ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 6, с.729-734
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
УДК 517.958:535.2
О МНОГОВОЛНОВЫХ РЕШЕНИЯХ ОДНОГО
НЕЛИНЕЙНОГО УРАВНЕНИЯ ШРЁДИНГЕРА
© 2021 г. А. Н. Волобуев
Рассматривается нелинейное уравнение Шрёдингера, возникающее в ряде физических
задач. Показано, что при выделении в этом уравнении действительной части возникает
нелинейное дифференциальное уравнение, имеющее по крайней мере два вида решений:
многоволновые и в виде стоячих волн. Представлены численные примеры многоволнового
решения и его перехода в решение в виде стоячих волн.
DOI: 10.31857/S0374064121060029
Введение. Нелинейные уравнения Шрёдингера возникают при решении различных физи-
ческих и технических задач. Наиболее часто исследуется нелинейное уравнение Шрёдингера с
кубической нелинейностью, имеющее особые виды решений в виде солитонов [1, гл. 1, § 1.7а; 2,
гл. 4, § 4.1]. Для такого уравнения различными методами, в частности методом обратной зада-
чи рассеяния, найдены одно- и многосолитонные решения. Однако в физических и технических
задачах возникают нелинейные уравнения Шрёдингера с другими видами нелинейностей. Од-
но из таких уравнений исследуется в данной работе.
1. Нелинейное уравнение Шрёдингера. Рассмотрим нелинейное уравнение Шрёдин-
гера следующего вида:
2
∂Φ
∂2Φ
(∂ ln|Φ|)
iμ
+V2
=
Φ,
(1)
∂t
∂X2
∂t
где μ и V - действительные постоянные, Φ = Φ(X, t) - искомая функция.
Несмотря на то, что уравнение (1) обычно не обсуждается в математической литературе,
оно возникает, например, при анализе самоиндуцированной прозрачности [3].
Исследуем бегущие волны, подчиняющиеся уравнению (1) и описывающиеся соотношением
Φ(X, t) = (ϕ - ϕ0) exp{i(kX - ωt)},
(2)
где k - волновое число бегущей волны, ω - её циклическая частота, ϕ0 - постоянная величина,
ϕ = ϕ(X,t) - действительнозначная функция, имеющая вторую производную по X и первую
по t, такая, что ϕ > ϕ0 при всех X и t; в частности, |Φ| = ϕ - ϕ0.
Подставляя выражение (2) для функции Φ в уравнение (1) и учитывая, что
∂ ln |Φ|
1
∂ϕ
=
,
∂t
(ϕ - ϕ0) ∂t
приходим к следующему уравнению относительно функции ϕ:
(
)
∂2ϕ
∂ϕ
∂ϕ
1
(∂ϕ)2
V2
+i μ
+ 2V 2k
+ (μω - ω2)(ϕ - ϕ0) =
(3)
∂X2
∂t
∂X
ϕ-ϕ0
∂t
Функция ϕ является действительнозначной, поэтому должно выполняться равенство
∂ϕ
∂ϕ
μ
+ 2V 2k
= 0.
(4)
∂t
∂X
Обозначим через ν множитель при ϕ - ϕ0 в левой части уравнения (3), т.е.
ν = μω - ω2.
(5)
729
730
ВОЛОБУЕВ
Тогда уравнение (3) (при выполнении условия (4)) запишется в виде
)2
∂2ϕ
1
(∂ϕ
V2
+ ν(ϕ - ϕ0) =
(6)
∂X2
ϕ-ϕ0
∂t
Уравнение вида (6) возникает также при исследованиях нервного импульса [4] и распростра-
нения электромагнитного поля в кириальной среде [5].
Таким образом, уравнение Шрёдингера (1) имеет решение вида (2) с действительнозначной
функцией ϕ тогда и только тогда, когда функция ϕ удовлетворяет уравнениям (4) и (6) и
неравенству ϕ > ϕ0.
Уравнение (4) является линейным однородным уравнением в частных производных перво-
го порядка с постоянными коэффициентами и поэтому легко решается: его общее веществен-
нозначное решение имеет вид ϕ-ϕ0 = f(ξ), где f : R → R - произвольная дифференцируемая
функция, а
ξ = μX - 2V 2kt.
Знак минус в переменной ξ соответствует распространению волны, как и в экспоненте (2),
слева направо.
Следовательно, уравнение Шрёдингера (1) имеет решение вида (2) тогда и только тог-
да, когда найдётся дважды дифференцируемая положительная функция f, определённая на
некотором (возможно, бесконечном) интервале, такая, что функция
ϕ(X, t) = ϕ0 + f(μX - 2V2kt)
(7)
удовлетворяет уравнению (6).
Подставляя в уравнение (6) вместо функции ϕ её представление (7), придём к следующему
обыкновенному дифференциальному уравнению:
1
V2μ2f′′ + νf = 4V4k2
(f′)2
(8)
f
(здесь штрих - производная по ξ).
Для упрощения будем считать, что V μ = 0. Уравнение (8) относится к типу уравнений,
не содержащих независимой переменной и поэтому стандартно интегрируется в квадратурах
(см., например, [6, с. 169]): в качестве новой искомой функции введём функцию p = df/dξ, а
за независимую переменную примем f. Тогда f′′ = pdp/df, и в этих обозначениях уравнение
(8) принимает вид
dp
a
p
+
p2 + bf = 0,
df
f
где a = -4V2k2/μ2, b = ν/(V2μ2). Это уравнение сводится к уравнению Бернулли.
Мы не будем записывать и анализировать общее решение уравнения (8) в случае произ-
вольных коэффициентов, поскольку наша цель состоит в том, чтобы указать для уравнения
(1) какое-либо параметрическое семейство решений (2), а также решения для уравнений (1) и
(6) в виде бегущих волн. Поэтому будем считать, что величина k в представлении (2) выбрана
такой, что имеет место равенство
4V2k2 = μ2.
(9)
Тогда в уравнении (8) числовые коэффициенты при f′′ и (f′)2 равны между собой, и, поделив
обе его части на 4V4k2, после очевидных преобразований придём с учётом равенства (5) к
уравнению
(f′)′
μω - ω2
=-
,
f
4V4k2
откуда находим
{
}
μω - ω2 ξ2
f (ξ) = C1 exp
-
+C2ξ
,
(10)
4V4k2
2
где C1 и C2 - произвольные действительные постоянные.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№6
2021
О МНОГОВОЛНОВЫХ РЕШЕНИЯ
731
Таким образом, если V μ = 0, то при каждом k = -μ/(2V ) и k = μ/(2V ) уравнение
Шрёдингера (1) имеет трёхпараметрическое семейство решений (2), где ϕ = f(μX - 2V2kt),
а функция f(ξ) задана равенством (10), в котором C1 > 0, C2 и ω - произвольные действи-
тельные постоянные.
2. Решения в виде бегущих волн. Перейдём к построению решений уравнений (1)
и (6) в виде бегущих волн. В этом пункте будем считать, что величина ν в равенстве (5)
неотрицательна, т.е. что
ω20 = μω - ω2
(11)
(если искать частное решение уравнения (6) в том виде, который предлагается ниже, то, как
показано, величина μω - ω2 должна быть неотрицательна; поэтому мы сразу обозначили её
ω20). Таким образом, далее мы ищем решения уравнения (1) и уравнения
)2
∂2ϕ
1
(∂ϕ
V2
+ ω20(ϕ - ϕ0) =
(12)
∂X2
ϕ-ϕ0
∂t
в виде бегущих волн.
Решение нелинейного уравнения (12) будем искать в виде бегущей уединённой волны
{
}
ϕ - ϕ0 = ϕmax exp
-(k0(X - X0) ± ω0(t - t0))2/2
,
(13)
где k0, X0 и t0 - действительные постоянные, и физический смысл входящих в представление
(13) величин следующий: ϕmax - амплитудное значение функции ϕ - ϕ0, X0 - координата
максимума (центра) волнового импульса, t0 - время достижения этого максимума. Знак минус
относится к волне, распространяющейся слева направо, а знак плюс - справа налево.
Непосредственной подстановкой функции ϕ, задаваемой равенством (13), в уравнение (12)
несложно убедиться, что эта функция будет его решением только при выполнении равенства
V2k20 = ω20.
(14)
Более того, функция (13) будет являться решением уравнения (4), если в (13) перед ω0 вы-
бран знак минус, а коэффициенты k0 и ω0 с одним и тем же множителем пропорциональны
соответственно коэффициентам μ и 2V2k линейной формы ξ, т.е.
2V2kk0 = μω0.
(15)
Действительно, в этом случае в силу (13), (15) и (11) получаем
{
}
μω - ω2 ξ2
ω0δ0
δ20
ϕ - ϕ0 = ϕmax exp
-
+
ξ+
,
4V4k2
2
V2k
2
где δ0 = -k0X0 + ω0t0, т.е. поскольку из ра-
венств (14) и (15) вытекает равенство (9), по-
лучаем найденное выше решение, соответству-
ющее функции (10), при условии, что μω -
- ω2 ≥ 0.
На рис. 1 показан график уединённого им-
пульса Φ(X, t), построенный по формуле (2) с
подстановкой в неё функции (13) при условиях:
ω0 = ω = 0 - отсутствие зависимости от вре-
мени, ϕmax = 1, X0 = 0, отношение волновых
чисел k/k0 = 5.
Нелинейное уравнение (12), а следователь-
но, и уравнение (1), допускает многоволновое
решение.
Рис. 1. Уединённый импульс функции Φ(X).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№6
2021
732
ВОЛОБУЕВ
Многоволновые решения найдены для очень ограниченного круга нелинейных уравне-
ний [1, 2]. Многоволновое решение уравнения (12) ищем в виде
∑
ϕ = ϕ0 + ϕmax ϕn(X,t),
(16)
n=1
где
ϕn(X, t) = ϕn = exp{-Δn(X, t)/2}, а Δn(X, t) = Δn = k0(X - X0n) - ω0(t - t0n).
(17)
В представлении (16), (17) число N - общее количество волн-импульсов, n - текущий
номер импульса, X0n - координаты максимумов волн-импульсов, t0n - времена достижения
этих максимумов.
Подставляя в уравнение (12) вместо функции ϕ её представления (16), (17), получаем
равенство
)2
∑ N∑
∑
ϕn ϕnΔn
=
ϕnΔn
(18)
n=1
n=1
n=1
Рассмотрим два подряд идущих одинаковых импульса n = 1, 2. Записывая для этого слу-
чая (N = 2) равенство (18), будем иметь
(ϕ1 + ϕ2)(ϕ1Δ21 + ϕ2Δ22) = (ϕ1Δ1 + ϕ2Δ2)2.
(19)
Очевидно, что равенство (19) равносильно равенству Δ1 - Δ2 = 0, или
k0(X02 - X01) - ω0(t02 - t01) = 0.
(20)
Соотношение (20) показывает, что расстояние между импульсами δ = X02 - X01 волна
проходит за время t02 - t01 со скоростью V = ω0/k0.
Если в Δn при каждом n взять t0n = X0n/V = k0X0n/ω0, то получим, что Δn = k0X -
-ω0t для всех n = 1,N, т.е. тогда Δ1 = Δ2 = ... = ΔN и в равенстве (18) их можно вынести
за знак суммы и сократить. В результате (18) превращается в тождество.
Следовательно, при таком выборе значений
t0n, n = 1,N, функция (16) является многовол-
новым решением нелинейного уравнения (12).
Наиболее простой вид многоволновое реше-
ние (16) приобретает в случае одинакового рас-
стояния δ между всеми волнами-импульсами.
В этом случае для координат максимумов им-
пульсов справедливо равенство X0n = nδ, а
для времён достижения максимумов - равен-
ство t0n = k0X0n/ω0 = k0nδ/ω0.
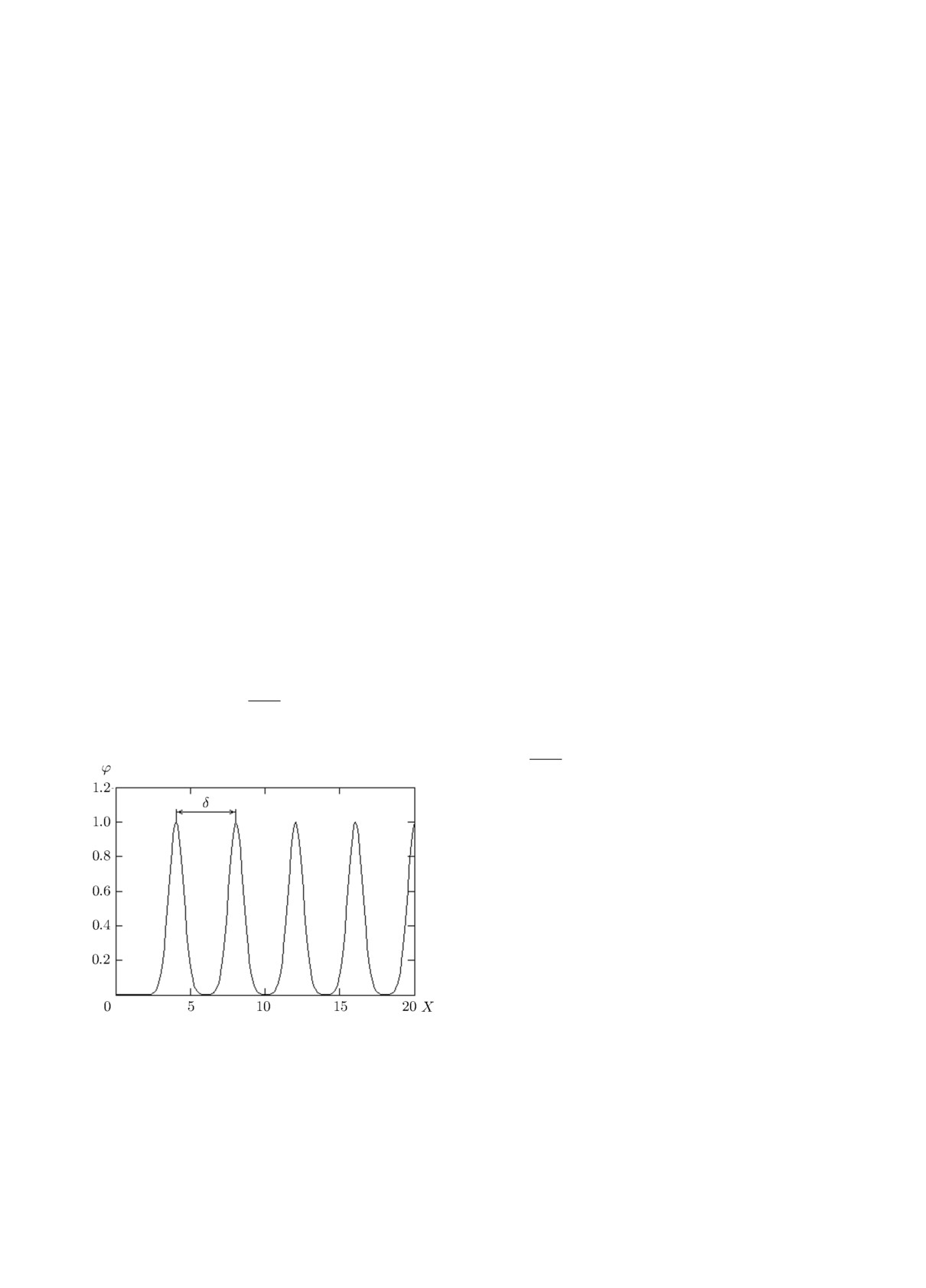
На рис. 2 показаны несколько следующих
друг за другом импульсов, построенных по фор-
муле (16) при условиях
ω0 = 0, ϕ0 = 0, ϕmax = 1, k0 = 2, δ = 4.
Рис. 2. Следующие друг за другом импульсы в
многоволновом решении.
Рассмотрим другой вид волны, представля-
ющий собой решение уравнения (16).
3. Решение в виде стоячих волн. Стоячие волны чаще всего образуются в линейных
системах в результате суперпозиции (интерференции) прямых и отражённых бегущих волн.
Однако известно, что стоячие волны могут возникать и в нелинейных системах [7, гл. 4, § 2].
Многие физические процессы носят принципиально нелинейный характер, и процесс возник-
новения стоячих волн в таких системах нетривиален. Мы не будем обсуждать физические
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№6
2021
О МНОГОВОЛНОВЫХ РЕШЕНИЯ
733
механизмы возникновения стоячих волн в этих системах. Исследуем математическую возмож-
ность возникновения стоячих волн, подчиняющихся нелинейному уравнению (12).
Некоторые решения нелинейного уравнения (12) можно найти методом разделения пере-
менных (см., например, [8, гл. 2, § 3]). Рассмотрим решение уравнения (12), имеющее вид
ϕ - ϕ0 = φ(X)T(t),
(21)
где φ(X) - функция только координаты X, T (t) - функция только времени t.
Подставив (21) в (12), получим
(
)2
d2φ(X)
dT (t)
V2φ(X)T2(t)
= φ(X)
- φ2(X)T2(t)ω20.
(22)
dX2
dt
Разделим обе части уравнения (22) на φ2(X)T2(t). В результате будем иметь
(
)2
1
d2φ(X)
1
dT (t)
V2
+ω20 =
= -α2,
(23)
φ(X) dX2
T (t) dt
где α - постоянная величина.
Равенства (23) распадаются на два не зависимых друг от друга уравнения. Одно из них -
уравнение относительно функции φ(X) - имеет вид
(
)
d2φ(X)
α2
+ k20 +
φ(X) = 0;
(24)
dX2
V2
здесь мы воспользовались равенством (14), в силу которого ω20/V2 = k20.
Обозначим k2S = k20 + α2/V2. Общим решением уравнения (24) является
φ(X) = φ(0) exp(ikS X),
(25)
где φ(0) - значение функции φ(X) в начале координат.
Другое уравнение, вытекающее из равенства (23), - уравнение относительно функции
T (t) - имеет вид
dT (t)
= iαT (t).
(26)
dt
Величина α может принимать как положительные, так и отрицательные значения, что не
влияет на дальнейшие выкладки. Общим решением уравнения (26) является
T (t) = T (0) exp(iαt),
(27)
где T (0) - начальное значение функции T (t).
Подставляя общие решения (25) и (27) в представление (21), получаем
ϕ - ϕ0 = ϕA exp(iαt)exp(ikSX),
(28)
где обозначено ϕA = T (0)φ(0).
Как показано выше, функция ϕ - ϕ0 должна быть действительнозначной. Использование
же экспонент с мнимыми показателями вводится исключительно для удобства преобразова-
ний. На самом деле в этих экспонентах нужно учитывать только действительные слагаемые.
Поэтому формула (28) описывает решение уравнения (12) в виде стоячих волн
ϕ - ϕ0 = ϕA cos(αt)cos(kSX) = ϕA cos(αt)cos(2πX/δ),
(29)
где ϕA - амплитудное значение стоячих волн, δ - длина волны.
Интересно проследить графически переход многоволнового решения (16) в решение в виде
стоячих волн (29). Этот переход осуществляется при сближении импульсов (см. рис. 2), т.е.
при уменьшении величины δ.
2
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№6
2021
734
ВОЛОБУЕВ
На рис. 3 показаны два графика. График 1
построен по формуле (16) при условиях ω0 =
= 0, ϕ0 = 0, ϕmax = 1, k0 = 2, δ = 2 для
N = 8 импульсов. График 2 (пунктиром) по-
строен по формуле (29) при условиях ϕ0 = 0.65
и ϕA cos(αt) = 0.38 для некоторого момента
времени t.
Заключение. В работе для рассмотренно-
го в ней нелинейного уравнения Шрёдингера
задача нахождения его решений, имеющих вид
бегущей волны, сведена к решению системы
двух уравнений в частных производных отно-
сительно одной и той же функции. Показано,
как найти все решения этой системы в замкну-
Рис. 3. Переход многоимпульсного решения в ре-
той форме. Одно из уравнений указанной сис-
шение в виде стоячей волны: 1
- многоволновое
решение, 2 - стоячая волна.
темы является нелинейным и возникает в раз-
личных задачах прикладного характера. Уста-
новлено, что это нелинейное уравнение имеет как многоволновые решения, так и решения
в виде стоячих волн. Многоволновое решение при уменьшении расстояния между волнами-
импульсами переходит в решение в виде стоячих волн.
СПИСОК ЛИТЕРАТУРЫ
1. Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М., 1987.
2. Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. М.,
1988.
3. Волобуев А.Н. Распространение импульса электромагнитного поля в диэлектрике в условиях само-
индуцированной прозрачности // Мат. моделирование. 2006. Т. 18. № 3. С. 93-102.
4. Волобуев А.Н. Индуктивно-емкостная модель возбудимой биоткани // Успехи совр. радиоэлектро-
ники. 2006. № 3. С. 33-60.
5. Volobuev A.N. The Nonlinear Analysis of Chiral Medium / Ed. Takashiro Akitsu. “Chirality from
Molecular Electronic States”. IntechOpen. 2018. P. 1-10.
6. Степанов В.В. Курс дифференциальных уравнений. М., 1953.
7. Красильников В.А., Крылов В.В. Введение в физическую акустику. М., 1984.
8. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1972.
Самарский государственный медицинский университет
Поступила в редакцию 24.12.2019 г.
После доработки 04.02.2021 г.
Принята к публикации 27.04.2021 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№6
2021