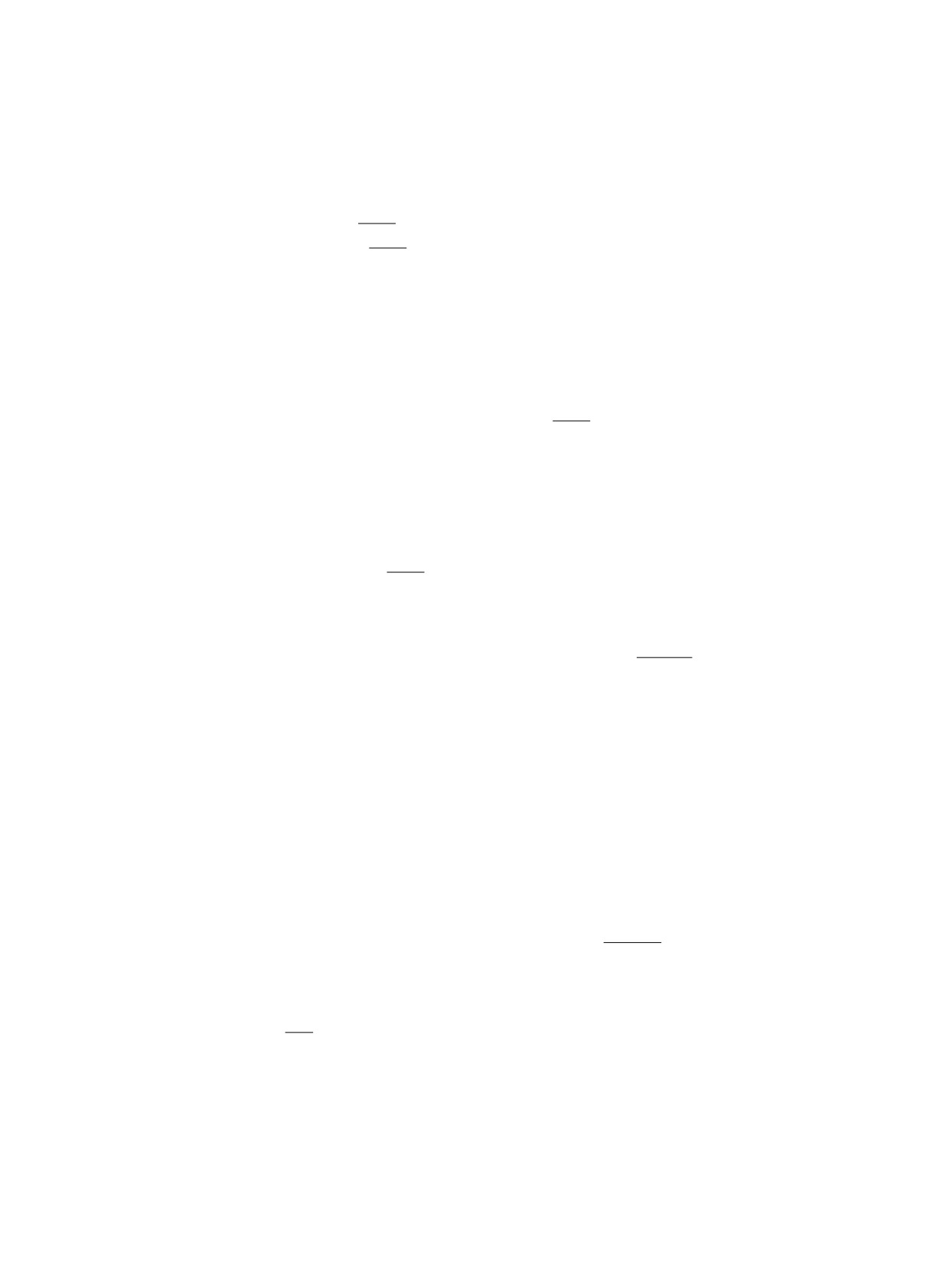ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 6, с.752-768

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956.8+517.956.328

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

ЗАДАЧ ДИРИХЛЕ И НЕЙМАНА

В ОБЛАСТИ С ДЫРЧАТЫМИ ПЕРЕГОРОДКАМИ

Найдена асимптотика собственных пар спектральных задач Дирихле и Неймана для опе-

ратора Лапласа в области, разделённой несколькими перегородками с отверстиями малых

диаметров и распадающейся на несколько независимых ячеек в пределе при стремлении

диаметров к нулю. При помощи асимптотических методов, обслуживающих сингулярно

возмущённые области, изучены расцепление кратного собственного числа предельных за-

дач, например, нулевого при краевых условиях Неймана, и локализация собственной функ-

ции в случае простого собственного числа.

DOI: 10.31857/S0374064121060042

1. Исходная и предельные задачи. Пусть Ω - ограниченная область в евклидовом

пространстве R^d, d ≥ 2. Систему декартовых координат x = (y, z) ∈ Rd-1 × R выберем так,

чтобы отрезок Υ = (z⁰, z^J ) оси z = x_d лежал внутри области Ω, а его концевые точки - на

её границе ∂Ω. Точками z¹ < . . . < zj-1 разобьём Υ на меньшие отрезки, а “перегородками”

Θ_j = {x ∈ Ω : z = z^j}, j = 1,J - 1,

область Ω - на “ячейки” ω₁, . . . , ω_J , которые считаем (связными) областями с липшицевыми

границами. На каждом сечении Θ_j , j = 1, J - 1, зафиксируем точку x^j = (y^j, z^j ) и образуем

вокруг неё мелкое отверстие

θ^εj = {x : η^j := ε-1(y - y^j) ∈ θ_j, z = z^j}, j = 1,J - 1.

(1)

Здесь θ_j - области в Rd-1 с липшицевыми границами ∂θj и компактными замыканиями

θ_j = θ_j

^⋃∂θ_j, ε > 0 - малый параметр, а число ε₀ > 0 таково, что θεj ⊂ Θ_j при ε ∈ (0,ε₀].

В области (рис. 1, а)

⋃

Ω^ε = Ω \ (Θ_j \ θ^εj)

j=1

рассмотрим для уравнения

-Δ_xu^ε(x) = λ^εu^ε(x), x ∈ Ω^ε,

(2)

спектральные задачи Дирихле

u^ε(x) = 0, x ∈ ∂Ω^ε,

(2)_D

и Неймана

∂_νu^ε(x) = 0, x ∈ ∂Ω^ε.

(2)_N

(а)

(б)

Рис. 1. Область с дырчатыми перегородками (а) и перегородка в ци-

линдре с одной дыркой (б).

752

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

753

Здесь Δ_x = ∇_x·∇_x - оператор Лапласа, ∇_x = grad, ∂_ν - производная вдоль внешней нормали,

λ^ε - спектральный параметр.

Из-за возможных иррегулярностей собственных функций u^ε нужна обобщённая постанов-

ка задач (2), (2)_D и (2), (2)_N как интегральных тождеств [1, гл. 2, § 2 и 5]

(∇_xu^ε, ∇_xψ^ε)_Ωε = λ^ε(u^ε, ψ^ε)_Ωε для всех ψ^ε ∈ H^εM .

(3)

Здесь ( · , · )_Ωε - натуральное скалярное произведение в пространстве Лебега L²(Ω^ε), индекс

M здесь и далее принимает значения D и N, H^εN = H¹(Ω^ε) - пространство Соболева, а

H^εD = H¹⁰(Ω^ε) - его подпространство, выделенное условием Дирихле (2)_D на ∂Ω^ε.

Ввиду компактности вложения H¹(Ω^ε) ⊂ L²(Ω^ε) задача (3) (или (2), (2)_D и (2), (2)_N )

имеет дискретный спектр, который образует неограниченную монотонную последовательность

0 ≤ λεM1 < λεM2 ≤ λεM3 ≤ ... ≤ λ^εMn ≤ ... → +∞,

(4)

составленную c учётом кратностей собственных чисел. Соответствующие собственные функ-

ции uεM1, uεM2, uεM3, . . . , u^εMn, . . . ∈ H^εM можно подчинить условиям ортогональности и норми-

ровки

(u^εMn, u^εMm)_Ωε = δ_m,n, m, n ∈ N,

(5)

где δ_m,n - символ Кронекера. Даже в случае гладких поверхностей ∂Ω и ∂θ1, ..., ∂θJ-1

функции u^εMn, вообще говоря, не принадлежат пространству Соболева H²(Ω^ε) из-за извест-

ных корневых сингулярностей градиента ∇_xu^εMn на рёбрах трещин (1) (см., например, [2; гл. 2

и 10]). Первое собственное число λεM1 простое, причём λεD1 > 0 и

λεN1 = 0, uεN1 = |Ω^ε|-1/2,

(6)

где |Ω^ε| - объём тела Ω^ε.

Основная цель статьи - построить асимптотику нескольких собственных пар {λ^εMn, u^εMn}.

Сама работа инициирована публикацией [3], в которой изучена первая собственная функция

задачи Дирихле на двух соосных цилиндрах с одинаковым сечением (рис. 1, б), соединён-

ных через малое отверстие θε1 (случай J = 2 для областей ω₁ и ω₂ частной формы). При

этом собственная функция раскладывается на цилиндрах в ряды Фурье, которые посредством

весьма громоздких вычислений согласуются на малом множестве θε1. Этот неоправданно тя-

желовесный подход назван в [3] “мощным методом”, который может быть применён и в “неци-

линдрических областях с вращательной симметрией”. Между тем более тридцати лет назад

были разработаны общие асимптотические методы исследования статических и спектральных,

скалярных и векторных эллиптических краевых задач в областях с разнообразными сингу-

лярно возмущёнными границами (см. монографии [4-6] и др.). Очень близкими по тематике

являются давние статьи [7-9], в которых используется метод сращиваемых разложений [10,

5] и конструируются полные асимптотические разложения решений спектральных задач для

эллиптических уравнений второго порядка со сменой краевых условий на малых участках

границы.

В данной работе применяется метод составных разложений (см. статьи [11-14], моногра-

фии [4, 6] и др.) к задачам в областях общих форм с произвольно перфорированными перего-

родками. Помимо упомянутой в [3] локализации собственной функции uεD1 в случае простого,

не обязательно первого, как в [3], собственного числа задач Дирихле и Неймана на ячейках

ω_j (см. п. 4), внимание уделяется кратным собственным числам, для которых в первую оче-

редь требуется построить младшие члены асимптотики и тем самым показать, как они (числа)

расцепляются при ε > 0.

Конкретизация асимптотических процедур [12, 4] для задач (2), (2)_D и (2), (2)_N требует

детального описания характеристик предельных (ε = 0) задач. В п. 2 вводится несколько

используемых в работе классических объектов гармонического анализа. В п. 3 изучается по-

ведение при ε → +0 первых J собственных пар задачи Неймана - построение и обоснование

асимптотик описано во всех деталях. Схема анализа повторяется с упрощениями в п. 4 для

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

754

НАЗАРОВ

возмущённого простого собственного числа предельных задач Дирихле в Ω⁰ = ω₁

^⋃...^⋃ω_J,

однако для сокращения объёма статьи обстоятельно рассматриваются только интересные для

приложений случаи d = 2 и d = 3. Наконец, в п. 5 обсуждаются доступные обобщения и

общие свойства спектральных пар в областях с перфорированными перегородками.

Перечислим возникающие предельные задачи. При ε = 0 отверстия θε1, . . . , θεJ-1 исчезают

и исходная задача распадается на J независимых спектральных задач

-Δ_xuj0(x) = λj0uj0(x), x ∈ ω_j,

(7)

uj0(x) = 0, x ∈ ∂ω_j, j = 1,J,

(7)_D

или

∂_νuj0(x) = 0, x ∈ ∂ω_j, j = 1,J.

(7)_N

Их собственные числа образуют последовательности

0 ≤ λj0M1 < λj0M2 ≤ λj0M3 ≤ ... ≤ λj0Mn ≤ ... → +∞,

(8)

а соответствующие собственные функции uj0M1, uj0M2, uj0M3, . . . , uj0Mn, . . . ∈ H0M (ω_j ) можно под-

чинить условиям ортогональности и нормировки

(uj0Mn, uj0Mm)ωj = δ_m,n, m, n ∈ N.

(9)

Понятно, что λj0D1 > 0, а для задачи Неймана верны формулы

λj0N1 = 0, uj0N1 = |ω_j|-1/2.

(10)

Задачи (7), (7)_D и (7), (7)_N нуждаются в обобщённой постановке [1, гл. 2, § 2 и 5], однако

соответствующие интегральные тождества приводить не будем ввиду их очевидности и про-

стоты.

Ещё одно семейство предельных задач появляется в результате растяжений координат

x → ξ^j = (η^j,ζ^j) = (ε-1(y - y^j),ε-1(z - z^j)),

(11)

где j = 1, J - 1. Замена (11) и формальный переход к ε = 0 превращают конечную область

Ω^ε в два полупространства R^d± = {ξ^j : ±ζ^j > 0}, соединённых через отверстие θ_j(0) = θ_j ×{0}

в стенке ∂R^d± :

Ξ^j = R^d-

^⋃θ_j(0)⋃ Rd+.

(12)

Поскольку Δ_x + λ = ε-2Δ_ξj + λ, главным членом оператора Гельмгольца в быстрых перемен-

ных ξ^j служит оператор Лапласа, т.е. предельная задача в области (12) выглядит так:

-Δ_ξj wj0(ξ^j) = 0, ξ^j ∈ Ξ^j,

(13)

wj0(η^j,±0) = 0 при η^j ∈ Rd-1 \ θ_j

(13)_D

или

∓∂_ζj wj0(ξ^j) = 0 при η^j ∈ Rd-1 \ θ_j.

(13)_N

В асимптотических конструкциях будут востребованы специальные решения однородных за-

дач (13), (13)_D и (13), (13)_N , описываемые в следующем пункте.

2. Вспомогательные объекты. 1^◦. Ёмкость. Пусть d ≥ 3 (см. замечание в конце п. 3

по поводу плоской задачи). Ёмкостной потенциал P_j - затухающее при |ξ^j| → ∞ решение

задачи Дирихле во внешности трещины θ_j (0) = {ξ^j : η^j ∈ θ_j, ζ^j = 0}

-Δ_ξj P_j(ξ^j) = 0, ξ^j ∈ R^d \ θ_j(0), P_j(ξ^j) = 1, ξ^j ∈ θ_j(0).

(14)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

755

Справедливо асимптотическое представление

P_j(ξ^j) = C(θ_j)Φ(ξ^j) + O(|ξ^j|1-d) при

|ξ^j| → +∞,

(15)

в котором Φ(ξ^j ) = |ξ^j |2-dΦ(|ξ^j |-1ξ^j ) - фундаментальное решение оператора Лапласа в R^d,

d ≥ 3, а C(θ_j) = ∥∇_ξjP_j;L²(R^d \ θ_j(0))∥² > 0 - коэффициент, пропорциональный гармониче-

ской емкости cap_d(θ_j) множества θ_j (0) (см. монографии [15, 16] и др.). Функция P_j чётная

относительно переменной ζ^j = ξ^jd, а значит, гармоническая функция W_j , определённая ра-

венством

W_j(ξ^j) = 1 - P_j(ξ^j), ζ^j > 0, W_j(ξ^j) = -1 + P_j(ξ^j), ζ^j < 0,

(16)

является нечётной по ζ^j и гладкой в области Ξ^j вплоть до границы вне ребра ∂θ^j × {0}, а

также удовлетворяет задаче Неймана (13), (13)_N .

2◦. Тензор виртуальной массы. При d ≥ 2 задача Неймана во внешности трещины

-Δ_ξj Q_j(ξ^j) = 0, ξ^j ∈ R^d \ θ_j(0),

∓∂_ζj Q_j(η^j,±0) = ±1, η^j ∈ θ_j(0),

(17)

имеет затухающее на бесконечности решение, допускающее асимптотическое представление

Q_j(ξ^j) = M(θ_j)∂_ζj Φ(ξ^j) + O(|ξ^j|^-d) при

|ξ^j| → ∞,

(18)

в котором M(θ_j ) = ∥∇_ξj Q_j; L²R^d \ θ_j(0))∥² - положительный коэффициент, зависящий от

формы трещины. Линейно растущее решение ζ^j + Q_j(ξ^j ) однородной задачи Неймана (17) -

классический объект гармонического анализа [15, приложение G], а M(θ_j) - единственный

ненулевой элемент матрицы (тензора) виртуальной массы, поскольку в случае прямой трещи-

ны θ_j (0) другие решения с линейным ростом - мономы ξ^p = η^p, p = 1, d - 1, - полностью удо-

влетворяют задаче Неймана. В пространственном случае d = 3 коэффициент M(θ_j ) известен,

например, для эллиптической трещины, а в плоском имеет место равенство M(θ_j) = πL2j/8,

где L_j - длина трещины θ_j, которое находится при помощи конформного преобразования Жу-

ковского и издавна используется в механике трещин (см. монографии [17, гл. XI; 18, гл. 12] и

др.).

Функция Q_j нечётна по переменной ζ^j, но далее понадобится чётная гладкая в Ξ^j функ-

ция W_j, являющаяся решением задачи Дирихле (13), (13)_D :

W_j(ξ^j) = ζ^j + Q_j(ξ^j) при ζ^j > 0, W_j(ξ^j) = -ζ^j - Q_j(ξ^j) при ζ^j < 0.

(19)

3◦. Матрица. Пусть T = T¹ + . . . + T^J , где T^j - блочно-диагональная J × J-матрица с

единственным ненулевым 2 × 2-блоком в строках и столбцах с номерами j и j + 1

(

)

C_jτ2j

-C_jτ_j

C_j > 0, τ_j > 0, j = 1,J - 1.

(20)

−C_jτ_j

C_j

Лемма 1. Матрица T положительная, и её (одномерное) корневое пространство натя-

нуто на столбец t = (t₁,... ,t_J)^т (^т - знак транспонирования) с компонентами t₁ = 1 и

t_j = τ₁ × ... × τj-1, j = 2,J.

Доказательство. Поскольку блоки (20) - положительные симметричные матрицы, ра-

венство a^тT a = 0 ∈ R^J для столбца a ∈ R^J означает, что T¹a = 0, . . . , T^J a = 0. Нужное

утверждение вытекает из записанных покомпонентно последних равенств:

C_jτ2ja_j - C_jτ_jaj+1 = 0,

-C_jτ_ja_j + C_jaj+1 = 0,

откуда следует, что aj+1 = τ_ja_j . Лемма доказана.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

756

НАЗАРОВ

3. Собственные числа задачи Неймана. Конечно же, далее речь пойдёт только о воз-

мущении положительных собственных чисел задачи (2), (2)_N (ср. собственные пары (10) и

(6)). Кроме того, считаем, что d ≥ 3, а двумерный случай обсудим в замечании в конце этого

пункта.

В качестве основного асимптотического приближения к собственной функции u^εk := u^εNk,

отвечающей собственному числу

λ^εk := λ^εnk = 0 + εd-2λ^′k +λεk,

(21)

возьмём кусочно-постоянную функцию u0k, т.е.

u0k(x) = a^kj, x ∈ ω_j, j = 1,J, a^k = (ak1,... ,a^kJ)^т ∈ R^J.

(22)

Числа λ^′k и столбцы a^k подлежат определению, а малые остаткиλεk - оцениванию, но, разу-

меется, λ′1 =λε1 = 0 и a¹¹ = . . . = a1J = |Ω⁰|-1/2.

Скачки функции (22) на отверстиях (1) компенсируем при помощи слагаемых типа погра-

ничного слоя

χ_j(x)w^′kj(ξ^j) :=

(a_j - aj-1)χ_j(x)w_j (ξ^j ), j = 1, J - 1,

(23)

где χ_j (x) = χ(r_j ) и r_j = |x - x^j|. Кроме того, χ ∈ C^∞c(R) - срезающая функция с малым

носителем, равная единице в окрестности начала координат и служащая для локализации

пограничного слоя, а w_j - функция, имеющая скачок -2 на множестве θ_j (0) и определяемая

при помощи гармонической функции (16) равенствами

w_j(ξ^j) = W_j(ξ^j) - 1 при ζ^j > 0, w_j(ξ^j) = W_j(ξ^j) + 1 при ζ^j < 0.

(24)

В качестве поправочных слагаемых члена регулярного типа εd-2u^′k возьмём функцию со

скачками на отверстиях (1), но принадлежащую пространствам H¹(ω_j), j = 1, J. К u0k +

+ εd-2u^′k добавим сумму выражений (23) и подставим результат в задачу (2), (2)_N со спек-

тральным параметром (21). При учёте соотношения Φ(ξ^j) = εd-2Φ(x - x^j) и представлений

(16), (15) для функций (24) соберём члены порядка εd-2. В итоге получим предельные задачи

-Δ_xu^′k(x) = λ^′ku0k(x) + f^′kj(x), x ∈ ω_j,

∂_νu^′k(x) = 0, x ∈ ∂ω_j,

(25)

с однородными условиями Неймана (поскольку ∂_ν χ_j = 0 на ∂Θ_j ) и следующими фрагментами

правых частей уравнений Пуассона:

f^′kj(x) =

(aj+1 - a_j)C(θ_j )[Δ_x, χ_j (x)]Φ(x - x^j) -

(a_j - aj-1)C(θj-1)[Δ_x, χj-1(x)]Φ(x - xj-1).

(26)

Подчеркнём, что при j = 1 и j = J выражения в (26) содержат только по одному члену, и

достаточно в (26) положить C(θ₀) = 0 и C(θ_J ) = 0 для несуществующих отверстий θε0 и θ^εJ .

Далее аналогичные и понятные упрощения формул отдельно оговаривать не будем.

Поскольку по предназначению фундаментального решения выполнено равенство

∫

[Δ_x, χ_j(x)]Φ(x) dx =

∂_|x|Φ(x)ds_x = -1,

(27)

R^d

S_R

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

757

∫

где S_R - сфера большого радиуса R > 0, условия разрешимости_ω

f^′kj(x)dx = 0 задач

Неймана (25) превращаются в соотношения

λ^′k|ω_j|a^kj =

(a_j - aj-1)C(θj-1) -

(aj+1 - a_j)C(θ_j ), j = 1, J,

(28)

где замена 1/2 → 1/4 (ср. формулы (26) и (28)) обусловлена тем, что в отличие от (27)

интегрирование ведётся по полусфере. В итоге получена система J линейных уравнений

Ta^k =λ^′kBa^k,

(29)

где T - J × J-матрица, составленная из диагональных 2 × 2-блоков (20), в которых τ_j = 1

и C_j = C(θ_j)/4, а B = diag{|ω₁|,...,|ω_J|} - диагональная J × J-матрица. В силу леммы 1

алгебраическая система (29) имеет собственные числа

0=λ′1 <λ′2 ≤...≤λ^′J,

(30)

а соответствующие собственные векторы a¹, . . . , a^J ∈ R^J можно подчинить условиям ортого-

нальности и нормировки

(a^ℓ)^тBa^k = δ_k,ℓ, k, ℓ = 1, J.

(31)

Компоненты особенного столбца a¹ указаны после формулы (22).

Итак, найдены все выделенные члены асимптотических анзацев для собственных пар за-

дачи (2), (2)_N . Обоснование асимптотики начнём с простого утверждения.

Лемма 2. На сегменте [0, Λ_N ) с концевой точкой Λ_N = max{λ10N2, . . . , λJ0N2} (см. после-

довательности (7_N ) расположено не более J собственных чисел задачи (2), (2)_N .

Доказательство. Применим максиминимальный принцип (см. [19, теорема 10.2.2])

∥∇_xψ^ε; L²(Ω^ε)∥

λ^εMm = max

inf

m ∈ N,

(32)

E^εMm

ψ^ε∈E^εMm\{0}

∥ψ^ε; L²(Ω^ε)∥²

где E^εMm - любое подпространство в H^εM с коразмерностью m - 1, в частности, EεM1 = H^εM .

В качестве пробного подпространства при m = J + 1 и M = N возьмём

E⊥NJ+1 = {ψ^ε ∈ H¹(Ω^ε) : (ψ^ε,1)ωj = 0, j = 1,J}.

(33)

На ячейках ω₁, . . . , ω_J в силу условий ортогональности из определения (33) выполняются

неравенства Пуанкаре, а значит, для функции ψ^ε ∈ E⊥NJ+1 справедливы неравенства

∑

∥∇_xψ^ε; L²(Ω^ε)∥² ≥

λj0N2∥ψ^ε;L²(ω_j)∥² ≥ Λ_N∥ψ^ε;L²(Ω^ε)∥².

(34)

j=1

Учитывая (33) и (34) в формуле (32) с m = J + 1 и M = N, уменьшаем максимум и оцени-

ваем снизу инфимум величиной Λ_N , которая тем самым оказывается меньше λεNJ+1. Лемма

доказана.

Введём в пространстве H^ε = H¹(Ω^ε) (индекс N не пишем) скалярное произведение

〈v^ε, ψ^ε〉 = (∇_xv^ε, ∇_xψ^ε)_Ωε + (v^ε, ψ^ε)_Ωε

(35)

и положительный самосопряжённый оператор K^ε,

〈K^εv^ε, ψ^ε〉 = (v^ε, ψ^ε)_Ωε для всех v^ε, ψ^ε ∈ H^ε.

(36)

В результате интегральное тождество (3) преобразуется в абстрактное уравнение с новым

спектральным параметром, а именно,

K^εU^ε = κ^εU^ε в H^ε, где κ^ε = (1 + λ^ε)-1.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

758

НАЗАРОВ

Справедливость следующего утверждения, известного [11] как лемма о “почти собствен-

ных” числах и векторах, обеспечена спектральным разложением резольвенты (см., например,

[19, гл. 6]).

Лемма 3. Пусть для v^ε ∈ H^ε и k^ε ∈ R₊ := (0, +∞) выполнены соотношения

∥v^ε; H^ε∥ = 1,

∥K^εv^ε - k^εv^ε; H^ε∥ =: h ∈ (0, k^ε).

(37)

Тогда у оператора K^ε имеется собственное число κ^ε, удовлетворяющее неравенству |κ^ε -

- k^ε| ≤ h. Более того, для любого h ∈ (h,k^ε) найдутся такие коэффициенты c^εNε, ...,

cεN ε+X ε-1, что



∑



∑



^ε -

cεpU^εp; H^ε

|c^εp|² = 1.

(38)

v

≤

p=N^ε

При этом {κ^εN ε , . . . , κ^εN ε+X ε-1} - набор всех собственных чисел оператора K^ε на замкнутом

сегменте [k^ε - h,k^ε + h], а соответствующие собственные векторы U^εNε, ..., U^εNε+Xε-1

подчинены условиям ортогональности и нормировки

〈U^εp, U^εq〉 = δ_p,q, p, q = N^ε, N^ε + X^ε - 1.

(39)

В качестве “почти собственных” пар оператора K^ε возьмём пары

k^εk = (1 + εd-2λ^′k)-1, v^εk = ∥u^εk;H^ε∥-1u^εk,

(40)

где

(

)

∑

⁽x-x^j)

r_j

u^εk(x) = u0k(x) + εd-2X^ε(x)u^′k(x) +

χ_j(x)w^′

X^ε(x) = 1 - χ

(41)

2Rε

j=1

Здесь u^′k ∈ H¹(Ω⁰) - какое-либо решение задач (25), существующее в силу равенств (28), а

срезка X^ε введена для уничтожения скачков функции u^′k на отверстиях, т.е. размер R > 0

выбран так, что X^ε = 0 на θε1

⋃ ... ^⋃θεJ-1. В результате u^εk ∈ H^εN. Отметим, что функция

u^′k гладкая внутри ячеек ω_j вплоть до прямых участков Θ_j и Θj-1 их границ. Благодаря

соотношению (31) и затуханию членов пограничного слоя получаем, что

|〈u^εk, u^εℓ〉 - δ_k,ℓ| = |〈u^εk, u^εℓ〉 - (a^ℓ)^тBa^k| = |〈u^εk, u^εℓ〉 - (u0k, u0ℓ)_Ωε | ≤

∫

((

)₂

)

∑

χ(r_j )

≤c

1+εd-2 +

-1

dx ≤ Cεd-2.

(42)

(1 + εr_j)d-2

j=1

Ω^ε

Теперь оценим величину h из (37) для конкретной пары (40) - обозначим эту величину h_k.

Согласно определениям (35) и (36) имеем

h_k = sup|〈K^εv^ε - k^εv^ε,ψ^ε〉| =

= (1 + εd-2λ^′k)-1∥u^ε; H^ε∥-1 sup |(∇_xu^ε, ∇_xψ^ε)_Ωε - εd-2λ^′k(u^ε, ψ^ε)_Ωε |;

(43)

здесь супремум вычисляется по всем функциям ψ^ε ∈ H^ε, для которых ∥ψ^ε; H^ε∥ = 1. В си-

лу одномерного неравенства Харди, записанного в радиальной переменной r_j = |x - x^j| и

проинтегрированного по угловым переменным, при d ≥ 3 выполнена весовая оценка

∥(ε + r_j )-1ψ^ε; L²(ω_j

^⋃ωj-1)∥ ≤ c∥ψ^ε;H¹(ω_j ⋃ ωj-1)∥.

(44)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

759

Разность скалярных произведений в L²(Ω^ε) под знаком модуля в (43) представим как

сумму выражений

I^uj(ψ^ε), S^uj(ψ^ε), j = 1,J, I^wℓ(ψ^ε), S^wℓ(ψ^ε), ℓ = 1,J - 1.

(45)

Укажем и преобразуем каждое из них. Прежде всего верны равенства

ε2-dI^uj(ψ^ε) = (∇_xu^′k,∇_x(X^εψ^ε))ωj + λ^′k(a^kj,X^εψ^ε)ωj ,

(46)

ε2-dS^uj(ψ^ε) = (u^′k∇_xX^ε,∇_xψ^ε)ωj - (∇_xu^′k,ψ^ε∇_xX^ε)ωj +

+ λ^′ka^kj(1 - X^ε,ψ^ε)ωj + εd-2λ^′k(X^εu^′k,ψ^ε)ωj.

(47)

Первые два слагаемых в правой части равенства (47) появились в результате переноса срезки

X^ε от u^′k к ψ^ε и сопутствующего коммутирования с оператор-градиентом, а третье - из-за

введения множителя X^ε в последнее скалярное произведение из (46). Примем во внимание

неравенства |u^′k(x)| + |∇_xu^′k(x)| ≤ n^′j при x ∈ ω_j

^⋂ (supp χ_j ⋃ supp χj-1) с некоторой мажо-

рантой n^′j (напоминаем, что u′k — гладкая функция вблизи прямых участков Θj и Θj-1

границы ∂ω_j ), а также соотношение r_j = min{r_j , rj-1} ≤ cε на пересечении ячейки ω_j и

множества supp (1 - X^ε), содержащего носитель функции |∇_xX^ε(x)| ≤ cε-1. В результате

получим, что

ε2-d|S^uj(ψ^ε)| ≤ c(ε-1n^′jI1/2Xj∥∇_xψ^ε;L²(ω_j)∥ +

+ I1/2Xj (n^′j + |a^kj|)∥(ε + r_j)-1ψ^ε;L²(ω_j)∥ + εd-2|λ^′k|∥u^′k;L²(ω_j)∥∥ψ^ε;L²(ω_j)∥) ≤

≤ c(ε-1+(d-2)/2 + εd/2 + εd-2)∥ψ^ε; H¹(ω_j)∥ ≤ Cεmin{-1+(d-2)/2,d-2}.

Наконец,

c_j

∫

I_Xj =

dx ≤ C_X rd-1jdr_j = C_j ε^d.

supp(1-X^ε)

Далее при ℓ = 1, J - 1 имеем

I^wℓ(ψ^ε) = (∇_xW_kℓ,∇_x(χ_ℓψ^ε))_ω

(48)

ℓ

^⋃ωℓ+1,

S^wℓ(ψ^ε) = εd-2λ^′k(χ_ℓw^′kℓ,ψ^ε)_ω

ℓ

^⋃ωℓ+1 + (wk ℓ∇xχℓ, ∇xψ^ε)ωℓ ^⋃ωℓ+1 ^-(∇xwk ℓ, ψε∇x^χℓ⁾ωℓ ^⋃ωℓ+1.(49)

При этом W_kℓ = ((akℓ+1 +a^kℓ)+(akℓ+1 -a^kℓ)W_ℓ)/2 ∈ H^1loc(Ξ^j ) - ограниченное решение задачи (13),

(13)_N , а значит, скалярное произведение (48) обращается в нуль, так как пробная функция

ξ^j → χ_ℓ(x)ψ^ε(x) обладает компактным носителем. Выделим из слагаемого типа пограничного

слоя (23) член

ϕεkℓ(x) =

(akℓ+1 + a^kℓ)C(θ_ℓ)Φ(ξ^ℓ) = εd-2

(akℓ+1 + a^kℓ)C(θ_ℓ)Φ(x - x^ℓ),

(50)

входящий в правую часть (26) задачи (25). Остаток представляет собой величину порядка

(1 + |ξ^ℓ|)1-d, превращающуюся в бесконечно малую O(ε1-d) на носителе supp |∇_xχ_ℓ| вектор-

функции ∇_xχ_ℓ, удалённом от точки x^ℓ. Отщепим от последних двух слагаемых, возникших

в (49) вследствие переброски срезки χ_j от w^′kℓ к ψ^ε, скалярные произведения, содержащие

функции (50), а оставшееся выражение преобразуем и оценим следующим образом:

|S^wℓ(ψ^ε) - (ϕ^εkℓ∇_xχ_ℓ, ∇_xψ^ε)_ω

ℓ

^⋃ωℓ+1 + (∇xϕkℓ,ψ^ε∇xχℓ)ωℓ ^⋃ωℓ+1^|≤ c(εd-2λ^k ×

× sup

|(ε+r_ℓ)w_ℓ(ξ^ℓ)| ∥(ε+r_ℓ)-1ψ^ε; L²(ω_ℓ

^⋃ωℓ+1)∥+εd-1∥ψ^ε;H¹(ω_ℓ ⋃ ωℓ+1)∥) ≤ cεd-1. (51)

⋃

x∈ω_ℓ

ωℓ+1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

760

НАЗАРОВ

Гармоническая в R^d± функция ϕ^εℓ с нулевыми данными Неймана на ∂R^d± \ {0} удовлетво-

ряет равенству

([Δ_x, χ_j ]ϕ^εkℓ, ψ^ε)_ω

(52)

ℓ

^⋃ωℓ+1 = (ϕkℓ∇xχj, ∇xψ^ε)ωℓ ^⋃ωℓ+1 ^-(∇xϕkℓ, ψε∇x^χj⁾ωℓ ^⋃ωℓ+1^.

Следовательно, сумма по ℓ = 1, J - 1 “лишних” слагаемых из левой части (51) и сумма по

j = 1,J выражений (45) взаимно уничтожаются благодаря интегральным тождествам, обслу-

живающим задачи (25) с правыми частями (26). Таким образом, при учёте определений (40)

и (41) приходим к следующей оценке величин (43):

h_k ≤ c_kεd-2+αd , α_d = min{1,-1 + d/2} ≥ 1/2.

(53)

Теорема 1. В случае d ≥ 3 найдутся такие положительные константы ε₀ и c₀, что

при ε ∈ (0,ε₀] первые J собственных чисел задачи Неймана (2), (2)_N удовлетворяют соот-

ношениям λεN1 = 0 и

|λ^εk - εd-2λ^′k| ≤ c₀εd-2+αd , k = 2, J,

где α_d - показатель из оценки (53), а λ′2, . . . , λ′J - положительные собственные числа

алгебраической системы (29).

Доказательство. Согласно лемме 3 и оценке (53) найдутся собственные числа κεNm(2),

..., κεNm(J) оператора K^ε и собственные числа λεNm(2),..., λεNm(J) задачи (2), (2)N , для

которых

|κεNm(k) - k^εk| ≤ h_k ≤ c_kεd-2+αd , k = 2, J,

и, следовательно,

{

|λεNm(k) - εd-2λ^′k| ≤ c_kεd-2+αd (1 + λεNm(k))(1 + εd-2λ^′k),

1 + λεNm(k) ≤ 2(1 + εd-2λ^′k) при c_kεd-2+αd(1 + εd-2λ^′k) ≤ 1/2,

а значит,

|λεNm(k) - εd-2λ^′k| ≤ 2c_kεd-2+αd (1 + εd-2λ^′k)² ≤ C_kεd-2+αd при ε ∈ (0, ε_k], ε_k > 0.

(54)

Если собственные числа λ′2, . . . , λ^′J системы (29) простые, то в силу неравенств (54) при

малом ε величины κεNm(2), . . . , κεNm(J) попарно не совпадают. В итоге на интервале (0, Cεd-2)

найдены различные удовлетворяющие последней оценке из (54) положительные собственные

числа задачи Неймана (2), (2)_N в количестве J - 1 штуки. По лемме 2 других собственных

чисел на интервале (0, Λ_N ) нет, т.е. утверждение теоремы проверено.

Рассмотрим теперь случай кратного собственного числа λ^′Nq. Пусть

λ′Nq-1 < λ^′Nq = ... = λ′Nq+Q

<λ′Nq+Q

Q_q > 1,

(55)

q-1

и убедимся в том, что обнаруженные собственные числа κ′Nm(q), ..., κ′Nm(q+Qq-1)^{операто-}

ра K^ε также можно взять различными. Применим вторую часть леммы 3, положив в ней

h = max{h₁,...,h_J} и h = hϱ, где ϱ > 1 - большое число. Пусть параметр ε настолько

мал, что сегмент σ^εq = [k^εq - h, k^εq + h] содержит среди найденных только точки κ′Nm(q),

, ..., Sεq+Q-1 указанные в (38) линейные комбина-

..., κ′Nm(q+Qq-1).Обозначимчерез

ции собственных векторов U^εp оператора K^ε, а через cε(q), . . . , cε(q+Q-1) - соответствующие

столбцы коэффициентов, нормированные в RXε . Поскольку векторы a¹, . . . , a^J и U^εN ε ,

..., U^εNε+Xε-1 подчинены условиям ортогональности и нормировки (31) и (39), выводим из

(38) и (42), (40) соотношения

|〈v^εk, v^εℓ〉 - δ_k,ℓ| ≤ cεd-2,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

761

Таким образом, при малом ε и большом ϱ столбцы cε(q), . . . , cε(q+Q-1) “почти ортонормиро-

ваны” в RXε , а значит, Q ≤ X^ε, и на сегменте σ^εq действительно присутствуют не менее Q

собственных чисел оператора K^ε. Именно в этом и требовалось убедиться, так как по лемме 2

строгое неравенство Q < X^ε невозможно. Теорема доказана.

Выполненные вычисления позволяют вывести асимптотические формулы для собственных

функций uεN2, . . . , u^εNJ . Вместе с тем поправочные слагаемые u^′k не определяются однознач-

но из задач (25), и то же самое можно сказать о собственных векторах системы (29) при

наличии кратных (55) среди собственных чисел (30). Поэтому ограничимся формулировкой

упрощённого результата - его переформулировка для случая (55) нуждается в стандартных,

но достаточно громоздких изменениях и доставляет менее явные формулы. Применим вторую

часть леммы 3, в которой возьмём h_k = c_kεd-2+αd и h_k = c_kεd-2. Множители c₁, . . . , c_J

зафиксируем малыми настолько, чтобы в c_kεd-2-окрестности точки (1 + εd-2λ^′k)-1 распола-

галось только одно собственное число оператора K^ε.

Теорема 2. Пусть d ≥ 3 и все собственные числа (30) простые. Тогда для собственных

функций uεN2, . . . , u^εNJ верны асимптотические формулы



∑



- u0k - χ_jw^′kj;H¹(Ω^ε)

c_kεαd , j = 2,J,

(56)

u

≤

j=1

функции в которых заданы равенствами (22), (23) и α_d = min{1, -1 + d/2} ≥ 1/2.

Подчеркнём, что H¹(ω_j)-нормы слагаемых w^′kj(ξ^j ) типа пограничного слоя равны O(εd-2),

однако эти слагаемые нельзя убрать из левой части оценок (56), так как кусочно-постоянные

функции u⁰², . . . , u0J не принадлежат пространству Соболева H¹(Ω^ε).

Замечание. При d = 2 асимптотические конструкции и процедура их обоснования разру-

шаются. Причина состоит в том, что для плоской задачи (14) решение P_j (ξ^j ) = 1 тривиально,

и вместо гармонической емкости вводится [16] логарифмическая ёмкость множества θ_j(0) как

коэффициент в разложении

Plogj(ξ^j) = -(2π)-1(ln |ξ^j| - ln c_log(θ_j)) + O(|ξ^j|-1),

|ξ^j| → +∞,

функции Plogj, гармонической в области Ξ^j = R² \ θ_j(0) и обращающейся в нуль на тре-

щине θ_j(0).

Разработано несколько подходов к вычислению асимптотики собственных пар спектраль-

ных задач в такой необычной ситуации. Во-первых, простейшим оказывается итерационный

процесс построения бесконечных рядов по обратным степеням большого параметра | ln ε|.

Во-вторых, при помощи усовершенствованного метода [13] (см. также [4, гл. 9]) можно про-

суммировать упомянутые ряды и вывести формулы

λ^εNk = |ln ε|-1Λ_k(|ln ε|-1) +λεNk,

|λεNk| ≤ c_kε^τ , τ ∈ (0,1),

где t → Λ_k(t) - вещественные аналитические функции. Первый подход обеспечивает малосо-

держательный результат, а второй, достаточно сложный и громоздкий в исполнении, воспро-

изводить в данной статье не будем.

4. Простое собственное число задачи Дирихле. Предположим, что для первых членов

последовательностей (8) собственных чисел задач (7), (7)_D справедливы неравенства

λj0D1 < λj0D1 при j = 1,J, j = j,

(57)

и построим асимптотику первого (заведомо простого; ср. п. 5, 3◦) собственного числа λεD1

задачи (2), (2)_D. Для определённости будем сначала считать, что 1 < j < J, - в случаях j = 1

и j = J формулы укорачиваются. Не будем писать индекс D и примем такие асимптотические

анзацы для собственных пар:

λε1 = λ^j01 + ε^dλ′1 + ... ,

(58)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

762

НАЗАРОВ

uε1(x) = u^j01(x) + ε^du′j(x) + εχ_j(x)w′j(ξ^j) + εχj-1(x)w′j-1(ξj-1) +

(59)

Здесь многоточие заменяет несущественные младшие асимптотические члены, причём три-

виальные анзацы uε1(x) = . . . на ячейках ω_j с номерами j = j при формальном анализе не

понадобятся. Поскольку λ^j01 - первое собственное число задачи Дирихле в ω_j и нормированная

в L²(ω_j) собственная функция выбрана положительной, справедливы неравенства

A_j := ∂_zu^j01(x^j) < 0, Aj-1 := ∂_zu^j01(xj-1) > 0.

(60)

Вспомнив, что uj±101 = 0, компенсируем скачки производной по z на отверстиях θεj и θεj-1

при помощи слагаемых типа пограничного слоя

w′j(ξ^j) = -

A_jw_j(ξ^j), w′j-1(ξj-1) =

Aj-1wj-1(ξj-1),

(61)

где фигурируют построенные по решению (19) задачи (13), (13)_D и затухающие при |ξ^j| →

→ +∞ функции

w_j(ξ^j) = W_j(ξ^j) - ζ^j при ζ^j > 0, w_j(ξ^j) = W_j(ξ^j) + ζ^j при ζ^j < 0,

(62)

у которых скачок производной по z на θ_j(0) равен -2. Учитывая поведение функций (62)

при ζ^j → ±∞, унаследованное от решений Q_j задачи (17) (см. формулы (19) и (18)), собираем

множители при ε^d в уравнении (2) на ячейке ω_j после подстановки в него анзацев (58) и (59).

В результате приходим к задаче Дирихле

-Δ_xu^′j(x) - λj01u^′j(x) = λ′1u0j(x) + f^′j(x), x ∈ ω_j,

u^′j(x) = 0, x ∈ ∂ω_j,

(63)

с индексом j = j и фрагментом правой части

f′j(x) =

A_jM(θ_j)Ψ_j(x) -

Aj-1M(θj-1)Ψj-1(x),

(64)

где

Ψ_j(x) = ([Δ_x,χ_j(x)] + λ^j01χ_j(x))∂_zΦ(x - x^j).

(65)

Способ вывода формул (64) и (65) мало отличается от представленного в п. 3 ввиду соотно-

шения ∂_ζj Φ(ξ^j ) = εd-1∂_zΦ(x - x^j) для выделенного в представлении (18) члена. Вместе с тем

из-за иррегулярности O(r1-dj) у функции (65) задача (63) с j = j не имеет решения в классе

H¹⁰(ω_j) при d ≥ 4. На помощь приходит теория Кондратьева [20] (см. также монографии [2, 21]

и др.), следуя которой введём весовое пространство Соболева V^lβ(ω_j) как пополнение линей-

ного множества C^∞c(ω_j \{x^j , xj-1}) (бесконечно дифференцируемые функции с компактными

носителями) по норме

(∑l

)1/2

∥g; V^lβ(ω_j)∥ =

∥rβ-l+pj∇^pxg; L₂(ω_j)∥2

p=0

Здесь ∇^xg - набор всех производных функции g порядка p, а l ∈ {0, 1, 2, . . .} и β ∈ R -

показатели гладкости и веса. Подпространство функций u ∈ V1β(ω_j), обращающихся в нуль

на ∂ω_j , обозначим V1β,0(ω_j ). Сопряжённое пространство V1β,0(ω_j)^∗ включено в V01-β(ω_j ), а

оператор B^jβ(λ) = -(Δ_x + λ) : V1β,0(ω_j) → V1β,0(ω_j )^∗ при |β| < d/2 наследует все основные

свойства отображения -(Δ_x + λ) : H¹⁰(ω_j ) → H¹⁰(ω_j )^∗ и, более того, при β = 0 совпадает с

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

763

ним. Иными словами, в силу предположения (57) оператор B^jβ(λ^j01) - изоморфизм при j =

= j, а Bjβ(λj01 ) - фредгольмово отображение с одномерными ядром и коядром, натянутыми на

собственную функцию u^j01. Все эти факты вытекают из общей теории, и их можно почерпнуть,

например, из источников [4, гл. 1; 2, гл. 2; 22, § 2 и теорема 2.7].

Учтём, что u^j01 ∈ V1β,0(ω_j), Ψ_j, Ψj-1 ∈ V01-β (ω_j) при β ∈ (-d/2, 2 - d/2) и

∫

(z - z^j + c)[Δ_x, χ_j(x)]∂_z Φ(x - x^j ) dx = (Φ(x)∂_|x|z - (z + c)∂_z Φ(x)) ds_x = 1.

(66)

R^d

S_R

В результате вытекающее из (64) и (65) условие разрешимости задачи (63) будет выглядеть так:

∫

λ′1 = λ′1∥u^j01;L²(ω_j)∥² = - u^j01(x)(Δ_xu′j(x) + λ^j01u′j(x))dx =

ω_j

∫

= u^j01(x)f′j(x)dx = -1(M(θj)|∂z uj01(xj)|2 + M(θj-1)|∂zuj01(xj-1)|2).

(67)

ω_j

Появление дроби 1/4 на месте дроби 1/2 обусловлено интегрированием по полусфере, а не

по сфере, как в формуле (66). В ситуациях j = 1 или j = J (ω_j - концевая ячейка) следует

положить M(θj-1) = 0 или M(θ_j) = 0 соответственно (отверстий θε0 и θ^εJ нет), а значит, в

правой части равенства (67) остаётся лишь одно слагаемое. Похожий, но частный случай при

помощи иного подхода рассматривался в публикации [3], а именно, J = 2 и j = 1, а ω₁ и

ω₂ - соосные цилиндры с одинаковым сечением.

Итак, получена формула (67) для поправки в представлении (58) первого собственного

числа λεN1 задачи (2), (2)_D, причём в дополнение к пограничным слоям (61) поправка ре-

гулярного типа u′1 в анзаце (59) для собственной функции uεD1 находится из ставшей по

причине (67) разрешимой задачи (63). Очевидное неравенство λ′1 < 0 согласуется с простым

следствием λεD1 < λj0D1 минимального принципа (см., например, [19, теорема 10.2.1]).

Сильные особенности O(r3-dj) при d > 3 у поправки u′j регулярного типа привносят но-

вые трудности в процедуру обоснования формальной асимптотики, устраняемые в методе [4]

введением в почти собственную спектральную пару младших асимптотических членов. Сфор-

мулируем результат, однако для сокращения объёма статьи исключим описание не нужных

по существу конструкций, т.е. ограничимся при доказательстве случаями d = 2 и d = 3.

При больших размерностях d ≥ 4 для проверки доказываемой далее оценки (68) нетрудно

приспособить упоминавшуюся общую схему оправдания асимптотики из монографии [4].

Теорема 3. При ограничениях (57) и d ≥ 2 найдутся такие положительные констан-

ты ε₁ и c₁, C₁, что при ε ∈ (0,ε₁] для первого собственного числа λεD1 задачи (2), (2)_D

справедливо неравенство

|λεD1 - λj0D1 - ε^dλ′1| ≤ c₁ε^dα_d(ε),

(68)

и других собственных чисел на интервале (0,Λ_D - C₁ε^d) нет. Здесь λ′1 > 0 - величина (57),

Λ_D = min{λj0D1+δ

|j = 1, J, } > 0 и α2(ε) = ε(1 + | ln ε|), α3(ε) = ε1/2, но αd(ε) = ε при

j,j

d ≥ 4.

Доказательство следует той же схеме, что и в п. 3. Укажем заменители леммы 3 и вы-

числений, приведших к теореме 1.

Сначала обратимся к смешанным краевым задачам

-Δ_xv^jε(x) = μ^jεv^jε(x), x ∈ ω_j,

v^jε(x) = 0, x ∈ ∂ω_j \ (θ^εj

^⋃θεj-1),

∂_zv^jε(x) = 0, x ∈ (θ^εj

^⋃θεj-1).

(69)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

764

НАЗАРОВ

Как известно (см. [7-9] и др.) и нетрудно проверить при помощи метода [4, гл. 5; 9; 13], для

первых двух собственных чисел задачи (69) верны оценки

|μ^jεq - λj0Dq| ≤ c^jqε^d при q = 1, 2 и ε ∈ (0, ε^jk]

(70)

с некоторыми положительными c^jk и ε^jk. Таким образом, применив неравенства Фридрихса-

Пуанкаре на ячейках ω₁, . . . , ω_J , обнаруживаем, что для функции ψ^ε ∈ H^εD лишь при одном

условии ортогональности (ψ^ε, vjε1)_ω

= 0 выполнено неравенство

∥∇_xψ^ε; L²(Ω^ε)∥² ≥ min{μ^jε

|j = 1,J}∥ψ^ε;L²(Ω^ε)∥².

1+δj,j

Осталось применить оценки (70) и соотношение (32) с индексами m = 2 и M = D, т.е. второе

утверждение теоремы проверено аналогично лемме 2.

Введём в пространстве H^εD скалярное произведение (35) и оператор (36), а в качестве

“почти собственной” пары возьмём

k^ε = (1 + λj0D1 + ε^dλ′1)-1, v^ε = ∥u^ε;H^εD∥-1u^ε,

(71)

где

∑

u^ε(x) = uj0D1(x) + ε^dX^ε(x)

u^′j(x) + ε

χ_j(x)w^′j(ξ^j).

(72)

j=j-1

Здесь собственная функция uj0D1 продолжена нулём с ячейки ω_j на всю область Ω^ε. Кроме

того, использованы те же срезки, что и в п. 3, функции w^′j взяты из (61), а функции u^′j -

решения задач (63), однако при j = j+1 и j = j-1, во-первых, u^′j = 0 и, во-вторых, f′j+1 или

f′j-1 содержат только первое или только второе слагаемое из формулы (64) соответственно.

Подчеркнём, что последние две задачи однозначно разрешимы согласно предположению (57).

Далее индекс D не пишем. Как и ранее, при j = 1 и j = J суммы в (72) укорачиваются.

Как уже упоминалось, считаем, что d = 2, 3, а значит, u^′j ∈ H¹(ω_j ), j = j, j±1, поскольку

из результатов работ [20, 23] (см. также [4, гл. 1; 2, гл. 3]) следует, что в окрестностях точек

x^j и xj-1 на прямых участках границы ∂ω_j верны такие неравенства:

|u^′j (x)| + r_j|∇_xu^′j (x)| ≤ c_j при d = 3,

(73)

Сразу же заметим, что вместо оценки (42) выполнена оценка

∫

((

)₂

)

∑

χ(r_j )

|〈u^ε, u^ε〉 - 1| ≤ c

1+ε^d +ε

-1

dx ≤ Cε^d.

(74)

(1 + εr_j)d-1

j=j-1

Ω⁰

Величину h, определённую в (37), для пары (71) преобразуем аналогично (43) и получим в

силу (71) и (74) неравенство

h ≤ csup|(∇_xu^ε,∇_xψ^ε)_Ωε - εd-2λ^′k(u^ε,ψ^ε)_Ωε|.

(75)

Выражение под знаком модуля представим как сумму скалярных произведений

Iu0(ψ^ε) = (∇_xu^j01,∇_xψ^ε)_ω

- λj01 (uj01 ,ψ^ε)_ω

Iuλ0(ψ^ε) = ε^dλ′1(u^j01,ψ^ε)_ω

I^uj(ψ^ε) = ε^d(∇_x(X^εu^′j),∇_xψ^ε)ωj -ε^dλ^j01(X^εu^′j,ψ^ε)ωj , I^uλj(ψ^ε) = ε2dλ′1(X^εu^′j,ψ^ε)ωj , j = j,j±1,

I^wj(ψ^ε) = ε(∇_x(χ_jw^′j),∇_xψ^ε)_ω

^⋃ωj+1,

(ψ^ε) = ε(λ^j01 + ε^dλ′1)(χ_j w^′j , ψ^ε)_ω

^⋃ωj+1, j = j - 1,j.

Для главного u^j01 и поправочных u^′j членов регулярного типа верны соотношения

Iu0(ψ^ε) = (∂_zu^j01,ψ^ε)_θε

- (∂_z uj01 , ψ^ε)_θε

|Iuλ0(ψ^ε) - ε^dλ′1(u^j01, X^εψ^ε)_ω

| ≤ cεd+1,

j-1

|I^uλj(ψ^ε)| ≤ cε2d∥u^′j ; L²(ω_j )∥ ∥ψ^ε; L²(ω_j )∥ ≤ Cε2d.

(76)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

765

Интегралы по отверстиям θεj и θεj-1 возникли потому, что пробная функция ψ^ε не обяза-

тельно обращается на них в нуль, а мажоранта во второй оценке (76) обусловлена тем, что

|u^j01(x)| ≤ cε на ω_j

^⋂supp(1 - X^ε) в силу условия Дирихле.

Отщепим от умноженных на ε членов (61) пограничного слоя (см. анзац (59)) величины

ϕεj(x) = -ε

(-1)j-j A_j M(θ_j )∂_ζj Φ(ξ^j) = -ε^d

(-1)j-j A_jM(θ_j )∂_zΦ(x - x^j), j = j - 1, j,

(77)

где A_j - коэффициенты (60). Вследствие соотношений (62) и (19), (18) остаток затухает как

O(|ξ^j |^-d) и оказывается бесконечно малой O(ε^d) на множестве supp |∇_xχ_j|, удалённом от

точки x^j . Таким образом,

|I^wλj(ψ^ε) - ελ^j01(χ_j ϕ^εj, ψ^ε)_ω

^⋃ωj+1|≤

(

∫

)1/2

(ε + r_j)² dx

≤ cεd+1

+ε2(d-1)

(ε + r_j)2d

(ε + r_j )2(d-1)

⋃

ω_j

ωj+1

ω_j

ωj+1

× ∥(ε + r_j )-1ψ^ε; L²(ω_j

^⋃ωj+1)∥ ≤ Cε^dα_d(ε).

(78)

Здесь выражения для множителей α₂(ε) и α₃(ε) указаны в формулировке теоремы, а весо-

вая норма пробной функции ψ^ε обеспечена неравенством (44), теряющим своё отношение к

неравенству Харди при d = 2, но справедливым вследствие неравенств Фридрихса по угловой

переменной φ ∈ (0, π) и в Rε-окрестностях точек x^j и xj-1 благодаря краевому условию

Дирихле на Θ_j \ θεj и Θj-1 \ θεj-1.

По тем же причинам, переводя срезку X^ε от u′j к ψ^ε, обнаруживаем, что при j = j, j ± 1

имеют место неравенства

|I^uj(ψ^ε) - ε^d(∇_xu^′j , ∇_x(X^εψ^ε))ωj - λ^j01(u^′j , X^εψ^ε)ωj | ≤

(

∫

)1/2

≤ cεd-1

(|u^′j (x)|² + r2j|∇_xu^′j (x)|²) dx

∥ψ^ε; H¹(Ω^ε)∥ ≤ cε^dα_d(ε),

(79)

supp|∇xX^ε|

в котором использованы оценки (73) и выполнено интегрирование. Подчеркнём, что при d >

> 3 нарушены именно оценки (73) и (79) из-за больших сингулярностей функций u^′j, однако

привлечение младших асимптотических членов по схеме [4] устраняет это препятствие в до-

казательстве.

Наконец, учитывая, что w^′j ∈ H^1loc(Ξ^j) - гармоническая функция в полупространствах

R^d± - обращается в нуль на ∂Ξ^j, но приобретает скачок производной на отверстии θ_j(0), при

помощи изложенных выше соображений выводим, что

|I^wj(ψ^ε) - (ϕ^εj∇_xχ_j, ∇_xψ^ε)_ω

^⋃ωj+1 + (∇xϕ^j, ψ^ε∇xχj)ω_j ⋃ωj+1 + (∂zu¹⁰, ψ^ε)θ^ε| ≤_j

≤ cε1+d∥ψ^ε; H¹(Ω^ε)∥ ≤ Cε1+d.

(80)

Закончим преобразования и подведём итог. Последние “лишние” члены из левых частей

неравенства (80), j = j и j = j - 1, взаимно уничтожаются с Iu0(ψ^ε) согласно первой фор-

муле в (76). Оставшиеся “лишние” члены из (80) вместе с вычитаемыми под знаками мо-

дуля в (78) и (76) также превращаются в нуль, так как u^′j - решения задач (63) с правы-

ми частями f^′j, а для функции (77) выполнено аналогичное (52) тождество. Следовательно,

h ≤ cε^dα_d(ε), и лемма 3 доставляет собственное число κ^ε оператора K^ε, расположенное в

cε^dα_d(ε)-окрестности точки k^ε. Повторив выкладки (54), находим собственное число задачи

(2), (2)D с асимптотикой (79). Поскольку по доказанному ранее других собственных чисел

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

766

НАЗАРОВ

на интервале

(0, λ^j01 + Cε^d) нет, проверка первого утверждения теоремы также закончена.

Теорема доказана.

Благодаря единственности собственного числа Дирихле на интервале (0, Λ_D -C₁ε^d) вторая

часть леммы 3 при доказательстве теоремы 3 не применялась. Вместе с тем, положив h = cε^d

и h = (ΛD -λj01 )/3 в неравенстве (38) и присоединив слагаемые ε^dX^εu^′j из (72) к остатку (это

нужно сделать из-за неопределённости в выборе u^′j и “плохой” мажоранты в неравенстве (75)

для нормы функции u^ε), получаем асимптотику собственной функции uεD1.

Теорема 4. При ограничениях (57) и d ≥ 2 найдутся такие положительные константы

ε₂ и c₂, что при ε ∈ (0,ε₂] для первой собственной функции задачи (2), (2)_D, нормированной

равенством (5), выполняется неравенство

∥uεD1 - uj0D1 - ε(χ_jw′j + χj-1w′j-1); H¹(Ω^ε)∥ ≤ c₂ε^τ , τ > 0.

(81)

Поскольку собственная функция uj0D1, продолженная нулём с ячейки ω_j на всю область

Ω^ε, возмущена в (81) слагаемыми типа пограничного слоя, приобретающими порядок εd-1

при удалении от точек x^j и xj-1 вовнутрь Ω^ε \ ω_j, теорема 4 как раз устанавливает свойство

локализации собственной функции uεD1. В отличие от теоремы 2 сама функция uj0D1 принад-

лежит пространству H^εD = H¹⁰(Ω^ε) и, поскольку H¹(ω_j )-нормы слагаемых типа пограничного

слоя - величины O(ε1+d/2), члены εχ_j w^′j из неравенства (81) можно убрать, уменьшив, может

быть, показатель τ > 0.

5. Несколько замечаний. 1^◦. Доступные обобщения. Многие геометрические ограни-

чения в работе введены исключительно для упрощения изложения. Так, лишь с понятными

изменениями в выкладках и рассуждениях можно допустить перфорацию несколькими отвер-

стиями, несвязные ячейки и косые или изломанные перегородки (рис. 2, а и б). Разработанные

в монографиях [4, 5] методы допускают многие другие в некотором смысле усложнения объ-

екта анализа, например, векторные краевые задачи, в том числе для систем уравнений теории

упругости. Наконец, метод составных разложений позволяет построить и обосновать беско-

нечные асимптотические ряды для собственных чисел и функций.

(а)

(б)

(в)

Рис. 2. Области с несвязными ячейками (а) и косыми или изломанными перего-

родками (б). Область, обладающая вращательной и зеркальной симметриями (в).

2◦. Локализация собственных функций. Описанные конструкции и приёмы асимптоти-

ческого анализа пригодны и для собственных чисел с любыми номерами. Пусть, например,

при d ≥ 3 собственное число λj0Np задачи Неймана (13), (13)_N с номером j ∈ {1, . . . , J} не

принадлежит спектрам (7)_N задач в других областях ω_j, т.е. при j = j. Тогда, совместив

рассуждения из п. 3 и п. 4, заключаем, что в последовательности (4)_N имеется собственное

число

λ^εNP = λj0Np + εd-2 1(C(θj)|uj0Np(xj)|2 + C(θj-1)|uj0Np(xj-1)|2) + O(εd-2+α), α > 0,

где P - количество членов последовательностей (7)_N , строго меньших λj0Np. Для соответству-

ющей собственной функции выполнено похожее на (7) неравенство



-uj0Np +1

(χ_jC(θ_j)uj0Np(x^j)w_j - χj-1C(θj-1)uj0Np(xj-1)wj-1); H¹(Ω^ε)

cε^τ , τ > 0.

^u

NP+1

≤

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

О СОБСТВЕННЫХ ЧИСЛАХ И ФУНКЦИЯХ

767

Конечно же схему обоснования асимптотик приходится изменить, так как лемма 2 стано-

вится бесполезной, и вместо неё нужно проверить так называемую “теорему о сходимости”, а

сильные сингулярности, обсуждавшиеся перед формулировкой теоремы 3, возникают не толь-

ко в задаче Дирихле, но и в задаче Неймана при λj0Np = 0.

Итак, замеченная в [3] локализация собственной функции не является прерогативой первой

собственной функции задачи Дирихле. На самом деле локализация обусловлена лишь тем

обстоятельством, что какое-то число является собственным для одной и только для одной из

предельных задач (13), (13)_D и (13), (13)_N .

3◦. Кратное собственное число задачи Дирихле. Предположим, что λ⁰ := λ10D1 = . . . = λJ0D1

(например, Ω - цилиндр ϖ × (0, J) ⊂ Rd-1 × R и z^p = p) и подчиним собственные функции

uj0D1 условиям нормировки (9). Тогда главный член асимптотики собственных функций uεDk,

отвечающих собственным числам

λ^εDk = λ⁰ - ε^dλ^′k + ... , k = 1,J,

(82)

задачи (2), (2)_D, имеет вид u0k(x) = a^kjuj0D1(x) при x ∈ ω_j, j = 1, J (ср. (57) и (22)). Повторив

асимптотический анализ из п. 4, видоизменённый согласно п. 3, получаем, что асимптотиче-

ские поправки (30) в анзаце (82) суть собственные числа J × J-матрицы T, образованной

2 × 2-блоками (20), в которых C_j = M(θ_j)(∂_zuj+10D1(xj+1))-2 и τ_j = ∂_zuj0D1(x^j)/∂_zuj+10D1(xj-1).

Обратим внимание на знак минус в правой части равенства в (82) (собственные числа умень-

шаются) и вспомним неравенства (60) (знаменатели не обращаются в нуль).

4◦. Расцепление собственных чисел. Найденные асимптотические формулы приводят к

выводу: расцепление кратных собственных чисел в задачах Дирихле и Неймана происходит

за счёт возмущений порядков ε^d при d ≥ 2 и εd-2 при d > 2 или | ln ε|-1 при d = 2 соот-

ветственно. Вместе с тем этот эффект может вообще отсутствовать или проявляться в членах

O(ε^q) c большими показателями q. Пусть, например, область Ω^ε обладает вращательной и

зеркальной симметриями относительно оси z и плоскости {x : z = 0} (рис. 2, в). Тогда, на-

пример, в задаче Неймана собственные функции uj0Np с номерами p > 1 и j = 1, 3 могут

обратиться (и обращаются) в нуль при z = 0, а значит, в аналогичных (21) асимптотиках

главная поправка λ^′p аннулируется. Кроме того, нетрудно проверить, что в случае λ20D1 >

> λ10D1 = λ30D1 несколько первых асимптотических членов в асимптотике собственных чисел

λεD1 и λεD2 совпадают. Наконец, из-за симметрии в последовательностях (4) заведомо имеют-

ся кратные собственные числа.

СПИСОК ЛИТЕРАТУРЫ

1. Ладыженская О.А. Краевые задачи математической физики. М., 1973.

2. Nazarov S.A., Plamenevsky B.A. Elliptic Problems in Domains with Piecewise Smooth Boundaries.

Berlin; New York, 1994.

3. Delitsyn A., Grebenkov D.S Mode matching methods for spectral and scattering problems // Q. J. Mech.

Appl. Math. 2018. V. 71. № 4. P. 537-580.

4. Mazja W.G., Nasarow S.A., Plamenewski B.A. Asymptotische Theorie elliptischer Randwertaufgaben in

singulär gestörten Gebieten. Bd. 1-2. Berlin, 1991.

5. Ильин А.М. Согласование асимптотических разложений решений краевых задач. М., 1989.

6. Kozlov V.A., Maz’ya V.G., Movchan A.B. Asymptotic Analysis of Fields in Multi-Structures. Oxford,

1999.

7. Гадыльшин Р.Р. Асимптотика собственного значения сингулярно возмущенной самосопряженной

эллиптической задачи с малым параметром в граничных условиях // Дифференц. уравнения. 1986.

Т. 22. № 4. С. 640-652.

8. Гадыльшин Р.Р. Расщепление кратного собственного значения задачи Дирихле для оператора Ла-

пласа при сингулярном возмущении граничного условия // Мат. заметки. 1992. Т. 52. № 4. С. 42-55.

9. Гадыльшин Р.Р. О возмущении спектра лапласиана при смене типа граничного условия на малой

части границы // Журн. вычислит. математики и мат. физики. 1996. Т 36. № 7. С. 77-88.

10. Van-Dyke M. Perturbation Methods in Fkuid Mechanics. New York; London, 1964.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021

4^∗

768

НАЗАРОВ

11. Вишик М.И., Люстерник Л.А. Регулярное вырождение и пограничный слой для линейных диф-

ференциальных уравнений с малым параметром // Успехи мат. наук. 1957. Т. 12. № 5. С. 3-122.

12. Мазья В.Г., Назаров С.А., Пламеневский Б.А. Об асимптотике решений эллиптических краевых

задач при нерегулярном возмущении области // Проблемы мат. анализа. Вып. 8. Л., 1981. С. 72-153.

13. Мазья В.Г., Назаров С.А., Пламеневский Б.А. Асимптотические разложения собственных чисел

краевых задач для оператора Лапласа в областях с малыми отверстиями // Изв. АН СССР. Сер.

Матем. 1984. Т. 48. № 2. С. 347-371.

14. Мазья В.Г., Назаров С.А. Об особенностях решений задачи Неймана в конической точке // Сиб.

мат. журн. 1989. Т. 30. № 3. С. 52-63.

15. Полиа Г., Сеге Г. Изопериметрические неравенства в математической физике. М., 1962.

16. Ландкоф Н.С. Основы современной теории потенциала. М., 1966.

17. Седов Л.И. Механика сплошной среды. Т. II. М., 1976.

18. Работнов Ю.Н. Механика деформируемого твердого тела. М., 1988.

19. Бирман М.Ш., Соломяк М.З. Спектральная теория самосопряженных операторов в гильбертовом

пространстве. Л., 1980.

20. Кондратьев В.А. Краевые задачи для эллиптических уравнений в областях с коническими или

угловыми точками // Тр. Московск. мат. о-ва. 1963. Т. 16. С. 219-292.

21. Kozlov V.A., Maz’ya V.G., Rossmann J. Elliptic Boundary Value Problems in Domains with Point

Singularities. Providence, 1997.

22. Назаров С.А. Полиномиальное свойство самосопряженных эллиптических краевых задач и алгеб-

раическое описание их атрибутов // Успехи мат. наук. 1999. Т. 54. № 5. С. 77-142.

23. Мазья В.Г., Пламеневский Б.А. О коэффициентах в асимптотике решений эллиптических краевых

задач в области с коническими точками // Math. Nachr. 1977. Bd. 76. S. 29-60.

Институт проблем машиноведения РАН,

Поступила в редакцию 23.08.2020 г.

г. Санкт-Петербург

После доработки 09.12.2020 г.

Принята к публикации 27.04.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№6

2021