ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 7, с.867-879

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.632+517.958:533.9

ВОПРОСЫ УСТОЙЧИВОСТИ В ДВУМЕРНЫХ

МАТЕМАТИЧЕСКИХ МОДЕЛЯХ РАВНОВЕСИЯ ПЛАЗМЫ

В МАГНИТНЫХ ЛОВУШКАХ-ГАЛАТЕЯХ

Ловушки-галатеи для удержания плазмы в магнитном поле, которое создаётся проводника-

ми с током, погружёнными в плазменный объём, составляют перспективный класс объек-

тов разработок в области управляемого термоядерного синтеза. После описания основных

свойств и количественных характеристик ловушек центральной проблемой является ис-

следование устойчивости равновесных магнитоплазменных конфигураций. Существенную

роль играют здесь математическое моделирование и расчёты, выполненные в терминах

дифференциальных уравнений магнитной газодинамики. Они изложены на примере рас-

прямлённой в цилиндр тороидальной ловушки “галатея-пояс”. В статье представлена её

плазмостатическая модель и несколько подходов к исследованию устойчивости конфигу-

раций: сходимость итерационных методов установления равновесия в двумерных моделях,

краткий обзор исследования магнитогазодинамической устойчивости одномерных конфи-

гураций, окружающих прямой проводник с током, и строгое исследование устойчивости

конфигураций относительно двумерных возмущений в линейном приближении. В числен-

ных расчётах получены критерии устойчивости в разных приближениях и их соотношения

между собой. Указаны пути обобщения результатов на трёхмерные возмущения.

DOI: 10.31857/S0374064121070013

Введение. Тематика, представленная названием нашей статьи, постоянно присутствует

в работах по приложениям вычислительной математики к проблемам физики плазмы, на-

чиная с середины прошлого столетия. Интерес к ней обусловлен многообещающими научно-

техническими приложениями и, в первую очередь, перспективой получить в большом количе-

стве дешёвую энергию управляемого термоядерного синтеза. Осуществить желаемую реакцию

синтеза лёгких элементов таблицы Менделеева предполагается в ловушках, в которых плотная

и нагретая до высоких температур плазма должна удерживаться магнитным полем в течение

требуемого времени. Особое внимание уделяется преодолению возникающих при этом много-

численных плазменных неустойчивостей. Поэтому основным объектом исследований в данной

области науки являются конфигурации плазмы, поля и создающего его электрического тока,

находящиеся в равновесии в разнообразных ловушках.

Наиболее распространены ловушки тороидальной формы, позволяющие максимально избе-

жать контактов горячей плазмы с элементами конструкции. В данной работе рассматривается

специальный класс тороидальных ловушек, в которых проводники с током, индуцирующим

магнитное поле, погружены в плазменный объём, но не соприкасаются с плазмой. Внимание

к ним привлечено А.И. Морозовым [1], который назвал их галатеями и инициировал серию

конкретных разработок таких ловушек [2-4]. Существенную роль в этих разработках играют

математические модели основных физических процессов и большие объёмы относящихся к

ним численных исследований. Они облегчают теоретическую часть работы, а также позво-

ляют более экономно вести громоздкие и дорогостоящие эксперименты и анализировать их

результаты. С численным моделированием равновесных магнитоплазменных конфигураций в

упомянутых выше ловушках-галатеях можно ознакомиться, например, по статьям [5-8], об-

зору [9] и монографиям [10, с. 65; 11, с. 152]. Математический аппарат моделей достаточно

плотной плазмы основывается на приближении механики сплошных сред, т.е. используются

дифференциальные уравнения магнитной газодинамики (МГД), а более конкретно - численное

решение краевых МГД-задач.

Основные проблемы в исследовании конфигураций в ловушках и соответствующих чис-

ленных моделей сводятся, во-первых, к описанию их возможных равновесных состояний и,

867

868

БРУШЛИНСКИЙ, СТЕПИН

во-вторых, к их устойчивости относительно хотя бы малых, но достаточно произвольных воз-

мущений.

Равновесия исследуются с помощью краевых задач для уравнений плазмостатики, в общем

случае трёхмерных и достаточно сложных. Однако широко распространены ловушки, которые

обладают симметрией (плоской, осевой, винтовой) или допускают её в каком-либо приближе-

нии. Симметрия позволяет понизить размерность задач о равновесии до двумерных, а в особо

простых случаях - даже до одномерных. В двумерных задачах систему уравнений плазмоста-

тики удаётся свести к одному скалярному уравнению Грэда-Шафранова для функции магнит-

ного потока [12, 13]. Одномерные задачи имеют дело с обыкновенными дифференциальными

уравнениями, которые несложно решаются аналитически. В исследованиях основных принци-

пиальных вопросов на качественном уровне допускается ещё одно упрощение: тороидальные

ловушки “распрямляются” в цилиндр, т.е. в тор бесконечного радиуса. Необходимые для этого

количественные поправки на тороидальность оцениваются, например, в работе [7].

Задачи об устойчивости равновесных магнитоплазменных конфигураций в ловушках об-

суждаются и рассматриваются во многих научных работах; в общем виде они поставлены

в [14-16; 17, с. 82] и решены в ряде конкретных случаев. Из работ последнего времени отме-

тим серию статей С.Ю. Медведева с соавторами (см. статью [18] и приведённую в ней библио-

графию).

В настоящей работе устойчивость рассматривается на примере двумерных равновесных

конфигураций в распрямлённом аналоге тороидальной “галатеи-пояса” - цилиндре с двумя

погружёнными в него прямыми проводниками. Приведена постановка задачи о МГД-устойчи-

вости относительно произвольных трёхмерных возмущений в линейном приближении. Эта за-

дача сведена к двумерным задачам для отдельных гармоник по координате z, указаны воз-

можные подходы к её решению, получен критерий устойчивости. Кроме того, рассмотрены

некоторые упрощения исходной задачи. Во-первых, сходимость итерационных методов уста-

новления в численном решении двумерных плазмостатических задач о равновесии трактуется

как разновидность устойчивости, но только относительно возмущений магнитного поля той

же размерности. Такая устойчивость названа “диффузионной” [19]. Она необходима, но недо-

статочна для МГД-устойчивости, однако может представлять интерес, поскольку оценивается

количественными критериями и указывает на обстоятельства, сопутствующие или препят-

ствующие общепринятой устойчивости. Во-вторых, общим элементом всех ловушек-галатей

являются погружённые в плазму проводники с током. Поэтому целесообразно рассмотреть

одномерную задачу о плазменной конфигурации, окружающей один прямой проводник и не

соприкасающейся с ним. В серии работ последнего времени [20-23] рассмотрены такие зада-

чи с заданным распределением давления по радиусу с различными его вариантами вблизи

внешней границы окрестности. Эти конфигурации оказались диффузионно устойчивыми при

допустимых значениях давления плазмы, но МГД-устойчивость потребовала более сильных

ограничений на давление, зависящих от его распределения у внешней границы.

В целях единообразного представления поставленных вопросов и их решения в п. 1 кратко

изложена двумерная математическая модель “галатеи-пояса”, даны определение диффузион-

ной устойчивости и её интерпретация в терминах спектральных свойств оператора линеаризо-

ванной задачи. В п. 2 кратко перечислены результаты об устойчивости одномерных конфигура-

ций, окружающих один прямой проводник с током. В п. 3 изложена логика МГД-устойчивости

двумерных конфигураций в галатеях и результаты численного исследования устойчивости от-

носительно двумерных возмущений, в том числе динамических. Указаны пути исследования

МГД-устойчивости относительно произвольных трёхмерных возмущений.

1. Математическая модель равновесия в “галатее-поясе”. Диффузионная устой-

чивость. Распрямлённый аналог тороидальной ловушки “галатея-пояс” [3] представляет со-

бой бесконечный цилиндр с двумя погружёнными в него прямыми проводниками конечного

диаметра. Математическая модель равновесных конфигураций в случаях круглого и квадрат-

ного сечений цилиндра плоскостью, перпендикулярной его оси, изложена в работах [6] и [7]

соответственно. Конфигурации расположены в приосевой части цилиндра и практически не

зависят от формы внешней границы. Поэтому кратко воспроизведём рассматриваемую мо-

дель для упрощения в случае квадратной области сечения цилиндра (см. рис. 1, на котором

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ВОПРОСЫ УСТОЙЧИВОСТИ В ДВУМЕРНЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЯХ

869

показаны сечения цилиндра и проводников плоскостью z = const; ось цилиндра совпадает с

осью z).

МГД-равновесие описывается уравнениями плазмостатики [10, с. 65; 11, с. 152; 14; 15]

∇p = j × H, j = rotH, div H = 0, j = j^pl + j^ex,

(1)

связывающими давление p, напряжённость магнитного поля H = (H_x, H_y, 0) и плотность

электрического тока j = (0, 0, j). Ток складывается из тока j^pl в плазме и заданного тока j^ex в

проводнике. Ток в проводниках вводится в задачу как непрерывная функция, сосредоточенная

в основном в области проводников. Такое задание тока позволяет ставить задачу в односвязной

области сечения цилиндра, не выделяя из неё “островки” с проводниками [5; 6; 10, с. 69; 11,

с. 157]. В наших работах эта функция имеет вид

∑

j^ex = j₀

exp{-((x - x_k)² + y²)/r2c}, j₀ = 2/r^2c,

(2)

k=1

где x₁ = 1, x₂ = -1 - абсциссы центров, r_c - условный радиус проводников, а множитель

j₀

обеспечивает равенство интеграла от функции (2), взятого по окрестности проводника,

величине заданного тока в нём.

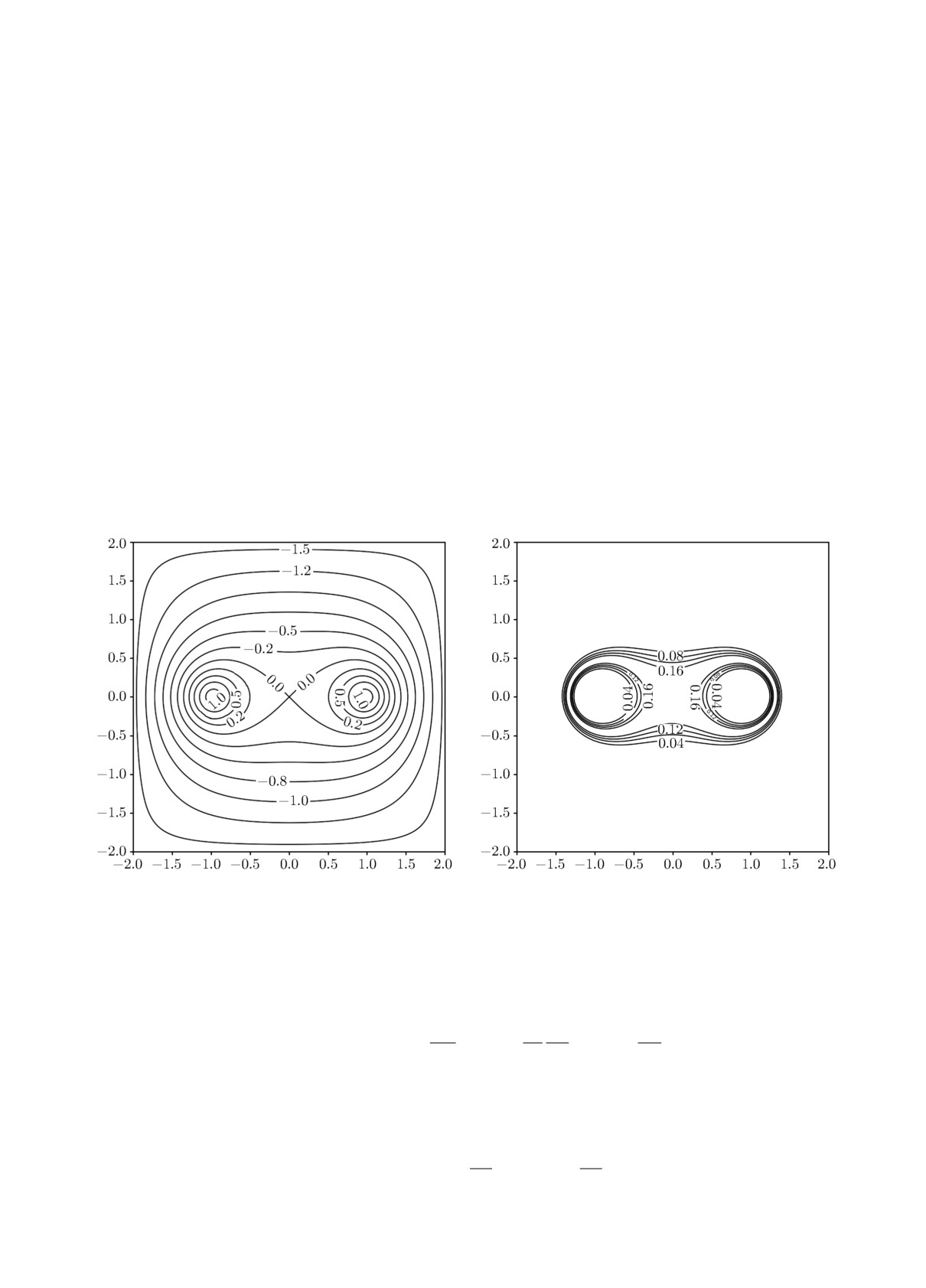
(а)

(б)

Рис. 1. Равновесные конфигурации магнитного поля (а) и давления плазмы (б) в сечении цилиндра при rc =

= 0.2, q = 0.2, p0 = 0.2.

Уравнения (1) и функция (2) представлены в безразмерной форме, т.е. все переменные в

них отнесены к единицам измерения, отмеченным индексом u, которые составлены из задан-

ных размерных величин: x₀ - расстояния от оси цилиндра до центров проводников и J_c -

электрического тока в каждом из них:

2J_c

c H_u

H^2u

x_u = y_u = x₀, H_u =

j_u =

p_u =

(3)

cx_u

4π x_u

4π

Рассматриваемая магнитоплазменная конфигурация обладает плоской симметрией (∂/∂z ≡

≡ 0), т.е. двумерна, что сильно упрощает математический аппарат модели. Магнитное поле

H выражается через z-компоненту вектор-потенциала ψ = ψ_z по формулам

∂ψ

H = rotΨ, H_x =

H_y = -

∂y

∂x

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

870

БРУШЛИНСКИЙ, СТЕПИН

Линии уровня ψ(x, y) = const - магнитные силовые линии в сечении цилиндра плоскостью

z = const, а физический смысл функции ψ - функция магнитного потока. Система уравнений

(1) сводится к одному скалярному уравнению - плоской разновидности уравнения Грэда-

Шафранова [12, 13]:

Δψ +

+ j^ex = 0.

(4)

dψ

Внешняя граница ловушки предполагается непрозрачной для магнитного поля, что отра-

жено в граничном условии ψ = ψ|_Γ = const. Давление p функционально зависит от ψ, и

зависимость p(ψ) должна быть задана при постановке конкретной задачи исходя из дополни-

тельных требований к исследуемой конфигурации.

В задачах о галатеях естественно требовать, чтобы проводники внутри плазменного объёма

не контактировали с плазмой. Это достигается, например, заданием p(ψ) в виде

p(ψ) = p₀ exp{-(ψ - ψ₀)²/q²}.

(5)

Здесь давление максимально на силовой линии ψ(x, y) = ψ₀ - сепаратрисе магнитного поля

в “поясе”, проходящей через центр (см. рис. 1), и быстро убывает при удалении от неё, если

параметр q достаточно мал. Таким образом, краевая задача для уравнения (4) содержит

параметр ψ₀, определяемый дополнительным условием

ψ₀ = ψ(0,0).

(6)

На внешней границе без ограничения общности можно положить ψ|_Γ = 0. Задача решается

итерационным методом установления. Уравнение (4) заменяется параболическим уравнением

∂ψ

= Δψ + g(x,y,ψ),

(7)

∂t

где g(x, y, ψ) - младшие члены в (4).

В его разностном аналоге переход от n-го слоя (итерации) к (n + 1)-му в главных членах с

производными от ψ осуществляется методом продольно-поперечной прогонки [11, с. 246; 24;

25], а нелинейное слагаемое g(x, y, ψ) в (7) и параметр ψ₀ в (6) берутся с предыдущего слоя.

Результаты расчётов “пояса”, полученные в работах [6, 7], проиллюстрированы на рис. 1.

Плазменная конфигурация сосредоточена в центре области и имеет форму криволинейного

четырёхугольника с выпуклыми внутрь границами и примыкающими к ним узкими полосками

вдоль магнитной сепаратрисы. Общий во всех вариантах расчётов результат состоит в том,

что итерационный процесс решения задачи сходится лишь при ограничении

p₀ < p^diff0

(8)

на максимальное значение давления, отнесённое к магнитной единице. Это позволяет считать

неравенство (8) условием так называемой диффузионной устойчивости [19] - устойчивости

только при возмущениях магнитного поля той же размерности, т.е. двумерных. Она не зависит

от численного метода решения задачи, поскольку связана с внутренней природой математи-

ческой модели - положительной определённостью дифференциального оператора

L[u] ≡ -Δu -

(9)

dψ

линеаризованной задачи. Сходимость итераций имеет место, если погрешность решения задачи

с уравнением (7) u = ψ - ψ_eq, где ψ_eq - искомое решение стационарной задачи, стремится к

нулю при t → ∞. Оно строится из экспонент

u(t, x, y) = e^-λtu(x, y),

(10)

удовлетворяющих уравнению

L[u] = λu.

(11)

Поэтому u → 0 в формуле (10) при любых “начальных” данных, если все собственные значения

задачи (11) положительны.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ВОПРОСЫ УСТОЙЧИВОСТИ В ДВУМЕРНЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЯХ

871

Диффузионная устойчивость, очевидно, необходима, но недостаточна для МГД-устойчи-

вости конфигураций, однако может быть полезна при анализе последней, так как содержит

грубый, но доступный критерий. Спектр оператора L[u] следует сравнить со спектром опе-

ратора L₀[u] ≡ -Δu, положительно определённого практически при любых однородных гра-

ничных условиях. Известно, что если коэффициент при u во втором слагаемом правой части

(9) положителен, то собственные значения оператора L[u] смещены вправо по сравнению со

спектром оператора L₀[u] [26, с. 86]. Отсюда вытекает достаточное условие диффузионной

устойчивости

d²p

≡

≤μ₁,

(12)

dψ

dψ²

где μ₁ - старшее (минимальное) собственное значение оператора L₀[u] [21], которое легко

находится аналитически и зависит только от геометрии задачи и граничных условий.

В квадратной области -2 < (x, y) < 2 на рис. 1 μ₁ = π²/8 ≈ 1.2321. Поскольку

(

)

d²p

2p₀

⁽ψ-ψ₀)²)(

(ψ - ψ₀)²

p₀

1-2

exp

≤ 0.4724

(13)

dψ²

q²

то из (12) и (13) следует, что p₀ ≤ 2.117μ₁q² = 2.61q².

Расчёты показали, что в этом примере со значением q = 0.2 итерационный процесс реше-

ния задачи сходится при гораздо более слабом ограничении p₀ ≤ 4.5 [7], что подтверждает

лишь достаточность критерия (12) для диффузионной устойчивости. В него коэффициент

при u во втором слагаемом оператора (9) входит только посредством максимального значе-

ния d²p/dψ², и поэтому без внимания остаётся существенный участок значений ψ, близких

к ψ₀, где d²p/dψ² < 0.

В серии расчётов конфигураций с параметрами r_c = 0.2, q = 0.2 получены равновесные

конфигурации, расположенные на конечном расстоянии от проводников. Пример распределе-

ния магнитного поля и давления при p₀ = 0.2 приведён на рис. 1. Электрический ток j равен

нулю в центре и на сепаратрисе магнитного поля, где давление максимально, и положителен в

области между сепаратрисой и внешней границей. Здесь он практически совпадает с j^pl = j -

-j^ex, так как заданный ток j^ex сосредоточен вблизи центров проводников. В области между

сепаратрисой и проводниками j^pl = j - j^ex < 0. Таким образом, сила Ампера (j × H)_z = -jH

направлена в сторону сепаратрисы и способствует изоляции проводников и внешней границы

от плазмы. При значениях p₀ < 0.8 границы четырёхугольника выпуклы внутрь, что бла-

гоприятствует устойчивости [27]. С возрастанием p₀ конфигурация увеличивается в объёме,

становится выпуклой в сторону внешней границы и стремится приблизиться к проводникам.

Время установления решения задачи с уравнением (7) возрастает, и по мере приближения

p₀ → p^diff0 установление прекращается.

Таким образом, двумерная математическая модель равновесия плазмы в ловушке “галатея-

пояс” основана на численном решении краевой задачи для уравнения Грэда-Шафранова. Рас-

смотрены свойства равновесных конфигураций и получено достаточное условие их диффу-

зионной устойчивости в терминах спектра дифференциального оператора линеаризованной

задачи.

2. Одномерная модель конфигураций, окружающих проводник с током. Ещё

один относительно простой, но достаточно общий подход к исследованию устойчивости рав-

новесия плазмы в галатеях можно рассмотреть в типичном для всех ловушек этого класса

элементе - окрестности одного отдельно взятого проводника. Здесь можно ограничиться од-

номерными задачами в кольцевой окрестности прямого токонесущего проводника и получить

определённую количественную информацию об окружающих его, но не соприкасающихся с

ним конфигурациях. Эти задачи можно считать обобщением задач о равновесных конфигу-

рациях в круглом цилиндре, в частности, хорошо известного Z-пинча (см., например, [15;

16; 10, с. 94; 11, с. 168]. Постановка задач и некоторые результаты их решений содержатся в

работах [20-23].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

872

БРУШЛИНСКИЙ, СТЕПИН

Подытожим их результаты и выводы из них кратким обзором, имея в виду, что постановка

задач более подробно изложена в работе [21]. Математические модели равновесных конфи-

гураций рассмотрены в кольцевой области 1 < r < R, содержащейся в сечении плазменного

цилиндра плоскостью z = const и охватывающей прямой круглый проводник радиуса 1. Моде-

ли одномерны: единственной независимой пространственной переменной является радиальная

координата r. Вектор плотности электрического тока j в проводнике и окружающей его плаз-

ме направлен вдоль оси z, а напряжённость магнитного поля H - только по азимуту ϕ. Три

скалярные функции p(r), j(r) и H(r) подчиняются двум уравнениям, к которым сводятся

уравнения плазмостатики (1):

1 d(Hr)

= -jH, j =

(14)

r dr

Они записаны в безразмерной форме. В качестве единицы измерения радиуса выбран ра-

диус проводника: r_u = r_c, остальные единицы те же, что и выше (см. (3)). Уравнений (14)

недостаточно для определения трёх функций, поэтому в математической модели каждой кон-

кретной конфигурации следует задать одну произвольную функцию в соответствии с допол-

нительными требованиями или имеющейся информацией. Естественно задать давление p(r)

так, чтобы проводник не соприкасался с горячей плазмой, например, в виде квадратичной

функции

(

⁽r₁ -r)2)

p=p₀

1<r<r₁,

(15)

r₁ - 1

возрастающей от нуля на поверхности проводника до своего максимального значения p₀ на

заданном от него расстоянии r₁ - 1 > 0. При r > r₁ давление остаётся постоянным или

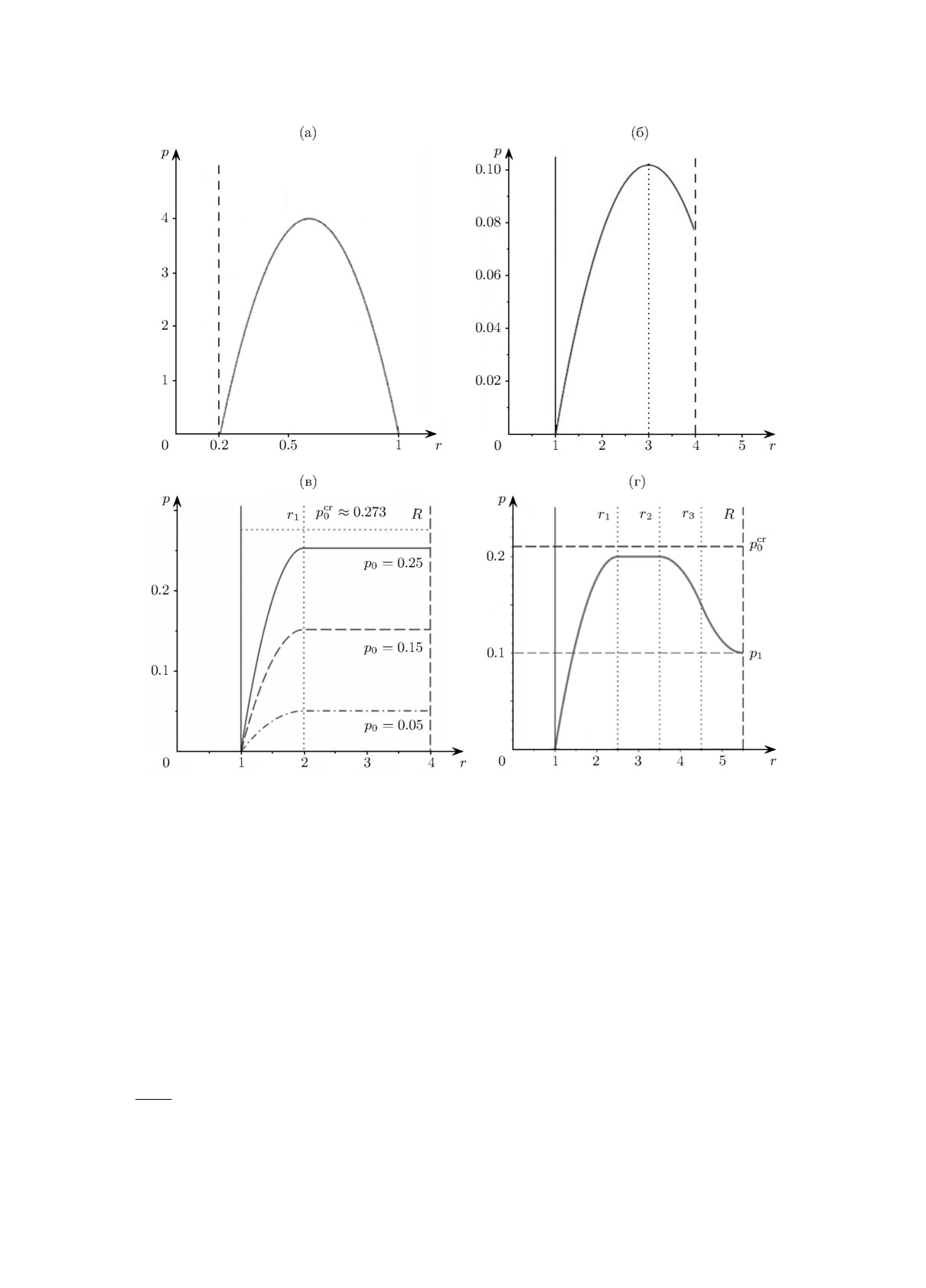
убывает в сторону внешней границы различными способами, как показано в работах [20-23].

Примеры рассматривавшихся распределений давления представлены на рис. 2.

Если задано распределение p(r), то магнитное поле H(r) и ток j(r) находятся интегри-

рованием уравнений (14). При этом возникает общее для всех конфигураций ограничение на

максимальное значение заданного давления

p₀ ≤ p^cr0 = 3/(r²¹ + 2r₁ + 3).

(16)

Устойчивость этих одномерных конфигураций исследована двумя способами. Первый из

них - в терминах рассмотренной выше диффузионной устойчивости, соответствующей схо-

димости итерационного метода решения краевых задач для уравнения Грэда-Шафранова.

Для математической модели одномерных конфигураций в этом уравнении нет необходимости,

поскольку она получается аналитически после задания p(r) формулой типа (15), однако их

устойчивость может, как уже отмечалось, представлять интерес. Одномерный вариант краевой

задачи для уравнения (4) в нашем случае имеет вид

(

)

1 d

dψ

+ g(ψ) = 0;

(1) = -1, ψ(R) = 0,

r dr

где

dp/dr

dψ

g(ψ) =

= j,

= -H.

dψ

dψ/dr

Численное решение её методом установления получено во всех рассчитанных вариантах

ловушки, достаточный критерий типа (12) также выполнен. Однако участвующий в этом кри-

терии коэффициент

⁽d²p

1 dp

⁽ dp)2)

dψ

H²

dr²

r dr

H²

может сильно возрастать при p₀ → p^cr0 и r₁ → 1. Это соответствовало бы неограниченному

приближению давления к критическому или конфигурации - к проводнику, что противоречит

физическому смыслу ловушек-галатей. С учётом этого замечания можно сделать вывод, что

исследованные варианты окружающих проводник конфигураций диффузионно устойчивы.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ВОПРОСЫ УСТОЙЧИВОСТИ В ДВУМЕРНЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЯХ

873

Рис. 2. Распределения давления в кольцевых конфигурациях плазмы вокруг проводника с

током [20-23].

Второй способ - строгое исследование МГД-устойчивости равновесных магнитоплазмен-

ных конфигураций относительно произвольных трёхмерных малых возмущений в линейном

приближении. Его общая логика в приложении к одномерным конфигурациям в цилиндре и,

в первую очередь, к Z-пинчу, известная из ранних работ [15; 16; 17, с. 71], изложена в мо-

нографиях [10, с. 90; 11, с. 165]. Результаты расчётов, относящиеся к рассматриваемым здесь

конфигурациям, окружающим прямой проводник, также представлены в работах последнего

времени [20-23].

Воспроизведём вкратце схему исследований [21] и полученные результаты. Состояние по-

коя (1), (14) возмущается малыми величинами p₁, H₁ и υ₁, зависящими от времени и всех

трёх пространственных координат. Уравнения магнитной газодинамики линеаризуются отно-

сительно этих величин. Из возникшей при этом системы семи линейных уравнений первого

порядка удаётся исключить p₁ и H₁ и привести её к следующему трёхмерному уравнению

второго порядка для вектора скорости υ₁:

∂²υ₁

= ∇(γp div υ₁ + ∇p · υ₁) + rotrot (υ₁ × H) × H + j × rot(υ₁ × H) ≡ -K[υ₁].

(17)

∂t

Решения линейного однородного уравнения с не зависящими от времени t коэффициента-

ми формируются из экспонент

υ₁(t,r,ϕ,z) = e^iωtυ(r,ϕ,z),

(18)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

874

БРУШЛИНСКИЙ, СТЕПИН

а параметр ω в показателе степени определяется спектральной задачей на собственные зна-

чения

ρω²υ = K[υ].

(19)

Дифференциальный оператор K[υ] с однородными краевыми условиями, например, υ_n =

= 0 на границе области, является самосопряжённым, следовательно, его собственные значения

ω² действительны. Отсюда следует, что решения (18) не возрастают со временем, если ω² > 0,

и экспоненциально возрастают, если ω² < 0, т.е. условием МГД-устойчивости конфигураций

является положительная определённость оператора K. В одномерных задачах его коэффици-

енты, составленные из функций p(r), H(r) и j(r) в состоянии покоя, не зависят также от ϕ

и z, поэтому возмущения (18) зависят от этих переменных также экспоненциально:

υ₁(t,r,ϕ,z) = eiωt+imϕ-ikzυ(r),

(20)

где m - целое, k - действительное, так как решения (20) должны быть периодическими по ϕ

и ограниченными при z → ±∞.

Спектральная задача (19) распадается на бесконечную серию одномерных задач для от-

дельных гармоник возмущений с параметрами m и k:

ρω2m,kυ_m,k = K_m,k[υ_m,k].

(21)

Из векторных уравнений (21) удаётся исключить компоненты υ_ϕ и υ_z и свести поиск

решений к задачам для одного скалярного уравнения относительно функции u = υ_rr:

(

)

+ G_m,ku = 0; u|_Γ = 0,

(22)

F^m,k dr

в котором коэффициенты F_m,k и G_m,k нелинейно зависят от собственного значения ω2m,k

(уравнение Соловьёва) [16]. Численно решая задачу (22), например, методом “стрельбы”, мож-

но найти старшие (минимальные) собственные значения ω2m,k, отвечающие за устойчивость

конфигураций относительно соответствующих гармоник возмущений.

Дальнейшие упрощения связаны с тем, что для качественного исследования устойчиво-

сти нет необходимости в вычислении собственных значений операторов K_m,k - достаточно

установить их положительность. Для этого достаточно лишь найти “границу устойчивости” в

области параметров равновесной конфигурации - условие на параметры, при котором стар-

шее собственное значение обращается в нуль, т.е. условие, при котором краевая задача для

уравнений (21), (22) при ω² = 0 имеет нетривиальное решение.

В частном случае m = 0 (т.е. когда возмущения не зависят от ϕ) уравнение (22) при ω² =

= 0 вырождается, и устойчивость определяется с помощью энергетического принципа [16; 28;

17, с. 75]: квадратичная форма K[υ]υ положительна при всех значениях k, если выполнено

условие

r dp

2γH

(23)

p dr

p+H²

где γ = 5/3 - показатель адиабаты.

Этому условию удовлетворяют все конфигурации на рис. 2 при 1 < r ≤ r₁, т.е. на воз-

растающей ветви p(r), и заведомо не удовлетворяют конфигурации на рис. 2, а, где левая

часть неравенства (23) неограниченно возрастает при r → R, а правая остаётся ограничен-

ной. В связи с этим рассмотрена конфигурация на рис. 2, б, где внешняя граница r = R₁ не

допускает обращения p(r) в нуль. В расчётах получена таблица значений R₁, допускающих

неравенство (23), в зависимости от параметров r₁ и p₀ [21]. Из неё следует, что попытки ото-

двинуть границу r = R от r = r₁ заметно усиливают ограничение на максимум давления p₀.

В остальных случаях m ≥ 1 уравнение (22) при ω² = 0 имеет вид

)

⁽H

^[m²H²

4α²H²

⁽ (2 - η)H² )]

u = 0,

(24)

dr ηr dr

r³

ηr

ηr²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ВОПРОСЫ УСТОЙЧИВОСТИ В ДВУМЕРНЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЯХ

875

где α = k/m, η = 1 + α²r². В численном решении краевой задачи для этого уравнения

показано, что конфигурации на рис. 2, б устойчивы при R < R₁ для гармоник с низкими

значениями волнового числа |k| ≲ 2. При возрастании |k| устойчивость требует более силь-

ных ограничений на p₀ при каждом значении R = R₁ по сравнению с упомянутой выше

таблицей [21].

Приведённые результаты показывают, что причины обнаруженной неустойчивости сосре-

доточены в основном у внешней границы кольцевой окрестности проводника, где плотность

плазмы уменьшается с ростом радиуса. Они же подтверждены анализом конфигурации на

рис. 2, в, где граница проведена непосредственно через область максимального давления. Здесь

все варианты устойчивы в пределах естественного ограничения давления (16) [22]. Отдельное

внимание уделено периферии конфигурации на рис. 2, г. Здесь давление ограничено снизу

p ≥ p₁ > 0, и переход от p(r₂) = p₀ к p(R) = p₁ осуществляется более плавно и разделён

значением r = r₃, где d²p/dr² = 0 и абсолютная величина dp/dr максимальна. Условие

устойчивости (23) при m = 0 выполнено везде, если оно выполнено при r = r₃. При m ≥ 1

в численном решении краевой задачи для уравнения (24) установлено, что неустойчивость

провоцируется скоростью убывания p(r) при r > r₂, т.е. сокращением области r₂ < r <

< R и уменьшением граничного значения p₁ [23]. Это соответствует известной тенденции

неустойчивости Z-пинча [15].

Изложенные результаты представляют интерес в первую очередь тем, что показывают вли-

яние распределения давления p(r) вблизи проводника на устойчивость. Здесь рассмотренная

одномерная модель наиболее оправдана. Результаты, относящиеся к периферии, следует счи-

тать ориентировочными, поскольку территории любых ловушек с двумя и более проводника-

ми, примыкающие к внешней границе, по существу неодномерны и нуждаются в исследованиях

в, как минимум, двумерных моделях.

Таким образом, в рассмотренных математических моделях равновесных магнитоплазмен-

ных конфигураций в окрестности прямого проводника с током исследована зависимость их

диффузионной и МГД-устойчивости от распределения давления плазмы вдоль радиуса ло-

вушки.

3. Двумерные задачи о МГД-устойчивости. Исследование устойчивости равновесных

конфигураций в ловушках, допускающих плоскую симметрию, в частности, в цилиндрическом

аналоге “галатеи-пояса”, ведётся в соответствии с упомянутой выше общей логикой линейной

теории. В основе такого исследования лежит анализ решений начально-краевой задачи для

уравнения

∂²υ₁

= ∇(γpdiv υ₁ + ∇p · υ₁) + rot rot(υ₁ × H) × H + (j - j^ex) × rot(υ₁ × H) ≡ -^K[υ₁] (25)

∂t

с граничным условием υ1n = 0 на внешней границе или, что то же самое, с условием по-

ложительной определённости линейного оператора

^K[υ₁]. Уравнение (25) отличается от (17)

заменой тока j на плазменный ток j^pl = j - j^ex, что позволяет рассматривать задачи в од-

носвязных областях, не исключая из них территории проводников. Коэффициенты уравнения

составлены из функций p(x, y), H(x, y) и j(x, y), т.е. не зависят от переменных t и z, по-

этому его решения зависят от них экспоненциально υ₁(t, x, y, z) = e^iωt-ikzυ(x, y) с действи-

тельными значениями параметра k, чтобы избежать неограниченного роста при z → ±∞.

Задача с уравнением (25) становится спектральной задачей типа (19), которая превращает-

ся в однопараметрическую серию двумерных векторных задач ρω2kυ_k =Kk[υ_k] для фурье-

гармоник возмущений скорости. Здесь оператор

K_k означает соответствующую гармонику

оператора

^K.

Собственные значения ω2k действительны, а вектор-функции υ_k, вообще говоря, комплекс-

ны. Действительные части этих вектор-функций удобно представить в терминах функций

u(x, y) = Re υ_xk, υ(x, y) = Re υ_yk, w(x, y) = Im υ_zk, опустив в дальнейшем индекс k:

ρω²u=L₁[u, υ]+kM₁[w], ρω²υ =L₂[u, υ]+kM₂[w], ρω²w =M₃[w]+kL₃[u, υ]+k²M₄[w], (26)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

876

БРУШЛИНСКИЙ, СТЕПИН

где

∂

∂j

∂

∂j^pl

L₁[u,υ] = -

(γp div υ) + H_yΔξ -

ξ, L₂[u,υ] = -

(γp div υ) - H_xΔξ -

ξ,

∂x

∂y

∂ξ

L₃[u,υ] = γp div υ + H_x

-H_y

+j^plξ,

∂y

∂x

)

∂

⁽∂H_yw

∂H_xw

M₁[w] = -

(γpw) - H_y

-j^plH_yw,

∂x

∂y

)

∂

⁽∂H_yw

∂H_xw

M₂[w] = -

(γpw) + H_x

+j^plH_xw,

∂y

∂x

∂y

M₃[w] = -(H · ∇)div Hw, M₄[w] = (γp + H2x + H2y)w, ξ = H_xυ - H_yu.

Заметим, что упростить уравнения (26) дальше, сведя их, например, к системе двух уравне-

ний для функций u и υ, аналогичной уравнению Соловьёва (22), здесь не удаётся, поскольку

третье из них не позволяет выразить функцию w аналитически через функции u, υ и их

производные. Однако из неё очевидно выделяется система уравнений, если положить в ней

k = 0, которая распадается на систему из двух уравнений

ρω²u = L₁[u, υ], ρω²υ = L₂[u, υ]

(27)

для u и υ и одно уравнение

ρω²w = M₃[w]

(28)

для w.

С ними естественно связать ещё один промежуточный вариант устойчивости - устойчи-

вость относительно двумерных возмущений, не зависящих от координаты z. Этот вариант

устойчивости шире рассмотренной в п. 1 диффузионной устойчивости, которая ограничена

возмущениями только магнитного поля, а здесь учитывается также возможность динамики

выведенной из равновесия плазмы.

Собственные значения задачи (28) всегда положительны, в чём легко убедиться с помощью

интеграла по квадрату |x| < 2,

|y| < 2:

∫∫

ω²

ρw² dx dy =

M₃[w]w dxdy = - Hw · ∇ div (Hw)dxdy =

∫∫

∮

= (div (Hw))² dx dy - H_nw div (Hw) ds,

(29)

в котором граница Γ непрозрачна для магнитного поля (H_n = 0). Отсюда следует, что осевая

компонента возмущений w(x, y), не зависящих от z, не может оказать влияние на неустой-

чивость двумерных конфигураций. Нетривиальным объектом на рассматриваемом двумерном

этапе исследования остаётся краевая задача (27) с граничным условием υ_n = 0:

u(±2, y) = 0, υ(x, ±2) = 0.

Здесь уместно обратить также внимание на квадратичную форму

ρω²(u² + υ²) = L₁[u, υ]u + L₂[u, υ]υ = -υ · ∇(γp div υ) - ξΔξ - ξυ · ∇j^pl

(30)

и её интеграл по упомянутому выше квадрату

∫∫

(L₁u + L₂υ) dx dy =

(γp(div υ)² + (∇ξ)² + j^pl div (ξυ)) dx dy.

(31)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ВОПРОСЫ УСТОЙЧИВОСТИ В ДВУМЕРНЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЯХ

877

Если эта форма неотрицательна на множестве всех собственных функций (u, υ) задачи (27), то

соответствующая равновесная конфигурация устойчива относительно двумерных возмущений.

Более сильное условие состоит в следующем: её неотрицательность при любых функциях (u, υ)

достаточна для устойчивости. Поскольку

∫∫

∮

j^pl div (ξυ) = div (j^plξυ) - ξ(υ · ∇)j^pl и

div (j^plξυ) dx dy = j^plξυ_n ds = 0,

это условие принимает вид

∫∫

ξυ · ∇j^pl ≤

(γp(div υ)² + (∇ξ)²) dx dy.

(32)

Устойчивость относительно двумерных возмущений скорости (u, υ) можно исследовать,

как и в п. 2, с помощью отыскания “границы устойчивости” в области параметров, т.е. усло-

вия, при котором ω² = 0 является собственным значением задачи (27), или, иначе говоря,

условия, при котором система линейных однородных уравнений L₁[u, υ] = 0, L₂[u, υ] = 0

имеет нетривиальное решение. Оно может быть найдено в процессе численного решения этих

уравнений итерационным методом установления:

∂u

∂υ

= -L₁[u,υ] = 0,

= -L₂[u,υ] = 0.

(33)

∂t

Здесь t - итерационный параметр, играющий роль “времени”, а знак минус в правых частях

обеспечивает корректность задачи Коши с уравнениями (33) параболического типа. “Началь-

ными условиями” (нулевой итерацией) могут быть любые функции u(x, y) и υ(x, y).

Равновесные конфигурации плазмы описываются решениями краевой задачи для уравне-

ния Грэда-Шафранова с фиксированными геометрией и параметрами r_c = 0.2, q = 0.2 в

формулах (2), (5). Искомой границей устойчивости является значение максимального давле-

ния p₀ в интервале 0 < p₀ < p^diff0 , допускающем диффузионную устойчивость относительно

двумерных возмущений магнитного поля.

В результате численного решения задачи (33) при небольших значениях параметра p₀ <

< p∗0 ∼ 3 устанавливается нулевая скорость в центральной части квадрата, где давление плаз-

мы заметно отличается от нуля (см. рис. 1). Время установления растёт вместе со значениями

p₀

и естественно зависит от выбора начальных условий. Вне конфигурации, где давление

практически нулевое, скорость может долго сохранять начальное значение, что можно отне-

сти к выбранным начальным условиям. При p₀ → p∗0 в области конфигурации появляются

ненулевые значения скорости, близкой по направлению к магнитному полю H. При этом об-

ращаются в нуль величины ξ, div υ и квадратичная форма (30), что соответствует собствен-

ному значению ω² = 0, т.е. границей устойчивости является значение p₀ = p∗0 < p^diff0 ∼ 5.

При значениях p₀ > p∗0 решения краевой задачи с уравнениями (33) неограниченно возрас-

тают, что соответствует неустойчивости конфигураций относительно двумерных возмущений

равновесия, включающих ненулевые значения скорости. Полученный результат конкретизи-

рует тенденцию, установленную выше при исследовании одномерных моделей конфигураций,

окружающих прямой проводник: устойчивость конфигураций в цилиндрическом аналоге “по-

яса” относительно двумерных возмущений, включая динамические, требует приблизительно

более сильного ограничения на максимальное давление p₀ < p∗0 по сравнению с диффузи-

онной устойчивостью p₀ < p^diff0 относительно возмущений магнитного поля. Таким образом,

справедливо следующее

Утверждение. Для МГД-устойчивости двумерных конфигураций плазмы в ловушке “га-

латея-пояс” произвольные малые двумерные возмущения, включая динамические, требуют

более сильного ограничения на давление плазмы, измеренного в магнитных единицах, по срав-

нению с диффузионной устойчивостью относительно возмущений магнитного поля. Пара-

метры ограничений находятся с помощью численного решения соответствующих задач.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

878

БРУШЛИНСКИЙ, СТЕПИН

Наконец, развитием и завершением изложенных исследований устойчивости в ловушках-

галатеях должно стать их распространение на трёхмерные малые возмущения равновесных

двумерных конфигураций. В основе лежит краевая задача с уравнениями (26) для фурье-

компонент произвольных возмущений с произвольными значениями действительного пара-

метра k. “Граница устойчивости” в области 0 < p0 < pdiff0 соответствует существованию

нетривиального решения уравнений (26) при ω² = 0, которое следует искать численными

методами. С другой стороны, устойчивость конфигураций равносильна положительной опре-

делённости квадратичной формы

F = F₀[u,υ,w] + kF₁[u,υ,w] + k²F₂[w],

(34)

где F₀ = L₁u + L₂υ + M₃w, F₁ = M₁u + M₂w + L₃w, F₂ = M₄w, или её интеграла по сечению

цилиндра. При этом F₀ можно упростить до рассмотренной выше формы (30), (31), поскольку

её последнее слагаемое положительно (см. (29)). Квадратный полином (34) с положительными

коэффициентами F₀ (что требуется для двумерной устойчивости) и F₂, очевидно, положи-

телен при любых значениях k ∈ R, если он не имеет действительных нулей, т.е. его дискри-

минант отрицателен. Отсюда следует условие, ограничивающее абсолютную величину формы

F₁ или её интеграла,

F²¹ ≤ 4F₀F₂.

(35)

В трёхмерных задачах оно играет ту же роль, что и неравенство (32) в двумерных.

Таким образом, МГД-устойчивость обсуждаемых конфигураций относительно произволь-

ных малых трёхмерных возмущений имеет место при выполнении условия, которое можно

сформулировать любым из двух эквивалентных между собой способов: 1) отсутствие нетриви-

альных решений краевой задачи с уравнениями (26) при ω² = 0; 2) выполнение неравенства

(35) для достаточно представительного набора функций (u, υ, w). Его проверка потребует

большого объёма вычислений.

Заключение. В статье представлена математическая модель равновесных магнитоплаз-

менных конфигураций в цилиндре с погружёнными в плазму двумя прямыми проводниками с

током - распрямлённом аналоге тороидальной магнитной ловушки “галатея-пояс”. Эта модель

основана на численном решении двумерных краевых задач для полулинейного дифферен-

циального уравнения Грэда-Шафранова эллиптического типа. Приведены примеры расчёта

геометрии конфигураций и их параметров, а также их зависимости от условий задачи. Прове-

дено достаточно полное исследование устойчивости конфигураций: одномерных - в окрестно-

сти одного отдельного проводника и двумерных - сначала относительно двумерных возмуще-

ний магнитного поля (диффузионная устойчивость), а затем МГД-устойчивости относительно

двумерных возмущений всех переменных, включая скорость. На всех этапах получены ограни-

чения на безразмерную величину давления плазмы, требуемые для устойчивости, и иерархия

этих ограничений. Указаны пути исследования устойчивости двумерных равновесных конфи-

гураций относительно произвольных трёхмерных возмущений.

Работа выполнена при поддержке Московского центра фундаментальной и прикладной ма-

тематики (соглашение с Министерством науки и высшего образования Российской Федерации

№ 075-15-2019-1623).

СПИСОК ЛИТЕРАТУРЫ

1. Морозов А.И. О галатеях - плазменных ловушках с омываемыми плазмой проводниками // Физика

плазмы. 1992. Т. 18. Вып. 3. С. 305-316.

2. Морозов А.И., Пустовитов В.Д. О стеллараторе с левитирующими обмотками // Физика плазмы.

1991. Т. 17. Вып. 10. С. 1276.

3. Морозов А.И., Франк А.Г. Тороидальная магнитная ловушка-галатея с азимутальным током // Фи-

зика плазмы. 1994. Т. 20. № 11. С. 982-989.

4. Морозов А.И., Бугрова А.И., Бишаев А.М., Липатов А.С., Козинцева М.В. Параметры плазмы

в модернизированной ловушке-галатее “Тримикс-М” // Журн. техн. физики. 2007. Т. 77. № 12.

С. 15-20.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ВОПРОСЫ УСТОЙЧИВОСТИ В ДВУМЕРНЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЯХ

879

5. Брушлинский К.В., Зуева Н.М., Михайлова М.С., Морозов А.И., Пустовитов В.Д., Тузо-

ва Н.Б. Численное моделирование прямых винтовых шнуров с проводниками, погруженными в

плазму // Физика плазмы. 1994. Т. 20. № 3. С. 284-292.

6. Брушлинский К.В., Игнатов П.А. Плазмостатическая модель магнитной ловушки “галатея-пояс”

// Журн. вычислит. математики и мат. физики. 2010. Т. 50. № 12. С. 2184-2194.

7. Брушлинский К.В., Кондратьев И.А. Сравнительный анализ расчётов равновесия плазмы в торои-

дальных и цилиндрических магнитных ловушках // Мат. моделирование. 2018. Т. 30. № 6. С. 76-94.

8. Tao B., Jin X., Li Z., Tong W. Equilibrium configuration reconstruction of multipole galatea magnetic

trap based on magnetic measurement // IEEE Trans. on Plasma Sci. 2019. V. 47. № 7. P. 3114-3123.

9. Морозов А.И., Савельев В.В. О галатеях - ловушках с погруженными в плазму проводниками

// Успехи физ. наук. 1998. Т. 168. № 11. С. 1153-1194.

10. Брушлинский К.В. Математические и вычислительные задачи магнитной газодинамики. М., 2009.

11. Брушлинский К.В. Математические основы вычислительной механики жидкости, газа и плазмы.

М., 2017.

12. Шафранов В.Д. О равновесных магнитогидродинамических конфигурациях // Журн. эксп. и теор.

физики. 1957. Т. 33. Вып. 3 (9). С. 710-722.

13. Grad H., Rubin H. Hydrodynamic equilibria and force-free fields // Proc. 2nd United Nations Int. Conf.

on the Peaceful Uses of Atomic Energy. Geneva, 1958. V. 31. P. 190-197.

14. Шафранов В.Д. Равновесие плазмы в магнитном поле // Вопросы теории плазмы / Под ред. М.А.

Леонтовича. М., 1963. Вып. 2. С. 92-131.

15. Кадомцев Б.Б. Гидромагнитная устойчивость плазмы // Вопросы теории плазмы / Под ред. М.А.

Леонтовича. М., 1963. Вып. 2. С. 132-176.

16. Соловьев Л.С. Гидромагнитная устойчивость замкнутых плазменных конфигураций // Вопросы

теории плазмы / Под ред. М.А. Леонтовича. М., 1972. Вып. 6. С. 210-290.

17. Бейтман Г. МГД-неустойчивости. М., 1982.

18. Медведев С.Ю., Мартынов А.А., Дроздов В.В., Иванов А.А., Пошехонов Ю.Ю., Коновалов С.В.,

Виллард Л. МГД-устойчивость и энергетический принцип без предположения о вложенности маг-

нитных поверхностей двумерных равновесий // Физика плазмы. 2019. Т. 45. № 2. С. 120-132.

19. Брушлинский К.В. Два подхода к задаче об устойчивости равновесия плазмы в цилиндре // Прикл.

математика и механика. 2001. Т. 65. Вып. 2. С. 235-243.

20. Брушлинский К.В., Кривцов С.А., Степин Е.В. Об устойчивости равновесия плазмы в окрестности

прямого проводника с током // Журн. вычислит. математики и мат. физики. 2020. Т. 60. № 4.

С. 153-163.

21. Брушлинский К.В., Степин Е.В. Математические модели равновесных конфигураций плазмы,

окружающей проводники с током // Дифференц. уравнения. 2020. Т. 56. № 7. С. 901-909.

22. Brushlinskii K.V., Stepin E.V. Mathematical model and stability investigation of plasma equilibrium

around a current-carrying conductor // J. Phys.: Conf. Ser. 2020. V. 1686. P. 012030.

23. Brushlinskii K.V., Stepin E.V. Plasma equilibrium and stability in a current-carrying conductor vicinity

// J. Phys.: Conf. Ser. 2020. V. 1640. P. 012018.

24. Peaceman D.W., Rachford H.H. The numerical solution of parabolic and elliptic differential equations

// J. Soc. Industr. Appl. Math. 1955. V. 3. № 1. P. 28-42.

25. Douglas J. On the numerical integration of ∂²u/∂x² + ∂²u/∂y² = ∂u/∂t by implicit method // J. Soc.

Industr. Appl. Math. 1955. V. 3. № 1. P. 42-65.

26. Арсенин В.Я. Методы математической физики и специальные функции. М., 1984.

27. Веденов А.А., Велихов Е.П., Сагдеев Р.З. Устойчивость плазмы // Успехи физ. наук. 1961. Т. 73.

Вып. 4. С. 701-766.

28. Bernstein I.B., Frieman E.A., Kruskal M.D., Kulsrud R.M. Energy principle for the hydromagnetic

stability problem // Proc. Roy. Soc. 1958. V. 244. P. 17-50. (Перевод: Бернштейн А.Б. и др. Энерге-

тический принцип для проблемы гидродинамической устойчивости // Управляемые термоядерные

реакции (сб. перев. материалов). М., 1960. Вып. 26. С. 226-260).

Институт прикладной математики

Поступила в редакцию 01.03.2021 г.

им. М.В. Келдыша РАН, г. Москва,

После доработки 01.03.2021 г.

Национальный исследовательский

Принята к публикации 27.04.2021 г.

ядерный университет “МИФИ”, г. Москва,

Московский государственный университет

им. М.В. Ломоносова

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021