ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 7, с.900-906
ЧИСЛЕННЫЕ МЕТОДЫ
УДК 519.642+517.956.3
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
НЕЛИНЕЙНОГО ОПЕРАТОРНОГО УРАВНЕНИЯ,
ВОЗНИКАЮЩЕГО В ОБРАТНОЙ
КОЭФФИЦИЕНТНОЙ ЗАДАЧЕ
© 2021 г. С. В. Гаврилов, А. М. Денисов
Рассматривается обратная задача для линейной системы уравнений в частных производ-
ных. Обратная задача состоит в определении двух неизвестных коэффициентов системы по
дополнительной информации об одной из компонент решения. Обратная задача сводится
к нелинейному операторному уравнению для одного из неизвестных коэффициентов. Для
численного решения этого операторного уравнения применяются метод последовательных
приближений и метод Ньютона. Приводятся результаты расчётов, иллюстрирующие схо-
димость численных методов решения обратной задачи.
DOI: 10.31857/S0374064121070049
1. Введение. Рассмотрим задачу определения функций u(x, t) и a(x, t) таких, что
ux + at = 0,
0≤x≤l,
0≤t≤T,
(1.1)
at = γ(t)(ϕ(t)u - a),
0≤x≤l,
0≤t≤T,
(1.2)
u(0, t) = μ(t),
0≤t≤T,
(1.3)
a(x, 0) = ψ(x),
0≤x≤l.
(1.4)
Эта задача представляет собой математическую модель процесса динамики сорбции [1, с. 174;
2, с. 6] в предположении, что свойства поглощающего вещества меняются со временем.
В работе [3] изучены вопросы существования и единственности решения следующей обрат-
ной задачи.
Пусть функции μ(t) и ψ(x) заданы, а функции γ(t) и ϕ(t) неизвестны. Требуется опре-
делить γ(t), ϕ(t), u(x, t) и a(x, t), если задана следующая дополнительная информация об
одной из компонент решения задачи (1.1)-(1.4):
u(l, t) = g(t),
0≤t≤T,
(1.5)
ux(l,t) = p(t),
0≤t≤T.
(1.6)
Будем предполагать, что для известных функций μ(t), ψ(x), g(t) и p(t) выполняются
Условия A. Функции μ(t), ψ(x), g(t) и p(t) таковы, что: μ, g, p ∈ C[0, T ]; ψ ∈ C[0, l];
μ(t) > 0, g(t) > 0, p(t) < 0 для 0 ≤ t ≤ T ; ψ(x) ≥ 0 для 0 ≤ x ≤ l, ψ(l) = 0, ψ(x) не равна
нулю тождественно.
Дадим определение решения обратной задачи. Пусть t0 ∈ (0, T ]. Введём прямоугольник
Qt0 = {(x,t) : 0 ≤ x ≤ l, 0 ≤ t ≤ t0}.
Определение. Четвёрка функций (γ(t), ϕ(t), u(x,t), a(x,t)) называется решением об-
ратной задачи при t ∈ [0, t0], если γ, ϕ ∈ C[0, t0], u, ux, a, at ∈ C(Qt0 ), γ(t) > 0, ϕ(t) > 0 для
0 ≤ t ≤ t0, u(x,t) > 0, a(x,t) ≥ 0 для (x,t) ∈ Qt0, γ(t), ϕ(t), u(x,t), a(x,t) удовлетворяют
уравнениям (1.1), (1.2) и условиям (1.3)-(1.6) в Qt0 .
Приведём некоторые результаты работы [3], которые будут использованы в дальнейшем.
900
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНОГО ОПЕРАТОРНОГО УРАВНЕНИЯ 901
Для функции u(x, t) при заданной функции γ(t) рассмотрим интегральное уравнение
{ ∫ t
}∫x
u(x, t) = μ(t) exp{-R(t; γ)x} + γ(t) exp
- γ(θ)dθ
exp{-R(t; γ)(x - s)}ψ(s) ds +
0
0
∫x
∫
t
{
∫
t
}
+ γ(t)
exp
- R(t;γ)(x - s) - γ(θ)dθ R(τ;γ)u(s,τ)dτ ds, (x,t) ∈ Qt0 ,
(1.7)
0
0
τ
где
[
∫
t
]
R(t; γ) = - p(t) + γ(t) p(τ) dτ (g(t))-1.
0
При выполнении условий А решение интегрального уравнения (1.7) существует и единственно.
Чтобы подчеркнуть зависимость этого решения от функции γ(t), будем обозначать его через
u(x, t; γ).
Определим оператор
[
∫
l
∫
t
]
(Aγ)(t) = g(t) - μ(t) exp{-R(t; γ)l} - γ(t)
H(l, s, t, τ; γ)R(τ; γ)u(s, τ; γ) dτ ds
×
0
0
(∫l
)-1
× H(l,s,t,0;γ)ψ(s)ds
,
0≤t≤t0,
(1.8)
0
где
{
∫
t
}
H(x, s, t, τ; γ) = exp
- R(t;γ)(x - s) - γ(θ)dθ
τ
В работе [3] показано, что решение обратной задачи сводится к решению нелинейного
операторного уравнения
γ(t) = (Aγ)(t),
0≤t≤t0.
(1.9)
Данная статья посвящена численным методам решения уравнения (1.9) и сформулирован-
ной обратной задачи. Для решения нелинейного операторного уравнения (1.9) используются
два итерационных метода: метод последовательных приближений и метод Ньютона. Итера-
ционным методам решения операторных уравнений, к которым сводятся обратные задачи,
посвящено достаточно много работ (см., например, [4-11]). Большое их число обусловлено
особенностями и спецификой каждой конкретной обратной задачи.
Рассмотрим метод последовательных приближений для решения операторного уравне-
ния (1.9).
Предположим, что выполнено неравенство
g(0) - μ(0) exp{(p(0)/g(0))l} > 0.
(1.10)
Определим положительную постоянную
(∫l
)-1
γ0 = (g(0) - μ(0)exp{(p(0)/g(0))l})
exp{(p(0)/g(0))(l - s)}ψ(s) ds
0
Введём множество функций
Γ0 = {γ(t) : γ ∈ C[0,t0], γ0/2 ≤ γ(t) ≤ 3γ0/2,
0 ≤ t ≤ t0}.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№7
2021
902
ГАВРИЛОВ, ДЕНИСОВ
Рассмотрим последовательность функций γn(t), n = 0, 1, 2, . . . , определяемую рекуррент-
но посредством метода последовательных приближений для решения уравнения (1.9):
γ0(t) ∈ Γ0, γn+1(t) = (Aγn)(t), n = 0,1,2,...
(1.11)
Из результатов работы [3] следует утверждение о сходимости метода последовательных при-
ближений.
Теорема 1. Пусть для функций μ(t), ψ(x), g(t) и p(t) выполнены условия А и нера-
венство (1.10). Тогда найдётся t0 ∈ (0, T ] такое, что для любой функции γ0(t) ∈ Γ0 по-
следовательность функций γn(t) принадлежит множеству Γ0 и при n → ∞ равномерно
сходится к непрерывной функции γ(t), являющейся решением уравнения (1.9).
2. Метод Ньютона. Рассмотрим вопрос о применении метода Ньютона для численного
решения исследуемой обратной задачи. Как уже отмечалось, для этого достаточно применить
метод Ньютона для решения нелинейного операторного уравнения (1.9).
Для построения метода Ньютона нужно знать производную оператора, определяемого фор-
мулой (1.8). Вначале рассмотрим вопрос о дифференцируемости по параметру решения инте-
грального уравнения (1.7).
Пусть функции γ(t), γΔ(t) и число ξ таковы, что функции γ(t) и γ(t) + ξγΔ(t) положи-
тельны и непрерывны на отрезке [0, t0] для всех ξ ∈ (-ε, ε).
Лемма. Если выполнены условия А, то у решения u(x, t; γ + ξγΔ) уравнения (1.7) суще-
∂u
ствует частная производная
(x, t; γ + ξγΔ)
∂ξ
ξ=0
Доказательство. Рассмотрим функцию
u(x, t; γ + ξγΔ) - u(x, t; γ)
v(x, t; γ, γΔ, ξ) =
ξ
Так как функции u(x, t; γ + ξγΔ) и u(x, t; γ) являются решением уравнения (1.7) для γ(t) +
+ ξγΔ(t) и γ(t) соответственно, то v(x,t;γ,γΔ,ξ) удовлетворяет уравнению
F1(x,t;γ,γΔ,ξ) - F1(x,t;γ,0,0)
v(x, t; γ, γΔ, ξ) =
+
ξ
∫x
∫
t
F2(x,t,s,τ;γ,γΔ,ξ) - F2(x,t,s,τ;γ,0,0)
+
u(s, τ; γ + ξγΔ) dτ ds +
ξ
0
0
∫x
∫
t
+
F2(x,t,s,τ;γ,0,0)v(s,τ;γ,γΔ,ξ)dτ ds, (x,t) ∈ Qt0 , (x,t) ∈ Qt0 ,
(2.1)
0
0
где
∫x
F1(x,t;γ,γΔ,ξ) = μ(t)exp{-R(t;γ + ξγΔ)x} + (γ(t) + ξγΔ(t)) H(x,s,t,0;γ + ξγΔ)ψ(s)ds,
0
а F2(x,t,s,τ;γ,γΔ,ξ) = (γ(t) + ξγΔ(t))H(x,s,t,τ;γ + ξγΔ)R(τ;γ + ξγΔ). Переходя к пределу
при ξ → 0, получаем, что
lim[F1(x, t; γ, γΔ, ξ) - F1(x, t; γ, 0, 0)]/ξ = F3(x, t; γ, γΔ),
(2.2)
ξ→0
lim
[F2(x, t, s, τ; γ, γΔ, ξ) - F2(x, t, s, τ; γ, 0, 0)]/ξ = F4(x, t, s, τ; γ, γΔ),
(2.3)
ξ→0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№7
2021
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНОГО ОПЕРАТОРНОГО УРАВНЕНИЯ 903
где
∫
t
∫
x
1
F3(x,t;γ,γΔ) = μ(t)exp{-R(t;γ)x}
p(θ) dθxγΔ(t) + γΔ(t) H(x, s, t, 0; γ)ψ(s) ds +
g(t)
0
0
∫x
(
∫
t
∫
t
)
1
+ γ(t) H(x,s,t,0;γ)
p(θ) dθ(x - s)γΔ(t) - γΔ(θ) dθ ψ(s) ds,
g(t)
0
0
0
а
F4(x,t,s,τ;γ,γΔ) = γΔ(t)H(x,s,t,τ;γ)R(τ;γ) +
(
∫
t
∫
t
)
1
+ γ(t)H(x,s,t,τ;γ)
p(θ) dθ(x - s)γΔ(t) - γΔ(θ) dθ R(τ; γ) -
g(t)
0
τ
τ
∫
1
- γ(t)H(x,s,t,τ;γ)
p(θ) dθγΔ(τ).
g(τ)
0
Уравнение (2.1) представляет собой интегральное уравнение Вольтерры второго рода для
функции v(x, t; γ, γΔ, ξ). Разрешив его относительно v(x, t; γ, γΔ, ξ), перейдя к пределу при
ξ → 0 и использовав формулы (2.2), (2.3), получим, что производная ∂u(x,t;γ + ξγΔ)/∂ξ су-
ществует при ξ = 0. Обозначим её w(x, t; γ, γΔ). Из уравнения (2.1) следует, что w(x, t; γ, γΔ)
является решением интегрального уравнения
∫x
∫t
w(x, t; γ, γΔ) = F3(x, t; γ, γΔ) +
F4(x,t,s,τ;γ,γΔ)u(s,τ;γ)dτ ds +
0
0
∫x
∫t
+
F2(x,t,s,τ;γ,0,0)w(s,τ;γ,γΔ)dτ ds, (x,t) ∈ Qt0 .
(2.4)
0
0
Лемма доказана.
Рассмотрим вопрос о дифференцируемости по Гато оператора A, определяемого равен-
ством (1.8). Из результатов [3] следует, что существует такое t0 ∈ (0, T ], что оператор A
отображает множество Γ0 в себя. Далее будем предполагать что число t0 удовлетворяет это-
му условию.
Введём множество
Γ00 = {γ(t) : γ ∈ C[0,t0], γ0/2 < γ(t) < 3γ0/2,
0 ≤ t ≤ t0}.
Теорема 2. Если выполнены условия А и неравенство (1.10), то для любой функции γ ∈
∈ Γ00 оператор A дифференцируем по Гато в Γ00.
Доказательство. Пусть γ(t) - произвольная функция из Γ00, а функция γΔ(t) и число
ξ таковы, что функция γ(t) + ξγΔ(t) также принадлежит множеству Γ00. Покажем, что при
ξ → 0 функции ((A(γ + ξγΔ))(t) - (Aγ)(t))/ξ равномерно сходятся на отрезке [0,t0].
Рассмотрим функции
[(∫ l
(∫l
)-1
)-1]
1
H(l, s, t, 0; γ + ξγΔ)ψ(s) ds
- H(l,s,t,0;γ)ψ(s)ds
ξ
0
0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№7
2021
904
ГАВРИЛОВ, ДЕНИСОВ
При ξ → 0 они равномерно на отрезке [0, t0] сходятся к функции
(∫l
)-2
F5(t;γ,γΔ) = -
H(l, s, t, 0; γ)ψ(s) ds
×
0
∫l
[
∫
t
∫
t
]
1
× H(l,s,t,0;γ)
p(θ) dθ(l - s)γΔ(t) - γΔ(θ) dθ ψ(s) ds.
(2.5)
g(t)
0
0
0
Из леммы следует, что при ξ → 0 функции
∫l
∫
t
u(s, τ; γ + ξγΔ) - u(s, τ; γ)
γ(t)
H(l, s, t, τ; γ)R(τ; γ)
dτ ds
ξ
0
0
равномерно на отрезке [0, t0] сходятся к функции
∫l
∫
t
γ(t)
H(l, s, t, τ; γ)R(τ; γ)w(s, τ; γ, γΔ ) dτ ds.
(2.6)
0
0
Из формул (2.3), (2.5) и (2.6) вытекает, что
(∫l
)-1
(A(γ + ξγΔ))(t) - (Aγ)(t)
lim
= H(l,s,t,0;γ)ψ(s)ds
×
ξ→0
ξ
0
t
l
t
[
∫
∫
∫
]
μ(t)
×
-
p(θ) dθ exp{-R(t; γ)l}lγΔ(t) -
F4(l,t,s,τ;γ,γΔ)u(s,τ;γ)dτ ds
-
g(t)
0
0
0
(
∫
l
∫
t
)(∫ l
)-1
− γ(t)
H(l, s, t, τ; γ)R(τ; γ)w(s, τ; γ, γΔ ) dτ ds
H(l, s, t, 0; γ)ψ(s) ds
+
0
0
0
[
∫
l
∫
t
]
+ g(t) - μ(t)exp{-R(t;γ)l} - γ(t)
H(l, s, t, τ; γ)R(τ; γ)u(s, τ; γ) dτ ds F5(t; γ, γΔ),
(2.7)
0
0
где функция w(x, t; γ, γΔ) определяется из уравнения (2.4). Таким образом, оператор A диф-
ференцируем по Гато на множестве Γ00 и его производная A′[γ]γΔ определяется правой ча-
стью равенства (2.7). Теорема доказана.
Итерационный процесс, соответствующий методу Ньютона [12, с. 669], определяется следу-
ющим образом. Задаётся функция γ0(t). Последующие функции γn+1(t), n = 0, 1, . . . , опре-
деляются по формуле γn+1(t) = γn(t)+ γΔn(t), где γΔn(t) - решение линейного интегрального
уравнения
γΔn - A′[γn]γΔn = -γn + Aγn.
(2.8)
3. Вычислительные эксперименты. Приведём результаты некоторых вычислительных
экспериментов, в которых для решения исследуемой обратной задачи использовались метод
последовательных приближений (1.11) и метод Ньютона (2.8).
Общая схема вычислительных экспериментов была следующей. На отрезке [0, T ] задава-
лись функции μ(t), γ(t) и ϕ(t), а на отрезке [0, l] - функция ψ(x). С этими функциями
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№7
2021
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНОГО ОПЕРАТОРНОГО УРАВНЕНИЯ 905
решалась задача (1.1)-(1.4) и определялись функции g(t) = u(l, t) и p(t) = ux(l, t). Затем с
функциями μ(t), g(t), p(t) и ψ(x) итерационными методами (1.11) и (2.8) решалось опера-
торное уравнение (1.9) и находилась приближённая функция γ(t). Для определения прибли-
жённой функции
ϕ(t) использовалась полученная в [3] формула
[
∫
t
]
ϕ(t) = - p(t) + γ(t) p(τ) dτ (g(t)γ(t))-1.
(3.1)
0
При приближённом решении операторного уравнения (1.9) для обоих итерационных мето-
дов использовалось одинаковое начальное приближение γ0(t) = γ0 и один и тот же критерий
останова
∥γn+1(t) - γn(t)∥C[0,T](∥γn(t)∥C[0,T])-1 ≤ δ.
В первом вычислительном эксперименте T = 0.5, l = 1 и
μ(t) = 1 + t, ψ(x) = 2 - 2x, γ(t) = 3 + sin(2πt), ϕ(t) = 0.5 + 0.1 cos(2πt).
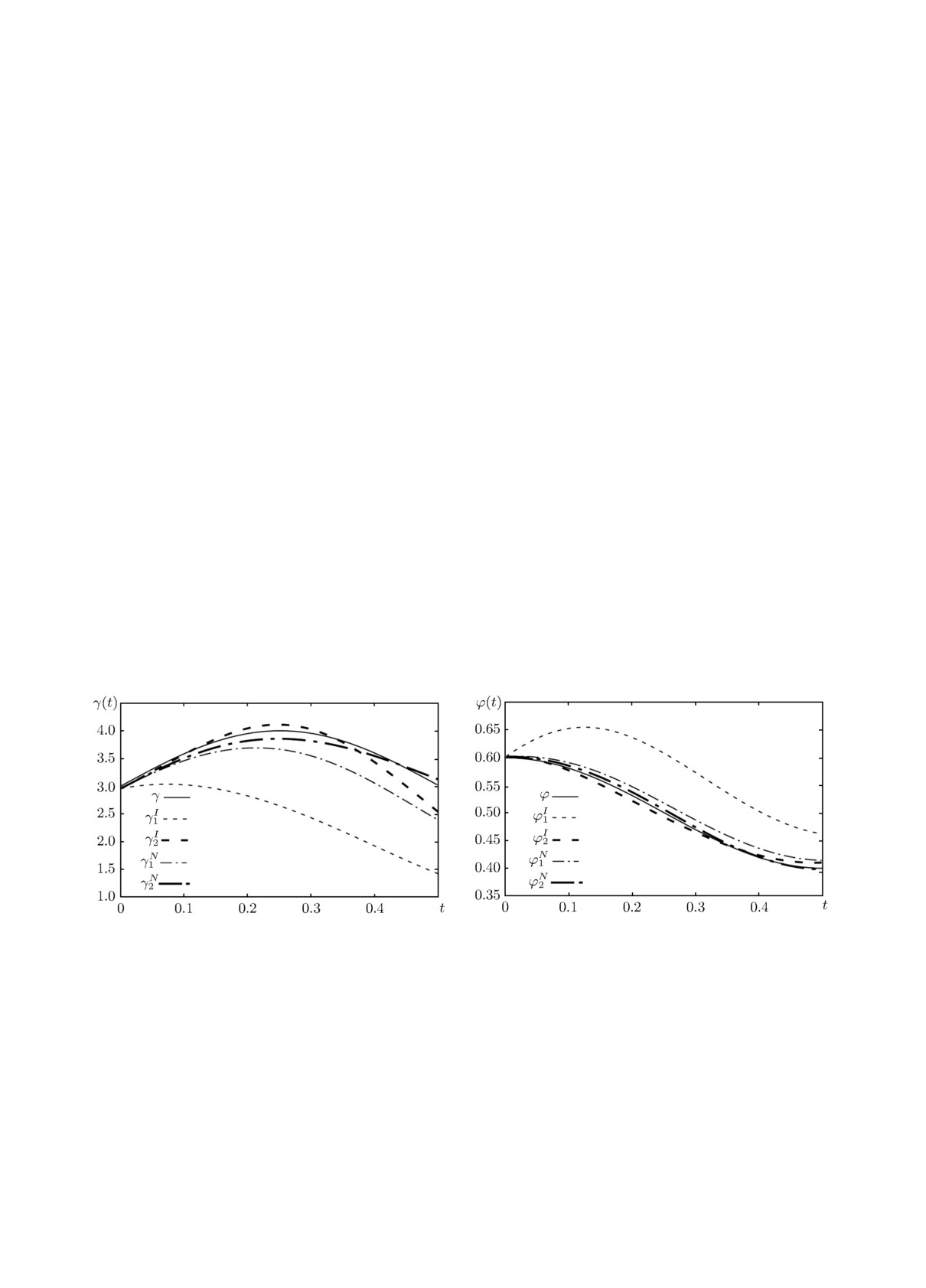
На рис. 1 приведены функция γ(t) = 3 + sin(2πt), первая γI1 (t) и вторая γI2 (t) итерации
метода последовательных приближений, а также первая γN1 (t) и вторая γN2 (t) итерации ме-
тода Ньютона. При величине δ = 0.001 метод последовательных приближений остановился
на 9-м шаге итераций, а метод Ньютона - на 6-м шаге итераций. Полученные при этом при-
ближённые решения γI (t) = γI9 (t) и
γN(t) = γN6(t), в рамках масштаба рис. 1, визуально
совпадают с точным решением γ(t) = 3 + sin(2πt) и поэтому не показаны.
На рис. 2 изображены функция ϕ(t) = 0.5 + 0.1 cos(2πt) и функции ϕI1(t), ϕI2(t), ϕN1 (t),
ϕN2 (t), полученные при подстановке функций γI1 (t), γI2 (t), γN1 (t), γN2 (t) в формулу (3.1) со-
ответственно. Найденные аналогично приближённые решения
ϕI (t) = ϕI9(t) и
ϕN (t) = ϕN6 (t)
визуально совпадают с точным решением ϕ(t) = 0.5 + 0.1 cos(2πt) и поэтому не показаны.
Рис. 1. Результаты первого вычислительного экспе-
Рис. 2. Результаты первого вычислительного экспе-
римента: точная функция γ(t) и функции, опреде-
римента: точная функция ϕ(t) и функции, опреде-
лённые на первых двух итерациях.
лённые на первых двух итерациях.
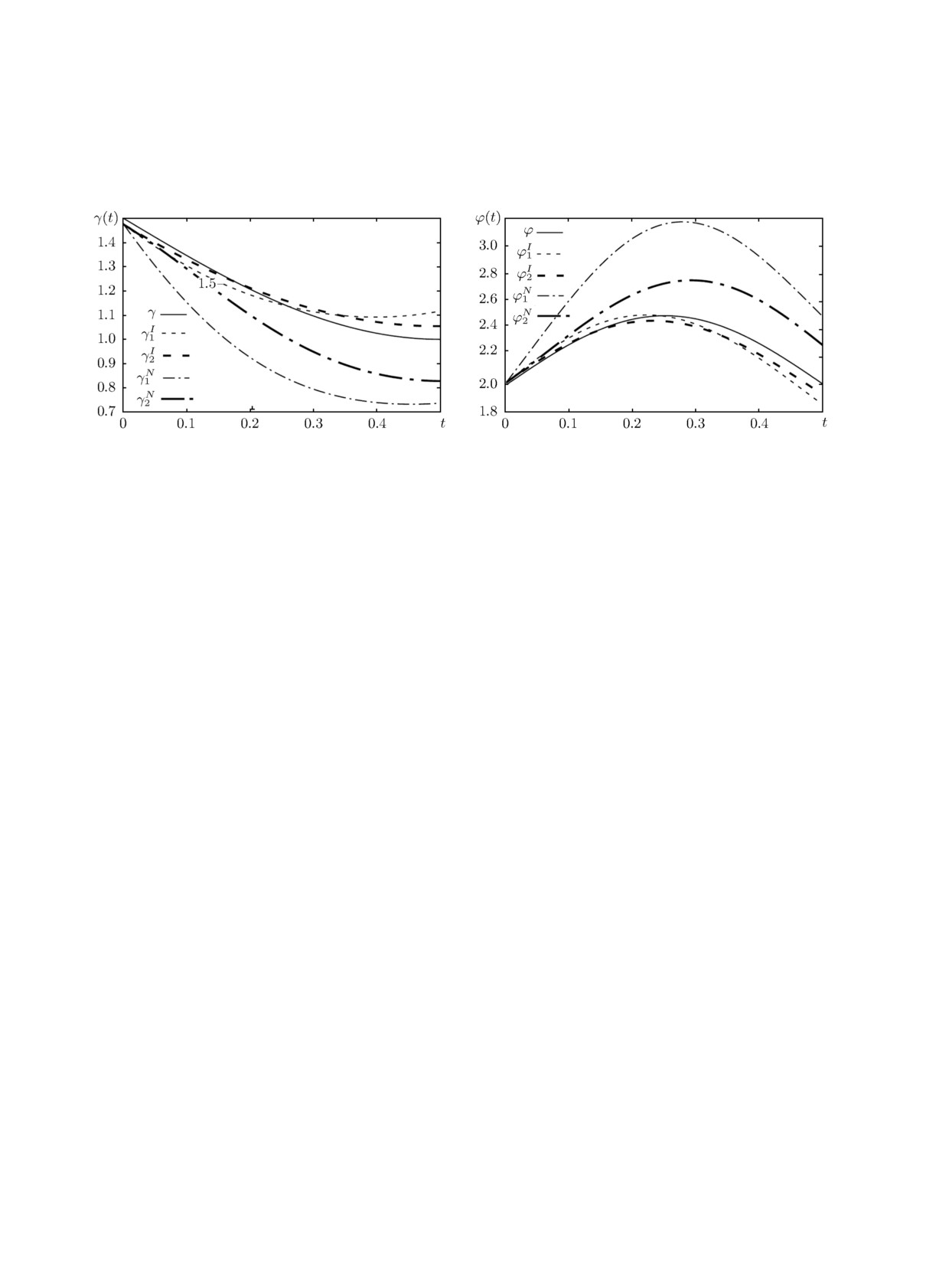
В втором вычислительном эксперименте T = 0.5, l = 1 и
μ(t) = 1 + t, ψ(x) = 2 - 2x, γ(t) = 1.5 - 0.5 sin(πt), ϕ(t) = 2 + 0.5 sin(2πt).
Величина δ выбиралась равной 0.001. Аналогично рис. 1 на рис. 3 показаны значения точной
функции γ(t), а также функции, полученные на первых двух итерациях для обоих методов.
Критерий сходимости был удовлетворён на 7-м шаге метода последовательных приближений и
на 9-м шаге метода Ньютона. В рамках масштаба рис. 3 приближённые решения, найденные на
заключительной итерации обоих методов γI (t) = γI7 (t) и γN (t) = γN9 (t), визуально совпадают
с точным решением.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№7
2021
906
ГАВРИЛОВ, ДЕНИСОВ
На рис. 4 изображена функция ϕ(t) = 2 + 0.5 sin(2πt), а также соответствующие первым
двум итерациям функции ϕI1(t), ϕI2(t), ϕN1 (t), ϕN2 (t). Функции
ϕI (t) = ϕI7(t) и
ϕN (t) =
= ϕN9 (t), найденные по формуле (3.1), совпадают на рисунке с ϕ(t) = 2 + 0.5sin(2πt).
Рис. 3. Результаты второго вычислительного экспе-
Рис. 4. Результаты второго вычислительного экспе-
римента: точная функция γ(t) и функции, опреде-
римента: точная функция ϕ(t) и функции, опреде-
лённые на первых двух итерациях.
лённые на первых двух итерациях.
Приведённые примеры, а также ряд других численных расчётов позволяют сделать вывод
о достаточно быстрой сходимости обоих методов и об отсутствии существенных преимуществ
в скорости сходимости одного из методов в сравнении с другим.
Работа выполнена при финансовой поддержке Минобрауки РФ в рамках реализации про-
граммы Московского центра фундаментальной и прикладной математики по соглашению
№ 075-15-2019-1621.
СПИСОК ЛИТЕРАТУРЫ
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1999.
2. Денисов А.М., Лукшин А.В. Математические модели неравновесной динамики сорбции. М., 1989.
3. Денисов А.М. Существование и единственность решения системы нелинейных интегральных урав-
нений // Дифференц. уравнения. 2020. Т. 56. № 9. С. 1174-1181.
4. Бимуратов С.Ш., Кабанихин С.И. Решение одномерной обратной задачи электродинамики мето-
дом Ньютона-Канторовича // Журн. вычислит. математики и мат. физики. 1992. Т. 32. № 12.
С. 1900-1915.
5. Monch L. A Newton method for solving inverse scattering problem for a sound-hard obstacle // Inverse
problems. 1996. V. 12. № 3. P. 309-324.
6. Kabanikhin S.I., Scherzer O., Shichlenin M.A. Iteration method for solving a two-dimensional inverse
problem for hyperbolic equation // J. of Inverse and Ill-Posed Problems. 2003. V. 11. № 1. P. 1-23.
7. Самарский А.А., Вабищевич П.Н. Численные методы решения обратных задач математической
физики. М., 2004.
8. Yan-Bo Ma. Newton method for estimation of the Robin coefficient // J. Nonlin. Sci. Appl. 2015. V. 8.
№ 5. P. 660-669.
9. Денисов А.М. Итерационный метод решения обратной коэффициентной задачи для гиперболиче-
ского уравнения // Дифференц. уравнения. 2017. Т. 53. № 7. С. 943-949.
10. Баев А.В., Гаврилов С.В. Итерационный метод решения обратной задачи рассеяния для систе-
мы уравнений акустики в слоисто-неоднородной среде с поглощением // Вестн. Моск. гос. ун-та.
Сер. 15. Вычислит. математика и кибернетика. 2018. № 2. С. 7-14.
11. Денисов А.М. Итерационный метод решения обратной задачи для гиперболического уравнения с
малым параметром при старшей производной // Дифференц. уравнения. 2019. Т. 55. № 7. С. 973-
981.
12. Канторович Л.В., Акилов Г.П. Функциональный анализ. М., 1977.
Московский государственный университет
Поступила в редакцию 03.02.2021 г.
им. М.В. Ломоносова
После доработки 03.02.2021 г.
Принята к публикации 27.04.2021 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№7
2021