ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 7, с.907-921

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.633+517.962.2+517.958

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ

РАЗНОСТНЫХ МЕТОДОВ РЕШЕНИЯ ЗАДАЧИ СТЕФАНА

НА ПОДВИЖНЫХ И ФИКСИРОВАННЫХ СЕТКАХ

Для двумерной задачи Стефана представлены разностные схемы, полученные методами с

явным выделением границы фазового перехода. Показано, что разностная схема, построен-

ная на подвижной сетке, и разностная схема, построенная методом выпрямления фронта,

эквивалентны.

DOI: 10.31857/S0374064121070050

Введение. Работа посвящена построению разностных схем для численного решения клас-

сической задачи Стефана. Задача состоит в определении поля температуры и положения гра-

ницы раздела фаз в области, содержащей два агрегатных состояния чистого вещества. На

движущейся границе раздела фаз задаётся фиксированная температура фазового перехода

и условие баланса внутренней энергии. В работе рассматриваются методы решения задачи

Стефана, основанные на процедуре явного выделения границы фазового перехода. При таком

подходе положение границы раздела фаз определяется положением закреплённых на ней уз-

лов сетки. Это обеспечивается за счёт либо использования подвижных сеток, согласованных в

исходном пространстве с формой границы фазового перехода [1-8], либо с помощью динами-

ческой замены переменных [9-17]; замена переменных выбирается так, чтобы в новых коор-

динатах расчётная область была регулярной, с фиксированными границами, совпадающими с

координатными линиями - метод выпрямления фронта [18]. В первом случае осуществляется

аппроксимация исходных дифференциальных уравнений, во втором - уравнений, полученных

в результате замены переменных. На уровне постановки дифференциальной задачи оба эти

подхода эквивалентны. В работе [19] для одномерной термодиффузионной задачи Стефана

построено семейство разностных схем, для которых подходы, основанные на использовании

подвижной и фиксированной сеток, эквивалентны.

В данной работе консервативные разностные схемы на подвижной и фиксированной сет-

ках построены для двумерной задачи Стефана. Доказана алгебраическая эквивалентность

построенных схем. Преобразование одной схемы в другую осуществляется с помощью замены

переменных, аналогично тому, как это делается в дифференциальной задаче.

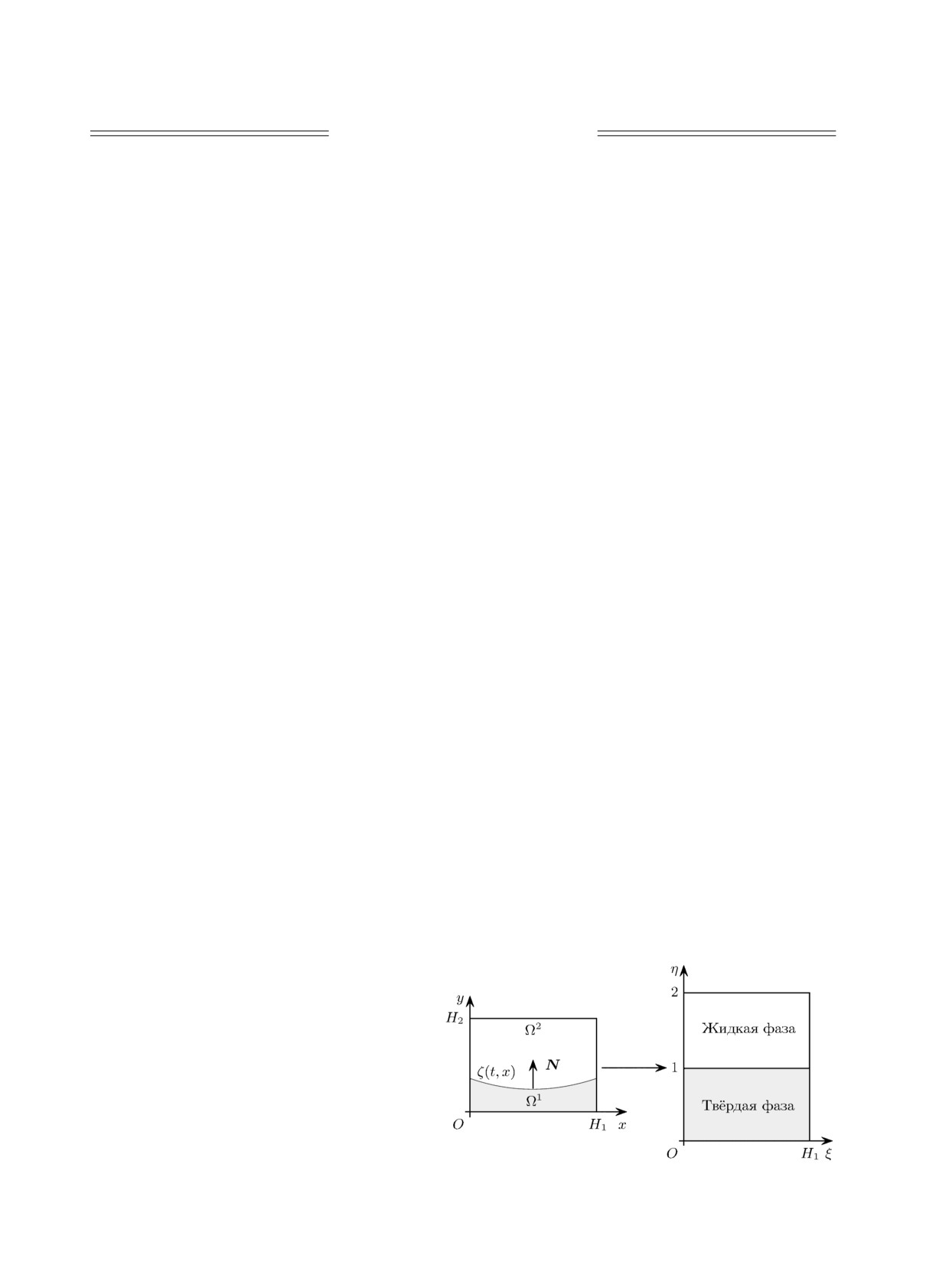
1. Постановка задачи. Задачу о фазовом переходе в чистом веществе рассмотрим в де-

картовой системе координат Oxy в прямоугольнике Ω = Ω(t, x, y) = [0, H₁] × [0, H₂]. В подоб-

ласти Ω¹(t, x, y) = {(x, y) : x ∈ [0, H₁], y ∈ [0, ζ(t, x)]} находится твёрдая фаза, а в оставшейся

части прямоугольника Ω, т.е. в подоб-

ласти Ω²(t, x, y) = {(x, y) : x ∈ [0, H₁],

y ∈ [ζ(t,x),H₂]}, располагается жидкая

фаза. Здесь и далее y = ζ(t, x) - диффе-

ренцируемая функция, представляющая

собой в каждый момент времени t гра-

ницу раздела фаз, положение которой ме-

няется в ходе процесса (см. левую часть

рис. 1).

Твёрдая и жидкая фазы имеют одина-

ковую плотность ρcr = ρ^lq = ρ и удель-

Рис. 1. Преобразование системы координат.

ную теплоёмкость c^crp = c^lp = c_p, но раз-

907

908

ГУСЕВ и др.

личные коэффициенты теплопроводности - k^cr и k^l соответственно. Распределение темпера-

туры в области описывается уравнением теплопроводности

∂_tT = ∇ · (κ∇T).

(1)

Здесь ∇ = (∂_x, ∂_y),

∂_x = ∂/∂x,

∂_y = ∂/∂y,

∂_t = ∂/∂t. Коэффициент температуропроводно-

сти является кусочно-постоянной функцией: κ(x, y) = κ^cr при (x, y) ∈ Ω¹, κ(x, y) = κ^l при

(x, y) ∈ Ω², где κ^cr = k^cr/(c_pρ) и κ^l = k^l/(c_pρ).

На межфазной границе температура равна температуре плавления чистого вещества

T|y=ζ(t,x) =T_melt

(2)

и выполняется закон сохранения энергии (условие Стефана):

(k^cr∇T · N)|y=ζ(t,x)-0 - (k^l∇T · N)|y=ζ(t,x)+0 = λρv^ph(e_y · N).

(3)

Здесь λ - скрытая теплота плавления, v^ph = v^ph(t, x) = ∂_tζ - скорость движения границы

раздела фаз, N - единичная нормаль к межфазной границе, направленная в жидкую фазу,

e_y - единичный вектор оси y.

На границе области Ω задана температура

T|∂Ω =T_b.

(4)

2. Метод выпрямления фронта.

2.1. Замена переменных. Для решения задачи с внутренней подвижной границей, поло-

жение которой необходимо определять в ходе решения задачи, применим метод выпрямления

фронта [18]. Основу этого метода составляет динамическая замена переменных специального

вида, при которой физическая область Ω(t, x, y) отображается в расчётную область Ω(t, ξ, η)

так, что в новой системе координат положение границы раздела фаз фиксировано и совпадает

с координатной линией η = const.

В данной работе используется замена переменных, при которой области Ω^m, m = 1, 2,

в новой системе координат становятся прямоугольниками (рис. 1), а границы областей y =

= Y₀ = 0, y = Y₁ = ζ(t,x) и y = Y₂ = H₂ переходят в прямые η = 0, η = 1 и η = 2

соответственно. Связь между системами координат имеет вид

t=t,ξ=x,η=(y-Ym-1)/l^m + m - 1, m = 1,2,

(5)

где l^m = l^m(t, ξ) = Y_m - Ym-1 - толщина зоны Ω^m.

Запишем задачу (1)-(4) в неподвижной системе координат [20]. Частные производные от

температуры преобразуются следующим образом:

∂T

∂η ∂T

∂T

∂η ∂T

∂T

∂η ∂T

(6)

∂t

∂t ∂η

∂x

∂ξ

∂x ∂η

∂y

∂y ∂η

Для вычисления метрических коэффициентов ∂η/∂t, ∂η/∂x, ∂η/∂y воспользуемся обратным

преобразованием координат

t = t, x = ξ, y = ϕ^m(t,ξ,η) = Ym-1 + l^m(η - m + 1), m = 1,2.

(7)

Якобиан преобразования (7): J^m = ∂(t, x, y)/∂(t, ξ, η) = l^m, m = 1, 2. Нетрудно показать [21,

22], что справедливы равенства

∂η

∂y

1 ∂ϕ^m

∂η

∂y

1 ∂ϕ^m

∂η

∂x

(8)

∂t

J^m ∂t

l^m

∂t

∂x

J^m

lm ∂ξ

∂y

J^m ∂ξ

l^m

Дифференциальные операторы в уравнениях (1)-(4) преобразуем с помощью соотношений

(6), (8) и умножим затем их на J^m. В дальнейшем для краткости будем опускать волну над

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ РАЗНОСТНЫХ МЕТОДОВ

909

t и верхний индекс m у функций l^m, ϕ^m, ϕ^mt = ∂ϕ^m/∂t, ϕ^mξ = ∂ϕ^m/∂ξ. Для производной

по времени получим

T (ξ,η)(T) = ∂_t(lT) - ∂_η(ϕ_tT).

(9)

Для диссипативных членов имеем

L(ξ,η)(T) = ∂_ξW^ξ + ∂_ηW^η.

(10)

Поток W(ξ,η) = (W^ξ, W^η) вычисляется по формуле

W^ξ = L^ξξ∂_ξT + L^ξη∂_ηT, W^η = L^ηξ∂_ξT + L^ηη∂_ηT,

где метрические коэффициенты L^ξξ, L^ξη, L^ηξ, L^ηη вычисляются следующим образом:

L^ξξ = κl, L^ξη = L^ηξ = κ(-ϕ_ξ), L^ηη = κ(1 + ϕ2ξ)/l.

Важно отметить, что метрические коэффициенты зависят от неизвестного положения границы

раздела фаз.

Таким образом, в расчётной области Ω(t, ξ, η) уравнение теплопроводности (1) имеет вид

T (ξ,η)(T) = L(ξ,η)(T).

(11)

2.2. Сетка и сеточные функции. В расчётной области Ω(t,ξ,η) введём прямоугольную

сетку ω(ξ,η)h = ω^ξh × ω^ηh, где ω^ξh = {ξ_i, i = 0, M, ξ₀ = 0, ξ_M = H₁}, ω^ηh = {η_j , j = 0, N, η₀ = 0,

η_j∗ = 1, η_N = 2}, шаги сетки: hξi+1/2 = ξi+1 - ξ_i, hηj+1/2 = ηj+1 - η_j. Введём также полуцелые

узлы: ξi+1/2 = (ξi+1 + ξ_i)/2, ηj+1/2 = (ηj+1 + η_j )/2. Расчётную область Ω(t, ξ, η) разобьём

на прямоугольные ячейки S(ξ,η)ij = [ξi-1/2, ξi+1/2] × [ηj-1/2, ηj+1/2]; длины граней ячейки S(ξ,η)ij

равны ℏ^ξi = 0.5(hξi+1/2 + hξi-1/2) и ℏ^ηj = 0.5(hηj+1/2 + hηj-1/2), её площадь dS(ξ,η)ij = ℏ^ξiℏ^ηj. Также

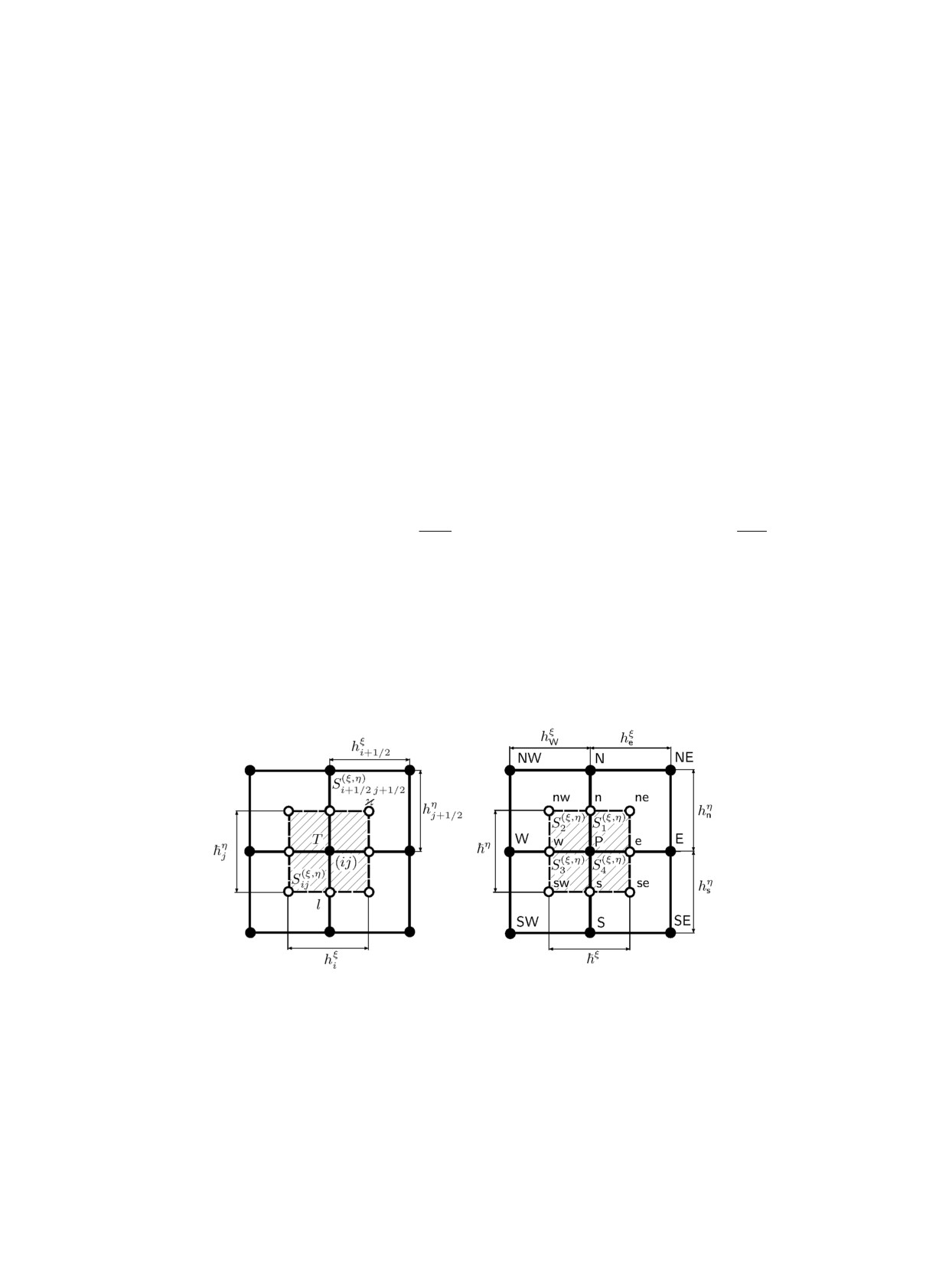
рассмотрим ячейки S(ξ,η)i+1/2j+1/2 с центрами в точках (ξi+1/2, ηj+1/2) (рис. 2). Сетка по времени

ω_τ = {t₀ = 0, tk+1 = t_k + τ, k = 0,1,...}, где τ - шаг по времени.

Рис. 2. Сетка и сеточные функции.

Сеточную функцию T^kij = T (t_k, ξ_i, η_j ) будем относить к узлам сетки ω(ξ,η)h. Доопределим

эту функцию внутри расчётных ячеек: T (t_k, ξ, η) = T^kij при (ξ, η) ∈ S(ξ,η)ij. Длины фаз l и

скорость движения границы раздела v^ph внутри ячеек доопределим линейным образом:

l(t_k, ξ, ηj+1/2) = lkij+1/2 + [lki+1j+1/2 - lkij+1/2](ξ - ξ_i)/hξi+1/2,

v^ph(t_k,ξ) = (v^ph)^ki + [(v^ph)ki+1 - (v^ph)^ki](ξ - ξ_i)/hξi+1/2 при ξ ∈ [ξ_i,ξi+1].

(12)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

910

ГУСЕВ и др.

Температуропроводность κ и метрические коэффициенты L^ξξ, L^ξη, L^ηη относятся к центрам

ячеек S(ξ,η)i+1/2j+1/2 (см. рис. 2).

Для обозначения узлов сетки также будем использовать локальную географическую нота-

цию [23]. Доопределим температуру в узлах n и s следующим образом: T_n = 0.5[T_P + T_N],

T_s = 0.5[T_P + T_S]. Введём сеточные операторы разностного дифференцирования. Для про-

странственных производных в направлении оси ξ имеем TP,ξ = (T_E - T_P)/h^e, TP,¯_ξ = TW,ξ;

разностные аппроксимации пространственных производных в направлении оси η: TP,η = (T_N-

- T_P)/hⁿ, TP,η = TS,η TP,̃η = (T_n - T_P)/(0.5hⁿ), TP,̃η = TS,̃η. Разностную производную по

времени обозначим через T_t =

T_P - T_P)/τ, где

T_P = T(t_k + τ,ξ_P,η_P). Контрольный объём

⋃₄

S(ξ,η)P =

Sqξ,η).

q=1

2.3. Разностная схема. Построим консервативную разностную схему с помощью интегро-

интерполяционного метода. Проинтегрируем уравнение (11) по ячейке S(ξ,η)P:

∫

T (ξ,η)(T)dξ dη dt =

L(ξ,η)(T)dξ dη dt.

t^k S(ξ,η)P

Подробное описание построения разностной схемы приведено в работе [20].

Аппроксимация диссипативных членов. Для диссипативных членов получаем

L(ξ,η)P(T)dS(ξ,η)P = (Wηn - Wηs)ℏ^ξ + (Wξe - Wξw)ℏ^η.

Аппроксимация потоков Wⁿ,

Wξe имеет вид

Wηnℏ^ξ = 0.5[hξeLηηne + hξwLηηnw]TP,η + 0.5[hξeLηξneTn,ξ + hξwLηξnwTn,¯_ξ],

(13)

Wξeℏ^η = 0.5[hηnLξξne + hηsLξξse]TP,ξ + 0.5[hηnLξηneTe,η + hηsLξηseTe,η],

(14)

здесь Tn,ξ = 0.5(TP,ξ +TN,ξ), T_n

= 0.5(T_P

+T_N

), Te,η = 0.5(TP,η +TE,η), Te,η = 0.5(TP,η+TE,η).

Метрические коэффициенты вычисляются следующим образом:

Lξξne = κ_nel_ne, Lξξse = κ_sel_se, Lηηne = κ_ne[1 + (ϕn,ξ)²]/l_n, Lηηnw = κ_nw[1 + (ϕn,¯_ξ)²]/ln,

Lξηne = Lηξne = κ_ne(-ϕn,ξ), Lξηse = κ_se(-ϕs,ξ), Lηξnw = κ_nw(-ϕn,¯_ξ).

Потоки

Wηs и W^w вычисляются аналогично.

На межфазной границе в разностной аппроксимации диссипативных членов возникает сла-

гаемое, обеспечивающее выполнение условия Стефана (3). Это слагаемое имеет вид

E(ξ,η)P∗(T)dS(ξ,η)P∗ = ℏ^ξλ(v^ph)^η.

Здесь P^∗ - индекс узлов сетки, лежащих на границе раздела фаз,^λ = λρ/c_p,

(v^ph)^η = (0.5[vphP + vphw]hξw + 0.5[vphP + vphe]hξe)/(2ℏ^ξ ).

(15)

Значения vwh и veh вычисляются по формуле (12).

С помощью несложных, но достаточно громоздких преобразований показывается, что пред-

ложенная аппроксимация диссипативных членов задаёт самосопряжённый отрицательно опре-

делённый разностный оператор.

Аппроксимация производной по времени. Построим пространственную аппроксима-

цию производной по времени. Для этого проинтегрируем выражение (9) по ячейке S(ξ,η)P. Для

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ РАЗНОСТНЫХ МЕТОДОВ

911

удобства интеграл по ячейке S(ξ,η) представим в виде суммы интегралов по ячейкам Sqξ,η),

q = 1,4:

∫

]

∑[∂∫

∂(ϕ_tT )

T (ξ,η)(T)dξ dη =

lT dξ dη -

dξ dη .

(16)

∂t

∂η

q=1

S(ξ,η)P

Sqξ,η)

Интегрируя первое слагаемое в (16) по ячейке S(ξ,η)1, c учётом формулы (12) получаем

∫

lT dξ dη = [l_n + l_ne]T_P(hξehηn)/8.

S(ξ,η)1

Интегралы по ячейкам S(ξ,η)2, S(ξ,η)3 и S(ξ,η)4 вычисляются аналогичным образом. Для второго

слагаемого в (16) имеем

∫

∂(ϕ_tT )

dξ dη +

dξ dη = 0.5[(ϕ_t)_n + (ϕ_t)_ne]T_nhξe/2 - 0.5[(ϕ_t)_s + (ϕ_t)_se]T_shξe/2,

∂η

(ξ,η)

S(ξ,η)

S₄

∫

∂(ϕ_tT )

dξ dη +

dξ dη = 0.5[(ϕ_t)_n + (ϕ_t)_nw]T_nhξw/2 - 0.5[(ϕ_t)_s + (ϕ_t)_sw]T_shξw/2.

∂η

(ξ,η)

S(ξ,η)

S₃

Таким образом, пространственная аппроксимация производной по времени принимает вид

∫

∂

T (ξ,η)(T)dξ dη =

(l_PT_P) dS(ξ,η)P - [(ϕ_t)_nT_n - (ϕ_t)_sT_s]ℏ^ξ,

(17)

∂t

S(ξ,η)

где

lP = [(0.5[ln + lne]h^e + 0.5[ln + lnw]h^w)hⁿ + (0.5[ls + lse]h^e + 0.5[ls + lsw]h^w)h^s]/(4ℏ^ξ ℏ^η),

(ϕ_t)_n = (0.5[(ϕ_t)_n + (ϕ_t)_ne]hξe + 0.5[(ϕ_t)_n + (ϕ_t)_nw]hξw)/(2ℏ^ξ ).

Пространственные аппроксимации операторов (9) и (10) проинтегрируем по отрезку

[t_k, tk+1], получившиеся выражения разделим на шаг по времени τ. В результате получим

следующую аппроксимацию по времени оператора (17):

T(ξ,η)P(T)dS(ξ,η)P = (lPT_P)_tdS(ξ,η)P - [(ϕ_t)

T_n - (ϕ_t)_s

T_s]ℏ^ξ.

(18)

Во внутренних точках сетки разностная схема для задачи (1)-(4), полученная с помощью

метода выпрямления фронта, имеет вид

T(ξ,η)P(T)dS(ξ,η)P = [L(ξ,η)P

T)+E(ξ,η)P∗

T )δ_PP∗ ] dS(ξ,η)P.

(19)

Здесь δ_PP∗ = 1, если P = P^∗, и δ_PP∗ = 0 в противном случае. Разностная схема (19) яв-

ляется консервативной, метрические коэффициенты L^ξξ, L^ξη, L^ηη в ней взяты с верхнего

временного слоя, соответствующая система нелинейных сеточных уравнений решается отно-

сительно вектора неизвестных, компонентами которого являются температуры в твёрдой и

жидкой фазах и скорость межфазной границы.

Несложно показать (см. [19]), что в регулярной точке выражение (18) преобразуется к виду

T(ξ,η)P(T)dS(ξ,η)P =lPTP,tdS(ξ,η)P - 0.5[hηn(ϕ_t)

T_η + hηs(ϕ_t)_s

T̃η]ℏ^ξ.

(20)

Заменив в системе уравнений (19) её левую часть представлением (20), получим разностную

схему, аппроксимирующую недивергентную форму записи задачи (11) в расчётной области.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

912

ГУСЕВ и др.

3. Метод расчёта на подвижной сетке.

3.1. Сетка и сеточные функции. В физической области Ω(t,x,y) введём подвиж-

ную сетку ω(x,y)h(t) = {(x_i, y_j(t, x_i)), i = 0, M, j = 0, N} таким образом, чтобы y₀(t, x_i) = 0,

y_N(t,x_i) = H₂, y_j∗(t,x_i) = ζ(t,x_i) для любого x_i. Сетка по времени ω_τ = {t₀ = 0, tk+1 =

= t_k + τ, k = 0,1,...}, где τ - шаг по времени.

Утверждение 1. Если в начальный момент времени координаты узлов сеток ω(x,y)h(0)

и ω(ξ,η)h связаны соотношениями

x_i = ξ_i, y_j(0,x_i) = ϕ(0,ξ_i,η_j), i = 0,M, j = 0,N,

(21)

и движение узлов сетки ω(x,y)h(t) определяется выражением

⎧

⎨

y_jvphi/ζ_i,

0<j ≤j^∗,

y_j(tk+1,x_i) = y_j(t_k,x_i) + τv^yj(x_i), v^y(xi) =

(22)

^⎩(H₂ - y_j)vphi/(H₂ - ζ_i), j^∗ < j < N,

то координаты узлов сеток ω(x,y)h(t) и ω(ξ,η)h связаны соотношениями

x_i = ξ_i, y_j(t_k,x_i) = ϕ(t_k,ξ_i,η_j), i = 0,M, j = 0,N,

(23)

для любого k > 0.

Доказательство. Для определённости рассмотрим узлы сетки, расположенные в твёрдой

фазе. Доказательство утверждения проведём методом математической индукции. Из форму-

лировки утверждения следует, что в начальный момент времени (т.е. при k = 0) равенство вы-

полнено. Пусть это равенство выполнено на k-м временном слое, т.е. y_j(t_k, x_i) = ϕ(t_k, ξ_i, η_j ) =

= η_jl(t_k,ξ_i). Покажем, что оно выполняется и в момент времени tk+1 = t_k + τ. Из равенств

(5) и (22) следует, что v^yj(x_i) = η_jvphi, поэтому в момент времени tk+1 имеем

y_j(tk+1,x_i) = y_j(t_k,x_i) + τv^yj(x_i) = [l(t_k,ξ_i) + τvphi]η_j = l(tk+1,ξ_i)η_j = ϕ(tk+1,ξ_i,η_j).

Для узлов сетки, лежащих в жидкой фазе, утверждение доказывается аналогично. Утвер-

ждение доказано.

В дальнейшем в физической области будем использовать сетку ω(x,y)h(t), удовлетворяющую

условиям (21), (22). Полуцелые узлы подвижной сетки определим равенствами

xi+1/2 = ξi+1/2, y_j(t,xi+1/2) = ϕ(t,ξi+1/2,η_j), yj+1/2(t,xi+1/2) = ϕ(t,ξi+1/2,ηj+1/2).

Шаги подвижной сетки

hxi+1/2 = xi+1 - x_i, hyij+1/2(t_k) = yj+1(t_k,x_i) - y_j(t_k,x_i),

hyi+1/2j+1/2(t_k) = yj+1(t_k,xi+1/2) - y_j(t_k,xi+1/2), ℏ^xi = xi+1/2 - xi-1/2,

ℏyi+1/2j(t_k) = yj+1/2(t_k,xi+1/2) - yj-1/2(t_k,xi+1/2).

В общем случае hyij+1/2 = hyi+1/2j+1/2 = hyi+1j+1/2.

Сетка ω(x,y)h(t) разбивает физическую область на четырёхугольные ячейки S(x,y)i+1/2,j+1/2(t)

c вершинами в точках (xi+α, yj+β(t, xi+α)), α, β = 0, 1. Соединим середины противоположных

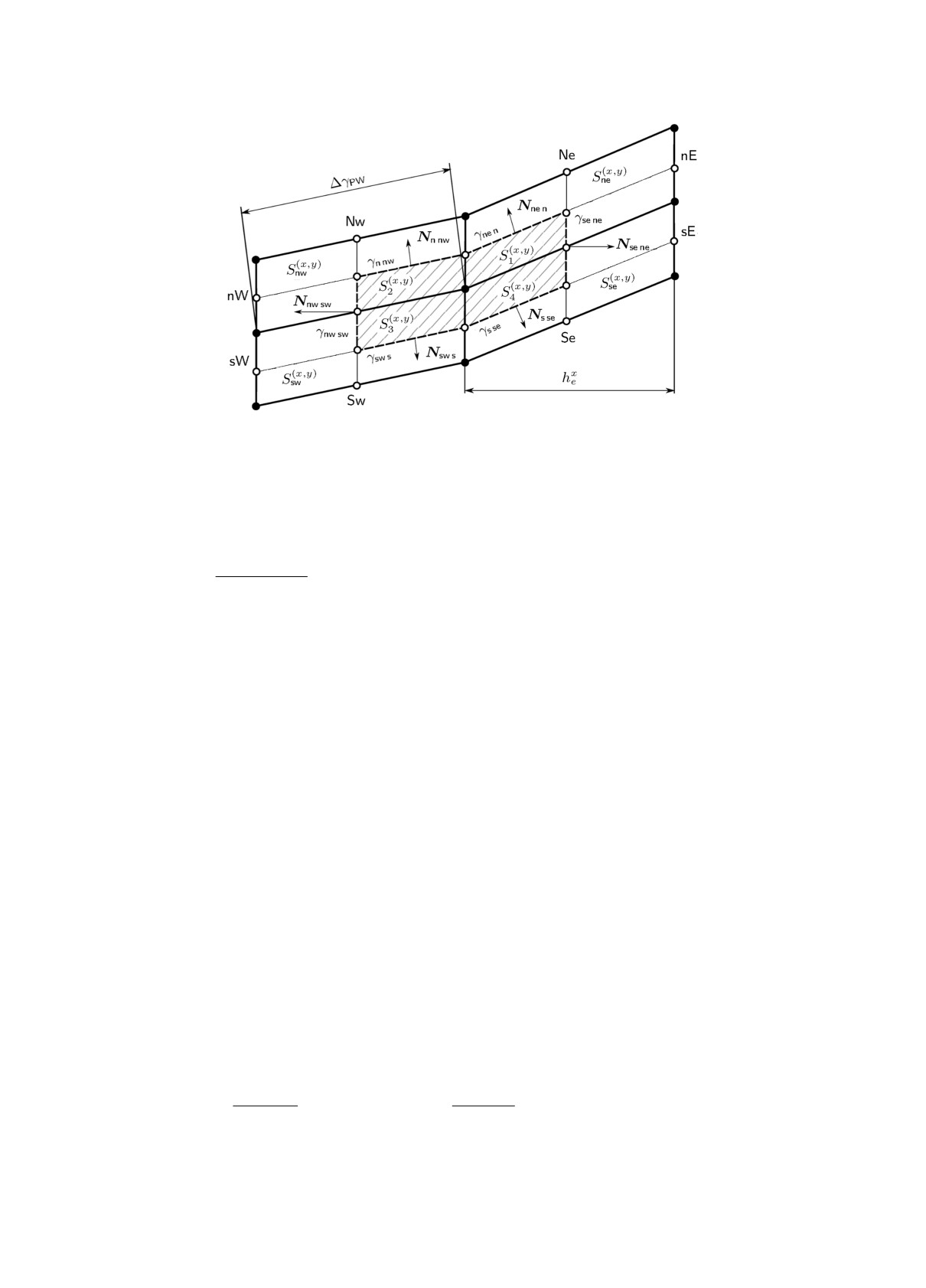
границ данных ячеек отрезками прямых. Полученные отрезки разбивают область на шести-

угольные ячейки S(x,y)ij(t), i = 0, M, j = 0, N (заштрихованная область на рис. 3). Из со-

отношения (23) следует, что S(x,y)ij(t_k) = {(x = ξ, y = ϕ(t_k, ξ, η)) : (ξ, η) ∈ S(ξ,η)ij}. Поэтому

температуру внутри расчётной ячейки S(x,y)ij(t) доопределим так же, как на фиксированной

сетке ω(ξ,η)h.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ РАЗНОСТНЫХ МЕТОДОВ

913

Рис. 3. Подвижная сетка.

Далее для обозначения узлов сетки будем использовать локальную географическую но-

тацию. Обозначим S(x,y)P =⋃4q=1 S(x,y)q (рис. 3) и dS(x,y)q - площадь ячейки S(x,y)q. Границу

ячейки S(x,y)P будем считать положительно ориентированной и введём упорядоченное в со-

ответствии с ориентацией границы множество вершин V = {ne, n, nw, sw, s, se}. Пусть γ_αβ -

участок границы с началом в точке α и концом в точке β (α, β ∈ V); Δγ_αβ - длина отрезка_√

γ_αβ, Δγ_αβ = δx2αβ + δy2αβ, где δx_αβ = x_β - x_α, δy_αβ = y_β - y_α; N_αβ - вектор внешней еди-

ничной нормали к границе γ_αβ с координатами (N^xαβ , N^yαβ ); μ_αβ - единичный направляющий

вектор границы, μ_αβ = (μ^xαβ, μ^yαβ ). В нашем случае

μ^xαβ = -N^yαβ, μ^yαβ = N^xαβ,

(24)

где N^xαβ = δy_αβ /Δγ_αβ , N^yαβ = -δx_αβ /Δγ_αβ . Производная вдоль участка границы γ_αβ вычис-

ляется по формуле Tμαβ = (T_β - T_α)/Δγ_αβ .

V={nE,n,nW,sW,s,sE},об-

Наряду с множеством V введём упорядоченное множество

разованное серединами вертикальных границ ячеек основной сетки Sνx,y), ν ∈ {ne, nw, sw, se}.

Доопределим функцию T в серединах границ ячейки основной сетки Sνx,y) как полусумму

её значений на концах соответствующих границ, т.е. T_n = 0.5[T_P + T_N], T_nE = 0.5[T_E + T_NE],

T_e = 0.5[T_P + T_E], T_Ne = 0.5[T_N + T_NE] и т.д; значение температуры в центре ячейки основной

сетки Sνx,y) равно среднему значению, вычисленному по значениям T в вершинах данной

ячейки, т.е. T_ne = 0.25[T_P + T_E + T_N + T_NE] и т.д. При такой переинтерполяции на “север-

ных” и “южных” границах ячейки S(x,y)P для сонаправленных векторов μ_αβ и μ˜α˜β, α, β ∈ V,

β ∈^V, имеем

Tμαβ = Tμ̃

= (T_̃

- T_α)/(2Δγ_αβ),

(25)

например, Tμnen = (T_n - T_nE)/(2Δγ_nen) = ([T_P + T_N] - [T_NE + T_E])/(4Δγ_nen). Производную ∂_yT

в центрах ячеек основной сетки Sνx,y) аппроксимируем следующим образом:

T_Ne - T_e

T_e - T_Se

[∂_y T ]hne = Te,y =

[∂_yT ]hse = Te,y =

[∂_yT ]hnw = Tw,y,

[∂_yT ]hsw = Tw,y.

(26)

h^ne

h^s

Остальные разностные аппроксимации пространственных производных на подвижной сетке

вычисляются стандартным образом.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

914

ГУСЕВ и др.

3.2. Разностная схема. Разностную схему будем строить с помощью интегро-интерполя-

ционого метода. Проинтегрируем уравнения (1)-(4) по контрольному объёму S(x,y)P(t):

∫

∂T

dx dy dt =

∇ · (κ∇T)dxdy dt.

∂t

t^k S(x,y)P

(t)

t^k S(x,y)P(t)

Аппроксимация диссипативных членов. Построим пространственную аппроксимацию

диссипативных членов

∫

[

]

∂

L(x,y)P(T)dS(x,y)P =

W^x +

W^y dxdy.

∂x

∂y

S(x,y)P(t)

Здесь W^x = κ∂_xT , W^y = κ∂_yT . В силу формулы Остроградского-Гаусса имеем

∫

[

]

∑∫

∂

W^x +

W^y dxdy =

[W^xN^xαβ + W^yN^yαβ] dγ.

∂x

∂y

α,β∈V_γ

S(x,y)P(t)

αβ

Вычислим интегралы вдоль “горизонтальных” границ γ_nen, γ_nnw, γ_sws, γ_sse. Воспользовав-

шись тем, что

(

)

∂T

-μ^y

∂x

μ^x

∂μ_αβ

^αβ ∂y

αβ

запишем интеграл вдоль границы следующим образом:

∫

[

]

∫

[

]

∂T

N^xαβ

∂T

μ^yαβ

∂T

N^xαβ + κ

N^y

dγ =

dγ +

N^yαβ -

N^x

dγ.

(27)

αβ

∂x

∂y

μ^xαβ

∂μ_αβ

μ^xαβ

∂y

γ_αβ

Для интегралов в правой части равенства (27) с учётом соотношений (24) получаем

∫

)

αβ

∂T

N^xαβ

∂T

⁽δy_αβ

dγ =

dγ ≈ Δγ_αβ

[κ]^hTμαβ

(28)

μ^xαβ

∂μ_αβ

N^yαβ κ∂μαβ

δx_αβ

γ_αβ

∫

[

]

∫

μ^yαβ

∂T

(N^xαβ)² + (N^yαβ )²

∂T

N_α

N^x

dγ =

dγ ≈

αβ

μ^xαβ

∂y

N_α

∂y

N^yαβ κ

∂y

γ_αβ

(

)

Δγ_αβ

≈ Δγ_αβ

[κ]^h[∂_yT ]^h

= -δx_αβ[1 + (δy_αβ/δx_αβ)²][κ]^h[∂_yT]hP.

(29)

δx_αβ

Здесь [κ]^h = κ_ne для γ_nen, [κ]h = κnw для γnnw, [κ]h = κse для γses и [κ]h = κsw для γssw;

[∂_yT ]hP - разностная аппроксимация оператора ∂_yT, [∂yT ]hP = TP,y для “северных” границ γnen

и γ_nnw, [∂yT ]hP = TP,y для “южных” границ γses и γssw.

Преобразуем теперь правые части в (28) и (29) к виду, удобному для сравнения с аппрокси-

мацией теплового потока (13) через образ отрезка γ_αβ в расчётной системе координат (t, ξ, η).

На границе γ_nen для ориентированной разности имеем δx_nen = -h_e/2; тогда δy_nen/δx_nen =

= yn,x = (y_nE - y_n)/hxe и, учитывая равенство (25), получаем Tμnen = -T_n,μ, где

T_n,μ = (T_nE - T_n)/(2Δγ_nen) = ([T_E + T_NE] - [T_P + T_N])/(4Δγ_nen).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ РАЗНОСТНЫХ МЕТОДОВ

915

На γ_nnw справедливы равенства

δx_nnw = -h_w/2, δy_nnw/δx_nnw = yn,x = (y_n - y_nW)/hxw и Tμnnw = -Tn,μ,

где Tn,μ = [T_n - T_nW]/(2Δγ_nen). Таким образом, поток I_n через “северную” границу представ-

ляется в виде

I_n = 0.5[hxeMyyne + hxwMyynw]TP,y + ΔγnenMyμneT_n,μ + Δγ_nnwMyμnwT_n,μ,

(30)

где коэффициенты M^yy и M^yμ вычисляются по формулам

Myyne = κ_ne[1 + (yn,x)²], Myynw = κ_nw[1 + (yn,x)²], Myμne = κ_ne(-yn,x), Myμnw = κ_nw(-yn,x).

На южных границах γ_sws и γ_sse выполняются равенства:

δx_sws = h_w/2, δy_sws/δx_sws = ys,x, Tμsws = Ts,μ = [T_s - T_sW]/(2Δγ_sws);

δx_sse = h_e/2, δy_sse/δx_sse = ys,x, Tμsse = Ts,μ = [T_sE - T_s]/(2Δγ_sse).

Поэтому поток I_s через “южную” границу представляется в виде

I_s = -0.5[hxeMyyse + hxwMyysw]TP,y - Δγ_sseMyμseT_s,μ - Δγ_swsMyμswT_s,μ,

(31)

где коэффициенты M^yy и M^yμ вычисляются по формулам

Myyse = κ_se[1 + (ys,x)²], Myysw = κ_sw[1 + (ys,x)²], Myμse = κ_se(-ys,x), Myμsw = κ_sw(-ys,x).

Запишем интегралы вдоль вертикальных границ γ_nwsw и γ_sene. В этом случае N^xαβ =

= δy_αβ/|δy_αβ|, N^yαβ = 0 и

∫

[

]

∫

∂T

δy_αβ

∂T

N^xαβ + κ

N^y

dγ =

dy.

αβ

∂x

∂y

|δy_αβ |

∂x

γ_αβ

Как и выше, производную ∂_xT выразим через производную по некоторому направлению.

В качестве такого направления выберем μ = μ_PE на “восточной” границе γ_sene и μ = μ_PW на

“западной” границе γ_nwsw. Для “восточной” границы γ_sene получим

∫

(

)

δy

se ne

∂T

μyPE

∂T

dy =

dy +

dy.

(32)

|δy_sene|

∂x

μxPE

∂μ_PE

μxPE

∂y

γse ne

Первое слагаемое в правой части равенства (32) аппроксимируем следующим образом:

∫

∂T

Δγ_PE

∂T

Δγ_PE

dy =

dy ≈

[hyne κ_ne + hyse κ_se]

TμPE =

μxPE

∂μ

δx_PE

∂μ_PE

δx_PE

γse ne

√

= 0.5[hyne κ_ne + hyse κ_se](|δx_PE|/δx_PE)

1 + (δy_PE/δx_PE)²TμPE.

(33)

Для аппроксимации второго слагаемого в правой части равенства (32) воспользуемся следую-

щей квадратурной формулой:

∫

(

)

[

(

)



(

)



]

μyPE

∂T

μ^nne

∂T



μ^sse

∂T



dy ≈

h^y

κ_ne



+h^y

κ_se



μxPE

∂y

μxnne

∂y

μxsse

∂y

γse ne

= 0.5[hyne(-δy_nne/δx_nne)κ_ne[∂_yT ]hne + hyse(-δy_sse/δx_sse)κ_se[∂_yT ]hse].

(34)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

4^∗

916

ГУСЕВ и др.

Интеграл вдоль “западной” границы γ_nwsw вычисляется аналогично:

∫

√

δy_nwsw

∂T

dy = -0.5[hynw κ_nw + hysw κ_sw](|δx_PW|/δx_PW)

1 + (δy_PW/δx_PW)²TμPW -

|δy_nwsw|

∂x

γnw sw

- 0.5[hynw(-δy_nnw/δx_nnw)κ_nw[∂_yT ]hnw + hysw(-δy_ssw/δx_ssw)κ_sw[∂_yT ]hsw].

(35)

Преобразуем правые части равенств (33), (34) и (35) к виду, удобному для сравнения с

аппроксимацией теплового потока (14) в расчётной области. На границе γ_sene имеем: δx_PE =

= hxe, δy_PE/δx_PE = yP,x = [y_E - y_P]/hxe, TμPE = TP,μ = [T_E - T_P]/Δγ_PE и, учитывая (26),

[∂_yT ]hne = Te,y,

[∂_yT ]hse = Te,y. Поэтому поток I_e через “восточную” границу ячейки можно

представить в виде

I_e = 0.5[hyneMμμne + hyseMμμse]TP,μ + 0.5[hyneMμyneTe,y + hyseMμyseTe,y],

(36)

где

√

Mμμne = κ_ne

1 + (yP,x)², M^μμ

=κ_se

1 + (yP,x)², Mμyne = Myμne , Mμyse = Myμse .

На границе γ_nwsw имеем: δx_PW = -hxw, δy_PE/δx_PE = yP,x = [y_P - y_W]/hxw, TμPW = -TP,μ,

где TP,μ = [T_P - T_W]/Δγ_PW и [∂_yT ]hnw = Tw,y, [∂yT ]hsw = Tw,y. Таким образом, поток Iw через

“западную” границу можно представить в виде

I_w = -0.5[hynwMμμnw + hyswMμμsw]TP,μ - 0.5[hynwMμynwTw,y + hyswMμyswTw,y],

(37)

где

√

Mμμnw = κ_nw

1 + (yP,x)², M^μμ

=κ_sw

1 + (yP,x)², Mμynw = Myμnw, Mμysw = Myμsw.

Аппроксимация диссипативных членов на подвижной сетке запишется следующим обра-

зом:

L(x,y)P(T)dS(x,y)P = I_n + I_s + I_e + I_w.

(38)

На фронте кристаллизации в аппроксимации диссипативных членов возникает дополни-

тельное слагаемое. Из условия Стефана (3) следует, что для скачка теплового потока справед-

ливо равенство

∫

E(x,y)P∗(T)dS(x,y)P∗ =

λ v^phNywP dγ +

λ v^phNyPe dγ ≈ ℏ^xλ(v^ph)^y,

(39)

γ_wP

γ_Pe

здесь

(v^ph)^y = (0.5[vphP + vphw]hxw + 0.5[vphP + vphe]hxe)/(2ℏxP).

(40)

Аппроксимация производной по времени. Для построения аппроксимации производ-

ной по времени воспользуемся транспортной теоремой Рейнольдса:

∫

∂T

T dx dy =

dx dy +

(T v · N) dγ,

(41)

∂t

S(x,y)P(t)

∂S(x,y)P(t)

где v - скорость движения границы ячейки S(x,y)P(t). Проинтегрировав соотношение (41) по

отрезку [t_k, tk+1], получим

∫

∂T

dx dy dt =

T dx dy dt -

(T v · N) dγ dt.

(42)

∂t

t^k S(x,y)P

(t)

S(x,y)P(t)

∂S(x,y)P(t)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ РАЗНОСТНЫХ МЕТОДОВ

917

Рассмотрим слагаемые, стоящие в правой части равенства (42). Первое слагаемое аппрок-

симируем следующим образом:

∫

∑

T dx dy dt

T_P

dS(x,y)

- T_P dS(x,y)q.

(43)

q=1

S(x,y)P(t)

(x,y)

Площади ячеек dSqx,y) и

будем вычислять по формуле трапеций, используя значения

координат вершин этих ячеек на слое t_k и tk+1 соответственно. Для dSqx,y), q = 1, 4, имеем

[hⁿ + h^ne]hxe

dS(x,y)1 =(yn -yP)+(yne -ye)he

dS(x,y)2 =[hn +hnw]hw,

dS(x,y)3 =[hs +hsw]hw,

dS(x,y)4 =[hs +hse]he

Расчётная ячейка S(x,y)P(t) перемещается только в направлении оси y, т.е. v = (0, v^y ). Поэто-

му для второго слагаемого в правой части соотношения (42) справедливо равенство

∫

∑∫

(T v · N) dγ dt =

Tv^yN^yαβ dγ dt.

(44)

α,β∈V_γ

αβ

∂S(x,y)P(t)

Для интегралов вдоль “горизонтальных” границ получаем

∫

(

)

(

v^α + v^yβ



v^α + v^yβ )



Tv^yN^yαβ dγ dt ≈ τ Δγ_αβ[T]^h

N^yαβ

=τ

-δx_αβ

T]^h

(45)



t=tk+1

tk γαβ

Здесь

T]^h

T_n для “северных” границ γ_nen, γ_nnw и

T]^h

T_s для “южных” границ γ_sws,

γ_sse. Скорости движения v^α, α ∈ V, вершин контрольного объёма равны средним значениям,

вычисленным по соответствующим значениям скоростей узлов сетки, например,

vyn = 0.5[vyP + vyN], v_ne = 0.25[vyP + vyN + vyE + vyNE]

и т.д. Суммируя равенства (45) по “северным” и “южным” границам ячейки, приходим к сле-

дующей формуле для приближённого вычисления интеграла (44):

∫

(T v · N) dγ dt ≈ -τ(v^yn

T_n - vysTs)ℏxP.

(46)

∂S(x,y)P(t)

Здесь скорость v^y вычисляется по формулам

vy_n = (0.5[vyn + vyne]hxe + 0.5[vyn + vynw]hxw)/(2ℏxP),

vy_s = (0.5[vys + vyse]hxe + 0.5[vys + vysw]hxw)/(2ℏxP).

Разделив равенства (43) и (46) на шаг τ, найдём аппроксимацию производной по времени на

подвижной сетке ω(x,y)(t):

T(x,y)P(T)dS(x,y)P = (T_P dS(x,y)P)_t - (v^yn

T_n - vysTs)ℏxP.

(47)

Разностный оператор (47) можно преобразовать к виду

T(x,y)P(T)dS(x,y)P = (T_P dS(x,y)P)_t - 0.5[hyn

T_PvyP)̃y +hys

T_PvyP)̃y]ℏxP,

(48)

где vyP = (0.5[vyP + v^e]hxe + 0.5[vyP + v^w]hxw)/(2ℏxP).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

918

ГУСЕВ и др.

По аналогии с [19] преобразуем аппроксимацию производной по времени (48) к недивер-

гентному виду. Рассмотрим верхнюю часть ячейки S(x,y)P, т.е. S(x,y)1

^⋃S(x,y)2. Воспользуемся

формулами разностного дифференцирования произведения [24]. Для разностной производной

по времени получаем

)

⁽h^x[hyn,t + hyne,t]

hxw[hyn,t + hynw,t]

([ dS(x,y)1 + dS(x,y)2]T_P)_t = ( dS(x,y)1 + dS(x,y)2)TP,t +

T_P.

Для разностной производной по переменной y имеем

TvyP)_y = vyP,̃yTP + vyn

TP,y.

В силу соотношения (23) производная по времени от шага по пространству выражается ра-

венствами

0.5(hyn,t + hyne,t) = [yn,t - yP,t] + [yne,t - ye,t] = [vyn - vyP] + [vyne - vye],

0.5(hyn,t + hynw,t) = [yn,t - yP,t] + [ynw,t - yw,t] = [vyn - vyP] + [vynw - vyw],

из которых вытекает, что

)

⁽hxe[hyn,t + hyne,t]

hxw[hyn,t + hynw,t]

ℏxPhⁿ

T_P =

vyP,̃yTP.

Откуда, приводя подобные члены, в регулярной точке сетки получаем равенство

([ dS(x,y)1 + dS(x,y)2]T_P)_t -ℏPhⁿ

T_PvyP)_y = (dS(x,y)1 + dS(x,y)2)TP,t -ℏPhⁿ

vy_n

TP,y.

(49)

Аналогично, для нижней части ячейки Sx,yP имеем

([ dS(x,y)3 + dS(x,y)4]T_P)_t -ℏPh^s

T_PvyP)¯˜y = (dS(x,y)3 + dS(x,y)4)TP,t -ℏPh^s

vy_s

TP,¯̃y.

(50)

Используя выражения (48)-(50), получим недивергентную форму записи аппроксимации про-

изводной по времени:

T(x,y)P(T)dS(x,y)P = TP,tdS(x,y)P - 0.5[hynv

TP,y +hysvys

TP,̃y]ℏxP.

(51)

Во внутренних точках сетки ω(x,y)(t) разностная схема для задачи (1)-(4) имеет вид

T(x,y)P(T)dS(x,y)P = [L(x,y)P(

T)+E(x,y)P∗

T )δ_PP∗ ]dS(x,y)P.

(52)

Разностная схема (52) является консервативной, коэффициенты M^ττ , M^τy, M^yy в ней взя-

ты с верхнего временного слоя, а соответствующая система нелинейных сеточных уравнений

решается относительно вектора неизвестных, компонентами которого являются температуры

в твёрдой и жидкой фазах и скорость межфазной границы.

4. Эквивалентность разностных схем.

Утверждение 2. Разностная схема (19), построенная с помощью метода выпрямления

фронта, и разностная схема (52), построенная на подвижной сетке, удовлетворяющей со-

отношению (23), алгебраически эквивалентны.

Доказательство. Выполним в разностной схеме (52) дискретный аналог замены перемен-

ных (5). Нетрудно проверить, что шаги сеток ω(x,y)h и ω(ξ,η)h связаны соотношениями

hxe = hξe, hxw = hξw,

(53)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ РАЗНОСТНЫХ МЕТОДОВ

919

hyn = y_N - y_P = ϕ(t_k,ξ_P,η_N) - ϕ(t_k,ξ_P,η_P) = l_n(η_N - η_P) = l_nhηn,

h^yα = l_αh^ηα,

=lαh^ηα, α ∈ V.

(54)

В силу равенств (7), (22) скорости движения вершин контрольного объёма v^α, α ∈ V, можно

записать следующим образом:

v^yα = ϕ_α,t, α ∈ V.

(55)

(x,y)

Выполним замену переменных в разностном операторе L(x,y)P

. Последовательно

рассмотрим потоки через все границы ячейки S(x,y)P. Начнём с “северной” границы, поток

через которую определяется выражением (30). Замена переменных в разностных аналогах

смешанных производных, входящих в (30), приводит к следующему равенству:

Δγ_nenMyμne

Tn,μ

Δγ_nnwMyμnw

Tn,μ = 0.5[hξeLηξneTn,ξ + hξwLηξnwTn

(56)

потому что

Δγ_nen

Tn,μ = 0.5h^eTn,ξ,

Δγ_nnw

Tn,μ = 0.5h^w

T_n

Myμne = κ_ne(-yn,x) = κ_ne(y_nE - y_n)/hxe = -κ_ne[ϕ(tk+1,ξ_E,η_n) - ϕ(tk+1,ξ_P,η_n)]/hξe =

=κ_ne(

=Lηξnw.

ϕn,ξ ) = L^ne ,

С помощью соотношений (54) преобразуем члены, связанные с

TP,y, к виду

Myyne

TP,y = κ_ne[1+(yn,x)²

TP,y = κ_ne[1+

ϕn,ξ )²]

T_N

T_P)/hyn = κ_ne[1+

ϕn,ξ )²]/(^ln

TP,η = Lyyne

TP,η,

Myynw

TP,y = Lyynw

TP,η,

откуда

0.5[hxeMyyne + hxwMyynw

TP,y = 0.5[hξeLηηne + hξwLηηnw

TP,η.

(57)

Аналогично выполним замену переменных в выражении (31) для потока через “южную”

границу:

Δγ_sseMyμse

T_s,μ

Δγ_swsMyμsw

T_s,μ = 0.5[hξeLηξseTs,ξ + hξwLηξswTs

(58)

0.5[hxeMyyse + hxwMyysw

TP,y = 0.5[hξeLηηse + hξwLηηsw

TP,η.

(59)

h^y

Рассмотрим поток (36) через “восточную” границу. Так какhne

Te,y

= h

Te,η,

seTe,y

=h^s

Te,η и

=L^ne,

e, то для смешанных производных в (36) будем иметь

0.5[hyneMμyneTe,y +hyseMμyse

Te,y] = 0.5[hηnLξηneTe,η + hηsLξηse

Te,η].

(60)

Для производной в направлении μ получаем

0.5[hyneMμμne +hyseMμμse

TP,μ = 0.5[hηnLξξne + hηsLξξse

TP,ξ.

(61)

Здесь воспользовались тем, что в силу соотношений (53) и (54) справедливы равенства

√

Mμμne

TP,μ =hyneκ_ne

1+(yP,x)

TP,μ =hyneκ_ne

T_E

T_P)/hxe =lnehηnκ_neTP,ξ = hηnLξξne

TP,ξ,

Mμμse

TP,μ = hηsLξξse

TP,ξ.

Для потока (37) на “западной” границе имеем

0.5[hynwMμynwTw,y +hyswMμysw

Tw,y] = 0.5[hηnLξηnwTw,η + hηsLξηsw

Tw,η],

(62)

0.5[hynwMμμnw +hyswMμμsw

TP,μ = 0.5[hηnLξξnw + hηsLξξsw

T_P

(63)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

920

ГУСЕВ и др.

Учитывая соотношения (56)-(63) в формуле (38), получаем

L(x,y)P

T)dS(x,y)P = L(ξ,η)P(

T)dS(ξ,η)P.

На фронте кристаллизации в уравнение (52) входит слагаемое, отвечающее за выполнение

условия Стефана и описывающее скачок теплового потока при изменении агрегатного состо-

яния вещества. Из формул (15) и (40) следует, что (v^ph)^y = (v^ph)^η, откуда вытекает, что на

границе раздела фаз выполняется равенство

(x,y)

E(x,y)

=E(ξ,η)

T)dS(ξ,η)P.

(64)

(x,y)

Выполним замену переменных в T(x,y)P(T )

. В силу соотношений (53) и (54) имеем

dS(x,y)1 = (hyn + hyne)hxe/8 = (l_n + l_ne)h^ξeh^ηn/8.

Площади остальных четвертей ячейки преобразуются аналогичным образом. Поэтому первое

слагаемое в аппроксимации (51) запишется в виде

TP,t dS(x,y)P = TP,tl_P dS(ξ,η)P.

(65)

Воспользовавшись формулой (55), для второго слагаемого в (51) получим

0.5[hyn vynTP,y +hysvys

TP,̃y]ℏxP = 0.5[hηn(ϕ_t)_nTP,η + hηs(ϕt)sTP,̃η]ℏξP.

(66)

Замена слагаемых в аппроксимации (51) их выражениями (65) и (66) приводит к равенству

(x,y)

T(x,y)P(T)

= T (ξ,η)P(T)dS(ξ,η)P.

В результате показано, что

(x,y)

[T(x,y)P(T ) - L(x,y)P

T)-E(x,y)P∗

T )δ_PP∗ ]

= [T(ξ,η)P(T ) - Lξ,ηP

T)-E(ξ,η)P∗

T )δ_PP∗ ] dS(ξ,η)P.

Таким образом, доказано, что схемы (52) и (19) алгебраически эквивалентны.

Заключение. Для классической двухфазной задачи Стефана выделен класс консерва-

тивных разностных схем, для которых метод выпрямления фронта и метод, основанный на

использовании подвижных сеток, алгебраически эквивалентны. Получены дивергентная и

недивергентная формы записи, аппроксимирующие соответствующие формы записи исходной

дифференциальной задачи. Для разностного оператора, аппроксимирующего на неподвижной

сетке диссипативные члены в уравнении теплопроводности, можно доказать свойства самосо-

пряжённости и отрицательной определённости. Доказательство указанных свойств является

несложным, но громоздким и поэтому в работе не приводится. В силу алгебраической эквива-

лентности предложенных разностных схем аналогичными свойствами обладает и разностный

оператор на подвижной сетке. Таким образом, построенный класс схем наследует основные

свойства исходной дифференциальной задачи.

СПИСОК ЛИТЕРАТУРЫ

1. Бакирова О.И. Численное моделирование процесса зонной плавки на основе решения задачи о фа-

зовом переходе в бинарной системе // Математическое моделирование. Получение металлов и по-

лупроводниковых структур. М., 1986. С. 142-158.

2. Дегтярев Л.М., Дроздов В.В., Иванова Т.С. Метод адаптивных к решению сеток в сингулярно-

возмущенных одномерных краевых задачах // Дифференц. уравнения. 1987. Т. 23. № 7. С. 1160-

1168.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

К ВОПРОСУ ОБ ЭКВИВАЛЕНТНОСТИ РАЗНОСТНЫХ МЕТОДОВ

921

3. Фрязинов И.В., Забелина М.П. Сеточный метод решения задачи Стефана для бинарной системы

// Дифференц. уравнения. 1987. Т. 23. № 7. С. 1188-1197.

4. Vermolen F.J., Vuik C. A mathematical model for the dissolution of particles in multi-component alloys

// J. of Comput. and Appl. Math. 2000. V. 126. P. 233-254.

5. Muray W.D., Landis F. Numerical and machine solutions of the transient heat conduction problems

involving melting or freezing // J. Heat Transfer. 1959. V. 81. P. 106-112.

6. Kutluay S. Numerical schemes for one-dimensional Stefan-like problems with a forcing term // Appl.

Math. and Comput. 2005. V. 168. P. 1159-1168.

7. Мажукин А.В., Мажукин В.И. Динамическая адаптация в параболических уравнениях // Журн.

вычислит. математики и мат. физики. 2007. Т 47. № 11. С. 1913-1936.

8. Sekhon M., Lent B., Dost S. Numerical study of liquid phase diffusion growth of SiGe subjected to

accelerated crucible rotation // J. of Crystal Growth. 2016. V. 438. P. 90-98.

9. Friazinov I.V., Marchenko M.P., Mazhorova O.S. Transient simulation of crystal growth by Bridgman

technique uder normal and low gravity // Proc. of Microgravity Science and Low Gravity / Aerospace

congress. Moscow, 1991. P. 179-187.

10. Lan C.W., Chen F.C. A finite volume method for solute segregation in directional solidification and

comparison with a finite element method // Comput. Methods Appl. Mech. Eng. 1996. V. 131. P. 191-

207.

11. Zhou Yu., North T.H. Kinetic modelling of diffusion-controled, two-phase moving interface problems

// Model. and Simul. in Material Science and Engineering. 1993. V. 1. № 4. P. 505-516.

12. Illingworth T.C., Golosnoy I.O. Numerical solutions of diffusion-controled moving boundary problems

which conserve solute // J. of Comput. Physics. 2005. V. 209. P. 207-225.

13. Pandelaers L., Verhaeghe F., Wollants P., Blanpain B. An implicit conservative scheme for coupled heat

and mass transfer problems with multiple moving interfaces // Int. J. of Heat and Mass Transfer. 2011.

V. 54. № 5-6. P. 1039-1045.

14. Самарский А.А, Вабищевич П.Н. Вычислительная теплопередача. М., 2003.

15. Мажорова О.С., Попов Ю.П., Щерица О.В. Алгоритм расчета задачи о фазовом переходе в мно-

гокомпонентной системе // Дифференц. уравнения. 2004. Т. 40. № 7. С. 1051-1060.

16. Мажорова О.С., Попов Ю.П., Щерица О.В. Метод численного решения задач кристаллизации мно-

гокомпонентных растворов / Препринт Ин-та прикладной математики им. М.В. Келдыша РАН. М.,

2002. № 18.

17. Nobeoka M., Takagi Y., Okano Y et al. Numerical simulation of InGaSb crystal growth by temperature

gradient method under normal- and micro-gravity fields // J. of Crystal Growth. 2014. V. 385. P. 66-71.

18. Landau H.G. Heat conduction in a melting solid // J. of Appl. Math. 1950. V. 8. P. 81-94.

19. Мажорова О.С., Попов Ю.П., Щерица О.В. Консервативные разностные схемы для термо-диффу-

зионной задачи Стефана // Дифференц. уравнения. 2013. T. 49. № 7. С. 897-905.

20. Gusev A.O., Shcheritsa O.V., Mazhorova O.S. Conservative finite volume strategy for investigation of

solution crystal growth techniques // Computers & Fluids. 2020. V. 202. P. 104501.

21. Vinokur M. Conservation equations of gasdynamics in curvilinear coordinate system // J. of Comput.

Phys. 1974. V. 14. P. 105-125.

22. Steger J. Implicit finite-difference simulation of flow about arbitrary two-dimensional geometries

// American Institute of Aeronautics and Astronautics Journal. 1978. V. 16. № 7. P. 679-686.

23. Patankar S.V. Numerical heat transfer and fluid flow. New York, 1981.

24. Самарский А.А. Введение в теорию разностных схем. М., 1971.

Институт прикладной математики

Поступила в редакцию 10.03.2021 г.

им. М.В. Келдыша РАН, г. Москва

После доработки 10.03.2021 г.

Принята к публикации 27.04.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021