ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 7, с.963-975

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.633

КОМПАКТНЫЕ РАЗНОСТНЫЕ СХЕМЫ

НА ТРЁХТОЧЕЧНОМ ШАБЛОНЕ

ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ

ВТОРОГО ПОРЯДКА

Для уравнений Клейна-Гордона с постоянными и переменными коэффициентами на трёх-

точечном шаблоне по пространству рассматриваются компактные разностные схемы 4+2

порядка аппроксимации. Предложены новые компактные схемы для одного типа квазили-

нейных гиперболических уравнений второго порядка. В случае постоянных коэффициентов

доказана сильная устойчивость разностного решения по отношению к малому возмущению

начальных условий, правой части и коэффициентов уравнения. Получены априорные оцен-

ки устойчивости и сходимости разностного решения в сильных сеточных нормах.

DOI: 10.31857/S0374064121070098

1. Введение. Повышение точности вычислительного метода для решения задач матема-

тической физики на минимальных шаблонах всегда представляло собой актуальную задачу

численного анализа (см., например, [1-4]). Среди методов построения разностных схем повы-

шенного порядка аппроксимации особое место занимают так называемые компактные схемы,

которые пишутся на шаблоне, несущественно отличающемся от традиционных для данного

уравнения [5]. Основополагающей работой по этой тематике для классических уравнений мате-

матической физики с самосопряжённым эллиптическим оператором является работа А.А. Са-

марского [6], опубликованная им более 50 лет назад. Для других классов уравнений, включая

уравнения типа конвекции-диффузии, нелинейные уравнения без смешанных производных и

задачи аэрогидродинамики, компактные разностные схемы построены в [7-9].

В настоящей работе для различных типов уравнения Клейна-Гордона исследуются на

обычном трёхточечном шаблоне компактные разностные схемы 4+2 порядка точности. Это

уравнение играет важную роль в математической физике; в частности, оно используется при

изучении солитонов и в физике конденсированного вещества [10]. Компактные разностные

схемы для такого уравнения строятся и изучаются, например, в [9, 11]. Некоторые резуль-

таты по данной тематике также анонсированы в [12, 13]. Для этого уравнения, несмотря на

линейность дифференциальной и разностной задач с переменными коэффициентами, для по-

лучения соответствующих априорных оценок не удаётся применить известные результаты по

теории Самарского устойчивости трёхслойных операторно-разностных схем [1, гл. VI, § 3].

В работе с использованием метода энергетических неравенств для компактных разностных

схем, аппроксимирующих уравнения Клейна-Гордона с переменными коэффициентами, полу-

чены априорные оценки устойчивости и сходимости разностного решения в сеточных нормах

L₂(ω_h), W¹²(ω_h), C(ω_h) или L_∞(ω_h). На примере вычислительного эксперимента для ква-

зилинейного уравнения, которое является следствием системы уравнений газовой динамики,

показывается, как использовать правило Рунге для определения разных порядков скорости

сходимости решения разностной схемы в случае двух независимых переменных.

1. Необходимые и достаточные условия устойчивости двух и трёхслойных опе-

раторно-разностных схем. При исследовании компактных разностных схем, аппроксими-

рующих линейные уравнения Клейна-Гордона, естественно воспользоваться общей теорией

Самарского [1, гл. VI, § 3] операторно-разностных схем. Ниже предлагается использовать дру-

гие канонические формы операторно-разностных схем, для которых условия устойчивости

формулируются значительно проще и не содержат условий на связь между операторами.

963

7^∗

964

МАТУС, ХОАНГ

Пусть задано действительное конечномерное евклидово пространство H и сетка по време-

ни ω_τ = {t_n = nτ, n = 0, N₀, τN₀ = T } = ω_τ

^⋃ {0}. Скалярное произведение в H обозначим

через (·, ·), и пусть A, B, D : H → H - линейные операторы, не зависящие от τ и t_n.

Рассмотрим задачу Коши для двухслойной операторно-разностной схемы

By_t + Ay(0.5) = ϕ(t), t ∈ ω_τ,

(1)

y₀ = u₀,

(2)

где yⁿ = y(t_n) ∈ H - искомая вектор-функция, а ϕⁿ = ϕ(t_n), u₀ заданы, y(σ) = σyn+1 + (1 -

- σ)yⁿ, yⁿ ∈ H. Тогда критерий Самарского (см. [1, с. 333]) при ϕ(t) ≡ 0 можно сформули-

ровать следующим образом.

Теорема 1. Условия

B = B(t) ≥ 0, A = A^∗ > 0, A - постоянный оператор,

необходимы и достаточны для устойчивости решения разностной задачи (1), (2) в H_A по

начальным данным, т.е. для выполнения оценки

∥yⁿ∥_A ≤ ∥u₀∥_A, n = 1, N₀,

где, как обычно, ∥v∥_A = (Av, v) для любого v ∈ H.

Для трёхслойных операторно-разностных схем будем использовать следующую канониче-

скую форму:

Dy_tt + A₁y(0.5,0.5) = ϕ(t),

0<t∈ω_τ,

(3)

y₀ = u₀, y₁ = u₁,

(4)

где y(σ1,σ2) = σ₁yn+1 + (1 - σ₁ - σ₂)yⁿ + σ₂yn-1, 0 ≤ σ1,σ2 ≤ 1.

В работе используются обозначения из [1, 2]. Далее будем предполагать, что D, A₁ -

положительные, самосопряжённые и постоянные операторы:

D = D^∗ > 0, A∗1 = A₁ > 0.

(5)

Тогда имеет место следующая

Теорема 2. Разностная схема (3), (4) устойчива в HA1 по начальным данным и правой

части, и имеет место априорная оценка

∑

Qn+1 ≤ Q¹ + τ∥ϕ(t_k)∥_D-1 .

k=1

Здесь Qⁿ = {∥y_t∥2D + (∥y∥2A1 + ∥y∥² )/2}1/2._A

Доказательство. Умножая уравнение (3) скалярно в H на 2τy◦

= τ(y_t + y_t), приходим

к энергетическому соотношению

Q2n+1 - Q2n = 2τ(y◦, ϕ) ≤ τ(∥yt∥D + ∥yt∥D)∥ϕ∥D-1 ≤ τ(Qn+1 + Qn)∥ϕ(tn)∥D-1 .

Отсюда и следует требуемая оценка.

2. Уравнение Клейна-Гордона с постоянными коэффициентами.

2.1. Постановка задачи и разностная схема. В области Q_T = {(x, t) : 0 ≤ x ≤ l, 0≤

≤ t ≤ T} рассмотрим начально-краевую задачу для уравнения Клейна-Гордона с постоянны-

ми коэффициентами

∂²u

- mu + f(x,t), m = const > 0,

(6)

∂t²

∂x²

∂u

u(x, 0) = u₀(x),

(x, 0) = u₀(x),

(7)

∂t

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

КОМПАКТНЫЕ РАЗНОСТНЫЕ СХЕМЫ НА ТРЁХТОЧЕЧНОМ ШАБЛОНЕ

965

u(0, t) = μ₁(t), u(l, t) = μ₂(t).

(8)

Отметим, что уравнение (6) является обобщением волнового уравнения и используется

для описания быстро движущихся частиц, имеющих массу покоя. Здесь и далее относительно

решения дифференциальной задачи будем предполагать, что оно существует, единственно и

обладает всеми непрерывными в Q_T производными, необходимыми по ходу изложения.

На равномерной сетке узлов ω = ω_h ×ω_τ = {(x_i, t_n) ∈ Q_T }, ω_h = {x_i = ih, 0 ≤ i ≤ N, h =

= l/N} = ω_h

^⋃ {0, l}, ω_τ = {t_n = nτ, 0 ≤ n ≤ N0, τ = T/N0} = ωτ

^⋃ {0} дифференциальную

задачу заменим разностной:

(

)

h²

y_tt = Λy(σ,σ) - m y +

Λy

+ ϕ, (x, t) ∈ ω_h × ω_τ ,

(9)

y(x, 0) = u₀(x), x ∈ ω_h, y_t(x, 0) = u₁(x), x ∈ ω_h,

(10)

y(0, t) = μ₁(t), y(l, t) = μ₂(t), t ∈ ω_τ ,

(11)

в которой

ŷ=yn+1,

y = yn-1, yⁿⁱ = y(x_i,t_n),

h²

Λy = y_xx, ϕ = f +

Λf, σ = σ -

12τ²

u₁(x) = u₀(x) +

[u′′0(x) - mu₀(x) + f(x, 0)], x ∈ ω_h.

Как и в монографии [1, с. 309], нетрудно показать, что для невязки

(

)

h²

ψ = -u_tt + Λu(σ,σ) - m u +

Λu

+ϕ

и погрешности аппроксимации второго начального условия имеют место априорные оценки

∥ψ∥ ≤ M(h⁴ + τ²), M = const > 0,

(12)

◦

∥ψ∥ = ∥u1 - u0t∥ ≤ M1τ2, M1 = const > 0,

(13)

т.е. разностная схема (9)-(11) аппроксимирует исходную дифференциальную задачу с четвёр-

тым порядком по пространству и вторым по времени.

2.2. Устойчивость по начальным данным и правой части. Для исследования этих

вопросов в линейном случае обычно применяют теорию трёхслойных операторно-разностных

схем, разработанную А.А. Самарским [1, гл. VI, § 3]. Требование самосопряжённости основного

пространственного оператора

(Ay)_i = -(Λy)_i, i = 1, N - 1, (Ay)₀ = 0, (Ay)_N = 0,

(14)

приводит к жёстким ограничениям на однородность граничных условий. Чтобы избежать это-

го, рассмотрим возмущённое решение

y, полученное по разностной схеме (9)-(11) с возму-

щённой правой частью

f и возмущёнными начальными условиями ũ₀,

ũ₁. Тогда задача для

возмущения y = y - y может быть записана в операторном виде:

Dy_tt + A₁y = ϕ, σ = 1,

(15)

y(0) = u₀, y_t(0) = u₁,

(16)

(

)

mh²

D = E + στ²A, A₁ = mE +

Здесь u₀ = ũ₀ - u₀, u₁ = ũ₁ - u₁, ϕ =

ϕ - ϕ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

966

МАТУС, ХОАНГ

Оператор A, определённый соотношением (14), является постоянным, положительным и

самосопряжённым, т.е. 0 < A^∗ = A : H → H, здесь H - пространство сеточных функций,

заданных на ω_h и равных нулю при x = 0 и x = l. Поэтому операторы D и A₁ также

являются положительными, постоянными и самосопряжёнными: D = D^∗ > E, A₁ = A∗1 > A.

Отметим следующие хорошо известные свойства оператора A [1, гл. II, § 3]:

λ₁E ≤ A ≤ λ₂E, A-1 ≤

E, δ =

(17)

l²

πh

λ₁ =

sin²

≥ δ, λ₂ =

cos²

(18)

h²

В дальнейшем нам понадобится следующая

Лемма 1 [1, с. 373]. Пусть в канонической форме (15), (16) операторы D и A₁ явля-

ются постоянными, положительными и самосопряжёнными в H и, кроме того, выполнено

неравенство

1+ε

D≥

τ²A₁, где ε > 0 - некоторое число.

(19)

Тогда для решения схемы (15), (16) имеет место априорная оценка

√

(

)

∑

1+ε

∥yn+1∥_D ≤

∥y(0)∥_D + ∥Dy_t(0)∥_A-1 +

τ ∥ϕ_s∥_A-1

(20)

s=1

В частности, если ε = 1, D ≥ E, A-11 < A-1 ≤ δ-1E, оценка (20) примет вид

(

)

√

∑

∥yn+1∥ ≤

∥y(0)∥_D +

∥Dy_t(0)∥ +

τ ∥ϕ_s∥

(21)

s=1

Применим оценку (21) к исследованию устойчивости компактной разностной схемы (9)-

(11). Далее будем предполагать, что

h²

√

≤τ ≤

(22)

√m,σ=1-

12τ²

Тогда условие (19) выполнено. Действительно,

)

[

(

)]

⁽1

mτ²

mh²

D-

A₁ =

E+

E+τ² σ-

A≥

Итак, имеет место следующая

Теорема 3. Пусть выполнено условие (22). Тогда разностная схема с неоднородными гра-

ничными условиями (9)-(11) условно устойчива по начальным данным и правой части, а для

её решения имеет место априорная оценка

(

)

√

∑

∥yn+1 -yn+1∥≤

∥ũ₀ -u₀∥_D +

∥D(ũ₁ - u₁)∥ +

ϕs - ϕs∥

s=1

Замечание. В линейном случае после замены

l-x

u=v+

μ₂(t) +

μ₁(t)

исходная дифференциальная задача сводится к задаче для v с однородными граничными

условиями. При этом устойчивость по граничным условиям и правой части решения разност-

ных схем для этих задач имеет место одновременно для обеих задач. Однако для нелинейного

уравнения Клейна-Гордона такая замена может не дать желаемого результата.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

КОМПАКТНЫЕ РАЗНОСТНЫЕ СХЕМЫ НА ТРЁХТОЧЕЧНОМ ШАБЛОНЕ

967

Итак, мы доказали устойчивость решения разностной схемы в слабой энергетической нор-

ме L₂(ω_h) при весьма слабых ограничениях на вес функции σ. Такие оценки полезны при

исследовании сходимости разностных схем с обобщёнными решениями [14]. Чтобы получить

априорные оценки в более сильных нормах W¹²(ω_h) и C(ω_h), воспользуемся теоремой 2 и

вложением (см. [1, с. 107])

√

∥y-y∥_C ≤

∥y_x - y_x]|.

(23)

√

Запишем разностную схему для возмущения y = y-y в каноническом виде (3) при h/

6≤

≤ τ ≤ 1/√m, σ = 1 - h2/(12τ2),

Dy_tt + A₁y(0.5,0.5) = ϕ, t ∈ ω_τ,

(24)

y(0) = u₀, y_t(0) = u₁,

(25)

где

(

)

mh²

D = E + τ²(σ - 0.5)A₁ = D^∗ ≥

E, D-1 ≤ 2E, A∗1 = A₁ = mE +

A>A≥δE.

Тогда имеет место следующая

√

Теорема 4. Решение разностной схемы (24), (25) при h/

6 ≤ τ ≤ 1/√m, σ = 1 -

− h²/(12τ²) устойчиво по начальным данным и правой части, и для всех n = 2,N₀ имеют

место априорные оценки

∑

√

(∥y^nx]|² + ∥yn-1x]|²)1/2 ≤ Q¹ + 2

ϕ(t_k) - ϕ(t_k)∥,

k=1

√

{

}

∑

∥yⁿ -yⁿ∥_C ≤

Q¹ + 2

ϕ(t_k) - ϕ(t_k)∥

(26)

k=1

√

Доказательство. При h/

6 ≤ τ ≤ 1/√m, σ = 1 - h2/(12τ2) выполнено условие (5),

поэтому в силу теоремы 2 имеем

∑

√

(∥yⁿ∥2A

+ ∥yn-1∥² )1/2 ≤ Q¹ +_A

τ ∥ϕ(t_k)∥_D-1 .

k=1

Так как A₁ > A и D-1 ≤ 2E, то справедлива оценка

∑

√

(∥y^nx]|² + ∥yn-1x]|²)1/2 ≤ Q¹ + 2

τ ∥ϕ(t_k)∥.

k=1

Следовательно, из леммы и вложения (23) вытекает, что

√

{

}

∑

∥yⁿ -yⁿ∥_C ≤

Q¹ + 2

ϕ(t_k) - ϕ(t_k)∥

k=1

Теорема доказана.

2.3. Сильная устойчивость. При исследовании корректности разностных схем основное

внимание уделяется устойчивости решения по начальным данным и правой части [1, 2]. Одна-

ко при численном решении дифференциальной задачи может оказаться, что коэффициенты

уравнения заданы не точно, а приближённо. Это показывает, насколько важно изучение схем с

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

968

МАТУС, ХОАНГ

возмущёнными коэффициентами. Под сильной устойчивостью понимается устойчивость ре-

шения разностной задачи по отношению к малому возмущению начальных условий, правой

части и коэффициентов уравнения [15].

Наряду с разностной схемой (9)-(11) рассмотрим соответствующую ей возмущённую задачу

(

)

h²

Λy

ϕ, (x, t) ∈ ω_h × ω_τ ,

(27)

ytt=Λy(σ,σ) - m

y(x, 0) = ũ₀(x), x ∈ ω_h,

yt(x, 0) = ũ1(x), x ∈ ωh,

(28)

y(0, t) = μ₁(t),

y(l, t) = μ₂(t), t ∈ ω_τ .

(29)

Вычитая из уравнений (27)-(29) соответствующие уравнения (9)-(11), получаем задачу для

возмущения y = y - y, которую запишем в операторном виде (15), (16):

Dy_tt

A₁y = ϕ -

A₁ - A₁)y,

y(0) = u₀, y_t(0) = u₁,

(

)

mh²

A₁ = mE +

Здесь D = D^∗ > E,

A₁

A∗1 > A ≥ δE - положительные, постоянные и самосопряжённые

операторы.

√

Заметим, что при h/

6 ≤ τ ≤

1/ m выполнено условие (19), поэтому на основании

априорной оценки (21) для y получаем неравенство

(

)

√

∑

∥yn+1∥ ≤

∥y(0)∥_D +

∥Dy_t(0)∥ +

τ {∥ϕ_s∥ + ∥

A₁ - A₁)y_s∥}

s=1

В силу соотношений (17), (18) имеем ∥A∥ < 4/h², и, следовательно, из (21) вытекает оценка



(

)



∥

A₁ - A₁)y_s∥ =^( m - m) E -h

A y_s

K_s| m - m|,

^<

в которой

(

)

√

∑

K_s =

∥u₀∥_D +

∥Du₁∥ +

τ ∥ϕ_r∥

r=1

Итак, мы можем сформулировать теорему о сильной устойчивости.

Теорема 5. Пусть выполнено следующее условие на шаги сетки:

√

≤τ ≤

√ , m = max{m, m}.

Тогда решение разностной схемы (9)-(11) сильно устойчиво и для её возмущения имеет

место априорная оценка

{

)}

√

∑(

∥yn+1-yn+1∥≤

2 ∥ũ₀-u₀∥_D+

∥D(ũ₁-u₁)∥+

ϕs-ϕs∥+

K_s| m-m|

n=1,N₀-1.

s=1

2.4. Теорема о сходимости. Обозначим через z = y - u погрешность метода. Заменяя

в разностных уравнениях (9)-(11) y на z + u , получаем задачу для z:

(

)

h²

z_tt = Λz(σ,σ) - m z +

Λz

+ ψ, (x,t) ∈ ω_h × ω_τ ,

(30)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

КОМПАКТНЫЕ РАЗНОСТНЫЕ СХЕМЫ НА ТРЁХТОЧЕЧНОМ ШАБЛОНЕ

969

◦

z(x, 0) = 0, x ∈ ω_h, z_t(x, 0) =

ψ, x ∈ ω_h,

(31)

z(0, t) = 0, z(l, t) = 0, t ∈ ω_τ .

(32)

Так как задачи (9)-(11) и (30)-(32) идентичны, то мы можем воспользоваться теоремой 4

для оценки погрешности метода.

Теорема 6. Пусть выполнены условия теоремы 4. Тогда решение разностной задачи (9)-

(11) сходится к точному решению дифференциальной задачи (6)-(8) в сеточной норме C(ω_h)

и для её решения имеет место оценка точности вида

max∥yⁿ - uⁿ∥_C ≤ M₂(h⁴ + τ²), M₂ = const > 0.

t∈ωτ

Доказательство. Действительно, из априорных оценок (12), (13) и (26) следует нера-

венство

√

{

}

∑

∥yⁿ - uⁿ∥_C ≤

Q(z¹) + 2 τ∥ψ(t_k)∥

≤ M₂(h⁴ + τ²).

k=1

Следовательно, разностное решение сходится к точному решению с четвёртым порядком по

пространству и вторым по времени.

3. Уравнение Клейна-Гордона с переменными коэффициентами.

3.1. Постановка задачи и разностная схема. В области Q_T = {(x, t) : 0 ≤ x ≤ l, 0≤

≤ t ≤ T} рассмотрим начально-краевую задачу для уравнения Клейна-Гордона с переменны-

ми коэффициентами

(

)

∂²u

∂

∂u

k(x, t)

- mu + f(x,t), m = const > 0,

(33)

∂t²

∂x

∂u

u(x, 0) = u₀(x),

(x, 0) = v₀(x),

(34)

∂t

u(0, t) = μ₁(t), u(l, t) = μ₂(t),

(35)

где 0 < k₁ ≤ k(x, t) ≤ k₂, u(x, t) ∈ C4,6(Q_T ), p ∈ C0,5(Q_T ), f ∈ C0,4(Q_T ).

На построенной сетке ω исходную дифференциальную задачу аппроксимируем разностной

схемой вида

[

]

h²

y_tt = Λy(σ,σ) -

Λ(py_tt) - m y(σ,σ) +

Λ(py(σ,σ)) + ϕ, (x, t) ∈ ωh × ωτ ,

(36)

y(x, 0) = u₀(x), x ∈ ω_h, y_t(x, 0) = u₁(x), x ∈ ω_h,

(37)

y(0, t) = μ₁(t), y(l, t) = μ₂(t), t ∈ ω_τ .

(38)

Здесь

Λy = (a(x, t_n)y_x)_x, σ = 0.5, ϕ = f +

Λ(pf), p(x, t) =

k(x, t)

[

(

)

]-1

a(x, t) = 6 p(x - h, t) + 4p x -

+ p(x,t)

0 < c₁ ≤ a(x,t) ≤ c₂,

u₁(x) = v₀(x) +

[(k(x, 0)u^′(x, 0))^′ - mu(x, 0) + f(x, 0)], x ∈ ω_h.

Следуя работам [5, 6, 8], нетрудно показать, что разностная схема (36)-(38) аппроксимирует

исходную задачу (33)-(35) с четвёртым порядком по пространству и вторым по времени, т.е.

для её невязки

[

]

h²

ψ = -u_tt + Λu(σ,σ) -

Λ(pu_tt) - m u(σ,σ) +

Λ(pu(σ,σ)) +ϕ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

970

МАТУС, ХОАНГ

и второго начального условия имеют место априорные оценки

∥ψ∥ ≤ M(h⁴ + τ²), M = const > 0,

◦

∥ψ∥ = ∥u1 - u0t∥ ≤ M1τ2, M1 = const > 0.

3.2. Устойчивость. Чтобы избежать громоздких выкладок, ограничимся случаем зави-

симости коэффициента k = k(x) только от пространственной переменной. Рассмотрим возму-

щённое решение y, полученное по разностной схеме (36)-(38) с возмущённой правой частью

f и возмущёнными начальными условиями ũ₀,

ũ₁. Тогда задача для возмущения y = y - y

примет вид

[

]

h²

y_tt = Λy(σ,σ) -

Λ(py_tt) - m y(σ,σ) +

Λ(py(σ,σ)) + ϕ, (x,t) ∈ ωh × ωτ ,

(39)

y(x, 0) = u₀(x), x ∈ ω_h, y_t(x, 0) = u₁(x), x ∈ ω_h,

(40)

y(0, t) = 0, y(l, t) = 0, t ∈ ω_τ .

(41)

Здесь u₀ = ũ₀ - u₀, u₁ = ũ₁ - u₁, ϕ =

ϕ - ϕ.

К сожалению, несмотря на линейность разностной задачи, к ней неприменима теория Са-

марского трёхслойных операторно-разностных схем [1]. При использовании метода энергети-

ческих неравенств в дальнейшем кроме некоторых известных фактов из теории разностных

схем: первая разностная формула Грина, неравенство Коши-Буняковского с ε [1, гл. II, § 3],

разностный аналог леммы Гронуолла [16, гл. III, § 1], нам понадобится также следующая

Лемма 2. Выражение

mh²

Qⁿ = ∥y_t∥² +

(a, y2x + y2x] +^m(∥y∥2 + ∥y∥2) -h

(ap(-1), y2xt] -

(ap(-1), y2x + y2x],

где p(-1) = pi-1, при выполнении условий

√

3k₁

h≤h₀, h₀ =

τ ≥

√

(42)

3k₁

неотрицательно: Qⁿ ≥ 0.

Доказательство. Достаточно показать, что выражение

mh²

I₁ =

(a, y2x + y2x] -h

(ap(-1), y2xt] -

(ap(-1), y2x + y2x]

(43)

неотрицательно. С учётом очевидных неравенств

h²

mh²

(ap(-1), y2xt] ≥ -

(a, y2x + y2x] и

(ap(-1), y2x + y2x] ≥ -mh2 (a, y2x + y2x]

6k₁τ²

24k₁

для выражения (43) имеет место оценка

mh²

I₁ ≥ c₃(a,y2x + y2x], c₃ =1

6k₁τ²

24k₁

При первом из условий (42) выполнено неравенство

mh²

≥

24k₁

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

КОМПАКТНЫЕ РАЗНОСТНЫЕ СХЕМЫ НА ТРЁХТОЧЕЧНОМ ШАБЛОНЕ

971

Следовательно,

c₃ ≥ -

≥0

6k₁τ²

при выполнении второго из условий (42). Лемма доказана.

Чтобы получить априорную оценку для y, умножим разностное уравнение (39) скалярно

на 2τy◦ и применим первую разностную формулу Грина. Получим следующее энергетическое

соотношение:

mτh²

Qn+1 -

(ap_x(y_t - y_t), y_xt + y_xt] = Qⁿ +

(ap_x(ŷ + y), y◦

] + 2τ(ϕ,y◦).

(44)

Рассмотрим в (44) слагаемые, отличные от Qⁿ и Qn+1. Применяя неравенство Коши-Буня-

ковского с ε, легко получаем следующие оценки:

(ap_x(y_t - y_t), y_xt + y_xt] ≥ -ch(∥y_t∥² + ∥y_t∥²),

(45)

[

]

mτh²

(ap_x(ŷ + y), y◦

] ≤ ch

(∥ŷ∥² + ∥y∥²) +^m(∥y∥2 + ∥y∥2) ,

(46)

2τ(ϕ, y◦) ≤ ετ∥ϕ∥2 +

(∥y_t∥² + ∥y_t∥²),

(47)

2ε

где c > 0 - константа, зависящая от m, ε, max|p_x(x)| и в каждом конкретном случае своя.

x∈ω_h

Учитывая неравенства (45)-(47) в (44), при выполнении условий (42) приходим к рекур-

рентному соотношению

Qn+1 ≤ (1 + τc)Qⁿ + τc∥ϕ∥² ≤ e^cτ Qⁿ + τc∥ϕ∥².

(48)

Итак, имеет место следующая

Теорема 7. Пусть выполнено условие

{

√

}

τ ≥ max

3k₁

Тогда имеет место оценка

(

)

∑

Qn+1 ≤ ectn Q¹ + c τ∥ϕ^k∥2 ,

(49)

k=1

означающая ρ-устойчивость решения разностной схемы (36)-(38) по начальным данным и

правой части в сеточных нормах L₂(ω_h), W¹²(ω_h), C(ω_h).

Доказательство теоремы следует из неравенства (48), леммы Гронуолла и вложения [1,

с. 107]

√

∥y-y∥_C ≤

∥y_x - y_x]|.

3.3. Сходимость разностной схемы в сеточной норме C(ω_h). Заменяя в разностных

уравнениях (36)-(38) y на z +u, где u - решение задачи (33)-(35), получаем для погрешности

z задачу

[

]

h²

z_tt = Λz(σ,σ) -

Λ(pz_tt) - m z(σ,σ) +

Λ(pz(σ,σ)) + ψ, (x,t) ∈ ωh × ωτ ,

(50)

◦

z(x, 0) = 0, x ∈ ω_h, z_t(x, 0) =

ψ, x ∈ ω_h,

ψ = O(τ²),

(51)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

972

МАТУС, ХОАНГ

z(0, t) = 0, z(l, t) = 0, t ∈ ω_τ .

(52)

Задачи (50)-(52) и (39)-(41) идентичны. Поэтому можно применить теорему 7 для оценки

погрешности метода. Тогда в соответствии с неравенством (49) получаем оценку

{

}

◦

4c₂

◦

∥z∥2C ≤ M₁

∥ψ∥2 +

∥ψx]|2 +

∥ψ∥2 + cTmax∥ψ(t)∥2

c²

t∈ωτ

где M₁ = const > 0.

Итак, мы можем сформулировать теорему о сходимости.

Теорема 8. Пусть выполнены условия теоремы 7. Тогда решение разностной схемы (36)-

(38) сходится к точному решению дифференциальной задачи (33)-(35) в сеточной норме

C(ω_h) и для её решения имеет место оценка точности

∥yⁿ - uⁿ∥_C ≤ M₂(h⁴ + τ²), n = 0, N₀,

где M₂ = const > 0.

4. Квазилинейные уравнения Клейна-Гордона. Недостатком предложенных А.А. Са-

марским компактных разностных схем для уравнений с переменными коэффициентами явля-

ется невозможность их обобщения на случай квазилинейных уравнений, так как соответству-

ющий шаблонный функционал должен вычисляться в несуществующей для квазилинейного

случая полуцелой точке. Тем не менее компактные схемы порядка 4 + 2, аналогичные схе-

мам для случая постоянных коэффициентов, можно строить и для квазилинейных уравнений

Клейна-Гордона

∂²u

∂²φ(u)

- mf₁(u) + f(x,t), m = const > 0,

∂t²

∂x²

∂u

u(x, 0) = u₀(x),

(x, 0) = u₀(x),

∂t

u(0, t) = μ₁(t), u(l, t) = μ₂(t),

с условием φ^′u = k(u) ≥ k₁ > 0.

Разностная схема 4 + 2 порядка аппроксимации на стандартном шаблоне имеет вид

y_tt = [φ(y)](σ,σ)xx - mf₁(y) + f -h

y_ttxx, (x,t) ∈ ω_h × ω_τ ,

y(x, 0) = u₀(x), x ∈ ω_h, y_t(x, 0) = u₁(x), x ∈ ω_h,

y(0, t) = μ₁(t), y(l, t) = μ₂(t), t ∈ ω_τ ,

где

v=v+

v_xx =

(v₊₁ + v-1),

0 < σ ≤ 1,

u₁(x) = u₀(x) +

[φ^′′(u₀(x)) - mf₁(u₀(x)) + f(x, 0)], x ∈ ω_h.

Для реализации этой схемы необходимо использовать итерационный метод Ньютона.

5. Вычислительный эксперимент. Ниже приводятся результаты численных расчётов

при решении начально-краевой задачи для уравнения вида

∂²u

1∂²u^-γ

(53)

∂t²

∂x²

c выбранными параметрами γ = 5, l = 2, T = 2. Начальные и краевые условия определяются

из точного решения

2/(1+γ)

⁽t+1⁾

u(x, t) =

x+1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

КОМПАКТНЫЕ РАЗНОСТНЫЕ СХЕМЫ НА ТРЁХТОЧЕЧНОМ ШАБЛОНЕ

973

Уравнение (53) является следствием системы уравнений газовой динамики в переменных

Лагранжа с уравнением состояния для политропного газа, в котором u = η - удельный объём.

Разностная схема 4+2 порядка аппроксимации для уравнения (53) имеет вид

y_tt = σ(φ(ŷ))_xx + (1 - 2σ)(φ(y))_xx + σ(φ(y))_xx -

y_ttxx,

(54)

где σ = 1, φ(u) = -u^-γ /γ.

Для нахождения решения разностной схемы (54) применяется итерационной метод Нью-

тона:

(k+1)

- 2y + y = τ²[φ(

ŷ )(

(k)ŷ)]_xx - τ²[φ(y)]_xx + τ²[φ(y)]_xx -h2(

- 2y + y)_xx,

⁽⁰⁾ŷ = 2y - y, k = 0, 1, 2, . . . - номер итерации.

На каждом слое этот процесс будет останавливаться, когда при некотором M будет выполнено

условие

(M+1)

∥

(M)ŷ∥_C ≤ ε, ε = 10-7.

Порядок сходимости по временной и пространственной переменным в норме L_∞ = C опре-

деляется по следующим формулам:

∥z(2h, τ)∥L∞

∥z(h, 2τ)∥L∞

p^h

∞

= log₂

p^τ

∞

= log₂

(55)

∥z(h, τ)∥L∞

Так как разностное решение сходится к точному решению с четвёртым порядком по прост-

ранству и вторым по времени, то для проверки скорости сходимости по временной переменной

мы выбираем такие шаги h и τ, чтобы выполнялось неравенство h⁴ ≤ τ². Тогда получается

схема O(τ²) и мы работаем со вторым правилом Рунге (55).

Аналогично, при рассмотрении порядка по h в расчётах следим, чтобы выполнялись нера-

венство h⁴ ≥ τ². Тогда можно применить первое правило Рунге (55).

В таблицах приведена скорость сходимости приближённого решения к точному.

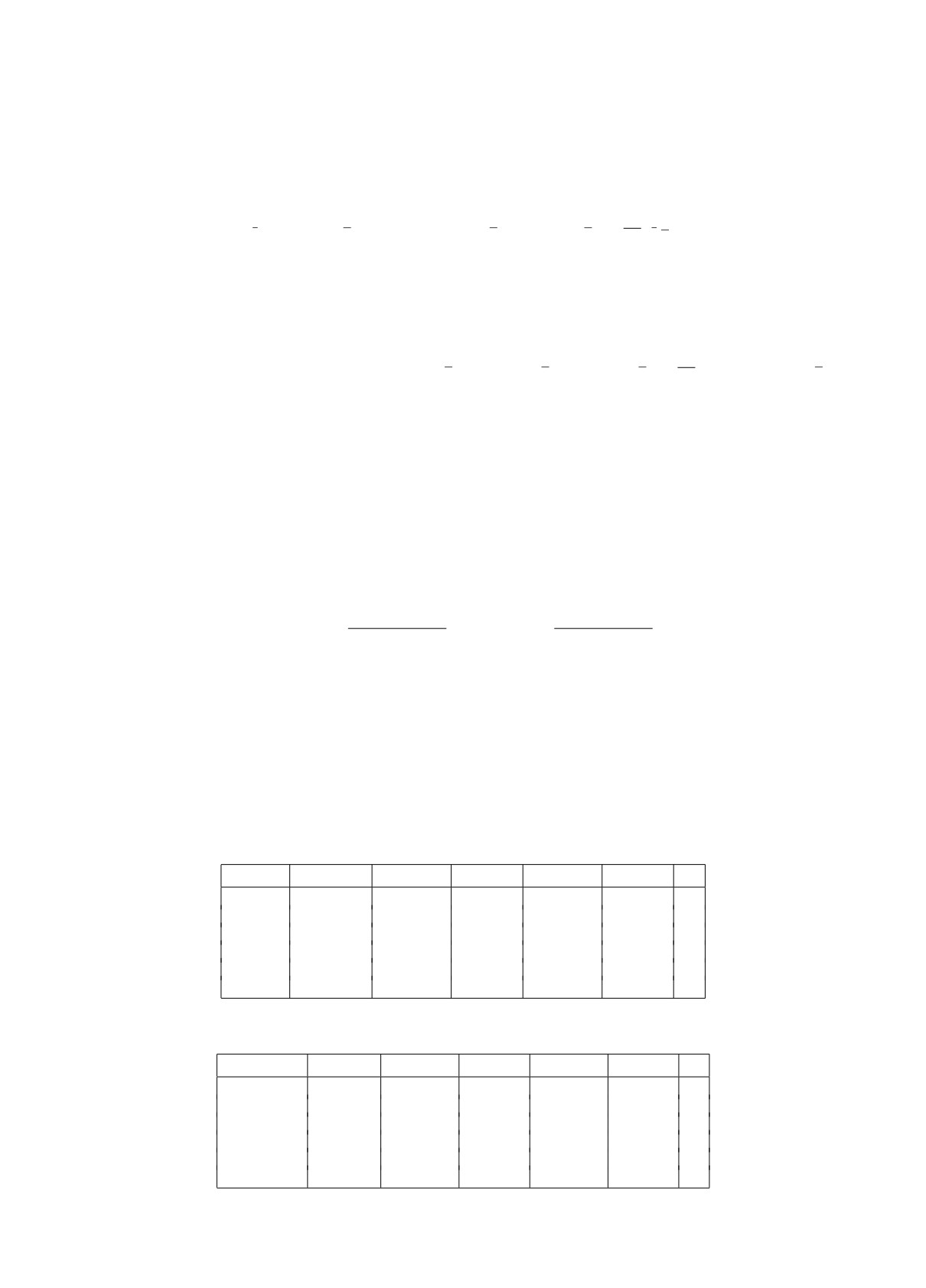
Таблица 1. Скорость сходимости по пространственному направлению

∥z∥L∞

p^hL∞

∥z∥L2

phL2

h0=0.5

τ0 = 0.25

1.29E-02

1.05E-02

h0/2¹

τ0/4¹

7.47E-04

4.10917

6.20E-04

4.08544

h0/2²

τ0/4²

4.49E-05

4.05519

3.82E-05

4.02065

h0/2³

τ0/4³

2.79E-06

4.00895

2.38E-06

4.00215

h0/2⁴

τ0/4⁴

1.75E-07

3.99592

1.49E-07

3.9998

h0/2⁵

τ0/4⁵

1.16E-08

3.91571

9.94E-09

3.90473

Таблица 2. Скорость сходимости по временному направлению

∥z∥L∞

p^τL∞

∥z∥L2

pτL2

h0 = 0.001 τ0=0.25

1.32E-02

1.11E-02

τ0/2¹

3.34E-03

1.97629

2.59E-03

2.09106

τ0/2²

7.66E-04

2.12479

6.25E-04

2.05417

τ0/2³

1.79E-04

2.10033

1.54E-04

2.02276

τ0/2⁴

4.49E-05

1.99439

3.82E-05

2.00736

τ0/2⁵

1.12E-05

1.99691

9.55E-06

2.00212

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

974

МАТУС, ХОАНГ

Отсюда видим, что построенная разностная схема имеет четвёртый порядок точности по

пространственной переменной и второй по временной.

Кроме того, на рис. 1, 2 по цветам и фигурам хорошо видна сходимость приближённого

решения к точному решению при измельчении шагов сетки h и τ. Для удобства визуального

наблюдения приведённые результаты получены в области 0 ≤ x ≤ 10,

0 ≤ t ≤ 10.

(а)

(б)

Рис. 1. Численное (а) и точное (б) решения при h = 0.5, τ = 0.5.

(а)

(б)

Рис. 2. Численное (а) и точное (б) решения при h = 0.25, τ = 0.125.

Проведённый вычислительный эксперимент подтверждает наши теоретические выводы.

СПИСОК ЛИТЕРАТУРЫ

1. Самарский А.А. Теория разностных схем. М., 1989.

2. Самарский А.А., Вабищевич П.Н., Матус П.П. Разностные схемы с операторными множителями.

Минск, 1998.

3. Lemeshevsky S., Matus P., Poliakov D. Exact Finite-Difference Schemes. De Gruyter, 2016.

4. Вабищевич П.Н. Двухслойные схемы повышенного порядка аппроксимации для нестационарных

задач математической физики // Журн. вычислит. математики и мат. физики. 2010. Т. 50. № 1.

С. 118-130.

5. Паасонен В.И. Компактные схемы для систем уравнений второго порядка с конвективными членами

// Числ. методы механики сплошной среды. 1998. Т. 3. № 1. С. 55-66.

6. Самарский А.А. Схемы повышенного порядка точности для многомерного уравнения теплопровод-

ности // Журн. вычислит. математики и мат. физики. 1963. Т. 3. № 5. С. 812-840.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

КОМПАКТНЫЕ РАЗНОСТНЫЕ СХЕМЫ НА ТРЁХТОЧЕЧНОМ ШАБЛОНЕ

975

7. Толстых А.И. Компактные разностные схемы и их применение в задачах аэрогидродинамики. М.,

1990.

8. Паасонен В.И. Обобщение методов повышенной точности для нелинейных уравнений 2-го порядка

в ортогональных системах координат // Числ. методы механики сплошной среды. 1977. Т. 8. № 2.

С. 94-99.

9. Паасонен В.И. Диссипативные асимметричные компактные схемы для уравнения колебаний // Вы-

числит. технологии. Спец. выпуск. 2001. Т. 6. № 2. С. 475-479.

10. Caudrey P.J., Eilbeck J.C., Gibbon J.D. The sine-Gordon equation as a model classical field theory // Il

Nuovo Cimento B. Ser. 11. 1975. V. 25. № 2. P. 497-512.

11. Luo Y., Li X., Guo C. Fourth-order compact and energy conservative scheme for solving nonlinear

Klein-Gordon equation // Numer. Methods Partial Differ. Equat. 2017. V. 33. № 4. P. 1283-1304.

12. Матус П.П., Хоанг Тхи Киеу Ань. Компактные разностные схемы для уравнения Клейна-Гордона

// Докл. НАН Беларуси. 2020. Т. 64. № 5. С. 526-533.

13. Матус П.П., Хоанг Тхи Киеу Ань. Компактные разностные схемы для уравнения Клейна-Гордона

с переменными коэффициентами // Докл. НАН Беларуси. 2021. Т 65. № 1. С. 25-32.

14. Москальков М.Н. О точности разностных схем, аппроксимирующих волновое уравнение с кусочно-

гладкими решениями // Журн. вычислит. математики и мат. физики. 1974. Т. 14. № 2. С. 390-401.

15. Матус П.П., Панайотова Й.Н. Коэффициентная устойчивость трехслойных операторно-разност-

ных схем // Журн. вычислит. математики и мат. физики. 2001. Т. 41. № 5. С. 722-731.

16. Самарский А.А., Гулин А.В. Устойчивость разностных схем. М., 1973.

Институт математики НАН Беларуси,

Поступила в редакцию 31.12.2020 г.

г. Минск,

После доработки 31.12.2020 г.

Католический университет им. Иоанна-Павла II,

Принята к публикации 27.04.2021 г.

г. Люблин, Польша,

Белорусский государственный университет,

г. Минск

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021