ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 7, с.988-1002

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.63+517.958:532.5

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ

РЕЛАКСАЦИОННОЙ МОДЕЛИ БАЕРА-НУНЦИАТО

С ПОМОЩЬЮ РАЗРЫВНОГО МЕТОДА ГАЛЁРКИНА

Предлагается численный метод для решения задач двухфазной двухскоростной гидроди-

намики в рамках модели Баера-Нунциато c релаксацией. Уравнения модели решаются

с помощью разрывного метода Галёркина с лимитером WENO-S, который применяется

непосредственно к консервативным переменным модели. Релаксационные процессы моде-

лируются с использованием неявного метода Рунге-Кутты второго порядка с адаптивным

выбором шага интегрирования. Алгоритм включает в себя метод Ньютона для решения

уравнений нелинейного метода Рунге-Кутты. Соответствующие матрицы Якоби вычисля-

ются с применением численного дифференцирования. Приводятся результаты численных

расчётов, демонстрирующих возможности предложенного алгоритма. Проводится сравне-

ние результатов численных расчётов с аналитическим решением, а также с результатами,

полученными другими авторами. Представлены результаты численных экспериментов с

различными скоростями релаксации, в том числе рассмотрен случай “жёсткой” релакса-

ции.

DOI: 10.31857/S0374064121070116

Введение. В настоящей работе рассматриваются вопросы численного решения двухфаз-

ной полностью неравновесной модели Баера-Нунциато (Б.-Н.) с релаксационными слагаемы-

ми. Впервые данная модель была предложена в работе [1] для анализа процесса перехода де-

флаграции в детонацию при моделировании динамики горения гранулированных взрывчатых

веществ. В дальнейшем она применялась для решения широкого спектра задач и в настоящее

время может рассматриваться как базовая модель для целого ряда обобщений [2-6].

Математическая формулировка модели приведена в п. 1 настоящей работы. Укажем здесь

основные свойства системы уравнений Б.-Н., которые усложняют задачу построения вычис-

лительных алгоритмов для её решения. Система уравнений Б.-Н. является гиперболической

системой первого порядка и включает в себя уравнения как в дивергентной форме, так и в

квазилинейной. Она не может быть записана в дивергентной форме. Система включает в себя

релаксационные слагаемые, которые описывают процесс релаксации механических и термо-

динамических параметров фаз к равновесному значению. По крайней мере в ряде приложе-

ний характерные времена релаксации могут быть значительно меньше характерных времён

протекания гидродинамических процессов. В этом смысле система уравнений Б.-Н. является

“жёсткой”.

Вследствие сказанного численное решение уравнений Б.-Н. представляет собой сложную

задачу, решению которой посвящено значительное число работ. Большая их часть направлена

на преодоление указанных выше трудностей.

Из многочисленных методов решения системы уравнений Б.-Н. далее будем рассматривать

только методы годуновского типа. Основой методов этого класса является способ постановки

и решения задачи Римана о распаде разрыва. Применительно к системе уравнений Б.-Н. ос-

новным вопросом является корректное определение обобщённого решения. Возникающая при

этом трудность связана с тем, что, как сказано выше, эта система включает в себя уравнения

как в дивергентной, так и в квазилинейной форме. Это делает классическое определение обоб-

щённого решения неприменимым в рассматриваемом случае. Наиболее хорошо разработанным

способом разрешения данной проблемы является теория, предложенная в фундаментальной

работе [7]. Этот подход используется в настоящей работе.

Способам построения схем высокого порядка для модели Б.-Н. посвящено значительное

число работ (см., например, [8-11]). Большинство из них основывается на применении методов

988

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ РЕЛАКСАЦИОННОЙ МОДЕЛИ

989

типа WENO. В настоящей работе применяется разрывный метод Галёркина/Рунге-Кутты

(RK/DG, Runge-Kutta/Discontinuous Galerkin method [12]). Такой выбор обусловлен тем, что

разрывный метод Галёркина допускает формальные обобщения на случай уравнений высокого

порядка, к которым сводятся модели типа Б.-Н.

В рамках настоящей работы модель Б.-Н. рассматривается в качестве основы для даль-

нейших обобщений. В силу этого используются алгоритмы, наиболее полно отвечающие идее

“physics-free”, т.е. минимально учитывающие особенности задачи, но, вместе с тем, пригодные

для получения конечных результатов с приемлемой точностью. По этой причине в настоящей

работе:

- используется максимально простой численный поток Русанова, гарантирующий устойчи-

вость аппроксимаций;

- лимитирование решения осуществляется в терминах консервативных переменных, без

перехода к характеристическим.

Для монотонизации решения используется лимитер WENO-S [13].

Одной из основных трудностей при решении задач с использованием модели Б.-Н. явля-

ется учёт релаксационных процессов. Более общая модель Б.-Н. с жёсткой релаксацией даёт

результаты в соответствии с менее общими равновесными моделями [3-5], причём при этом

делается значительно меньше предположений относительно протекающих физических процес-

сов в многофазной среде. В этой модели релаксация скоростей фаз и их термодинамических

параметров учитывается в виде источниковых слагаемых, при наличии которых система урав-

нений может становиться жёсткой. С вычислительной точки зрения операция интегрирования

таких систем является сложной, поскольку характерные времена релаксации могут быть зна-

чительно меньше, чем шаг интегрирования по времени в вычислительной схеме.

Разработка эффективных методов аппроксимаций уравнений Б.-Н. в настоящее время не

вполне завершена. Основные усилия направлены здесь на разработку методов интегрирования

жёстких систем уравнений специального вида и алгоритмов решения полной задачи с учётом

релаксационных слагаемых, в частности, разработку соответствующих схем расщепления по

физическим процессам. Работы в этой области сосредоточены в основном в направлении раз-

вития так называемых асимптотически корректных разностных схем (“asymptotic preserving

schemes”) (см. [14, 15]), которые, в частности, имеют равномерную по малому времени релак-

сации скорость сходимости численных аппроксимаций.

Целью настоящей работы является реализация и демонстрация возможностей алгоритма,

который основывается на таких сравнительно простых средствах численных методов как:

- разрывный метод Галёркина для построения пространственных аппроксимаций уравне-

ний модели;

- лимитирование консервативных переменных с использованием геометрического лимитера

WENO-S;

- теория Dal Maso-Le Floch-Murat для формулировки задачи Римана и, как следствие,

численных потоков для неконсервативной “части” задачи;

- простейшее расщепление по физическим процессам для учёта жёстких релаксационных

слагаемых;

- неявный метод Рунге-Кутты для интегрирования уравнений модели.

Эффективность предложенной методики иллюстрируется результатами численных экспе-

риментов в одномерном случае.

Структура работы следующая. Математическая модель Б.-Н. и её особенности представ-

лены в п. 1. Разрывный метод Галёркина для гиперболических уравнений с неконсерватив-

ными слагаемыми кратко описан в пп. 2.1. Алгоритм вычисления релаксационных слагаемых

изложен в пп. 2.2. Схема лимитирования представлена в пп. 2.3. Результаты численных экс-

периментов приведены в п. 3.

1. Модель Баера-Нунциато с релаксацией. Модель Б.-Н. с релаксационными слага-

емыми, описывающая двухфазное течение, может быть представлена в виде системы гипер-

болических уравнений [5]

∂α_k

+ u_I · ∇α_k = ν(P_k - P_k),

(1.1a)

∂t

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

990

ТУХВАТУЛЛИНА и др.

∂α_kρ_k

+ ∇ · (α_kρ_ku_k) = 0,

(1.1b)

∂t

∂α_kρ_ku_k

+ ∇ · (α_kρ_ku_k

^⊗u_k) + ∇(α_kP_k) - P_I∇α_k = μ(u_k - u_k),

(1.1c)

∂t

∂α_kρ_kE_k

+ ∇ · (α_k(ρ_kE_k + P_k)u_k) - P_Iu_I∇α_k = μ(u_k - u_k) · u_I + ν(P_k - P_k)P_I.

(1.1d)

∂t

Здесь α_k, ρ_k, u_k, P_k, E_k - объёмная доля, плотность, поле скоростей, давление и полная

энергия фазы k = 1, 2 соответственно; k = {1, 2} \ {k}; ν, μ - релаксационные параметры.

Для объёмных долей выполнено условие нормировки α₁ + α₂ = 1. Полная энергия k-й фазы

определяется равенством

E_k = U_k + u_k · u_k/2,

где U_k - внутренняя энергия фазы.

Уравнения модели (1.1) включают в себя уравнение динамики для объёмной доли (1.1a),

законы сохранения массы (1.1b), импульса (1.1c) и энергии (1.1d).

Величины u_I и P_I являются так называемыми “интерфейсными” скоростью и давлени-

ем. Для замыкания модели необходимо указать их конкретную зависимость от переменных

задачи. Она может быть определена целым рядом способов, причём выбор замыкающих соот-

ношений непосредственно влияет на структуру волн и поведение фаз в модели (см. [1, 16-18]).

В настоящей работе используется вариант, предложенный в основополагающей работе [1]:

u_I = u₁, P_I = P₂,

где k = 1 соответствует менее плотной фазе (более сжимаемой), k = 2 - более плотной фазе

(менее сжимаемой). Термодинамические свойства фаз определяются уравнениями состояния

вида U_k = U_k(P_k, ρ_k). В данной работе они определены равенствами

P_k + γ_kP_∞,k

U_k =

(γ_k - 1)ρ_k

где P_∞,k и γ_k - параметры.

Отметим, что система уравнений (1.1) содержит недивергентные члены вида P_I∇α_k и не

может быть записана в консервативном виде. Эта особенность является типичной для целого

ряда многофазных многоскоростных моделей (см. [19]).

2. Вычислительные алгоритмы. Рассматриваемый алгоритм численного решения сис-

темы уравнений (1.1) основан на следующих подходах: использовании расщепления по физиче-

ским процессам для расчёта релаксационных правых частей системы; применении разрывного

метода Галёркина для решения однородной системы (1.1) и неявного метода Рунге-Кутты для

интегрирования “жёстких” правых частей системы (1.1). Далее описаны основные компоненты

полного алгоритма решения задачи.

2.1. Разрывный метод Галёркина. В данном пункте представлена схема разрывно-

го метода Галёркина [11] для одномерного варианта неоднородной гиперболической системы

уравнений (1.1), записанной в абстрактной форме

∂Q(x,t)

∂Q

+ B(Q)

= S(Q),

(2.1)

∂t

∂x

где x ∈ Ω = [0, L] ⊂ R, t ∈ [0, T ] ⊂ R, Q = Q(x, t) = (Q₁, . . . , Q_M )^т - решение уравнения (2.1),

M = 7 - число компонент вектора Q,

B(Q) = ∂F(Q)/∂Q + A(Q).

(2.2)

Здесь A - заданная матрица, зависящая от решения задачи и определяющая квазилинейную

“часть” системы уравнений, F - заданный вектор потоков, B - матрица системы, записанной

в квазилинейной форме, S - плотность источников. Далее считается, что матрицы A, B и

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ РЕЛАКСАЦИОННОЙ МОДЕЛИ

991

вектор поток F являются непрерывными и имеют требуемое количество производных как

функции вектора переменных Q. Обобщённое решение данной задачи для консервативных

систем (в случае, когда A(Q) = 0) может быть определено в классе обобщённых функций.

Для неконсервативных систем (т.е. в случае, когда A(Q) = 0) обобщённое решение не может

быть определено так же, как в случае консервативных систем. Для решения этой проблемы в

настоящей работе используется распространённый подход, основанный на применении теории

DLM (Dal Maso-Le Floch-Murat [7]). В рамках этого подхода для корректного определения

“неконсервативного произведения” вида A(Q) вводится липшицево отображение Ψ : [0, 1] ×

× R⁷ → R⁷ (путь), которое “соединяет” левое значение решения в точке разрыва с правым:

Ψ(Q⁺, Q^-; 0) = Q^-, Ψ(Q⁺, Q^-; 1) = Q⁺, Ψ(Q, Q; s) = Q.

Введём разбиение {ω_i}i=Ni=0 области Ω и обозначим ячейку сетки (конечный элемент)

ω_i = [xi-1/2,xi+1/2],

1≤i≤N.

Обозначим через V^kh(Ω) подпространство в L¹(Ω), состоящее из тех элементов, сужения (огра-

ничения) которых на ячейки ω_i принадлежат векторному пространству P^k(ω_i) полиномов

степени не выше k:

V^kh = {v ∈ L¹(Ω) : v|ωi ∈ P^k(ω_i);

1 ≤ i ≤ N}.

Представим решение Q(x, t) в ячейке ω_i конечномерной аппроксимацией Q_h ∈ V^kh:

∑

Q_h(x,t)|ωi =

ψ(l)i(x)Q(l)i(t),

(2.3)

l=0

где ψ(l)i - полином Лежандра степени l. Здесь и в дальнейшем индекс i обозначает при-

надлежность i-й ячейке. Чтобы получить полудискретную систему уравнений для Q_h(x, t),

умножим уравнение (2.1) на пробную функцию v_h ∈ V^kh и проинтегрируем получившееся

тождество по отрезку ω_i:

∫

]

∫

∂Q_h(x,t)

∂Q(·,t)

v_h(x)dx + B(Q(·,t))

,v_h

S(Q_h)v_h(x) dx.

∂t

∂x

ω_i

Неконсервативное произведение может быть определено в обобщённом смысле следующим

образом [20]:

]

∫

∂Q

∂Q(x,t)

B(Q)

,v_h

^def=

B(Q(x, t))

v_h(x)dx +

∂x_Ψ

∂x

ω_i

(∫1

)

∑

∂Ψ

B(Ψ(Q+d, Q^-d, s))

(Q+d, Q^-d, s) ds v_h(x_d),

(2.4)

∂s

где индекс d нумерует точки разрыва решения Q, при этом Q+d и Q^-d - предельные значения

решения соответственно справа и слева от разрыва в точке x_d в момент времени t. Заметим,

что данное определение существенно зависит от выбранного пути Ψ. В случае, когда A = 0

произведение (2.4) не зависит от выбранного пути и совпадает с классическим определением

обобщённого произведения. Следствием определения (2.4) и системы (2.1) без релаксационных

слагаемых является условие Гюгонио, которому должно удовлетворять обобщённое решение

в точках разрыва x_d:

∫

∂Ψ

(ξ_dI - B(Ψ(Q^-d, Q+d; s)))

(Q^-d, Q+d; s)ds = 0,

∂s

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

992

ТУХВАТУЛЛИНА и др.

где ξ_d - скорость движения разрыва, I - единичная матрица. С учётом равенства (2.2) полу-

чим

]

∫

(

)

∂Q

∂Q(x,t)

∂F(Q)

B(Q)

,v_h

A(Q(x, t))

v_h(x)dx +

∂x_Ψ

∂x

ω_i

(

(∫1

))

∑

∂Ψ

F (Q+d) - F(Q^-d) +

A(Ψ(Q+d, Q^-d, s))

(Q+d, Q^-d, s) ds v_h(x_d).

∂s

Постановка задачи Римана для соответствующей неконсервативной системы представлена

в [20]. На основе сделанных выше построений могут быть выведены соответствующие схе-

мы типа Годунова. В частности, численная схема для разрывного метода Галёркина может

быть записана в виде

∫

(

)

∂Q_h

v_h(x)dx +

A(Q_h)

+ F(Q_h) v_h(x)dx +

∂t

∂x

ω_i

∫

+ (v_h(xi+1/2)^-D^-

+ v_h(xi+1/2)⁺D⁺

) = S(Q_h)v_h(x)dx,

i+1/2

i-1/2

ω_i

где D∓i±1/2 и v_h(xi±1/2)^∓ определены на границах соответствующих ячеек,

∫1

D-i+1/2 = F(Qi+1) - F(Q-i+1/2) + A(Ψ(Q-i+1/2,Qi+1;s))∂Ψ(Q-i+1/2,Qi+1; s) ds,

∂s

∫1

D+i+1/2 = F(Q+i+1/2) - F(Qi+1) + A(Ψ(Qi+1,Q+i+1/2;s))∂Ψ( Qi+1,Q+i+1/2;s)ds,

∂s

здесь

Qi+1 - решение задачи Римана на границе ячеек.

Пусть выбран линейный путь Ψ(Q^-, Q⁺; s) = Q^-d + s(Q+d - Q^-d) и в качестве численного

потока используется поток Русанова. Тогда в точках разрыва x_d = xi±1/2 будем иметь

∫

D^±d = F(Q+d) - F(Q^-d) + A^±d(Q+d - Q^-d), A^±d =

(A(Q^-d + s(Q+d - Q^-d)) ± IΛ) ds,

где Λ = λ(s) - максимальные собственные значения матрицы B(Q^-d + s(Q+d - Q^-d)). От-

метим, что применение более простого потока Лакса-Фридрихса приводит, вообще говоря, к

неустойчивой схеме (см. приложение 2).

Рассматривая произвольный полином v_h(x) ∈ span {ψ(l)i}, получаем следующую полудис-

кретную систему уравнений относительно переменных

{Q(l)i}, определённых в представле-

нии (2.3):

dQi

= H( Qi) + I( Qi).

(2.5)

Q_i

Здесь

= (Q(0)1,i, . . . , Q(0)M,i, . . . , Q(k)M,i) - вектор неизвестных. Его компоненты Q(l)m,i в даль-

нейшем будем называть l-й гармоникой (l = 0, k) m-й компоненты вектора Q_i. Матри-

ца M ∈ RM(k+1)×M(k+1) является матрицей Грама указанной системы базисных функций,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ РЕЛАКСАЦИОННОЙ МОДЕЛИ

993

вектор H(Qi) представляет собой аппроксимацию дифференциального оператора в левой час-

ти системы уравнений (2.1), а вектор I(Qi) - аппроксимацию правой части (2.1),

∫

I(l)m = S_m(Q_h)ψ(l)i dx.

(2.6)

ω_i

Одна из наиболее простых стратегий решения системы (2.5) - расщепление по процессам

первого порядка. Разобьём временной интервал на части точками {tn}. Далее на каждом

временном шаге t ∈ [tⁿ, tn+1] сначала решается задача Коши для системы ОДУ

dQi

= H( Qi), t ∈ (tⁿ,tn+1],

(2.7)

c начальными данными

= Q_i(tⁿ) для определения “промежуточного” решения

Qi,H

= Q_i(tn+1). Затем решается задача Коши для системы ОДУ

dQi

= I( Qi), t ∈ (tⁿ,tn+1],

(2.8)

с начальными данными

Qi,H.

Для интегрирования по времени однородной системы (2.7) далее используется вариант ме-

тода Рунге-Кутты TVD/RK3 [12] с лимитированием консервативных переменных на каждом

шаге метода. В настоящей работе используется лимитер WENO-S, описанный в п. 2.3. Для

интегрирования по пространству применяется метод квадратур Гаусса-Лежандра.

Для интегрирования системы уравнений (2.8) используется неявный алгоритм Рунге-Кут-

ты с автоматическим выбором шага интегрирования, описанный в п. 2.2.

2.2. Алгоритм расчёта релаксационных слагаемых. Задача Коши для ОДУ (2.8) ре-

шается неявным методом Рунге-Кутты второго порядка на временном интервале t ∈ (tⁿ, tn+1].

Разобьём временной интервал на части точками (tn0, tn1, . . . , tnM-1), где tnj+1 = t^nj + τ_j, tn0 = t_n,

tnM-1 = tn+1. Таким образом, Δt = tn+1 - tⁿ - шаг интегрирования газодинамической час-

ти задачи, а τ_j - шаг интегрирования релаксационной части. При этом шаг τ_j может быть

переменным. Разностная схема решения задачи Коши для системы (2.8) имеет следующий

вид:

Qj+1

= Q_i(tⁿ);

= Q^ji +1τk(R(Qj+1i) + R(Qji)), j = 0,1,... ,

(2.9)

где R = M-1I. Аппроксимации релаксационных членов I, определённые в (2.6), рассчиты-

ваются численно методом квадратур Гаусса-Лежандра.

Нелинейная система уравнений (2.9) решается численно методом Ньютона:

∂F (Qj+1i)/∂Qj+1i|_̃

(2.10)

Qj+1,si ·(Qi+1,s+1 -Qi+1,s)=-F(Qi+1,s)^,

Qj+1,0

где индекс s обозначает номер итерации,

= Q^ji соответствует s = 0. Функция F

имеет следующий вид:

F(Qj+1i) =Qj+1i -Qji - 0.5τ_j(R(Qj+1i) + R(Qji)).

Якобиан ∂F (Qj+1i)/∂Qj+1i в (2.10) вычисляется с применением численного дифференциро-

вания. Итерации метода Ньютона продолжаются до тех пор, пока величина r = max|rm| не

станет меньше заданного значения. Здесь r_m определены равенством

⎧

⎨₍ Qj+1,s+1

- Qj+1,si,m)/Qj+1,s+1i,m, если

|Qj+1,s+1i,m| > 1,

i,m

r_m =

⎩̃Qj+1,s+1

- Qj+1,si,m

в противном случае.

i,m

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

994

ТУХВАТУЛЛИНА и др.

В реализованном алгоритме предусмотрен автоматический выбор шага интегрирования.

В начальный момент τ₀ = 0.2Δt. В случае, если превышено максимальное число N_max нью-

тоновских итераций (далее N_max = 20) или если решение сходится к нефизичным результа-

там (отрицательное давление или объёмная доля и т.д.), то шаг интегрирования уменьшается.

В случае, когда число итераций меньше минимального значения N_min (далее N_min = 6), шаг

интегрирования увеличивается.

2.3. Лимитирование переменных. Применение лимитера WENO-S состоит из двух ша-

гов [13].

1. Идентификация ячеек, в которых решение подлежит лимитированию. В данной работе

используется TVB-идентификатор, основанный на функции minmod.

2. Применение лимитера WENO-S для реконструкции решения в отмеченных ячейках.

Идентификация ячеек, в которых решение подлежит лимитированию. Обозна-

чим через

m,i

усреднённое по объёму решение в ячейке ω_i, т.е.

∫

m,i

Q_mdx.

(2.11)

Δx_i

ω_i

Здесь, как и выше, индекс i обозначает пространственную ячейку, а индекс m обозначает

компоненту вектора

Q, m = 1,M · k.

Q+

Q-

Определим скачки численного решения в ячейках как

= Q-m,i+1/2 -Qm,i,

m,i

= Q_m,i - Q⁺

. Рассмотрим в каждой ячейке функции

m,i-1/2

(Q+m,i)^(mod) = minmod(Q+m,i,Qm,i+1 -Qm,i,Qm,i -Qm,i-1),

(Q-m,i)^(mod) = minmod(Q-m,i,Qm,i+1 -Qm,i,Qm,i -Qm,i-1),

(2.12)

где

{

s min(a₁, . . . , a_N ), если s = sign (a_k), k = 1, N ,

minmod(a₁,... ,a_N) =

в противном случае.

Решение в ячейке ω_i подлежит лимитированию, если в (2.12) (Q±m,i)^(mod) = (Q±m,i), т.е. какая-

либо из функций в (2.12) возвращает не первый аргумент.

Применение лимитера WENO-S состоит из следующих шагов.

1. Обозначим полиномы в ячейках ω_j, j = i - 1, i, i + 1, через p-1(x), p₀(x) и p₁(x)

соответственно и модифицируем решения в соседних ячейках следующим образом:

pmod-1(x) = p-1 - p-1 + p₀, p^mod1(x) = p₁ - p₁ + p₀,

где p - усреднённое по объёму решение, представленное равенством (2.11).

2. Индикаторы гладкости β_i рассчитываем по формуле

∫

(

)₂

∑

∂^l

β_i =

Δx2l-1

p_j(x) dx,

∂x^l

l=1_ω

где k - степень полинома p_j (x).

3. Весы κ_j рассчитываем по формуле

∑

γ_n

κ_j = κ_j/

κ_n, κ_n =

n = -1,0 + 1.

(ε + β_n)^r

n=-1,0,+1

Здесь γ_n - линейный вес, ε = 10-6 и r = 2. Линейные веса должны удовлетворять следующим

требованиям: γ₀ ≫ γ±1, γ-1 + γ₀ + γ₊₁ = 1. В настоящей работе γ₀ = 0.998, γ±1 = 0.001.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ РЕЛАКСАЦИОННОЙ МОДЕЛИ

995

4. Реконструкция решения в центральной ячейке ω₀ проводится по формуле

p^new0(x) = κ-1pmod-1(x) + κ₀p₀(x) + κ₁p^mod1(x).

Применение лимитера в одномерном случае может быть записано в операторном виде

p^new0 = Λ_αp₀ для направления Oxα . Для многомерного случая и декартовых сеток p^new0 =

= Λp₀, где Λ = Λ_zΛ_yΛ_x.

Общая схема решения однородной гиперболической системы с применением описанного

выше лимитера имеет приведённый ниже вид.

Для интегрирования по времени системы обыкновенных дифференциальных уравнений

(2.7) используется TVD/RK3 метод Рунге-Кутты, представленный ниже. На k-й стадии ме-

тода Рунге-Кутты используется способ лимитирования переменных, описанный выше:

= Qⁿⁱ + ΔtP( Qni ),

= ΛQ1i,

ΔtP(Q1i),

= ΛQ2i,

Qn+1

ΔtP(Q2i),

= ΛQn+1i,

где P = M-1H (см. (2.5)).

3. Вычислительные эксперименты. В настоящем пункте рассмотрен ряд тестовых рас-

чётов, которые демонстрируют возможности предложенного алгоритма. В тесте 1 проводит-

ся тестирование численного алгоритма решения системы ОДУ (2.8). Приводится сравнение

с численными результатами, полученными другими авторами [21], а также с аналитическим

решением (см. приложение 1). В тесте 2 численно исследуется метод для решения полной

задачи (1.1). Рассматриваются численные расчёты задачи Римана с различными коэффици-

ентами релаксации. Приводится сравнение с численными результатами, полученными конечно-

объёмной схемой первого порядка с численным потоком HLLEM (соответствующие решения

далее называются “решения HLLEM”). Все расчёты предложенным методом приведены для

разрывного метода Галёркина с линейным восполнением решения в ячейках сетки, что соот-

ветствует k = 1 в аппроксимации (2.3).

Результаты расчётов представлены для примитивных переменных (фазовые давления и

скорости).

Тест 1. Рассматривается задача Коши для уравнения (2.8).

Начальные условия имеют следующие вид: для нулевых гармоник

u₁ = -5, u₂ = 5, P₁ = 0.1, P₂ = 20, α₁ = 0.9, ρ₁ = 1.1111, ρ₂ = 40,

для первых гармоник

Q⁽¹⁾

= 0.01 · Q(0)2,3,6,7,

= 0.

2,3,6,7

1,4,5,8,9

Параметры уравнения состояния: γ₁ = 6, π₁ = 0 Па, γ₂ = 1.4, π₂ = 0 Па. Значения пара-

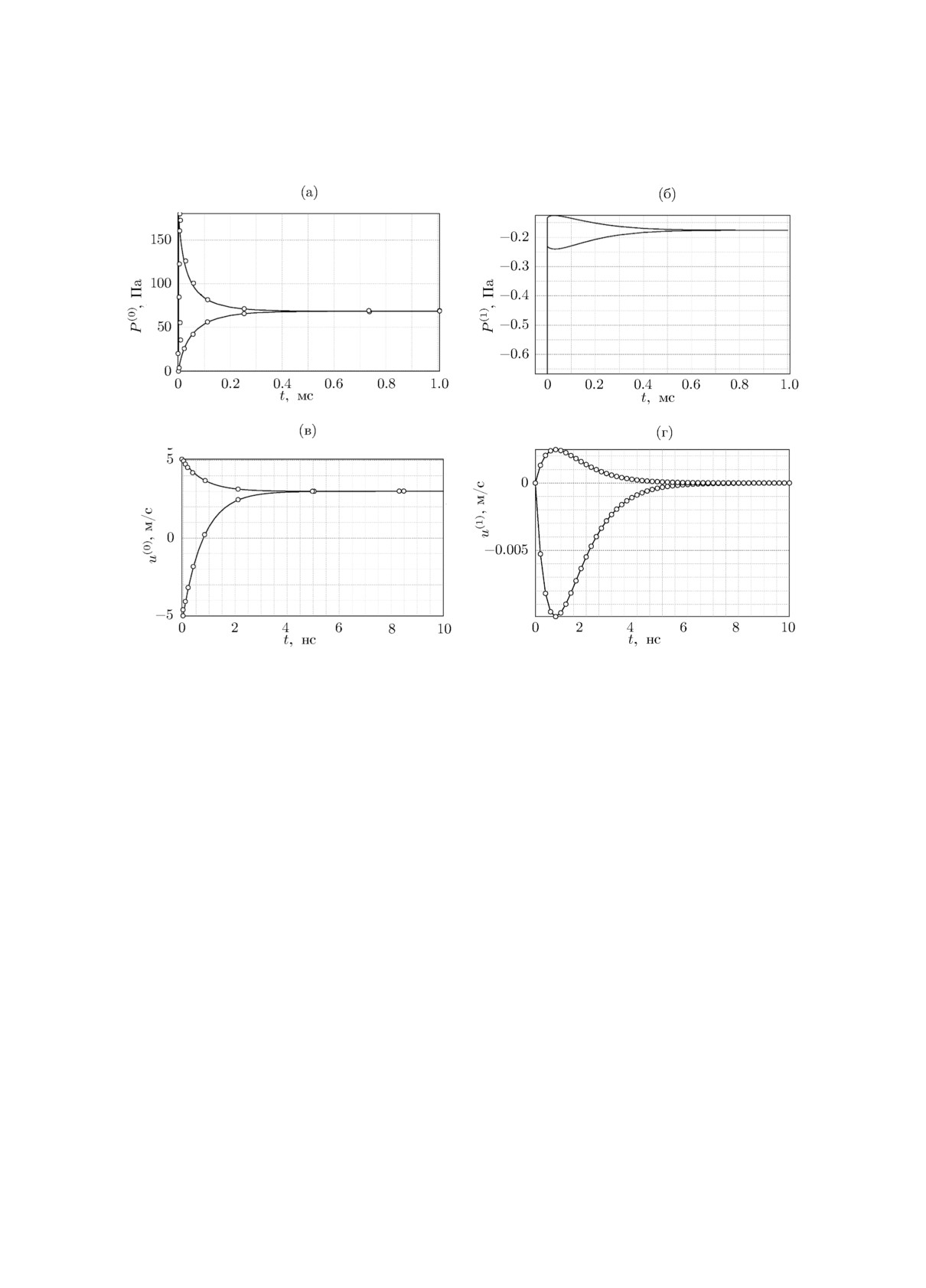
метров релаксации μ = 10⁹ кг/(м ·c) и ν = 10 Па-1 ·c-1. На рис. 1, а и рис. 1, б представлены

результаты расчётов для нулевой и первой гармоник фазовых давлений соответственно с τ₀ =

= 2·10-4 c. При расчёте с шагом τ₀ = 2·10-4 c скорости фаз сразу выходят на стационарное

значение 3 м/с (эти результаты не показаны на рис. 1). На рис. 1, в и рис. 1, г представлены

результаты расчётов для нулевой и первой гармоник фазовых скоростей соответственно с τ₀ =

= 2 · 10-9 c. Видим, что численный расчёт хорошо согласуется с результатами, полученными

в [21] для нулевых гармоник (фазовые скорости и давления), а также хорошо согласуется с

аналитическим решением для первых гармоник (фазовые скорости). Аналитическое решение

для первых гармоник фазовых давлений в данной работе получено не было и сравнение с ним

не приводится. Также видно, что нулевые и первые гармоники для фазовых давлений и ско-

ростей релаксируют на одних и тех же временах. Резкое изменение давления (см. рис. 1, а и

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

9^∗

996

ТУХВАТУЛЛИНА и др.

рис. 1, б) в начальный момент времени связано с релаксацией скоростей, которая происходит

на временах порядка 10 нс.

Рис. 1. Тест 1. Сплошные кривые - результаты численного расчёта, символы на (а) и (в) - результаты

численного расчёта в [21], символы на (г) - аналитическое решение.

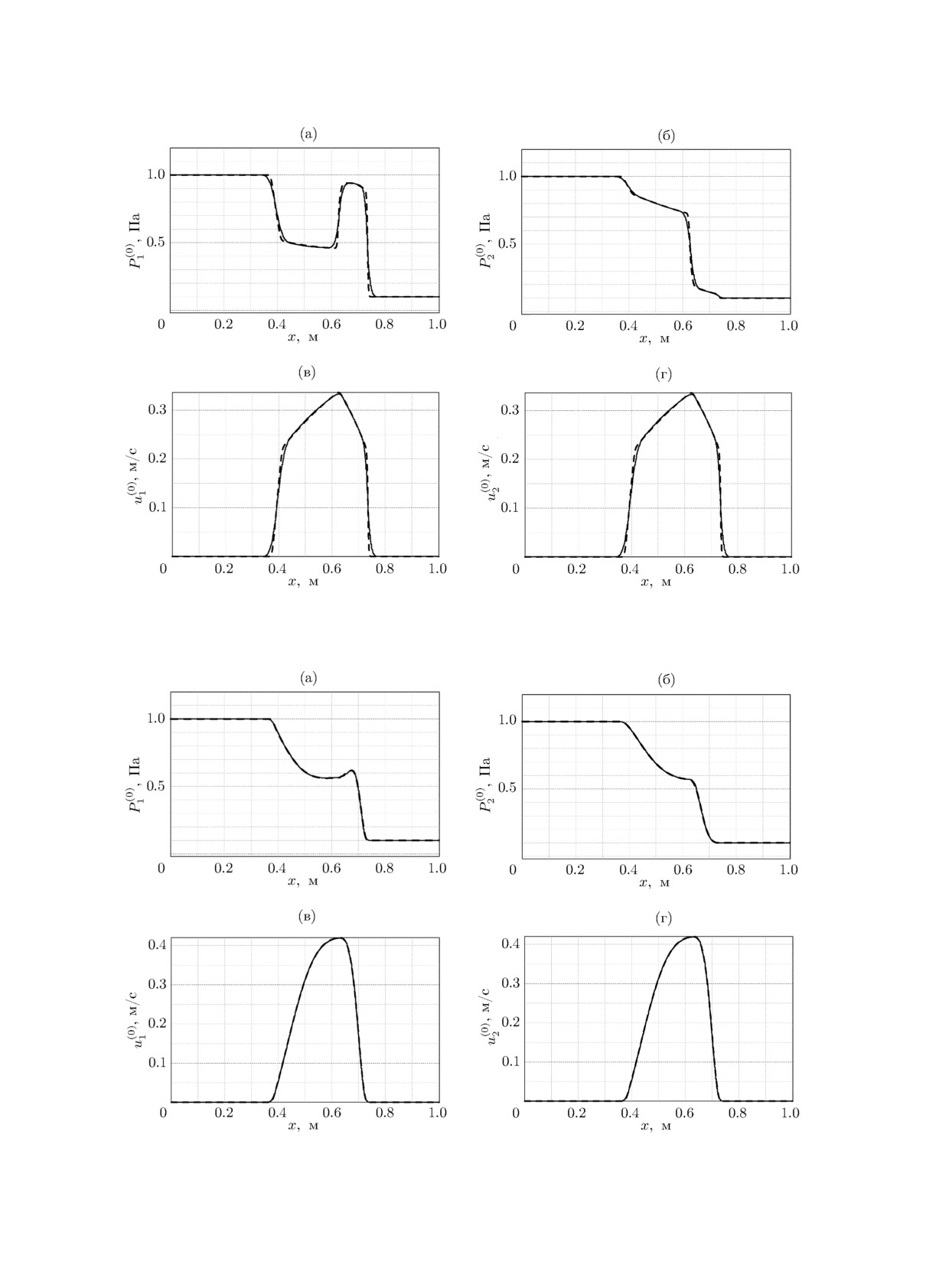
Тест 2. В данном тесте рассматривается задача Римана о распаде разрыва системы урав-

нений (1.1). В начальный момент времени разрыв находится в точке x₀ = 0.6 м. Длина рас-

чётной области 1 м. Слева от разрыва P₁ = P₂ = 1, ρ₁ = 1, ρ₂ = 0.2, u₁ = u₂ = 0, α₁ = 0.55,

справа от разрыва P₁ = P₂ = 0.1, ρ₁ = 0.125, ρ₂ = 2, u₁ = u₂ = 0, α₁ = 0.45. Параметры

уравнения состояния

γ₁ = 2, π₁ = 2Па, γ₂ = 1.4, π₂ = 0Па.

Число узлов сетки и шаг по времени задавались как N = 500 и Δt = 10-6 c. Значение па-

раметра релаксации μ = 10⁶кг/(м · c), что соответствует времени релаксации меньшему, чем

газодинамический шаг интегрирования по времени. Значения параметра релаксации ν = 1,

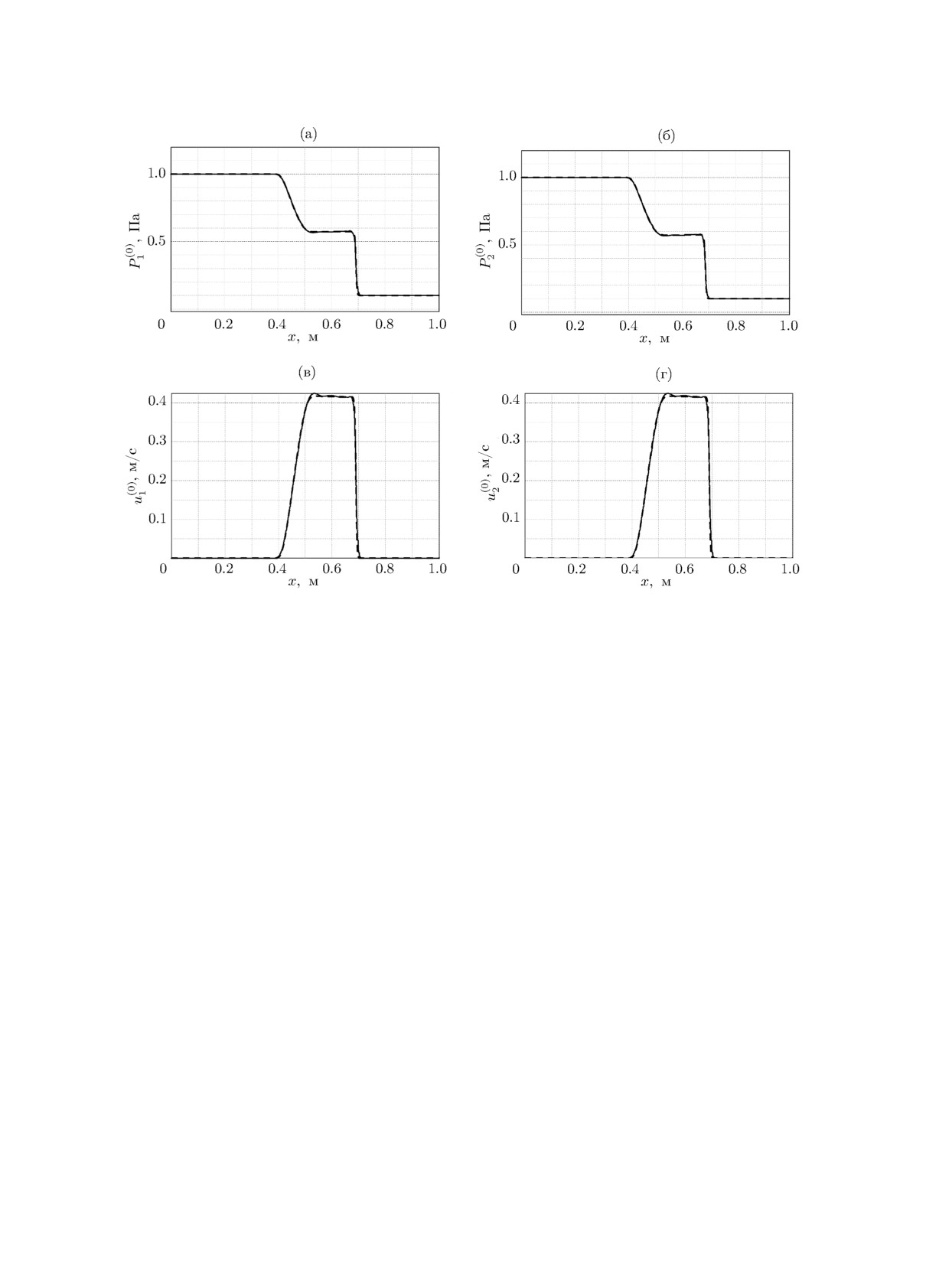
10 и 100 Па-1 · c-1 (рис. 2-4). На графиках показаны только нулевые гармоники. Видим,

что результаты численных расчётов хорошо согласуются с результатам HLLEM для всех ко-

эффициентов релаксации (см. рис. 2-4), а также что величина времени релаксации принципи-

ально меняет структуру разрывов. Небольшая немонотонность результатов, представленных

на рис. 4, по-видимому, связана с численным расчётом матрицы Якоби в методе Ньютона, а

именно, с выбором шага численного дифференцирования.

Результаты расчётов при помощи конечно-объёмной схемы с потоком HLLEM получены на

сетке с N = 10 000 шагами. Все остальные параметры не менялись.

Представленные результаты демонстрируют, что предложенный алгоритм обеспечивает

устойчивый расчёт решения задачи при достаточно широком диапазоне изменения парамет-

ров релаксации, в том числе при жёсткой релаксации, и позволяет добиться сходного каче-

ства разрешения фронтов по сравнению с конечно-объёмной схемой первого порядка с потока-

ми HLLEM при условии одновременного использования: (а) значительно более грубых сеток;

(б) наиболее простых численных потоков типа Русанова; (в) лимитирования консервативных

переменных.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

998

ТУХВАТУЛЛИНА и др.

Рис. 4. Тест 2. Коэффициенты релаксации μ = 10⁶ кг/(м · c) и ν = 100 Па-1 · c-1. Сплошные

линии - результаты численного расчёта (N = 500), штриховые линии - результаты численного

расчёта HLLEM (N = 10 000).

Заключение. В работе представлен подход к численному решению многофазной полно-

стью неравновесной модели Баера-Нунциато с релаксационными слагаемыми в одномерном

случае. В качестве численной схемы используется разрывный метод Галёркина с применением

численного потока Русанова. Для монотонизации решения используется лимитер WENO-S,

применяемый непосредственно к консервативным переменным модели. Учёт релаксационных

слагаемых в численной схеме проводится неявным методом Рунге-Кутты второго порядка с

адаптивным выбором шага интегрирования. Соответствующая нелинейная система уравнений

решается методом Ньютона. Представленный комплексный подход применяется к одномерным

тестовым задачам. Результаты соответствуют полученным ранее для численных схем с пото-

ком HLLEM. В работе показано, что использование разрывного метода Галёркина позволяет

добиться сходного разрешения волновых фронтов при значительно меньшем числе расчётных

ячеек, чем в методах с использованием большей информации об исходной системе уравнений.

4. Приложения.

Приложение 1. Для уравнения релаксации скоростей (см. систему ОДУ (2.8)) можно

выписать точное аналитическое решение задачи, которое имеет вид

Q(l)

W (t) = exp(At)W (t₀), t > t₀;

(t) =Q(l)2,3(t₀), t = t₀,

2,3

где l = 0, 1, а вектор W и матрица A имеют следующий вид:

⎛

⎞

Q⁽⁰⁾

⎛

⎞

a₁₁

a₁₂

a₁₃

a₁₄

⎜

(1)

⎟

⎜Q

⎟

⎜

b₁₁

b₁₂

b₁₃

b₁₄

⎟

W =

⎜

⎟,

⎝

⎠.

⎝

Q⁽⁰⁾

⎠

−a₁₁

-a₁₂

-a₁₃

-a₁₄

−b₁₁

-b₁₂

-b₁₃

-b₁₄

Q⁽¹⁾

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ РЕЛАКСАЦИОННОЙ МОДЕЛИ

999

Q(0,1)

Согласно (1.1) имеем

= (α₁ρ₁)(0,1),

= (α₂ρ₂)(0,1),

= (α₁ρ₁u₁)(0,1),

= (α₂ρ₂u₂)(0,1), где u1,2 - скорость 1-й или 2-й фазы. Постоянные коэффициенты a_ij и b_ij

имеют следующий вид:

)

(0)

⁽Q

- Q⁽¹⁾²

1 μQ(0)2

⁽ Q(0)

+ Q⁽¹⁾²

a₁₁ =

log

a₁₂ = -

log

2 Q⁽¹⁾

Q⁽⁰⁾

+ Q⁽¹⁾²

Q⁽¹⁾

2(Q⁽¹⁾²)²

Q⁽⁰⁾

- Q⁽¹⁾

(0)

)

⁽Q

⁽ Q(0)

+ Q⁽¹⁾³

1 μQ(0)3

- Q⁽¹⁾³

a₁₃ =

log

a₁₄ =

log

2 Q⁽¹⁾

Q⁽⁰⁾

Q⁽¹⁾

Q⁽⁰⁾

- Q⁽¹⁾³

2(Q⁽¹⁾³)²

+ Q⁽¹⁾

)

(0)

3 μQ

⁽ Q(0)

+ Q⁽¹⁾²

μQ(0)2

3 μ( Q(0)2)²

⁽ Q(0)

- Q⁽¹⁾²

b₁₁ = -3

log

b₁₂ = 3

log

Q⁽¹⁾

2(Q⁽¹⁾²)²

Q⁽⁰⁾

- Q⁽¹⁾²

(Q(1)2)²

2 (Q⁽¹⁾²)³

Q⁽¹⁾

+ Q⁽⁰⁾

(0)

)

⁽ Q(0)

3μ

3 μQ

- Q⁽¹⁾³

b₁₃ =

log

Q⁽¹⁾

2(Q⁽¹⁾³)²

Q⁽¹⁾

+ Q⁽⁰⁾

(0)

)

⁽ Q(0)

μQ

μ(Q(0)3)²

- Q⁽¹⁾³

b₁₄ = -3

-4

log

Q⁽⁰⁾

(Q(1)3)²

(Q(1)3)³

+ Q⁽¹⁾

Приложение 2. В настоящем приложении показывается, что простейший поток Лакса-

Фридрихса при его применении в рамках разрывного метода Галёркина с интегрированием по

времени методом TVD/RK3 приводит к неустойчивой схеме.

Утверждение. Для линейного одномерного уравнения переноса

∂q

∂f(q)

= 0; f(q) = aq, a = const,

(4.1)

∂t

∂x

с начальными условиями в виде кусочно-линейных функций

2Q₁x_i

2Q₁

q_h(x,0)|ωi = Q₀ -

x, Q0,1 = const,

(4.2)

заданными на каждом конечном элементе ω_i = [xi-1/2, xi+1/2], дискретное решение, полу-

ченное с использованием разрывного метода Галёркина с линейным восполнением решения

в ячейках, интегрированием по времени с помощью схемы TVD/RK3, описанной в п. 2.3, и

численного потока Лакса-Фридрихса вида

f (q_l, q_r) =

[f(q_l) + f(q_r)] -

(q_r - q_l),

(4.3)

2Δt

удовлетворяет неравенству

|qn+1h|>|q^nh|.

Доказательство. Считаем, что все ячейки сетки (конечные элементы) ω_i = [xi-1/2, xi+1/2]

имеют одинаковую длину h. Каждая из них может быть отображена на канонический ко-

нечный элемент ω_i = [-1, +1]. В канонических координатах базисные функции разрывного

метода Галёркина имеют вид ψ₀ = 0, ψ₁ = ξ, а начальные условия - вид q_h|ωi = Q₀ + Q₁ξ.

В соответствии с п. 2.1 сначала получим полудискретное уравнение. Для этого умножим

уравнение (4.1) на ψ ∈ span (ψ₀, ψ₁) и проинтегрируем результат по ω_i. Тогда получим

∫

∂q

∂f(q)

ψ(ξ) dξ +

ψ(ξ) dξ = 0.

(4.4)

∂t

∂ξ

−1

-1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

1000

ТУХВАТУЛЛИНА и др.

Полудискретное решение задачи в каждой ячейке сетки (конечном элементе) можно пред-

ставить в виде

q_i := q_h(ξ,t)|ωi = si0(t) + si1(t)ξ,

где si0,1 = si0,1(t) - гармоники решения в ячейке ωi.

Введём следующие обозначения:

q^-i = q_h(-1,t)|ωi = si0 - si1, q+i = q_h(1,t)|ωi = si0 + si1.

После стандартных преобразований уравнения (4.4) получим

∫

∂q

∂ψ(ξ)

ψ(ξ) dξ - f(q_i)

dξ +

f (q_i)ψ|ξ=1

f (q_i)ψ|ξ=-1] = 0,

∂t

∂ξ

−1

-1

где

f - численный поток. Отсюда получаем следующие уравнения для определения гармоник

решения в ячейке ω_i:

∫

(si0(t) + si1(t)ξ) dξ +

f (qi+1/2)

f (qi-1/2)] = 0,

−1

∫

(si0(t) + si1(t)ξ)ξ dξ +

f (qi+1/2)

f (qi-1/2)] - f(q_i) dξ = 0.

−1

-1

Тогда с учётом ортогональности полиномов ψ₀ и ψ₁ будем иметь

ds₀

f (qi+1/2)

f (qi-1/2)),

(

∫

)

ds₁

f (qi+1/2)

f (qi-1/2) - f(q_i) dξ

-1

При использовании численного потока Лакса-Фридрихса (4.3) получаем

f (qi+1/2) =

[f(q-i+1) + f(q+i)] -

(q-i+1 - q+i) =

(q-i+1 + q+i) -

(q-i+1 - q+i),

2Δt

f (qi-1/2) =

[f(q^-i) + f(q+i-1)] -

(q^-i - q+i-1) =

(q^-i + q+i-1) -

(q^-i - q+i-1),

2Δt

или, вводя число Куранта λ = aΔt/h,

f (qi+1/2) =

[(λ - 1)q-i+1 + (1 + λ)q+i],

f (qi-1/2) =

[(λ - 1)q^-i + (1 + λ)q+i-1].

2Δt

Помимо этого в частном случае линейного уравнения переноса верно равенство

∫

2λhsi0

f (q_i) dξ = a (si0 + si1ξ) dξ = 2asi0 =

Δt

−1

-1

В результате система обыкновенных дифференциальных уравнений для определения гар-

моник решения в конечном элементе ω_i примет вид

dsi0

(-si0 - λsi1) +

[(1 + λ)q+i-1 + (1 - λ)q-i+1],

Δt

2Δt

dsi1

(λsi0 - si1) +

[(1 - λ)q-i+1 - (1 + λ)q+i-1].

Δt

2Δt

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ РЕЛАКСАЦИОННОЙ МОДЕЛИ

1001

Подставляя в последние уравнения выражения для численных потоков q+i-1 и q-i+1, получаем

dsi0

(-si0 - λsi1) +

[(1 + λ)(si-10 + si-11) + (1 - λ)(si+10 - si+11)],

Δt

2Δt

dsi1

(λsi0 - si1) +

[(1 - λ)(si+10 - si+11) - (1 + λ)(si-10 + si-11)],

Δt

2Δt

или

dsi0

dsi1

= G₀(q_h),

= G₁(q_h).

Учитывая начальные условия (4.2), находим, что

6Q₁

G₀(q_h) = 0, G₁(q_h) = -

Δt

Непосредственной проверкой несложно убедиться в том, что для данной системы ОДУ

применение аппроксимаций по времени вида TVD/RK3 приводит к следующим соотношениям:

si,(1)1 = Q₁ - 6Q₁ = -5Q₁,

si,(2)1 =3Q1 +

(-5Q₁) +

(-6)(-5Q₁) = 7Q₁,

si,new1 =1Q1 +

(7Q₁) +

- 6(7Q₁) = -23Q₁.

Поэтому значения решения на временном шаге n + 1 имеют вид

(si0)n+1 = Q₀ (si1)n+1 = (-23)ⁿQ₁.

Таким образом, |qn+1h|>|q^nh|, что доказывает утверждение.

Обратим внимание, что в рассмотренном выше случае алгоритм корректно пересчитывает

нулевые гармоники дискретного решения в ячейках (которые соответствуют среднему значе-

нию решения в ячейках). При этом первые гармоники решения неограниченно возрастают, как

только в начальном условии существуют соответствующие сколь угодно малые, но конечные

возмущения. Одновременно с этим применение потока Лакса-Фридрихса для метода конечных

объёмов первого порядка даёт устойчивое корректное решение.

Описанные теоретические построения подтверждаются результатами расчётов авторов (см.

также работу [22]).

Исследование Р.Р. Тухватуллиной (введение, пп. 2.2, п. 3, приложение 1) выполнено при

финансовой поддержке Российского научного фонда (проект 19-71-30004). Исследование

М.В. Алексеева и Е.Б. Савенкова (введение, п. 1, пп. 2.1, 2.3, приложение 2) выполнено при

поддержке Московского центра фундаментальной и прикладной математики (соглашение с

Министерством науки и высшего образования Российской Федерации № 075-15-2019-1623).

СПИСОК ЛИТЕРАТУРЫ

1. Baer M., Nunziato J. A two-phase mixture theory for the deflagration-to-detonation transition (DDT)

in reactive granular materials // Int. J. Multiph. Flow. 1986. № 12. P. 861-889.

2. Drew D., Passman S. Theory of Multicomponent Fluids. Springer, 2014.

3. Favrie N., Gavrilyuk S., Saurel R. Solid-fluid diffuse interface model in cases of extreme deformations

// J. Comput. Phys. 2009. V. 228. № 16. P. 6037-6077.

4. Kapila A., Son S., Bdzil J., Menikoff R. Two-phase modeling of DDT: structure of the velocity-relaxation

zone // Phys. Fluids. 1997. V. 9. № 12. P. 3885-3897.

5. Kapila A., Menikoff R., Bdzil J., Son S., Stewart S. Two-phase modeling of deflagration-to-detonation

transition in granular materials: Reduced equations // Phys. Fluids. 2001. V. 13. № 10. P. 3002-3024.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021

1002

ТУХВАТУЛЛИНА и др.

6. Murrone A., Guillard H. A five-equation reduced model for compressible two phase flow problems // J.

Comput. Phys. 2005. V. 202. № 2. P. 664-698.

7. Dal Maso G., Le Floch P., Murat F. Definition and weak stability of nonconservative products // J.

Math. Pures Appl. 1995. V. 74. № 6. P. 483-548.

8. Tokareva S., Toro E. HLLC-type Riemann solver for the Baer-Nunziato equations of compressible two-

phase flow // J. Comput. Phys. 2010. V. 229. № 10. P. 3573-3604.

9. Dumbser M., Toro E. A simple extension of the Osher Riemann solver to non-conservative hyperbolic

systems // J. Sci. Comput. 2011. V. 48. P. 70-88.

10. Franquet E., Perrier V. Runge-Kutta discontinuous Galerkin method for the approximation of Baer and

Nunziato type multiphase models // J. Comput. Phys. 2012. V. 291. P. 4096-4141.

11. de Frahan H., Varadan S., Johnsen E. A new limiting procedure for discontinuous Galerkin methods

applied to compressible multiphase flows with shocks and interfaces // J. Comput. Phys. 2015. V. 280.

P. 489-509.

12. Cockburn B., Shu C.-W. The Runge-Kutta local projection-discontinuous Galerkin finite element method

for scalar conservation laws // ESAIM Math. Model. Numer. Anal. 1991. V. 25. № 3. P. 337-361.

13. Zhong X., Shu C.-W. A simple weighted essentially nonoscillatory limiter for Runge-Kutta discontinuous

Galerkin methods // J. Comput. Phys. 2013. V. 232. № 1. P. 397-415.

14. Jin S., Xin Z. The relaxation schemes for systems of conservation laws in arbitrary space dimensions

// Comm. Pure Appl. Math. 1995. V. 48. № 3. P. 0010-3640.

15. Jin S. Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations // SIAM J.

Sci. Comput. 1999. V. 21. P. 441-454.

16. Andrianov N., Warnecke G. The Riemann problem for the Baer-Nunziato two-phase flow model // J.

Comput. Phys. 2004. V. 195. № 2. P. 434-464.

17. Daude F., Berry R., Galon P. A Finite-volume method for compressible non-equilibrium two-phase flows

in networks of elastic pipelines using the Baer-Nunziato model // Comput. Methods in Appl. Mech. Eng.

2019. V. 354. P. 820-849.

18. Saurel R., Abgrall R. A simple method for compressible multifluid flows // SIAM J. Sci. Comput. 1999.

V. 21. № 3. P. 1115-1145.

19. Nigmatulin R. Dynamics of Multiphase Media. N.Y., 1990.

20. Pares C. Numerical methods for nonconservative hyperbolic systems: a theoretical framework // SIAM

J. Numer. Anal. 2006. V. 44. № 1. P. 300-321.

21. Chiocchetti S., Muller C. A solver for stiff finite-rate relaxation in Baer-Nunziato two-phase flow model

// Droplet Interactions and Spray Processes. 2020. P. 31-44.

22. Rider W., Lowrie R. The use of classical Lax-Friedrichs Riemann solvers with discontinuous Galerkin

methods // Int. J. Numer. Methods Fluids. 2002. V. 40. P. 479-486.

Институт прикладной математики

Поступила в редакцию 01.03.2021 г.

им. М.В. Келдыша, г. Москва

После доработки 01.03.2021 г.

Принята к публикации 27.04.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№7

2021