ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 8, с.1063-1070

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956

МЕТОД РИМАНА-АДАМАРА ДЛЯ ОДНОЙ СИСТЕМЫ

В ТРЁХМЕРНОМ ПРОСТРАНСТВЕ

Для линейной неоднородной системы в частных производных первого порядка с тремя

независимыми переменными доказаны существование и единственность решения задачи

Дарбу, которое построено в терминах определяемой в работе матрицы Римана-Адамара.

DOI: 10.31857/S0374064121080070

Линейная система уравнений в частных производных первого порядка

∑

∂u_i

a_ik(x₁,... ,x_n)u_k + f_i(x₁,... ,x_n), i = 1,n,

(1)

∂x

k=1

коэффициенты a_ik и свободные члены f_i, i, k = 1, n, которой непрерывны, исследовалась

многими авторами [1-3]. Эта система представляет интерес, в частности, с точки зрения при-

менения получаемых результатов к изучению важных в теоретическом и практическом от-

ношении дифференциальных уравнений смешанного типа. Отметим, что наибольшее число

публикаций относится к случаю, когда в системе (1) n = 2.

В работе [4] предложен вариант метода Римана для гиперболических систем дифференци-

альных уравнений, и в терминах матрицы Римана построены решения задач Коши и Гурса.

В статьях [5, 6] метод Римана применяется для исследования задач для систем уравнений с

двумя и тремя независимыми переменными с кратными характеристиками. Системы гипер-

болических уравнений исследовались ранее рядом авторов в различных направлениях [7-13].

Отметим, что В.И. Жегаловым и его учениками разработан метод Римана для класса

уравнений с доминирующими частными производными

(D₁ + D₂)u = f(x₁, . . . , x_n),

(2)

здесь D₁ ≡ ∂k1+...+kn /∂xk11 · · · ∂xnn , а D2 - линейная комбинация с переменными коэффици-

0 ≤ l_i ≤ k_i, i = 1,n, и l_j < k_j хотя бы

ентами операторов вида ∂l1+...+ln /∂xl11 · · · ∂xnn , где

для одного j ∈ {1, . . . , n} (см., например, работы [14-16]). Уравнение (2) имеет приложения

в теориях фильтрации жидкости в трещиноватых средах, поглощения влаги корнями расте-

ний, колебаний стержней с учётом эффектов поперечной инерции, распространения волн в

диспергирующих средах.

Большой интерес представляет задача Дарбу для гиперболического уравнения второго

порядка с двумя независимыми переменными. Эта задача рассматривалась, в частности, в

работах [17, гл. 3, § 1; 18-23].

В статье [24] для уравнения Бианки третьего порядка исследованы существование и един-

ственность решения задачи Дарбу, а также определена функция Римана-Адамара, доказаны

её существование и единственность, построено решение задачи Дарбу в терминах функции

Римана-Адамара. При этом определение функции Римана-Адамара основывается на опреде-

лении функции Римана [14].

Решение задачи Дарбу для системы (1) с двумя независимыми переменными построено в

терминах матрицы Римана-Адамара в работе [25].

В настоящей работе для системы вида (1) с тремя независимыми переменными предложен

метод решения задачи Дарбу, являющийся определённым развитием метода Римана, который

естественно назвать методом Римана-Адамара.

1063

1064

МИРОНОВ, МИРОНОВА

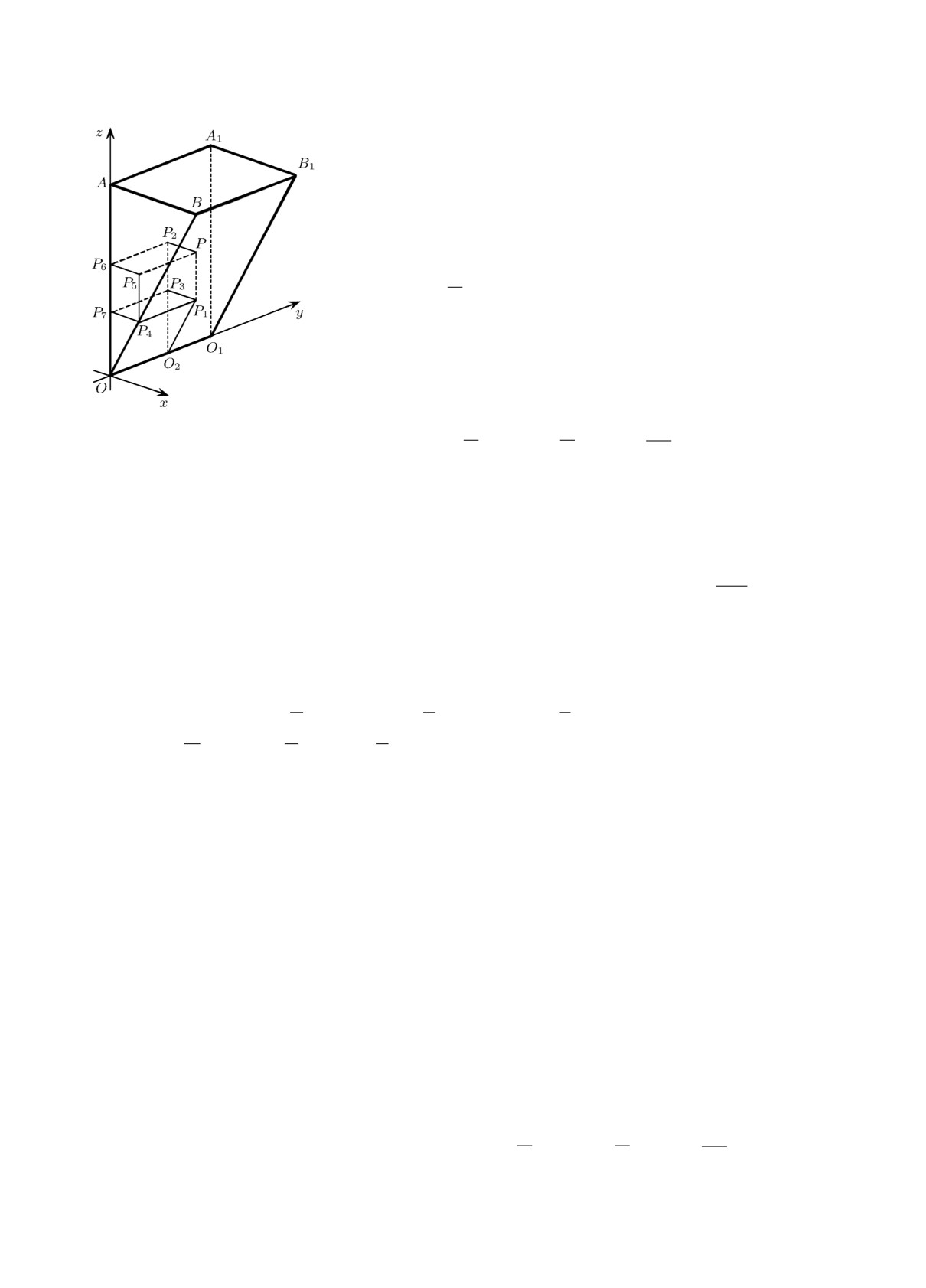
Пусть D - область в R³ , ограниченная призмой Π =

= OABO₁A₁B₁, задаваемой плоскостями (рисунок):

x = 0 (AA₁O₁O), y = 0 (AOB), y = y₀ > 0 (A₁O₁B₁),

z = x (OBB₁O₁), z = z₀ > 0.

Обозначим боковые грани призмы Π при x = 0 и z = x че-

рез X и T соответственно, а через Y её основание при y = 0.

В области D рассмотрим гиперболическую систему

u_x = a₁₁(x,y,z)u + a₁₂(x,y,z)v + a₁₃(x,y,z)w + f₁(x,y,z),

v_y = a₂₁(x,y,z)u + a₂₂(x,y,z)v + a₂₃(x,y,z)w + f₂(x,y,z),

w_z = a₃₁(x,y,z)u + a₃₂(x,y,z)v + a₃₃(x,y,z)w + f₃(x,y,z).

(3)

Рисунок. Области D и DP ,

Считаем, что её коэффициенты и свободные члены непре-

D1, D2 (призмы Π, ΠP , Π2 и

рывны: a_ij ∈ C(D), f_i ∈ C(D), i, j = 1, 3. Линейное преобра-

параллелепипед Π1).

зование искомых функций u → b₁u, v → b₂v, w → b₃w, где

∫_x

b₁ = b₁(x,y,z) = exp

a₁₁(α,y,z)dα и аналогичный вид имеют функции b₂ и b₃, приводит

систему (3) к случаю, в котором

a₁₁ = a₂₂ = a₃₃ ≡ 0.

(4)

Далее считаем эти условия выполненными.

Определим класс C(k,l,m) функций: включение f ∈ C(k1,k2,k3) равносильно существова-

нию у функции f непрерывных производных ∂r1+r2+r3 f/∂xr1 ∂yr2 ∂zr3 (r_i = 0, k_i). Решение

(u, v, w) системы (3) такое, что u ∈ C(1,0,0)(D), v ∈ C(0,1,0)(D), w ∈ C(0,0,1)(D), назовём

регулярным в области D.

Задача Дарбу. В области D найти регулярное решение системы (3), удовлетворяющее

граничным условиям

u|_X = ϕ₁(y, z), v|_Y = ϕ₂(x, z), w|_T = ψ(x, y),

(5)

где ϕ₁ ∈ C(X), ϕ₂ ∈ C(Y ), ψ ∈ C(T ) - заданные функции.

Докажем существование и единственность решения задачи Дарбу.

Сведём систему (3) с учётом условий (4) и (5) к системе интегральных уравнений

∫x

u(x, y, z) = ϕ₁(y, z) + (a₁₂v + a₁₃w + f₁)(α, y, z) dα,

∫

v(x, y, z) = ϕ₂(x, z) + (a₂₁u + a₂₃w + f₂)(x, β, z) dβ,

∫z

w(x, y, z) = ψ(x, y) + (a₃₁u + a₃₂v + f₃)(x, y, γ) dγ.

(6)

Решение системы интегральных уравнений Вольтерры (6) существует и единственно в классе

непрерывных функций. Задача Дарбу (3)-(5) и система (6) эквивалентны. Действительно,

система (6) - следствие (3)-(5). Обратно, дифференцируя уравнения системы (6), получаем

систему (3) с условиями (4) и (5).

Таким образом, справедлива

Теорема 1. Если выполняются условия a_ij ∈ C(D), f_i ∈ C(D), i, j = 1, 3, то решение

задачи Дарбу (3), (4) существует и единственно.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

МЕТОД РИМАНА-АДАМАРА ДЛЯ ОДНОЙ СИСТЕМЫ

1065

Перейдём к построению решения задачи Дарбу в терминах матрицы Римана-Адамара.

Запишем систему (3), (4) в векторно-матричной форме

L(U) = F, L(U) ≡ A₁U_x + A₂U_y + A₃U_z - BU, U = colon (u, v, w),

(7)

⎛

⎞

⎛

⎞

⎛

⎞

⎛

⎞

a₁₂

a₁₃

A₁ =^⎝0

0⎠,A2 = ⎝0

0⎠,A3 = ⎝0

0⎠,B= ⎝a21

a₂₃⎠,

a₃₁

a₃₂

F = colon(f₁,f₂,f₃).

Введём матрицу Римана [4] R = colon (R₁, R₂, R₃), где вектор-функции R_i(x, y, z, ξ, η, ζ)=

= (ri1, ri2, ri3), i = 1, 3, являются решениями систем

∫x

ri1(x,y,z) = δi1 - (a₂₁ri2 + a₃₁ri3)(α,y,z)dα,

∫

ri2(x,y,z) = δi2 - (a₁₂ri1 + a₃₂ri3)(x,β,z)dβ,

∫z

ri3(x,y,z) = δi3 - (a₁₃ri1 + a₂₃ri2)(x,y,γ)dγ,

(8)

в которых δ_ij - символ Кронекера. Решения систем (8) при каждом i = 1, 3 существуют и

единственны в классе непрерывных функций. По первой тройке аргументов (x, y, z) матрица

R удовлетворяет сопряжённой к (7) системе

L^∗(V) = 0, L^∗(V) ≡ -(VA₁)_x - (VA₂)_y - (VA₃)_z - VB.

Справедливо тождество

(RA₁U)_x + (RA₂U)_y + (RA₃U)_z = RL(U),

(9)

которое может быть проверено непосредственно. Интегрированием этого тождества получаем

решение задачи Дарбу.

Возьмём внутри области D произвольную точку P (ξ, η, ζ). Она определяет (см. рисунок)

область D_P , ограниченную призмой Π_P = O₂P₁P P₂OP₄P₅P₆ и состоящую из двух частей -

области D₁, ограниченной прямоугольным параллелепипедом Π₁ = P₁P P₂P₃P₄P₅P₆P₇, и

области D₂, ограниченной призмой Π₂ = O₂P₁P₃OP₄P₇.

Определим матрицу Римана-Адамара задачи Дарбу H(x, y, z, ξ, η, ζ) = (h_ij ), i, j = 1, 3,

равенством

{

R(x, y, z, ξ, η, ζ), (x, y, z) ∈ D₁,

H(x, y, z, ξ, η, ζ) =

Q(x, y, z, ξ, η, ζ), (x, y, z) ∈ D₂.

Здесь Q = colon (Q₁, Q₂, Q₃), где вектор-функции Q_i = (qi1, qi2, qi3), i = 1, 3, являются

решениями задачи Дарбу в D₂ для сопряжённой системы

qi1x = -a₂₁qi2 - a₃₁qi3, qi2y = -a₁₂qi1 - a₃₂qi3, qi3z = -a₁₃qi1 - a₂₃qi2

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

1066

МИРОНОВ, МИРОНОВА

с условиями

qi1|z=x = 0, qi2|y=η = 0, qi3|z=ξ = ri3|z=ξ.

(10)

Последнее условие в (10) можно записать в виде [hi3]|z=ξ = 0, где [hi3]|z=ξ - скачок функции

hi3 на плоскости z = ξ.

Очевидно, что матрица Римана-Адамара существует и единственна.

Проинтегрируем тождество (9) по области D₁ (она определяется неравенствами 0 < x < ξ,

0 < y < η, ξ < z < ζ):

∫

r₁₁u(ξ,β,γ)dγ dβ -

r₁₁u(0,β,γ)dγ dβ +

r₁₂v(α,η,γ)dγ dα -

∫

r₁₂v(α,0,γ)dγ dα +

r₁₃w(α,β,ζ)dβ dα -

r₁₃w(α,β,ξ)dβ dα =

∫

(r₁₁f₁ + r₁₂f₂ + r₁₃f₃)(α, β, γ) dγ dβ dα,

(11)

∫

r₂₁u(ξ,β,γ)dγ dβ -

r₂₁u(0,β,γ)dγ dβ +

r₂₂v(α,η,γ)dγ dα -

∫

r₂₂v(α,0,γ)dγ dα +

r₂₃w(α,β,ζ)dβ dα -

r₂₃w(α,β,ξ)dβ dα =

∫

(r₂₁f₁ + r₂₂f₂ + r₂₃f₃)(α, β, γ) dγ dβ dα,

(12)

∫

r₃₁u(ξ,β,γ)dγ dβ -

r₃₁u(0,β,γ)dγ dβ +

r₃₂v(α,η,γ)dγ dα -

∫

r₃₂v(α,0,γ)dγ dα +

r₃₃w(α,β,ζ)dβ dα -

r₃₃w(α,β,ξ)dβ dα =

∫

(r₃₁f₁ + r₃₂f₂ + r₃₃f₃)(α, β, γ) dγ dβ dα.

(13)

В равенствах (11)-(13) у r_ij указана только первая тройка аргументов, вторая их тройка -

(ξ, η, ζ). В этих равенствах учтено также, что согласно (8) справедливы равенства

r₁₁(ξ,β,γ,ξ,η,ζ) = 1, r₁₂(α,η,γ,ξ,η,ζ) = 0, r₁₃(α,β,ζ,ξ,η,ζ) = 0,

r₂₁(ξ,β,γ,ξ,η,ζ) = 0, r₂₂(α,η,γ,ξ,η,ζ) = 1, r₂₃(α,β,ζ,ξ,η,ζ) = 0,

r₃₁(ξ,β,γ,ξ,η,ζ) = 0, r₃₂(α,η,γ,ξ,η,ζ) = 0, r₃₃(α,β,ζ,ξ,η,ζ) = 1.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

МЕТОД РИМАНА-АДАМАРА ДЛЯ ОДНОЙ СИСТЕМЫ

1067

Теперь проинтегрируем тождество (9) по области D₂. Очевидно, область D₂ может быть

задана любой из двух систем неравенств:

1) 0 < x < ξ, 0<y<η, x<z<ξ;

2) 0 < x < z, 0<y<η, 0<z<ξ.

Интегрируя равенство для первых компонент векторов в (9), получаем

∫

dy dz (q₁₁u)_x(x, y, z) dx +

dz dx (q₁₂v)_y(x, y, z) dy +

∫

∫∫∫

+ dy dx (q₁₃w)_z(x, y, z) dz =

(q₁₁f₁ + q₁₂f₂ + q₁₃f₃)(x, y, z) dx dy dz.

D₂

Отсюда

∫

dy (q₁₁u(z, y, z) - q₁₁u(0, y, z)) dz + dz (q₁₂v(x, η, z) - q₁₂v(x, 0, z)) dx +

∫

∫∫∫

+ dy (q₁₃w(x, y, ξ) - q₁₃w(x, y, x)) dx =

(q₁₁f₁ + q₁₂f₂ + q₁₃f₃)(x, y, z) dx dy dz.

(14)

D₂

Здесь q₁₁(z, y, z) = q₁₂(x, η, z) ≡ 0 в силу условий (10).

Интегрируем равенство для вторых компонент векторов в (9):

∫

dy dz (q₂₁u)_x(x, y, z) dx + dz dx (q₂₂v)_y(x, y, z) dy +

∫

∫∫∫

+ dy dx (q₂₃w)_z(x, y, z) dz =

(q₂₁f₁ + q₂₂f₂ + q₂₃f₃)(x, y, z) dx dy dz.

D₂

Отсюда

∫

dy (q₂₁u(z, y, z) - q₂₁u(0, y, z)) dz + dz (q₂₂v(x, η, z) - q₂₂v(x, 0, z)) dx +

∫

∫∫∫

+ dy (q₂₃w(x, y, ξ) - q₂₃w(x, y, x)) dx =

(q₂₁f₁ + q₂₂f₂ + q₂₃f₃)(x, y, z) dx dy dz.

(15)

D₂

Снова q₂₁(z, y, z) = q₂₂(x, η, z) ≡ 0 в силу условий (10).

Аналогично, интегрируя равенство для третьих компонент векторов в (9), будем иметь

∫

dy dz (q₃₁u)_x(x, y, z) dx + dz dx (q₃₂v)_y(x, y, z) dy +

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

1068

МИРОНОВ, МИРОНОВА

∫

∫∫∫

+ dy dx (q₃₃w)_z(x, y, z) dz =

(q₃₁f₁ + q₃₂f₂ + q₃₃f₃)(x, y, z) dx dy dz.

D₂

Отсюда

∫

dy (q₃₁u(z, y, z) - q₃₁u(0, y, z)) dz + dz (q₃₂v(x, η, z) - q₃₂v(x, 0, z)) dx +

∫

∫∫∫

+ dy (q₃₃w(x, y, ξ) - q₃₃w(x, y, x)) dx =

(q₃₁f₁ + q₃₂f₂ + q₃₃f₃)(x, y, z) dx dy dz,

(16)

D₂

где q₃₁(z, y, z) = q₃₂(x, η, z) ≡ 0 в силу условий (10).

Складывая почленно равенства (11) и (14), получаем

∫

u(ξ, β, γ) dγ dβ +

(q₁₃ - r₁₃)w(α, β, ξ) dβ dα =

∫

r₁₁u(0,β,γ)dγ dβ +

r₁₂v(α,0,γ)dγ dα +

∫

q₁₁u(0,β,γ)dγ dβ +

q₁₂v(α,0,γ)dγ dα+

∫

∫∫∫

q₁₃w(α,β,0)dβ dα +

(h₁₁f₁ + h₁₂f₂ + h₁₃f₃)(α, β, γ) dγ dβ dα.

(17)

D_P

Второе слагаемое в левой части равенства (17) обращается в нуль в силу (10).

Обозначим грани D₁ и D₂ при z = x через S, при x = 0 через X₁ и X₂, а при y = 0

через Y₁ и Y₂ соответственно. Запишем формулу (17) в виде

∫

∫∫

u(ξ, β, γ) dγ dβ =

h₁₁udγ dβ +

h₁₂v dγ dα +

X₁+X₂

Y₁+Y₂

∫∫

∫∫∫

+ h₁₃w dβ dα +

(h₁₁f₁ + h₁₂f₂ + h₁₃f₃) dγ dβ dα.

(18)

D_P

Обозначим правую часть равенства (18) через F₁(ξ, η, ζ). Очевидно, что F₁(ξ, η, ζ) может

считаться известной функцией, так как выражается через элементы матрицы H и данные

задачи Дарбу. Дифференцируя (18), получаем

∂²F₁(ξ,η,ζ)

u(ξ, η, ζ) =

(19)

∂η∂ζ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

МЕТОД РИМАНА-АДАМАРА ДЛЯ ОДНОЙ СИСТЕМЫ

1069

Аналогично складывая равенства (12) и (15), (13) и (16), находим соответственно, что

∫

∫∫

v(α, η, γ) dγ dα =

h₂₁udγ dβ +

h₂₂v dγ dα +

X₁+X₂

Y₁+Y₂

∫∫

∫∫∫

+ h₂₃w dβ dα +

(h₂₁f₁ + h₂₂f₂ + h₂₃f₃)dγ dβ dα,

(20)

D_P

∫

∫∫

w(α, β, ζ) dβ dα =

h₃₁udγ dβ +

h₃₂v dγ dα +

X₁+X₂

Y₁+Y₂

∫∫

∫∫∫

+ h₃₃w dβ dα +

(h₃₁f₁ + h₃₂f₂ + h₃₃f₃) dγ dβ dα,

(21)

D_P

откуда дифференцированием получаем

∂²F₂(ξ,η,ζ)

∂²F₃(ξ,η,ζ)

v(ξ, η, ζ) =

w(ξ, η, ζ) =

(22)

∂ξ∂ζ

∂ξ∂η

где F₂(ξ, η, ζ) и F₃(ξ, η, ζ) - известные правые части равенств (20) и (21), выражающиеся

через элементы матрицы H и данные задачи Дарбу.

Формулы (19) и (22) представляют собой решение задачи Дарбу (3), (5) в терминах мат-

рицы Римана-Адамара H.

СПИСОК ЛИТЕРАТУРЫ

1. Бицадзе А.В. О структурных свойствах решений гиперболических систем уравнений с частными

производными // Мат. моделирование. 1994. Т. 6. № 6. С. 22-31.

2. Чекмарев Т.В. Формулы решения задачи Гурса для одной линейной системы уравнений с частными

производными // Дифференц. уравнения. 1982. Т. 18. № 9. С. 1614-1622.

3. Плещинская И.Е. Об эквивалентности некоторых классов эллиптических и гиперболических систем

первого порядка и уравнений второго порядка с частными производными // Дифференц. уравне-

ния. 1987. Т. 23. № 9. С. 1634-1637.

4. Миронова Л.Б. О методе Римана в Rⁿ для одной системы с кратными характеристиками // Изв.

вузов. Математика. 2006. № 1. С. 34-39.

5. Жегалов В.И., Миронова Л.Б. Об одной системе уравнений с двукратными старшими частными

производными // Изв. вузов. Математика. 2007. № 3. С. 12-21.

6. Миронова Л.Б. Применение метода Римана к одной системе в трехмерном пространстве // Изв.

вузов. Математика. 2019. № 6. С. 48-57.

7. Романовский Р.К. О матрицах Римана первого и второго рода // Мат. сб. 1985. Т. 127. № 4. С. 494-

501.

8. Жегалов В.И. Задача с нормальными производными в граничных условиях для системы диффе-

ренциальных уравнений // Изв. вузов. Математика. 2008. № 8. С. 70-72.

9. Воронова Ю.Г. О задаче Коши для линейных гиперболических систем уравнений с нулевыми обоб-

щёнными инвариантами Лапласа // Уфимский мат. журн. 2010. Т. 2. № 2. С. 20-26.

10. Жибер А.В., Костригина О.С. Задача Гурса для нелинейных гиперболических систем уравнений

с интегралами первого и второго порядка // Уфимский мат. журн. 2011. Т. 3. № 3. С. 67-79.

11. Созонтова Е.А. О характеристических задачах с нормальными производными для системы гипер-

болического типа // Изв. вузов. Математика. 2013. № 10. С. 43-54.

12. Андреев А.А., Яковлева Ю.О. Задача Коши для системы дифференциальных уравнений гипербо-

лического типа порядка n с некратными характеристиками // Вестн. Самарск. гос. техн. ун-та.

Сер. физ.-мат. науки. 2017. Вып. 4. С. 752-759.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

5^∗

1070

МИРОНОВ, МИРОНОВА

13. Жегалов В.И., Миронов А.Н. Вариант метода исключения для одной системы уравнений с частны-

ми производными // Дифференц. уравнения. 2017. Т. 53. № 6. С. 841-845.

14. Жегалов В.И. О трехмерной функции Римана // Сиб. мат. журн. 1997. Т. 38. № 5. С. 1074-1079.

15. Миронов А.Н. Метод Римана для уравнений со старшей частной производной в Rⁿ // Сиб. мат.

журн. 2006. Т. 47. № 3. С. 584-594.

16. Миронов А.Н. К методу Римана решения одной смешанной задачи // Вестн. Самарск. гос. техн.

ун-та. Сер. физ.-мат. науки. 2007. Вып. 2. С. 27-32.

17. Бицадзе А.В. Некоторые классы уравнений в частных производных. М., 1981.

18. Моисеев Е.И. Об одном интегральном представлении решения задачи Дарбу // Мат. заметки. 1982.

Т. 32. Вып. 2. С. 175-186.

19. Моисеев Е.И. О приближении классического решения задачи Дарбу гладкими решениями // Диф-

ференц. уравнения. 1984. Т. 20. № 1. С. 73-87.

20. Моисеев Е.И. Уравнения смешанного типа со спектральным параметром. М., 1988.

21. Сабитов К.Б. Построение в явном виде решений задач Дарбу для телеграфного уравнения и их

применение при обращении интегральных уравнений. I // Дифференц. уравнения. 1990. Т. 26. № 6.

С. 1023-1032.

22. Сабитов К.Б., Шарафутдинова Г.Г. Задачи Коши-Гурса для вырождающегося гиперболического

уравнения // Изв. вузов. Математика. 2003. № 5. С. 21-29.

23. Джохадзе О.М., Харибегашвили С.С. Некоторые свойства функций Римана и Римана-Адамара для

линейных гиперболических уравнений второго порядка и их приложения // Дифференц. уравнения.

2011. Т. 47. № 4. С. 477-492.

24. Миронов А.Н. Задача Дарбу для уравнения Бианки третьего порядка // Мат. заметки. 2017. Т. 102.

Вып. 1. С. 64-71.

25. Mironova L.B. Boundary-value problems with data on characteristics for hyperbolic systems of equations

// Lobachevskii J. of Math. 2020. V. 41. № 3. P. 400-406.

Елабужский институт (филиал)

Поступила в редакцию 21.09.2020 г.

Казанского (Приволжского) федерального университета,

После доработки 21.09.2020 г.

Самарский государственный технический университет

Принята к публикации 08.06.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021