ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 8, с.1104-1115

ТЕОРИЯ УПРАВЛЕНИЯ

УДК 517.935.4

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКОГО РЕЖИМА

В ОДНОЙ НЕЛИНЕЙНОЙ СИСТЕМЕ

П. А. Крылов, Т. С. Тодоров

Рассматривается управляемая нелинейная система, замкнутая обратной связью в форме

двухпозиционного реле с гистерезисом, представляющая собой упрощённую модель одной

термомеханической установки. Получены условия на регулятор и параметры системы, га-

рантирующие существование в этой системе периодического режима.

DOI: 10.31857/S0374064121080124

Введение. В работе [1] рассматривалась заданная на полуоси t ≥ 0 управляемая нели-

нейная система

mÿ(t) + β y(t) + ky(t) = αl-1E(T (t))(Δ - y(t)) - mg,

αγ-1 T˙ (t) + T (t) = u

(1)

с начальными условиями

y(0) = y₀,

y(0) = 0, T (0) = T₀,

(2)

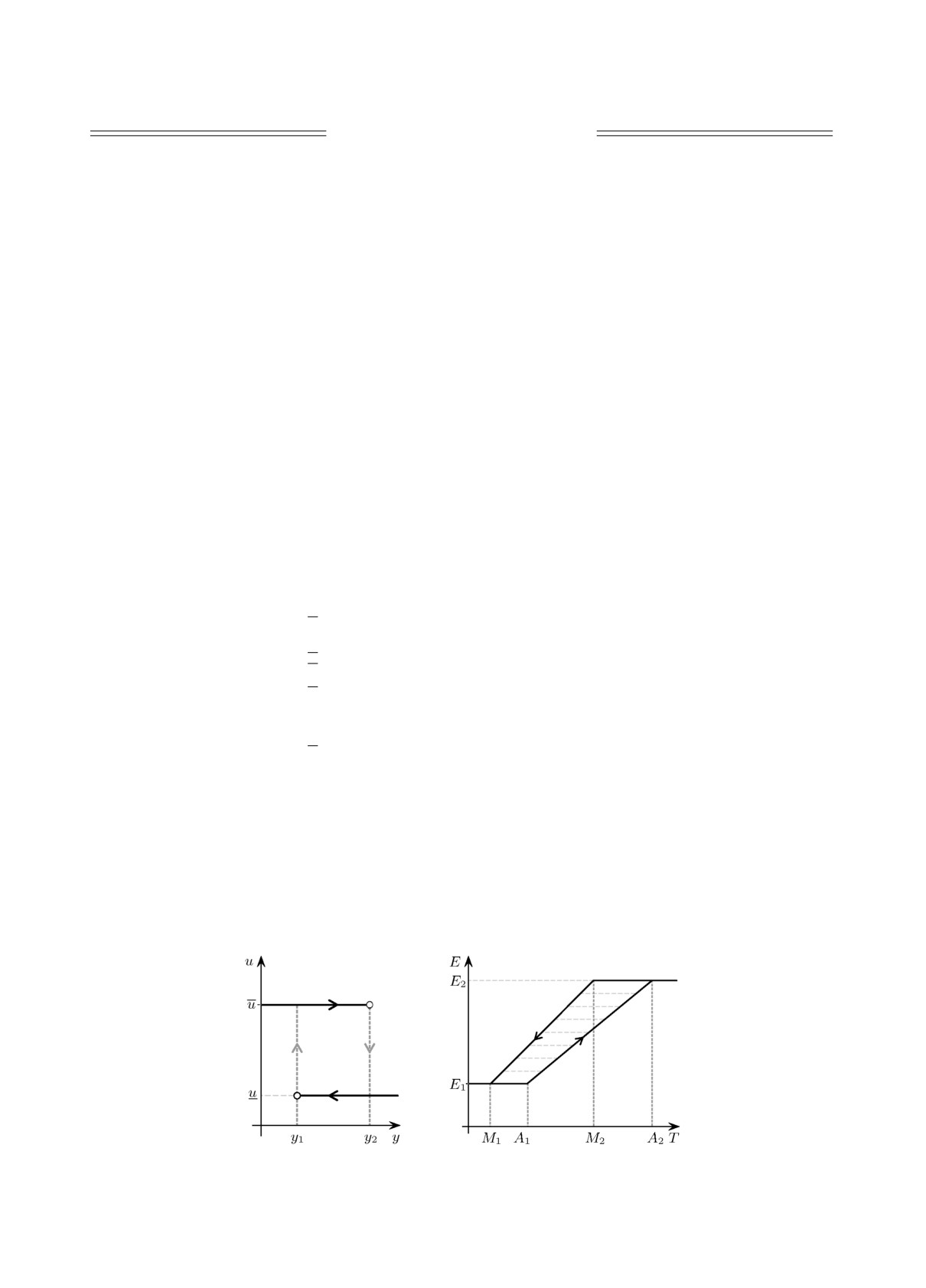
замкнутая обратной связью в форме двухпозиционного реле с гистерезисом (рис. 1):

⎧

⎪u, если y(t) ≤ y1;

⎪

⎪u, если y(t) ≥ y2;

⎪

⎨u, если y(τ) ∈ (y1, y2) при всех τ ∈ [0, t];

u = u_r(y(t)) =

u, если y(t) ∈ (y₁, y₂) и существует s ∈ [0, t) такое, что

(3)

⎪

y(s) = y₁ и y(τ) ∈ (y₁, y₂) при всех τ ∈ (s, t];

⎪

если y(t) ∈ (y₁, y₂) и существует s ∈ [0, t) такое, что

⎩^u

y(s) = y₂ и y(τ) ∈ (y₁, y₂) при всех τ ∈ (s, t].

Система (1) представляет собой упрощённую модель одной термомеханической установ-

ки [2], для которой используются следующие обозначения: y - выходная переменная, харак-

теризующая величину механической деформации материала с памятью формы [3], при этом

предполагается, что 0 < y₀ < Δ; T - температура деформируемого материала, причём T₀ ≥ 0;

положительные числа m, β, k, α, l, Δ, γ являются физическими параметрами термоме-

ханической установки; g - ускорение свободного падения; u - управление в форме обратной

связи по переменной y (u = u(y)); E - модуль Юнга деформируемого материала (нелинейная

характеристика с гистерезисом и насыщением, рис. 2).

Рис. 1. Обратная связь

Рис. 2. Возможный вид характе-

в виде реле.

ристики E(T) с гистеризисом.

1104

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКОГО РЕЖИМА

1105

Отображение E(T ) можно рассматривать как многозначное отображение E : R₊ → R₊

⎧

⎪E1,

если T ≤ M₁;

⎪

{

⎪[

]

⎪

T -M₁

M₂ < A₁,

⎪

E₁,

(E₂ - E₁) + E₁ ,

если

⎪

M₂ - M₁

T ∈ (M₁,M₂];

⎪

{

⎪[

]

⎪

T -A₁

T -M₁

A₁ ≤ M₂,

⎪

(E₂ - E₁) + E₁,

(E₂ - E₁) + E₁ , если

⎪

A₂ - A₁

M₂ - M₁

T ∈ (A₁,M₂];

⎪

{

⎨

M₂ < A₁,

E(T ) =

[E₁, E₂],

если

⎪

T ∈ (M₂,A₁];

⎪

{

[

]

⎪

T -A₁

M₂ < A₁,

⎪

(E₂ - E₁) + E₁, E₂ ,

если

⎪

A₂ - A₁

T ∈ (A₁,A₂];

⎪

{

⎪[

]

⎪

T -A₁

A₁ ≤ M₂,

⎪

(E₂ - E₁) + E₁, E₂ ,

если

⎪

A₂ - A₁

T ∈ (M₂,A₂];

⎪

^⎩E₂,

если T > A₂.

Здесь A₁, A₂, M₁, M₂, E₁, E₂ - положительные константы, определяемые физическими

свойствами материала с памятью формы. Далее будем считать, что они связаны следующими

неравенствами:

0<A₁ <A₂,

0<M₁ <M₂, M₁ <A₁, M₂ <A₂,

0<E₁ <E₂.

Отметим, что для каждой конкретной непрерывной функции T (t) из отображения E(T )

выделяется однозначная ветвь, являющаяся непрерывной функцией, множество значений ко-

торой принадлежит отрезку [E₁, E₂] (см. [1]).

Считаем, что пороговые значения y₁, y₂, характеризующие управление (3), удовлетворяют

условию 0 < y₁ < y₂ < Δ.

В работе [1] получены эффективно проверяемые условия на коэффициенты и начальные

значения переменных состояния системы (1), (2) и на параметры регулятора (3), обеспечиваю-

щие возникновение колебательных движений [4, с. 10] в соответствующей замкнутой системе.

При этом в [1] использовалось следующее определение колебательного движения (колебатель-

ного режима). Решение системы (1), (2), т.е пару (y(t), T (t)) функций, удовлетворяющих этой

системе и начальным условиям при управлении u, задаваемом условиями (3), называем коле-

бательным режимом, если найдутся такие положительные константы (параметры режима)

t∗1, t∗2, y, y (0 < t∗1 < t∗2 и 0 < y < y < Δ), что выполняются следующие условия:

1) найдётся момент t ≥ 0, для которого y(t) = y;

2) для любого момента t такого, что y(t) = y, существует момент ξ ∈ [t + t∗1, t + t∗2], при

котором справедливо равенство y(ξ) = y и y(τ) = y для всех τ ∈ (t, t + t∗1);

3) для любого момента t такого, что y(t) = y, существует такой момент ξ ∈ [t + t∗1, t + t∗2],

при котором справедливо равенство y(ξ) = y и y(τ) = y для всех τ ∈ (t, t + t∗1).

Анализируя результаты работы [1], можно утверждать, что проблема определения усло-

вий на параметры замкнутой системы (1)-(3), гарантирующих существование колебательных

режимов, оказалась весьма непростой. Однако с прикладной точки зрения более актуальной

является задача определения условий существования периодического режима для указанной

замкнутой системы.

Основываясь на результатах работы [1], в настоящей статье получены достаточные условия

существования периодического режима в замкнутой системе (1)-(3).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

1106

ФУРСОВ и др.

1. Постановка задачи. Запишем систему (1), (2) в нормальной форме Коши:

x₁(t) = x₂(t),

(

)

x₂(t) = -

E(x₃(t)) x₁(t) -

x₂(t) - g +

ΔE(x₃(t)),

(4)

x₃(t) = -

(x₃(t) - u),

x₁(0) = y₀, x₂(0) = 0, x₃(0) = T₀,

где x₁ = y, x₂ = y, x₃ = T, а 0 < y₀ < Δ, T₀ ≥ 0.

Замкнём систему (4) регулятором (3) и при t ≥ 0 рассмотрим соответствующую замкнутую

систему

x₁(t) = x₂(t),

(

)

x₂(t) = -

E(x₃(t)) x₁(t) -

x₂(t) - g +

ΔE(x₃(t)),

(5)

x₃(t) = -

(x₃(t) - u_r(x₁(t))),

x₁(0) = y₀, x₂(0) = 0, x₃(0) = T₀,

где 0 < y₀ < Δ, T₀ ≥ 0, для которой будем предполагать, что y₀ < y₁, T₀ < M₁. Запишем

замкнутую систему (5) в векторной форме

x(t) = P (x(t), u_r), x = (x₁, x₂, x₃)^т.

Тогда если выход реле принимает значение u, то считаем, что активной является система

x(t) = P (x(t), u),

(6)

если же выход реле принимает значение u, то считаем, что активной является система

x(t) = P (x(t), u).

(7)

Тогда при заданных начальных условиях x(0) = (y₀, 0, T₀)^т решение замкнутой системы (5)

с учётом того, что y₀ < y₁, ищется в классе непрерывных вектор-функций x(t) в соответствии

со следующим алгоритмом чередования активных режимов:

⎧

⎪P (x(t), u), если x1(t) ≤ y1;

⎪

⎪P (x(t), u), если x1(t) ≥ y2;

⎨

P (x(t), u), если x₁(t) ∈ (y₁, y₂) и существует s ∈ [0, t) такое, что

x(t) =

(8)

⎪

x₁(s) = y₁ и x₁(τ) ∈ (y₁,y₂) при всех τ ∈ (s,t];

⎪

(x(t), u), если x₁(t) ∈ (y₁, y₂) и существует s ∈ [0; t) такое, что

⎩^P

x₁(s) = y₂ и x₁(τ) ∈ (y₁,y₂) при всех τ ∈ (s,t].

При этом в точках разрыва правой части системы (на гиперплоскостях x₁ = y₁, x₁ =

= y₂) происходит “склейка по непрерывности” соответствующих решений систем (6) и (7).

Далее определённую на полуоси t ≥ 0 функцию f будем называть Θ-периодической, если

f (t + Θ) = f(t) для всех t ≥ 0.

Сформулируем теперь задачу управления для системы (4).

Задача. Найти ограничения на числовые параметры m, k, α, l, β, Δ, γ системы (4),

а также на параметры y₁, y₂, u, u регулятора (3), при выполнении которых в замкнутой

системе (5) существует периодическое решение (периодический режим).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКОГО РЕЖИМА

1107

2. Периодический режим в системе с программным управлением. Решение постав-

ленной задачи о существовании периодического решения в системе (5) разобьём на несколько

шагов. Вначале исследуем вопрос о существовании периодического решения системы (4), замк-

нутой программным управлением вида

{

u, если t ∈ [qΘ, qΘ + Θ₁),

u_p(t) =

q = 0,1,2,... ; Θ₁ + Θ₂ = Θ.

(9)

u, если t ∈ [qΘ + Θ₁, qΘ + Θ₁ + Θ₂),

Здесь u, u, Θ₁, Θ - положительные параметры указанного программного управления.

Рассмотрим теперь задачу выбора таких параметров управления (9), которые обеспечивают

существование периодического решения в соответствующей замкнутой системе (4), (9).

Прежде всего заметим, что рассматриваемое управление u(t) является кусочно-постоян-

ной периодической функцией с периодом Θ. Покажем, что для любых u, u, Θ > Θ₁ > 0

уравнение

x₃(t) = -

(x₃(t) - u_p(t))

(10)

имеет периодическое решение с периодом Θ. Действительно, при любых t ≥ s ≥ 0 для

решений уравнения (10) справедлива формула Коши

∫t

x₃(t) = x₃(s)e-γ(t-s)/α + e-γ(t-τ)/α

u(τ) dτ.

(11)

Пусть x₃(0) = T₀. Тогда, учитывая, что u_p(t) ≡ u на промежутке [0, Θ₁), и используя фор-

мулу (11), найдём x₃(Θ₁):

∫Θ1

x₃(Θ₁) = T₀e-γΘ1/α +

u e-γ(Θ1-τ)/α dτ =

= T₀e-γΘ1/α + u(1 - e-γΘ1/α) = u + (T₀ - u)e-γΘ1/α.

(12)

Далее, учитывая, что u_p(t) ≡ u на промежутке [Θ₁, Θ), для x₃(Θ) получаем

x₃(Θ) = u + (x₃(Θ₁) - u)e-γΘ2/α = u + (u + (T₀ - u)e-γΘ1/α - u)e-γΘ2/α =

= u(1 - e-γΘ2/α) + u(1 - e-γΘ1/α)e-γΘ2/α + T₀e-γΘ/α.

(13)

Учитывая Θ-периодичность функции u_p(t), заключаем, что решение x₃(t) будет Θ-пери-

одическим, если и только если выполняется равенство x₃(Θ) = T₀. Тогда из представления

(13) находим начальное условие для Θ-периодического решения x^Θ3(t):

-γΘ₂/α

u(1 - e-γΘ2/α) + u(1 - e-γΘ1/α)e

T₀ = T =

(14)

1-e-γΘ/α

Из равенств (13) и (14) следует, что

-γΘ₁/α

u(1 - e-γΘ1/α) + u(1 - e-γΘ2/α)e

x^Θ3(Θ₁) =

1-e-γΘ/α

Теперь, обозначая T = x^Θ3(Θ₁) и γ = γ/α, запишем в явном виде Θ-периодическое реше-

ние уравнения (10):

{

u + (T - u)e-γ(t-qΘ),

если t ∈ [qΘ, qΘ + Θ₁),

x^Θ3(t) =

q = 0,1,2,...

u + (T - u)e-γ(t-qΘ-Θ1),

если t ∈ [qΘ + Θ₁, qΘ + Θ),

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

1108

ФУРСОВ и др.

Будем теперь предполагать, что параметры u, u, Θ₁, Θ регулятора (9) выбраны так,

что выполняются неравенства

T <M₁, T >A₂.

(15)

Полагая, что компонента x₃ решения замкнутой системы (4), (9) удовлетворяет началь-

ному условию x₃(0) = T , рассмотрим её подсистему

x₁(t) = x₂(t),

(

)

x₂(t) = -

ϕ(t) x₁(t) -

x₂(t) - g +

Δϕ(t),

(16)

x₁(0) = y₀, x₂(0) = 0,

где ϕ(t) = E(x^Θ3(t)). В силу условий (15) и того, что x^Θ3(t) является Θ-периодическим ре-

шением уравнения (10), функция ϕ(t) также будет Θ-периодической, и при этом её можно

описать следующим образом:

⎧

⎪E1,

t ∈ [qΘ,qΘ + ΘA1),

⎪

⎪u + (T - u)e-γ(t-qΘ) - A1

⎪

(E₂ - E₁) + E₁,

t ∈ [qΘ + ΘA1,qΘ + ΘA2),

⎪

A₂ - A₁

⎨

E₂,

t ∈ [qΘ + ΘA2,qΘ + Θ₁),

ϕ(t) =

(17)

⎪E2,

t ∈ [qΘ + Θ₁,qΘ + ΘM2),

⎪

⎪u + (T - u)e-γ(t-qΘ-Θ1) - M1

⎪

(E₂ - E₁) + E₁, t ∈ [qΘ + ΘM2 , qΘ + ΘM1 ),

⎪

M₂ - M₁

⎩

E₁,

t ∈ [qΘ + ΘM1,qΘ + Θ),

где

T -u

ΘA1 =

ΘA2 =

A₁ - u

A₂ - u

T -u

ΘM1 = Θ₁ +

ΘM2 = Θ₁ +

M₁ - u

M₂ - u

и учтено, что T₀ < M₁.

На рис. 3, 4 схематично изображены графики функций x^Θ3(t) и ϕ(t) при t ∈ [0, Θ].

Рис. 3. График функции x^Θ3(t).

Рис. 4. График функции ϕ(t).

Из сказанного выше следует, что система (16) фактически является линейной нестацио-

нарной системой вида

x(t) = A(t)x(t) + f(t),

(18)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКОГО РЕЖИМА

1109

где x = (x₁, x₂)^т,

(

)

(

)

A(t) =

f (t) =

(19)

ϕ(t)

Δϕ(t) - g

причём матрица A(t) и вектор-столбец f(t) - непрерывные и периодические с периодом Θ

функции, т.е., в частности, A(t + Θ) = A(t), f(t + Θ) = f(t) для любого t ≥ 0.

Известно [5, с. 215], что если линейная однородная Θ-периодическая система

x(t) = A(t)x(t)

(20)

не имеет нетривиального Θ-периодического решения, то соответствующая неоднородная сис-

тема (18) имеет единственное Θ-периодическое решение. Теперь заметим, что если однород-

ная система (20) является асимптотически устойчивой, то она не может иметь нетривиального

Θ-периодического решения.

Получим условия, при которых рассматриваемая линейная однородная система (20) яв-

ляется асимптотически устойчивой. Для этого воспользуемся методом, предложенным в [5,

с. 197]. Рассмотрим систему (20), матрица A(t) коэффициентов которой задана в (19). Эта

система эквивалентна дифференциальному уравнению второго порядка

ÿ(t) + a y(t) + b(t)y(t) = 0,

(21)

где y(t) = x₁(t),

y(t) = x₂(t), а

b(t) =

ϕ(t) +

Сделаем в уравнении (21) стандартную замену зависимой переменной y = e-at/2z, тогда

(

)

(

)

a²

Ż-

z e-at/2 и

ÿ=

z-aŻ+

z e-at/2.

Поэтому в результате указанной замены уравнение (21) приводится к виду

z(t) + p(t)z(t) = 0,

(22)

где

p(t) =

ϕ(t) +

4m²

В соответствии с результатами, изложенными в монографии [5, с. 202], если для Θ-перио-

дической функции p(t) выполнены неравенства

∫Θ

p(t) ≥ 0,

0 < Θ p(t)dt ≤ 4,

то все решения z(t) уравнения (22) ограничены вместе с их производными первого порядка.

Но из ограниченности z(t) и Ż(t) вытекает, что решения y(t) уравнения (21) вместе с их про-

изводными

y(t) стремятся к нулю и, следовательно, система (20) асимптотически устойчива.

Тогда, учитывая, что E₁ ≤ ϕ(t) ≤ E₂, получаем достаточное условие того, чтобы система (20)

с матрицей коэффициентов A(t), заданной в (19), была асимптотически устойчива:

β²

E₁ +

> 0,

E₂ +

≤

(23)

4m²

Θ²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

1110

ФУРСОВ и др.

Следовательно, при выполнении условия (23) линейная неоднородная система (18) имеет,

и при том единственное, Θ-периодическое решение. Обозначим это решение через x^Θ(t) =

= (xΘ1 (t), xΘ2 (t))^т.

Таким образом, доказана следующая

Теорема 1. Пусть параметры u, u, Θ₁, Θ программного управления (9) для системы

(4) выбраны так, что выполняются следующие условия:

1) справедливы неравенства

-γ(Θ-Θ₁)/α

u(1 - e-γ(Θ-Θ1)^/α) + u(1 - e-γΘ1/α)e

M₁ < T =

1-e-γΘ/α

-γΘ₁/α

u(1 - e-γΘ1/α) + u(1 - e-γ(Θ-Θ1)^/α)e

A₂ > T =

;

1-e-γΘ/α

2) имеет место условие (23).

Тогда в системе (4), замкнутой программным управлением (9), существует единствен-

ное периодическое движение x^Θ(t) = (x^Θ1(t),x^Θ2(t),x^Θ3(t))^т, причём x^Θ3(0) = T.

3. Периодический режим в системе с обратной связью. Вернёмся к исходной задаче

(см. п. 2) о построении регулятора в форме обратной связи (3), обеспечивающего существо-

вание периодического режима в замкнутой системе (5). Основная идея решения этой задачи

состоит в выборе параметров обратной связи (3) на основе результатов работы [1], позволяю-

щих гарантировать существование колебательного режима в замкнутой системе (5), а также

на основе рассчитанного, в соответствии с теоремой 1, программного управления (9) и обеспе-

чиваемого им периодического решения x^Θ(t).

Итак, на основании теоремы 1 и достаточных условий существования колебательных ре-

жимов, полученных в работе [1], справедлива следующая

Теорема 2. Пусть

1) для параметров системы (4) выполняется неравенство

mg + kΔ

Δ-

> 0;

k + αE₁/l

2) спектр каждой матрицы

(

)

(

)

kl + αE₁

kl + αE₂

−

лежит на отрицательной полуоси и является простым;

3) параметры u, u, Θ₁, Θ удовлетворяют условиям теоремы 1 и, кроме того,

u<M₁, u>A₂;

4) величины y₁ = x^Θ1(0), y₂ = x^Θ1(Θ₁) удовлетворяют неравенствам

mg + kΔ

y₁ > Δ -

y₂ < Δ -

k + αE₁/l

k + αE₂/l

где x^Θ(t) = (x^Θ1(t), x^Θ2(t), x^Θ3(t))^т - периодическое решение системы (4), замкнутой программ-

ным управлением (9) с параметрами u, u, Θ₁, Θ;

5) для системы (4), замкнутой обратной связью (3) с параметрами u, u, y₁, y₂, вы-

полняются неравенства

)

(

)₂

E₂

βC²³

⁽m²g²

αE₂

< 1,

Δ2 ν0 < k Δ +

E₁

t∗

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКОГО РЕЖИМА

1111

где

{

√

}

E₁m

t∗

= min

√

, (y₂ - y₁)

C₂

2E₂C₁

(

)₂

(

)

E₂

√

^√α

C₁ = k y₁ +

E₂(y₁ - Δ)², C₂ =

E₂

mE₁

√m⁺

√

E₁

4mgΔE₁

C₃ =

ν₀ = max{H_max/H₀,2}, H₀ =

E₂(k + αE₂/l)

k+E₁

)₂

(

)₂}

⁽E₂

^{m²g²

H_max =

H^∗,

H^∗ = max{H^∗, H},

H= max

E₂Δ²,k Δ +

E₁

)₂

}

^{(2βC₃C₄/t∗1

C²⁴

H^∗ = max

+ βC²³/t∗1

C₄ =

+Δ+y₁;

1 - E₂/E₁

C²³

6) для момента времени t₀ выполняются условия

0 < xΘ1 (t₀) < ζ₊, xΘ2 (t₀) = 0, t₀ < ΘA2,

где ζ₊ - положительный корень квадратного трёхчлена

(

)₂

(

)₂

αν₀E₂

p(ζ) ≡ kν₀ ζ +

(ζ - Δ)² - k Δ +

Тогда решение x(t) замкнутой системы (5) с начальными условиями

x₁(0) = x^Θ1(t₀),

x₂(0) = x^Θ2(t₀),

x₃(0) = x^Θ3(t₀)

(24)

является колебательным режимом с параметрами t∗1, t∗2, y₁, y₂, где

√

t∗1 = (y₂ - y₁)

m/H_max

(алгоритм для расчёта константы t∗2 достаточно громоздкий и полностью приведён в [1]).

Кроме того, для решения x(t) верно тождество x(t) ≡ x^Θ(t + t₀) при t ∈ [0,t∗1].

Теперь покажем, что при некоторых дополнительных условиях на константу t∗1 колеба-

тельный режим

x(t) системы (5) с начальными условиями (24) является, на самом деле,

периодическим режимом. Для этого достаточно установить, что при начальных условиях (24)

переключения реле обратной связи (3) с параметрами u, u, y₁, y₂, удовлетворяющими усло-

виям теоремы 2, на промежутке [0, Θ] происходят при t₁ = Θ₁ - t₀ и t₂ = Θ - t₀.

Итак, пусть выполнены условия теоремы 2 и для t∗1 справедливо неравенство

ΘA2 - t₀ < t∗1 ≤ Θ₁ - t₀.

(25)

Тогда в силу колебательности решения x(t) замкнутой системы (5) с начальными условиями

(24) выполнено неравенство

x₁(t) < y₂, t ∈ [0,ΘA2 - t₀].

(26)

Отсюда вытекает, что в силу теоремы 2 при t ∈ [0, ΘA2 -t₀] верно тождество x(t) ≡ x^Θ(t+t₀).

Далее рассмотрим поведение функций x1(t) и

x₂(t) на промежутке [ΘA2 - t0, Θ1 - t0].

Прежде всего заметим, что вследствие определения обратной связи (3) тождества

x₁(t) ≡

≡ xΘ1 (t+t₀) и x₂(t) ≡ xΘ2 (t+t₀) на промежутке [ΘA2-t₀,Θ₁-t₀] остаются верными вплоть до

момента t_∗ ∈ [ΘA2 - t₀, Θ₁ - t₀], для которого выполняется равенство x₁(t_∗) = x^Θ1(t_∗ + t₀) = y₂.

Покажем, что x^Θ1(t+t₀) = y₂ при t ∈ [ΘA2 -t₀, Θ₁ -t₀). Так как ϕ(t+t₀) ≡ E₂ на промежутке

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

1112

ФУРСОВ и др.

[ΘA2 - t₀, Θ₁ - t₀], то функции x^Θ1(t + t₀) и x^Θ2(t + t₀) на нём тождественно совпадают с

соответствующими компонентами x₁(t) и x₂(t) решения x(t) линейной стационарной системы

x₁(t) = x₂(t),

)

(27)

⁽k

x₂(t) = -

E₂

x₁(t) -

x₂(t) - g +

ΔE₂

с начальными условиями

x₁(ΘA2 - t₀) = x^Θ1(ΘA2 ), x₂(ΘA2 - t₀) = x^Θ2(ΘA2 ).

(28)

Согласно условию 2) теоремы 2 матрица коэффициентов системы (27) является устойчивой и

имеет простой спектр. Покажем, что для решения x(t) этой системы с начальными условиями

(28) выполняется соотношение x₁(t) = y₂ при t ∈ [ΘA2 - t₀, Θ₁ - t₀).

Действительно, первая компонента x₁(t) любого решения x(t) системы (27) обладает свой-

ством

x₁(t) → x∗1 > y₂ при t → +∞,

(29)

где x∗1 = Δ - (mg + kΔ)/(k + αE₂/l); в (29) сходимость доказана в работе [1], а неравенство -

это второе неравенство в условии 4) теоремы 2.

Рассмотрим уравнение

x₁(t) = y₂, t ≥ ΘA2 - t₀.

(30)

Так как вектор-функция (x₁(t), x₂(t))^т на промежутке [ΘA2 -t₀, Θ₁-t₀] является решением

системы (27), собственные значения λ₁ и λ₂ матрицы коэффициентов которой отрицательны

и различны, то справедливо представление

x₁(t) = C₁eλ1t + C₂eλ2t + x∗1,

где C₁ и C₂ - некоторые постоянные. При этом, поскольку

x₁(ΘA2 - t₀) < y₂ < x∗1,

постоянные C₁ и C₂ не равны одновременно нулю.

Поэтому уравнение (30) можно записать в виде

C₁eλ1t + C₂eλ2t = y₂ - x∗1, где λ₁ < 0, λ₂ < 0, C²¹ + C²² > 0, t > ΘA2.

Заметим, что функция в левой части рассматриваемого уравнения может иметь не более одной

точки экстремума при t > 0, а значит, в силу свойства (29) уравнение (30) может иметь не

более одного корня. Следовательно, уравнение x^Θ1(t + t₀) = y₂ может иметь не более одного

корня на промежутке t ∈ [ΘA2 - t₀, Θ₁ - t₀]. Поэтому, так как в силу условия теоремы 2

функция x^Θ1(t + t₀) принимает значение y₂ при t = Θ₁ - t₀, то x^Θ1(t + t₀) = y₂ при t ∈

∈ [ΘA2 - t₀, Θ₁ - t₀). Таким образом,

x₁(t) = y₂, t ∈ [ΘA2 - t₀,Θ₁ - t₀), и

x₁(Θ₁ - t₀) = y₂.

(31)

Теперь предположим, что для t∗1 дополнительно выполнено условие

ΘM1 - Θ₁ < t∗1 ≤ Θ₂.

(32)

Тогда в силу того, что решение x(t) замкнутой системы (5) с начальными условиями (24)

является колебательным режимом, выполнено неравенство x₁(t) > y₁, t ∈ [Θ₁ - t₀, ΘM1 - t₀].

Отсюда, учитывая соотношения (31) и (26), получаем тождество

x(t) ≡ x^Θ(t + t₀) при t ∈ [0, ΘM1 - t₀].

(33)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКОГО РЕЖИМА

1113

Рассмотрим теперь поведение функций x1(t) и x2(t) на промежутке [ΘM1 - t0, Θ - t0].

Аналогично приведённым выше рассуждениям заметим, что тождества x₁(t) ≡ x^Θ1(t + t₀) и

x₂(t) ≡ x^Θ2(t+t₀) на промежутке [ΘM1 -t₀,Θ-t₀] остаются верными вплоть до момента t_∗ ∈

∈ [ΘM1 - t₀, Θ - t₀], для которого выполняется равенство x₁(t_∗) = xΘ1 (t_∗ + t₀) = y₁. Покажем,

что x^Θ1(t + t₀) = y₁ при t ∈ [ΘM1 - t₀, Θ - t₀). Так как ϕ(t + t₀) ≡ E₁ на промежутке

[ΘM1 - t₀, Θ - t₀], то функции x^Θ1(t + t₀) и x^Θ2(t + t₀) тождественно совпадают на нём с

соответствующими компонентами x₁(t) и x₂(t) решения x(t) линейной стационарной системы

x₁(t) = x₂(t),

)

(34)

⁽k

x₂(t) = -

E₁

x₁(t) -

x₂(t) - g +

ΔE₁

с начальными условиями

x₁(ΘM1 - t₀) = x^Θ1(ΘM1 ), x₂(ΘM1 - t₀) = x^Θ2(ΘM1 ).

(35)

Согласно условию 2) теоремы 2 матрица коэффициентов системы (34) является устойчивой и

имеет простой спектр. Покажем, что для решения x(t) этой системы с начальными условиями

(35) выполняется соотношение x₁(t) = y₁ при t ∈ [ΘM1 - t₀, Θ - t₀).

Действительно, первая компонента x₁(t) любого решения x(t) системы (34) обладает свой-

ством

x₁(t) → x∗∗1 < y₁ при t → ∞,

(36)

где x^∗∗ = Δ - (mg + kΔ)/(k + αE₁/l); в (36) сходимость доказана в работе [1], а неравенство -

первое неравенство в условии 4) теоремы 2.

Рассмотрим уравнение

x₁(t) = y₁, t ≥ ΘM1 - t₀.

(37)

Так как вектор-функция (x^Θ1(t), x^Θ2(t))^т на промежутке [ΘM1 - t₀, Θ - t₀] является реше-

нием системы (34), собственные значения λ′1 и λ′2 матрицы коэффициентов которой отрица-

тельны и различны, то справедливо представление

x₁(t) = C₁eλ1t + C₂eλ2t + x∗∗1,

где C₁ и C₂ - некоторые постоянные. При этом, поскольку

x₁(ΘM1 - t₀) > y₁ > x∗∗1,

C₁ и C₂ не равны одновременно нулю.

Поэтому уравнение (37) можно записать в виде

C₁eλ1t + C₂eλ2t = y₁ - x∗∗1, где λ′1 < 0, λ′2 < 0, C²¹ + C²² > 0, t ≥ ΘM1 - t₀.

Заметим, что функция в левой части рассматриваемого уравнения может иметь не более одной

точки экстремума при t > 0, а тогда в силу свойства (36) уравнение (37) может иметь не более

одного корня. Следовательно, уравнение x^Θ1(t + t₀) = y₁ может иметь не более одного корня

на промежутке t ∈ [ΘM1 - t₀, Θ - t₀]. Поэтому, так как в силу условия теоремы 2 функция

x^Θ1(t + t₀) принимает значение y₁ при t = Θ - t₀, x^Θ1(t + t₀) = y₁ при t ∈ [ΘM1 - t₀,Θ - t₀).

Таким образом,

x₁(t) = y₁, t ∈ [ΘM1 - t₀,Θ - t₀), и

x₁(Θ - t₀) = y₁.

Отсюда и из тождества (33) вытекает, что

x(t) ≡ x^Θ(t + t₀) при t ∈ [0, Θ - t₀].

(38)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

1114

ФУРСОВ и др.

Наложим ещё одно ограничение на константу t∗1, а именно, пусть

t∗1 > t₀.

(39)

Тогда вследствие того, что решение x(t) замкнутой системы (5) с начальными условиями (24)

является колебательным режимом, выполнено неравенство

x₁(t) < y₂, t ∈ [Θ - t₀,Θ].

(40)

Отсюда и из тождества (38) вытекает, что при t ∈ [0, Θ] моменты переключений реле обрат-

ной связи (3) и реле программного управления (9) совпадают. Но тогда на этом промежутке

справедливо тождество x(t) ≡ x^Θ(t + t₀), а в силу Θ-периодичности функции x^Θ(t + t₀) это

тождество верно при всех t ≥ 0.

Следовательно, колебательное решение

x(t) системы (5) с начальными условиями (24)

является периодическим режимом. Таким образом, доказана следующая теорема о существо-

вании периодического режима в замкнутой системе (5).

Теорема 3. Пусть выполняются условия теоремы 2 и имеют место неравенства (25),

(32) и (39). Тогда в замкнутой системе (5) существует периодический режим с начальными

условиями (24).

4. Результаты моделирования. Рассмотрим систему (1) со следующими параметрами:

m = 0.018, β = 0.7, k = 0.07, α = 1.32 · 10-8, l = 0.2, Δ = 0.009, γ = 1.76 · 10⁹,

M₁ = 24.3, M₂ = 52.7, A₁ = 32.8, A₂ = 57.5, E₁ = 3 · 10⁸, E₂ = 8 · 10⁸.

Используя результаты настоящей статьи, удаётся рассчитать параметры

u = 80, u = 1, y₁ = 0.00172, y₂ = 0.0063

обратной связи (3), при которых в соответствующей замкнутой системе при E(0) = 4.73 · 10⁸

и начальных условиях

y(0) = 0.0032,

y(0) = 0, T (0) = 41.067

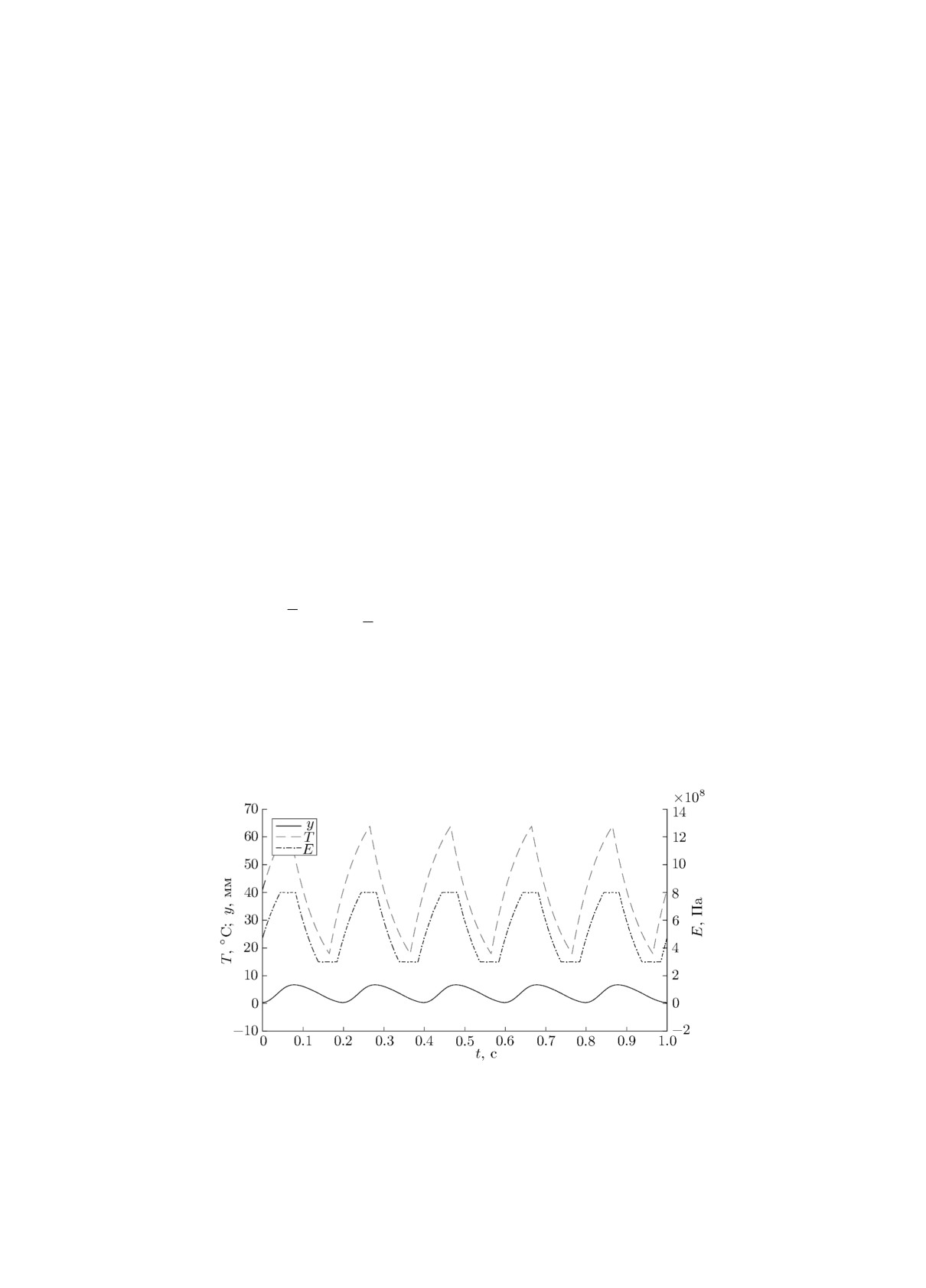
возникает периодическое движение (рис. 5) с периодом Θ = 0.2. При этом моменты переклю-

чения реле обратной связи t₁ = Θ₁ - t₀, t₂ = Θ - t₀, где Θ₁ = 0.1 и t₀ = 0.036.

Рис. 5. Графики функций y(t), T (t), E(t), соответствующих перио-

дическому режиму системы (1).

Заключение. В работе рассмотрена математическая модель одной термомеханической

установки [1] в виде управляемой нелинейной динамической системы (1), коэффициенты ко-

торой - положительные числовые параметры. При этом основная задача состояла в выборе

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКОГО РЕЖИМА

1115

алгоритма управления, обеспечивающего в замкнутой системе возникновение периодическо-

го движения. В качестве алгоритма управления предложено использовать обратную связь по

выходу с оператором обратной связи в форме двухпозиционного реле с гистерезисом. В ре-

зультате получены достаточные условия на коэффициенты и начальные значения переменных

состояния системы (1) и на параметры регулятора (3), обеспечивающие возникновение пери-

одического режима в соответствующей замкнутой системе.

Исследование выполнено при финансовой поддержке Российского фонда фундаменталь-

ных исследований и Национального научного фонда Болгарии (проект 19-57-18006), Россий-

ского фонда фундаментальных исследований (проекты 20-57-0001, 20-07-00827, 19-07-00294),

Минобрнауки РФ в рамках реализации программы Московского центра фундаментальной и

прикладной математики по соглашению № 075-15-2019-1621.

СПИСОК ЛИТЕРАТУРЫ

1. Фурсов А.С., Тодоров Т.С., Крылов П.А., Митрев Р.П. О существовании колебательных режимов в

одной нелинейной системе с гистерезисами // Дифференц. уравнения. 2020. Т. 56. № 8. С. 1103-1121.

2. Todorov T., Nikolov N., Todorov G., Ralev Y. Modelling and investigation of a hybrid thermal energy

harvester // MATEC Web of Conferences. 2018. V. 148. P. 12002.

3. Pai A. A phenomenological model of shape memory alloys including time-varying stress: master’s thesis

of applied science. Waterloo, Ontario, Canada, 2007.

4. Обморшев А.Н. Введение в теорию колебаний. М., 1965.

5. Демидович Б.П. Лекции по математической теории устойчивости. М., 1967.

Электротехнический университет,

Поступила в редакцию 01.03.2021 г.

г. Ханчжоу, Китай,

После доработки 19.05.2021 г.

Московский государственный университет

Принята к публикации 08.06.2021 г.

им. М.В. Ломоносова,

Институт проблем передачи информации

им. А.А. Харкевича, г. Москва,

Технический университет, г. София, Болгария

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№8

2021