ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 9, с.1177-1190

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.958:621.372.8+517.984.4

ИССЛЕДОВАНИЕ СПЕКТРА ПОВЕРХНОСТНЫХ ВОЛН

ОТКРЫТОГО НЕОДНОРОДНОГО ПРЯМОУГОЛЬНОГО

ДИЭЛЕКТРИЧЕСКОГО ВОЛНОВОДА

Рассматривается задача о поверхностных волнах регулярной открытой неоднородной вол-

новедущей структуры прямоугольного сечения. Эта задача сводится к краевой задаче для

продольных компонент электромагнитного поля в пространствах Соболева. Для нахож-

дения решения использована вариационная формулировка задачи. Доказаны теоремы о

дискретности спектра и о распределении характеристических чисел оператор-функции на

комплексной плоскости. Характеристические числа задачи соответствуют постоянным рас-

пространения волновода.

DOI: 10.31857/S0374064121090041

Введение. Важный класс существенно векторных электродинамических задач составляют

задачи о распространении электромагнитных волн в волноведущих структурах. При исследо-

вании процессов распространения волн в волноведущих структурах с неоднородным заполне-

нием возникают краевые задачи на собственные значения для систем уравнений Гельмгольца

с разрывными коэффициентами. При этом на линиях (поверхностях) разрыва коэффициентов

ставятся дополнительные условия, называемые условиями сопряжения. В простейших зада-

чах спектральный параметр присутствует лишь в уравнениях, в результате возникает задача

на собственные значения для некоторого самосопряжённого оператора. Однако при анализе

достаточно сложных моделей спектральный параметр входит уже не только в уравнения, но

и в условия сопряжения, причём нелинейным образом. Задача становится несамосопряжён-

ной [1-3].

Для исследования спектральных свойств таких задач оказывается естественным и эффек-

тивным использовать метод операторных пучков. После того как исходная краевая задача

сведена к изучению некоторого операторного пучка, для изучения его спектральных свойств

можно применять аппарат функционального анализ (см. [2-4]). В работах [1-5] в целом по-

строена теория распространения нормальных волн в закрытых (экранированных) волноводах:

доказана дискретность спектра задачи, получены результаты о распределении (локализации)

характеристических чисел на комплексной плоскости, а также доказан ряд теорем о кратной

полноте по Келдышу системы собственных и присоединённых векторов задачи в специальных

пространствах.

Открытые (неэкранированные) волноведущие структуры исследовались рядом авторов [1,

6, 7]. Однако для таких структур достаточно полной теории распространения волн не по-

строено. В этом случае задача становится значительно сложнее (в силу некомпактности соот-

ветствующих операторов из-за неограниченности области). В статье рассматриваются именно

открытые структуры - случай неограниченной внешней области. Первые результаты по ис-

следованию этой задачи получены недавно в работах [8-11].

Указанные трудности удаётся преодолеть при помощи введения фиктивной внешней облас-

ти - внешности круга - и представления решения в этой области через функцию Грина. Это

приводит к тому, что в вариационном соотношении появляется оператор следа (на границе

фиктивной области), сложным нелинейным образом зависящий от спектрального параметра.

Поэтому в данном случае нужно анализировать уже не операторный пучок (как в [5]), а опера-

тор-функцию. Тем не менее удаётся достаточно подробно изучить свойства оператор-функции

и получить результаты о её спектре. В статье доказывается дискретность спектра задачи о

нормальных волнах неоднородной волноведущей структуры.

1177

1178

СМОЛЬКИН

Отметим, что в работе рассматриваются лишь волны, убывающие на удалении от волно-

вода (удовлетворяющие соответствующим условиям на бесконечности). Другие типы волн не

рассматриваются.

1. Постановка задачи. Рассмотрим трёхмерное пространство R³ с цилиндрической сис-

темой координат Oρϕz. Пространство заполнено изотропной средой без источников с диэлек-

трической проницаемостью ε = ε_cε₀ ≡ const и магнитной проницаемостью μ = μ_cμ₀ ≡ const,

где ε0 и μ0 - диэлектрическая и магнитная проницаемости вакуума, а εc ≥ 1 и μc ≥ 1 -

относительные диэлектрическая и магнитная проницаемости.

Пусть Q ⊂ R² - ограниченная область с кусочно-гладкой границей Γ₁. Рассмотрим об-

ласть Ω₀ ⊂ Q с кусочно-гладкой границей Γ₀ такую, что Γ₁

^⋂Γ₀ = ∅. Обозначим Ω₁ :=

:= Q \ Ω₀.

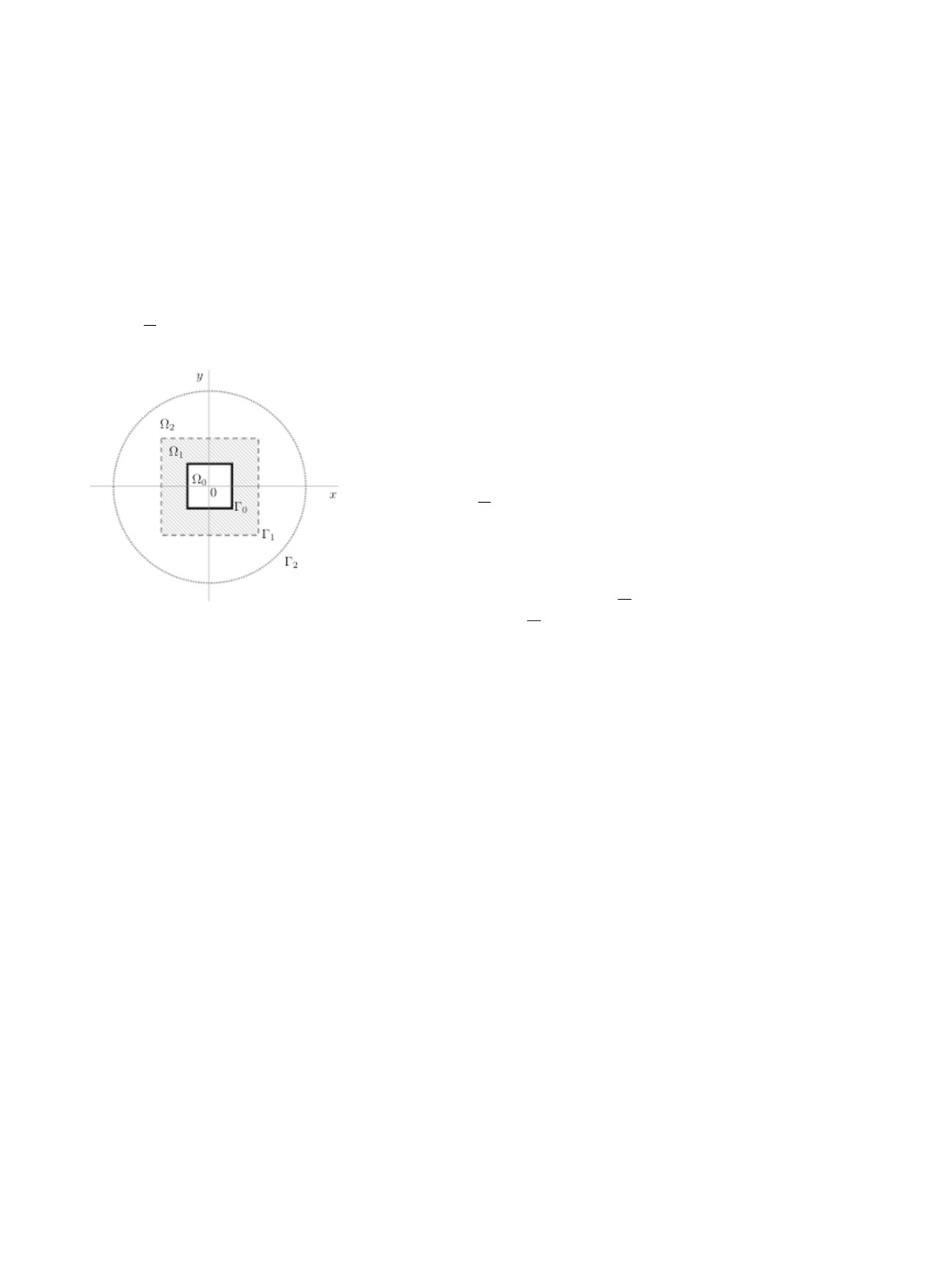
Будем рассматривать математическую модель регуляр-

ной (вдоль оси Oz) открытой волноведущей структуры W,

поперечное сечение которой плоскостью z = const пред-

ставляет собой двухсвязную область Ω₁ с границами Γ₀

и Γ₁. Волновод заполнен неоднородным изотропным ма-

териалом с относительными диэлектрической и магнитной

проницаемостями ε(ρ, ϕ), Im ε = 0, и μ(ρ, ϕ), Im μ =

= 0, соответственно. Мы также предполагаем, что ε(ρ, ϕ),

μ(ρ, ϕ) ∈ C1(Ω1) и minε > εc, min μ > μc. Границы

Γ₀ - проекция поверхности идеально проводящего бесконеч-

но тонкого экрана, Γ₁ - проекция поверхности соприкосно-

вения диэлектриков.

Выберем r > 0 так, чтобы выполнялось включение

:= {x = (ρ, ϕ) : ρ < r} ⊃ Q. Введём в рассмотрение

B_r

Рисунок. Геометрия задачи.

область Ω₂ := B_r \ Q; обозначим Γ₂ := {x : ρ = r} (ри-

сунок).

Диэлектрическая и магнитная проницаемости во всём пространстве имеют вид ε₀ ε и

μ₀μ, где

⎧

⎨ε(x), x ∈ Ω1,

⎨μ(x), x ∈ Ω1,

ε=

ε_c,

x∈Ω₂,

μ=

μ_c,

x∈Ω₂,

^⎩ε_c,

x ∈ R² \ (Ω₁

^⋃Ω₂),

^⎩μ_c,

x ∈ R² \ (Ω₁

^⋃Ω₂).

Будем рассматривать монохроматические волны

Ee^-iωt = e^-iωt(E_ρ,E_ϕ,E_z)^т, He^-iωt = e^-iωt(H_ρ,H_ϕ,H_z)^т,

где ω - частота.

Задача об электромагнитных поверхностных волнах, распространяющихся в неоднородном

волноводе прямоугольного сечения, состоит в отыскании нетривиальных решений однородной

системы уравнений Максвелла:

rot H = -iεE, rot E = iμH,

(1)

причём должны быть удовлетворены следующие условия: обращение в нуль на поверхности

идеального проводника касательных составляющих электрического поля

E_τ |Γ0 = 0,

(2)

непрерывность касательных составляющих полей на границе раздела сред

[E_τ ]|Γ1 = 0,

[H_τ ]|Γ1 = 0,

[E_τ ]|Γ2 = 0,

[H_τ ]|Γ2 = 0,

(3)

ограниченность энергии поля в любом конечном объёме волновода

∫

(ε|E|² + μ|E|²) dX < ∞,

(4)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

ИССЛЕДОВАНИЕ СПЕКТРА ПОВЕРХНОСТНЫХ ВОЛН

1179

а также условие излучения на бесконечности: электромагнитное поле затухает как O(1/ρ)

при ρ → ∞.

Здесь X = (ρ, ϕ, z), V ⊂ R³ - любой конечный объём. Система уравнений Максвелла (1)

записана в нормированном виде. Осуществлён переход к безразмерным величинам [5]: k₀x →

√

→ x, γ → γ/k₀,

μ₀/ε₀H → H, E → E, где k²⁰ = ω²μ₀ε₀ (временной множитель e^-iωt

всюду опущен).

Будем искать решение системы (1) в виде бегущей волны [12, 13], т.е. с зависимостью e^iγz

от координаты z, вдоль которой структура регулярна:

E_x = E_x(x)e^iγz, E_y = E_y(x)e^iγz, E_z = E_z(x)e^iγz,

H_x = H_x(x)e^iγz, H_y = H_y(x)e^iγz, H_z = H_z(x)e^iγz,

где γ - постоянная распространения (неизвестный спектральный параметр задачи).

Задача о поверхностных волнах является задачей на собственные значения для системы

уравнений Максвелла относительно спектрального параметра γ - нормированной постоянной

распространения (затухания) волноведущей структуры.

Принята следующая классификация волн [12-15] по параметру γ:

1) распространяющаяся волна, если Im γ = 0;

2) затухающая волна, если Re γ = 0;

3) комплексная волна, если Re γIm γ = 0.

Мы будем рассматривать комплексные и распространяющиеся поверхностные волны.

Запишем систему уравнений Максвелла (1) в координатном виде

1 ∂H_z

∂H_z

1 ∂(ρH_ϕ)

1 ∂H_ρ

- iγH_ϕ = -iεE_ρ, iγH_ρ -

= -iεE_ϕ,

= -iεE_z,

ρ ∂ϕ

∂ρ

ρ ∂ϕ

1 ∂E_z

∂E_z

1 ∂(ρE_ϕ)

1 ∂E_ρ

- iγE_ϕ = iμH_ρ, iγE_ρ -

= iμH_ϕ,

= iμH_z

(5)

ρ ∂ϕ

∂ρ

ρ ∂ϕ

и, выразив функции E_ρ, H_ρ, E_ϕ, H_ϕ через E_z и H_z из 1, 2, 4 и 5-го уравнений системы (5),

получим

(

)

(

)

1 i

∂E_z

∂H_z

1 i

∂H_z

∂E_z

E_ρ = -

γρ

+μ

H_ρ = -

γρ

-ε

ρκ²

∂ρ

∂ϕ

ρκ²

∂ρ

∂ϕ

(

)

(

)

1 i

∂E_z

∂H_z

1 i

∂H_z

∂E_z

E_ϕ = -

- ρμ

H_ϕ = -

+ ρε

(6)

ρκ²

∂ϕ

∂ρ

ρκ²

∂ϕ

∂ρ

где κ² = γ² - εμ.

Из последних формул следует, что поле нормальной волны в волноводе может быть пред-

ставлено при помощи двух скалярных функций: Π(ρ, ϕ) := E_z(ρ, ϕ), Φ(ρ, ϕ) := H_z(ρ, ϕ).

Тем самым задача сводится к нахождению функций Π и Φ - продольных компонент элек-

трического и магнитного полей.

Для продольных компонент Π и Φ поля имеем следующую задачу на собственные зна-

чения: найти такие γ ∈ C, при которых существуют нетривиальные решения следующей

системы дифференциальных уравнений:

(

)

(

)

∇ε

∇εμ

LΠ := ΔΠ - κ²Π = -

∇Π -

εμ, Φ

κ²

εκ²

(

)

(

)

∇μ

∇εμ

LΦ := ΔΦ - κ²Φ = -

∇Φ +

εμ, Π

(7)

κ²

μκ²

где

1 ∂u ∂v

J (u, v) :=

ρ ∂ρ ∂ϕ

ρ ∂ϕ ∂ρ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

1180

СМОЛЬКИН

удовлетворяющие краевым условиям на Γ₀:



∂Φ



Π|Γ0 = 0,

= 0,

(8)



∂n

Γ₀

условиям сопряжения на Γ₁:

[Π]|Γ1 = 0,

[Φ]|Γ1 = 0,

[

]

[

]

[

]

[

]

1 ∂Π



μ ∂Φ



1 ∂Φ



ε ∂Π



= 0, γ



= 0,

(9)



κ² ∂τ

κ² ∂n

κ² ∂τ

κ² ∂n

Γ₁

условиям сопряжения на Γ₂:

]

^[∂Π



^[∂Φ



[Π]|Γ2 = 0,

[Φ]|Γ2 = 0,



= 0,



= 0,

(10)



∂ρ

Γ₂

условию ограниченности энергии:

∫

(|∇Π|² + |∇Φ|² + |Π|² + |Φ|²) dx < ∞,

(11)

где Ω = Ω₁

^⋃Ω2 ⋃Γ₁, и условию излучения на бесконечности:

Π(ρ, ϕ) = O(1/ρ), Φ(ρ, ϕ) = O(1/ρ) при ρ → ∞ равномерно по ϕ.

(12)

Зная продольные компоненты Π и Φ поля, его поперечные составляющие находим по форму-

лам (6). Определённое так поле E, H удовлетворяет всем условиям (1)-(4). Эквивалентность

перехода к задаче (7)-(12) нарушается лишь при γ² = εμ; в этом случае требуется отдельное

рассмотрение системы (1).

2. Вариационная формулировка. Будем искать решения Π и Φ задачи (7)-(12) в

пространствах Соболева

H¹⁰(Ω) = {f : f ∈ H¹(Ω), f|Γ0 = 0} и H¹(Ω)

соответственно; скалярное произведение и норма в них задаются равенствами

∫

(f, g)₁ =

(∇f∇g + fg) dx,

∥f∥²¹ = (f, f)₁.

Здесь мы используем обозначение для пространства Соболева H¹⁰(Ω), не совпадающее со

стандартным: в нашем случае f|Γ0 = 0, но, вообще говоря f|Γ1 = 0.

Дадим другую, вариационную, формулировку задачи (7)-(12). Умножим уравнения (7)

на произвольные пробные функции u ∈ H¹⁰(Ω) и v ∈ H¹(Ω) соответственно, считая их пока

непрерывно дифференцируемыми в Ω₁ и Ω₂, и применим формулу Грина [16, с. 329] отдельно

для каждой области (возможность применения формулы Грина обоснована в [5]). Тогда с

учётом граничного условия (8) будем иметь

∫



∫

(

)

∫

εu

∂Π



LΠdx =

τ -

∇Π∇u dx -

∇ε +

∇εμ ∇Π dx - εΠu dx

 d

κ²

∂n

κ²

Γ₁

Ω₁

Γ₁

Ω₁

∫



∫

(

)

∫

μv

μv ∂Φ

LΦ dx =



τ-

∇Φ∇v dx -

∇μ +

∇εμ ∇Φ dx - μΦv dx,

 d

κ²

κ² ∂n

κ²

Γ₁

Ω₁

Γ₁

Ω₁

где κ² = γ² - εμ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

ИССЛЕДОВАНИЕ СПЕКТРА ПОВЕРХНОСТНЫХ ВОЛН

1181

Принимая во внимания правые части уравнений системы (7), получаем

∫

(

)

∫

εu

γu

LΠdx = -

∇ε +

∇εμ ∇Π dx -

J (εμ, Φ) dx

κ²

κ⁴

Ω₁

∫

(

)

∫

μv

γv

LΦ dx = -

∇μ +

∇εμ ∇Φ dx +

J (εμ, Π) dx.

κ²

κ⁴

Ω₁

Таким образом, приходим к равенствам

∫



γu

εu

∂Π



∇Π∇u dx + εΠu dx -

J (εμ, Φ) dx =

(13)

 d

κ²

κ⁴

κ²

∂n

Γ₁

Ω₁

Γ₁

∫



γv

μv ∂Φ



∇Φ∇v dx + μΦv dx +

J (εμ, Π) dx =

τ.

(14)

 d

κ²

κ⁴

κ² ∂n

Γ₁

Ω₁

Γ₁

Аналогично, для области Ω₂ выполняются равенства

∫



∫



ε_cu

∂Π

ε_cu

∂Π



∇Π∇u dx -

Πu dx +

τ =

(15)

 d

κ²

∂n

κ²⁰

∂n

Γ₂

Γ₁

Ω₂

Γ₂

Γ₁

∫



∫



μ_cv

∂Φ

μ_cv

∂Φ

∇Φ∇v dx -

Φv dx +



τ =



τ,

(16)

 d

κ²

∂n

κ²

∂n

Γ₂

Γ₁

Ω₂

Γ₂

Γ₁

где κ²⁰ = γ² - ε_cμ_c.

В силу условий сопряжения (9) из равенств (13), (15) и равенств (14), (16) соответственно

следует, что

∫



∫



γu

εμ - ε_cμ_c

∂Φ



ε_cu

∂Π



εΠu dx +

∇Π∇u dx -

J(εμ,Φ)dx +

τ-

τ =0

 d

κ²

κ⁴

κ²⁰κ2

∂τ

κ²

∂n

Γ₁

Γ₂

Γ₁

Γ₂

∫



∫



γv

εμ - ε_cμ_c

∂Π



μ_cv

∂Φ



μΦv dx +

∇Φ∇v dx +

J(εμ,Π)dx -

τ -

τ = 0.

 d

κ²

κ⁴

κ²⁰κ2

∂τ

κ²

∂n

Γ₁

Γ₂

Γ₁

Γ₂

Так как граница Γ₂ - окружность с радиусом r, последние формулы, можно записать

следующим образом:

∫



ε_cu

∂Π

γu

εμ - ε_cμ

∂Φ



dl =

εΠu dx +

∇Π∇u dx -

J(εμ,Φ)dx + γ

u

 d

κ²

∂ρ

κ²

κ⁴

κ²⁰κ2

∂τ

Γ₁

Γ₂

Γ₁

∫



μ_cu

∂Φ

γv

εμ - ε_cμ

∂Π



dl =

μΦv dx +

∇Φ∇v dx +

J(εμ,Π)dx - γ

τ.

 d

κ²

∂ρ

κ²

κ⁴

κ²⁰κ2

∂τ

Γ₁

Γ₂

Γ₁

Вне области Ω₂ имеем ε = μ = 1. Тогда система (7) примет вид

LΠ := ΔΠ - κ²⁰Π = 0, LΦ := ΔΦ - κ²⁰Φ = 0.

(17)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

1182

СМОЛЬКИН

Функция Грина G внешней задачи Дирихле для уравнения Гельмгольца (17) во внешности

окружности Γ₂ определяется как решение следующей краевой задачи:

δ(ρ - ρ₀)δ(ϕ - ϕ₀)

LG = -

ρ₀ > r;

G(x, x₀)|Γ2 = 0,

G(x, x₀) = O(1/ρ) при ρ → ∞.

Здесь G(x, x₀) = G(x₀, x), x = (ρ, ϕ) и x₀ = (ρ₀, ϕ₀).

Имеем [17, с. 203] в смысле распределений

∑

δ(ϕ - ϕ₀) =

cos(m(ϕ - ϕ₀)),

2π

m=-∞

где в качестве основного пространства берётся пространство C∞0(-π, π) бесконечно диффе-

ренцируемых функций, определённых на интервале (-π, π) и обращающихся в нуль в окрест-

ности его концов. Тогда функция Грина G(x, x₀) примет вид

∑

G(x, x₀) =

Gm(ρ, ρ0) cos(m(ϕ - ϕ0)),

2π

m=-∞

где G_m(ρ, ρ₀) - функция Грина следующей краевой задачи:

(

)

1 d

dG_m

⁽m²

δ(ρ - ρ₀)

L_mG_m :=

+k²

Gm = -

ρ₀ ≥ r;

ρ dρ

dρ

ρ²

2πρ

Gm(r, ρ0) = 0,

Gm(ρ, ρ0) = O(1/ρ) равномерно по m при ρ → ∞.

Нетрудно проверить, что функция Грина G_m имеет вид

⎧

K_m(κ₀ρ₀)

⎪

⎨

(I_m(κ₀r)K_m(κ₀ρ) - I_m(κ₀ρ)K_m(κ₀r)), r ≤ ρ < ρ₀,

K_m(κ₀r)

Gm(ρ, ρ0) =

⎪Km(κ0ρ)

⎩

(I_m(κ₀ρ₀)K_m(κ₀r) - I_m(κ₀r)K_m(κ₀ρ₀)), r ≤ ρ₀ < ρ,

K_m(κ₀r)

где функция K_m - модифицированная функция Бесселя (функция Макдональда), функция

I_m - модифицированная функция Бесселя (функция Инфельда) [18, с. 198].

В силу условия на бесконечности выбираем следующую ветвь корня:

√

κ₀ =

γ² - ε_cμ_c =

√

(

|γ² - ε_cμ_c| + Re (γ² - ε_cμ_c) +

√

+ isignIm(γ² - ε_cμ_c)

|γ² - ε_cμ_c| - Re (γ² - ε_cμ_c)).

Функция κ₀(γ) является аналитической [16] в области C\Λ₀, где Λ₀ := {γ : Im γ² = 0,

γ² ≤ ε_cμ_c}.

Окончательно получаем

⎧

⎪

^∑K_m(κ₀ρ₀)

(I_m(κ₀r)K_m(κ₀ρ)-I_m(κ₀ρ)K_m(κ₀r)) cos (m(ϕ-ϕ₀)), r ≤ρ<ρ₀,

⎪

K_m(κ₀r)

m=-∞

G(x, x₀)=

2π ⎪

∑

K_m(κ₀ρ)

⎪

(I_m(κ₀ρ₀)K_m(κ₀r)-I_m(κ₀r)K_m(κ₀ρ₀)) cos (m(ϕ-ϕ₀)), r ≤ρ₀ <ρ.

⎩

K_m(κ₀r)

m=-∞

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

ИССЛЕДОВАНИЕ СПЕКТРА ПОВЕРХНОСТНЫХ ВОЛН

1183

Вследствие второй формулы Грина справедливо равенство

∫

2π

(

)

∂v

∂u



(uLv - vLu) dx = r

-v

dϕ.



∂ρ

ρ=r

R²\Br

Далее, пусть v = G, тогда будем иметь

∫

2π



∂G



(uLG - GLu) dx = r

dϕ.



∂ρ

ρ=r

R²\Br

Кроме того,

∫

(uLG - GLu) dx = -u(x₀), x₀ ∈ R² \ B_r.

R²\Br

Окончательно получаем

∫2π



∂G(x, x₀)



u(x₀) = -r

u(x)

dϕ, x₀ ∈ R² \ B_r,

(18)



∂ρ

ρ=r

где



∂G(x, x₀)

∑ K_m(κ₀ρ₀)



cos [m(ϕ - ϕ₀)].

(19)



∂ρ

2πr

K_m(κ₀r)

ρ=r

m=-∞

Учитывая теорему о непрерывности нормальной производной потенциала двойного слоя на

границе [16, с. 115] и используя равенство (18), определим на границе Γ₂ значение нормальной

производной:



∫

2π



∂u



∂²G(x,x₀)



= -r

u(x)

ϕ,



ρ=r d

∂ρ₀

∂ρ₀∂ρ

ρ₀=r

причём



∂²G(x,x₀)

κ₀

∑ K^′m(κ₀r)



cos(m(ϕ - ϕ₀)).

(20)

ρ=r

∂ρ₀∂ρ

2πr

K_m(κ₀r)

ρ₀=r

m=-∞

Сходимость рядов (19) и (20) понимается в смысле распределений [17, с. 203].

Далее, переставив переменные x и x₀ местами, домножив на тестовые функции u и v и

∫

∂u

взяв интегралы

vdl, получим

Γ₂ ∂ρ

2π

∫



∂Π

∂²G(x,x₀)



udl = -r²

Π(x₀)u(x)

dϕ dϕ₀.

ρ=r

∂ρ

∂ρ∂ρ₀

ρ₀=r

Γ₂

∫

2π

∫

2π



∂Φ

∂²G(x,x₀)



vdl = -r²

Φ(x₀)v(x)

dϕ dϕ₀.

ρ=r

∂ρ

∂ρ∂ρ₀

ρ₀=r

Γ₂

Воспользовавшись условиями сопряжения (10), будем иметь

∫

2π

∫

2π



∂²G(x,x₀)



ε_cΠ(x₀)u(x)

dϕ dϕ₀ =

κ²

∂ρ∂ρ₀

 ρ=r

ρ₀=r

∫



γu

εμ - ε_cμ_c

∂Φ



εΠu dx +

∇Π∇u dx -

J(εμ,Φ)dx + γ

τ,

 d

κ²

κ⁴

κ²⁰κ2

∂τ

Γ₁

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

1184

СМОЛЬКИН

2π

∫



∂²G(x,x₀)

μ_cΦ(x₀)v(x)

dϕ dϕ₀ =

ρ=r

κ²

∂ρ∂ρ₀

ρ₀=r

∫



γv

εμ - ε_cμ_c

∂Π



μΦv dx +

∇Φ∇v dx +

J(εμ,Π)dx - γ

τ.

 d

κ²

κ⁴

κ²⁰κ2

∂τ

Γ₁

Складывая последние выражения и домножая на γ², получаем вариационное соотношение

∫

γ²

(εΠu + μΦv) dx +

(ε∇Π∇u + μ∇Φ∇v + εΠu + μΦv) dx -

(εΠu + μΦv) dx +

∫

εμ

(ε∇Π∇u + μ∇Φ∇v + εΠu + μΦv) dx -

(εΠu + μΦv) dx +

κ²

∫

)

γ³

εμ - ε_cμ

⁽∂Π

∂Φ



(μvJ(μ, Π) - εuJ(εμ, Φ)) dx - γ³



τ +

 d

κ⁴

κ²κ²

∂τ

Γ₁

∫

2π

∫

2π



∂²G(x,x₀)

+r²

(ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x))

dϕ dϕ₀ = 0.

(21)

κ²

∂ρ∂ρ₀

 ρ=r

ρ₀=r

Вариационное соотношение (21) получено для гладких функций u и v. Соотношение (21)

распространяется на любые функции u ∈ H¹⁰(Ω), v ∈ H¹(Ω) по непрерывности, поскольку

непрерывность соответствующих форм будет доказана в следующем пункте.

Определение. Пару функций Π ∈ H¹⁰(Ω), Φ ∈ H¹(Ω), (∥Π∥₁ +∥Φ∥₁ = 0) будем называть

собственным вектором задачи (7)-(12), отвечающим характеристическому числу (х.ч) γ₀ ∈

∈ C, если при γ = γ₀ вариационное соотношение (21) выполнено для любых u ∈ H¹⁰(Ω),

v ∈ H¹(Ω).

3. Задача о спектре оператор-функции. Пусть H = H¹⁰(Ω) × H¹(Ω) - декартово про-

изведение гильбертовых пространств со стандартным скалярным произведением и нормой:

(u, v) = (u₁, v₁)₁ + (u₂, v₂)₁,

∥u∥² = ∥u₁∥²¹ + ∥u₂∥²¹; u, v ∈ H,

u = (u₁,u₂)^т, v = (v₁,v₂)^т, u₁,v₁ ∈ H¹⁰(Ω), u₂,v₂ ∈ H¹(Ω).

Тогда интегралы, входящие в соотношение (21), можно рассматривать как полуторалинейные

формы над полем C от аргументов u = (Π, Φ)^т, v = (u, v)^т, заданные на H. Каждая

полуторалинейная форма t(u, v), u, v ∈ H, задаёт [19, с. 67] линейный оператор T : H → H

по формуле

t(u, v) = (Tu, v) для любого v ∈ H.

Оператор T ограничен, если форма ограничена: |t(u, v)| ≤ C∥u∥∥v∥. Линейность оператора

следует из линейности формы по первому аргументу, а непрерывность - из оценок

∥Tu∥² = t(u, Tu) ≤ C∥u∥∥Tu∥.

Рассмотрим полуторалинейные формы и порождаемые ими линейные операторы:

∫

k(u, v) :=

(εΠu + μΦv) dx = (Ku, v) для любого v ∈ H,

∫

εμ

k_γ(u,v) :=

(εΠu + μΦv) dx = (K_γ(γ)u, v) для любого v ∈ H,

κ²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

ИССЛЕДОВАНИЕ СПЕКТРА ПОВЕРХНОСТНЫХ ВОЛН

1185

∫

a(u, v) :=

(ε∇Π∇u + ∇Φ∇v + εΠu + Φv) dx = (Au, v) для любого v ∈ H,

∫

εμ

aγ (u, v) :=

(ε∇Π∇u + μ∇Φ∇v + εΠu + μΦv) dx = (A_γ(γ)u, v) для любого v ∈ H,

κ²

∫

γ³

b(u, v) :=

(vJ(μ, Π) - εuJ(εμ, Φ)) dx = (B(γ)u, v) для любого v ∈ H,

κ⁴

∫

)

εμ - ε_cμ_c

⁽∂Π

∂Φ



s(u, v) := γ

τ = (S(γ)u,v) для любого v ∈ H,

 d

κ²

∂τ

Γ₁

∫2π

2π

∫

p(u, v) :=

F (ϕ, ϕ₀)(ε_cΠ(x₀)u(x) +



+ μ_cΦ(x₀)v(x))^

dϕ dϕ₀ = (P(γ)u, v) для любого v ∈ H,

ρ=r

ρ₀=r



∂²G(x,x₀)



F (ϕ, ϕ₀) := r²

ρ=r .

κ²

∂ρ∂ρ₀

ρ₀=r

Известно [16, с. 428], что функция Грина G(x, x₀) имеет логарифмическую особенность,

которую можно выделить. Тогда аналогично [20, с. 61] находим



∂²G(x,x₀)

κ₀

∑ K^′m(κ₀r)



cos (m(ϕ - ϕ₀)) =

ρ=r

∂ρ₀∂ρ

2πr

K_m(κ₀r)

ρ₀=r

m=-∞

∑

κ₀ K₁(κ₀r)

κ₀

K^′m(κ₀r)

cos (m(ϕ - ϕ₀)) =

πr K₀(κ₀r)

πr

K_m(κ₀r)

m=1

(

)

∑

κ₀ K₁(κ₀r)

K^′m(κ₀r)

κ₀r

+ m cos(m(ϕ - ϕ₀)) +

m cos (m(ϕ - ϕ₀)) =

πr K₀(κ₀r)

πr²

K_m(κ₀r)

πr²

m=1

(

)

∑

κ₀ K₁(κ₀r)

K^′m(κ₀r)

κ₀r

+ m cos(m(ϕ - ϕ₀)) -

πr K₀(κ₀r)

πr²

K_m(κ₀r)

πr² 1 - cos (ϕ - ϕ₀)

m=1

Для общего члена последнего ряда имеем

K^′m(κ₀r)

κ₀r

+ m = O(1/m) при m → ∞,

K_m(κ₀r)

а значит, ряд сходится условно при ϕ = ϕ₀.

Оператор P(γ) представим как сумму компактного и гиперсингулярного операторов

P(γ) = K_P + P_G,

(22)

где

∫

2π

∫

2π

(

)

κ₀r K₁(κ₀r)



k_p(u,v) :=

ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x)



dϕ dϕ₀ -

ρ=r

π K₀(κ₀r)

ρ₀=r

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

3^∗

1186

СМОЛЬКИН

∫

2π

∫

2π

(

)



∑



K^′m(κ₀r)

κ₀r

+ m cos(m(ϕ - ϕ₀))(ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x))

dϕ dϕ₀ =

ρ=r

K_m(κ₀r)

m=1

ρ₀=r

= (K_P(γ)u, v) для любого v ∈ H

∫

2π

∫

2π



ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x)



p_G(u,v) := -

dϕ dϕ₀ = (P_Gu, v) для любого v ∈ H.

ρ=r

2π

1 - cos(ϕ - ϕ₀)

ρ₀=r

Так как функции Π, u, Φ, v ∈ H¹(Ω), то следы этих функций на Γ₂ принадлежат прост-

ранству H1/2(Γ₂) [21, с. 59]. Гиперсингулярный оператор P_G : H1/2(Γ₂) → H-1/2(Γ₂) ограни-

чен [22, с. 19]. В силу антидуального спаривания пространств H1/2(Γ₂) и H-1/2(Γ₂) [23, с. 258]

получаем, что полуторалинейная форма p_G(u, v) ограничена в H. Далее, учитывая скорость

убывания коэффициентов ряда для k_p(u, v), заключаем, что этот ряд определяет интеграль-

ный оператор с логарифмической особенностью ядра и оператор K_P : H1/2(Γ₂) → H1/2(Γ₂)

будет компактным. Таким образом, оператор-функция P (γ) : H → H ограничена.

Ограниченность форм a(u, v) и a_γ (u, v) очевидна, а форм k(u, v) и k_γ(u, v) следует из

неравенства Пуанкаре [21, с. 59]. Ограниченность форм b(u, v) и s(u, v) установлена в [10].

Теперь вариационную задачу (21) можно записать в операторном виде

(N(γ)u, v) = 0 для любого v ∈ H,

или равносильно

N(γ)u = 0, N(γ) : H → H,

N(γ) := γ²K + A - K + A_γ - K_γ + B - S + P.

(23)

Уравнение (23) - операторная запись вариационного соотношения (21). Характеристиче-

ские числа и собственные векторы оператор-функции N совпадают по определению с соб-

ственными значениями и собственными векторами задачи (7)-(10) при γ² = εμ.

4. Свойства оператор-функции. Приведём следующие утверждения о свойствах опе-

раторов, входящих в оператор-функцию N(γ) (доказательства в [5, 10]).

Лемма 1. Операторы K и K_γ компактные. Оператор K положительно определён и

для его собственных чисел верна асимптотика

λ_n(K) = O(n-1) при n → ∞.

Лемма 2. Ограниченный оператор A : H → H является положительно определённым:

A ≥ I.

Лемма 3. Оператор B_γ компактен. Оператор-функция B_γ (γ) голоморфна в области

C\Λ_B, где

{

}

Λ_B := γ : Imγ = 0,

|γ| =

√ε_cμ_c, min^√ε(x)μ(x) ≤ |γ| ≤ max^√ε(x)μ(x)

x∈Ω₁

Обозначим через ϱ(N) резольвентное множество оператор-функции N(γ), т.е. совокуп-

ность тех γ ∈ C, при которых оператор N(γ) имеет ограниченный обратный. Спектр опера-

тор-функции N(γ) будем обозначать через σ(N), т.е. σ(N) = C \ ϱ(N).

Лемма 4. Существует γ ∈ R такое, что оператор N(γ) непрерывно обратим, т.е.

резольвентное множество ϱ(N) оператор-функции N(γ) не пусто; ϱ(N) = ∅.

Доказательство. Пусть γ ∈ R, γ > 0 и γ → +∞. Рассмотрим следующую оператор-

функцию:

N(γ) = N₁(γ) + N₂(γ),

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

ИССЛЕДОВАНИЕ СПЕКТРА ПОВЕРХНОСТНЫХ ВОЛН

1187

где N₁(γ) = γ²K+A-K+γP₀ и N₂(γ) = A_γ -K_γ +B-S+P(γ)-γP₀, а оператор P₀ : H → H

определяется полуторалинейной формой

∫2π

∑

p₀(u,v) :=

cos (m(ϕ - ϕ₀)) dϕ ×

m=-∞

∫2π



(ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x))

ϕ₀ = (P₀u,v) для любого v ∈ H.

ρ=r d

ρ₀=r

Известно [17, с. 203], что (в смысле распределений)

∑

cos(mφ) = 2π

δ(φ - 2πl) = 2πδ(φ),

m=-∞

l=-∞

где φ = |ϕ - ϕ₀|,

0 ≤ |φ| ≤ π и в качестве основного пространства берётся, как и в п. 2,

пространство C∞0(-π, π). Получаем, что

∑

cos (m(ϕ - ϕ₀)) = 2πδ(ϕ - ϕ₀).

m=-∞

Тогда оператор P₀ определяется формой

∫2π

(P₀u, v) := 2π (ε_cΠ(x)u(x) + μ_cΦ(x)v(x))|ρ=r dϕ для любого v ∈ H.

∫2π

Очевидно, что (P₀u, u) = 2π

(ε_c|Π(x)|² + μ_c|Φ(x)|²)|ρ=r dϕ > 0 при ∥u∥ = 0. Так как

следы функций Π, u, Φ, v на Γ₂ принадлежат пространству H1/2(Γ₂), заключаем, что

оператор P₀ : H → H ограничен.

Принимая во внимание асимптотику функций K_m при γ → +∞ [18, с. 198], имеем

F (ϕ, ϕ₀) ∼ γ + O(1/γ)

и, следовательно,

∥P(γ) - γP₀∥ = O(1/γ) при γ → +∞.

Тогда оператор-функцию N(γ) можно рассматривать как возмущение операторного пучка N₁

оператор-функцией N₂ при больших γ.

Из свойств операторов K и A вытекает, что найдётся такое большое γ > 0, при котором

для любого u справедливо неравенство

Re (N₁(γ)u, u) = γ²(Ku, u) + (Au, u) - (Ku, u) + γ(P₀u, u) ≥ ∥u∥².

Поэтому γ ∈ ϱ(N₁), где ϱ(N₁) - резольвентное множество пучка N₁. Причём, используя

лемму 7.1 из [24, с. 309], имеем оценку ∥N-11(γ)∥ ≤ 1. Выберем γ так, чтобы ∥N₂(γ)∥ < 1.

Получаем, что существует и ограничен оператор

(N₁(γ) + N₂(γ))-1 = (I + N-11(γ)N₂(γ))N-11(γ).

Лемма доказана.

Замечание. В дальнейшем нам понадобится продолжение функций ε(x) и μ(x) в Ω₂

с сохранением гладкости. Так как ε, μ ∈ C¹(Ω₁), такое продолжение легко осуществить [25,

с. 122]. При этом сохраним старые обозначения за продолженными функциями ε и μ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

1188

СМОЛЬКИН

Поскольку соотношение (21) справедливо для любых u ∈ H¹⁰(Ω), v ∈ H¹(Ω), введём

пробные функции u и v такие, что u = η-1u, v = η-1v, где η = γ²χ - ϵ, χ = (εμ - ε_cμ_c)-1 >

> 0, ϵ = εμ(εμ - ε_cμ_c)-1 > 0. Очевидно, что так определённые функции u и v принадлежат

тем же пространствам, что и исходные функции u и v.

Соотношение (21) примет вид

∫

κ²⁰

ηκ²⁰(1 - κ-2)(εΠu + μΦv)dx + η

(ε∇Π∇u + μ∇Φ∇v + εΠu + μΦv) dx +

κ²

∫

)

κ²

⁽∂Π

∂Φ



(εu∇Π∇η+ μv∇Φ∇η) dx+ γη

(μvJ(μ, Π)-εuJ(εμ, Φ)) dx-γ

τ+

 d

κ²

κ⁴

∂τ

Γ₁

∫2π

∫

2π



∂²G(x,x₀)



+r²

η(ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x))

dϕ dϕ₀ = 0.

(24)



∂ρ∂ρ₀

ρ=r

ρ₀=r

Имеем следующие ограниченные операторы:

k(u, v) := ηκ²⁰(1 - κ-2)(εΠu + μΦv) dx = (K(γ)u, v) для любого v ∈ H,

∫

a₁(u,v) := χ(ε∇Π∇u + μ∇Φ∇v + εΠu + μΦv)dx = (A1u,v) для любого v ∈ H,

∫

a₂(u,v) :=

ϵϵ(ε∇Π∇u + μ∇Φ∇v + εΠu + μΦv)dx = (A2u, v) для любого v ∈ H,

∫

)

⁽∂Π

∂Φ



s(u, v) :=

τ = (Su,v) для любого v ∈ H,

 d

∂τ

Γ₁

∫

b(u, v) :=κ0((εu∇Π∇η + μv∇Φ∇η) +

κ²

γη

(μvJ(μ, Π) - εuJ(εμ, Φ))) dx = (B(γ)u, v) для любого v ∈ H,

κ²

2π

∫



η(ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x))

dϕ dϕ₀ -

kp(u, v) =κ0rK1(κ0r⁾

ρ=r

π K₀(κ₀r)

ρ₀=r

∫

2π

∫

2π

(

)



∑



K^′m(κ₀r)

κ₀r

+ m cos[m(ϕ - ϕ₀)](ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x))

ϕ dϕ₀ =

K_m(κ₀r)

 ρ=r^d

m=1

ρ₀=r

= (KP(γ)u,v) для любого v ∈ H,

∫

2π

∫

2π



ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x)



p₁(u,v) = -

dϕ dϕ₀ = (P1u, v) для любого v ∈ H

ρ=r

2π

1 - cos(ϕ - ϕ₀)

ρ₀=r

∫

2π

∫

2π



ε_cΠ(x₀)u(x) + μ_cΦ(x₀)v(x)



p₂(u,v) = -

dϕ dϕ₀ = (P2u, v) для любого v ∈ H,

ρ=r

2π

1 - cos(ϕ - ϕ₀)

ρ₀=r

здесь ϵ = ε_cμ_cεμε-1 μ-1.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

ИССЛЕДОВАНИЕ СПЕКТРА ПОВЕРХНОСТНЫХ ВОЛН

1189

Таким образом, мы получили следующую оператор-функцию:

N(γ)u = 0, u ∈ H,

N(γ) : H → H,

N(γ) :=K +KP +B + γ²(A1 +P1) - γ^S - (A2 +P2).

(25)

Уравнение (25) - операторная запись вариационного соотношения (24). Спектры оператор-

A₁

функций N иN совпадают: σ(N(γ)) = σ(N(γ)). Операторы

K(γ),

B(γ),

K_P (γ),

и A₂

сохраняют все свойства операторов K, B(γ), K_P (γ) и A, перечисленные в леммах 1-3.

Справедливы следующие леммы [5, 11].

Лемма 5. Оператор^S самосопряжён,S =S∗, и имеют место неравенства

I≤^S≤1I.

(26)

Лемма 6. ОператорыP1 иP2 положительные,P1 > 0,

P₂ > 0.

Теорема 1. Оператор-функция

N(γ) : H → H является ограниченной, голоморфной и

фредгольмовой в области Λ := C\(Λ_B

^⋃Λ0 ⋃Λ_F), где Λ_F := {γ : Imγ = 0, γ_∗ ≤ |γ| ≤ γ^∗}, а

√

-1/2 +

1/4 + 4(maxεμ - εcμc)-2

1/2 +

1/4 + 4(∥A2∥ + ∥P2∥)(∥A1∥ + ∥P1∥)

x∈Ω

γ_∗ =

γ^∗ =

2(∥A1∥ + ∥P1∥)

2(maxεμ - εcμc)-1

x∈Ω

Доказательство. В области C\Λ₀ функция

K^′m(κ₀r)

Km+1(κ₀r)

= -κ₀

κ₀ K_m(κ₀r)

K_m(κ₀r)

является аналитической (как функция от γ). Так как Re κ₀ > 0, функции K_m(κ₀r) не имеют

нулей [18, с. 198]. Принимая во внимание лемму 3, получаем, что в области C\(Λ_B

^⋃Λ₀)

оператор-функцияN(γ) является аналитической.

Запишем оператор-функцию

N(γ) следующим образом:

N(γ) :=NK (γ) +N0(γ), где

N_K(γ) =K +KP +B иN0(γ) = γ²(A1 +P1) - γ^S - (A2 +P2).

Покажем, что операторN0(γ) является обратимым. Пусть γ = γ^′ + iγ^′′, γ^′′ = 0, тогда

A₂

⁽N₀(γ)⁾

= A₁ +

≥ I.

γ^′′

|γ|²

Далее, пусть Im γ = 0. Для квадратичной формы (N₀(γ)u, u) рассмотрим уравнение

(N₀(γ)u, u) = ((γ²(A1 +P1) - γ^S - (A2 +P2))u, u) = 0.

Выражая из этого уравнения (Su, u) и принимая во внимание оценку (26), получаем двойное

неравенство

I≤

(A2 +P2) - γ(A1 +P1) ≤1I.

(27)

Решая неравенства (27) относительно γ, получаем, что вне множества γ_∗ ≤ |γ| ≤ γ^∗ оператор

N₀(γ) положительно или отрицательно определён и поэтому непрерывно обратим [24, с. 37],

и, следовательно, оператор-функция

N(γ) является фредгольмовой как сумма обратимого

N₀(γ) и компактного

N_K(γ) операторов. Теорема доказана.

Теорема 2. Спектр оператор-функции N(γ) : H → H является дискретным в Λ, т.е.

имеет конечное число характеристических точек конечной алгебраической кратности в лю-

бом компакте I₀ ⊂ Λ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021

1190

СМОЛЬКИН

Доказательство. Утверждение теоремы следует из теоремы 1 и теоремы о голоморфной

оператор-функции [24].

Заключение. Доказаны теоремы о дискретности спектра на поверхностных волнах регу-

лярной открытой неоднородной волноведущей структуры прямоугольного сечения.

Исследование выполнено при финансовой поддержке Российского фонда фундаменталь-

ных исследований (проект 20-31-70010).

СПИСОК ЛИТЕРАТУРЫ

1. Ильинский А.С., Шестопалов Ю.В. Применение методов спектральной теории в задачах распро-

странения волн. М., 1989.

2. Смирнов Ю.Г. Метод операторных пучков в краевых задачах сопряжения для системы эллиптиче-

ских уравнений // Дифференц. уравнения. 1991. Т. 27. № 1. С. 140-147.

3. Смирнов Ю.Г. Применение метода операторных пучков в задаче о собственных волнах частично

заполненного волновода // Докл. АН СССР. 1990. Т. 312. № 3. С. 597-599.

4. Делицин А.Л. Об одном подходе к вопросу о полноте нормальных волн волновода с магнитодиэлек-

трическим заполнением // Дифференц. уравнения. 2000. Т. 36. № 5. С. 629-633.

5. Смирнов Ю.Г. Математические методы исследования задач электродинамики. Пенза, 2009.

6. Ложечко В.В., Шестопалов Ю.В. О задачах возбуждения открытых цилиндрических резонаторов

с нерегулярной границей // Журн. вычислит. математики и мат. физики. 1995. Т. 35. № 1. C. 71-82.

7. Даутов Р.З., Карчевский Е.М. Метод интегральных уравнений и точные нелокальные граничные

условия в теории. Казань, 2009.

8. Смирнов Ю.Г., Смолькин Е.Ю. О дискретности спектра в задаче о нормальных волнах открытого

неоднородного волновода // Дифференц. уравнения. 2017. Т. 53. № 10. С. 1298-1309.

9. Смирнов Ю.Г., Смолькин Е.Ю. Исследование спектра в задаче о нормальных волнах закрытого ре-

гулярного неоднородного диэлектрического волновода произвольного сечения // Докл. РАН. 2018.

Т. 478. № 6. С. 1-4.

10. Смирнов Ю.Г., Смолькин Е.Ю. Метод оператор-функций в задаче о нормальных волнах неодно-

родного волновода // Дифференц. уравнения. 2018. Т. 54. № 9. С. 1196-1206.

11. Smirnov Y., Smolkin E. Mathematical theory of normal waves in an open metal-dielectric regular

waveguide of arbitrary cross section // Math. Model. and Anal. 2020. V. 25. № 3. P. 391-408.

12. Адамс М. Введение в теорию оптических волноводов. М., 1984.

13. Снайдер А., Лав Дж. Теория оптических волноводов. М., 1987.

14. Вайнштейн Л.А. Электромагнитные волны. М., 1988.

15. Маркузе Д. Оптические волноводы. М., 1974.

16. Владимиров В.С. Уравнения математической физики. М., 1981.

17. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М., 2004.

18. Абрамовиц М., Стиган И. Справочник по специальным функциям. М., 1979.

19. Като Т. Теория возмущений линейных операторов. М., 1972.

20. Shestopalov Yu.V., Smirnov Yu.G., Chernokozhin E.V. Logarithmic Integral Equations in Electromag-

netics. Holland, 2000.

21. Adams R.A. Sobolev Spaces. New York, 1975.

22. Ильинский А.С., Смирнов Ю.Г. Дифракция электромагнитных волн на проводящих тонких экра-

нах: псевдодифференциальные операторы в задачах дифракции. М., 1996.

23. Трибель Х. Теория интерполяции, функциональные пространства, дифференциальные операторы.

М., 1980.

24. Гохберг И.Ц., Крейн М.Г. Введение в теорию линейных несамосопряжённых операторов в гильбер-

товом пространстве. М., 1965.

25. Хирш М. Дифференциальная топология. М., 1979.

Пензенский государственный университет

Поступила в редакцию 04.03.2021 г.

После доработки 04.03.2021 г.

Принята к публикации 08.06.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№9

2021