ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 10, с. 1380-1399

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.955.8

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

С ЛОКАЛИЗОВАННЫМИ НАЧАЛЬНЫМИ ДАННЫМИ

ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ

С МАЛЫМИ ДИСПЕРСИОННЫМИ ЭФФЕКТАМИ

Построено асимптотическое решение задачи Коши для многомерного волнового уравне-

ния с учётом малых дисперсионных эффектов и с локализованной начальной функцией.

Отдельно рассмотрены трёхмерный случай и построение асимптотики для него. При спе-

циальном выборе начальной функции в трёхмерном случае представлена асимптотика в

явном виде с помощью функций Эйри и Скорера. В качестве примера, где возникают

дисперсионные эффекты, рассмотрено усреднение волнового уравнения с быстроосцилли-

рующим коэффициентом и построено асимптотическое решение такого уравнения.

DOI: 10.31857/S0374064122100089, EDN: KQNPGZ

Введение. Во многих задачах математической физики, например, при описании распро-

странения звука в воде [1, гл. 2] или распространения электромагнитных волн в неоднородных

средах [2, гл. 4], возникает волновое уравнение в недивергентной форме. Часто в таких задачах

в уравнении следует учитывать и дисперсионные эффекты, появляющиеся при распростране-

нии волн.

В данной работе строится асимптотика решения задачи Коши с локализованными началь-

ными данными, сформулированной для многомерного волнового уравнения в недивергентной

форме с учётом малых дисперсионных эффектов

∂²v(x,t)

= Δv(x,t) + ε²Φ(x)Δ²v(x,t) + ε²Lˆv(x,t), x ∈ Rⁿ,

(1)

c²(x)

∂t²



∂v



v(x, 0) = V (x/μ),

= 0.

(2)



∂t

t=0

Предполагается, что функция c(x) является гладкой и ограниченной, 0 < c_m ≤ c(x) ≤ c_M ,

где c_m и c_M - некоторые константы; функция Φ(x) ≥ 0 также является гладкой и ограни-

ченной; функция V (ξ) - достаточно гладкая и убывающая на бесконечности вместе со своими

производными. Малый параметр 0 < μ ≪ 1 отвечает за локализацию начальной функции, а

малый параметр 0 < ε ≪ 1 характеризует дисперсионные эффекты, при этом предполагаем,

что справедливо соотношение ε² ≤ μ³. Оператор

L - дифференциальный или псевдодиффе-

ренциальный, устроенный таким образом, что стоящий в правой части уравнения (1) оператор

является симметричным и положительно определённым в подходящем пространстве. Если в

(1) отбросить

L, то получим уравнение, которое, вообще говоря, является некорректным, так

как его символ не является положительным при больших значениях производных. Однако с

учётом оператора

L задача (1), (2) является корректной, а символ оператора в (1) положи-

тельный.

В работе [3] для задачи Коши для двумерного волнового уравнения, записанного в дивер-

гентной форме, со слабыми дисперсионными эффектами асимптотика решения была представ-

лена с помощью функций Эйри. В статье [4] изучалась задача Коши для многомерных строго

гиперболических систем, в частности, трёхмерное волновое уравнение без учёта дисперсион-

ных эффектов. В данной работе представлена асимптотика решения задачи (1), (2) с помощью

функций Эйри и связанных с ними других специальных функций. Полученное представление

1380

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1381

иллюстрируется на примере построения асимптотики решения задачи Коши для волнового

уравнения с быстроосциллирующей скоростью.

В уравнении (1) удобно перейти к оператору

p = -iμ∇, умножив уравнение на

-μ².

Определим следующие функции:

L₀(x,p) = c²(x)|p|², L₁(x,p) = i

c²(x)Φ(x)|p|⁴.

μ³

После умножения на c²(x) уравнение (1) принимает вид

(

)

∂²v(x, t)

-μ²

= L₀(x,

p) + iμL₁(x,

p) + iμL1(2x,

p, μ) v(x, t),

(3)

∂t²

где цифры показывают порядок действия операторов: сначала оператор дифференцирова-

ния p, а потом - оператор умножения на функцию от x (см. [5, с. 56; 6, с. 279]). Функцию

L₀(x,p) будем называть главным символом оператора.

Через L1(2x,

p, μ) в соотношении (3) обозначен результат соответствующих преобразований

оператора

L из (1). Предполагается, что функция L¹(x, p, μ) является гладкой и ограничен-

ной порядка μ. Таким образом, оператор

L¹ не играет роли при построении асимптотики и

его явный вид не является существенным. Асимптотика определяется коэффициентами при

вторых и четвёртых производных, т.е. видом функций L₀(x, p) и L₁(x, p).

Отметим, что из вида функции L₁(x, p) и из (3) следует, что при ε²/μ² = O(μ1+α), где

α > 0, асимптотика решения задачи (1), (2) переходит в асимптотику решения волнового

уравнения.

Для широкого класса дифференциальных и псевдодифференциальных уравнений с началь-

ными условиями, заданными в виде канонического оператора, имеется общая схема В.П. Мас-

лова [5], позволяющая представить асимптотику решения в виде канонического оператора на

лагранжевом многообразии Λ_t (или нескольких многообразиях Λ_t,j ), полученном сдвигом за

время t вдоль траекторий подходящей гамильтоновой системы (или гамильтоновых систем)

начального многообразия Λ₀.

В рассматриваемом случае соответствующие гамильтонианы определяются с помощью

главного символа оператора

√

H^±(x,p) = ±

L₀(x,p) = ±c(x)|p|.

Для наших целей локализованную функцию V (x/μ) удобно представить с помощью пре-

образования Фурье, что с точностью до множителя совпадает с определением канонического

оператора Маслова [7-9]

∫

V (x/μ) =

V (p)e^{i〈x,p〉/μ} dp ≡ μn/2e-iπn/4K^μ

V (p)](x),

(4)

Λ₀

(2π)n/2

Rⁿ

где

V (p) - образ фурье-функции V (ξ). В этом случае канонический оператор K^μ задаётся_Λ

на многообразии

Λ₀ = {x = 0,p = α ∈ Rⁿ},

представляющем собой вертикальную плоскость в фазовом пространстве. Это многообразие

проектируется в одну точку x = 0 на конфигурационном пространстве, и с точки зрения

классической теории канонического оператора (см. [5, с. 153]) состоит из особых точек.

В случае представления начальных условий на многообразии Λ₀ гамильтонианы H^±(x, p)

оказываются негладкими при p = 0, что приводит к появлению негладких так называемых

проколотых многообразий Λ_t,j , и общий подход Маслова нуждается в серьёзной модифика-

ции. Одна из таких модификаций, основанная на представлении асимптотики решения в виде

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1382

СЕРГЕЕВ

проинтегрированного по дополнительному параметру канонического оператора, была предло-

жена в статьях [10, 11].

В работе [12] была предложена серьёзная модификация канонического оператора Маслова,

которая позволила не только сделать существенно эффективными его интегральные представ-

ления в окрестности каустик, но и расширить возможности применения канонического опера-

тора на классы негладких многообразий, в том числе и на “проколотые” многообразия [8, 9, 13,

14]. Использование указанной модификации канонического оператора позволяет прямо приме-

нять схему Маслова для решения рассматриваемой задачи Коши, что и продемонстрировано

в данной работе.

Асимптотика решения задачи (1), (2) в каждый фиксированный момент времени t ло-

кализована в окрестности некоторой поверхности. В случае постоянной функции c(x) ≡ c₀

эта поверхность является гладкой и представляет собой фронт волны. В случае переменной

функции c(x) на этой поверхности могут возникать точки самопересечения, а сама поверх-

ность может уже быть не гладкой. Тем не менее, будем продолжать называть эту поверхность

фронтом волны. С точки зрения теории модифицированного канонического оператора фронт

волны является каустикой специального вида [9, 12-14].

В п. 1 приводятся асимптотические формулы для решения задачи (1), (2) в трёхмерном

случае. В п. 2 рассматриваются волновое уравнение с быстроосциллирующим коэффициентом

и усреднённое уравнение с гладкими коэффициентами, имеющее вид (1). В п. 3 приводятся

асимптотические формулы для задачи (1), (2) в многомерном случае, из которых следуют

формулы для трёхмерного случая. В п. 4 описана процедура вывода усреднённого уравнения

для волнового уравнения с быстроосциллирующим коэффициентом.

1. Трёхмерный случай. В данном пункте строится асимптотическое при μ → 0 решение

задачи (1), (2) в трёхмерном случае (x ∈ R³). Также рассматривается специальный случай

выбора вида начальной функции, когда асимптотику можно представить с помощью функций

Эйри и других функций, связанных с ними. Приводятся формулы для асимптотики решения

волнового уравнения в бездисперсионном случае.

Рассмотрим задачу Коши для уравнения (3) с локализованными начальными данными (2).

Этим начальным данным отвечает многообразие Λ₀, на котором удобно перейти к сфериче-

ским координатам p = ρn(ϕ, θ), где ρ ≥ 0, а вектор n(ϕ, θ) = (cos ϕ cos θ, sin ϕ cos θ, sin θ).

Следуя схеме построения асимптотики решения с помощью модифицированного канониче-

ского оператора [8, 12-14], построим для гамильтониана H(x, p) = c(x)|p| решение следующей

системы Гамильтона:

x=H_p(x,p),

p=-H_x(x,p), x|t=0=0, p|t=0=n(ϕ,θ), ϕ∈[0,2π], θ∈[-π/2,π/2].

(5)

Обозначим через X(ϕ, θ, t) и P (ϕ, θ, t) решение этой системы.

Замечание 1. Будем рассматривать только положительную ветвь корня H(x, p) =

√

L₀(x,p), так как канонические операторы, отвечающие положительной и отрицательной

ветвям корня, связаны комплексным сопряжением (см. [11, лемма 14]).

Лагранжево многообразие в момент времени t, отвечающее асимптотике, имеет вид

Λ_t = {x = X(ϕ,θ,t),p = ρP(ϕ,θ,t)}, ρ ≥ 0, ϕ ∈ [0,2π], θ ∈ [-π/2,π/2].

Предельный переход ρ → 0 + 0 определяет край многообразия

∂Λ_t = {x = X(ϕ,θ,t),p = 0}, ϕ ∈ [0,2π], θ ∈ [-π/2,π/2].

Так как якобиан J = det ∂X(ϕ, θ, t)/∂(ρ, ϕ, θ) проектирования многообразия Λ_t на кон-

фигурационное пространство x ∈ R³ равен нулю, то данное многообразие состоит только из

особых точек.

Проекция края многообразия (как и всего многообразия Λ_t) на конфигурационное прост-

ранство есть поверхность γ_t = {x = X(ϕ, θ, t)}, которую будем называть фронтом волны. Эта

поверхность может быть негладкой и иметь точки самопересечения. С точки зрения теории

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1383

модифицированного канонического оператора эта поверхность является каустикой специаль-

ного вида.

Далее перейдём к описанию вида асимптотики задачи (1), (2) в трёхмерном случае в окрест-

ности переднего фронта. Более подробное описание алгоритма построения модифицированного

канонического оператора Маслова для задачи (1), (2) приведено в п. 3, где рассматривается

n-мерный случай.

Многообразие Λ_t можно покрыть счётным числом карт Ω_j. В каждой карте рассмотрим

систему относительно (ϕ, θ) ∈ Ω_j :

〈X_ϕ(ϕ, θ, t), x₀ - X(ϕ, θ, t)〉 = 0,

〈X_θ(ϕ, θ, t), x₀ - X(ϕ, θ, t)〉 = 0,

(6)

где x₀ - некоторая фиксированная точка на фронте, x₀ ∈ γ_t.

Определим для каждой карты Ω_j её ранг k_j = rank Ω_j как наименьшее значение ранга

матрицы системы (6)

k_j = min rank(X_ϕX_θ).

(ϕ,θ)∈Ω_j

Пусть в точке f = (ρ_f , ϕ_f , θ_f ) ∈ Λ_t ранг матрицы rank (X_ϕX_θ)|_f < 2, тогда точка f назы-

вается фокальной. Так как функция X(ϕ, θ, t) не зависит от ρ, то фокальными точками будут

и точки (ρ, ϕ_f , θ_f ) для любого ρ ≥ 0. Таким образом, приходим к определению фокальных

точек на крае многообразия.

Определение 1. Точка (ϕ, θ) ∈ ∂Λ_t, в которой rank (X_ϕX_θ) = 2, называется регулярной.

Если же в этой точке rank (X_ϕX_θ) < 2, то точка называется фокальной.

Предполагаем, что на крае многообразия фокальные точки являются изолированными.

Далее будем рассматривать карты многообразия, содержащие точки края этого многообразия,

и строить асимптотику, отвечающую именно таким картам.

Определение 2. Выберем некоторую карту Ω. Пусть Γ = (X(ϕ, θ, τ), P (ϕ, θ, τ)), τ ∈

∈ [0, t], - траектория системы Гамильтона (5) такая, что при τ = t эта траектория задаёт

регулярную точку r ∈ Ω с координатами (ϕ, θ, t). Индексом Маслова карты Ω называется

число

m(Ω) = ind Γ + σ.

(7)

Здесь ind Γ - индекс Морса траектории Γ, равный числу фокальных точек на траектории

при τ ∈ (0, t). Число σ определяется в зависимости от ранга карты. При k = 2 число σ = 0,

а при k = 0 число σ = inerdex ((X_ϕ,θ)^тP_ϕ,θ), где матрица вычислена в точке r. При k = 1

определение числа σ будет приведено в утверждении 3.

В зависимости от значения k введём функции

+^∞

U_k(s,λ,ϕ,θ) =

ρ2-k/2

V (ρn(ϕ, θ))ei(ρs+λρ3 )dρ, k = 0, 1, 2.

Далее сформулируем утверждения о представлении асимптотики решения задачи (1), (2) в

окрестности переднего фронта в зависимости от значения k. Все эти утверждения вытекают

из общего n-мерного случая, разобранного в п. 3.

Определим следующие функции:

∫

c(0)

λ(ϕ, θ, t) =

Q(ϕ, θ, t), Q(ϕ, θ, t) =

Φ(X(ϕ, θ, τ))|P (ϕ, θ, τ)|² dτ.

(8)

μ³

Сформулируем сначала утверждение о виде асимптотики в карте ранга k = 2. В этом

случае фронт представляет собой гладкую поверхность и вектор P (ϕ, θ, t) будет совпадать с

внешней нормалью к фронту.

В картах ранга k = 2 естественным образом определены координаты (ϕ, θ) ∈ ∂Λ_t в силу

системы (6). Это приводит к представлению асимптотики решения в параметрической форме,

где ещё одним параметром выступает координата ξ, определённая по нормали к фронту.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1384

СЕРГЕЕВ

С вычислительной точки зрения параметрическое представление асимптотики представля-

ется наиболее эффективным в силу того, что не требуется разрешать систему (6) относительно

(ϕ, θ) для всех точек x₀ в заданной области фронта.

Пусть точка x₀ ∈ γ_t и пусть она принадлежит проекциям карт Ω_j, j = 1, N , ранги

которых равны k = 2. Введём параметр ξ ∈ [-d, d], определяющий координату по нормали к

фронту, причём ξ = 0 на фронте, ξ > 0 за пределами фронта и ξ < 0 в области, ограниченной

фронтом. Величина d определяет окрестность фронта по нормали.

Утверждение 1. В окрестности точки x₀ асимптотика решения задачи (1), (2) пред-

ставляется в виде суммы

∑

v_as(x,t) =

v_j(x,t).

j=1

Функции v_j (x, t) определяются для каждой карты Ω_j и задаются параметрическим образом

v_j(x,t) = (v_j = W_j(ξ,ϕ,θ,t),x = Ξ_j(ξ,ϕ,θ,t)) с параметрами (ξ,ϕ,θ), где

√

(

)

2πμ

| cos θ|

c(X)

|P |

W_j(ξ,ϕ,θ,t) =

Ree-iπ(indΓ+1)/2U2

, λ(ϕ, θ, t), ϕ, θ

|det (Xт(ϕ,θ)

X(ϕ,θ))|1/4

c(0)

Ξ_j(ξ,ϕ,θ,t) = ξ

+ X, ξ ∈ [-d,d], (ϕ,θ) ∈ Ω_j.

(9)

|P |

Здесь для краткости обозначили X = X(ϕ,θ,t), P = P(ϕ,θ,t), матрица X(ϕ,θ) = (X_ϕ,X_θ),

а индекс т - транспонирование. Число indΓ - индекс Морса соответствующей траектории

(X(ϕ, θ, τ), P (ϕ, θ, τ)) системы Гамильтона (5).

Сформулируем теперь утверждение о виде асимптотики, отвечающей карте ранга k = 0.

Утверждение 2. Пусть точка x₀ ∈ γ_t принадлежит проекции карты Ω ранга k = 0.

В окрестности точки x₀ асимптотика решения задачи (1), (2) имеет вид

∫

√

c(X(ϕ, θ, t))

v_as(x,t) = Ree-iπm(Ω)/2 g(ϕ,θ)

| cos θ|

|det (P, P_ϕ, P_θ)|

c(0)

R²

(

)

〈P (ϕ, θ, t), x - X(ϕ, θ, t)〉

×U₀

, λ(ϕ, θ, t), ϕ, θ dϕ dθ.

Здесь g(ϕ, θ) - срезающая функция, отвечающая карте Ω, а m(Ω) - её индекс Маслова.

Теперь опишем асимптотику в окрестности точки x₀ ∈ γ_t, которая лежит в проекции карты

Ω ранга k = 1. В этой карте существует точка, в которой либо X_θ = 0, либо X_ϕ = 0, или же

векторы X_ϕ и X_θ являются линейно зависимыми. Во всех этих случаях можно определить в

Ω локальные координаты (φ, η) : в первом случае φ = ϕ, η = θ, во втором - φ = θ, η = ϕ,

а в третьем можно выбрать один из двух вариантов, в зависимости от вычислений. Во всех

этих случаях вектор X_φ отличен от нуля и существует такая областьΩ, что для всех η ∈^Ω

система (6) определяет в области (φ, η) ∈ Ω функцию φ = φ(x₀, t, η).

Утверждение 3. Пусть точка x₀ ∈ γ_t и содержится в проекциях карт Ω_j, j = 1, N ,

ранга k = 1. Обозначим через φ_j = φ_j (x₀, t, η), η ∈Ωj, решения системы (6), отвечающие

картам Ω_j.

Асимптотика решения задачи (1), (2) в окрестности точки x₀ имеет следующий вид:

∫

√

∑

√

c(X(φ, η, t))

v_as(x, t) =

2πμ Re e-iπ/4

e-i2 m(Ωj) g_j(η)

| cos θ|

|det M|

c(0)

j=1

)

⁽ 〈P (φ, η, t), x - X(φ, η, t)〉



×U₁

, λ(φ, η, t), φ, η

dη.

(10)



φ=φ_j(x₀,t,η)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1385

Функции g_j (η) - срезающие функции, отвечающие областямΩj. Матрица M определяется

по формуле

(

)

X_φ

〈X_φ, X_η〉

M =

,P,P_η - P_φ

|X_φ|2

|X_φ|²

Индекс Маслова m(Ω_j ) вычисляется согласно (7), где σ = 1, если W < 0, и σ = 0, если

W ≥ 0; число W определяется в регулярной точке карты по формуле

(

)(

)

〈X_φ, X_η〉

W =Xтη E₃ -

X_ηX^т

P_η - P_φ

|X_φ|²

Матрица E₃ - единичная размера 3 × 3.

Замечание 2. В (10) присутствует функция cos θ вне зависимости от выбора локальных

координат (φ, η), и чтобы не усложнять формулу, косинус не выражается через эти коорди-

наты. Также у функций X и P вместо аргументов (ϕ, θ) в (10) записаны (φ, η), что, вообще

говоря, не является корректным, однако полностью корректная запись сильно усложнит фор-

мулы и их восприятие. Отметим, что при φ = θ и η = ϕ соответствующие аргументы в

функциях следует поменять местами.

Далее рассмотрим случай, когда функция V (ξ) имеет специальный вид

(

)-2

ξ²¹

ξ²²

ξ²³

V (ξ) = A

(11)

b²¹

b²²

b²

где A, b₁, b₂ и b₃ - некоторые параметры. Преобразование Фурь

V (p) такой функции имеет

вид [4]

√

2π

V (p) = Ab₁b₂b₃

e^-

p²¹b²¹+p²²b²²+p²³b²³ .

В этом случае функции U_k можно вычислить и представить с помощью специальных функ-

ций, связанных с функцией Эйри. Введём обозначения

√

s + iβ(ϕ,θ)

β(ϕ, θ) = b²¹ cos² ϕ cos² θ + b²² sin² ϕ cos² θ + b²³ sin² θ,

(3λ)1/3

тогда

(

)

⁽π)3/2

eiπ/2

U₂(s,λ,ϕ,θ) = -Ab₁b₂b₃

Ai^′(z) + i Gi^′(z)

(3λ)2/3



⁽π)2 e-iπ/4Ab₁b₂b₃ d



U₁(s,λ,ϕ,θ) = -

(Ai²(ζ) + iAi (ζ) Bi (ζ))



(12λ)1/3(3λ)1/2 dζ²

ζ=z/41/3

)

⁽π)3/2 1⁽

U₀(s,λ,ϕ,θ) = -Ab₁b₂b₃

z(Ai (z) + i Gi (z)) -

3λ

Здесь Ai (z) и Bi (z) - функции Эйри, а Gi (z) - функция Скорера [15], являющаяся ограни-

ченным решением неоднородного уравнения Эйри f^′′ - zf = -1/π, равная

∫

(

)

t³

Gi (z) =

sin zt +

dt.

Отметим, что в двумерном случае профиль волны описывается с помощью функций Эйри, а

функция Скорера отсутствует.

Замечание 3. При k = 2 асимптотика решения задачи представляется в виде суммы

комбинаций производной функции Эйри и производной функции Скорера. При k = 1 или

k = 2 уже требуется интегрирование соответствующих функций.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1386

СЕРГЕЕВ

При вычислении функций U0,2 мы воспользовались соотношением

∫

ei(ρ(s+iβ)+λρ3)dρ =

(Ai (z) + i Gi (z))

(3λ)1/3

и соотношениями, вытекающими из него после дифференцирования по s. При вычислении

функции U₁ использовалось соотношение, справедливое при λ > 0 (см. [9, 16]):

∫

e-iπ/4

√

√ρe^iρse^-ρβ eiλρ3 dρ =

√

(Ai²(ζ) + i Ai (ζ) Bi (ζ))|ζ=z/41/3,

2π

6λ dζ

а также равенства, получающиеся после дифференцирования по s.

Замечание 4. Если λ = 0, т.е. дисперсионные эффекты отсутствуют, то утверждения 1-3

дают асимптотику решения волнового уравнения [4]. При этом для специального начального

условия (11) функции U_k(ξ, 0, ϕ, θ) становятся рациональными:

√

(

)

2π

eiπ(3-k/2)/2

U_k(s,0,ϕ,θ) = Ab₁b₂b₃

Γ 3-

k = 0,1,2,

(s + iβ(ϕ, θ))3-k/2

где Γ(ζ) - гамма-функция Эйлера, cоответственно асимптотика решения волнового уравнения

в данном случае принимает более простой вид.

При k = 2 асимптотика решения для волнового уравнения, по аналогии с утверждением 1,

представима в виде суммы параметрически заданных функций v_j(x, t) = (W_j , Ξ_j )|:

√

(

)

-2

μ Ab₁b₂b₃(2π)3/2

cos θ c(X(ϕ, θ, t))

|P |

W_j(ξ,ϕ,θ,t) =

Re eiπ(1-indΓ)/2 ξ

+ iβ(ϕ, θ)

4 |det (X(ϕ,θ))^тX(ϕ,θ)|1/4

c(0)

Ξ_j(ξ,ϕ,θ,t) = ξ

+ X.

(12)

|P |

При k = 0 асимптотика решения для волнового уравнения имеет вид

√

∫

2π

c(X(ϕ, θ, t))

v_as(x,t) = Ab₁b₂b₃

Reeiπ(3-m(Ω))/2 g(ϕ,θ)

c(0)

R²

√

(

)-3

√

〈P (ϕ, θ, t), x - X(ϕ, θ, t)〉

| cos θ|

|det (P, P_ϕ, P_θ)|

+ iβ(ϕ, θ)

dϕ dθ.

При k = 1, по аналогии с утверждением 3, переходим к координатам (φ, η), что приводит

к следующему виду асимптотики волнового уравнения:

√

∫

∑

3π

c(X(φ, η, t))

v_as(x,t) = -

√μAb₁b₂b₃ Re

eiπm(Ωj )/2 g_j(η)

c(0)

j=1

)-5/2^

√

⁽ 〈P (φ, η, t), x - X(φ, η, t)〉



| cos θ|

|det M|

+ iβ(φ, η)

dη.

(13)



φ=φ_j(x₀,t,η)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1387

2. Волновое уравнение с быстроосциллирующим коэффициентом. В качестве при-

мера где возникает волновое уравнение с дисперсионными поправками рассмотрим задачу о

построении асимптотики решения задачи Коши для трёхмерного волнового уравнения с быст-

роосциллирующим коэффициентом и локализованной начальной функцией

(

)

∂²

Θ(x)

u=C²

,x Δu, x ∈ R³, u|t=0 = V (x/μ), u_t|t=0 = 0.

(14)

∂t²

Здесь вектор-функция Θ(x) = (θ₁(x), . . . , θ_m(x)), m ≤ 3, где θ_k(x) - гладкие вещественные

функции, и градиенты ∇θ_k(x) линейно независимы при всех x. Функция C²(y, x), y ∈ R^m,

является 2π-периодической по каждой переменной y_j и гладкой по всем переменным, и спра-

ведливо неравенство 0 < cm ≤ C2(y,x) ≤ cM. Малый параметр 0 < ε ≪ 1 отвечает за

скорость быстрых осцилляций, описываемых фазами θ_k(x), считаем что ε ≤ μ3/2.

Поскольку начальная функция является быстроменяющейся, то и главный член асимп-

тотического решения также будет быстроменяющейся функцией. Поэтому прямое примене-

ние подходов усреднения, развитых в работах [17-23], приводит, вообще говоря, к неверным

результатам, и здесь следует применять подходы, предложенные в [16, 24-27]. Усреднённое

уравнение здесь также появляется и в случае гладких решений (μ = 1) переходит в “обычное”

усреднённое уравнение из [17-23].

Согласно статьям [16, 25-27] процесс построения асимптотического решения задачи (14)

разумно разбить на две задачи. Первая задача состоит в построении “приближённого” усред-

нённого уравнения с гладкими коэффициентами, что осуществляется с помощью операторного

усреднения (см. [16, 25-27]). Вторая задача - построение асимптотического решения усреднён-

ной задачи с помощью представленных выше формул.

Отметим важный момент, связанный с построением усреднённого уравнения. В случае

дивергентной записи волнового уравнения для построения усреднённого уравнения возникает

необходимость в решении вспомогательной задачи на ячейке при любом соотношении между

ε и μ [25, 26], при этом явно найти решение этой задачи удаётся в редких случаях. Однако

при предположении о малости осцилляций, т.е. когда функция C²(y, x) имеет вид

C²(y,x) = C²⁰(x) + δa(y,x),

(15)

где C₀(x) - гладкая функция, δ - малый параметр, а функция a(y, x) имеет нулевое среднее

по y, решение задачи на ячейке можно построить с необходимой точностью.

Для случая уравнения в недивергентной форме ситуация меняется: необходимость решать

задачу на ячейке возникает, в частности, при ε ∼ μ3/2. Если же μ ∼ 1, то в качестве усред-

нённого уравнения получается волновое, и для определения его коэффициента решать задачу

на ячейке уже не требуется.

Отметим, что используемый нами метод построения усреднённого уравнения обобщается

и на n-мерный случай.

Метод операторного усреднения для уравнения (14) приводит к задаче с псевдодифферен-

циальным уравнением вида (3):

-μ²v_tt(x,t) =

L(x,

p; ε, μ)v(x, t), v|t=0 = V (x/μ), v_t|t=0 = 0.

(16)

ε²

Цифры над операторами показывают их порядок действия: первым действует p = -iμ∇, а

вторым - оператор умножения на функцию от x. Оператор L(x, p; ε, μ) является симметрич-

ным и положительно определённым.

Утверждение 4. Для символа оператора L(x, p; ε, μ) справедливо следующее разложение

по степеням ε/μ:

μ²

ε²

ε⁴

L(x, p; ε, μ) = L₀(x, p) +

L⁴⁰(x,p) +

L(x, p, ε/μ),

ε²

μ²

μ⁴

L₀(x,p) = c²(x)|p|², L⁴⁰(x,p) = -Φ(x)c²(x)|p|⁴.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1388

СЕРГЕЕВ

Функция c(x) определяется через среднее по ячейке y ∈ T^m = [0, 2π]^m от функции

1/C²(y, x):

(

∫

-1

)-1

c²(x) =

(17)

C²(y,x)Tm

(2π)^m

C²(y,x)

T^m

где скобки 〈·〉_Tm обозначают среднее на ячейке.

Функция Φ(x) = 〈|∇^θyψ₂(y, x)|²〉_Tm , где ψ₂(y, x) является решением задачи на ячейке

c²(x) - C²(y,x)

(-Δ^θy)ψ₂ =

〈ψ₂(y, x)〉_Tm = 0.

(18)

C²(y,x)

Операторы (-Δ^θy) = 〈-i∇^θy, -i∇^θy〉,

∇^θy = ∇Θ(x)∇_y, градиент ∇_y = (∂/∂y₁,... ,∂/∂y_m) и

матрица ∇Θ(x) = (∇θ₁(x), . . . , ∇θ_m(x)). Поправка L содержит производные старшего (по

сравнению с |p|⁴) порядка.

Обоснование этого утверждения приведено в п. 4.

Зная асимптотику решения v_as(x, t) усреднённой задачи (16), можно построить асимпто-

тику задачи (14) в виде действия некоторого оператора

χ на функцию v_as(x, t). В общем

случае точно вычислить оператор χ не представляется возможным, но его можно вычислить

с требуемой точностью.

Определим операторы

χ₃ = χ₃(y,x,

p) и

χ₄ = χ₄(y,x,

p) следующим образом: пусть их

символы являются периодическими по y с нулевым средним решениями следующих задач:

(-Δ^θy)χ₃(y, x, p) = -2p²〈p, -i∇^θyψ₂(y, x)〉,

(19)

(-Δ^θy)χ₄(y, x, p) = -2〈p, -i∇^θyχ₃(y, x; p)〉 +

(

)

c²(x)

+p4 ψ2(y,x)(-Δθy)ψ2(y,x) - 〈|∇θyψ2(y,x)|2

(20)

〉_Tm C2(y,x)

Утверждение 5. Пусть ε ∼ μ3/2, а функция v_as(x, t) является асимптотическим ре-

шением усреднённой задачи (16). Тогда функция

(

)

))

ε²

Θ(x)

ε³

⁽Θ(x)

ε⁴

⁽Θ(x)

u_as(x,t) =

ψ₂

p² +

χ₃

, x,

χ₄

, x,

p v_as(x,t),

(21)

μ²

μ³

μ⁴

где символы операторов χ3,4 определены в (19), (20), удовлетворяет волновому уравнению

(14) с точностью O(μ3/2), а начальным данным - с точностью O(μ).

Под выражением O(μ^α) в формулировке утверждения 5 понимается гладкая и ограничен-

ная функция порядка μ^α.

Определение 3. В рамках утверждения 5 функция v_as(x, t) называется главной частью

асимптотического решения задачи (14).

Обоснование утверждения 5 приведено в п. 4.

Случай малых осцилляций. Отдельно рассмотрим случай, когда коэффициент уравне-

ния (14) имеет вид (15):

C²(y,x) = C²⁰(x) + δa(y,x),

где C₀(x) - гладкая функция, а параметр δ является малым. Функция a(y, x) является 2π-

периодичной по каждой переменной y_j и имеет нулевое среднее. Для неё справедливо разло-

жение в ряд Фурье

∑

a(y, x) =

a_k(x)e^i〈k,y〉.

(22)

|k|=0

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1389

Вычислим функцию c²(x), определённую в (17). Непосредственным вычислением получаем

〈a²(y, x)〉_Tm

c²(x) = C²⁰(x) - δ²

+ O(δ³).

C²⁰(x)

Из этого равенства следует, что гамильтониан H(x, p) имеет представление

∑

|p|

H(x, p) = |p|C₀(x) -

a_k(x)a_-k(x) + O(δ³).

(23)

2 C³⁰(x)

|k|=0

Обозначим через X(ϕ, θ, t) и P (ϕ, θ, t) решение системы Гамильтона (5) с гамильтонианом

(23). Отметим, что поправку порядка δ² к гамильтониану можно учесть и в уравнении пе-

реноса, вместо самой системы Гамильтона. В таком случае гамильтониан приобретает вид

H(x, p) = C₀(x)|p|, но при этом сдвигается фронт волны и поправляется амплитуда.

Теперь определим коэффициент усреднённого уравнения Φ(x) при дисперсионных поправ-

ках. Для правой части уравнения в задаче на ячейке (18) справедливо равенство

c²(x) - C²(y,x)

a(y, x) + O(δ²).

C²(y,x)

C²⁰(x)

С учётом (22) решение ψ₂(y,x) задачи на ячейке (18) также ищется в виде ряда Фурье.

Непосредственным вычислением действия оператора ∇^θy на экспоненту e^i〈k,y〉 получаем

∑

a_k(x)a_-k(x)

Φ(x) = 〈|∇^θyψ₂(y, x)|²〉_Tm =

+ O(δ³).

C⁴⁰(x)

|∇Θ(x)k|²

|k|=0

После определения функции Φ(x) можно определить функцию Q(ϕ, θ, t) согласно фор-

муле (8). Эта функция описывает профиль волны и дисперсионные эффекты. В случае малых

осцилляций мы имеем Q(ϕ, θ, t) = δ²F (ϕ, θ, t) + O(δ³), где

∫t

)

(∑

C₀(0)

|P |²

a_k(X(ϕ,θ,τ))a_-k(X(ϕ,θ,τ))

F (ϕ, θ, t) =

dτ.

(24)

C⁴⁰(X(ϕ,θ,τ))

|∇Θ(X(ϕ, θ, τ))k|²

|k|=0

Из (24) и (8) следует, что в случае малых осцилляций параметр λ, определяющий дис-

персионные эффекты решения, равен λ = (ε²δ²/μ³)F (ψ, t). Это означает, что дисперсионные

эффекты начинают оказывать влияние на решение в случае εδ ∼ μ3/2, т.е. при наличии малых

осцилляций эффективным параметром дисперсии становится произведение δε вместо ε.

Пример. Приведём пример реализации полученных выше асимптотических формул в слу-

чае малых осцилляций и при dim y = m = 1. Выбираем следующий вид коэффициента урав-

нения (14):

( (

))

(x₂ - 5)²

C²(y,x) = C²⁰(x) + δk(x)cos y, C₀(x) = 1 -

k(x), k(x) = exp -α x²¹ +

+x²

Функция Θ(x) = 8x²¹/7 + 2x₂ + 2x²³, а параметры задачи α = 0.4, a = 2, δ = 0.1, ε = 0.5.

Проводя вычисления, получаем

k²(x)

δ² k²(x)

c²(x) = C²⁰(x) -

〈|∇^θyψ₂|²〉[0,2π] =

2 C²⁰(x)

2 C⁴⁰(x) |∇Θ(x)|²

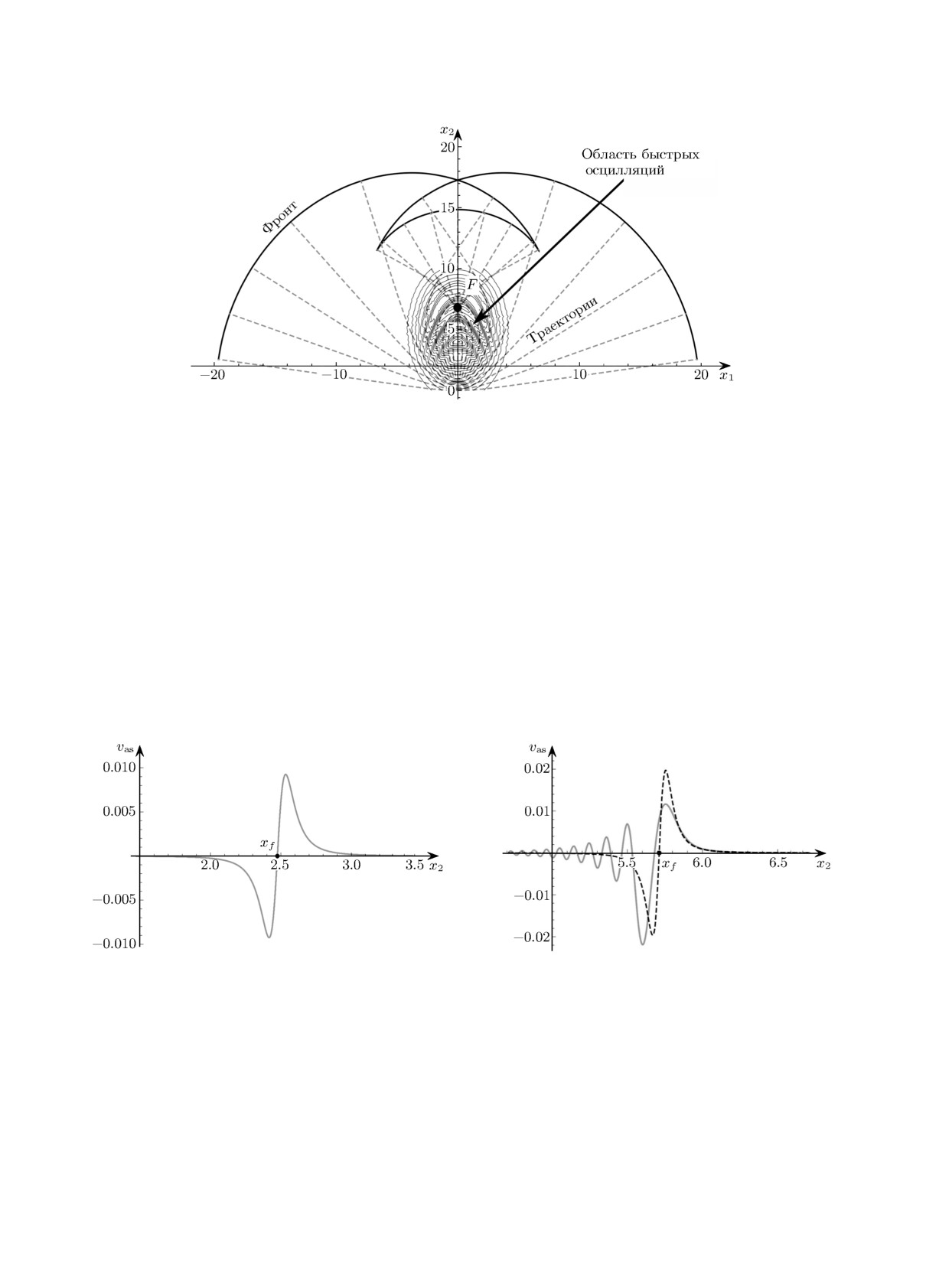
На рис. 1 представлены сечение волнового фронта γ_t = {X(ϕ, θ, t)} при t = 20 плоскостью

x₃ = 0 при ϕ ∈ [0,π] и проекции некоторых траекторий системы Гамильтона (5) на конфи-

гурационное пространство при x₃ = 0, отмечены проекция фокальной точки F и область

быстрых осцилляций коэффициента исходного уравнения.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1390

СЕРГЕЕВ

Рис. 1. Сечение волнового фронта γt (жирная непрерывная линия) плоско-

стью x3 = 0 при ϕ ∈ [0, π] и проекции траектории системы Гамильтона (5)

(штриховые линии). Контурные линии показывают область быстрых осцилля-

ций коэффициента уравнения.

Начальное возмущение V (ξ) выбирается в специальном виде (11), где A = 1, b₁ = b₂ =

= b₃ = 1, параметр локализации начальной функции μ = (δε)2/3 ≈ 0.135.

На рис. 2 и 3 представлены профили главной части асимптотического решения задачи (14)

вдоль луча, выходящего из начала координат и совпадающего с положительным направлением

оси x₂. Для сравнения на обоих рисунках показана асимптотика решения волнового уравне-

ния с коэффициентом c²(x) без учёта дисперсионной поправки. На рис. 2 показаны профили

волны до возникновения фокальной точки. Вначале дисперсионные эффекты не оказывают

существенного влияния и главная часть определяется асимптотикой решения волнового урав-

нения (12). После прохождения области осцилляций дисперсионные эффекты начинают ока-

зывать влияние на амплитуду волны и главная часть асимптотического решения определяется

формулой (9).

Рис. 2. Графики главной части асимптотического решения до прохождения фокальной точки: слева - в момент

времени t = 3 до прохождения волной области осцилляций, точка x_f ≈ 2.47 лежит на фронте; cправа - в

момент времени t = 9 после прохождения зоны осцилляций, точка x_f ≈ 5.71 лежит на фронте. Штриховой

линией показана асимптотика волнового уравнения без учёта дисперсии.

На рис. 3 приведён график главной части асимптотики вдоль указанного луча после воз-

никновения фокальной точки. В этом случае луч пересекает фронт в точках xf1 и xf2. Точка

xf2 является точкой самопересечения фронта, и в её окрестности, в зависимости от значений

ϕ и θ, в нуль обращается либо |X_θ|, либо |X_ϕ|. На соответствующих траекториях систе-

мы Гамильтона (5) дисперсионные эффекты не играют существенной роли, поэтому главная

часть асимптотики в окрестности этой точки представляется суммой функций вида (13), а

индекс Маслова в этих случаях равен нулю. Асимптотика решения в окрестности точки xf1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1391

описывается с помощью формулы (9), так как соответствующая траектория системы Гамиль-

тона проходит через область осцилляций. Так как соответствующая траектория прошла через

фокальную точку, то её индекс Морса равен единице, и вместо головной волны получается

впадина.

Рис. 3. График главной части асимптотического ре-

шения после фокальной точки в момент времени t =

= 20. Точки xf1 ≈ 14.8, xf2 ≈ 17.2 лежат на фронте.

Штриховой линией показана асимптотика волнового

уравнения без учёта дисперсии.

3. Асимптотика решения многомерного волнового уравнения с дисперсионными

эффектами. Приведём формулы для построения асимптотики решения задачи Коши (1), (2)

для волнового уравнения с дисперсионными поправками в n-мерном случае.

Перейдём к оператору p = -iμ∇ в уравнении (1), умножив его на

- μ². После преобра-

зований получим задачу



∂²v(x,t)

∂v



-μ²

= c²(x)|p|²v(x,t) -

c²(x)Φ(x)|p|⁴v(x,t), v(x,0) = V (x/μ),

= 0. (25)



∂t²

μ²

∂t

t=0

Начальная функция V (x/μ) определена формулой (4).

Асимптотика задачи (25) представляется с помощью модифицированного канонического

оператора Маслова [8, 12-14]

v_as(x,t) = Re [μn/2e-iπn/4K^μ

V (p)](x, t)].

Λt

Далее кратко опишем процедуру построения модифицированного канонического оператора

Маслова в n-мерном случае.

Перейдём на начальном многообразии Λ₀ к сферическим координатам α = ρn(ψ), где

ρ ≥ 0 и вектор n(ψ) ∈ Sn-1, а Sn-1 - единичная сфера размерности n - 1. Пусть функции

X (ρ, ψ, t) и P(ρ, ψ, t) являются решением следующей системы Гамильтона:

x = H_p(x,p),

p = -H_x(x,p), x|t=0 = 0, p|t=0 = ρn(ψ), ρ = 0,

(26)

где гамильтониан H(x, p) = c(x)|p|. Справедливы равенства X (ρ, ψ, t) = X(ψ, t), P(ρ, ψ, t) =

= ρP (ψ, t), где функции X и P являются решением системы Гамильтона

x = H_p(x,p),

p = -H_x(x,p), x|t=0 = 0, p|t=0 = n(ψ).

(27)

Система (26) не определена при ρ = 0, однако её решение можно по непрерывности про-

должить на ρ = 0 (см. [13]), так как функции X(ψ, t) и P (ψ, t) не зависят от ρ. С учётом

такого продолжения можно построить многообразие с краем

Λ_t = {x = X(ρ,ψ,t) ≡ X(ψ,t),p = P(ρ,ψ,t) ≡ ρP(ψ,t)}.

Краю многообразия в фазовом пространстве соответствуют точки на многообразии, отвечаю-

щие значению ρ = 0.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1392

СЕРГЕЕВ

Проекция этого многообразия на конфигурационное пространство в каждый момент време-

ни t представляет собой поверхность γ_t = {x = X(ψ, t)}, которую будем называть фронтом

волны. Асимптотика решения задачи (25) локализована в окрестности этой поверхности.

В любой точке многообразия Λ_t якобиан проектирования det ∂X (ρ, ψ, t)/∂(ρ, ψ) этого мно-

гообразия на конфигурационное пространство равен нулю. Это означает, что данное много-

образие, с точки зрения классической теории канонического оператора [5], состоит только

из особых точек. При этом, в силу построения, край многообразия Λ_t рассматривается как

особенность специального вида. В окрестности края канонический оператор Маслова опреде-

ляется согласно результатам работ [8, 12-14].

Многообразие Λ_t можно покрыть счётным набором карт Ω_j, так что каждый компакт

на многообразии покрывается конечным числом карт [5]. Определим ранг k_j = rank Ω_j кар-

ты Ω_j как наименьшее значение ранга матрицы ∂X (ρ, ψ, t)/∂(ρ, ψ) при (ρ, ψ) ∈ Ω_j. Точки на

многообразиях, в которых ранг этой матрицы равен n - 1 (максимально возможный ранг),

называем регулярными, остальные точки - фокальными.

Обозначим через g_j (ρ, ψ) разбиение единицы, подчинённое покрытию многообразия кар-

тами Ω_j. Канонический оператор Маслова, действующий на функцию

V (ρ, ψ), заданную на

многообразии Λ_t, определяется следующим образом:

∑

K^μ

V (ρ, ψ)](x, t) =

KΩj [g_j(ρ,ψ

V (ρ, ψ)](x, t).

Λt

Здесь KΩj [g_j (ρ, ψ

V (ρ, ψ)] - предканонический оператор, записанный в карте Ω_j и определя-

ющий действие канонического оператора на функцию

V (ρ, ψ) в этой карте.

Определим предканонический оператор согласно [8, 12-14], учитывая, что карта может

содержать точки края многообразия. Пусть ранг карты Ω равен k, тогда в этой карте ком-

поненты вектора ψ можно перенумеровать так, чтобы rank ∂X/∂φ = k, где φ = (ψ₁, . . . , ψ_k).

Оставшиеся компоненты обозначим через η = (ψk+1, . . . , ψn-1), таким образом ψ = (φ, η).

В этой карте определена невырожденная матрица размера n × n

M (ψ, t) = (Π, P, P_η - P_φΠ^тX_η),

(28)

где матрица Π = Π(ψ, t) имеет размер n × k и определяется равенством Π^тX_φ = E_k, E_k -

единичная матрица размера k × k, а верхний индекс т обозначает транспонирование.

Пусть точка x₀ лежит на фронте γ_t, тогда в карте Ω существует решение φ = φ(x₀, t, η)

системы уравнений (см. лемму 6 в [12])

Π^т(ψ,t)(x₀ - X(ψ,t)) = 0.

(29)

Определим индекс Маслова карты Ω следующим образом:

m(Ω) = ind Γ(ψ, t) + σ.

Здесь ind Γ(ψ, t) - приращение индекса Маслова вдоль пути, отвечающего траектории Γ =

= {X(ψ, τ), P (ψ, τ)} системы Гамильтона (27) при τ ∈ (0, t], заканчивающейся в регулярной

точке карты Ω. В случае гамильтониана H(x, p) = c(x)|p| величина ind Γ(ψ, t) совпадает

с индексом Морса соответствующего пути и равна числу фокальных точек на нём (см. [4;

5, с. 155]).

Число σ при k = n-1 определяется как число отрицательных собственных чисел матрицы

размера n - k - 1 × n - k - 1

W = (X_η)^т(E_n - Π(X_φ)^т)(P_η - P_φΠ^тX_η),

вычисленной в регулярной точке карты Ω. Если k = n - 1, то положим σ = 0.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1393

Введём функции

+∞

∫t

U_k(s,λ,ψ) =

ρn-1-k/2

V (ρn(ψ))ei(ρs+λρ3 )dρ, Q(ψ, t) = c(0)

Φ(X(ψ, τ))|P⁰(ψ, τ)|² dτ.

Утверждение 6. Пусть точка x₀ ∈ γ_t и содержится в проекции на конфигурационное

пространство карты Ω ранга k. Пусть ψ = (φ,η), а функция φ = φ(x₀,t,η) - решение

системы (29), тогда в окрестности точки x₀ при ε ∼ μ3/2 справедливо равенство

∫

iπ(n-k-2m(Ω))/4

√

c(X(ψ, t))

K_Ω

V ](x, t) =

g(ψ)

|det (n(ψ), n^′(ψ))|| det M|U_k(s, λ, ψ) dη,

(2πμ)(n-k)/2

c(0)

Rn-k-1

где M - матрица, определённая в (28), а n^′(ψ) - матрица производных вектора n(ψ) по

координатам ψ. Функция g(ψ) является срезающей функцией, отвечающей карте Ω. Здесь

〈P (ψ, t), x - X(ψ, t)〉

s = s(x,ψ,t) =

λ = λ(ψ,t) =

Q(ψ, t).

μ³

Из утверждения 6 следуют асимптотические формулы для трёхмерного случая, приведён-

ные в утверждениях 1-3.

4. Вывод усреднённого уравнения. В данном пункте описываются процедура опера-

торного усреднения и вывод усреднённого уравнения, а также приводится обоснование утвер-

ждения 5 о малости соответствующей невязки. Мы не будем концентрироваться на вопросах,

связанных с корректностью усреднённой задачи и свойствах операторов, возникающих в про-

цессе вывода усреднённого уравнения.

Операторное усреднение. Следуя работам [16, 25-27], воспользуемся операторным

усреднением для построения усреднённого уравнения. Решение волнового уравнения (14)

(

)

∂²

Θ(x)

u(x, t) = C²

,x Δu(x,t)

∂t²

ищем в виде u(x, t) = Ψ(Θ(x)/ε, x, t), где функция Ψ(y, x, t)

2π-периодична по переменным

y ∈ R^m. Функция u(x,t) будет решением уравнения (14), если функция Ψ удовлетворяет

уравнению

-ε²Ψ_tt(y,x,t) =^Ĥ(x,y,-iε∇,-i∇^θy)Ψ(y,x,t),

(30)

^Ĥ(x, y, -iε∇, -i∇^θy ) = C²(y, x)〈(-iε∇ - i∇^θy), (-iε∇ - i∇^θy)〉,

где -i∇^θy = -i∇Θ(x)∇_y, матрица ∇Θ(x) = (∇θ₁(x), . . . , ∇θ_m(x)), а ∇_y = (∂/∂y₁, . . . , ∂/∂y_m).

Оператор

Ĥ с областью определения на функциях, периодических и гладких по y на

ячейке T^m = {y ∈ [0, 2π]^m}, а по переменной x из пространства Шварца S(Rⁿ), являет-

ся симметричным и положительно определённым в пространстве L2,C (T^m × Rⁿ) с весовым

скалярным произведением

∫

(f(y, x), g(y, x))L2,C (Tm×Rn) =

f (y, x)g(y, x) dy dx.

(2π)^m

C²(y,x)

T^m Rⁿ

Решение уравнения (30) ищется в виде действия псевдодифференциального оператора χ

на функцию v :

Ψ(y, x, t) = χ(x,-iε∇, y)v(x, t),

(31)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1394

СЕРГЕЕВ

где цифры обозначают порядок действия операторов. При этом предполагается, что функция

v не зависит от y и удовлетворяет усреднённому уравнению с гладкими коэффициентами

-ε²v_tt =Lv,

L= L(2x,

-iε∇).

(32)

Отметим, что операторы χ и

L зависят от параметра ε, но для краткости записи эта зави-

симость не указывается.

Подстановка (32) и (31) в уравнение (30) приводит к соотношению между операторами

( Ĥχ - χL) = 0.

(33)

Если функция v(x, t) - решение уравнения (32), то соотношение (33) является достаточным

условием (см. [26]), чтобы функция Ψ была решением уравнения (30). Из этого соотношения

определяются операторы^L и χ.

Введём пространство L2,c(Rⁿ) со скалярным произведением

∫

(w(x), v(x))L2,c =

w(x)v(x) dx,

c²(x)

Rⁿ

где функция c²(x) определена в (17) и равна c²(x) = 〈1/C²(y, x)〉-1Tm . Следуя [26], потребуем

совпадения нормы функции Ψ = χv в пространстве L2,C (T^m × Rⁿ) и нормы функции v в

пространстве L2,c(Rⁿ). Это требование приводит к условию нормировки для оператора χ:

∫

χ(p

-iε∇,x,y)

χ(p, x, y) dy =

(34)

(2π)^m

C²(y,x)

c²(x)

T^m

с учётом равенства для сопряжённого оператора

χ^∗ = χ(-iε∇,x,y).

Отметим, что оператор^L является симметричным и положительно определённым. Дейст-

вительно, пусть Ψ = χv, тогда из (33) и (34) вытекает равенство (Lv, v)L2,c = (^ĤΨ, Ψ)_L

2,C

Из симметричности и положительной определённости оператора

Ĥ вытекают аналогичные

свойства и для оператора

Доказательство утверждения 4. Напомним, что в утверждении 4 строится символ

усреднённого оператора

Перейдём в уравнениях (30) и (32) к оператору p = -iμ∇:

(

)

-μ²Ψ_tt(y,x,t) =

x,y,

p, -i∇^θ

Ψ(y, x, t),

(35)

ε²

(

)

-μ²v_tt(x,t) =

p; ε v(x, t).

(36)

ε²

Операторнозначный символ оператора

Ĥ можно представить в виде суммы

(

)

(

)

μ²

H x,y,

p,-i∇^θ

H₀(x,y,

p,-i∇^θy) + εH₁(x,y,∇_y) ,

(37)

ε²

где

H₀ = H⁰⁰ +

H¹⁰ +

H²⁰; H₁ = -C²(y,x)〈ΔΘ(x),∇_y〉;

μ²

H⁰⁰ = C²(y,x)(-Δ^θy); H¹⁰ = 2C²(y,x)〈p,-i∇^θy〉; H²⁰ = C²(y,x)p².

Здесь (-Δ^θy) = 〈-i∇^θy, -i∇^θy〉, вектор ΔΘ(x) = (Δθ₁(x), . . . , Δθ_m(x)).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1395

Предполагается, что для символа оператора χ справедливо разложение

χ(y, x, εp/μ; ε) = χ₀(y, x, εp/μ) + εχ₁(y, x, εp/μ) + . . . ,

∑

⁽ε)m

χ₀(y,x,εp/μ) =

χm0(y,x,p),

(38)

m=0

где χm0 - однородные полиномы по степеням |p|. Символ L(x, p; ε) ищем в виде

L(x, εp/μ; ε) = L₀(x, εp/μ) + εL₁(x, εp/μ) + ε²L₂(x, εp/μ) + . . . ,

(39)

∑

⁽ε)m

L₀(x,εp/μ) =

Lm0(x,p), L₁(x,εp/μ) =

Lm1(x,p),

(40)

m=0

где Lm0(x, p) и Lm1(x, p) являются однородными полиномами по p степени m.

По аналогии с [16] можно оценить количество членов в (39) и (40), необходимое для то-

го, чтобы асимптотика усреднённой задачи удовлетворяла уравнению с точностью O(μ²)

при ε ∼ μ3/2. Для этого подставим функцию v(x, t) = A(x, t)eiS(x,t)/μ в уравнение (36), что

приведёт к равенству

(

)

[

∂²

μ²

L(x,ε

p /μ) A(x, t)eiS(x,t)/μ = eiS(x,t)/μ

-S2t+iμS_ttA+iμS_tA_t+

L₀(x,ε∇S/μ)A+

∂t²

ε²

]

μ²

⁽∂²L₀(x,ε∇S/μ) ∂²S⁾

L₁(x,ε∇S/μ)A-i

〈∇_ξL₀(x, ε∇S/μ), ∇A〉-i

A+μ² ĜA . (41)

∂ξ²

∂x²

Через ξ обозначен второй аргумент символа оператора L(x, (ε/μ)p) : ξ = (ε/μ)p. Оператор

Ĝ такой, что его действие на гладкую функцию A даёт ограниченную функцию. Зависимость

оператора

L от ε и μ для сокращения записи не указывается.

Для того чтобы выражение в правой части равенства (41) было порядка O(μ²), достаточно

определить члены разложения Lm0, m = 0, 5, L⁰¹ и L¹¹, что следует из (40).

Лемма. Справедливы следующие равенства:

L⁰⁰(x,p) = L¹⁰(x,p) = L³⁰(x,p) = L⁵⁰(x,p) = 0, L⁰¹(x,p) = L¹¹(x,p) = 0,

L²⁰(x,p) = c²(x)|p|², L⁴⁰(x,p) = -c²(x)〈|∇^θyψ₂(y,x)|²〉_Tm p⁴,

где функция c²(x) = 〈1/C²(y, x)〉_Tm и определена в (17). Функция ψ₂(y, x) является периоди-

ческим решением с нулевым средним задачи на ячейке

c²(x) - C²(y,x)

(-Δ^θy)ψ₂ =

〈ψ₂(y, x)〉_Tm = 0.

(42)

C²(y,x)

Доказательство. Существование гладкого по переменным x и y и 2π-периодичного по

y решения задачи (42) следует из работы [26].

С учётом равенств (37)-(39) символы произведений операторов

Ĥχ и χL можно предста-

вить в виде рядов по степеням ε. Подстановка этих рядов в (33) приводит к уравнениям на

L₀, L₁ и χ₀, χ₁ :

H₀χ₀ = χ₀L₀,

(43)

H₀χ₁ = χ₁L₀ + χ₀L₁ - H₁χ₀ + i(〈H0p,∇〉 - 〈L0x,∇_p〉)χ₀.

(44)

Уравнение (43) означает, что функция χ₀ при фиксированных x и малых фиксирован-

ных p является собственной функцией оператора H₀ с областью определения на гладких и

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

7^∗

1396

СЕРГЕЕВ

периодических функциях на ячейке y ∈ T^m (см. [26]). Этот оператор при фиксированных x

и малых p является симметричным в смысле скалярного произведения

∫

u(x, y, p)v(x, y, p)

(u(x, y, p), v(x, y, p)) =

dy.

(45)

(2π)^m

C²(y,x)

T^m

Для χ₀(p, x, y) из условия нормировки (34), а также из (38) и правил вычисления символа

произведения двух операторов, получаем равенство

∫

|χ₀|²

dy =

(46)

(2π)^m

C²(y,x)

c²(x)

T^m

Оператор H₀ при p = 0 переходит в оператор H⁰⁰ = C²(y, x)(-Δ^θy ), поэтому с учётом (46)

получаем (см. [26]), что L⁰⁰ = 0 и χ⁰⁰ = 1.

Из уравнения (43) с помощью (40) определяем следующие члены в разложении символа

L(x, p; ε). Из симметричности оператора H⁰⁰ следует, что L¹⁰ = 0 и χ¹⁰ = 0. Для L²⁰ и χ²⁰

получаем задачу

H⁰⁰χ²⁰ + H²⁰χ⁰⁰ = χ⁰⁰L²⁰.

Согласно (45) скалярно умножим это равенство на χ⁰⁰ и после некоторых вычислений получим

L²⁰ = c²(x)|p|² и χ²⁰ = ψ₂(y,x)|p|², где функция ψ₂(y,x) определена в (42). Аналогичные

рассуждения приводят к следующим значениям: L³⁰ = 0 и L⁴⁰ = -〈|∇^θyψ₂|²〉_Tm c²(x)|p|⁴. При

этом функция χ³⁰(y, x, p) является периодическим решением с нулевым средним задачи на

ячейке

(-Δ^θy)χ³⁰(y, x, p) = -2p²〈p, -i∇^θyψ₂(y, x)〉.

(47)

При вычислении L⁴⁰ использовалось равенство

ψ₂(y,x)

c²(x) - C²(y,x)

c²(x)

= ψ₂(y,x)

(48)

C²(y,x)Tm

C²(y, x)

T^m

а также факт, что функция ψ₂(y, x) является периодическим решением задачи на ячейке (42).

Величина L⁵⁰ = 0, что следует из цепочки равенств

χ³⁰(y,x,p)

L⁵⁰ = -p²c⁴(x)

= -p²c²(x)〈χ³⁰(y,x,p)(-Δ^θy)ψ₂(y,x)〉_Tm =

C²(y, x)Tm

= -p²c²(x)〈(-Δ^θy)χ³⁰(y,x,p)ψ₂(y,x)〉_Tm = 2p⁴c²(x)〈〈p,-i∇^θyψ₂(y,x)〉ψ₂(y,x)〉_Tm = 0.

Здесь использовалось равенство, аналогичное равенству (48), где вместо ψ₂ стоит χ³⁰. Опера-

тор (-Δ^θy) мы перенесли на χ³⁰ с помощью интегрирования по частям. Последнее выражение

в цепочке равенств равно нулю в силу того, что функция ψ₂(y, x) является периодической с

нулевым средним на ячейке T^m, и произведение её самой и производной также будет иметь

нулевое среднее.

Функция χ⁴⁰(y, x, p) по y является периодическим решением с нулевым средним следую-

щей задачи:

(-Δ^θy)χ⁴⁰(y, x, p) = -2〈p, -i∇^θyχ³⁰(y, x, p)〉 +

(

)

c²(x)

+p4 ψ2(y,x)(-Δθy)ψ2(y,x) - 〈|∇θyψ2(y,x)|2

(49)

〉_Tm C2(y,x)

Перейдём теперь к вычислению символа L₁. Умножим выражение (44) скалярно, согласно

(45), на функцию χ₀ и воспользуемся равенством (43) и условием (46), после чего для L₁

получим выражение

)

∑

∂H₀ ∂χ₀

∂L₀ ∂χ₀

L₁ = (χ₀,H₁χ₀) - i χ₀,

c²(x)

∂p_j ∂x_j

∂x_j ∂p_j

j=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1397

Минимальная степень p у выражения справа равна 2, поэтому L⁰¹ и L¹¹ равны нулю. Лемма

доказана.

На основании леммы доказано утверждение 4.

В процессе доказательства леммы также определяюся члены разложения (38) для опера-

тора χ₀ :

χ⁰⁰ = 1, χ¹⁰ = 0, χ²⁰ = ψ₂(y,x)|p|²,

где функция ψ₂(y, x) - решение задачи на ячейке (42). Функции χ³⁰(y, x, p) и χ⁴⁰(y, x, p) яв-

ляются периодическими решениями с нулевым средним задач (47) и (49).

Отметим, что так как не учитывается L₁ из разложения оператораL, то нас не интересует

и вид поправки χ₁ из разложения оператора χ.

Если полученные в лемме выражения для L(x, p; ε) подставить в (41), то в него будут

входить только L²⁰(x, p) и L⁴⁰(x, p). При этом функция L²⁰(x, p) определяет уравнение Гамиль-

тона-Якоби, а поправка L⁴⁰(x, p) попадает в уравнение переноса, добавляя дисперсионные

эффекты к асимптотике решения.

Доказательство утверждения 5. Пусть функция v_as(x, t) является формальным асимп-

тотическим решением уравнения (16) с локализованными начальными данными из (14). Для

такой функции справедливо равенство

∂

ε²

-μ²

v_as(x,t) = c²(x)|p|²v_as(x,t) -

c²(x)〈|∇^θyψ₂|²〉_Tm |p|⁴v_as(x,t) + O(μ²).

∂t²

μ²

Построим функцию

(

)

ε²

ε³

ε⁴

Ψ_as(y,x,t) =

ψ₂(y,x)|p|² +

χ30(y,2x,

p) +

χ40(y,2x,

p) v_as(x, t),

(50)

μ²

μ³

μ⁴

где χ3,40(y, x, p) определены в (47), (49). Отметим, что в момент времени t = 0 при ε ∼ μ3/2

справедливо равенство Ψ_as(y, x, 0) = V (x/μ) + O(μ).

Покажем, что при подстановке функции (50) в уравнение (35) для невязки выполнена

оценка

(

)

R(y, x, t) = -μ²(Ψ_as)_tt -

H x,y,

p, -i∇^θ

Ψ_as = O(μ3/2),

ε²

из которой следует, что функция (21), равная u_as(x, t) = Ψ_as(Θ(x)/ε, x, t), будет удовлетворять

волновому уравнению с быстроосциллирующим коэффициентом (14) с такой же точностью.

Справедливо равенство

(

)

ε²

ε³

ε⁴

-μ²(Ψ_as)_tt =

ψ₂(y,x)|p|² +

χ³⁰(y,x, p) +

χ⁴⁰(y,x, p) (-μ2(vas)tt) =

μ²

μ³

μ⁴

(

)

ε²

= c²(x)|p|² -

c²(x)〈|∇^θyψ₂|²〉_Tm |p|⁴ +

ψ₂(y, x)|p|2c2(x)|p|2 vas(x, t) + O(μ2 + ε3/μ3).

μ²

Непосредственное вычисление действия оператора

Ĥ на функцию Ψ_as(y, x, t) с учётом

уравнения на ячейке (42) и формул (47) и (49) приводит к следующему выражению:

(

)

μ²

ε²

ε³

ε⁴

^ĤΨ_as =μ2

H₀ + εĤ1) 1+

ψ₂(y,x)|p|² +

χ³⁰(y,x, p) +

χ⁴⁰(y,x, p) v_as =

ε²

μ²

μ³

μ⁴

ε²

= c²(x)|p|²v_as -

c²(x)〈|∇^θyψ₂|²〉_Tm |p|⁴v_as +

c²(x)ψ₂(y,x)|p|⁴v_as + O(ε + ε³/μ³).

μ²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

1398

СЕРГЕЕВ

Здесь также учитывалось, что действие оператора

p на гладкие функции аргумента x, в

частности на ψ₂(y, x) и χ3,40(y, x, p), есть O(μ). Таким образом, для невязки R получаем

выражение

(

)

ε³

R(y, x, t) = -μ²(Ψ_as)_tt -

^ĤΨ_as =ε2

ψ₂(y,x)(|p|²c²(x)|p|² - c²(x)|p|⁴)v_as + O ε +

+μ²

ε²

μ²

μ³

В силу того, что функция c²(x) является гладкой, справедливо равенство |p|²c²(x)|p|²v_as =

= c²(x)|p|⁴v_as + O(μ). В итоге для невязки при условии ε ∼ μ3/2 получаем нужную оценку

R(y, x, t) = O(μ3/2). Утверждение 5 доказано.

Автор выражает благодарность Доброхотову С.Ю., Шафаревичу А.И., Толченникову А.А.

и Аникину А.Ю. за ценные советы и указания.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования

Российской Федерации (номер госрегистрации АААА-А20-120011690131-7).

СПИСОК ЛИТЕРАТУРЫ

1. Tolstoy I., Clay C.S. Ocean Acoustics. Theory and Experiment in Underwater Sound. New York, 1966.

2. Laufer G. Introduction to Optics and Lasers in Engineering. New York, 1996.

3. Dobrokhotov S.Yu., Sergeev S.A., Tirozzi B. Asymptotic solutions of the Cauchy problem with localized

initial conditions for linearized two-dimensional Boussinesq-type equations with variable coefficients

// Rus. J. of Math. Phys. 2013. V. 20. № 2. P. 155-171.

4. Аллилуева А.И., Доброхотов С.Ю., Сергеев С.А., Шафаревич А.И. Новые представления канони-

ческого оператора Маслова и локализованные асимптотические решения строго гиперболических

систем // Докл. РАН. 2015. Т. 464. № 3. С. 261-266.

5. Маслов В.П., Федорюк М.В. Квазиклассическое приближение для уравнений квантовой механики.

М., 1976.

6. Маслов В.П. Операторные методы. М., 1973.

7. Доброхотов С.Ю., Тироцци Б., Шафаревич А.И. Представления быстроубывающих функций ка-

ноническим оператором Маслова // Мат. заметки. 2007. Т. 82. № 5. С. 792-796.

8. Доброхотов С.Ю., Назайкинский В.Е. Эффективные асимптотики в задачах о распространении

волн, порождённых локализованными источниками, в линейных многомерных неоднородных и дис-

персионных средах // Журн. вычислит. математики и мат. физики. 2020. Т. 60. № 8. С. 107-120.

9. Доброхотов С.Ю., Назайкинский В.Е. Проколотые лагранжевы многообразия и асимптотические

решения линейных уравнений волн на воде с локализованными начальными условиями // Мат.

заметки. 2017. Т. 101. № 6. С. 936-943.

10. Доброхотов С.Ю., Секерж-Зенькович С.Я., Тироцци Б., Тудоровский Т.Я. Описание распростра-

нения волн цунами на основе канонического оператора Маслова // Докл. РАН. 2006. Т. 409. № 2.

С. 171-175.

11. Dobrokhotov S.Yu., Shafarevich A.I., Tirozzi B. Localized wave and vortical solutions to linear hyperbolic

systems and their application to linear shallow water equations // Rus. J. Math. Phys. 2008. V. 15. № 2.

P. 192-221.

12. Доброхотов С.Ю., Назайкинский В.Е., Шафаревич А.И. Новые интегральные представления кано-

нического оператора Маслова // Изв. РАН. Сер. мат. 2017. Т. 81. № 2. С. 53-96.

13. Dobrokhotov S.Yu., Nazakinskii V.E., Shafarevich A.I. Canonical operator on punctured Lagrangian

manifolds // Rus. J. of Math. Phys. 2021. V. 28. № 1. P. 22-36.

14. Доброхотов С.Ю., Назайкинский В.Е., Шафаревич А.И. Эффективные асимптотики решений за-

дачи Коши с локализованными начальными данными для линейных систем дифференциальных и

псевдодифференциальных уравнений // Успехи мат. наук. 2021. Т. 76. Вып. 5 (461). С. 3-80.

∫x2

15. Scorer R. S. Numerical evaluation of integrals of the form I =

f (x)eiφ(x) dx and the tabulation of

∫_∞

the function Gi (z) = (1/π)

sin(uz + (1/3)u³) du // Quart. J. Mech. and Appl. Math. 1950. V. 3.

Pt. 1. P. 107-112.

16. Dobrokhotov S.Yu., Grushin V.V., Sergeev S.A., Tirozzi B. Asymptotic theory of linear water waves in a

domain with nonuniform bottom with rapidly oscillating sections // Rus. J. of Math. Phys. 2016. V. 23.

№ 4. P. 455-474.

17. Санчес-Паленсия Э. Неоднородные среды и теория колебаний. М., 1984.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ

1399

18. Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. М., 1984.

19. Bensousan A., Lions J.L., Papanicolau G. Asymptotic Analysis for Periodic Structures. Amsterdam;

New York; Oxford, 1978.

20. Жиков В.В., Козлов С.М., Олейник О.А. Усреднение дифференциальных операторов. М., 1993.

21. Marchenko V.A., Khruslov E.Ya. Homogenization of Partial Differential Equations. Boston, 2006.

22. Пастухова С.Е., Тихомиров Р.Н. Об операторных оценках усреднения для эллиптических уравне-

ний с младшими коэффициентами // Алгебра и анализ. 2017. Т. 29. № 5. С. 179-207.

23. Дородный М.А., Суслина Т.А. Операторные оценки погрешности при усреднении гиперболических

уравнений // Функц. анализ и его прил. 2020. Т. 54. № 1. С. 69-74.

24. Буслаев В.С. Квазиклассическое приближение для уравнений с периодическими коэффициентами

// Успехи мат. наук. 1987. Т. 42. Вып. 6 (258). С. 77-98.

25. Грушин В.В., Доброхотов С.Ю., Сергеев С.А. Осреднение и дисперсионные эффекты в задаче о

распространении волн, порожденных локализованным источником // Тр. Мат. ин-та им. В.А. Стек-

лова. 2013. Т. 281. С. 170-187.

26. Брюнинг Й., Грушин В.В., Доброхотов С.Ю. Осреднение линейных операторов, адиабатическое

приближение и псевдодифференциальные операторы // Мат. заметки. Т. 92. № 2. С. 163-180.

27. Brüning J., Grushin V.V., Dobrokhotov S.Yu. Approximate fromulas for eigenvalues of the Laplace

operator on a torus arising in linear problems with oscillaing coefficients // Rus. J. of Math. Phys.

2012. V. 19. № 3. P. 261-272.

Институт проблем механики

Поступила в редакцию 08.04.2022 г.

имени А.Ю. Ишлинского РАН, г. Москва

После доработки 24.08.2022 г.

Принята к публикации 30.08.2022 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 10

2022