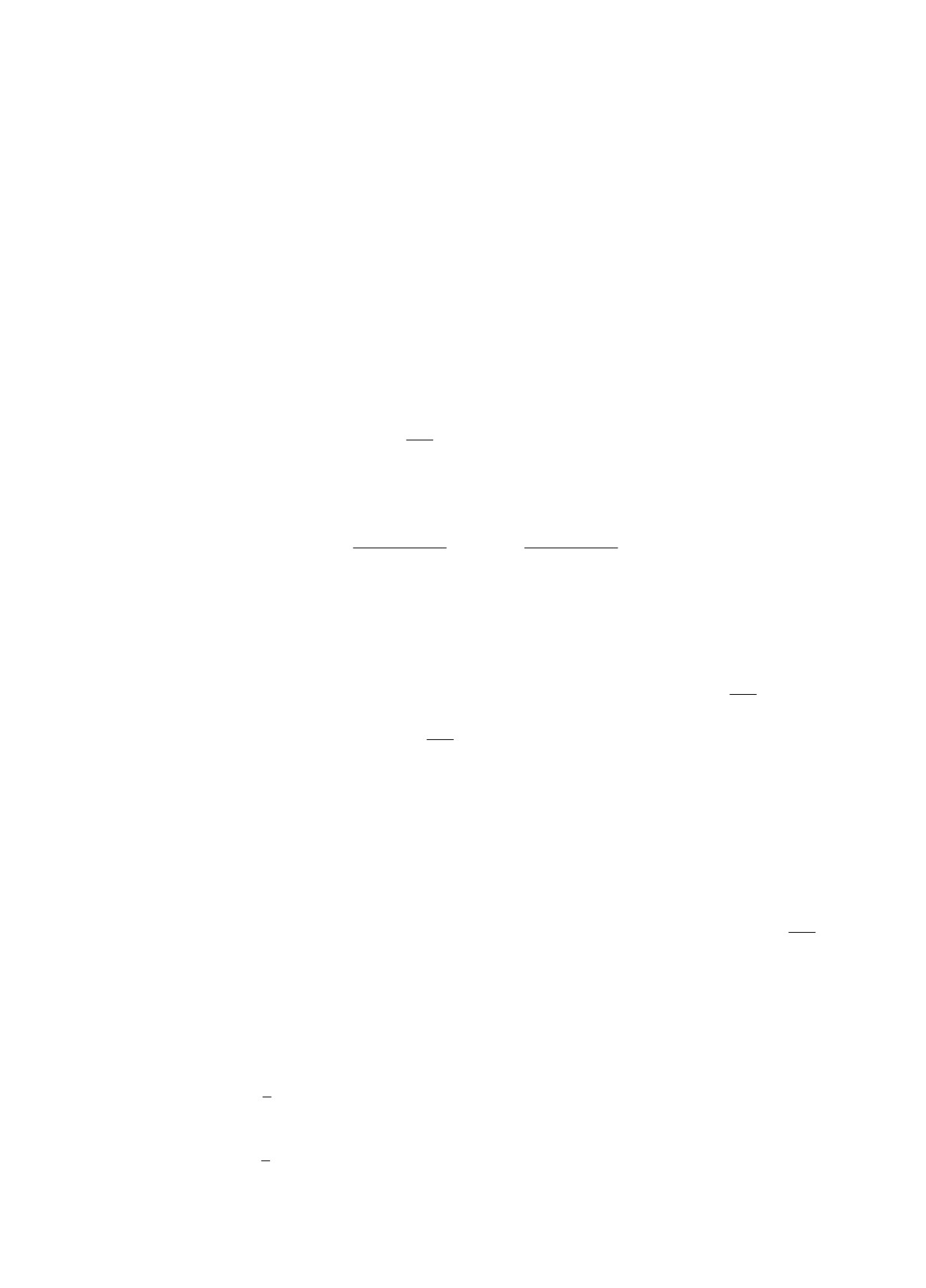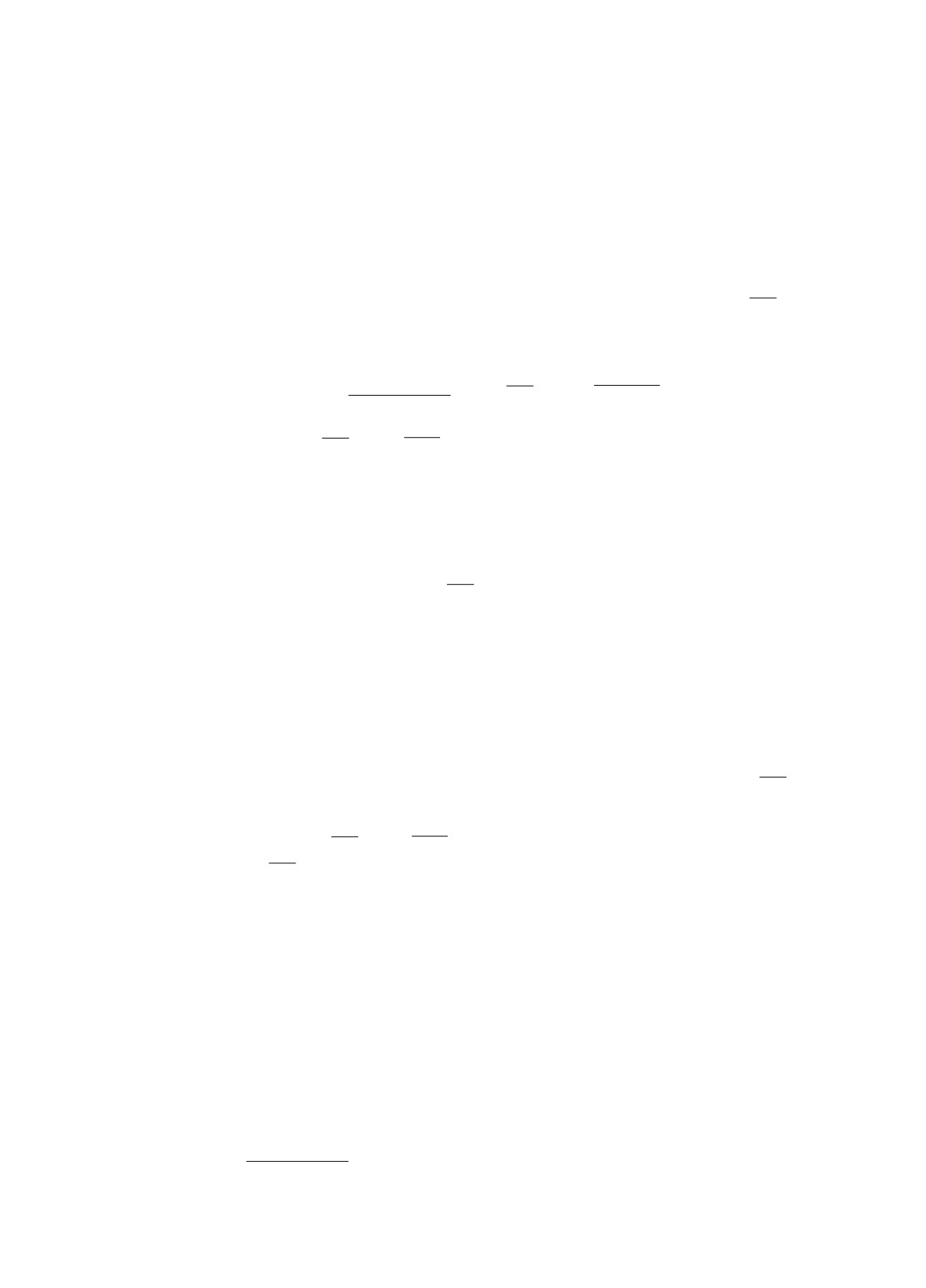ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 11, с. 1537-1547

ТЕОРИЯ УПРАВЛЕНИЯ

УДК 517.977

О ПОСТРОЕНИИ КУСОЧНО-АФФИННОГО

СТАБИЛИЗАТОРА ДЛЯ НЕЛИНЕЙНОЙ СИСТЕМЫ

Рассмотрена задача стабилизации системы нелинейных по фазовым переменным обык-

новенных дифференциальных уравнений с управляющими параметрами. На допустимые

значения позиционного управления наложены жёсткие поточечные ограничения. В предпо-

ложении достаточной гладкости функций из правой части дифференциальных уравнений

построена кусочно-аффинная система, аппроксимирующая исходную нелинейную систему

на прямоугольной сетке в заданной области фазового пространства. Стабилизатор может

быть найден также в кусочно-аффинной форме, ему соответствует непрерывная, но не

везде дифференцируемая функция Ляпунова схожей структуры. Сформулирована и дока-

зана основная теорема о достаточных условиях стабилизируемости системы при помощи

кусочно-аффинного управления. Предложен алгоритм построения такого управления, а

также функции Ляпунова в некоторой малой окрестности нулевого положения равновесия.

Рассмотрен пример численного решения задачи стабилизации для конкретной модельной

системы в трёхмерном пространстве.

DOI: 10.31857/S0374064122110097, EDN: MBOXCW

Введение. Работа посвящена приближённому решению задачи стабилизации для управля-

емой системы [1, с. 476-478], заданной при помощи нелинейных дифференциальных уравнений

с гладкой правой частью. Необходимо построить позиционное управление - стабилизатор, для

которого заведомо выполнены жёсткие поточечные ограничения и который делает нулевое

положение равновесия замкнутой им системы локально асимптотически устойчивым. Необхо-

димо также оценить область притяжения положения равновесия для замкнутой системы.

Указанную задачу можно решать с помощью кусочной линеаризации исходных нелиней-

ных уравнений на заданной сетке из многогранников в фазовом пространстве. На этой сетке

необходимо построить кусочно-аффинную функцию Ляпунова, а также соответствующее ей

кусочно-аффинное позиционное управление.

Кусочно-аффинные функции Ляпунова успешно используются для изучения устойчивости

нелинейных (в частности, кусочно-аффинных) систем. Так, в работе [2] показано, что для сис-

темы дифференциальных уравнений с гладкой правой частью и экспоненциально устойчивым

нулевым положением равновесия всегда можно построить локальную непрерывную кусочно-

линейную функцию Ляпунова. Данная функция может быть далее достроена до непрерывной

кусочно-аффинной функции Ляпунова, позволяющей оценить область притяжения нулевого

положения равновесия.

В работе [3] предложен алгоритм построения непрерывной кусочно-аффинной функции

Ляпунова для задачи синтеза управлений в нелинейной системе дифференциальных уравне-

ний. Задача стабилизации сведена к проблеме исследования слабой асимптотической устойчи-

вости для вспомогательного дифференциального включения. Функцию цены, определённую

на совокупности симплексов в фазовом пространстве, предлагается определять за счёт реше-

ния вспомогательной задачи линейного программирования. При этом используется кусочно-

постоянное позиционное управление, относительно которого априори неизвестно, будет ли оно

допустимым, т.е. порождающим траектории рассматриваемой системы. В упомянутой работе

этот вопрос остался неисследованным.

Статья [4] посвящена построению непрерывной кусочно-аффинной функции Ляпунова, а

также кусочно-аффинного позиционного управления для задачи стабилизации системы с пе-

реключениями - гибридной системы [5]. Условия переключений между несколькими разными

дифференциальными уравнениями (режимами функционирования) являются частью управ-

ления совокупной гибридной системой. Предложен алгоритм построения указанных функций

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

1538

ТОЧИЛИН

с разными областями притяжения положения равновесия замкнутой системы, получена оценка

этой области. Обоснована допустимость построенного кусочно-аффинного управления.

В работе [6] рассмотрена задача оптимального управления нелинейной системой с инте-

гральным функционалом на бесконечном отрезке времени. Для решения задачи использована

функция цены, построенная на совокупности симплексов в фазовом пространстве, а искомое

субоптимальное позиционное управление найдено в кусочно-аффинной форме. В отличие от

предыдущих результатов здесь также предложен более общий подход к построению разрывной

кусочно-аффинной функции цены. Этот метод может быть также применён и при решении

задачи стабилизации для нелинейной системы.

В настоящей статье предложен альтернативный к упомянутым выше подход к парамет-

ризации кусочно-аффинных функций Ляпунова в задаче стабилизации нелинейной системы:

вместо сетки из симплексов в фазовом пространстве используется совокупность прямоуголь-

ных параллелепипедов. Теперь функции цены и управления нельзя однозначно определить

своими (независимыми) значениями в вершинах. В результате получаются другие формулы

для расчёта указанных функций, более простые с точки зрения расчётов, поскольку не нуж-

но вычислять матрицы перехода от глобальных декартовых координат к барицентрическим

координатам в рамках каждого конкретного симплекса. При этом, однако, повышается размер-

ность во вспомогательных задачах оптимизации, которые необходимо решать при построении

функции цены. Для вычисления этой функции, а также позиционного управления, предло-

жен алгоритм, основой которого является решение цепочки вспомогательных задач линейно-

го программирования. Вычисления по такому алгоритму могут быть проведены достаточно

эффективно, в том числе и для систем большой размерности. Работа этого алгоритма проде-

монстрирована на конкретном модельном примере.

1. Задача стабилизации для нелинейной системы. Рассмотрим систему обыкновен-

ных дифференциальных уравнений с управляющими параметрами

x = f(x) + g(x)u, x ∈ Rⁿ, t ∈ [0,+∞).

(1)

Здесь гладкие функции f(x) ∈ C²(Ω), f(x) ∈ Rⁿ, f(0) = 0, g(x) ∈ C¹(Ω), g(x) ∈ R^n×m опре-

делены при x ∈ Ω = [a₁, b₁]×. . .×[a_n, b_n]. Точка x = 0 является внутренней для множества Ω,

т.е. a_i < 0 < b_i для любых i = 1, n.

На допустимые значения позиционного управления u = u(x) ∈ R^m наложены жёсткие

поточечные ограничения: u ∈ P ⊂ R^m, где множество P является выпуклым компактом.

Допустимым управлением назовём такую функцию u = u(x), которая удовлетворяет ука-

занному выше поточечному ограничению, а также порождает траектории системы (1), т.е. для

любого начального условия x(0) = x₀ ∈ Ω задача Коши для дифференциального уравнения

x = f(x)+g(x)u(x) должна иметь единственное решение x(t) = x(t,t₀,x₀), определённое при

t ≥ 0, по крайней мере до момента выхода траектории на границу Ω. Эти условия, в част-

ности, будут выполнены, если функция u(x) удовлетворяет условию Липшица при x ∈ Ω.

Также предположим, что для допустимого управления u(x) должно быть выполнено усло-

вие u(0) = 0. Будем далее рассматривать траектории замкнутой системы лишь до момента

возможного выхода на границу Ω, не накладывая в связи с этим никаких дополнительных

априорных ограничений на допустимые управления.

Решаемая в данной работе задача стабилизации состоит в поиске таких множества X ⊂ Ω

и допустимого управления u(x), определённого при x ∈ X , что система дифференциальных

уравнений x = f(x)+g(x)u(x) будет обладать асимптотически устойчивым нулевым положе-

нием равновесия с областью притяжения X , т.е. для любых x₀ ∈ X и t ≥ 0 должно быть

выполнено условие существования предела

lim

∥x(t, 0, x₀)|u(·)∥ = 0, x(t, 0, x₀)|u(·) ∈ X ,

t→+∞

где x(t, 0, x₀)|u(·), t ∈ [0, +∞), - траектория системы x = f(x)+g(x)u(x), выпущенная из на-

чальной позиции x(0) = x₀. Заметим, что данное определение асимптотической устойчивости

является более сильным, чем традиционное, так как здесь сочетаются требования инвари-

антности множества X и принадлежности ему начальной позиции, т.е. не рассматриваются

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

О ПОСТРОЕНИИ КУСОЧНО-АФФИННОГО СТАБИЛИЗАТОРА

1539

траектории, которые стартуют вне X и попадают в это множество в какой-то промежуточный

момент времени. Даное ограничение связано с особенностями основного алгоритма, который

будет приведён далее. Кроме того, это сильное требование позволяет не следить за возможным

выходом траектории замкнутой системы за границу Ω в какие-то промежуточные моменты

времени, так как X ⊂ Ω.

Для решения задачи стабилизации далее воспользуемся традиционным подходом, пред-

полагающим поиск наряду с управлением u(x) также соответствующей функции Ляпуно-

ва V (x). Последняя может быть использована для доказательства асимптотической устойчи-

вости нулевого положения равновесия замкнутой системы.

2. Кусочная линеаризация дифференциальных уравнений. Каждый из отрезков

[a_i, b_i] разобьём на N_i ∈ N частей:

⋃

x_i ∈ [a_i,b_i] =

[x(j)i, x(j+1)i], x(0)i = a_i, x(Ni)_i = b_i.

j=0

Будем считать, что для каждого i = 1, n найдётся номер j^∗i ∈ {1, . . . , N_i - 1} такой, что

x(ji)_i = 0, т.е. начало координат является одной из точек разбиения.

Для каждой пары индексов i, j введём обозначения

(j)

+x(j+1)i

z(j)i =xi

δ(j)i =xij+1) -xij)

Для нумерации вершин и многогранных частей полученного разбиения области Ω будем далее

использовать мультииндексы

j=(j1,... ,j_n) ∈ {0,... ,N₁} × ... × {0,... ,N_n}.

Множество всех таких индексов

j обозначим через J . Кроме того, через J₀ обозначим

совокупность всех мультииндексовj ∈ J , для которых j_i < N_i при любом i = 1, n. Мульти-

индекс, соответствующий нулевому положению равновесия, обозначим черезj∗. Пусть z(j) ∈

∈ Rⁿ - вектор с компонентами z(ji)_i, i = 1,n. Аналогично δ(j) ∈ Rⁿ - вектор с компонента-

ми δ(ji)_i. Введём также обозначение для части области Ω:

Ω(j) = [x(j1)1,x(j1+1)1] × ... × [x(jn)_n,x(jn+1)n] для любого

j=(j1,... ,j_n) ∈ J₀.

Точка x(j) = (x(j1)1, . . . , xnjn)) является вершиной многогранника Ω(j), обладающей наимень-

шими координатами.

Рассмотрим теперь линеаризованную систему (1):

x_i = f_i(z(j)) + (f^′i(z(j)))^т(x - z(j)) + g_i(z(j))u + ν(j)i(x), если x_i ∈ [x(ji)_i,x(ji+1)i], i = 1,n.

Здесь f^′i(·) - градиент функции f_i(·), g_i(·) - i-я строка матрицы g(·). Погрешность линеа-

ризации ν(j)i(x), далее интерпретируемую как неопределённость, можно оценить следующим

образом:

ν(j)i(x) ∈ [R(j)i,-,R(j)i,+],

(2)

∑

R(j)i,- =1∥δ(j)∥2

min

λ_min(f^′′i(ξ)) - ∥δ(j)∥

max

∥g^′ik(η)∥ρ(e_k|P),

ξ∈Ω(j)

η∈Ω(j)

k=1

∑

R(j)i,+ =1∥δ(j)∥2 max

λ_max(f^′′i(ξ)) + ∥δ(j)∥

max

∥g^′ik(η)∥ρ(e_k|P).

ξ∈Ω(j)

η∈Ω(j)

k=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

7^∗

1540

ТОЧИЛИН

Здесь f^′′i(·) - матрица из вторых производных функции fi(·), λmin(Q), λmax(Q) - соот-

ветственно наименьшее и наибольшее собственные значения некоторой симметричной мат-

рицы Q, ρ(l|P) - значение опорной функции ко множеству P в направлении l ∈ R^m, а e_k -

k-й орт в пространстве R^m.

3. Кусочно-аффинные функции V (x) и u(x). Для решения задачи стабилизации

далее используем непрерывную кусочно-аффинную функцию Ляпунова, которая может быть

задана следующей формулой:

∑

V (x) = (α(ji)(x_i)v(ji)_i + (1 - α(ji)(x_i))v(ji+1)i), если x_i ∈ [x(ji)_i, x(ji+1)i], i = 1, n.

(3)

i=1

Здесь

(j_i+1)

-x_i

α(ji)(x_i) =

i = 1,n, j_i = 0,N_i - 1,

x(ji+1)i - x(ji)

а параметры v(j)i ∈ R, i = 1, n, j = 0, N_i, будут найдены далее. Эти величины однознач-

но задают непрерывную кусочно-аффинную функцию V (x) на совокупности областей Ω(j),

j∈J0. Данная функция является дифференцируемой по любому направлению в любой точ-

ке x ∈ int Ω. На границах множеств Ω(j) эта функция может быть недифференцируема в

обычном смысле.

На величины v(j)i наложим следующие ограничения:

v(ji)_i = 0 для любого i = 1,n, т.е. V (x(j∗)) = V (0) = 0,

(4)

∑

j∈Jтакого,что

j= j∗_.

V (x(j)) =

v(ji)_i > 0 для любого индекса

(5)

i=1

Заметим, что так как функция V (x) является аффинной в каждой из областей Ω(j), то при

выполнении условий (4), (5) V (x) > 0 при любом x = 0.

Далее будем использовать непрерывное кусочно-аффинное позиционное управление вида

∑

u(x) = (α(ji)(x_i)u(ji)_i + (1 - α(ji)(x_i))u(ji+1)i), если x_i ∈ [x(ji)_i, x(ji+1)i], i = 1, n,

(6)

i=1

где векторы u(ji)_i ∈ R^m, i = 1, n, j = 0, N_i, необходимо определить. Кроме того, положим

u(ji)_i = 0 при всех i = 1,n. Пусть для любой вершины x(j) рассматриваемых многогранников

∑

u(x(j)) =

u(ji)_i ∈ P.

(7)

i=1

Поскольку каждая компонента вектор-функции u(x) является аффинной в каждой облас-

ти Ω(j), то из условия (7) вытекает, что u(x) ∈ P, x ∈ Ω.

При любых фиксированных значениях u(ji)_i кусочно-аффинная функция u(x) удовлетво-

ряет условию Липшица в области Ω, а потому данное управление является допустимым.

Пусть x ∈ int Ω(j) для некоторого индекса j. Рассмотрим производную функции Ляпунова

вдоль траектории линеаризованной системы, замкнутой кусочно-аффинным управлением u(x)

при x ∈ Ω(j) :

∑

v(ji+1)i - v(ji)_i

V (x) =

(f_i(z(j)) + (f^′i(z(j)))^т(x - z(j)) + g_i(z(j))u(x) + ν(j)i(x)).

(8)

(j_i+1)

-x(ji)

i=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

О ПОСТРОЕНИИ КУСОЧНО-АФФИННОГО СТАБИЛИЗАТОРА

1541

Используя (8) и (2), запишем теперь достаточное условие определённой отрицательности пол-

ной производной функции цены в какой-либо вершине h многогранника Ω(j) :

[

^∑v(ji+1)i - v(ji)_i

R(j)i,- + R(j)i,+

R(j)i,+ - R(j)i,- ]

f_i(z(j)) +

+ sgn (v(ji+1)i - v(ji)_i)

(j_i+1)

-x(ji)

i=1

∑

v(ji+1)i - v(ji)_i

((f^′i(z(j)))^т(h - z(j)) + g_i(z(j))u(h)) ≤ -ε min{∥h∥, 1}.

(9)

(j_i+1)

-x(ji)

i=1

Здесь ε > 0 - малое фиксированное число.

Далее для некоторого множества X через ∂X обозначим множество его граничных точек,

а через int X - множество всех внутренних точек.

Приведённые выше предварительные построения позволяют теперь сформулировать ос-

новное утверждение, задающее достаточные условия для решения задачи стабилизации с ис-

пользованием кусочно-аффинных функций V (x) и u(x).

⋃

Теорема. Пусть J^∗ ⊂ J₀ - некоторое множество мультииндексовj, X₀ =

j∈J^∗ Ω(j).

Пусть найдены такие v(ji)_i, u(ji)_i (для различных i, j_i), что для любых j ∈ J^∗, i = 1, n,

выполнены условия (4), (5), (7), (9) (последнее условие выполнено для любой вершины h мно-

жества Ω(j)). Построим множество

X = {x ∈ X₀ : V (x) ≤ V_min},

(10)

V_min = min{V (h) : h - вершина Ω(j), j ∈ J^∗, h ∈ ∂X₀}.

(11)

Предположим, что 0 ∈ int X . Тогда кусочно-аффинное управление u(x), определённое со-

гласно формуле (6), решает задачу стабилизации для системы (1), причём областью при-

тяжения нулевого положения равновесия замкнутой этим управлением системы является

множество int X.

Доказательство. Рассмотрим произвольную точку x ∈ Ω(j) ⋂ int X₀,

j ∈ J^∗, и оценим

производную функции Ляпунова V (x), построенной согласно формуле (3), вдоль траектории

системы (1), замкнутой при помощи управления (6). Предположим, что x и^j выбраны таким

образом, что вектор f(x) + g(x)u(x) указывает либо внутрь Ω(j), либо вдоль границы этого

многогранника. Для любого x всегда можно подобрать подходящий индексj ∈ J^∗.

Для оценки производной функции Ляпунова используем условие (9), а также оценку для

погрешности линеаризации (2):

(

∑

v(ji+1)i - v(ji)_i

V (x) ≤

f_i(z(j)) + (f^′i(z(j)))^т(x - z(j)) +

(j_i+1)

-x(ji)

i=1

)

∑

+ g_i(z(j))

(α(ji)(x_i)u(ji)_i + (1 - α(ji)(x_i))u(ji+1)i)

i=1

{

}

∑

max R(j) viji+1) -viji)_i,-

,R(j) viji+1) -viji)i,+

x(ji+1)i - x(ji)_i

x(ji+1)i - x(ji)

i=1

Полученная функция является линейной относительно переменной x. Эта функция достигает

своего максимума хотя бы в одной вершине многогранника Ω(j). Кроме того, выражение в

третьей строке можно записать через функцию sgn аналогично (9). В итоге получим, что

[

(j_i+1)

^∑v_i

−v(ji)_i

R(j)i,- + R(j)i,+

R(j)i,+ - R(j)i,- ]

V (x) ≤ max

f_i(z(j)) +

+ sgn (v(ji+1)i - v(ji)_i)

x(ji+1)i - x(ji)

i=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

1542

ТОЧИЛИН

}

∑

v(ji+1)i - v(ji)_i

((f^′i(z(j)))^т(h - z(j)) + g_i(z(j))u(h)) : h - вершина Ω(j)

≤

(j_i+1)

-x(ji)

i=1

≤ -εmin(min{∥h∥,1}) ≤ 0.

Заметим, что полученное выражение может быть равно нулю только в том случае, если h = 0

является одной из вершин Ω(j). При этом в других вершинах этого многогранника анализи-

руемая линейная функция принимает значения, отличные от нуля. Следовательно, равенство

нулю этой линейной функции возможно только при x = 0, т.е. доказано, что

V (x) < 0 для любого x ∈ int X₀, x = 0.

Более того, можно показать, что для любого η > 0 существует число δ > 0 такое, что

V (x) ≤ -δ при всех x ∈ int X₀, ∥x∥ ≥ η.

Из доказанного свойства монотонности функции V (x) вдоль траекторий системы, а также

из определения множества X следует, что если траектория замкнутой системы стартует из

int X , то она не может достичь границы ∂X , а значит, никогда не выйдет за пределы этого

множества.

Заметим также, что из условий (4) и (5) следует, что V (x) является определённо поло-

жительной функцией в X₀. Далее, следуя схеме доказательства классической теоремы Ля-

пунова об асимптотической устойчивости [7, с. 25; 8, с. 81-82], можно показать, что нулевое

положение равновесия замкнутой системы является асимптотически устойчивым с областью

притяжения int X .

4. Алгоритм построения кусочно-аффинных функций V (x) и u(x). Рассмот-

рим теперь конкретный алгоритм построения кусочно-аффинной функции Ляпунова V (x), а

также управления u(x), удовлетворяющих условиям теоремы. Попутно будет построена, по

возможности максимальная по включению, область притяжения X нулевого положения рав-

новесия. Множество X , вообще говоря, зависит от Ω, но в данной работе эта зависимость

подробно не исследуется.

Основная идея алгоритм схожа с предложенной в работе [4], но с учётом другой структу-

ры используемых кусочно-аффинных функций. В этом алгоритме проводятся многократные

попытки добавлять совокупности соседних множеств Ω(j) к ранее обработанным, подсчиты-

вая значения v(ji)_i, u(ji)_i в соответствующих вершинах. При этом на каждом шаге алгоритма

следует проверять выполнение условий основной теоремы. Если на очередном шаге не удастся

добавить (обработать) какие-либо новые множества Ω(j), то алгоритм завершит работу.

Для упрощения расчётов будем далее считать, что множество допустимых значений управ-

лений P является выпуклым многогранником в R^m и может быть задано при помощи сово-

купности линейных неравенств∗) :

P = {u ∈ R^m : Du ≼ γ}, D ∈ R^l×m, γ ∈ R^l.

Каждой вершине x(k) множеств Ω(j) сопоставим вспомогательную величину σ(k), прини-

мающую значения, равные нулю и единице, и показывающую, были ли уже в этой вершине

подсчитаны значения v(k)i, u(k)i. Кроме того, каждому множеству Ω(j) сопоставим вспомо-

гательную величину η(j), которая может принимать три значения: η(j) = 0, если данное

множество ещё не было обработано алгоритмом; η(j) = 1, если множество уже было успешно

обработано алгоритмом и было добавлено ко множеству X₀; η(j) = -1, если множество уже

было обработано алгоритмом, но за его счёт не удалось расширить область притяжения.

Будем говорить, что два разных множества Ω(j) и Ω(k) являются соседними, если они

пересекаются по общей грани максимальной возможной размерности (т.е. имеют ровно n об-

щих вершин). Множества Ω(j), . . . , Ω(s) назовём соседними, если их можно упорядочить так,

∗) Символ “ ≼ ” соответствует покомпонентному неравенству для векторов одинаковой длины.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

О ПОСТРОЕНИИ КУСОЧНО-АФФИННОГО СТАБИЛИЗАТОРА

1543

что в полученной цепочке каждое следующее множество является соседним по отношению к

какому-либо предыдущему.

Зафиксируем также вспомогательный параметр - натуральное число S.

Шаг 1. Изначально положим v(j∗)_i = 0, u(j∗)_i = 0 для любого i = 1, n. Также пусть σ(j∗) =

= 1. Для всех других вершин σ(j) = 0. Также пусть J^∗ = ∅, X₀ = ∅, V_min = 0. Для каждого

j пусть η(j) = 0.

Шаг 2. Возьмём некоторую совокупность соседних множеств Ω(j),

j ∈

⊂ J₀, для ко-

торых либо x(j∗) = 0 является одной из их вершин, либо хотя бы одно из этих множеств

является соседним со множеством Ω(k), для которого η(k) = 1. Кроме того, для каждого из

таких множеств должно быть выполнено условие η(j) = 0. Если удовлетворяющих этим усло-

виям множеств не существует, то алгоритм переходит к завершающему шагу 12. В противном

случае начинается описанная ниже обработка найденных многогранников.

Шаг 3. Выполняется последовательный перебор разных вариантов значений функций sgn

в формулах (9) для всех возможных

j ∈

только для ещё не найденных величин v(ji)_i

или v(ji+1)i. Каждый такой вариант соответствует некоторой системе неравенств для искомых

величин v(k)i, а выражения в квадратных скобках в (9) можно далее считать постоянными.

Следующие четыре шага алгоритма выполняются отдельно для каждого такого варианта.

Шаг 4. Для каждого^j

J используем далее вспомогательный вектор d(j) ∈ Rⁿ. Изна-

чально пусть

∑

d(j) =

sgn (v(ji+1)i - v(ji)_i)g_i(z(j)).

i=1

Здесь учитывается, что значения функций sgn ранее были зафиксированы.

Если вектор d(j) не нулевой, то дополнительно нормируем его: d(j) = d(j)/∥d(j)∥.

Положим s = 1 (вспомогательный индекс).

⋃

Шаг 5. Поиск управлений. Определим значения u(k)i, i = 1, n, x(k) ∈

Ω(j), σ(k) = 0,

j∈J

решив вспомогательную задачу линейного программирования:

}

∑

j∈ Jˆ

d(j)

u(k)i : x(k) ∈ Ω(j), σ(k) = 0,

→ min

i=1

при линейных ограничениях

)

∑

⋃

D u(k)

≼ γ для любого

k такого, что x(k) ∈

Ω(j), σ(k) = 0.

i=1

j∈J

Шаг 6. Поиск значений функции Ляпунова. Определим значения v(k)i, i = 1, n, x(k) ∈

⋃

∈

Ω(j), σ(k) = 0, решив вспомогательную задачу линейного программирования. Задача

j∈J

оптимизации при этом имеет вид

}

∑∑{

⋃

v(k)i : x(k) ∈

Ω(j), σ(k) = 0

→ min .

(12)

i=1

j∈Jˆ

Линейные ограничения на искомые параметры v(k)i определяются следующим образом:

(a) Условия положительности значений функции Ляпунова и одновременно расширения

потенциальной области притяжения X₀ :

∑

⋃

v(k)i ≥ max{εmin{∥x(k)∥,1},V_min} для любого x(k) ∈

Ω(j) такого, что σ(k) = 0.

i=1

j∈

ˆJ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

1544

ТОЧИЛИН

(b) Ограничения на v(k)i для вычисления sgn в (9) (см. шаг 3 алгоритма).

той системы (9) для каждого^j

J и каждой соответствующей вершины h (в том числе для

вершин, уже обработанных на предыдущих итерациях). При этом в формулах (9) использу-

ются управляющие параметры u(k)i, найденные на предыдущем шаге 5, на данной итерации

работы алгоритма.

Шаг 7. Если удалось решить задачи линейного программирования и найти значения u(k)i

и v(k)i, то проверяется выполнение следующего условия:

- либо s = 1 (т.е. это первая итерация работы);

- либо s > 1, и значение функционала (12), найденное на этой итерации, меньше анало-

гичного значения, найденного на предыдущей итерации, с номером s - 1.

Если указанное условие выполнено и s < S, то производятся следующие действия:

- значение s увеличивается на единицу;

- для каждого^j

J заново рассчитывается вектор

∑

v(ji+1)i - v(ji)_i

d(j) =

g_i(z(j)),

(j_i+1)

x_i

−x(ji)

i=1

если вектор d(j) не нулевой, то дополнительно нормируем его: d(j) = d(j)/∥d(j)∥;

- алгоритм снова переходит к шагу 5.

В противном случае алгоритм переходит либо к обработке следующего варианта значе-

ний функций sgn в соответствующих формулах (9), либо к шагу 8, завершающему такую

обработку.

Шаг 8. Задачи линейного программирования из шага 7 должны быть решены для разных

вариантов значений функций sgn в соответствующих формулах (9). Среди задач, которые

имеют решения, выделим ту, в которой значение функции (12) получилось наименьшим.

Шаг 9. Если в предыдущих шагах удалось найти решение задачи линейного программиро-

вания для оптимального варианта значений функций sgn в формулах (9), то ко множеству X₀

j∈ Jˆ,акомножествуJ ∗_{-соответствующиеиндексы}

добавляются многогранники Ω(j),

Для каждого обработанного на данном шаге множества Ω(j) положим η(j) = 1. Для каждой

вершины x(k) указанных множеств положим σ(k) = 1. Запоминаются значения v(k)i, u(k)i, по-

лученные в результате решения задачи линейного программирования. Кроме того, необходимо

заново пересчитать величину V_min по формуле (11).

Шаг 10. Если же выше не удалось найти решения задач линейного программирования, то

для каждого рассмотренного на данном шаге множества Ω(j) положим η(j) = -1.

Шаг 11. Алгоритм переходит снова к шагу 2, т.е. к следующей попытке добавить какие-то

множества Ω(j) к конструируемому множеству X₀.

Шаг 12. Завершение работы. На выходе имеем множества X₀ и J^∗, задающие область

притяжения нулевого положения равновесия, а также величины v(j)i, u(j)i, i = 1, n,

j∈J ∗_.

Теперь можно определить множество X согласно (10), а также построить кусочно-аффинные

функции Ляпунова и позиционного управления (стабилизатора) по формулам (3), (6).

Для одной и той же системы (1) приведённый алгоритм может построить разные множества

X₀ и определённые на них кусочно-аффинные функции V (x) и u(x). Это связано с тем, что в

шаге 2 можно выбирать очередные обрабатываемые области Ω(j) разными способами. Одна

из возможностей - обрабатывать эти множества по одному за шаг работы алгоритма (рис. 1, a)

аналогично тому, как было описано в работе [4] для случая системы с переключениями и сетки

из симплексов. Такой подход минимизирует сложность вычислений на каждом отдельном шаге

работы алгоритма, однако количество таких шагов может быть большим. Возможны и другие

подходы, когда за один шаг работы алгоритма обрабатывается сразу совокупность множеств

Ω(j), например, как показано на рис. 1, б.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

О ПОСТРОЕНИИ КУСОЧНО-АФФИННОГО СТАБИЛИЗАТОРА

1545

(а)

(б)

Рис. 1. Множества X , полученные при разных правилах выбо-

ра очередных обрабатываемых многогранников Ω(j). Числами обо-

значены номера итераций алгоритма, на которых Ω(j) добавлены

в X.

Заметим, что поскольку на каждом шаге работы алгоритма отслеживается выполнение

условий теоремы, то если 0 ∈ int X , можно утверждать, что множество X является множе-

ством притяжения для нулевого положения равновесия системы (1) при использовании по-

строенного кусочно-аффинного стабилизатора вида (6).

Решаемые на каждом шаге работы алгоритма подзадачи линейного программирования мо-

гут быть решены эффективно (см. [9, с. 297-303]) за полиномиальное время в зависимости как

от количества переменных (v(k)i, u(k)i), так и от количества линейных неравенств (ограниче-

ний). Это позволяет применять алгоритм для решения задач стабилизации сложных систем с

большой размерностью вектора фазовых переменных.

5. Пример. В качестве примера рассмотрим задачу стабилизации угловых скоростей квад-

рокоптера, зависшего в заданной точке пространства. Для этого используем математическую

модель, подробно описанную в статье [10]. Дифференциальные уравнения для трёх компонент

угловой скорости выглядят следующим образом:

I_xxw˙_ϕ =

√

F₂ - w_ψw_θ(I_zz - I_yy), I_zzw˙_ψ = dF₄ - w_ϕw_θ(I_yy - I_xx),

I_yyw˙_θ =

√

F₃ - w_ϕw_ψ(I_xx - I_zz),

(13)

где F₁ = p₁ + p₂ + p₃ + p₄, F₂ = -p₁ + p₂ + p₃ - p₄, F₃ = -p₁ - p₂ + p₃ + p₄, F₄ = -p₁ + p₂ - p₃ +

+p₄, p_i, i = 1,4, - тяги, создаваемые отдельными двигателями. На каждый из управляющих

параметров p_i задано поточечное ограничение: p_i ∈ [0, p_max]. Величина F₁ соответствует

подъемной силе для центра масс аппарата и считается фиксированной: F₁ = p₁ + p₂ + p₃ +

+p₄ = mg. Другие величины F₂, F₃, F₄ могут изменяться, позволяя квадрокоптеру изменять

ориентацию в пространстве.

Введём обозначения x = (w_ϕ, w_ψ, w_θ)^т для вектора фазовых переменных и запишем сис-

тему (13) в виде

x = f(x) + Bu, u ∈ P,

где

⎛

⎞

√

⎛

⎞

⎜

2I_xx

⎟

c₁x₂x₃

⎜

⎟

⎜

⎟

f (x) =^⎝c₂x₁x₃⎠,B=

⎜

⎟,

⎜

I_zz

⎟

c₃x₁x₂

⎝

⎠

√

2I_yy

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

1546

ТОЧИЛИН

I_yy - I_zz

I_xx - I_yy

I_zz - I_xx

c₁ =

c₂ =

c₃ =

I_xx

I_zz

I_yy

Множество P - выпуклый многогранник в пространстве переменных u = (F₂, F₄, F₃)^т, кото-

рый задаётся следующими неравенствами:

0 ≤ mg - F₂ - F₃ - F₄ ≤ 4p_max,

0 ≤ mg + F₂ - F₃ + F₄ ≤ 4p_max,

0 ≤ mg + F₂ + F₃ - F₄ ≤ 4p_max,

0 ≤ mg - F₂ + F₃ + F₄ ≤ 4p_max.

Используемые при линеаризации уравнений градиенты функций f_i имеют вид

⎛

⎞

⎛

⎞

⎛

⎞

c₂x₃

c₃x₂

f′1(x) = ⎝c₁x₃⎠, f′2(x) = ⎝

⎠, f′3(x) = ⎝c3x1⎠.

c₁x₂

c₂x₁

Матрицы вторых производных выглядят следующим образом:

⎛

⎞

⎛

⎞

⎛

⎞

c₂

c₃

f′′1(x) = ⎝0

c₁⎠, f′′2(x) = ⎝0

⎠_,f′′

(x) =^⎝c3

0⎠.

c₁

c₂

Теперь можно легко найти оценки на погрешности линеаризации:

R(j)i,- = -ci∥δ(j)∥2, R(j)i,+ =ci∥δ(j)∥2, i = 1, 2, 3.

Для расчётов используем параметры квадрокопте-

ра из работы [10]: d = 0.09 м, m = 0.5 кг, I_xx = I_yy =

= 0.0021435 кг·м/рад, I_zz = 0.001 кг·м/рад, p_max =

= 1.33 Н. При помощи приведённого выше алгоритма

удалось построить кусочно-аффинные функции Ляпу-

нова и управления в малой окрестности нулевого по-

ложения равновесия. На рис. 2 изображена получен-

ная в результате расчётов область притяжения замк-

нутой системы, являющаяся множеством уровня ку-

сочно-аффинной функции Ляпунова V (x). В приме-

ре Ω = [0, 1] × [0, 1] × [0, 1], отрезки [0, 1] были раз-

биты на n = 10 частей. Алгоритм проработал

100

итераций с максимальным количеством попыток ре-

шения подзадач линейного программирования S = 3.

На каждой итерации обрабатывалась одна очередная

Рис. 2. Область притяжения X .

многогранная область Ω(j), соседняя по отношению к

ранее обработанным.

Заключение. Рассмотрена задача стабилизации для нелинейной системы дифференци-

альных уравнений. Предложен метод приближённого построения непрерывного кусочно-аф-

финного управления, а также соответствующей функции Ляпунова. Доказана теорема о доста-

точных условиях решения задачи стабилизации при помощи такого управления. Предложен-

ные в работе методы и идеи будут в дальнейшем использованы для решения задач стабилиза-

ции систем большой размерности, что потребует более тщательного анализа соответствующих

численных методов и алгоритмов.

Результаты пп. 1-4 получены при финансовой поддержке Российского научного фонда

(проект 22-11-00042). Результаты п. 5 получены при поддержке Министерства науки и высше-

го образования Российской Федерации в рамках реализации программы Московского центра

фундаментальной и прикладной математики по соглашению № 075-15-2022-284.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

О ПОСТРОЕНИИ КУСОЧНО-АФФИННОГО СТАБИЛИЗАТОРА

1547

СПИСОК ЛИТЕРАТУРЫ

1. Красовский Н.Н. Проблемы стабилизации управляемых движений // Малкин И.Г. Теория устой-

чивости движения. Дополнение 4. М., 1966. С. 475-515.

2. Giesl P., Hafstein S. Existence of piecewise linear Lyapunov functions in arbitrary dimensions // Discret.

and Contin. Dyn. Syst. 2012. V. 32. № 10. P. 3539-3565.

3. Baier R., Hafstein S. Numerical computation of control Lyapunov functions in the sense of generalized

gradients // 21st International Symposium on Mathematical Theory of Networks and Systems (MTNS

2014). Groningen, 2014. P. 1173-1180.

4. Атанесян А.А., Точилин П.А. Задача стабилизации системы с переключениями при помощи ку-

сочно-линейного управления // Вестн. Московского ун-та. Сер. 15: Вычислит. математика и кибер-

нетика. 2019. № 4. С. 22-32.

5. Куржанский А.Б., Точилин П.А. Слабо инвариантные множества гибридных систем // Диффе-

ренц. уравнения. 2008. Т. 44. № 11. С. 1523-1533.

6. Точилин П.А. О построении кусочно-аффинной функции цены в задаче оптимального управления

на бесконечном отрезке времени // Тр. Ин-та математики и механики УрО РАН. 2020. Т. 26. № 1.

С. 223-238.

7. Барбашин Е.А. Введение в теорию устойчивости. М., 2014.

8. Красовский Н.Н. Некоторые задачи теории устойчивости движения. М., 1959.

9. Схрейвер А. Теория линейного и целочисленного программирования. М., 1991.

10. Каплунова Е.П., Точилин П.А. Задача целевого управления квадрокоптером при движении в го-

ризонтальной плоскости с огибанием препятствий // Вестн. Московского ун-та. Сер. 15: Вычислит.

математика и кибернетика. 2021. № 4. С. 21-36.

Московский государственный университет

Поступила в редакцию 03.06.2022 г.

имени М.В. Ломоносова,

После доработки 03.09.2022 г.

Университет МГУ-ППИ в Шэньчжэне,

Принята к публикации 21.10.2022 г.

Институт проблем управления

имени В.А. Трапезникова РАН, г. Москва

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022