ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 11, с. 1548-1556

ТЕОРИЯ УПРАВЛЕНИЯ

УДК 517.977

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ

НЕЙРОРЕГУЛЯТОРА ДЛЯ ПЕРЕКЛЮЧАЕМЫХ СИСТЕМ

Рассматривается задача стабилизации переключаемой линейной системы с медленными

переключениями, недоступными для наблюдения. Решение ищется в классе регуляторов

переменной структуры. Для обеспечения работоспособности такого регулятора необходимо

построение наблюдателя переключающего сигнала. В качестве наблюдателя предлагается

использовать нейросеть, теоретическим аспектам настройки которой и посвящена настоя-

щая работа.

DOI: 10.31857/S0374064122110103, EDN: MCFCOP

1. Постановка задачи. Рассматривается непрерывная скалярная переключаемая линей-

ная система

x = A_σx + b_σu, σ ∈ S_τ,

(1)

где σ : R₊ → I = {1, . . . , m} - непрерывная справа кусочно-постоянная функция (переключа-

ющий сигнал) с конечным числом разрывов (переключений) на любом конечном промежутке;

S_τ - множество всех переключающих сигналов σ, для которых время между любыми дву-

мя соседними переключениями не меньше τ (τ > 0); I - множество индексов, нумерующих

режимы функционирования системы (1); A_σ = A ◦ σ - композиция отображения A : I →

→ {A₁, . . . , A_m} (A_i ∈ R^n×n) и переключающего сигнала σ, b_σ = b ◦ σ - аналогичная ком-

позиция для отображения b : I → {b₁, . . . , b_m} (b_i ∈ Rⁿ); пары матриц (A_i, b_i), i = 1, m,

определяют режимы функционирования системы (1); x ∈ Rⁿ - вектор состояния, u ∈ R¹ -

управляющий вход.

Задача. Требуется стабилизировать систему (1) в заданной окрестности нуля D(0; γ) =

= {x ∈ Rⁿ : ∥x∥ ≤ γ}, т.е. построить обратную связь u = u(x) такую, что для некоторого

γ > 0 и любых x(0) ∈ D(0;γ), σ ∈ S_τ норма соответствующего решения x(t) удовлетворяет

условиям:

1) ∥x(t)∥ → 0 при t → ∞;

2) ∥x(t)∥ ≤ γ при t ∈ [0, ∞).

При этом вектор-функция x(t) определяется как решение следующей нестационарной сис-

темы с кусочно-постоянными коэффициентами:

x = Aσ(t)x + bσ(t)u(x), x(0) = x₀, σ ∈ S_τ.

Далее для векторов будем рассматривать норму ∥x∥ = max|xi|, а для матриц - норму ∥A∥ =

∑

= max

|a_ij |.

Известные подходы к решению сформулированной выше задачи стабилизации можно раз-

бить на две группы. К первой группе относятся методы, предполагающие построение единого

регулятора для семейства динамических систем, включающего все различные режимы (A_i, b_i)

переключаемой системы (1). Фактически в этом случае речь идет о нахождении одновременно

стабилизирующего регулятора для конечного семейства линейных систем. При этом данный

регулятор должен обеспечивать не только устойчивость каждого режима системы (1), но и

устойчивость траекторий этой системы при любом переключающем сигнале из множества

S_τ . Одним из наиболее известных методов, позволяющих синтезировать подобные регулято-

ры, является метод квадратичной стабилизации [1, с. 49], основанный на поиске регулятора

в форме статической линейной обратной связи, обеспечивающий существование общей функ-

ции Ляпунова для системы (1), замкнутой этим регулятором. Популярность данного подхода

1548

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ НЕЙРОРЕГУЛЯТОРА

1549

обусловлена возможностью сведения задачи синтеза такого регулятора к задаче поиска реше-

ний системы линейных матричных неравенств, которая, в свою очередь, допускает численное

решение. Также можно отметить метод сверхстабилизации [2], предполагающий поиск единой

статической обратной связи и обеспечивающей свойство сверхустойчивости для всех замкну-

тых режимов системы (1). В этом случае поиск стабилизатора может быть сведён к решению

задачи линейного программирования [3]. Отметим, что упомянутые методы имеют свои до-

стоинства и недостатки. К достоинствам можно отнести тот факт, что регуляторы, найденные

в соответствии с методом квадратичной стабилизации или методом сверхстабилизации, на са-

мом деле решают более общую задачу, а именно, обеспечивают устойчивость переключаемой

системы при произвольных переключениях (когда отсутствует ограничение снизу на время пе-

реключений для различных режимов). С другой стороны, с увеличением количества режимов

шансы на нахождение единого регулятора существенно уменьшаются, поскольку его существо-

вание становится связанным с разрешимостью линейных неравенств большой размерности.

Качественно другой подход к решению поставленной задачи заключается в построении

регулятора переменной структуры (переключаемого регулятора)

u = u_σ(x),

(2)

каждый режим которого является стабилизирующей обратной связью u = u_i(x) для i-го

режима x = A_ix + b_iu переключаемой системы (1), т.е. обеспечивает асимптотическую устой-

чивость замкнутой системы

x = A_ix + b_iu_i(x).

(3)

Отметим, что в предположении полной управляемости пары (A_i, b_i) стабилизирующую об-

ратную связь для каждого режима системы (1) можно искать в форме линейной статической

обратной связи u = -k_ix. Известно [4, с. 249], что такая обратная связь всегда существует

как решение задачи модального управления.

Таким образом, система (1), замкнутая регулятором (2), будет иметь вид

x = A_σx + b_σu_σ(x), σ ∈ S_τ.

Укажем теперь две основные проблемы, которые необходимо решать для обеспечения ра-

ботоспособности указанного выше регулятора переменной структуры. Первая состоит в том,

что для реализации указанного регулятора необходимо знать моменты переключения режи-

мов и номера активных режимов в каждый момент времени, для того чтобы обеспечить син-

хронность переключений регулятора. Но, как правило, такая информация о переключаемой

системе в режиме реального времени недоступна. Вторая проблема заключается в том, что

устойчивость каждого режима (3) переключаемой системы в отдельности не является доста-

точным условием устойчивости самой переключаемой системы (1).

Одно из возможных решений первой проблемы, позволяющее использовать данный регу-

лятор, заключается в построении наблюдателя переключающего сигнала (в дальнейшем бу-

дем называть его просто наблюдателем), который определял бы номер активного режима

для текущего момента времени, что, в свою очередь, позволило бы обеспечить синхронность

переключения регулятора с переключениями режимов. Учитывая известные оценки времени

задержки τ для обеспечения устойчивости переключаемой системы c устойчивыми режимами

(см., например, [5, с. 56; 6; 7]), решение второй проблемы естественно искать, используя эти

оценки при построении регуляторов (2).

2. Подход к решению. В настоящей работе исследуются теоретические аспекты решения

задачи из п. 1 на основе нейросетевого подхода, который заключается в том, что в качестве

упомянутого выше наблюдателя режимов предлагается использовать нейронную сеть [8, с. 55].

Можно считать, что выходом такой нейросети является оценка σ(t) недоступного для изме-

рения переключающего сигнала. При этом регулятор переменной структуры ищем в виде

u = -k_σx,

(4)

где σ(t) - оценка переключающего сигнала, σ(t) ∈ {1, . . . , m}, а векторы k_i ∈ Rⁿ выбираются

из условий устойчивости матриц A_i - b_ik_i.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

1550

ФУРСОВ, МОСОЛОВА

Пару - переключаемый регулятор и нейронную сеть - далее будем называть нейрорегуля-

тором. Систему (1), замкнутую нейрорегулятором, можно представить переключаемой систе-

мой следующего вида:

x = (A_σ - b_σk_σ)x, σ ∈ S_τ,

σ ∈ [S]εp,

(5)

где ε_p = τ/p - достаточно малая положительная константа, p ∈ N - некоторый фиксиро-

ванный параметр алгоритма наблюдения, [S]εp - множество переключающих сигналов, для

которых моменты переключений принадлежат множеству {lε_p}, l = 0, 1, 2, . . . Перенумеруем

(от 1 до m²) все возможные режимы

x = (A_i - b_ik_j)x (i,j = 1,m)

переключаемой системы (5), присвоив каждому (ij)-му режиму соответствующий номер s =

= (i - 1)m + j. Введём функцию ξ : {1, . . . , m²} → {1, . . . , m}, отображающую каждый номер

s в соответствующий ему индекс i, т.е. ξ(s) = i.

Работа нейронной сети в качестве наблюдателя переключающего сигнала осуществляется

в процессе функционирования системы и состоит в следующем: для заданной дискретной по-

следовательности моментов времени lε_p , l = 0, 1, 2, . . . , по каждой паре измерений вектора

состояния (x(lε_p), x((l + 1)ε_p)) нейронная сеть должна определять номер s текущего режима

переключаемой системы (5) в момент t = (l + 1)ε_p. Обозначим выход нейросети в момент

lε_p через N[lε_p]. На основе данной информации оценка σ[lε] переключающего сигнала σ(t)

строится следующим образом:

σ(t) ≡ ξ(N[lε_p]) при t ∈ [lε_p, (l + 1)ε_p), l = 1, 2, . . .

(6)

В результате переключение векторов k_i стабилизирующей обратной связи задаёт переключа-

ющий сигнал (6) с некоторым заданным начальным условием σ(0) = σ₀

(σ₀ ∈ {1,... ,m }).

Описанный наблюдатель далее будем обозначать через Nεp .

Таким образом, основная задача функционирования нейронной сети состоит в построении

оценки σ неизвестного переключающего сигнала σ ∈ Sτ . Дискретную ошибку оценивания

e_σ[lτ] (l = 0,1,2,...) сигнала σ(t) определим по формуле

e_σ[lτ] = max

μ(i+1)τiτ ,

i=0,l-1

где μ(i+1)τiτ - количество промежутков вида [jε_p, (j + 1)ε_p) ⊂ [iτ, (i + 1)τ], для которых σ(t) ≡

≡ σ(jε_p). Заметим, что такой выбор ошибки e_σ[lτ] удобен для дальнейшего оценивания

окрестности положения равновесия (см. п. 5), используемой для формирования обучающей

выборки для нейросетевого наблюдателя.

Можно выделить несколько основных шагов настройки нейрорегулятора:

1) выбор структуры нейросети;

2) выбор регуляторов u = -k_ix, обеспечивающих достаточно быстрое затухание переход-

ных процессов замкнутых режимов переключаемой системы с учётом времени задержки τ;

3) выбор величины ε_p c учётом ограничений на ошибку оценивания и времени задержки τ;

4) расчёт величины γ (см. условие задачи в п. 1) с учётом ограничений на ошибку оцени-

вания и размера окрестности D(0; γ);

5) построение обучающей выборки для нейросети с учётом величины γ;

6) обучение нейросети на промежутке [0, ε_p];

7) проверка работоспособности нейросети по определению текущего активного режима;

8) моделирование переключаемой системы (1), замкнутой построенным нейрорегулятором.

Далее обсуждаются теоретические вопросы, связанные с настройкой и работоспособностью

нейрорегулятора. К ним относятся, главным образом, задачи, сформулированные в перечис-

ленных выше пп. 2)-5).

3. Выбор режимов переключаемого регулятора. Построение стабилизирующего ре-

гулятора переменной структуры для системы (1) в случае ненаблюдаемых переключающих

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ НЕЙРОРЕГУЛЯТОРА

1551

сигналов включает два основных шага: построение стабилизирующих регуляторов для каж-

дого режима в отдельности и настройка алгоритма их переключений. Рассмотрим первый

шаг. Как было указано выше, необходимым условием устойчивости переключаемой системы

является асимптотическая устойчивость каждого её режима. К сожалению, это условие не яв-

ляется достаточным и требует усиления в зависимости от класса допустимых переключающих

сигналов. Поскольку в работе рассматривается случай медленных переключений с заданным

временем задержки τ, то при синтезе регулятора переменной структуры, при построении ста-

билизаторов для каждого режима системы (1) можно использовать подход, основанный на

достаточном условии устойчивости переключаемых линейных систем, сформулированный в

работе [7].

Итак, в предположении полной управляемости пар (A_i, b_i), i = 1, m, для каждого режима

x=A_ix+b_iu

построим обратную связь u = -k_ix, обеспечивающую простой вещественный и устойчивый

спектр матрицы замкнутой системы

x = (A_i - b_ik_i)x,

(7)

т.е. Spec (A_i - b_ik_i) ⊂ R_- и для любых s_j, s_m ∈ Spec (A_i - b_ik_i) следует, что s_j = s_m.

В этом случае для нормы вектора решения системы (7) можно записать [9, с. 57] следую-

щую оценку:

∥x(t)∥ ≤ ∥eΛii(t-s)∥ · ∥x(s)∥ ≤ c_iieαii(t-s)∥x(s)∥, t ≥ s ≥ 0,

где

Λ_ii = A_i - b_ik_i, α_ii =

max

λ^ik < 0, c_ii = ∥M-1ii∥ · ∥M_ii∥.

λ^ik∈Spec {Λ_ii}

Здесь M_ii - матрица преобразования, приводящая матрицу Λ_ii к диагональному виду J_ii =

= diag {λi1,... ,λⁱⁿ}, т.е.

J_ii = M-1iiΛ_iiM_ii.

Заметим, что столбцами матриц M_ii являются собственные векторы соответствующих мат-

риц Λ_ii.

Обозначим

α = max

α_ii, c = max c_ii.

i=1,m

В соответствии с достаточным условием устойчивости [7] переключаемая система с режимами

(7) является устойчивой при любых переключающих режимах из множества S_τ , если

2 ln c

τ >

(8)

|α|

Для выполнения условия (8) можно рекомендовать строить регуляторы u = -k_ix, обес-

печивающие достаточно большую величину α, что всегда возможно в силу предположения о

полной управляемости пар (A_i, b_i). Известно, как правило, что c = O(|α|n-1).

4. Квантование времени работы наблюдателя переключающего сигнала. Как уже

отмечалось выше, основная проблема при реализации регулятора переменной структуры сос-

тоит в том, что для его работоспособности нужна информация о текущем переключающем

сигнале, что позволит обеспечить синхронность переключения режимов регулятора с пере-

ключениями режимов системы, и если переключающий сигнал недоступен для измерения, то

необходимо использовать наблюдателя для оценки текущего значения переключающего сигна-

ла. Выше (см. п. 2) был определён наблюдатель, работающий на основе нейросети. Фактически

данный наблюдатель представляет собой дискретную систему, выход которой управляет пере-

ключением режимов регулятора переменной структуры. В идеале режимы регулятора должны

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

1552

ФУРСОВ, МОСОЛОВА

переключаться синхронно с переключениями режимов системы (1). Однако моменты переклю-

чений системы (1), обусловленные переключающими сигналами σ ∈ S_τ , совершенно не обя-

зательно должны совпадать с дискретной последовательностью {lε} моментов срабатывания

нейросети. В результате этого могут возникать ошибки нейросети в определении номера актив-

ного режима замкнутой системы (5), что, в свою очередь, влечёт за собой неверное включение

очередного режима регулятора. Более того, нельзя исключать и того факта, что нейросеть мо-

жет самопроизвольно выдавать ошибочное значение активного режима. Достаточно полную

информацию о корректности работы нейросети содержит введённая выше ошибка оценивания

переключающего сигнала e_τ [lτ], на основе которой ниже будет сформулировано достаточное

условие устойчивости переключаемой системы (1), замкнутой нейрорегулятором (4), (6).

Далее потребуется следующая лемма, доказательство которой аналогично рассуждениям

теоремы 6 работы [7].

Лемма. Пусть для системы

x = A_σx, σ ∈ S_τ,

(9)

существуют константы d > 1 и q > 0 такие, что для любого переключающего сигнала

σ ∈ S_τ и начального условия x(0) ∈ Rⁿ для соответствующего решения x(t) справедливы

неравенства:

1) ∥x((i + 1)q)∥ < ∥x(iq)∥/d для всех i = 0, 1, . . . ;

2) ∥x(t)∥ < ∥x(iq)∥ для всех t ∈ [(i + 1)q, (i + 2)q], i = 0, 1, . . .

Тогда для любого начального условия x(0) ∈ Rⁿ и любого переключающего сигнала σ ∈ S_τ

норма соответствующего решения системы (9) стремится к нулю, т.е.

∥x(t)∥ → 0, t → ∞.

Далее будем использовать обозначение

Λ_ij = A_i - b_ik_j, i,j = 1,m.

Пусть J_ij - жорданова нормальная форма для Λ_ij, а M_ij - матрица, приводящая Λ_ij к

соответствующей жордановой форме J_ij . Положим

α_ij =

max

Re (λ(ij)k).

λ(ij)∈Spec Λij

Для систем

x = (A_i - b_ik_j)x, i = j,

можно записать следующие оценки для норм решений [8]

∥x(t)∥ ≤ ∥eΛij (t-s)∥∥x(t)∥ ≤ c_ij eαij (t-s)P_ij(t - s)∥x(t)∥,

∑rij-1

здесь c_ij = ∥M-1ij∥∥M_ij ∥, P_ij (t) =

(t^k/k!), r_ij - размер максимальной клетки Жордана

k=0

в жордановой нормальной форме J_ij матрицы Λ_ij .

Обозначим

ρ = max

α_ij, β = max

c_ij,

r = max

r_ij.

i,j=1,m

i=j

Без ограничения общности будем считать, что ρ > 0.

Сформулируем теперь достаточное условие устойчивости замкнутой системы (5).

Теорема 1. Пусть для замкнутой системы (5) при любом переключающем сигнале σ ∈

∈ S_τ и любом начальном условии x(0) ∈ Rⁿ наблюдатель Nεp генерирует оценку σ ∈ [S]εp

с ошибкой, удовлетворяющей условию

e_σ[lτ] ≤ θ, l = 1,2,... ,

для некоторого θ ∈ N,

0 ≤ θ ≤ [p/2].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ НЕЙРОРЕГУЛЯТОРА

1553

Тогда, если

τ >

где h = cθ+2β^θP^θ(ε_p)e(ρ-α)θεp , для любого начального условия x(0) ∈ Rⁿ и любого переключа-

ющего сигнала σ ∈ S_τ норма соответствующего решения системы (5) стремится к нулю:

∥x(t)∥ → 0, t → ∞.

Доказательство. Прежде всего заметим, что h > 1, а из определения наблюдателя Nεp

следует, что θ ≥ 1. Далее, в силу условия теоремы на каждом отрезке [iτ, (i + 1)τ], i =

= 0, 1, . . . , максимальное число промежутков [lε_p, (l + r)ε_p) (l ∈ N

^⋃ {0}, r ∈ N), на которых

σ(t) ≡ σ[lε_p], не более θ (при этом для каждого l число r фактически равно количеству “скле-

енных” промежутков длины ε_p, на которых выполнено указанное тождество), максимальное

число промежутков вида [lε_p, (l + r)ε_p) (l ∈ N

^⋃ {0}, r ∈ N), на которых σ(t) ≡ σ[lε_p], не

более θ + 1 и не более одного промежутка вида [lε_p, (l + 1)ε_p), содержащего точку разрыва

переключающего сигнала σ(t) (соответственно на таком промежутке σ(t) ≡ σ[lε_p]). Заметим,

что для всех l ∈ N

^⋃ {0} верны следующие неравенства:

∥x((l + 1)ε_p)∥ ≤ c∥x(lε_p)∥eαεp , если σ(t) ≡ σ[lε_p],

∥x((l + 1)ε_p)∥ ≤ β∥x(lε_p)∥P (ε_p)eρεp , если σ(t) ≡ σ[lε_p],

(10)

а если σ(t) ≡ σ[lε_p] на промежутке [lεp, (l + 1)εp), внутри которого лежит точка разрыва

переключающего сигнала σ(t), то справедлива оценка

∥x((l + 1)ε_p)∥ ≤ cβP (ε_p)eρεp ∥x(lε_p)∥.

(11)

Из неравенств (10) и (11) нетрудно получить следующую оценку для решений системы (5):

∥x((i + 1)τ)∥ ≤ h∥x(iτ)∥e^ατ , i = 0, 1, . . .

(12)

Учитывая, что α < 0, в силу условия теоремы получаем цепочку неравенств

τ >

ln h-1, ατ < ln h-2, e^ατ < h-2,

∥x(iτ)∥e^ατ < h-2∥x(iτ)∥,

откуда

h²∥x(iτ)∥e^ατ < ∥x(iτ)∥.

(13)

Далее из (12) и (13) имеем

h∥x((i + 1)τ)∥ ≤ h²∥x(iτ)∥e^ατ < ∥x(iτ)∥.

Отсюда окончательно получаем

∥x((i + 1)τ)∥ <

∥x(iτ)∥, i = 0, 1, . . .

(14)

Таким образом, показано, что для замкнутой системы (5) выполнен п. 1) леммы при q = τ,

d = h. Докажем теперь, что для этой системы выполняется также и п. 2) леммы.

Действительно, зафиксируем произвольное t ∈ [(i+1)τ, (i+2)τ], i = 0, 1, . . . , и рассмотрим

два случая.

1) Пусть t ∈ [lε_p, (l + 1)ε_p) ⊂ [(i + 1)τ, (i + 2)τ] и на этом промежутке σ(t) ≡ σ[lε_p]. Далее,

пусть на отрезке [(i + 1)τ, (i + 2)τ] левее t располагается κ промежутков вида [lε_p, (l + 1)ε_p),

для которых σ(t) ≡ σ[lε_p] и r промежутков такого же вида, где σ(t) ≡ σ[lε_p]. Тогда, учитывая

(10) и (11), получаем оценку

∥x(t)∥ ≤ cr+1β^κP^κ(ε_p)e(ρ-α)κεp c∥x((i + 1)τ)∥eα(t-(i+1)τ).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

1554

ФУРСОВ, МОСОЛОВА

Поскольку eα(t-(i+1)τ) < 1, то справедливо неравенство

∥x(t)∥ ≤ cr+2β^κP^κ(ε_p)e(ρ-α)κεp ∥x((i + 1)τ)∥.

(15)

Отсюда, учитывая (14), получаем

∥x(t)∥ ≤ cr+2β^κP^κ(ε_p)e(ρ-α)κεp c∥x((i + 1)τ)∥ <

cr+2β^κP^κ(ε_p)e(ρ-α)κεp

< cr+2β^κP^κ(ε_p)e(ρ-α)κεp

∥x(i)τ)∥ =

∥x(i)τ)∥.

cθ+2β^θP^θ(ε_p)e(ρ-α)θεp

В силу того, что в рассматриваемом случае r ≤ θ, κ ≤ θ, дробь в последнем неравенстве не

превосходит единицы и тогда окончательно имеем

∥x(t)∥ < ∥x(iτ)∥.

(16)

2) Пусть теперь t ∈ [lε_p, (l + 1)ε_p) ⊂ [(i + 1)τ, (i + 2)τ] и на этом промежутке σ(t) ≡

≡ σ[lε_p]. Также, как и в случае 1), пусть на отрезке [(i + 1)τ,(i + 2)τ] левее t располагается

κ промежутков вида [lε_p, (l + 1)ε_p), для которых σ(t) ≡ σ[lε_p] и r промежутков такого же

вида, где σ(t) ≡ σ[lε_p]. Тогда, рассуждая как и в случае 1) и учитывая (10) и (11), получаем

оценку

∥x(t)∥ ≤ cr+1β^κP^κ(ε_p)e(ρ-α)κεp βP (ε_p)∥x((i + 1)τ)∥eρ(t-(i+1)τ) ≤

≤ cr+1βκ+1Pκ+1(ε_p)e(ρ-α)(κ+1)εp∥x((i + 1)τ)∥.

(17)

Отсюда с учётом (14) имеем

∥x(t)∥ ≤ cr+1βκ+1Pκ+1(ε_p)e(ρ-α)(κ+1)εp ∥x((i + 1)τ)∥ <

cr+1βκ+1Pκ+1(ε_p)e(ρ-α)(κ+1)εp

< cr+1βκ+1Pκ+1(ε_p)e(ρ-α)(κ+1)εp

∥x(iτ)∥ =

∥x(iτ)∥.

cθ+2β^θP^θ(ε_p)e(ρ-α)θεp

В силу того, что в рассматриваемом случае r ≤ θ, κ + 1 ≤ θ, дробь в последнем неравенстве

не превосходит единицы, и в случае 2) также имеет место неравенство (16).

Таким образом, получили, что при выполнении условий теоремы 1 выполняются условия

леммы, а тогда для любого начального условия x(0) ∈ Rⁿ и любого переключающего сигнала

σ ∈ S_τ норма соответствующего решения замкнутой системы (5) стремится к нулю. Теорема 1

доказана.

5. Оценка окрестности положения равновесия для формирования обучающей

выборки. Как было отмечено в п. 2, задача нейросети состоит в том, чтобы по каждой паре

измерений вектора состояния (x(lε_p), x((l + 1)ε_p)) нейронная сеть определяла бы номер s

текущего режима переключаемой системы (5) в момент t = (l + 1)ε_p. Причём считаем, что

эту задачу нейросеть должна правильно решать в предположении, что на рассматриваемом

отрезке [lε_p, (l + 1)ε_p] отсутствуют точки разрыва сигнала σ(t). И поскольку в этом случае

на таких отрезках будет активен один из линейных стационарных режимов системы (5), то

x((l + 1)ε_p) = x(ε_p), если x(lε_p) = x(0). Таким образом, нейронную сеть достаточно обучить

на векторах вида (x(0), x(ε_p)), построенных для всех возможных режимов системы (5). При

этом необходимо решить вопрос об окрестности нуля, по которой будет строиться выборка для

обучения нейросети. В качестве таковой можно выбрать окрестность D(0; γ) (см. постановку

задачи в п. 1). Следующая теорема даёт оценку величины γ по заданной ошибке оценивания

переключающего сигнала e_σ[lτ].

Теорема 2. Пусть выполнены условия теоремы 1. Тогда при любом начальном условии

x(0) ∈ D(0; γ) и любом переключающем сигнале σ ∈ S_τ выполнено неравенство

∥x(t)∥ ≤ γ, t ∈ [0, +∞),

где

γ = hγ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ НЕЙРОРЕГУЛЯТОРА

1555

Действительно, если выполнены условия теоремы 1, то из полученных в ходе её доказа-

тельства неравенств (14) и (16) следует, что для любого переключающего сигнала σ ∈ S_τ и

начального условия x(0) ∈ Rⁿ для соответствующего решения x(t) справедливы неравенства:

1) ∥x((i + 1)τ)∥ < ∥x(iτ)∥/h для всех i = 0, 1, . . . ;

2) ∥x(t)∥ < ∥x(iτ)∥ для всех t ∈ [(i + 1)τ, (i + 2)τ], i = 0, 1, . . .

Из этих неравенств следует, что для расчёта величины γ достаточно оценить наибольшее

значение нормы вектора x(t) на промежутке [0, τ]. Учитывая оценки (15) и (17), получаем

∥x(t)∥ ≤ cθ+2β^θP^θ(ε_p)e(ρ-α)θεp ∥x(0)∥ ≤ hγ

при всех t ∈ [0, τ]. Теорема доказана.

6. Численное моделирование. Полученные результаты продемонстрируем на численном

примере. Рассмотрим задачу стабилизации (см. п. 1) для переключаемой линейной системы

x = A_σx + b_σu, σ ∈ S_τ, σ(t) ∈ I = {1,2,3},

(18)

где

(

)

(

)

(

)

(

)

(

)

(

)

-2

-1

A₁ =

b₁ =

A₂ =

b₂ =

A₃ =

b₃ =

−1

-1

-2

Считаем, что τ = 1, γ = 2.

Стабилизирующий регулятор для системы (18) ищем в виде

u = -k_σx,

σ(t) ∈ {1, 2, 3}.

(19)

)

Используя рассуждения п. 3, выберем следующие значения k_i : k₁ =

⁽-0.4

-0.1

, k₂ =

)

⁽-0.2

0.3

, k₃ =

⁽-1.4

-1.8

. Пусть p = 20, тогда ϵ_p = 0.05. В качестве наблюдателя

Nεp выберем обобщённую регрессионную двухуровневую нейронную сеть. При условии, что

наблюдатель Nεp генерирует оценку

σ ∈ [S]εp с ошибкой e_σ[lτ] ≤ 1 (априорная ошибка

θ = 1), рассчитаем величины h, γ в соответствии с результатами пп. 4, 5: h = 24.3, γ = 68.9.

Далее с использованием величины γ осуществляется обучение нейросети с помощью функции

newgrnn пакета Matlab.

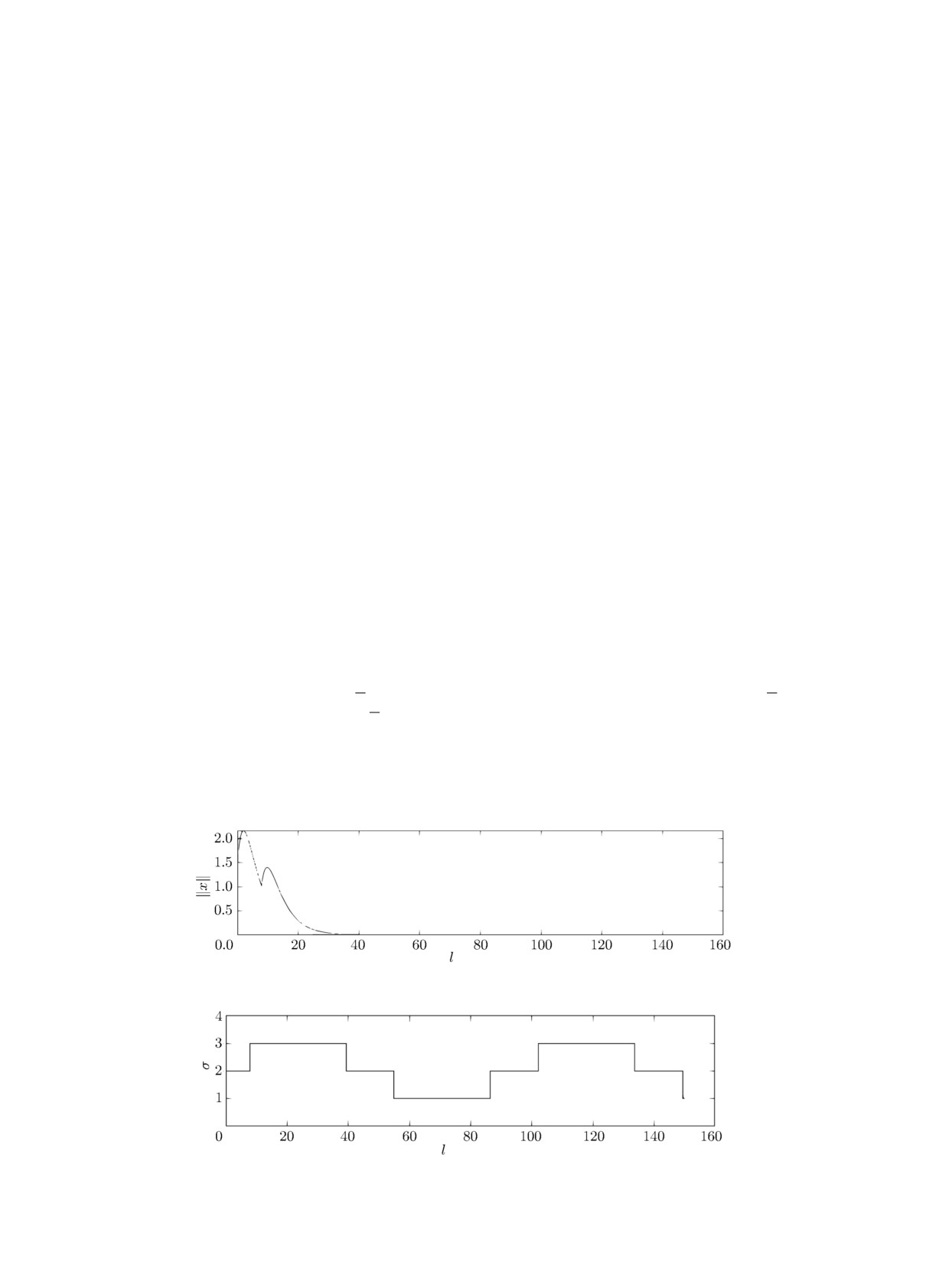
На рис. 1 представлены результаты численного моделирования в пакете Matlab решения

замкнутой системы (18), (19) при начальных условиях x₁(0) = 1.5, x₂(0) = 1 и некотором

переключающем сигнале σ (рис. 2).

Рис. 1. Поведение нормы решения замкнутой системы.

Рис. 2. Переключающий сигнал.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022

8^∗

1556

ФУРСОВ, МОСОЛОВА

Моделирование проведено для t ∈ [0, 150]. Его результаты показали, что апостериорная

ошибка наблюдателя равна также единице, а норма решения стремится к нулю, что подтвер-

ждает работоспособность построенного стабилизатора.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 22-21-

00162).

СПИСОК ЛИТЕРАТУРЫ

1. Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных матричных неравенств.

М., 2007.

2. Поляк Б.Т., Щербаков П.С. Сверхустойчивые линейные системы управления. I. Анализ // Автома-

тика и телемеханика. 2002. № 8. С. 37-53.

3. Фурсов А.С., Мосолова Ю.М., Миняев С.И. Цифровая сверхстабилизация переключаемой интер-

вальной линейной системы // Дифференц. уравнения. 2020. Т. 56. № 11. С. 1516-1527.

4. Андреев Ю.Н. Управление конечномерными линейными объектами. М., 1976.

5. Liberzon D. Switching in Systems and Control. Boston, 2003.

6. Фурсов А.С., Хусаинов Э.Ф. К вопросу о стабилизации переключаемых линейных систем // Диф-

ференц. уравнения. 2015. Т. 51. № 11. C. 1522-1533.

7. Фурсов А.С., Хусаинов Э.Ф. Сверхстабилизация линейных динамических объектов при действии

операторных возмущений // Дифференц. уравнения. 2014. Т. 50. № 7. C. 865-876.

8. Хайкин С. Нейронные сети. М., 2006.

9. Демидович Б.П. Лекции по математической теории устойчивости. М., 1967.

Электротехнический университет, г. Ханчжоу, Китай,

Поступила в редакцию 31.05.2022 г.

Московский государственный университет

После доработки 21.07.2022 г.

имени М.В. Ломоносова,

Принята к публикации 15.08.2022 г.

Институт проблем передачи информации

имени А.А. Харкевича, г. Москва

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№ 11

2022