ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 2, с.164-173

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.925.52

УСЛОВИЯ СУЩЕСТВОВАНИЯ ЦИКЛОВ У ОДНОЙ

СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Рассматривается дифференциальная система третьего порядка, представляющая собой

обобщение системы, описывающей математическую модель явления фазовой синхрони-

зации. Получены достаточные условия существования у этой системы седлового цикла

первого рода. Доказательство условий основывается на построении положительно инвари-

антного тороидального множества с использованием двух цилиндрических поверхностей,

границы которых определяются предельными циклами дифференциальной системы вто-

рого порядка.

DOI: 10.31857/S0374064122020030

Введение. В настоящей работе рассматривается система дифференциальных уравнений

x = Ax + bϕ(σ),

σ = c^тx + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ,

(1)

где x ∈ R², σ ∈ R - фазовые переменные, точка над символом - производная по времени t,

векторы b, c ∈ R², числа u ∈ [0, 1] и α₁, ρ₁, ρ₀ ∈ R и постоянная 2 × 2-матрица A заданы, за-

данная функция ϕ(σ) является непрерывной и Δ-периодической. При выполнении равенства

u = 0 система (1) является математической моделью системы фазовой синхронизации с филь-

тром, имеющим дробно-рациональную частотную характеристику с запаздыванием [1-14]. За-

паздывание в системе фазовой автоподстройки определяется значением параметра ρ = ρ₁ +

+ρ₀ > 0, при отсутствии запаздывания значение ρ равно нулю [1, 12]. В случае ρ = 0, u = 0

изучению системы фазовой автоподстройки посвящены многочисленные работы [1-14]. Для

системы (1) рассматривается задача определения седловых и устойчивых предельных циклов

первого рода [1, 4, 5, 10-13]. Наличие предельных циклов обеспечивает для системы фазовой

синхронизации существование режимов скрытой квазисинхронизации и мультистабильности.

При этом скрытая квазисинхронизация определяется скрытыми предельными циклами, для

∫_T

которых 〈 σ〉 = T-1

σ(t) dt = 0 [5-7, 9, 12].

В данной работе на основе метода нелокального сведения [1-5] с использованием резуль-

татов работ [10, 11] получены достаточные условия существования нескольких предельных

циклов первого рода у системы (1).

1. Условия существования седлового цикла системы.

Теорема 1. Пусть для системы (1) выполняются следующие предположения:

1) верно неравенство c^тb = -Γ < 0, а вектор l, задаваемый равенством l^т = c^тA, линей-

но независим с вектором c и имеют место соотношения: l^тb = -ν₁, l^тA = -α₁l^т - β₁c^т,

где β₁ > 0 и ν₁β-11 = ρ₁;

2) Δ-периодическая функция ϕ(σ) имеет на отрезке [0, Δ] два нуля σ₁ и σ₂, в кото-

рых её производная удовлетворяет неравенствам dϕ(0)/dσ > 0 и dϕ(σ₂)/dσ < 0, а сама

производная dϕ(σ)/dσ на отрезке [0,Δ] ограничена;

3) существуют положительные числа λ₁, λ₂ и r₁, при которых система дифференци-

альных уравнений второго порядка

y = -λ₁y - λ₂σ - Γϕ(σ) - ε,

σ = y + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ

(2)

при ε = -ε-1 таком, что r₁ < ε-1, имеет решение, определяющее функцию f-1(σ), неполо-

жительную на некотором отрезке [-σ₁, σ₂], где σ₁ > 0, σ₂ > 0, и обращающуюся в нуль

только в его концах;

164

УСЛОВИЯ СУЩЕСТВОВАНИЯ ЦИКЛОВ

165

4) существует положительное число r₂, для которого система (2) при ε = ε⁺¹ таком,

что ε⁺¹ > r₂, имеет решение, определяющее неотрицательную на отрезке [0, σ₂] функцию

f⁺¹¹(σ), равную нулю только в точке σ₂, и неотрицательную на отрезке [-σ₁,0] функцию

f⁺¹²(σ), равную нулю только в точке -σ₁, причём f⁺¹²(0) < f⁺¹¹(0);

5) система (2) при ε = ε-2 таком, что r₂ < ε-2, имеет решение, определяющее на неко-

тором отрезке [-σ₃,σ₄], где -σ3 < -σ1 и σ2 < σ4, функцию f-2(σ), обращающуюся в

нуль в концах этого отрезка и удовлетворяющую неравенству f-2(σ) < f-1(σ) на интервале

(-σ₁, σ₂);

6) система (2) при ε = -ε⁺² таком, что r₁ < ε⁺², имеет решение, определяющее на от-

резке [0,σ₄] функцию f⁺²¹(σ), обращающуюся в нуль в точке σ₄ и удовлетворяющую нера-

венству f⁺²¹(σ) > f⁺¹¹(σ) на полуинтервале [0, σ₂), и на отрезке [-σ3, 0] функцию f+22(σ),

обращающуюся в нуль в точке -σ₃ и удовлетворяющую неравенству f⁺²²(σ) > f⁺¹²(σ) на

полуинтервале [-σ₁, 0), причём f⁺²²(0) > f⁺²¹(0);

7) для всех σ ∈ [-σ₃, -σ₁] справедливо неравенство λ₂σ + r₂ + Γϕ(σ) < 0;

8) имеет место равенство λ₂ = β₁ + λ₁(λ₁ - α₁), и для значений σ ∈ [-σ₃,σ₄] выполня-

ется неравенство

ψ₁(σ) = (λ₂ρ₁ - ν₁ - λ₁Γ + λ₂ρ₀(1 - u))ϕ(σ) - λ₂(α₁u + λ₁ - α₁)σ - (α₁ - λ₁)r₁ < 0;

9) для любого σ ∈ [-σ₃, σ₄] справедливо неравенство

ψ₂(σ) = (λ₂ρ₁ - ν₁ - λ₁Γ + λ₂ρ₀(1 - u))ϕ(σ) - λ₂(α₁u + λ₁ - α₁)σ + (α₁ - λ₁)r₂ > 0;

10) если для функции

ψ₄(σ) = Γϕ(σ) - λ₁ψ₃(σ) + λ₂σ,

где ψ₃(σ) = ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ, при некотором значении σ выполняются нера-

венства -r₂ < ψ₄(σ) < r₁, то справедливо включение σ ∈ [-τ₂, τ₁], где τ₁ > 0, τ₂ > 0;

11) функция ψ₅(σ) = -α₁Γϕ(σ)-ν₁ϕ(σ)+β₁ψ₃(σ) на сегменте [-τ₂, τ₁]

^⋂ [-σ₃, σ₄] имеет

единственный нyль ψ₅(0) = 0.

Тогда система (1) имеет седловой предельный цикл первого рода.

Доказательство. Рассмотрим функции W_i(z) = l^тx + λ₁c^тx + λ₂σ + (-1)ⁱr_i, P (z) = c^тx,

V+1i(z) = c^тx - f+1i(σ), V+2i(z) = c^тx - f+2i(σ), V^-i(z) = c^тx - f^-i(σ), где i = 1,2, z = (x^т,σ)^т,

числа r₁, r₂, λ₁, λ₂ и функции f⁺¹¹(σ), f⁺¹²(σ), f-1(σ), f⁺²¹(σ), f⁺²²(σ), f-2(σ) удовлетворяют

условиям 3)-11) теоремы.

Используя значения σ₁, σ₂ из условия 3) теоремы, определим поверхности

∂Q₁₁ = {z : V⁺¹¹(z) = c^тx - f⁺¹¹(σ) = 0, σ ∈ [0,σ₂]},

∂Q₁₂ = {z : V⁺¹²(z) = c^тx - f⁺¹²(σ) = 0, σ ∈ [-σ₁,0]},

∂Q₂ = {z : V-1(z) = c^тx - f-1(σ) = 0, σ ∈ [-σ₁,σ₂]},

∂Q₀₁ = {z : f₀(σ) = σ = 0, f⁺¹²(0) ≤ c^тx ≤ f⁺¹¹(0)}.

Пусть ∂Q = ∂Q₁₁

^⋃∂Q12 ⋃ ∂Q2 ⋃∂Q₀₁, тогда ∂Q является цилиндрической поверхно-

стью. Обозначим внешность цилиндрической поверхности вместе с поверхностью ∂Q через Q.

Значения σ₃, σ₄ из условия 5) теоремы позволяют определить поверхности

∂D₂₁ = {z : V⁺²¹(z) = c^тx - f⁺²¹(σ) = 0, σ ∈ [0,σ₄]},

∂D₂₂ = {z : V⁺²²(z) = c^тx - f⁺²²(σ) = 0, σ ∈ [-σ₃,0]},

∂D₂ = {z : V-2(z) = c^тx - f-2(σ) = 0, σ ∈ [-σ₃,σ₄]},

∂Q₀₂ = {z : f₀(σ) := σ = 0, f⁺²¹(0) ≤ c^тx ≤ f⁺²²(0)}.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

166

МАМОНОВ и др.

Пусть ∂D = ∂D₂₁

^⋃∂D22 ⋃∂D2 ⋃ ∂D₀₂, тогда ∂D является цилиндрической поверхно-

стью. Обозначим внутренность цилиндрической поверхности ∂D вместе с поверхностью ∂D

через D. Используя области Q и D, определим множество

G=Q

^⋂D^⋂{z : W₁(z) ≤ 0}^⋂{z : W₂(z) ≥ 0}.

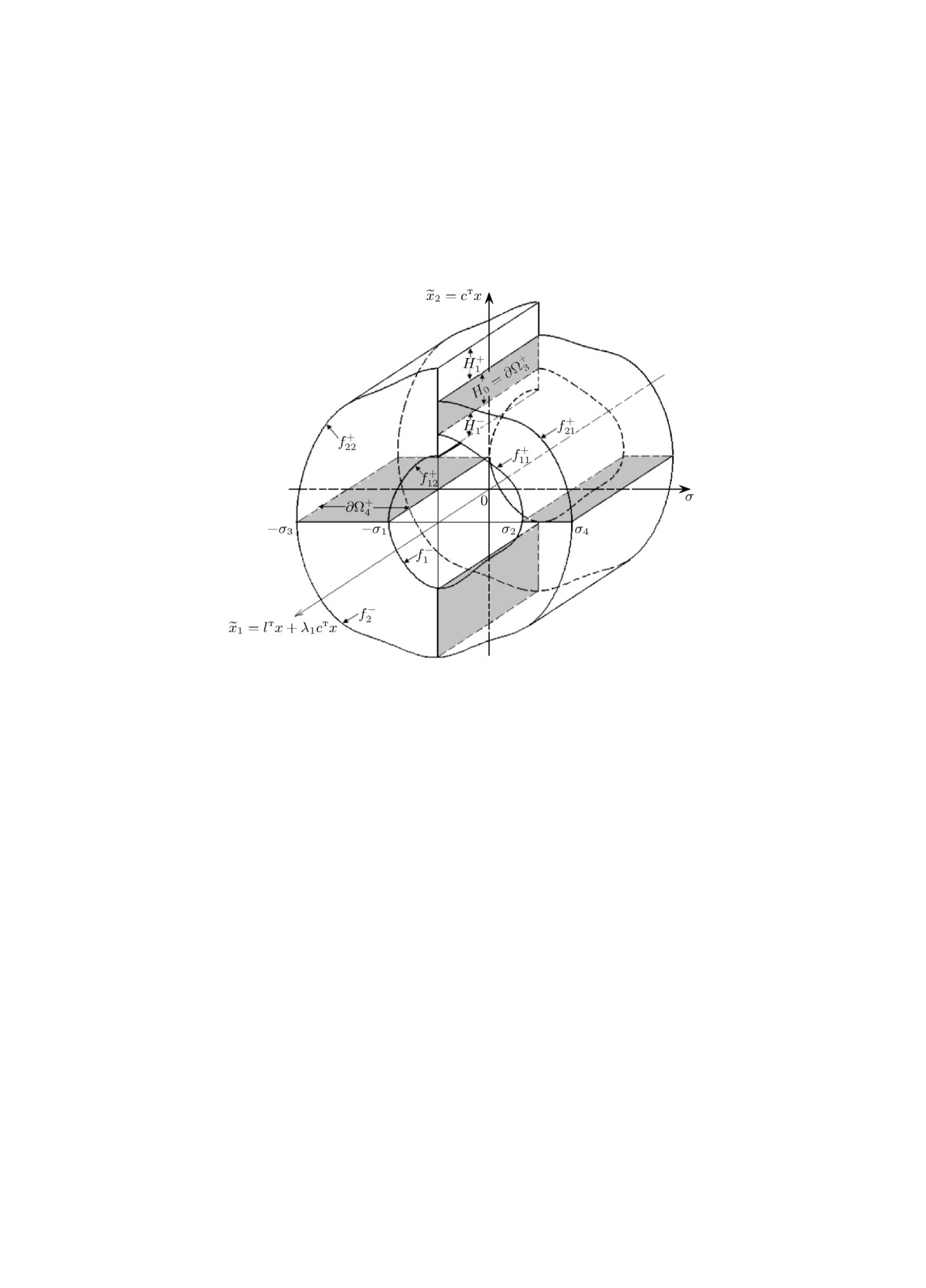
Строение множества G представлено на рис. 1.

Рис. 1. Множество G в координатах x1 = l^тx + λ1c^тx,

x2 = c^тx, σ.

Множество G представим в виде объединения G = G₁

^⋃G₂ множеств G₁ и G₂, где

G₁ = (G

^⋂ {z : c^тx ≤ 0})^⋃ (G^⋂ {z : c^тx ≥ 0, σ ≥ 0}),

G₂ = G

^⋂ {z : c^тx ≥ 0, σ ≤ 0}.

Рассмотрим множества G₁, L = {z : W₁ ≤ 0, W₂ ≥ 0},

∂Q₀₃ = {z : f₀(σ) = σ = 0, f⁺¹¹(0) ≤ c^тx ≤ f⁺²¹(0)},

∂Q₃ = {z : P(z) = c^тx = 0,-σ₃ ≤ σ ≤ -σ₁}.

Граница ∂G₁ множества G₁ определяется равенствами

∂G₁ = ∂Ω⁺¹

^⋃∂Ω⁺²⋃ ∂Ω⁺³⋃ ∂Ω⁺⁴⋃∂Ω-5⋃∂Ω-6⋃∂Ω-7⋃ ∂Ω⁺⁸,

∂Ω⁺¹ = ∂Q₁₁

^⋂L, ∂Ω+2 = ∂Q2

^⋂L, ∂Ω+3 = ∂Q03

^⋂L,

∂Ω⁺⁴ = ∂Q₃

^⋂L, ∂Ω-5 = ∂D21

^⋂L, ∂Ω-6 = ∂D2

^⋂L,

∂Ω-7 = G₁

^⋂ {z : W₁(z) = 0}, ∂Ω+8 = G1

^⋂ {z : W₂(z) = 0}.

Для вектора z ∈ ∂Ω⁺¹ справедливы соотношения

c^тx = f⁺¹¹(σ), σ ∈ [0,σ₂],

l^тx ≥ -r₂ - λ₁c^тx - λ₂σ.

(3)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

УСЛОВИЯ СУЩЕСТВОВАНИЯ ЦИКЛОВ

167

Используя эти соотношения и условия 1) и 4) теоремы, найдём и оценим снизу производную

функции V⁺¹¹(z) в силу системы (1) на множестве ∂Ω⁺¹:

df⁺¹¹(σ)

V+

(z) = l^тx - Γϕ(σ) -

(f⁺¹¹(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) ≥

dσ

df⁺¹¹(σ)

≥ -r₂ - λ₂σ - λ₁f⁺¹¹(σ) - Γϕ(σ) -

(f⁺¹¹(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) =

dσ

= -r₂ + ε⁺¹ > 0.

(4)

Для вектора z ∈ ∂Ω⁺² выполняются соотношения

c^тx = f-1(σ), σ ∈ [-σ₁,σ₂],

(5)

l^тx ≤ r₁ - λ₁c^тx - λ₂σ.

(6)

Найдём и оценим сверху производную функции V-1(z) в силу системы (1) на множестве ∂Ω⁺².

Используя соотношения (5), (6) и условия 1) и 3) теоремы, получаем

df-1(σ)

V-

(z) = l^тx - Γϕ(σ) -

(f-1(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) ≤

dσ

df-1(σ)

≤ r₁ - λ₂σ - λ₁f-1 (σ) - Γϕ(σ) -

(f-1(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) =

dσ

= r₁ - ε-1 < 0.

(7)

Найдём и оценим снизу производную функции f₀(σ) ≡ σ в силу системы (1) на множестве

∂Ω⁺³. Применяя условие 2) теоремы, будем иметь

0(σ) = c^тx + ρ1ϕ(0) + ρ0(1 - u)ϕ(0) - α1uσ = c^тx ≥

(0) > 0.

(8)

Рассмотрим множество ∂Ω⁺⁴. Если z ∈ ∂Ω⁺⁴, то справедливы оценка (3) и равенство

c^тx = 0, σ ∈ [-σ₃,-σ₁].

(9)

В силу условий 1) и 7) теоремы и соотношений (3), (9) заключаем, что производная функции

P (z) = c^тx в силу системы (1) удовлетворяет на множестве ∂Ω⁺⁴ соотношению

(z) = l^тx - Γϕ(σ) ≥ -r₂ - λ₂σ - Γϕ(σ) > 0.

(10)

Пусть z ∈ ∂Ω-5, тогда справедливы оценка (6) и равенство

c^тx = f⁺²¹(σ), σ ∈ [0,σ₄].

(11)

Используя соотношения (6), (11) и условия 1) и 6) теоремы найдём и оценим сверху производ-

ную функции V⁺²¹(z) в силу системы (1) на множестве ∂Ω-5:

df⁺²¹(σ)

V+

(z) = l^тx - Γϕ(σ) -

(f⁺²¹(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) ≤

dσ

df⁺²¹(σ)

≤ r₁ - λ₂σ - λ₁f⁺²¹(σ) - Γϕ(σ) -

(f⁺²¹(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) =

dσ

= r₁ - ε⁺² < 0.

(12)

Для множества ∂Ω-6 выполняется оценка (3) и равенство

c^тx = f-2(σ), σ ∈ [-σ₃,σ₄].

(13)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

168

МАМОНОВ и др.

Найдём и оценим снизу производную функции V-2(σ) в силу системы (1) на множестве ∂Ω-6.

Применяя соотношения (3), (13) и условия 1) и 5) теоремы, получаем

^-(z) ≥ -r₂ - λ₂σ - λ₁f-2(σ) - Γϕ(σ) -

df-2(σ)

−

(f-2(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) = -r₂ + ε-2 > 0.

(14)

dσ

Пусть z ∈ ∂Ω-7, тогда выполняется условие 8) теоремы и справедливо равенство l^тx =

= r₁ - λ₂σ - λ₁c^тx. Воспользовавшись этим равенством и условиями 1) и 8) теоремы, найдём

и оценим сверху производную функции W₁(z) в силу системы (1) на множестве ∂Ω-7 :

W₁(z) = -α₁l^тx - β₁c^тx - ν₁ϕ(σ) + λ₁l^тx - λ₁Γϕ(σ) + λ₂c^тx + λ₂ρ₁ϕ(σ) +

+ λ₂ρ₀(1 - u)ϕ(σ) - λ₂α₁uσ = (λ₁ - α₁)l^тx + (λ₂ - β₁)c^тx +

+ (λ₂ρ₁ - ν₁ - λ₁Γ + λ₂ρ₀(1 - u))ϕ(σ) - λ₂α₁uσ = (λ₁ - α₁)r₁ - (λ₁ - α₁)λ₂σ -

- (λ₁ - α₁)λ₁c^тx + (λ₂ - β₁)c^тx + (λ₂ρ₁ - ν₁ - λ₁Γ + λ₂ρ₀(1 - u))ϕ(σ) -

- λ₂α₁uσ = (λ₂ - β₁ - λ₁(λ₁ - α₁))c^тx - (λ₂α₁u + λ₂(λ₁ - α₁))σ +

+ (λ₂ρ₁ - ν₁ - λ₁Γ + λ₂ρ₀(1 - u))ϕ(σ) - (α₁ - λ₁)r₁ = ψ₁(σ) < 0.

(15)

Для z ∈ ∂Ω⁺⁸ выполняются равенства λ₂ = β₁ + λ₁(λ₁ - α₁) и l^тx = -r₂ - λ₂σ - λ₁c^тx.

Учитывая эти равенства и условия 1) и 9) теоремы, найдём и оценим снизу производную

функции W₂(z) в силу системы (1) на множестве ∂Ω⁺⁸ :

W₂(z) = (λ₂ - β₁ - λ₁(λ₁ - α₁))c^тx - (λ₂α₁u + λ₂(λ₁ - α₁))σ +

+ (λ₂ρ₁ - ν₁ - λ₁Γ + λ₂ρ₀(1 - u))ϕ(σ) + (α₁ - λ₁)r₂ = ψ₂(σ) > 0.

(16)

Обозначим

∂Ω⁺³ = {z : f₀(σ) = σ = 0, f⁺¹¹(0) ≤ c^тx ≤ f⁺²¹(0), W₁(z) ≤ 0, W₂(z) ≥ 0},

∂Ω⁺⁴ = {z : P(z) = c^тx = 0,

-σ₃ ≤ σ ≤ -σ₁, W₁(z) ≤ 0, W₂(z) ≥ 0}.

Пусть T₁ - оператор сдвига по траекториям системы (1), определённый на множестве ∂Ω⁺³.

Покажем, что T₁(∂Ω⁺³) ⊂ ∂Ω⁺⁴. Из построения множества G₁ следует существование ε > 0

такого, что при любом z ∈ G₁ выполняется неравенство

(c^тx)² + σ² ≥ ε.

(17)

Для множества G₁ поверхности ∂Ω⁺³ и ∂Ω⁺⁴ являются частью границы. Пусть z₀ ∈ ∂Ω⁺³,

покажем, что для решения z(t, z₀) системы (1) с начальными условиями z(0, z₀) = z₀ найдётся

t1 такое, что z(t1, z0) ∈ G1. Предположим противное, т.е. что для любого t > 0 выполняется

включение z(t, z₀) ∈ G₁. Множество G₁ является ограниченным, следовательно, ограничено

и решение z(t, z₀).

В силу системы (1) справедливо соотношение

∫

σ(t) dt = (c^тx + ψ₃(σ)) dt = (c^тx + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) dt = (σ(t) - σ(0)) ∈ R,

из которого вследствие леммы Барбалата [14, с. 230] вытекает равенство

lim

(c^тx + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) dt = lim

(c^тx + ψ₃(σ)) = 0.

(18)

t→+∞

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

УСЛОВИЯ СУЩЕСТВОВАНИЯ ЦИКЛОВ

169

Используя условие 1) теоремы, найдём интегралы

∫

c^т x dt = (l^тx - Γϕ(σ))dt = c^т(x(t) - x(0)) ∈ R,

(19)

∫

l^т xdt =

(-α₁l^тx - β₁c^тx - ν₁ϕ(σ)) dt = l^т(x(t) - x(0)) ∈ R.

(20)

С учётом (19), (20) и леммы Барбалата справедливы равенства

lim (l^тx - Γϕ(σ)) = 0,

(21)

t→+∞

lim

(-α₁l^тx - β₁c^тx - ν₁ϕ(σ)) = 0.

(22)

t→+∞

Так как z(t, z₀) ∈ G₁, то выполняется двойное неравенство

-r₂ ≤ l^тx + λ₁c^тx + λ₂σ ≤ r₁.

(23)

В силу (18), (21), (23) для функции σ(t) справедливы соотношения

- r₂ ≤ lim

(Γϕ(σ) - λ₁ψ₃(σ) + λ₂σ) = lim

ψ₄(σ) ≤ r₁,

t→+∞

из которых и условия 10) теоремы следует, что

-τ₂ ≤ σ ≤ τ₁.

(24)

Используя равенства (22), (21) и (18), получаем

lim

(-α₁Γϕ(σ) + β₁ψ₃(σ) - ν₁ϕ(σ)) = lim

ψ₅(σ) = 0.

(25)

t→+∞

Из условий 2) и 11) теоремы и соотношений (24), (25), (18) следует, что

lim

σ(t) = 0,

lim

c^тx = 0, lim ((c^тx)² + σ²) = 0.

(26)

t→+∞

Равенства (17) и (26) одновременно выполняться не могут, поэтому существует

t1 такое, что

z(t₁, z₀) ∈ G₁. С учётом соотношений (4), (7), (8), (10), (12), (14)-(16) заключаем, что решение

z(t, z₀) может пересечь границу множества G₁ только через поверхность ∂Ω⁺⁴. Следователь-

но, существует t₁, для которого z(t₁, z₀) ∈ ∂Ω⁺⁴. Итак, оператор T₁ отображает множество

∂Ω⁺³ в множество ∂Ω⁺⁴, T₁(∂Ω⁺³) ⊂ ∂Ω⁺⁴.

Рассмотрим множества G₂ и L = {z : W₁(z) ≤ 0, W₂(z) ≥ 0}. Граница ∂G₂ множества

G₂ определяется равенствами

∂G₁ = ∂Ω⁺⁴

^⋃∂Ω⁺⁹⋃ ∂Ω⁺¹⁰⋃ ∂Ω-11⋃∂Ω-12⋃ ∂Ω⁺¹³,

∂Ω⁺⁴ = ∂Q₃

^⋂L, ∂Ω+9 = ∂Q12

^⋂L, ∂Ω+10 = ∂Q02

^⋂L, ∂Ω-11 = ∂D22

^⋂L,

∂Ω-12 = G₂

^⋂ {z : W₁(z) = 0}, ∂Ω+13 = G2

^⋂ {z : W₂(z) = 0}.

Обозначим через

V∂Ω производную функции V (z) в силу системы (1) на множестве ∂Ω.

Вследствие оценок (8), (10), (15), (16) верны неравенства

0(σ)∂Ω+

> 0,

(z)∂Ω+

> 0,

W₁(z)∂Ω-

< 0,

W₂(z)∂Ω+ > 0.

(27)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

170

МАМОНОВ и др.

Пусть z ∈ ∂Ω⁺⁹, тогда справедливо равенство c^тx = f⁺¹²(σ), σ ∈ [-σ₁, 0], используя которое

и условия 1) и 4) теоремы, найдём и оценим снизу производную функции V ⁺¹²(z) в силу системы

(1) на множестве ∂Ω⁺⁹:

df⁺¹²(σ)

V+

(z)∂Ω+

= l^тx - Γϕ(σ) -

(f⁺¹²(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) ≥

dσ

≥ -r₂ + ε⁺¹ > 0.

(28)

Для z ∈ ∂Ω-11 выполняется равенство

c^тx = f⁺²²(σ), σ ∈ [-σ₃,0].

(29)

Найдём и оценим сверху производную функции V⁺²²(z) в силу системы (1) на множестве ∂Ω-11.

С учётом соотношений (29), (7) и условий 1) и 6) теоремы получаем

df⁺²²(σ)

V+

(z)∂Ω-

= l^тx - Γϕ(σ) -

(f⁺²²(σ) + ρ₁ϕ(σ) + ρ₀(1 - u)ϕ(σ) - α₁uσ) ≤

dσ

≤ r₁ - ε⁺² < 0.

(30)

Обозначим через T₂ оператор сдвига по траекториям системы (1), определённый на мно-

жестве ∂Ω⁺⁴. Множество G₂ является ограниченным. Рассмотрим решение z(t, z₂) системы

(1) с начальными условиями z(0, z₂) = z₂ ∈ ∂Ω⁺⁴. Повторяя рассуждения, проведённые для

множества G₁, и учитывая оценки (27), (28), (30), заключаем, что существует значение

t₂,

для которого z(t₂, z₂) ∈ ∂Ω⁺¹⁰. Следовательно, оператор T₂ отображает множество ∂Ω+4 в

множество ∂Ω⁺¹⁰, T₂(∂Ω⁺⁴) ⊂ ∂Ω⁺¹⁰.

Используя операторы T₁ и T₂, определим оператор T = T₂ ◦ T₁. Тогда оператор T отоб-

ражает множество ∂Ω⁺³ в множество ∂Ω⁺¹⁰, T (∂Ω⁺³) ⊂ ∂Ω⁺¹⁰, ∂Ω+3 ⊂ ∂Ω+10. В данном случае

нет отображения множества ∂Ω⁺³ в себя. Для определения неподвижной точки оператора T

используем понятие вращения векторного поля [15].

Из условия 1) линейной независимости векторов l и c теоремы следует, что для матрицы

B = ∥(l+λ₁)c,c∥ существует обратная матрица B-1. В системе (1) сделаем замену переменных

x = (B^т)-1(x + q), q = colon(q₁,k₀), q₁ = 0, (f⁺²¹(0) + f⁺¹¹(0))/2 = k₀, (f⁺²¹(0) - f⁺¹¹(0))/2 =

= k₁ > 0. Для отображения B_L, заданного равенством x = Bтx - q, имеем x1 = lтx +

+ λ₁c^тx,

x₂ = c^тx - k₀. Сделанная замена переменных является линейной, следовательно,

отображает периодические функции в периодические. После сделанной замены переменные x

переобозначим снова через x. Множества ∂Ω⁺³, ∂Ω⁺¹⁰ отображаются в множества B_L(∂Ω⁺³) =

= H₀, B_L(∂Ω⁺¹⁰) = H = H₀

^⋃H⁺¹⋃H-1 , где (ниже x = (x₁,x₂)^т)

H₀ = {x : x₂ ≤ k₁, x₂ ≥ -k₁, x₁ ≤ r₁,

-r₂ ≤ x₁},

∂H₀ = L₁

^⋃L₂⋃L₃⋃L₄,

L₁ = {x : x₂ = k₁, x₁ ≤ r₁,

-r₂ ≤ x₁}, L₂ = {x : x₂ ≤ k₁, x₂ ≥ -k₁, x₁ = r₁},

L₃ = {x : x₂ = -k₁, x₁ ≤ r₁,

-r₂ ≤ x₁}, L₄ = {x : x₂ ≤ k₁, x₂ ≥ -k₁, x₁ = -r₂},

H⁺¹ = {x : x₂ ≥ k₁, x₂ ≤ f⁺²²(0) - k₀ = k₂, x₁ ≤ r₁,

-r₂ ≤ x₁},

H-1 = {x : x₂ ≥ f⁺¹²(0) - k₀ = -k₃, x₂ ≤ -k₁, x₁ ≤ r₁,

-r₂ ≤ x₁}.

Пусть U - оператор сдвига по траекториям системы (1) после замены переменных B_L. В

силу свойств оператора T = T₂ ◦ T₁ выполняются включения

U (H₀) ⊂ H, U(L₁) ⊂ H⁺¹, U(L₂) ⊂ H, U(L₃) ⊂ H-1, U(L₄) ⊂ H.

(31)

Оператор U(x) = (x∗1, x∗2)^т = x^∗ определяет на границе ∂H₀ ограниченной области H₀

векторное поле S_U (x) = x-Ux = (x₁ -x∗1, x₂ -x∗2)^т = x^∗ Для векторного поля S_U рассмотрим

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

УСЛОВИЯ СУЩЕСТВОВАНИЯ ЦИКЛОВ

171

линейный оператор U_L(x) = A_Lx, где A_L = diag [μ₁, μ₂],

0 < μ₁ < 1, μ₂ > 1. Оператор U_L

определяет векторное поле S_L = x - A_Lx = ((1 - μ₁)x₁, (1 - μ₂)x₂)^т. Обозначим

S_L(x)

S_U (x)

S₀(x) =

∥S_L(x)∥

∥S_U (x)∥

и покажем, что для любого x ∈ ∂H₀ вектор S₀(x) ненулевой.

Пусть x ∈ L₁, U(L₁) ⊂ H⁺¹, e₁ = (1, 0)^т, e₂ = (0, 1)^т, тогда x = (x₁, k₁)^т, x1 ∈ [-r2,r1].

Для вектора U(x) = x^∗ = (x∗1, x∗2)^т в силу включения U(L₁) ⊂ H⁺¹ справедливы неравенства

0 < k₁ < x∗2 < f⁺²²(0) - k₀ = k₂,

-r₂ < x∗1 < r₁.

(32)

Вследствие (32) и неравенства μ₂ > 1 получаем, что

(

)т

S_L(x)

S_U (x)

S₀(x)^тe₂ =

e₂ =

(1 - μ₂)k₁ +

(k₁ - x∗2) < 0,

∥S_L(x)∥

∥S_U (x)∥

∥S_L(x)∥

∥S_U (x)∥

откуда вытекает, что для любого x ∈ L₁ вектор S₀(x) отличен от нулевого.

Пусть x ∈ L4, U(L4) ⊂ H, тогда x = (-r2, x2)т,

x₂ ∈ (-k₃,k₂). Пусть U(x) = x^∗ =

= (x∗1, x∗2)^т. В силу включения U(L₄) ⊂ H верны неравенства

-r₂ < x∗1 < r₁,

0 > -r₂ - x∗1,

из которых и неравенства μ₁ < 1 следует, что

(

)т

S_L(x)

S_U(x)

S₀(x)^тe₁ =

e₁ =

(μ₁ - 1)r₂ -

(r₂ + x∗1) < 0.

∥S_L(x)∥

∥S_U (x)∥

∥S_L(x)∥

∥S_U (x)∥

Другими словами, для любого x ∈ L₄ вектор S₀(x) отличен от нулевого. Аналогично тому,

как это сделано для множеств L₁, L₄, с использованием включений (31) показывается, что и

на множествах L₂, L₃ вектор S₀(x) ненулевой. В силу [15, теорема 5.6] вращение γ(S_U , ∂H₀)

векторного поля S_U на множестве ∂H₀ равно вращению γ(S_L, ∂H₀) линейного векторного

поля S_L на множестве ∂H₀. Пусть B_L = diag [1 - μ₁, 1 - μ₂]. Так как сумма кратностей

β(B_L) вещественных отрицательных собственных значений матрицы B_L равна единице, то

γ(S_L, ∂H₀) = (-1)β(BL) = -1 и γ(S_U , ∂H₀) = -1. В силу [15, теорема 5.15] оператор U имеет

на H₀ по крайней мере одну неподвижную точку x^∗ ∈ H₀, Ux^∗ = x^∗. Неподвижная точка

z^∗ = (x∗т,0)^т определяет начальные условия предельного цикла первого рода. Таким образом,

система (1) имеет седловой предельный цикл первого рода, содержащийся во множестве G.

Теорема доказана.

Теорема 2. Пусть для системы (1) выполнены условия 1)-3), 5), 7)-11) теоремы 1, в

условии 4) вместо последнего неравенства выполняется неравенство f⁺¹²(0) ≥ f⁺¹¹(0), а в

условии 6) вместо последнего неравенства - неравенство f⁺²²(0) ≤ f⁺²¹(0). Тогда система (1)

имеет предельный цикл.

Доказательство. Используя обозначения и рассуждения теоремы 1, показывается, что

оператор U отображает замкнутое выпуклое множество H₀ в себя: U(H₀) ⊂ H₀. В силу

теоремы Брауэра [15] оператор U имеет на H₀ по крайней мере одну неподвижную точку

x^∗ ∈ H₀, Ux^∗ = x^∗. Неподвижная точка z^∗ = (x∗т,0)^т определяет начальные условия пре-

дельного цикла первого рода. Таким образом, система (1) имеет предельный цикл первого

рода, содержащийся во множестве G. Теорема доказана.

2. Проверка условий теоремы. Рассмотрим систему дифференциальных уравнений (1),

в которой

(

)

(

)

(

)

-α₁

-β₁

-ν₁

-Γ

α₁ > 0, β₁ > 0, ρ₁ = ν₁β-11, ρ = ρ₁ + ρ₀.

(33)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

172

МАМОНОВ и др.

Тогда c^тb = -Γ < 0, c^тA = l^т, l^тb = -ν₁ < 0, rang ||c, l|| = 2, l^тA = -α₁l^т - β₁c^т. Для

системы (1), (33) условие 1) теоремы 1 выполняется.

Пусть α₁ = 0.02, β₁ = 2.1, Γ = 4, ν₁ = 1.24, γ = 0.18, u = 0.958, ρ₁ = 0.59, ρ₀ = 0.029,

ϕ(σ) = -γ + sin(σ + arcsin γ),

σ₁ = 0,

σ₂ = π - 2arcsin γ = 2.8. Тогда ϕ(σ₁) = ϕ(σ₂) = 0,

ϕ(0) > 0,

ϕ(σ₂) < 0, функция ϕ(σ) - периодическая с периодом Δ = 2π. Уравнение ϕ(σ) =

= 0 на сегменте [0,Δ] имеет два корня ϕ(σ₁) = ϕ(σ₂) = 0,

0 = σ₁ < σ₂ < Δ, при этом

ϕ(σ)

ограничена на сегменте [0, Δ]. Для системы (1), (33) условие 2) теоремы 1 выполнено.

Для того чтобы выполнялись условия 3) и 4) теоремы 1, возьмём λ₁ = 0, λ₂ = β₁ = 2.1,

ε-1 = ε⁺¹ = ε⁺² = ε-2 = 0.92, r₁ = r₂ = 0.92 · 10-10 < ε-1. Пусть -σ₁ = -3.11, σ₂ = 5.34.

Тогда при выбранных значениях σ₁, σ₂, ε-1, ε⁺¹, r₁, r₂ система второго порядка (2) имеет

решения, определяющие функции f-1(σ), f⁺¹¹(σ), f⁺¹²(σ), для которых выполнены условия 3)

и 4) теоремы 1. Графики функций f-1(σ), f⁺¹¹(σ), f⁺¹²(σ) представлены на рис. 1.

Пусть -σ₃ = -8.93, σ₄ = 8.48. Тогда при выбранных значениях σ₃, σ₄, ε-2, ε⁺², r₁, r₂

система второго порядка (2) имеет решения, определяющие функции f-2(σ), f⁺²¹(σ), f⁺²²(σ),

для которых выполнены условия 5) и 6) теоремы 1. Графики функций f-2(σ), f⁺²¹(σ), f⁺²²(σ)

показаны на рис. 1.

При σ ∈[-8.93, -3.11] верно неравенство λ₂σ +r₂ +Γϕ(σ) < 0, а для любого σ ∈[-8.93, 8.48]

справедливы соотношения λ₂ = β₁ = 2.1, ψ₁(σ) < 0 и ψ₂(σ) > 0. Условия 7)-9) теоремы 1

выполнены.

При τ₁ = 0.154, τ₂ = 0.151 выполняется условие 10) теоремы 1, а функция ψ₅(σ) на

сегменте [-τ₂, τ₁]

^⋃ [-σ₃, σ₄] имеет единственный нyль ψ₅(0) = 0 (условие 11)). Для системы

(1), (33) с приведёнными выше значениями выполнены все условия теоремы 1, поэтому эта

система имеет седловой предельный цикл первого рода.

Из доказательства теоремы 1 следует, что начальные условия седлового цикла находятся в

множестве H₀. Используя деление множества H₀ на части и вычисляя вращение векторного

поля, численно определяются начальные условия седлового цикла. Система (1), (33) с ука-

занными значениями параметров (в частности, u = 0.958) имеет седловой предельный цикл

первого рода z₁(t) = (x₁, x₂, σ)^т с начальными условиями x₁ = -0.0063142, x₂ = 10.36968,

σ = 0 и периодом Tz1 = 4.35562692. Мультипликаторы найденного седлового цикла z₁(t)

соответственно равны μ₁ = 1, μ₂ = 1.69, μ₃ = 0.92. Неравенство μ₂ > 1 является характе-

ристикой неустойчивости цикла.

С использованием теоремы 2 показывает-

ся, что у этой системы наряду с седловым пре-

дельным циклом z₁(t) существуют два устой-

чивых предельных цикла первого рода: внут-

ренний цикл z₂(t) с начальными условиями

x₁ = -0.0101, x₂ = 7.1956, σ = 0, периодом

Tz3 = 4.6930 и мультипликаторами μ1 = 1,

μ₂ = 0.39, μ₃ = 0.92; внешний цикл z₃(t) с

начальными условиями x₁ = -0.0021, x₂ =

= 14.8285, σ = 0, периодом Tz2 = 4.2732 и

мультипликаторами μ₁ = 1, μ₂ = 0.54, μ₃ =

= 0.92. Цикл z₃(t) определяет скрытые ко-

лебания [7]. Взаимное расположение всех цик-

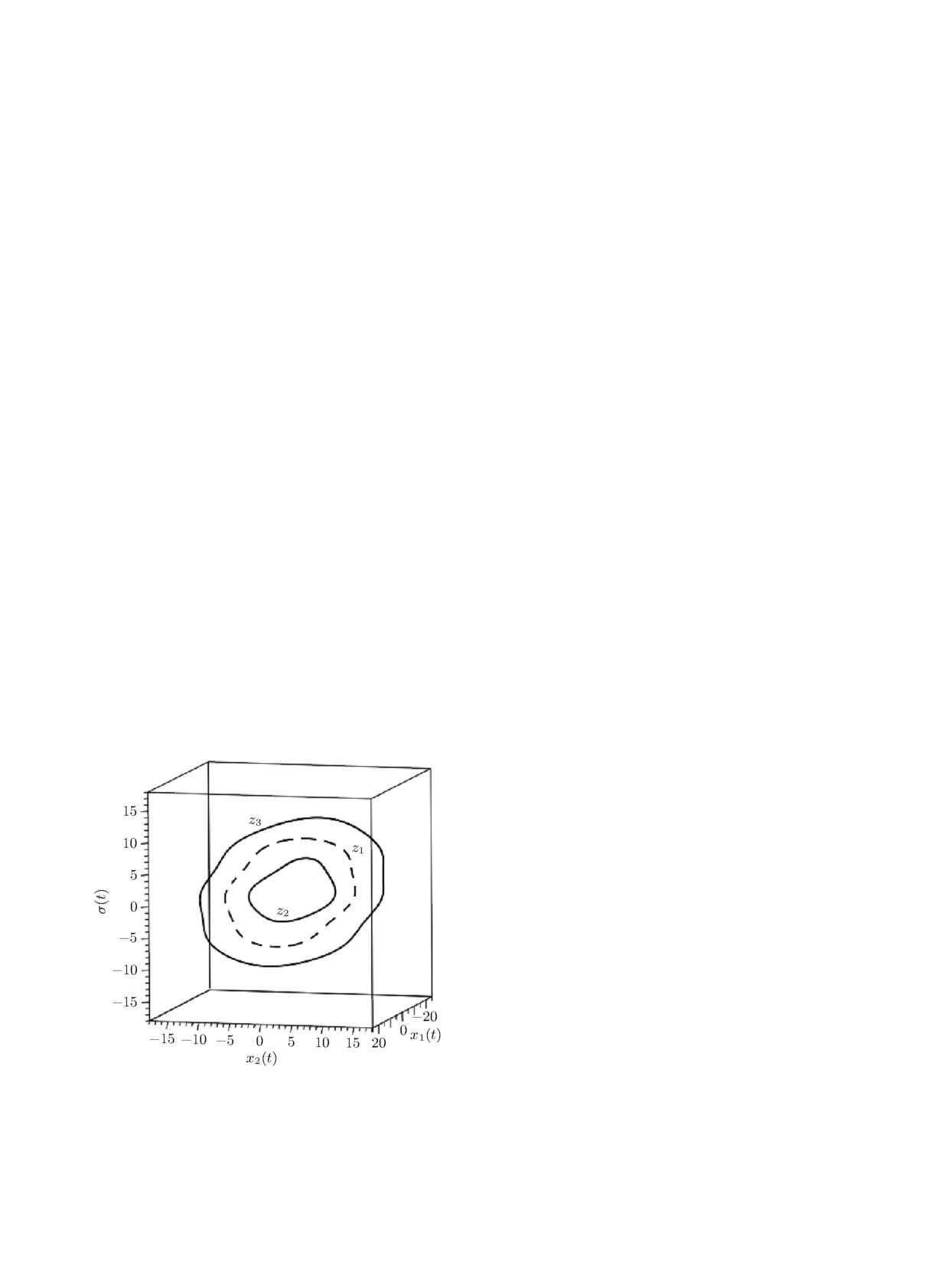
лов рассматриваемой системы в пространстве

(x₁, x₂, σ) изображено на рис. 2.

Рассмотрим систему (1) при u = 0

Рис. 2. Циклы системы (1) в пространстве (x1; x2, σ)

x = Ax + bϕ(σ),

при u = 0.958.

σ = c^тx + ρ₁ϕ(σ) + ρ₀ϕ(σ).

(34)

Система (34) является фазовой системой дифференциальных уравнений [2, с. 9] и опреде-

ляет математическую модель фазовой автоподстройки частоты с фильтром второго порядка с

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

УСЛОВИЯ СУЩЕСТВОВАНИЯ ЦИКЛОВ

173

запаздыванием [1-13]. Численный анализ рассмотренной выше системы (1), (33) при уменьше-

нии значения u с u = 0.985 до u = 0 позволяет сделать вывод о трансформации трёх циклов

z₁(t), z₂(t), z₃(t) в циклы z1(t),

z₂(t),

z₃(t) системы (34). Используя начальные условия

цикла z₁(t), рассмотрим для системы (34) множество ω₁, которое определим следующим

образом:

ω₁ = {(σ,x) : (x₁ + 0.00631)² + (x₂ - 10.36968)² ≤ 1.12², σ = 0}.

Пусть U₁ - оператор сдвига по траекториям фазовой системы (34). Обозначим Q₁(x) =

= x - U₁(x). Вращение γ(Q₁,∂ω₁) векторного поля Q₁(x) на границе ∂ω₁ множества ω₁

отлично от нуля, γ(Q₁, ∂ω₁) = 0. Множество ω₁ содержит неподвижную точку оператора

U₁, определяющую начальные условия седлового цикла первого рода

z₁(t) системы (34) с

начальными условиями x₁ = 0.374,

x₂ = 10.21184, σ = 0 и периодом Tz2 = 4.3702.

Система (34) имеет устойчивые циклы: внутренний цикл z₂(t) с начальными условиями

x₁ = 0.01, x₂ = 7.2768, σ = 0 и периодом Tz2(t) = 4.6771; внешний цикл z3(t) с начальными

условиями x₁ = 0.591, x₂ = 14.721, σ = 0 и периодом Tz3(t) = 4.2982. Для устойчивых циклов

∫_T

z₂(t),

z₃(t) определяются характеристики 〈σ˙₂〉 = T-1

σ(t) dt = -0.00075 и 〈σ˙₃〉 = -0.0044.

Полученные значения 〈σ˙₂〉 и 〈σ˙₃〉 позволяют сделать вывод о наличии в фазовой системе

скрытых квазисинхронных режимов [5-7, 9, 12]. Существование в системе (34) разночастотных

предельных циклов первого рода говорит о фазовой мультистабильности в этой системе, при

этом предельные циклы первого рода системы (34) определяют квазисинхронные режимы.

СПИСОК ЛИТЕРАТУРЫ

1. Леонов Г.А., Буркин И.М., Шепелявый А.И. Частотные методы в теории колебаний. В 2-х ч. СПб,

1992.

2. Леонов Г.А., Смирнова В.Б. Математические проблемы теории фазовой синхронизации. СПб, 2000.

3. Буркин И.М., Леонов Г.А. О существовании нетривиальных периодических решений у одной нели-

нейной системы третьего порядка // Дифференц. уравнения. 1984. Т. 20. № 12. С. 2036-2042.

4. Буркин И.М., Буркина Л. И., Леонов Г.А. Проблема Барбашина в теории фазовых систем // Диф-

ференц. уравнения. 1981. Т. 17. № 11. С. 1932-1944.

5. Burkin I.M. Transition into space of derivatives // Differ. Equat. 2015. V. 51. № 13. P. 1717-1751.

6. Шалфеев В.Д., Матросов В.В. Нелинейная динамика систем фазовой синхронизации. Н. Новгород,

2013.

7. Кузнецов Н.В. Теория скрытых колебаний и устойчивость систем управления // Изв. РАН. Теория

и системы управления. 2020. № 5. С. 5-27.

8. Кузнецов Н.В., Лобачев М.Ю., Юлдашев М.В., Юлдашев Р.В. О проблеме Гарднера для систем

управления фазовой автоподстройкой частоты // Докл. АН СССР. 2019. Т. 489. № 6. С. 541-544.

9. Матросов В.В. Автомодуляционные режимы системы фазовой автоподстройки частоты с фильтром

второго порядка // Изв. вузов. Радиофизика. 2006. Т. 49. № 4. С. 357-368.

10. Мамонов С.С. Условия существования предельных циклов второго рода системы дифференциаль-

ных уравнений. I // Дифференц. уравнения. 2010. Т. 46. № 5. С. 637-646.

11. Мамонов С.С. Условия существования предельных циклов второго рода системы дифференциаль-

ных уравнений. II // Дифференц. уравнения. 2010. Т. 46. № 8. С. 1075-1084.

12. Мамонов С.С., Ионова И.В., Харламова А.О. Механизмы возникновения скрытой синхронизации

динамических систем // Чебышёвcкий сб. 2019. Т. 20. № 3. С. 333-348.

13. Mamonov S.S., Kharlamova A. O. First-kind cycles of systems with cylindrical phase space // J. Math.

Sci. 2020. V. 248. № 4. P. 457-466.

14. Попов В.М. Гиперустойчивость автоматических систем. М., 1970.

15. Красносельский М.А. Оператор сдвига по траекториям дифференциальных уравнений. М., 1966.

Рязанский государственный университет

Поступила в редакцию 03.12.2021 г.

имени С.А. Есенина

После доработки 03.12.2021 г.

Принята к публикации 24.02.2022 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022