ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 2, с.260-269

ТЕОРИЯ УПРАВЛЕНИЯ

УДК 517.977.8

ОЦЕНКА ВРЕМЕНИ ПОИМКИ И ПОСТРОЕНИЕ

СТРАТЕГИИ ПРЕСЛЕДОВАТЕЛЯ В НЕЛИНЕЙНОЙ

ДИФФЕРЕНЦИАЛЬНОЙ ИГРЕ ДВУХ ЛИЦ

В конечномерном евклидовом пространстве рассматривается дифференциальная игра двух

лиц - преследователя и убегающего, описываемая нелинейной автономной управляемой

системой дифференциальных уравнений в нормальной форме, правая часть которой пред-

ставляет собой сумму двух функций, одна из которых зависит только от фазовой пере-

менной и управления преследователя, а другая - только от фазовой переменной и управ-

ления убегающего. Множество значений управления преследователя является конечным,

а множество значений управления убегающего - компактом. Цель преследователя сос-

тоит в приведении траектории системы из начального положения в любую наперёд задан-

ную окрестность нуля за конечное время. Стратегия преследователя конструируется как

кусочно-постоянная функция со значениями в заданном конечном множестве, для постро-

ения которой разрешается использовать лишь информацию о значении текущих фазовых

координат. Управление убегающего - измеримая функция, для построения которой нет

ограничений по доступной информации. Показано, что для перевода системы в любую

наперёд заданную окрестность нуля преследователю достаточно использовать стратегию

с постоянным шагом разбиения временного промежутка. Величина фиксированного шага

разбиения найдена в явном виде. Выделен класс систем, для которых получена оценка

времени перевода из произвольного начального положения в заданную окрестность нуля.

Оценка является неулучшаемой в некотором точно указанном смысле. В решении суще-

ственно используется понятие положительного базиса векторного пространства.

DOI: 10.31857/S037406412202011X

Введение. Дифференциальные игры двух лиц, рассмотренные первоначально Р.Ф. Ай-

зексом [1], в настоящее время представляют собой достаточно развитую теорию, имеющую

многочисленные практические приложения [2-7]. В ней разработаны методы решения различ-

ных классов игровых задач: метод Айзекса, основанный на анализе некоторого уравнения в

частных производных и его характеристик, метод экстремального прицеливания Красовского,

метод Понтрягина и другие. Н.Н. Красовским и его научной школой создана теория пози-

ционных игр, в основе которой лежит понятие максимального стабильного моста и правило

экстремального прицеливания. Однако эффективное построение таких мостов для реальных

конфликтно управляемых процессов, в первую очередь, нелинейных дифференциальных игр,

весьма затруднительно или даже невозможно. Удобнее строить мосты, не являющиеся макси-

мальными, но обладающие свойством стабильности и дающие эффективно реализуемые про-

цедуры управления для отдельных классов игр. Достаточные условия разрешимости задачи

преследования в нелинейном примере Л.С. Понтрягина получены в [8]. В работе [9] представле-

ны достаточные условия разрешимости задачи преследования в нелинейной дифференциаль-

ной игре при некоторых дополнительных условиях на вектограмму системы и терминальное

множество. Приближённое построение стабильных мостов в нелинейных дифференциальных

играх, в том числе численно, рассматривается, в частности, в работах [10, 11].

В работе [12] введено понятие положительного базиса векторного пространства, которое в

работах [12, 13] эффективно использовалось для исследования свойства управляемости нели-

нейных систем, описываемых дифференциальными уравнениями в конечномерном евклидовом

пространстве. Свойства положительного базиса в работах [14-16] использовались для исследо-

вания управляемых систем на многообразиях, а в работах [17-21] - для исследования задачи

преследования группой преследователей одного или нескольких убегающих в линейных диф-

ференциальных играх с равными возможностями игроков. В работе [22] получены достаточные

260

ОЦЕНКА ВРЕМЕНИ ПОИМКИ И ПОСТРОЕНИЕ СТРАТЕГИИ ПРЕСЛЕДОВАТЕЛЯ

261

условия разрешимости задачи поимки для дифференциальной игры двух лиц, описываемой

нелинейной дифференциальной системой первого порядка при дискретном управлении и с

неполной информацией. Доказано, что существует окрестность нуля, из каждой точки кото-

рой происходит поимка.

В данной работе в продолжение исследования [22] получены следующие результаты. По-

казано, что для перевода системы в любую наперёд заданную окрестность нуля достаточно

использовать стратегию с постоянным шагом разбиения временного интервала. Выделен класс

систем, для которого получена оценка времени поимки из заданного начального положения,

являющаяся неулучшаемой в некотором описанном в работе смысле. Свойства положительно-

го базиса векторного пространства играют в дальнейшем существенную роль.

1. Постановка задачи. В пространстве R^k (k ≥ 2) рассматривается дифференциальная

игра двух лиц: преследователя P и убегающего E. Динамика игры описывается системой

дифференциальных уравнений

x = f(x,u) + g(x,v), u ∈ U, v ∈ V, x(0) = x₀,

(1)

где x ∈ R^k - фазовый вектор, u, v - управляющие воздействия. Множество U = {u₁, . . . , u_m}

конечно, u_i ∈ R^l, i = 1, m; множество V ⊂ R^s - компакт. Функция f : R^k × U → R^k - для

каждого u ∈ U липшицева по x. Функция g : R^k × V → R^k - липшицева по совокупности

переменных, т.е. существуют положительные числа L₁, . . . , L_m, L₂ такие, что

∥f(x¹, u_i) - f(x², u_i)∥ ≤ L_i∥x¹ - x²∥, x¹, x² ∈ R^k, i = 1, m,

∥g(x¹, v¹) - g(x², v²)∥ ≤ L₂(∥x¹ - x²∥ + ∥v¹ - v²∥), x¹, x² ∈ R^k, v¹, v² ∈ V.

(2)

Здесь и всюду далее норма считается евклидовой. Обозначим L₁ = max{L₁, . . . , L_m}.

Под разбиением σ промежутка [0, T ] будем понимать конечное множество {τ_q}ηq=0 точек

этого промежутка такое, что 0 = τ₀ < τ₁ < τ₂ < . . . < τ_η = T.

Определение 1. Кусочно-постоянной стратегией W преследователя P называется пара

(σ, W_σ), где σ = {τ_q}nq=0 - разбиение промежутка [0, T ], а W_σ - семейство отображений d_r,

r = 0,η - 1, ставящих в соответствие парам (τ_r,x(τ_r)) ∈ [0,T] × R^k постоянное управление

u_r(t) ≡ u_r ∈ U, t ∈ [τ_r,τr+1).

Под управлением убегающего понимаем произвольную измеримую функцию v : [0, ∞) → V.

Обозначим данную игру через Γ(x₀).

Определение 2. Будем говорить, что в игре Γ(x₀) происходит ε-поимка, если существу-

ет T > 0 такое, что для любого ε > 0 существует кусочно-постоянная стратегия W пре-

следователя P такая, что для любого допустимого управления убегающего v(·) выполняется

неравенство ∥x(τ)∥ < ε для некоторого τ ∈ [0, T ].

Целью преследователя является осуществление ε-поимки.

Целью убегающего - воспрепятствовать этому.

Определение 3 [12]. Совокупность векторов a₁,... ,a_n ∈ R^k называется положительным

базисом в R^k, если для любой точки ξ ∈ R^k существуют неотрицательные числа μ₁, . . . , μ_n

∑_n

такие, что ξ =

μ_ia_i.

i=1

Используем следующие обозначения: Int A - внутренность множества A; co A - выпуклая

оболочка множества A; O_ε(x) - ε-окрестность точки x; D_ε(x) - замкнутый шар радиуса ε

с центром в точке x.

Справедлива следующая теорема о поимке [22].

Теорема 1 [22]. Пусть векторы f(0, u₁), . . . , f(0, u_m) образуют положительный базис и

имеют место включения -g(0, V ) ⊂ Int (co {f(0, u₁), . . . , f(0, u_m)}). Тогда существует ε₀ > 0

такое, что для любой точки x₀ ∈ Oε0 (0) в игре Γ(x₀) происходит ε-поимка.

Замечание 1. Согласно доказательству теоремы 1 движение, порождаемое выигрыш-

ной стратегией преследователя, находится внутри шара Dx0 (0). Поэтому достаточно считать

функции f( · , · ), g( · , · ) определёнными в некоторой окрестности нуля фазового пространст-

ва. При этом данные функции могут быть локально липшицевы в указанном выше смысле.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

262

ЩЕЛЧКОВ

Замечание 2. Без ограничения общности можно считать, что U = {1, . . . , m}, так как

управление преследователя на интервалах разбиения постоянно, т.е. функция f имеет вид

f (x, j) = f_j(x), где f_j : Rk → Rk - липшицева по x функция. Кроме того, множество U

может быть произвольным непустым подмножеством в R^l при условии, что для каждого

u ∈ U функция f является липшицевой по x. В этом случае, если существует конечный

набор величин {u₁, . . . , u_m} ⊂ U, который удовлетворяет условию теоремы 1, то происходит

ε-поимка.

2. Стратегия поимки, сконструированная в [22]. Приведём выигрышную стратегию

преследователя, найденную в [22], сопутствующие обозначения и некоторые установленные в

доказательстве теоремы 1 результаты. Считаем, что условия этой теоремы выполнены. Су-

ществование указанных в данном пункте параметров установлено в [22] при доказательстве

теоремы 1.

Существуют α > 0, ε₀ > 0 такие, что для любых точки x ∈ Dε0 (0) и вектора p ∈ R^k,

∥p∥ = 1, найдётся i ∈ {1, . . . , m}, для которого при любом v ∈ V выполнено неравенство

〈f(x, u_i) + g(x, v), p〉 ≥ α,

где

α = min

min

min max 〈f(x, u_i) + g(x, v), p〉.

x∈Dε₀ (0)

∥p∥=1

v∈V i=1,m

Существует число h > 0 такое, что для каждого x₀ ∈ Dε0 (0) \ {0} и любого v ∈ V

справедливо неравенство

〈f(x, u₀) + g(x, v), -x₀/∥x₀∥〉 ≥ α/2 = α

(3)

при всех x ∈ D_h(x₀). Здесь u₀ находится из следующего максимума:

max〈f(x0, u), -x0/∥x0∥〉 = 〈f(x0, u0), -x0/∥x0∥〉.

(4)

u∈U

При этом достаточно взять h = α/(2L₁ + 2L₂).

Пусть D - число, при котором имеет место неравенство ∥f(x, u_i) + g(x, v)∥ ≤ D для всех

x ∈ Dε0(0), любого v ∈ V и каждого i ∈ {1,...,m}.

Обозначим

Δ(ξ) = min{α∥ξ∥/D², h/D}.

(5)

В работе [22] показано, что при реализации стратегии преследователя длина отрезка разбиения

[τ_j , τj+1), j = 0, 1, . . . , выбирается с использованием определённой равенством (5) функции

Δ(·) и задаётся равенством τj+1 - τ_j = Δ(x(τ_j )). Управление u_j находится из следующего

максимума:

max〈f(x(τj), u), -x(τj )/∥x(τj )∥〉 = 〈f(x(τj ), uj), -x(τj )/∥x(τj )∥〉.

(6)

u∈U

Для каждого j = 0, 1, . . . справедлива следующая оценка:



∫



²

∥x(τj+1)∥² = ∥x(τ_j )∥² +^

(f(x(s), u_j) + g(x(s), v(s))) ds

 +

τ_j

∫

〈f(x(s), u_j ) + g(x(s), v(s)), x(τ_j )〉 ds ≤

τ_j

≤ ∥x(τ_j )∥² + D²(Δ(x(τ_j )))² - 2Δ(x(τ_j ))α∥x(τ_j )∥ ≤ ∥x(τ_j )∥² - Δ(x(τ_j ))α∥x(τ_j )∥.

(7)

Кроме того, ∥x(t)∥ < ∥x(τ_j )∥, t ∈ (τ_j , τj+1).

При использовании данной стратегии происходит ε-поимка. В доказательстве теоремы 1

(см. [22]) получена общая, т.е. для всех x₀ ∈ Dε0 (0) \ {0}, верхняя оценка времени ε-поимки.

Геометрический смысл такого выбора параметров для описанной выше стратегии заклю-

чается в следующем.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

ОЦЕНКА ВРЕМЕНИ ПОИМКИ И ПОСТРОЕНИЕ СТРАТЕГИИ ПРЕСЛЕДОВАТЕЛЯ

263

Пусть начальное положение находится в точке b ∈

∈ Dε0(0) (рис. 1). Управление преследователя выбира-

ется в соответствии с максимумом (4), где x₀ = b. Тог-

да для всех t ∈ [0, Δ(b)] справедливо включение x(t) ∈

∈ D_h(b) (рис. 1, малая окружность). Поэтому до момен-

та Δ(b) для скорости будет справедливо неравенство (3),

т.е. вектор скорости будет находиться в выпуклом кону-

се, определяемом положительным числом α. Таким об-

разом, траектория также будет содержаться в выпуклом

конусе, определяемом числом α, но с вершиной в точке

b (рис. 1, лучи, выходящие из точки b). В силу определе-

ния функции Δ(·) к моменту Δ(b) траектория в конусе

уйдёт не дальше некоторого расстояния (рис. 1, большая

дуга). Причём это расстояние равно половине длины про-

извольной хорды, проведённой из точки b вдоль границы

Рис. 1. Геометрический смысл выбора

конуса. Так как в силу (3) для всех t ∈ [0, Δ(b)] верно

параметров.

неравенство ∥ x(t)∥ ≥ α, то в момент Δ(b) точка тра-

ектории будет находиться в конусе на расстоянии от точки b не ближе, чем αΔ(b) (рис. 1,

малая дуга). Из описанного выше следует, что к моменту Δ(b) траектория системы будет

находиться в закрашенной области (рис. 1).

3. Гарантированное время поимки. Обозначим через S множество систем, удовле-

творяющих постановке задачи и теореме 1. Другими словами, под элементом s ∈ S будем

понимать набор (f( · , · ), g( · , · ), U, V ), для которого выполнены следующие условия:

1) k, l, s, m ∈ N, k ≥ 2;

2) множество U = {u₁, . . . , u_m} конечно, u_i ∈ R^l, i = 1, m;

3) множество V ⊂ R^s - компакт;

4) функция f : R^k × U → R^k при каждом u ∈ U липшицева по x, функция g : R^k × V →

→ R^k липшицева по совокупности переменных, т.е. существуют положительные числа L₁, L₂

такие, что выполняются оценки (2);

5) векторы f(0, u₁), . . . , f(0, u_m) образуют положительный базис в R^k, и имеет место

включение -g(0, V ) ⊂ Int (co {f(0, u₁), . . . , f(0, u_m)}).

Дифференциальную игру (1), соответствующую четвёрке s ∈ S и начальному положению

x₀, обозначим Γ(s,x₀).

Пусть s ∈ S. Определим число ε₀(s) условием

ε₀(s) = sup{r ≥ 0 : -g(x,V ) ⊂ Int(co {f(x,u₁),... ,f(x,u_m)}), x ∈ D_r(0)}.

Далее, определим множество O(s) ⊂ R^k равенством

{

Oε0(s)(0), ε0(s) < +∞,

O(s) =

R^k,

ε₀(s) = +∞.

Отметим, что согласно теореме 1 для каждого s ∈ S и любого x₀ ∈ O(s) в игре Γ(s, x₀)

происходит ε-поимка.

Обозначим

D(s, r) = max{∥f(x, u) + g(x, v)∥ : x ∈ D_r(0), u ∈ U, v ∈ V },

α(s, x₀) = min

min

min max 〈f(x, u_i) + g(x, v), p〉.

(8)

x∈D∥x0∥(0)

∥p∥=1

v∈V i=1,m

Для μ ∈ [0, 1] определим следующие функции:

μα(s, x₀)

h(s, μ) =

(9)

2(L₁ + L₂)

(

)

α(s, μ) = α(s, x₀)

(10)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

264

ЩЕЛЧКОВ

Теорема 2. Пусть s ∈ S, x₀ ∈ O(s), x₀ = 0, L₁ и L₂ - константы Липшица, соот-

ветствующие четвёрке s. Тогда в игре Γ(s, x₀) для любого δ > 0, δ < ∥x₀∥, траекторию

системы можно перевести в шар D_δ(0), используя кусочно-постоянную стратегию пресле-

дователя с фиксированным шагом разбиения Δ = h(s,μ₀)/D(s,∥x₀∥) за время

∥x₀∥² - δ

T_δ ≤

+ Δ,

2α(s, μ₀)δ - (D(s, ∥x₀∥))²Δ

где

μ₀ = min{1,(L₁ + L₂)δ/D(s,∥x₀∥)}.

(11)

Доказательство. Так как четвёрка s фиксирована, то для упрощения записи обозначим:

D(s, ∥x₀∥) = D, α(s, x₀) = α(x₀), h(s, μ) = h(μ), α(s, μ) = α(μ).

1⁰. В этом пункте доказательства получим оценки, соответствующие функциям α(x₀),

h(μ), α(μ).

Пусть p ∈ R^k,

∥p∥ = 1, μ ∈ (0, 1], ξ ∈ D∥x0∥(0), x ∈ Dh(μ)(ξ). Выберем такое значение

u ∈ U, на котором достигается следующий максимум:

max〈f(ξ, u), p〉 = 〈f(ξ, u), p〉.

u∈U

Докажем, что для любого v ∈ V справедливо неравенство

〈f(x, u) + g(x, v), p〉 ≥ α(μ).

(12)

Используя определения (8), оценим скалярное произведение в (12):

〈f(x, u) + g(x, v), p〉 = 〈f(x, u) - f(ξ, u) + f(ξ, u) + g(x, v) - g(ξ, v) + g(ξ, v), p〉 =

= 〈f(ξ, u) + g(ξ, v), p〉 + 〈f(x, u) - f(ξ, u), p〉 + 〈g(x, v) - g(ξ, v), p〉 ≥

≥ α(x₀) - ∥f(x, u) - f(ξ, u)∥ - ∥g(x, v) - g(ξ, v)∥ ≥

≥ α(x₀) - L₁∥x - ξ∥ - L₂∥x - ξ∥ ≥ α(x₀) - (L₁ + L₂)h(μ) =

μα(x₀)

= α(x₀) - (L₁ + L₂)

= α(μ).

2(L₁ + L₂)

Таким образом, неравенство (12) доказано.

Заметим, что функция h(μ) является строго возрастающей, функция α(μ) - строго убы-

вающей и имеют место двойные неравенства

α(x₀)

0 ≤ h(μ) ≤

≤ α(μ) ≤ α(x₀), μ ∈ [0, 1].

(13)

2(L₁ + L₂)

2⁰. В этом пункте доказательства построим стратегию, переводящую траекторию системы

в шар D_δ(0).

В силу определений (9), (11) и неравенств (13) справедлива оценка

h(μ₀) ≤ α(μ₀)δ/D.

(14)

Определим фиксированный шаг разбиения Δ = h(μ₀)/D. Фиксированное управление пре-

следователя u_j ∈ U на интервале [τ_j, τj+1), j = 0, η, будем выбирать из условия (6).

Оценим квадрат нормы, используя неравенства (12), (14), (8). Для всех t ∈ (0, τ₁] имеем



∫



²



∥x(t)∥² =^x₀ + (f(x(s), u₀) + g(x(s), v(s))) ds



∫



∫



²



= ∥x₀∥² + ^ (f(x(s), u₀) + g(x(s), v(s))) ds

〈f(x(s), u₀) + g(x(s), v(s)), x₀〉 ds ≤

 +

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

ОЦЕНКА ВРЕМЕНИ ПОИМКИ И ПОСТРОЕНИЕ СТРАТЕГИИ ПРЕСЛЕДОВАТЕЛЯ

265

≤ ∥x₀∥² + D²t² - 2tα(μ₀)∥x₀∥ ≤

≤ ∥x₀∥² + D²tΔ - 2tDh(μ₀) = ∥x₀∥² + Dth(μ₀) - 2tDh(μ₀) < ∥x₀∥².

(15)

Отметим, что при рассматриваемых условиях в силу выбора (6) управления преследователя

траектория системы не покидает шар D∥x0∥(0). Поэтому при выводе неравенств (15) коррект-

но оценивать норму скорости системы величиной D = D(s, ∥x₀∥).

В силу (15) справедливо следующее неравенство:

∥x(τ₁)∥² ≤ ∥x₀∥² + D²Δ² - 2Δα(μ₀)δ < ∥x₀∥².

(16)

Пусть x(τ₁), . . . , x(τη-1) ∈ D_δ(0). Тогда аналогично (16) для всех j = 1, η справедливы

неравенства ∥x(τ_j )∥² ≤ ∥x(τj-1)∥² + D²Δ² - 2Δα(μ₀)δ < ∥x(τj-1)∥². Следовательно,

∥x(τ_η)∥² ≤ ∥x₀∥² + ηD²Δ² - 2ηΔα(μ₀)δ.

Отсюда, если ∥x₀∥² + ηD²Δ² - 2ηΔα(μ₀)δ ≤ δ², то x(τ_η) ∈ D_δ(0). Таким образом,

[

]

∥x₀∥² - δ

η≤

+ 1.

(17)

2Δα(μ₀)δ - D²Δ²

Здесь

[·] - целая часть числа. Если η строго больше правой части неравенства (17), то

x(τη-1) ∈ D_δ(0), что противоречит предположению x(τη-1) ∈ D_δ(0).

Оценим величину τ_η :

([

]

)

(

)

∥x₀∥² - δ

∥x₀∥² - δ²

τ_η = ηΔ ≤

+1 Δ≤

+1 Δ=

+ Δ.

2Δα(μ₀)δ - D2Δ2

2α(μ₀)δ - D²Δ

Таким образом,

∥x₀∥² - δ

T_δ ≤

+ Δ,

2α(μ₀)δ - D²Δ

где μ₀ = min{1, (L₁ + L₂)δ/D}, Δ = h(μ₀)/D. Теорема доказана.

Обозначим

T (s, x₀) = ∥x₀∥/α(s, x₀).

Теорема 3. Для множества S справедливы следующие свойства.

1) Для любого s ∈ S и любого x₀ ∈ O(s) в игре Γ(s, x₀) происходит ε-поимка за время

T (s, x₀).

2) Существуют c ∈ S и x₀ ∈ O(c), для которых за любое время T < T (c, x₀) в игре

Γ(c, x₀) ε-поимка не происходит.

Доказательство. Так как четвёрка s фиксирована, то для упрощения записи обозначим:

D(s, ∥x₀∥) = D, α(s, x₀) = α(x₀), h(s, μ) = h(μ), α(s, μ) = α(μ), T (x₀) = T (s, x₀).

1⁰. В этом пункте доказательства построим стратегию поимки, используя теорему 2.

Зафиксируем произвольно число ω ∈ (0, 1). Выберем μ₁ таким, что

0 < μ₁ ≤ min{1,(L₁ + L₂)ω∥x₀∥/D}.

(18)

Тогда аналогично (14) справедлива оценка

h(μ₁) ≤ α(μ₁)ω∥x₀∥/D.

(19)

Обозначим Δ₁ = h(μ₁)/D. Аналогично п. 2⁰ доказательства теоремы 2, используя фик-

сированный шаг Δ₁ разбиения, показывается, что траектория системы переводится в шар

Dω∥x0∥(0) за время T1, где

∥x₀∥²(1 - ω²)

T₁ ≤

+Δ₁.

2α(μ₁)ω∥x₀∥ - D²Δ₁

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

266

ЩЕЛЧКОВ

Далее, обозначим μ₂ = ωμ₁. Тогда h(μ₂) = ωh(μ₁). Следовательно, так как α(·) является

строго убывающей функцией, то в силу (19) справедлива оценка

h(μ₂) ≤ α(μ₁)ω²∥x₀∥/D ≤ α(μ₂)ω²∥x₀∥/D.

(20)

Обозначим Δ₂ = h(μ₂)/D. Таким образом, используя фиксированный шаг Δ₂ разбиения,

видим, что траектория системы переводится в шар D_ω2∥x0∥(0) из положения x(T1) за время

T₂. Так как ∥x(T₁)∥ ≤ ω∥x₀∥, то

∥x(T₁)∥² - ω⁴∥x₀∥

ω²∥x₀∥²(1 - ω²)

T₂ ≤

+Δ₂ ≤

+Δ₂.

(21)

2α(μ₂)ω²∥x₀∥ - D²Δ₂

Далее, повторяем процедуру. Обозначим μ₃ = ωμ₂, тогда h(μ₃) = ωh(μ₂) и в силу (20)

справедливо неравенство

h(μ₃) ≤ α(μ₂)ω³∥x₀∥/D ≤ α(μ₃)ω³∥x₀∥/D.

Фиксированный шаг Δ₃ = h(μ₃)/D. Аналогично (21) оценим T₃ :

ω⁴∥x₀∥²(1 - ω²)

T₃ ≤

+Δ₃.

2α(μ₃)ω³∥x₀∥ - D²Δ₃

И так далее для каждого q ∈ N. В результате получаем

μ_q = ωq-1μ₁, h(μ_q) = ωq-1h(μ₁), Δ_q = ωq-1Δ₁,

ω2(q-1)∥x₀∥²(1 - ω²)

T_q ≤

+Δ_q.

(22)

2α(μ_q)ω^q∥x₀∥ - D²Δ_q

В силу построения данной процедуры верно неравенство

x(T₁ + . . . + T_q) ≤ ω^q∥x₀∥.

Таким образом, можем перевести траекторию системы в любую наперёд заданную окрест-

ность нуля. Следовательно, для того чтобы при использовании данной процедуры происходила

∑_∞

ε-поимка, осталось показать, что величина

T_q ограничена сверху.

q=1

Используя неравенства (22), преобразуем оценку для T_q :

ω2(q-1)∥x₀∥²(1 - ω²)

T_q ≤

+Δ_q =

+ωq-1Δ₁ =

2α(μ_q)ω^q∥x₀∥ - D²Δ_q

2α(μ_q)ω^q∥x₀∥ - D²ωq-1Δ₁

∥x₀∥²(1 - ω²)

ωq-1 + ωq-1Δ₁ ≤

ωq-1 + ωq-1Δ₁.

(23)

2α(μ_q)ω∥x₀∥ - Dh(μ₁)

2α(μ₁)ω∥x₀∥ - Dh(μ₁)

Теперь, используя (23), оценим следующую сумму:

∑

∥x₀∥²(1 - ω²)

T_q ≤

ωq-1 + ωq-1Δ₁ =

2α(μ₁)ω∥x₀∥ - Dh(μ₁)

q=1

∥x₀∥²(1 - ω²)

∥x₀∥²(1 + ω)

h(μ₁)

Δ₁ =

2α(μ₁)ω∥x₀∥ - Dh(μ₁) 1 - ω

1-ω

2α(μ₁)ω∥x₀∥ - Dh(μ₁)

D(1 - ω)

Таким образом, из начального положения x₀ ε-поимка происходит за конечное время

T (ω, μ₁), которое определяется равенством

∥x₀∥²(1 + ω)

h(μ₁)

T (ω, μ₁) =

(24)

2α(μ₁)ω∥x₀∥ - Dh(μ₁)

D(1 - ω)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

ОЦЕНКА ВРЕМЕНИ ПОИМКИ И ПОСТРОЕНИЕ СТРАТЕГИИ ПРЕСЛЕДОВАТЕЛЯ

267

2⁰. В этом пункте доказательства оценим время поимки, используя равенство (24). На

основе построения данной оценки покажем выполнение свойств из условия теоремы.

Обозначим

μ = min{1,(L₁ + L₂)ω∥x₀∥/D}.

Отметим, что в силу (18) число T (ω, μ₁) определено для каждого μ₁ ∈ (0, μ]. Так как функция

h(·) является строго возрастающей, a α(·) - строго убывающей, то

inf

T (ω, μ₁) = lim

T (ω, μ₁).

μ₁∈(0,μ]

μ₁→0+

Найдём, используя определения (9) и (10), значение последнего предела, которое обозначим

через T (ω, 0), т.е.

(

)

∥x₀∥²(1 + ω)

h(μ₁)

∥x₀∥²(1 + ω)

lim

T (ω, μ₁) = lim

μ₁→0+

2α(μ₁)ω∥x₀∥ - Dh(μ₁)

D(1 - ω)

2α(x₀)ω∥x₀∥

Таким образом, для любого ω ∈ (0, 1) ε-поимка происходит за любое время T > T (ω, 0).

Функция T (ω, 0) является строго убывающей при ω ∈ (0, 1). Поэтому

∥x₀∥²(1 + ω)

∥x₀∥

inf

T (ω, 0) = lim

= T(x₀).

ω∈(0,1)

ω→1-

ω→1- 2α(x₀)ω∥x₀∥

α(x₀)

Покажем, что за время T (x₀) происходит ε-поимка. В силу построения ε-поимка проис-

ходит за любое время T > T (x₀). Пусть δ > 0, T = T (x₀) + δ/(2D). Тогда за время T

происходит ε-поимка. Следовательно, существует кусочно-постоянная стратегия преследова-

теля такая, что ∥x(τ)∥ < δ/2 для некоторого τ ∈ [0, T ]. В силу определений (8) справедливо

неравенство

|∥x(τ)∥ - ∥x(τ - δ/(2D))∥| ≤ Dδ/(2D) = δ/2.

Поэтому ∥x(τ - δ/(2D))∥ ≤ ∥x(τ)∥ + δ/2 < δ. При этом τ - δ/(2D) ≤ T (x₀). Таким образом,

доказано, что за время T (x₀) происходит ε-поимка. Следовательно, свойство 1) из формули-

ровки теоремы выполнено.

Приведём пример, для которого выполнено свойство 2) из формулировки теоремы. Рас-

смотрим в случае k = s = 2 систему

x₁ = u₁ + v₁,

x₂ = u₂ + v₂,

(

)

(

)

(

)

u₁

v₁

f (x, u) =

g(x, v) =

x₀ =

u₂

v₂

{(

)

(

)

(

)

(

)}

(

)

1.5

-1.5

1.5

U =

V = [-1,1] × [-1,1], v(t) ≡

t ≥ 0.

1.5

-1.5

Отметим, что здесь, согласно теореме 1, ε-поимка будет происходить из любого начального

положения x₀ ∈ R². Для данного примера α(x₀) = 0.5, T (x₀) = 2.

Оценим x₂(t):

∫t

∫

x₂(t) = 1 + (u₂(s) + 1)ds ≥ 1 +

(-1.5 + 1) ds = 1 - 0.5t.

Отсюда если T ∈ [0, 2), то x(T ) ∈ O1-0.5T (0). Следовательно, ε-поимка не происходит за

время T < 2 = T (x₀). Таким образом, справедливо и свойство 2) из формулировки теоремы.

Теорема доказана.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

268

ЩЕЛЧКОВ

4. Компьютерное моделирование. Рассмотрим дифференциальную игру в R². Систе-

ма (2) дифференциальных уравнений имеет вид

(

)

(

)

x₁ = u₁ cos(|x₁| + |x₂|) - u₂ sin(|x₁| + |x₂|) + v₁ cos

- |x₁| - |x₂|

- v2 sin

- |x₁| - |x₂|

(

)

(

)

x₂ = u₁ sin(|x₁| + |x₂|) + u₂ cos(|x₁| + |x₂|) + v₁ sin

- |x₁| - |x₂|

+ v2 cos

- |x₁| - |x₂|

{(

)

(

)

(

)

(

)}

-1

u(t) = (u₁(t), u₂(t)) ∈ U =

-1

{(

)

(

)

(

)

(

)}

0.5

-0.5

0.5

v(t) = (v₁(t), v₂(t)) ∈ V = co

0.5

-0.5

с начальным условием

(

)

(

)

x₀₁

0.2

x₀ =

x₀₂

Таким образом,

(

)

f (x, u) = A(|x₁| + |x₂|)u, g(x, v) = A

- |x₁| - |x₂| v,

где A(·) - матрица поворота, u = (u₁, u₂)^т, v = (v₁, v₂)^т.

Данная система удовлетворяет условиям теоремы 1, причём ε-поимка происходит при лю-

бом x₀ ∈ R². Система имеет следующие параметры:

√

α(x₀) = 1 - 0.5

2, L₁ = 2

2, L₂ =

2, D = 1.5

Выберем δ = 0.1. Тогда согласно теореме 2 для перевода траектории системы в шар D_δ(0)

√

достаточно использовать фиксированный шаг разбиения Δ ≤ (1 - 0.5

2)/18. Выберем Δ =

= 0.0162.

Приближённое решение данной системы находим методом Рунге-Кутты третьего порядка с

шагом 10-4. Управление убегающего на каждом шаге метода постоянное, его выбор осуществ-

ляется из следующего максимума: max〈g(x, v), x/∥x∥〉 = 〈g(x, v), x/∥x∥〉, где

x - положение

v∈V

на начало шага метода.

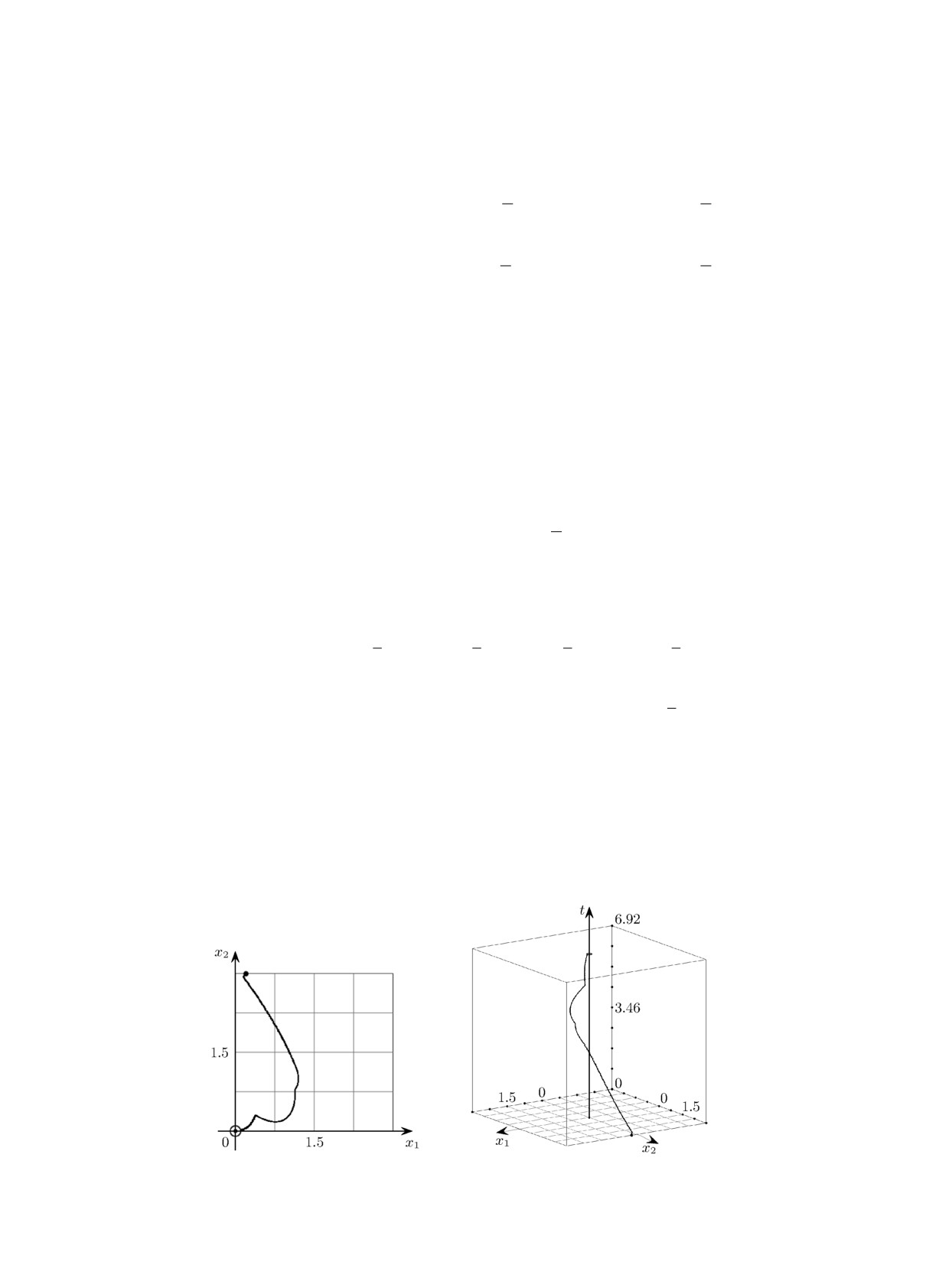
Результат моделирования: время достижения шара D_δ(0) равно T_δ = 6.9187; траекто-

рия системы и полученное решение представлены на рис. 2 и 3. Отметим, что T_δ < T ((1 -

- δ/∥x₀∥)x₀) ≈ 9.9239.

Рис. 2. Полученная траектория

Рис. 3. Полученное решение

(x1(t),x2(t)).

(x1(t),x2(t), t).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022

ОЦЕНКА ВРЕМЕНИ ПОИМКИ И ПОСТРОЕНИЕ СТРАТЕГИИ ПРЕСЛЕДОВАТЕЛЯ

269

Заключение. Для одного класса нелинейных дифференциальных игр преследования по-

казано, что можно использовать стратегию преследователя с постоянным шагом разбиения

временного интервала. Получена оценка времени поимки из заданного начального положе-

ния, которая в определённом смысле является неулучшаемой.

Работа выполнена при поддержке Минобрнауки РФ в рамках государственного задания

№ 075-01265-22-00 (проект FEWS-2020-0010) и Российского фонда фундаментальных иссле-

дований (проект 20-01-00293). При выполнении исследований использовались вычислитель-

ные ресурсы центра коллективного пользования ИММ УрО РАН “Суперкомпьютерный центр

ИММ УрО РАН”.

СПИСОК ЛИТЕРАТУРЫ

1. Isaacs R. Differential Games. New York, 1965.

2. Blaquiere A., Gerard F., Leitmann G. Quantitative and Qualitative Differential Games. New York, 1969.

3. Красовский Н.Н. Игровые задачи о встречe движений. М., 1970.

4. Friedman A. Differential Games. New York, 1971.

5. Hajek O. Pursuit Games. New York, 1975.

6. Leitmann G. Cooperative and Noncooperative Many-Player Differential Games. Vienna, 1974.

7. Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М., 1974.

8. Никольский М.С. Одна нелинейная задача преследования // Кибернетика. 1973. № 2. С. 92-94.

9. Пшеничный Б.Н., Шишкина Н.Б. Достаточные условия конечности времени преследования

// Прикл. математика и механика. 1985. Т. 49. Вып. 4. С. 517-523.

10. Двуреченский П.Е., Иванов Г.Е. Алгоритмы вычисления операторов Минковского и их применение

в дифференциальных играх // Журн. вычислит. математики и мат. физики. 2014. Т. 54. № 2.

С. 224-255.

11. Ушаков В.Н., Ершов А.А. К решению задачи управления с фиксированным моментом окончания

// Вестн. Удмуртского ун-та. Математика. Механика. Компьютерные науки. 2016. Т. 26. Вып. 4.

С. 543-564.

12. Петров Н.Н. Об управляемости автономных систем // Дифференц. уравнения. 1968. Т. 4. № 4.

C. 606-617.

13. Петров Н.Н. Локальная управляемость автономных систем // Дифференц. уравнения. 1968. Т. 4.

№ 7. C. 1218-1232.

14. Нарманов А.Я., Петров Н.Н. Нелокальные проблемы теории оптимальных процессов. I // Диффе-

ренц. уравнения. 1985. Т. 21. № 4. C. 605-614.

15. Нарманов А.Я. О стабильности вполне управляемых систем // Дифференц. уравнения. 2000. Т. 36.

№ 10. C. 1336-1344.

16. Нарманов А.Я. О стабильности вполне управляемых систем // Мат. тр. 2001. Т. 4. № 1. C. 94-110.

17. Банников А.С., Петров Н.Н. К нестационарной задаче группового преследования // Тр. Ин-та

математики и механики УрО РАН. 2010. Т. 16. № 1. C. 40-51.

18. Петров Н.Н. Одна задача простого преследования с фазовыми ограничениями // Автоматика и

телемеханика. 1992. № 5. C. 22-26.

19. Петров Н.Н. Одна задача группового преследования с дробными производными и фазовыми огра-

ничениями // Вестн. Удмуртского ун-та. Математика. Механика. Компьютерные науки. 2017. Т. 27.

№ 1. С. 54-59.

20. Петров Н.Н., Соловьева Н.А. Многократная поимка в рекуррентном примере Л.С. Понтрягина с

фазовыми ограничениями // Тр. Ин-та математики и механики УрО РАН. 2015. Т. 21. № 2. С. 178-

186.

21. Виноградова М.Н., Петров Н.Н., Соловьева Н.А. Поимка двух скоординированных убегающих в

линейных рекуррентных дифференциальных играх // Тр. Ин-та математики и механики УрО РАН.

2013. Т. 19. № 1. С. 41-48.

22. Щелчков К.А. Об одной нелинейной задаче преследования с дискретным управлением и неполной

информацией // Вестн. Удмуртск. ун-та. Математика. Механика. Компьютерные науки. 2018. Т. 28.

№ 1. С. 111-118.

Удмуртский государственный университет,

Поступила в редакцию 03.06.2021 г.

г. Ижевск

После доработки 14.01.2022 г.

Принята к публикации 24.02.2022 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№2

2022