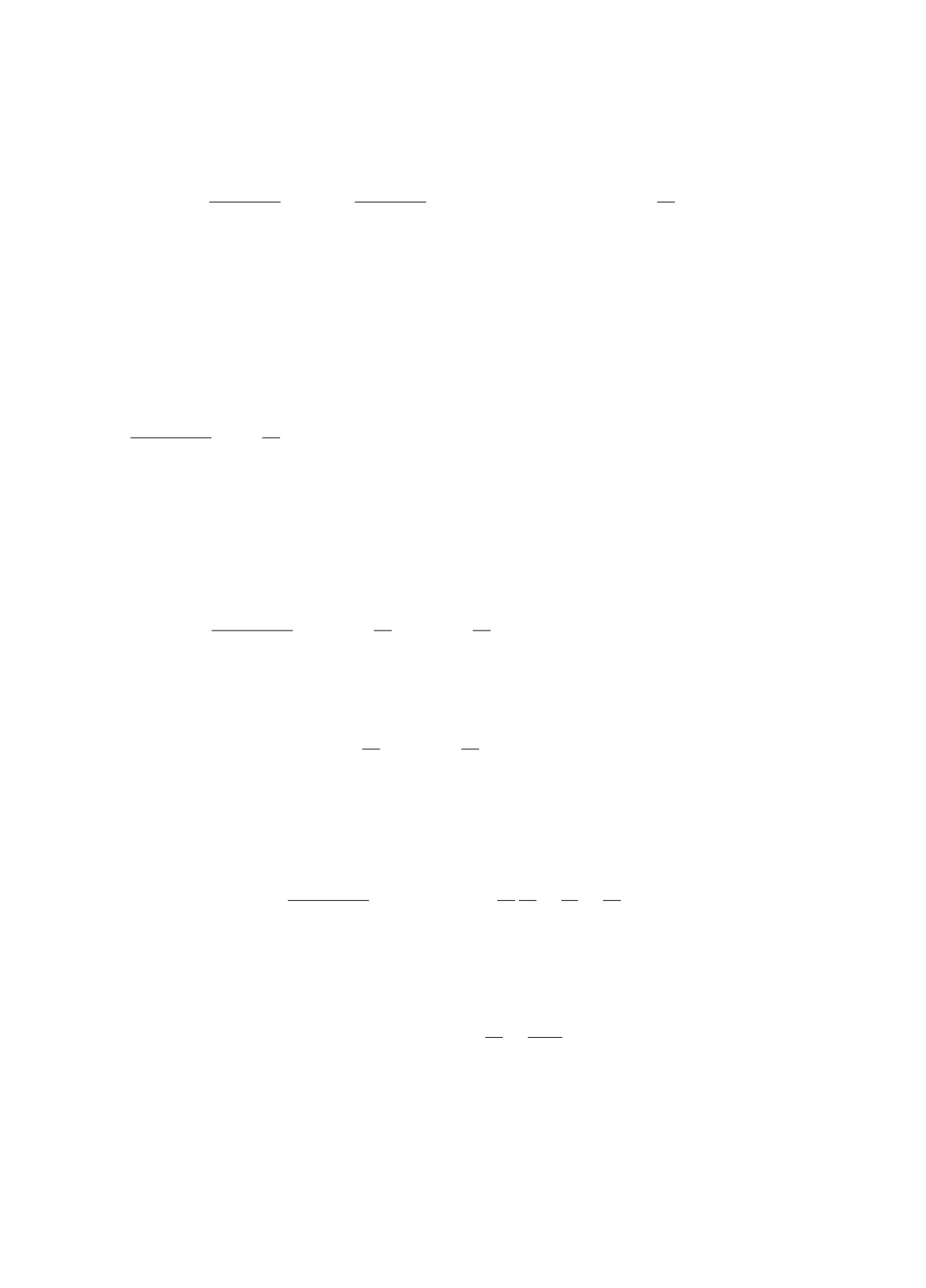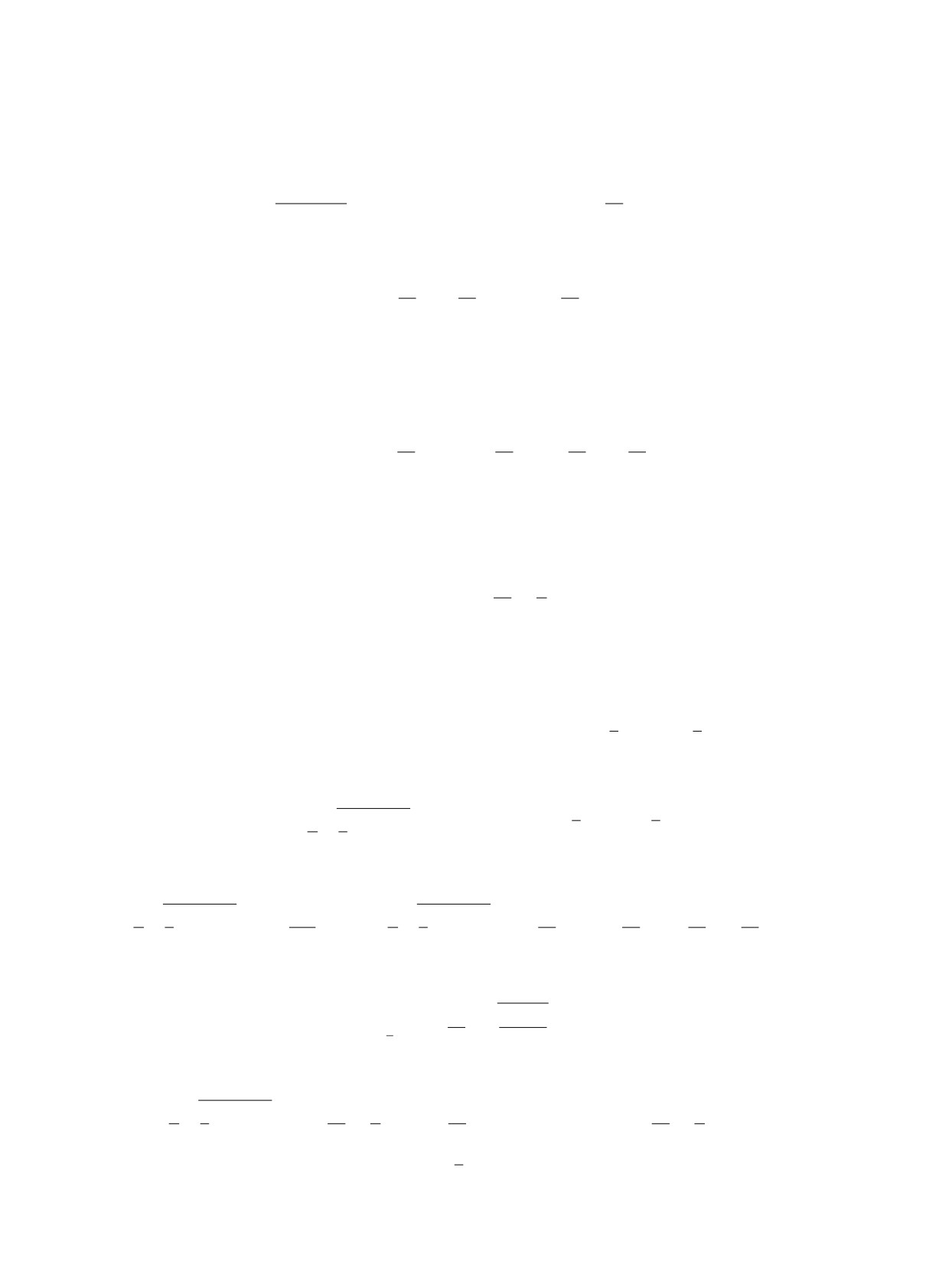ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 3, с.291-300

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.925.42

ГЛОБАЛЬНОЕ АЛГЕБРАИЧЕСКОЕ

КОЛЬЦО ПУАНКАРЕ-БЕНДИКСОНА

ДЛЯ СИСТЕМЫ ВАН ДЕР ПОЛЯ

Для системы Ван дер Поля аналитически построены две замкнутые алгебраические кри-

вые, образующие кольцо Пуанкаре-Бендиксона для вceх значений eё параметра. Внут-

ренняя граница кольца представляет собой замкнутую кривую нулевого уровня функции

Дюлака-Черкаса, поэтому это кольцо содержит не более одного предельного цикла. Внеш-

няя граница кольца строится с помощью специальной процедуры.

DOI: 10.31857/S0374064122030013, EDN: BWZAUY

Введение. В качественной теории автономных систем на плоскости

= P(x,y),

= Q(x,y)

(1)

фундаментальную роль играет специальный класс ω-предельных множеств, называемых пре-

дельными циклами. Общий подход к доказательству существования хотя бы одного предельно-

го цикла в системе (1) состоит в построении на фазовой плоскости такого кольца (кольцеобраз-

ной области) A, которое не содержит состояний равновесия и границы которого представляют

собой простые замкнутые кривые (называемые далее овалами), обладающие тем свойством,

что любая траектория системы (1) сразу после попадания в некоторый момент времени на

границу кольца A входит в него либо при увеличении, либо при уменьшении времени t (см.,

например, [1, с. 159]). Указанное кольцо называют кольцом Пуанкаре-Бендиксона, поскольку

применение теоремы Пуанкаре-Бендиксона [2, с. 187; 3, с. 244] к этому кольцу гарантиру-

ет существование хотя бы одного лежащего в нём предельного цикла системы (1). Далее мы

называем трансверсальными овалами системы (1) гладкие замкнутые кривые, которые не про-

ходят через особые точки системы и такие, что в любой их точке касательный вектор и вектор

поля системы не коллинеарны. Будем также предполагать, что границы кольца Пуанкаре-

Бендиксона являются трансверсальными овалами.

Ключевая проблема в этом подходе заключается в построении трансверсальных вектор-

ному полю овалов. Общей процедуры их построения нет. Ранее кольца Пуанкаре-Бендиксона

были найдены для систем типа Льенара; в них границы состоят из кусочно гладких кривых,

построенных довольно сложным образом (см., например, [4; 5, с. 249; 3, с. 253; 1, с. 303; 6].

В недавних работах [7, 8] для полиномиальных систем (1) построены гладкие трансверсаль-

ные овалы, являющиеся границами кольца Пуанкаре-Бендиксона. Для обеих работ харак-

терно, что каждый трансверсальный овал строится с помощью аппроксимации траекторий

системы (1). В статье [7] для построения внутренней и внешней границ кольца A требуется

аппроксимация двух разных траекторий, а в статье [8] - аппроксимация только одной траек-

тории, но предполагается, что эта траектория является предельным циклом.

В данной работе для системы Ван дер Поля для построения её трансверсальных овалов,

зависящих от параметра λ системы и образующих кольцо Пуанкаре-Бендиксона A(λ), пред-

лагается чисто аналитический подход, который не требует аппроксимации какой-либо траек-

тории. Особенности этого подхода заключаются в следующем.

(а) Овалы представляют собой алгебраические кривые и образуют кольцо Пуанкаре-Бен-

диксона при всех значениях параметра λ, при этом никаких ограничений на расположение

содержащегося в нём предельного цикла не предполагается (кольцо Пуанкаре-Бендиксона,

291

292

ГРИНЬ, ШНАЙДЕР

при построении которого не накладывается никаких ограничений на значения параметра и ло-

кализацию содержащегося в нём предельного цикла, будем называть глобальным, а поскольку

его границы, как сказано, - алгебраические кривые, то глобальным алгебраическим кольцом

Пуанкаре-Бендиксона).

(б) Внутренний трансверсальный овал состоит из овала, содержащегося в множестве ну-

левого уровня функции Дюлака-Черкаса для системы Ван дер Поля. Это свойство означает,

что система Ван дер Поля имеет не более одного предельного цикла Γ(λ) и, если цикл Γ(λ)

существует, он является грубым.

(в) Способ построения внешнего трансверсального овала состоит в нахождении многочлена

∑2N

O(x, y, λ) от x и y вида

p_i(x,λ)yⁱ, где N ∈ N - некоторое число, такого, что его мно-

i=0

жество O нулевого уровня содержит овал, который можно использовать в качестве внешней

границы. Полиномы p_i(x, λ) от переменной x с коэффициентами, зависящими от λ, опреде-

ляются с помощью решения дифференциальных уравнений с разделяющимися переменными.

(г) Если A(λ) является кольцом Пуанкаре-Бендиксона для системы Ван дер Поля, то

по нему можно построить кольцо Пуанкаре-Бендиксона для любой системы на плоскости,

которая линейно топологически эквивалентна системе Ван дер Поля.

Структура работы следующая. В п. 1 содержатся нужные в дальнейшем сведения о функ-

ции Дюлака-Черкаса и доказывается инвариантность свойства трансверсальности для ова-

ла при линейном гомеоморфизме. В п. 2 вводятся три системы, которые линейно топологи-

чески эквивалентны уравнению Ван дер Поля при λ > 0. Построению кольца Пуанкаре-

Бендиксона, внутренняя граница которого представляет собой множество нулевого уровня

функции Дюлака-Черкаса, посвящён п. 3. В этом пункте подробно описывается новая проце-

дура построения внешней границы в виде алгебраического овала. В п. 4 представлены глобаль-

ные алгебраические кольца Пуанкаре-Бендиксона для системы Ван дер Поля и двух линейно

топологически эквивалентных систем, включая сингулярно возмущённую систему.

1. Предварительные сведения. Начнём с определения линейной топологической экви-

валентности планарных автономных систем. Далее предполагаем, что выполнено условие

(A). Множества G и G₁ - открытые подмножества плоскости R², Λ - открытый интервал

прямой R, функции P и Q принадлежат классу C1(x,y)0λ(G × Λ, R), а функции P₁ и Q₁ -

классу C1(x,y)0λ(G₁ × Λ, R).

При λ ∈ Λ рассмотрим планарную автономную параметрическую систему

= P(x,y,λ),

= Q(x,y,λ)

(2)

на множестве G и планарную автономную параметрическую систему

= P₁(u,v,λ),

= Q₁(u,v,λ)

(3)

dτ

на множестве G₁.

Определение 1. Пусть выполняется условие (A). Системы (2) и (3) называются (линейно)

топологически эквивалентными, если для каждого λ ∈ Λ существует (линейный) гомеомор-

физм h(λ), отображающий G на G₁ и переводящий траектории системы (2) в траектории

системы (3), а независимые переменные t и τ этих систем связаны равенством τ = g(λ)t, где

g(λ) - возрастающий гомеоморфизм интервала Λ.

Согласно этому определению топологически эквивалентные планарные автономные систе-

мы имеют одинаковую топологическую структуру своих траекторий. Позже будет использо-

вана следующая

Лемма 1. Пусть выполняется условие (A) и системы (2) и (3) линейно топологически

эквивалентны при λ ∈ Λ, где соответствующий линейный гомеоморфизм представляется

2×2-матрицей T(λ). Тогда если O(λ) - трансверсальный овал системы (2), то T(λ)O(λ) -

трансверсальный овал системы (3).

Доказательство. Пусть p(λ) - точка на O(λ) такая, что вектор t_a(λ) поля системы

(2) в точке p(λ) не коллинеарен касательному вектору t_o(λ) к овалу O(λ) в точке p(λ).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

ГЛОБАЛЬНОЕ АЛГЕБРАИЧЕСКОЕ КОЛЬЦО

293

Если предположить, что вектор T (λ)t_a(λ) векторного поля системы (3) в точке T (λ)p(λ)

коллинеарен касательному вектору T (λ)t_o(λ) к овалу T (λ)O(λ) в точке T (λ)p(λ), то из

обратимости матрицы T (λ) при λ ∈ Λ следует, что вектор t_a(λ) векторного поля системы

(2) в точке p(λ) коллинеарен касательному вектору t_o(λ) к овалу O(λ) в p(λ). Полученное

противоречие доказывает лемму. Лемма доказана.

Важным инструментом качественного исследования топологической структуры траекто-

рий системы (2) является функция Дюлака (см., например, [3, с. 264]). Для её определения

обозначим через X(λ) векторное поле, задаваемое системой (2).

Определение 2. Пусть выполняется условие (A). Функция B ∈ C1(x,y)0λ(G × Λ, R) назы-

вается функцией Дюлака для системы (2) при λ ∈ Λ в области G, если выражение

∂(BP )

∂(BQ)

div (BX) ≡

≡ (grad B, X) + B div X

∂x

∂y

не изменяет знак в G и обращается в нуль только на множестве нулевой меры Лебега.

Из существования функции Дюлака вытекает следующая оценка числа предельных циклов

системы (2) в области G [2, с. 189].

Предложение. Пусть выполняется условие (A) и в p-связной (p ≥ 1) области G ⊂ R²

для системы (2) при λ ∈ Λ существует функция Дюлака B. Тогда система (2) имеет не

более p - 1 предельных циклов, целиком расположенных в G.

Метод функции Дюлака обобщён Л.А. Черкасом в 1997 г. (см. [9]). Соответствующая обоб-

щённая функция Дюлака, называемая также функцией Дюлака-Черкаса (см. [10]), определя-

ется следующим образом.

Определение 3. При выполнении условия (A) функция Ψ ∈ C1(x,y)0λ(G ×Λ, R) называется

функцией Дюлака-Черкаса системы (2) в области G, если существует действительное число

κ = 0 такое, что

Φ := (grad Ψ, X) + κΨ div X > 0

(< 0) в G.

(4)

Замечание 1. В случае κ = 1 функция Ψ является функцией Дюлака.

Замечание 2. Условие (4) можно ослабить, допуская, что функция Φ может обращаться в

нуль в G на множестве меры нуль и что ни один овал этого множества не является предельным

циклом системы (2).

Аналитический подход к построению функций Дюлака-Черкаса для класса систем Льена-

ра описан в [11].

Введём множество W(λ) := {(x, y) ∈ G : Ψ(x, y, λ) = 0}.

Из неравенства (4) и замечания 2 вытекает

Лемма 2. Если подмножество W(λ) содержит овал, то он является трансверсальным

овалом системы (2).

Следующую теорему можно найти в [9].

Теорема 1. Пусть при выполнении условия (A) функция Ψ является функцией Дюлака-

Черкаса для системы (2) при λ ∈ Λ в области G. Тогда любой предельный цикл Γ(λ) этой

системы, расположенный целиком в G, обладает следующими свойствами:

(i) Γ(λ) не пересекается с множеством W(λ);

(ii) предельный цикл Γ(λ) является грубым;

(iii) устойчивость цикла Γ(λ) определяется знаком выражения κΦΨ на Γ(λ).

Следствие. Из свойства (ii) следует, что существование функции Дюлака-Черкаса озна-

чает отсутствие у системы (2) кратного предельного цикла.

Следующий результат о верхней границе числа предельных циклов доказан в [10].

Теорема 2. Пусть при выполнении условия (A) в p-связной области G для системы (2)

при λ ∈ Λ существует функция Дюлака-Черкаса Ψ такая, что множество W(λ) состоит

из s овалов в G. Тогда система (2) имеет для λ ∈ Λ не более p - 1 + s предельных циклов

в G и все предельные циклы гиперболические.

В случае p = s = 1 теорема 2 формулируется следующим образом.

Теорема 3. Пусть при выполнении условия (A) в односвязной области G для систе-

мы (2) при λ ∈ Λ существует функция Дюлака-Черкаса Ψ такая, что множество W(λ)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

294

ГРИНЬ, ШНАЙДЕР

состоит из одного овала. Тогда система (2) имеет при λ ∈ Λ не более одного предельного

цикла Γ(λ) в G. Если цикл Γ(λ) существует, то он окружает множество W(λ).

Отметим, что метод функций Дюлака-Черкаса использовался также в работах [12, 13].

2. Система Ван дер Поля и три линейно топологически эквивалентные ей систе-

мы. Скалярное автономное параметрическое дифференциальное уравнение второго порядка

d²x

+ λ(x² - 1)

+ x = 0,

(5)

dt²

где λ - вещественный параметр, введено Бальтазаром Ван дер Полем [14] в 1926 г. для опи-

сания автоколебаний в триодной схеме. Если заменить t на -t и λ на -λ, то уравнение (5)

не изменится. Таким образом, при изучении фазового портрета системы

= -y,

= x - λ(x² - 1)y,

(6)

которая соответствует уравнению (5), можно ограничиться случаем λ > 0.

Хорошо известно (см., например, [3, с. 254]), что система (6) имеет для любого λ = 0

единственный предельный цикл Γ(λ), который рождается из периодического решения, когда

параметр λ переходит через нулевое значение.

С помощью линейного преобразования

u = x, λv = y, τ = λt

(7)

получаем из системы (6) при λ > 0 линейно топологически эквивалентную ей систему

= -v,

u - (u² - 1)v.

(8)

dτ

λ²

Для системы (8) при достаточно больших λ в работе [6] построено кольцо Пуанкаре-

Бендиксона такое, что внутренняя его граница при любом λ представляет собой трансверсаль-

ный овал системы (8) и определяется множеством нулевого уровня функции Дюлака-Черкаса

для этой системы, а для построения внешней границы кольца разработана специальная мето-

дика, основанная на теории поворота векторных полей.

Далее представлен новый подход к построению трансверсального алгебраического овала

системы, который при любом λ > 0 можно использовать в качестве внешней границы B^o(λ)

для глобального алгебраического кольца Пуанкаре-Бендиксона B(λ) системы (8). Этот под-

ход применён в работе к построению трансверсальных алгебраических овалов системы Ван

дер Поля и получающихся из этой системы линейными преобразованиями вводимых ниже

дифференциальных систем (10) и (12).

Используя линейное преобразование

√

λx, v =

λy,

(9)

получаем из системы (6) линейно топологически эквивалентную ей систему

= -v,

= u + λv - u²v.

(10)

Понятно, что системы (6) и (10) имеют при λ > 0 единственный предельный цикл, но в

отличие от системы (6) предельный цикл системы (10) порождается бифуркацией Андронова-

Хопфа, когда параметр λ переходит через нулевое значение.

Наконец, применяя к системе (6) при λ > 0 линейное преобразование

u = x, v = λy, τ = t/λ, ε = 1/λ²,

(11)

получаем линейно топологически эквивалентную ей систему

= -v, ε

= u - (u² - 1)v,

(12)

dτ

представляющую собой при больших значениях λ сингулярно возмущённую систему.

В следующем пункте строится глобальное алгебраическое кольцо Пуанкаре-Бендиксона

для системы (8).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

ГЛОБАЛЬНОЕ АЛГЕБРАИЧЕСКОЕ КОЛЬЦО

295

3. Построение глобального алгебраического кольца Пуанкаре-Бендиксона для

системы (8). Система (8) имеет при всех λ в начале координат единственное состояние рав-

новесия, являющееся фокусом или узлом. Таким образом, любой её предельный цикл должен

окружать начало координат. Наша цель - построить два непересекающихся алгебраических

трансверсальных овала Bⁱ(λ) и B^o(λ) этой системы, окружающих начало координат, которые

можно взять в качестве границ алгебраического кольца Пуанкаре-Бендиксона B(λ). Соглас-

но лемме 2 одна из возможностей построения трансверсального овала автономной системы

состоит в использовании множества нулевого уровня W(λ) функции Дюлака-Черкаса. В ра-

боте [6] доказан следующий результат.

Лемма 3. Полином Ψ(u, v, λ) := u² + λ²v² - 1 представляет собой функцию Дюлака-

Черкаса для системы (8) при λ > 0 в R², множество нулевого уровня W(λ) которой явля-

ется эллипсом

Bⁱ(λ) := {(u,v) ∈ R² : u² + λ²v² = 1}.

Производная функции Ψ в силу системы (8) на Bⁱ(λ) положительна за исключением точек

(-1, 0) и (1, 0), в которых эта производная принимает нулевое значение.

Согласно лемме 2 справедлива

Лемма 4. Эллипс Bⁱ(λ) может быть использован в качестве внутренней границы коль-

ца Пуанкаре-Бендиксона для системы (8) при любых λ > 0.

Опишем новый подход, о котором говорилось выше, к построению трансверсального ал-

гебраического овала системы (8). Этот овал можно использовать в качестве внешней грани-

цы B^o(λ) для глобального алгебраического кольца Пуанкаре-Бендиксона.

Наша дальнейшая цель заключается в построении многочлена O(u, v, λ) от u и v в одном

из следующих видов:

∑

O(u, v, λ) :=

a_ij(λ)uⁱv^j, O(u,v,λ) :=

p_j(u,λ)v^j или O(u,v,λ) :=

q_i(v,λ)uⁱ,

i+j=0

j=0

i=0

где N - натуральное число, которое необходимо выбрать, p_j - многочлены от u с коэффи-

циентами, зависящими от λ, а q_i - многочлены от v с коэффициентами, зависящими от λ,

такого, что:

1) множество N (λ), на котором производная функции O в силу системы (8) принимает

нулевые значения и изменяет знак, состоит из овала C(λ), окружающего внутреннюю грани-

цу Bⁱ(λ);

2) множество нулевого уровня многочлена O(u, v, λ) содержит при λ > 0 овал O(λ),

окружающий C(λ).

Тогда овал O(λ) представляет собой глобальный трансверсальный алгебраический овал

системы (8).

Далее полагаем N = 1 и используем представление

O(u, v, λ) := O₀(u, λ) + O₁(u, λ)v + O₂(u, λ)v²,

где функции O_i(u, λ), i = 0, 1, 2, являются полиномами по u, которые нужно определить.

Дифференцируя функцию O в силу системы (8), получаем



(

)

dO(u, v, λ)

dO₀(u, λ)



= O₁(u,λ)

- O₁(u,λ)(u² - 1) + O₂(u,λ)

u v-



dτ

λ²

(8)

(

)

dO₁(u, λ)

dO₂(u, λ)

−

+ O₂(u,λ)2(u² - 1) v² -

v³.

(13)

Для того чтобы множество

{



}

dO(u, v, λ)



N (λ) := (u, v) ∈ R² :



dτ

(8)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

296

ГРИНЬ, ШНАЙДЕР

в фазовой плоскости содержало овал C(λ), на котором производная dO(u, v, λ)/dτ |₍₈₎ изме-

няет знак, потребуем выполнения тождеств

dO₂(u, λ)

dO₀(u, λ)

≡ 0,

- O₁(u,λ)(u² - 1) + O₂(u,λ)

u≡0

(14)

λ²

и будем предполагать, что функция O₁(u, λ)u является чётной по u.

Функцию O₁ будем искать в виде

O₁(u,λ) ≡ c₁(λ)u + c₃(λ)u³;

(15)

в силу (14) имеем

O₂(u,λ) ≡ c₂(λ).

(16)

С учётом тождеств (14)-(16) производная (13) принимает вид



dO(u, v, λ)



(c₁(λ)u² + c₃(λ)u⁴) + (-(c₁(λ) + 3c₃(λ)u²) - 2c₂(λ)(u² - 1))v².

(17)



dτ

λ²

(8)

Далее мы хотим гарантировать, чтобы знак выражения в квадратных скобках из равенства

(17) не зависел от u. Для этого полагаем

c₁(λ) = 2c₂(λ)

(18)

и, таким образом, имеем



)

dO(u, v, λ)

⁽ 1



=u²

c₃(λ)u² +

c₂(λ) - (3c₃(λ) + 2c₂(λ))v2



dτ

λ²

(8)

Если потребовать выполнения неравенств c₃(λ) < 0, c₂(λ) > 0 и 3c₃(λ) + 2c₂(λ) > 0, то

множество N (λ) содержит эллипс

C(λ) := {(u, v) ∈ R² :

c₃(λ)u² +

c₂(λ) - (3c₃(λ) + 2c₂(λ))v² = 0},

λ²

на котором производная dO(u, v, λ)/dτ |₍₈₎ изменяет знак. Затем, положив

c₂(λ) = -3c₃(λ),

(19)

получим



(

)

dO(u, v, λ)

1 u²

v²



= 6u²c₃(λ)

(20)



dτ

λ² 6

λ²

(8)

В итоге пришли к следующему результату.

Лемма 5. Производная dO(u, v, λ)/dτ |₍₈₎ при λ > 0 принимает нулевое значение при

u = 0 и положительна (отрицательна) во всех остальных точках области, расположенных

внутри (вне) эллипса

{

}

u²

λ²v²

C(λ) := (u, v) ∈ R² :

=1 .

Очевидна

Лемма 6. Эллипс C(λ) окружает эллипс Bⁱ(λ) при любом λ > 0.

На последнем шаге мы должны убедиться, что внешняя граница O(λ) окружает эллипс

C(λ). Из тождеств (15), (18) и (19) следуют равенства

O₁(u,λ) = c₃(λ)(-6u + u³), O₂(u,λ) = -3c₃(λ).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

ГЛОБАЛЬНОЕ АЛГЕБРАИЧЕСКОЕ КОЛЬЦО

297

Подставляя эти выражения для функций O₁ и O₂ во второе тождество в (14), получаем для

функции O₀(u, λ) дифференциальное уравнение

(

)

dO₀(u, λ)

= -c₃(λ) (u² - 1)(-6u + u³) +

λ²

которое имеет первый интеграл

(

)

O₀(u,λ) = -3c₃(λ)

u⁶ -

u⁴ +

u² + c₀(λ) ;

λ²

здесь c₀(λ) - произвольная непрерывная функция. Следовательно, имеем

O(u, v, λ) = -3c₃(λ)P (u, v, λ),

где

(

)

(

)

u²

P (u, v, λ) := v² + vu 2-

+ 1+

u² -

u⁴ +

u⁶ + c₀(λ).

(21)

λ²

Поэтому множество нулевого уровня полинома O(u, v, λ) совпадает с множеством нулевого

уровня P(λ) полинома P (u, v, λ).

Далее докажем, что справедлива

Лемма 7. Для непрерывной функции c₀ : R⁺ → R^-, заданной равенством

c₀(λ) := -18 -

(22)

λ²

множество P(λ) представляет собой овал, который является центрально симметричным

и окружает эллипс C(λ).

Доказательство. Заметим, что множество P(λ) инвариантно относительно преобразо-

вания (u, v) → (-u, -v), т.е. центрально симметрично. Из равенств (21) и (22) следует, что

P(λ) - овал, окружающий начало координат.

√

Очевидно, что эллипс C(λ) пересекает ось u в точках (-

6,0) и (

6,0). Так как обе

кривые P(λ) и C(λ) центрально симметричны, то чтобы доказать, что P(λ) окружает C(λ),

достаточно установить неравенство

(

√

)

√

P u,

(6 - u²), λ

при

6≤u≤

Имеем

(

√

)

√

(

) (

)

u³

P u,

(6 - u²), λ

(6-u²)+

(6 - u²)

2u-

+ 1+

u²-

u⁴+

u⁶+c₀(λ).

3λ²

λ²

Используя очевидную оценку

(

)√

u³

6-u²

max

√

2u -

< 3,

0≤u≤

получаем

(

√

)

(

)

P u,

(6 - u²), λ

+ 1+

6 + 12 + c₀(λ) < 18 +

+ c₀(λ) = 0.

λ²

√

Такое же неравенство справедливо и при -

6 ≤ u < 0. Лемма доказана.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

298

ГРИНЬ, ШНАЙДЕР

Лемма 8. Овал

{

(

)

(

)

}

u²

B^o(λ) := (u,v) ∈ R : v² + vu 2-

+ 1+

u² -

u⁴ +

u⁶ - 18 -

λ²

может использоваться как внешняя граница кольца Пуанкаре-Бендиксона для системы (8).

Доказательство. По лемме 7 овал B^o(λ) является алгебраической кривой, окружающей

эллипс C(λ) при λ > 0. Из леммы 5 вытекает, что производная dO(u, v, λ)/dt|₍₈₎ принимает

на B^o(λ) отрицательные значения, за исключением двух точек на оси u = 0, в которых

производная обращается в нуль. Это означает, что любая траектория системы (8), попавшая

на овал B^o(λ), пересекает его. Лемма доказана.

Из лемм 4 и 8 следует основной результат работы.

Теорема 4. При всех λ > 0 кольцо B(λ), ограниченное овалами Bⁱ(λ) и B^o(λ), явля-

ется глобальным алгебраическим кольцом Пуанкаре-Бендиксона, содержащим единственный

предельный цикл Γ(λ) системы (8).

Кольцо B(λ) вместе с предельным циклом Γ(λ) системы (8) для случаев λ² = 10 и λ² =

= 0.1 представлено на рис. 1.

Рис. 1. Кольцо B(λ) с предельным циклом Γ(λ) системы (8) при λ² = 10 (слева)

и λ² = 0.1 (справа).

4. Глобальные алгебраические кольца Пуанкаре-Бендиксона для системы Ван

дер Поля и линейно топологически эквивалентных ей систем. В п. 3 построено гло-

бальное алгебраическое кольцо Пуанкаре-Бендиксона для системы (8). Те же рассуждения,

что и для системы (8), можно применить к системе Ван дер Поля (6) и системам (10) и (12)

и получить соответствующие результаты. Однако нужные утверждения тривиально вытека-

ют из теоремы 4 и того, что системы (6), (10), (12) и (8) попарно линейно топологически

эквивалентны друг другу.

Согласно лемме 1, применив преобразование (7) к трансверсальным овалам Bⁱ(λ) и B^o(λ)

системы (8), получим трансверсальные овалы Aⁱ(λ) и A^o(λ) системы Ван дер Поля (6), об-

разующие кольцо A(λ), содержащее единственный предельный цикл Γ(λ). Далее, применяя

преобразование (9) к трансверсальным овалам системы Ван дер Поля, получаем трансвер-

сальные овалы для системы (10). Наконец, применяем преобразование (11) к трансверсальным

овалам системы Ван дер Поля для получения трансверсальных овалов системы (12). В итоге

приходим к следующим результатам.

Теорема 5. При λ > 0 овалы Aⁱ(λ) := {(x, y) ∈ R² : x² + y² = 1} и

{

(

)

}

x²

7λ²

λ²

A^o(λ) := (x,y) ∈ R² : y² + λyx 2-

+ (1 + λ²)x² -

x⁴ +

x⁶ - 8 - 3λ - 18λ² = 0

являются трансверсальными овалами системы Ван дер Поля (6) и образуют её глобальное ал-

гебраическое кольцо Пуанкаре-Бендиксона A(λ), содержащее единственный предельный цикл

Γ(λ) этой системы.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

ГЛОБАЛЬНОЕ АЛГЕБРАИЧЕСКОЕ КОЛЬЦО

299

На рис. 2 показано кольцо A(λ) вместе с предельным циклом Γ(λ) при значениях пара-

метра λ = 0.001 и λ = 3.

Рис. 2. Кольцо A(λ) с предельным циклом Γ(λ) системы (6) при λ = 0.001 (слева)

и λ = 3 (справа).

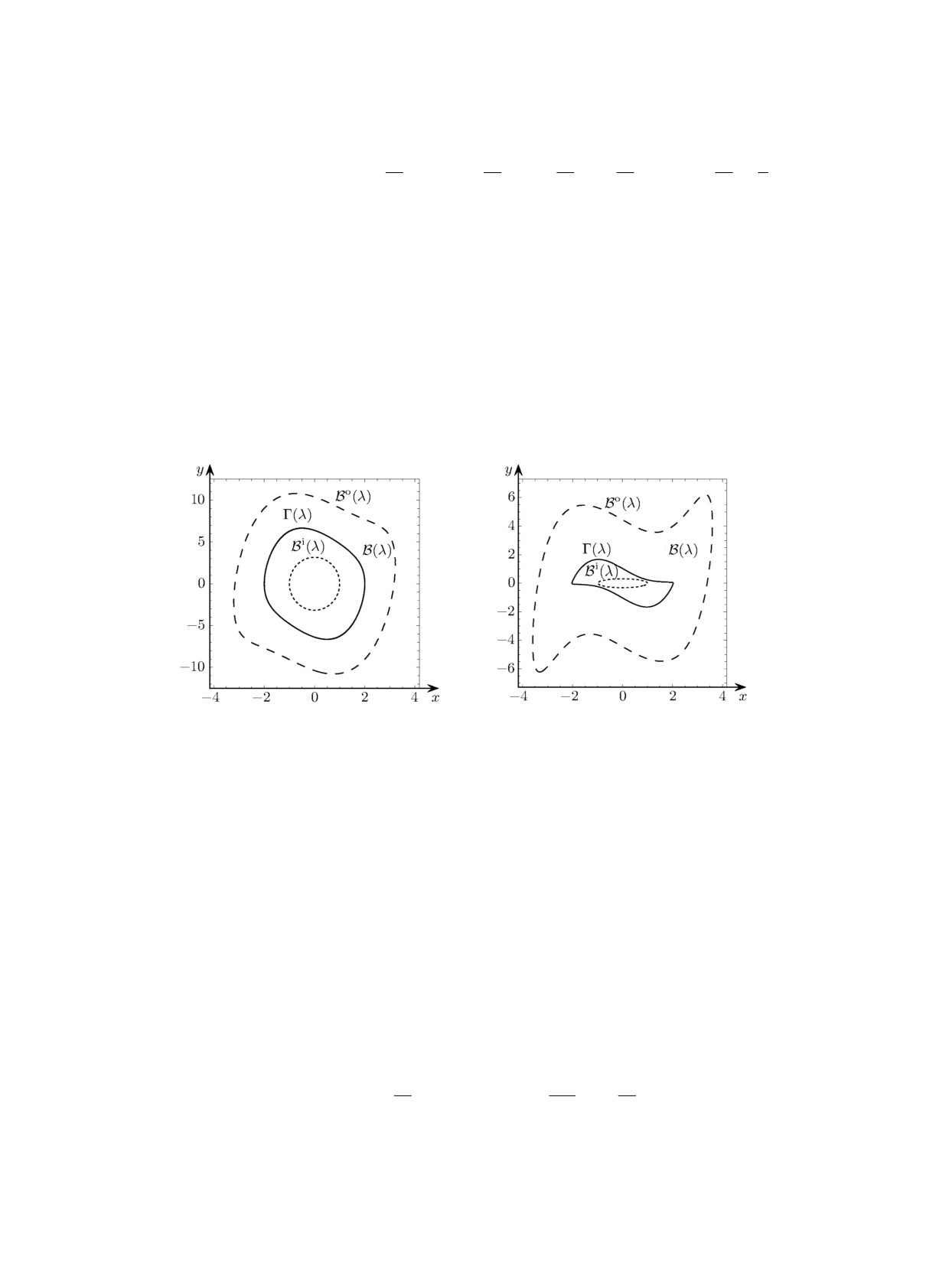
Теорема 6. При λ > 0 овалы Hⁱ(λ) := {(u, v) ∈ R² : u² + v² = λ} и

{

(

)

}

u²

7λ

u⁶

H^o(λ) := (u,v) ∈ R² : v² + vu 2λ -

+ (1 + λ²)u² -

u⁴ +

- 8λ - 3λ² - 18λ³ = 0

являются трансверсальными овалами системы (10) и образуют её глобальное алгебраическое

кольцо Пуанкаре-Бендиксона H(λ), содержащее единственный предельный цикл Γ(λ) этой

системы.

Замечание 3. Так как оба овала стягиваются к началу координат при стремлении λ к ну-

лю, то кольцо Пуанкаре-Бендиксона H(λ) отражает бифуркацию предельного цикла Γ(λ) из

начала координат (бифуркация Андронова-Хопфа) при переходе параметра λ через нулевое

значение.

На рис. 3 показано кольцо H(λ) вместе с предельным циклом Γ(λ) при значениях пара-

метра λ = 0.01 и λ = 1.

Рис. 3. Кольцо H(λ) с предельным циклом Γ(λ) системы (10) при λ = 0.01 (слева)

и λ = 1 (справа).

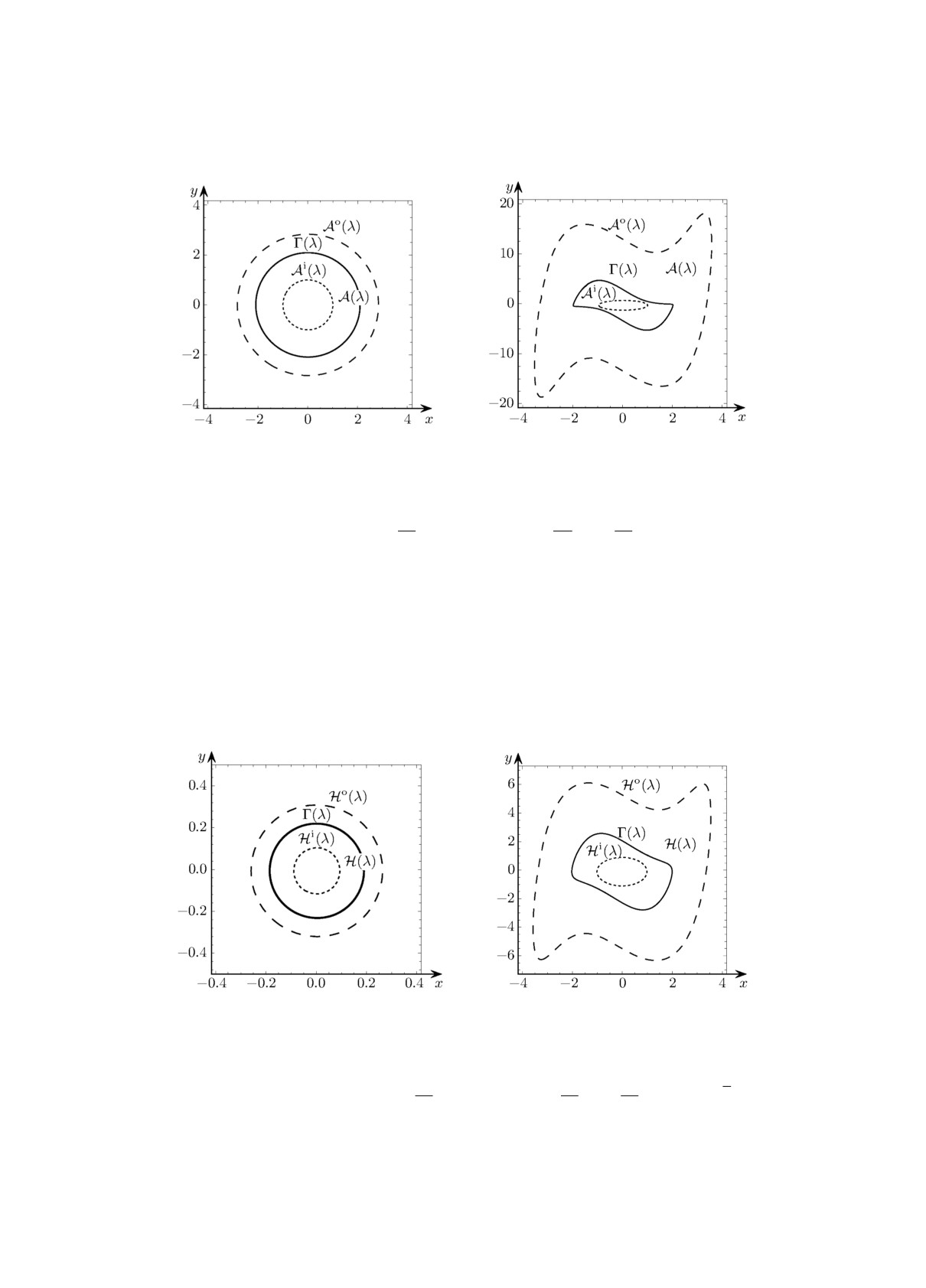
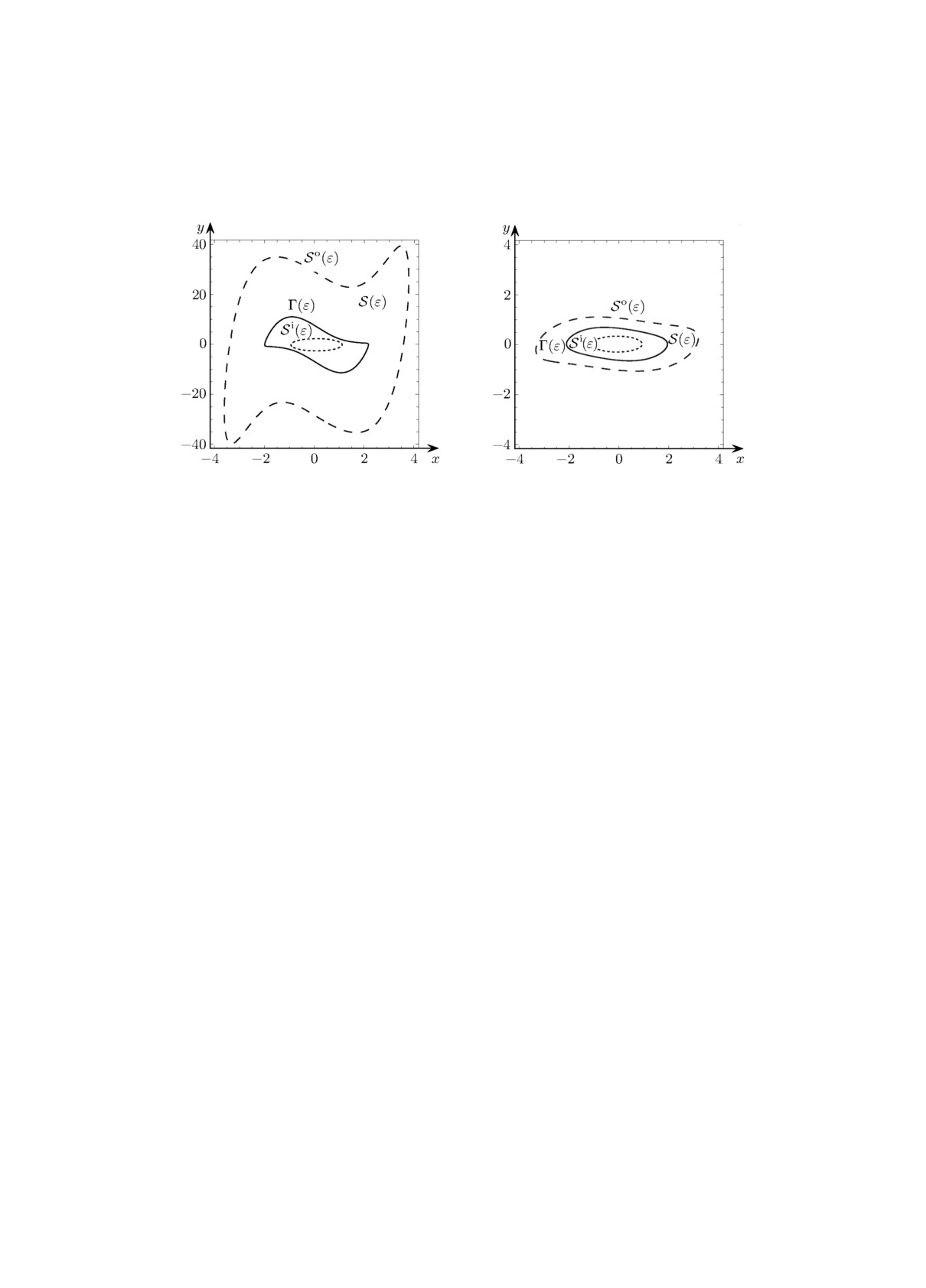
Теорема 7. При ε > 0 овалы Sⁱ(ε) := {(u, v) ∈ R² : u² + εv² = 1} и

{

(

)

}

u²

u⁶

√

S⁰(ε) := (u,v) ∈ R² : ε²v² + εvu 2-

+ (1 + ε)u² -

u⁴ +

- 8ε - 3

ε - 18 = 0

являются трансверсальными овалами системы (12) и образуют её глобальное алгебраическое

кольцо Пуанкаре-Бендиксона S(ε), содержащее единственный предельный цикл Γ(ε) этой

системы.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

300

ГРИНЬ, ШНАЙДЕР

Замечание 4. При малых ε предельный цикл Γ(ε) представляет собой релаксационные

колебания.

На рис. 4 показано кольцо S(ε) вместе с предельным циклом Γ(ε) при значениях пара-

метра ε = 0.15 и ε = 10.

Рис. 4. Кольцо S(ε) с предельным циклом Γ(ε) системы (12) при ε = 0.15 (слева)

и ε = 10 (справа).

Гринь А.А. признателен Немецкой службе академических обменов (DAAD) за финансовую

поддержку, а также за гостеприимство сотрудникам Берлинского технического университета

и Института прикладного анализа и стохастики им. К. Вейерштрасса в Берлине.

СПИСОК ЛИТЕРАТУРЫ

1. Sansone G., Conti R. Non-linear Differential Equations. V. 67. New York, 1964.

2. Dumortier F., Llibre L., Artes J.C. Qualitative Theory of Planar Differential Systems. Berlin, 2006.

3. Perko L. Differential equations and dynamical systems. Texts Appl. Math. V. 7. New York, 2001.

4. Flanders D.A., Stoker J.J. The limit case of relaxation oscillations // Studies in Nonlin. Vibration Theory,

Inst. Math. Mech. New York University, 1946. P. 51-64.

5. Lynch S. Dynamical Systems with Applications Using Mathematica. Birkhäuser, 2007.

6. Schneider K.R. New approach to study the van der Pol equation for large damping // Electron. J. Qual.

Theory Differ. Equat. 2018. № 8. P. 1-10.

7. Giacomini H., Grau M. Transversal conics and the existence of limit cycles // J. Math. Anal. Appl. 2015.

V. 428. P. 563-586.

8. Gasull A., Giacomini H., Grau M. Effective construction of Poincaré-Bendixson regions // J. Appl. Anal.

Comp. 2017. V. 7. P. 1549-1569.

9. Черкас Л.А. Функция Дюлака полиномиальных автономных систем на плоскости // Дифференц.

уравнения. 1997. Т. 33. № 5. С. 689-699.

10. Grin A.A, Schneider K.R. On some classes of limit cycles of planar dynamical systems // Dyn. Contin.

Discrete Impuls. Syst. Ser. A. Math. Anal. 2007. V. 14. P. 641-656.

11. Cherkas L.A., Grin A.A., Schneider K.R. Dulac-Cherkas functions for generalized Liénard systems

// Electron. J. Qual. Theory Differ. Equat. 2011. № 35. P. 1-23.

12. Gasull A., Giacomini H. Upper bounds for the number of limit cycles through linear differential equations

// Pacific J. Math. 2006. V. 226. № 2. P. 277-296.

13. Gasull A., Giacomini H. Some applications of the extended Bendixson-Dulac theorem // In Progress

and challenges in dynamical systems. V. 54. Heidelberg, 2013. P. 233-252.

14. Van der Pol B. On relaxation-oscillations // The London, Edinburgh and Dublin Phil. Mag. & J. of Sci.

1926. V. 14. P. 978-992.

Гродненский государственный университет

Поступила в редакцию 03.01.2022 г.

им. Янки Купалы, Беларусь

После доработки 03.01.2022 г.

Институт прикладного анализа и стохастики

Принята к публикации 09.03.2022 г.

им. К. Вейерштрасса, г. Берлин, Германия

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022