ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 3, с.301-308

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.938.5

ХАОТИЧЕСКАЯ ДИНАМИКА ОДНОРОДНЫХ ПОЛЕЙ

ЯНГА-МИЛЛСА С ТРЕМЯ СТЕПЕНЯМИ СВОБОДЫ

Рассматривается сценарий перехода к хаотической динамике в гамильтоновой системе од-

нородных полей Янга-Миллса с тремя степенями свободы при наличии механизма Хиггса.

Показано, что в этой системе, как и в других гамильтоновых и консервативных системах

уравнений, на начальной стадии перехода от регулярного движения к хаотическому клю-

чевую роль играет нелокальный эффект размножения гиперболических и эллиптических

циклов и торов вокруг эллиптических циклов в окрестностях сепаратрисных поверхностей

гиперболических циклов. Численно обнаружено, что новые эллиптические и гиперболи-

ческие циклы гамильтоновой системы рождаются не только в результате седло-узловых

бифуркаций и бифуркаций типа вилки, но также в результате субгармонического каскада

бифуркаций, характерного для универсального бифуркационного сценария перехода к ха-

осу в соответствии с теорией Фейгенбаума-Шарковского-Магницкого (ФШМ).

DOI: 10.31857/S0374064122030025, EDN: BWZBWO

Введение. Анализ хаотической динамики классических неабелевых калибровочных полей

Янга-Миллса считается чрезвычайно важным с точки зрения решения знаменитой пробле-

мы конфайнмента (невылетания цветных объектов) в квантовой хромодинамике, что, в свою

очередь, играет ключевую роль в построении Стандартной модели физики элементарных ча-

стиц [1, 2]. Поэтому неслучайно проблема решения уравнений Янга-Миллса вошла в число

семи проблем тысячелетия, сформулированных Институтом математики Клэя [3]. Система

уравнений Янга-Миллса чрезвычайно сложна, так как представляет собой в общем случае

систему из восемнадцати нелинейных уравнений с частными производными. Рассмотрение

однородных зависящих только от времени полей Янга-Миллса приводит к гамильтоновой

системе уравнений с девятью степенями свободы, анализ решений которой также является

чрезвычайно сложной задачей.

Автором настоящей работы в [4] рассмотрен переход к хаосу в наиболее простом случае

гамильтоновой системы однородных полей Янга-Миллса-Хиггса с двумя степенями свободы,

являющейся системой уравнений Янга-Миллса с учётом взаимодействия калибровочного поля

с так называемым хиггсовским вакуумом. Гамильтониан такого взаимодействия имеет вид

H = (˙x² + y²)/2 + x²y²/2 + ν(x² + y²)/2,

(1)

где ν ≥ 0 - числовой параметр, а x и y - зависимые переменные. Соответствующая гамиль-

тониану (1) система уравнений движения имеет вид

x + x(ν + y²) = 0,

ÿ+ y(ν + x²) = 0.

(2)

При фиксированных значениях полной энергии системы уравнений Янга-Миллса-Хиггса

(2) и достаточно больших значениях параметра ν решения системы (2) ведут себя регуляр-

но, так как в этом случае влияние члена x²y²/2 в гамильтониане (1) сколь угодно мало.

При малых значениях параметра ν решения системы (2) ведут себя хаотически аналогич-

но решениям системы уравнений Янга-Миллса, в гамильтониане которой хиггсовский член

ν(x² + y²)/2 равен нулю.

В работе [4] показано, что структура решений гамильтоновой системы (1), (2) полностью

определяется каскадами бифуркаций циклов расширенной диссипативной системы при стрем-

лении параметра диссипации к нулю. Рождающиеся в результате каскадов бифуркаций устой-

чивые циклы диссипативной системы переходят в эллиптические циклы гамильтоновой сис-

темы, а их области устойчивости - в торы вокруг этих эллиптических циклов. Касание обра-

зовавшихся торов гамильтоновой системы происходит по гиперболическим циклам, в которые

301

302

МАГНИЦКИЙ

переходят соответствующие неустойчивые циклы диссипативной системы, рождающиеся в ней

либо вместе с устойчивыми циклами в результате седло-узловых бифуркаций, либо при потере

устойчивости циклов в результате бифуркаций типа вилки или бифуркаций удвоения периода.

В окрестностях сепаратрисных поверхностей гиперболических циклов происходит образование

новых более сложных гиперболических и эллиптических циклов в соответствии с нелокальным

эффектом размножения циклов и торов в консервативных системах, открытым и проанализи-

рованным автором в работах [5-8]. Показано, что именно последний эффект играет ключевую

роль в системе уравнений Янга-Миллса-Хиггса на начальной стадии перехода от регуляр-

ного движения к хаотическому. Однако существенную роль играют также субгармонические

каскады бифуркаций в соответствии с порядком Шарковского, происходящие в расширенной

диссипативной системе и частично сохраняющиеся в гамильтоновой системе при стремлении

параметра диссипации к нулю [9].

В настоящей работе рассмотрен переход к хаосу в существенно более сложном случае га-

мильтоновой системы однородных полей Янга-Миллса-Хиггса с тремя степенями свободы,

имеющей гамильтониан

H = (˙x² + y² + Ż² + x²y² + x²z² + y²z²)/2 + ν(x² + y² + z²)/2,

(3)

и соответствующую гамильтониану (3) систему уравнений

x + x(ν + y² + z²) = 0,

ÿ+ y(ν + x² + z²) = 0,

z+ z(ν + x² + y²) = 0.

(4)

При ν = 0 система уравнений (4) переходит в систему уравнений Янга-Миллса с тремя

степенями свободы

x + x(y² + z²) = 0,

ÿ+ y(x² + z²) = 0,

z+ z(x² + y²) = 0.

(5)

Всюду далее считаем постоянной полную энергию системы уравнений Янга-Миллса-Хиггса

H = 1, а динамику решений системы (4) рассматриваем при уменьшении значений пара-

метра ν.

1. Аналитическое исследование. Нетрудно видеть, что система (4) уравнений Янга-

Миллса-Хиггса имеет набор основных периодических решений, которым соответствует в фа-

зовом пространстве набор основных замкнутых траекторий (циклов):

C_x : z = y = 0, ( x)² + νx² = 2; C_y : x = z = 0, ( y)² + νy² = 2; C_z : x = y = 0, ( Ż)² + νz² = 2;

C^±xy : z = 0, y = ±x, ( x)² + νx² + x⁴/2 = 1; C^±xz : y = 0, z = ±x, ( x)² + νx² + x⁴/2 = 1;

C^±yz : x = 0, z = ±y, ( y)² + νy² + y⁴/2 = 1; C^±xyz : y = ±x, z = ±x, ( x)² + νx² + x⁴ = 2/3.

Очевидно, что циклу C_x с начальным условием x(0) = 0 отвечает периодическое решение

√

x(t) =

2/ν sin(√νt). Аналогично, циклам Cy и Cz с таким же начальным условием отве-

√

чают периодические решения y(t) =

2/ν sin(√νt) и z(t) =√2/ν sin(√νt) соответственно.

Найдём аналитические выражения для периодических решений, соответствующих другим

основным циклам системы (4). Решая уравнение

( x)² + νx² + α²x⁴ = β²

с начальным условием x(0) = 0, получаем

∫

√

β² - νx² - α²x⁴,

√

= t.

β² - νu² - α²u⁴

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

ХАОТИЧЕСКАЯ ДИНАМИКА ОДНОРОДНЫХ ПОЛЕЙ ЯНГА-МИЛЛСА

303

Представляя интеграл в последнем выражении в виде

∫

dθ

√

(u² + a²)(b² - u²)

² +b²

1 - k2 sin2 θ

где

√

a² = (

ν² + 4β²α² +ν)/(2α²), b² = (

ν² + 4β²α² -ν)/(2α²), k = b/ a² + b², cos ϕ = x/b,

получаем окончательно

√

x(t) = b cn (K(k) - α

(a² + b²)t),

(6)

где cn (·) - эллиптический косинус Якоби, а K(k) - полный эллиптический интеграл первого

рода. Циклы C^± задаются выражением (6) при α² = 1/2, β² = 1 и α² = 1, β² = 2/3

соответственно.

Нетрудно убедиться в том, что функция (6) при ν → ∞ поточечно сходится к функции

x(t) = β cos(π/2-

√νt)/√ν = β sin(√νt)/√ν. В другом предельном случае при ν = 0 получим

периодические решения, задающие циклы C^± системы уравнений Янга-Миллса (5), в виде

√

x(t) =

β/α cn (K(1/

2) -

^√2βαt). Следовательно, система уравнений Янга-Миллса (5) со-

вершает периодические колебания вдоль осей симметрии z = 0, y = ±x, y = 0, z = ±x

и y = ±x, z = ±x по закону эллиптического косинуса. Аналогичные колебания происходят

вдоль осей x = 0, z = ±y. Численные расчёты, проведённые в работах [1, 10], показали, что

эти решения системы уравнений Янга-Миллса являются крайне неустойчивыми. Более того,

численные расчёты показали полную хаотичность поведения решений этой системы.

Для выяснения природы динамического хаоса в системе уравнений Янга-Миллса (5) про-

анализируем численно сценарий перехода к хаосу в системе уравнений Янга-Миллса-Хиггса

(4) при ν → 0.

2. Численное исследование сценария перехода к хаосу. Для численного исследова-

ния сценария перехода к хаосу в системе уравнений (4) применим подход, предложенный и

развитый автором в работах [5-8]. Будем аппроксимировать эллиптические циклы гамильто-

новой системы (4) устойчивыми циклами расширенной диссипативной системы, а двумерные

торы вокруг эллиптических циклов системы (4) - областями устойчивости соответствующих

устойчивых циклов расширенной диссипативной системы.

В качестве одной из возможных расширенных диссипативных систем рассмотрим систему

x = u,

u = -x(ν + y² + z²) - μu,

y = v + (1 - H(x,y,z))y,

v = -y(ν + x² + z²) - μv,

Ż = r,

r = -z(ν + x² + y²),

(7)

где μ - числовой параметр.

Дивергенция правой части системы (7) на решениях системы (3), (4) равна -2μ - (ν +

+ x² + z²)y² и, следовательно, отрицательна при всех μ > 0, а расширенная диссипативная

двухпараметрическая система уравнений (7) удовлетворяет условиям 1) и 2) теоремы 3.1 ра-

боты [5].

Нетрудно видеть, что решения гамильтоновой системы (4) с начальными условиями z₀ =

= r₀ = 0 являются решениями гамильтоновой системы уравнений Янга-Миллса-Хиггса с

двумя степенями свободы

x = u,

u = -x(ν + y²),

y=v,

v = -y(ν + x²).

(8)

Система (8) рассматривалась в работе [4] при значениях параметра ν = 2, 1, 0.55. Чтобы

иметь возможность сравнить полученные результаты, проанализируем численно влияние ве-

личин параметров ν и μ на динамику системы (7) при фиксированном значении H = 1 и тех

же значениях параметра ν = 2,

0.55. В работе [4] показано, что при больших значениях

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

304

МАГНИЦКИЙ

параметра ν = 2 топология траекторий гамильтоновой системы (8) определяется основными

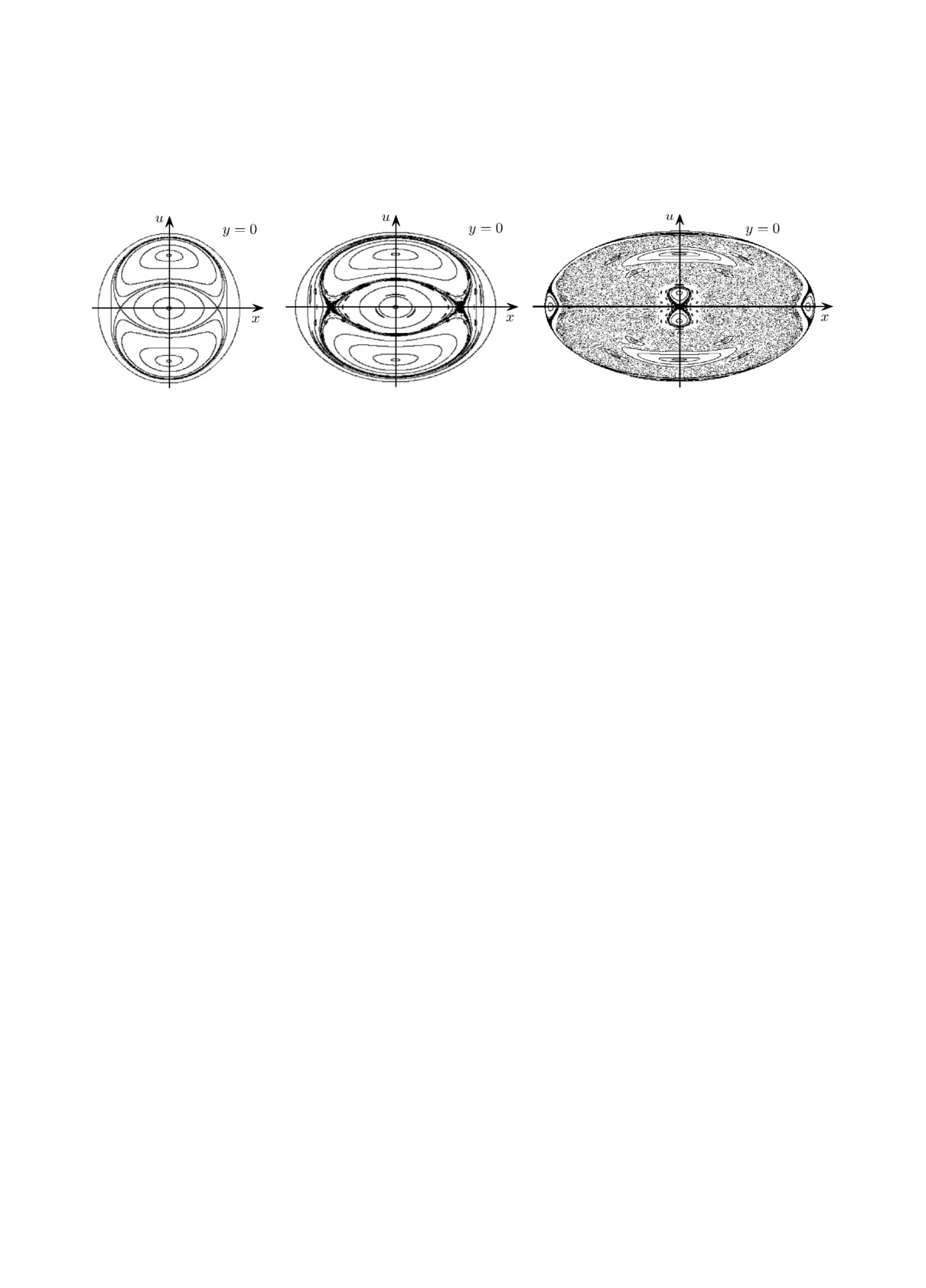
торами вокруг четырёх основных эллиптических циклов C_x, C_y и C^±xy системы (рис. 1, a).

(а)

(б)

(в)

Рис. 1. Проекции сечения плоскостью y = 0 двумерных торов системы (8): вокруг её основных эллиптических

циклов при ν = 2, x0 = y0 = 0 и u0 = 1.4142,

1.35,

1.33795,

1.33,

1.3,

1.2,

1.1,

1.02,

0.4,

0.2,

0.03

(а);

вокруг основных и более сложных эллиптических циклов при ν = 1, x0 = y0 = 0 и u0 = 1.4142, 1.37,

1.3524,

1.335,

1.318,

1.313,

1.305,

1.25,

1.2,

1.02,

0.5499,

0.5384,

0.52,

0.508,

0.4,

0.2,

0.03 (б); вокруг основных,

более сложных эллиптических циклов и циклов удвоенного периода при ν = 0.55, x0 = y0 = 0 и u0 = 1.4142,

1.41,

1.398,

1.35047,

1.349,

±1.3396,

1.14,

1.09,

1.04,

1.015,

0.42,

0.395,

0.3665,

±0.35,

±0.3,

±1.139

(y0 = 0.645942),

±1.155

(y0 = 0.645942) (в).

Численно можно убедиться в том, что в расширенной диссипативной системе

x = u,

u = -x(ν + y²) - μu,

y = v + (1 - H(x,y))y,

v = -y(ν + x²)

(9)

при всех малых значениях параметра диссипации μ > 0 имеются три устойчивых цикла, пе-

реходящих в эллиптические циклы C_y и C^±xy гамильтоновой системы (8) при μ = 0, и один

неустойчивый цикл, переходящий в эллиптический цикл C_x гамильтоновой системы (8) при

μ = 0. Области устойчивости (и неустойчивости) этих циклов переходят в двумерные торы

гамильтоновой системы (8) вокруг её эллиптических циклов, а касание образовавшихся торов

происходит по двум гиперболическим циклам D^±, которые являются пределами неустойчи-

вых седловых циклов расширенной диссипативной системы при μ → 0, родившихся в дис-

сипативной системе одновременно с устойчивыми циклами C^±xy в результате седло-узловой

бифуркации при μ ≈ 0.08. Циклам D^± гамильтоновой системы (8) соответствуют начальные

условия u(0) = y(0) = 0, x(0) ≈ ±0.6864269. Аналитические выражения для циклов D^±

получить не удалось.

На рис. 1, a представлены проекции на плоскость (x, u) сечений плоскостью y = 0 дву-

мерных торов гамильтоновой системы (8) вокруг её четырёх основных эллиптических циклов

C_x, C_y и C^±xy. Циклу C_y соответствует в проекции точка (0,0), циклу C_x - внешний контур

рисунка, циклам C^±xy - две эллиптические точки, лежащие на оси u, причём каждой из двух

точек в проекции соответствуют две точки пересечения плоскостью y = 0 двух циклов C^±xy.

Гиперболическим циклам D^± соответствуют на рис. 1, а лежащие на оси x две точки пере-

сечения сепаратрис (проекций сечений сепаратрисных поверхностей, по которым происходит

касание различных двумерных торов). При этом каждой из двух точек в проекции соответ-

ствуют две точки пересечения плоскостью y = 0 двух циклов D^±. Заметим, что циклы C^±xy,

определяющие, в основном, динамику системы (8), существуют в ней и являются отличными

от циклов C_x, C_y при любых ν > 0. Поэтому проведённый выше анализ динамики реше-

ний системы (8) при достаточно больших значениях параметра ν не может быть осуществлён

методами теории возмущений, исходя из решений невозмущённой системы, получающейся из

системы (8) удалением кубических членов.

При значении параметра возмущения ν = 1 ситуация заметно усложняется. Теперь топо-

логия траекторий системы (8) определяется основными торами системы (т.е. торами вокруг

четырёх основных эллиптических циклов C_x, C_y и C^±xy ) и набором торов вокруг более слож-

ных эллиптических циклов, родившихся изначально устойчивыми в диссипативной системе (9)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

ХАОТИЧЕСКАЯ ДИНАМИКА ОДНОРОДНЫХ ПОЛЕЙ ЯНГА-МИЛЛСА

305

при уменьшении значений параметра μ до нуля в результате седло-узловых бифуркаций.

Причём вследствие нелокального эффекта размножения циклов и торов [6] более сложные

многооборотные циклы и торы рождаются в окрестностях сепаратрисных поверхностей ги-

перболических циклов D^±, а менее сложные - вне этих окрестностей. Движение траектории

по поверхностям таких сложных многооборотных торов, расположенных в окрестностях сепа-

ратрисных поверхностей гиперболических циклов, создаёт иллюзию хаотического движения,

хорошо наблюдаемого в различных сечениях Пуанкаре (рис. 1, б). Касание различных вит-

ков сложных торов происходит по гиперболическим циклам, родившимся в диссипативной

системе совместно с устойчивыми циклами в результате седло-узловых бифуркаций. Так как

в окрестностях сепаратрисных поверхностей гиперболических циклов системы расположены,

переплетаясь и, по всей видимости, касаясь друг друга, различные системы многооборотных

сложных торов (внутренние по отношению к сепаратрисному контуру, внешние и смешанные),

то глобальная в смысле теории КАМ (Колмогорова-Арнольда-Мозера) устойчивость решений

системы (8) сохраняться не может.

Таким образом, усложнение динамики решений в окрестностях сепаратрисных поверхно-

стей гиперболических циклов D^± системы (8) определяется наличием многочисленных слож-

ных многооборотных двумерных торов вокруг эллиптических циклов системы. Касание торов

происходит по гиперболическим циклам. Кроме того, поскольку в окрестностях гиперболиче-

ских циклов движение траектории замедляется, то это ведёт к образованию в этих окрестно-

стях новых ещё более сложных эллиптических и гиперболических циклов и соответствующих

им двумерных торов. Следовательно, на начальном этапе перехода к хаосу рост области хао-

тического движения в системе (8) при уменьшении значений параметра ν объясняется, как и

в других гамильтоновых и консервативных системах [4-9], нелокальным эффектом размноже-

ния гиперболических и эллиптических циклов, а также торов вокруг эллиптических циклов.

Более простые циклы рождаются достаточно далеко от сепаратрисных поверхностей гипербо-

лических периодических решений, а более сложные - вблизи этих поверхностей.

Вместе с тем пример системы (8) показывает, что гиперболические и эллиптические циклы

гамильтоновой или консервативной системы могут являться предельным случаем устойчивых

и седловых циклов расширенной диссипативной системы, родившихся не только в результате

седло-узловых бифуркаций, но также и в результате бифуркаций типа вилки и удвоения пе-

риода. Так при ν ≈ 0.594 в диссипативной расширенной системе (9) при μ → 0 устойчивый

цикл C_y теряет устойчивость в результате бифуркации типа вилки, становясь седловым, а

в его окрестности рождаются два устойчивых цикла C^±y, переходящие в эллиптические цик-

лы гамильтоновой системы (8) при μ = 0. Возникающие вокруг этих двух эллиптических

циклов торы касаются по ставшему гиперболическим циклу C_y. То же самое происходит с

циклом C_x при ν ≈ 0.594 в модифицированной расширенной диссипативной системе со сла-

гаемым (1-H(x, y))x в первом уравнении и вычитаемым -μr - в четвёртом. Он также теряет

устойчивость при μ → 0 в результате бифуркации типа вилки, становясь седловым, а в его

окрестности рождаются два устойчивых цикла C^±x, переходящие в эллиптические циклы га-

мильтоновой системы (8) при μ = 0. Возникающие вокруг этих двух эллиптических циклов

торы касаются по ставшему гиперболическим циклу C_x. В отличие от циклов C_y и C_x с

циклами C^±xy происходят бифуркации удвоения периода при ν ≈ 0.733. Сами циклы ста-

новятся седловыми, а в их окрестностях рождаются устойчивые циклы удвоенного периода,

переходящие при μ → 0 в эллиптические циклы гамильтоновой системы (8).

Всё это хорошо видно на рис. 1, в при ν = 0.55. Гиперболическому циклу C_y соответствует

в проекции точка (0, 0), гиперболическому циклу C_x - внешний контур рисунка, эллиптиче-

ским циклам C^±xy соответствуют две эллиптические точки, лежащие на оси u, причём каждой

из двух точек в проекции соответствуют две точки пересечения плоскостью y = 0 двух циклов

C^±xy. Эллиптическим циклам C^±y соответствуют лежащие на оси u в окрестности нуля две

эллиптические точки, а эллиптическим циклам C^±x - лежащие на оси x в окрестностях внеш-

него контура две эллиптические точки. При этом каждой из последних четырёх эллиптических

точек в проекции на плоскость (x, u) соответствуют две точки пересечения плоскостью y = 0

каждого из четырёх эллиптических циклов C^±y, C^±x, а каждому замкнутому контуру вокруг

каждой эллиптической точки - два контура в сечении двумерного тора вокруг соответствую-

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

306

МАГНИЦКИЙ

щего эллиптического цикла плоскостью y = 0. Чтобы наглядно увидеть это, достаточно взять

проекцию сечения тора плоскостью, отличной от плоскости y = 0, например y = 0.2. Эллип-

тическим циклам удвоенного периода соответствуют на рис. 1, в восемь эллиптических точек,

лежащих в окрестностях эллиптических точек циклов C^±xy. Гиперболические циклы D^± уже

совсем скрыты на рис. 1, в хаотической динамикой, порождённой в их окрестностях эффектом

размножения гиперболических и эллиптических циклов и торов вокруг эллиптических цик-

лов. Этот же эффект, как видно из рис. 1, в, в полной мере уже работает и в окрестностях

ставших гиперболическими циклов C_y и C_x.

При дальнейшем уменьшении значений параметра ν происходит субгармонический кас-

кад бифуркаций циклов C^±xy. Циклы C^±xy периодов четыре рождаются при ν ≈ 0.54, а циклы

периодов шесть - при ν ≈ 0.508 (рис. 2). Бифуркационные значения параметра ν субгармо-

нического каскада циклов для гамильтоновой системы (8) находились численно предельным

переходом ν = lim ν(μ), μ → 0, где ν(μ) - значение параметра, при котором происходит

рождение соответствующего цикла субгармонического каскада в расширенной диссипативной

системе (9).

(а)

(б)

(в)

(г)

Рис. 2. Проекции на плоскость (x, u) циклов C^±xy периодов один, два, четыре и шесть

при ν = 0.74, 0.73, 0.54, 0.508.

Таким образом, численно установлено, что пятимерная энергетическая поверхность га-

мильтоновой системы (4) имеет четырёхмерное подпространство, в котором при ν = 2 хао-

тическая динамика вообще отсутствует, а при ν = 1 наблюдается исключительно локальный

псевдохаос. Это, естественно, происходит в окрестности тех начальных условий z₀ = r₀ = 0,

при которых решения лежат на поверхностях касающихся двумерных торов системы (8) или

близки к ним (окрестность сепаратрисы на рис. 1, б). Топология траекторий системы (4) с

начальными условиями z₀ = r₀ = 0 определяется основными торами системами (т.е. тора-

ми вокруг основных циклов системы) и набором торов вокруг более сложных эллиптических

циклов, появившихся в окрестности сепаратрисной поверхности гиперболического периодиче-

ского решения в результате нелокального эффекта размножения циклов и торов. Псевдохаос,

возникший в окрестности гиперболического цикла D^±, не является гомоклиническим хаосом,

а всего лишь следствием ошибок вычислений из-за неустойчивости решаемой задачи. Эффект

хаотичности создают точки, лежащие в сечении Пуанкаре на поверхностях тех торов, обмот-

ки которых расположены, переплетаясь, вокруг различных сложных эллиптических циклов,

образовавшихся вследствие эффекта размножения циклов и торов и имеющих тот же вид, что

и сложные циклы системы, представленные на рис. 1, в и рис. 2, б, в работе [4].

Рассмотрим теперь, что происходит вне окрестностей касающихся двумерных торов сис-

темы (4) при ν = 2 и ν = 1. Численные расчёты показывают, что вне этих окрестностей

траектории гамильтоновой системы (4) двигаются по поверхностям трёхмерных торов вокруг

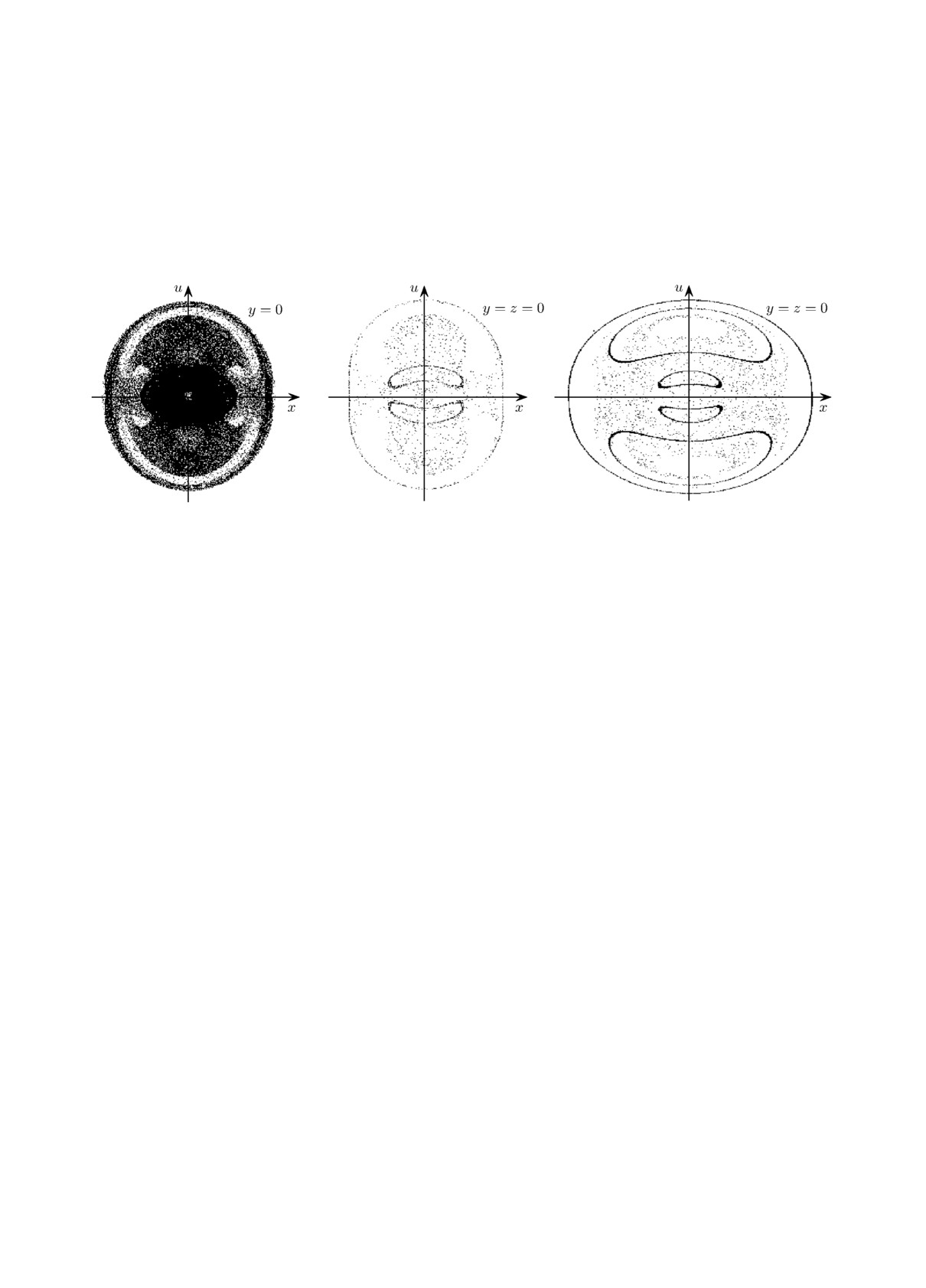
двумерных торов системы (4). Сечения некоторых из таких трёхмерных торов представлены

на рис. 3, б, в.

Из рис. 3, б видно, что при ν = 2 область существования трёхмерных торов окружена

областью глобального хаотического поведения траекторий системы (4). Таким образом, чис-

ленно установлено совместное сосуществование в гамильтоновой системе (4) при ν = 2 обла-

стей регулярного движения по двумерным торам вокруг основных циклов системы, областей

регулярного движения по трёхмерным торам вокруг упомянутых выше двумерных торов и

областей глобального хаотического поведения траекторий системы в остальной части энерге-

тической поверхности.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

ХАОТИЧЕСКАЯ ДИНАМИКА ОДНОРОДНЫХ ПОЛЕЙ ЯНГА-МИЛЛСА

307

При значении ν = 1, как видно из рис. 3, в, гамильтонова система (4) имеет области

регулярного движения по двумерным торам вокруг основных циклов системы, области регу-

лярного движения по трёхмерным торам вокруг упомянутых выше двумерных торов, области

локального хаотического поведения траекторий системы в четырёхмерном подпространстве

пятимерной энергетической поверхности и области глобального хаотического поведения тра-

екторий системы в остальной части энергетической поверхности.

(а)

(б)

(в)

Рис. 3. Проекции сечений коразмерности 1 (а) и 2 (б) системы (4) при ν = 2, z0 = 0.16, r0 = -0.16 и

u0 = 1.33,

1.05,

1.0,

0.44,

0.4273,

0.427,

0.423,

0.4; проекция сечения коразмерности 2 (в) системы (4) при

ν = 1, z0 = 0.16, r0 = -0.16 и u0 = 1.37,

1.25,

1.15,

0.55,

0.35.

Таким образом, в гамильтоновой системе (4) с тремя степенями свободы даже при достаточ-

но малых значениях параметра ν одновременно существуют области регулярного движения по

двумерным торам вокруг основных циклов системы, области регулярного движения по трёх-

мерным торам вокруг упомянутых выше двумерных торов, области локального хаотического

поведения траекторий системы в четырёхмерном подпространстве пятимерной энергетической

поверхности и области глобального хаотического поведения траекторий системы, содержащей

гетероклинические сепаратрисные многообразия, натянутые на гиперболические циклы сис-

темы, и все циклы и непериодические траектории, родившиеся изначально устойчивыми в

диссипативной системе (7) при μ > 0 и потерявшие устойчивость в результате субгармониче-

ских, гомоклинических или каких-либо более сложных каскадов бифуркаций в соответствии

с теорией ФШМ. Все торы системы, кроме торов вокруг основных циклов, рождаются в ре-

зультате различных бифуркаций. Заметим, что в системе (4), имеющей три степени свободы,

переход к хаосу в соответствии с теорией ФШМ может происходить также и субгармоническим

каскадом бифуркаций устойчивых двумерных торов в расширенной диссипативной системе,

однако двумерных торов удвоенного периода обнаружить пока не удалось.

На основе проведённых численных расчётов для гамильтоновой системы уравнений Янга-

Миллса-Хиггса с тремя степенями свободы показано, что при достаточно больших значениях

параметра возмущения ν хаотическая динамика в системе отсутствует, а движение идёт по

основным двумерным или трёхмерным торам вокруг основных циклов системы, причём эти

торы не являются торами невозмущённой системы. При уменьшении значений параметра ν

никакого разрушения торов невозмущённой системы и расщепления сепаратрисы не происхо-

дит; движение идёт по основным торам вокруг основных циклов системы и набору сложных

многооборотных переплетающихся торов вокруг более сложных эллиптических циклов, ро-

дившихся изначально устойчивыми в расширенной диссипативной системе при уменьшении

значений параметра диссипации до нуля; видимость хаотичности создают точки, лежащие в

сечениях Пуанкаре на поверхностях таких сложных многооборотных торов. При достаточно

малых значениях параметра ν хаотическая динамика в возмущённой системе присутствует, но

переход к хаосу происходит не через разрушение двумерных или трёхмерных торов невозму-

щённой системы, как это постулируется теорией КАМ, а, наоборот, через каскады бифуркаций

рождения новых сложных двумерных и трёхмерных торов в соответствии с бифуркационной

теорией ФШМ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022

2^∗

308

МАГНИЦКИЙ

Заключение. В работе рассмотрен переход к хаосу в сложном случае гамильтоновой сис-

темы однородных полей Янга-Миллса-Хиггса с тремя степенями свободы. Показано, что в

этой системе, как и во многих других гамильтоновых и консервативных системах уравнений,

на начальной стадии перехода от регулярного движения к хаотическому ключевую роль иг-

рает нелокальный эффект размножения гиперболических и эллиптических циклов и торов

вокруг эллиптических циклов в окрестностях сепаратрисных поверхностей гиперболических

циклов. Обнаружено, что новые эллиптические и гиперболические циклы гамильтоновой сис-

темы рождаются не только в результате седло-узловой бифуркации и бифуркации типа вилки,

но также и в результате субгармонического каскада бифуркаций, характерного для универ-

сального бифуркационного сценария перехода к хаосу в соответствии с теорией Фейгенбаума-

Шарковского-Магницкого, справедливой как для диссипативных, так и для консервативных

систем дифференциальных уравнений.

Работа выполнена при частичной финансовой поддержке Российского фонда фундамен-

тальных исследований (проекты 18-029-10008mk и 20-07-00066a).

СПИСОК ЛИТЕРАТУРЫ

1. Матинян С.Г. Динамический хаос неабелевых калибровочных полей // Физика элементарных ча-

стиц и атомного ядра. 1985. Т. 16. Вып. 3. С. 522-550.

2. Goldfain E. Bifurcations and pattern formation in particle physics: An introductory study // Eur. Phys.

Lett. 2008. V. 82. P. 11001.

3. Carlson J., Jaffe A., Wiles A. The Millennium Prize Problems. Cambridge; Massachusetts, 2006.

4. Магницкий Н.А. Хаотическая динамика однородных полей Янга-Миллса с двумя степенями сво-

боды // Дифференц. уравнения. 2009. Т. 45. № 12. С. 1698-1703.

5. Магницкий Н.А. Новый подход к анализу гамильтоновых и консервативных систем // Дифференц.

уравнения. 2008. Т. 44. № 12. С. 1618-1627.

6. Магницкий Н.А. О природе динамического хаоса в окрестности сепаратрисы консервативной сис-

темы // Дифференц. уравнения. 2009. Т. 45. № 5. С. 647-654.

7. Магницкий Н.А. Теория динамического хаоса. М., 2011.

8. Magnitskii N.A. Universality of transition to chaos in all kinds of nonlinear differential equations

// Chapter in Nonlinearity, Bifurcation and Chaos - Theory and Applications. Rijeca, 2012. P. 133-174.

9. Рябков О.И. Об исследовании седло-узловых бифуркаций и бифуркации вилки методом стабили-

зации Н.А. Магницкого // Дифференц. уравнения. 2010. Т. 46. № 11. С. 1657-1661.

10. Чириков Б.В., Шепелянский Д.Л. Динамика некоторых однородных моделей классических полей

Янга-Миллса // Ядерная физика. 1982. Т. 36. № 6 (12). С. 1563-1576.

Федеральный исследовательский центр

Поступила в редакцию 06.10.2021 г.

“Информатика и управление” РАН, г. Москва

После доработки 09.03.2022 г.

Принята к публикации 09.03.2022 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№3

2022