ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 3, с.309-318
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
УДК 517.952
О ЗАДАЧЕ КОШИ ДЛЯ ОДНОМЕРНОГО ЗАКОНА
СОХРАНЕНИЯ С НАЧАЛЬНЫМИ УСЛОВИЯМИ,
СОВПАДАЮЩИМИ СО СТЕПЕННОЙ
ИЛИ ЭКСПОНЕНЦИАЛЬНОЙ ФУНКЦИЕЙ
НА БЕСКОНЕЧНОСТИ
© 2022 г. Л. В. Гаргянц
Для квазилинейного уравнения первого порядка со степенной функцией потока построены
обобщённые энтропийные решения задач Коши с начальными условиями, совпадающими
со степенной или экспоненциальной функцией на минус бесконечности. В случае экспо-
ненциально растущего начального условия установлена односторонняя периодичность по
пространственной переменной найденного решения. Доказано несуществование положи-
тельных решений у рассматриваемых задач Коши.
DOI: 10.31857/S0374064122030037, EDN: BXLRJB
1. Введение и постановка задачи. Для заданных f ∈ C1(R) и u0 ∈ L∞loc(R) рассмотрим
задачу Коши для уравнения
ut + (f(u))x = 0, (t,x) ∈ ΠT = (0,T) × R,
0 < T ≤ ∞,
(1)
с начальным условием
u|t=0 = u0(x), x ∈ R.
(2)
В работах [1, 2] (см. также [3, c. 39-40 и 65]) дано
Определение 1. Функция u: ΠT → R, u ∈ L∞loc(ΠT ), называется обобщённым энтропий-
ным решением задачи (1), (2), если выполняются следующие условия:
1) для любого k ∈ R имеет место неравенство
|u - k|t + (sign (u - k)(f(u) - f(k)))x ≤ 0 в D′(ΠT );
(3)
2) esslimu(t, · ) = u0(·) в L1loc(R), т.е. существует множество E ⊂ (0,T) полной меры
t→0+
Лебега такое, что u(t, · ) ∈ L1loc(R), t ∈ E, и u(t, · ) → u0(·) в L1loc(R) при t → 0+, t ∈ E.
Условие (3) означает, что для любой пробной функции ϕ ∈ C∞0(ΠT ), ϕ ≥ 0, выполнено
неравенство
∫
(|u - k|ϕt + sign (u - k)(f(u) - f(k))ϕx) dx dt ≥ 0.
ΠT
При u0 ∈ L∞(R) существование и единственность ограниченного обобщённого энтропий-
ного решения u ∈ L∞(ΠT ) задачи (1), (2) установлены в работах С.Н. Кружкова [1, 2] в общем
случае многих пространственных переменных. В этих работах также доказано свойство моно-
тонной зависимости решения от начальных данных:
если u, v ∈ L∞(ΠT ) - обобщённые энтропийные решения задачи (1), (2) с начальными
условиями u0 ∈ L∞(R) и v0 ∈ L∞(R) соответственно, причём u0(x) ≤ v0(x) п.в. на R, то
u(t, x) ≤ v(t, x) п.в. на ΠT .
Из этого свойства вытекает принцип максимума/минимума: если a ≤ u0 ≤ b почти всюду
на R и u - ограниченное обобщённое энтропийное решение задачи (1), (2), то a ≤ u ≤ b
почти всюду на ΠT . Из него, в частности, следует единственность постоянного решения при
постоянных начальных условиях в классе ограниченных измеримых функций.
309
310
ГАРГЯНЦ
В работе Е.Ю. Панова [4] доказана теорема существования и единственности локально
ограниченного обобщённого энтропийного решения задачи (1), (2) в общем случае многих
пространственных переменных в классе функций, удовлетворяющих степенному ограничению
на рост по пространственным переменным. Решения, рассматриваемые в данной статье, не
входят в найденные Е.Ю. Пановым классы корректности.
Будем строить кусочно-гладкие обобщённые энтропийные решения задачи (1), (2), поэтому
заменим определение 1 на свойство (см. [5, с. 74-77]), которое содержит
Предложение 1. Пусть u: ΠT → R - кусочно-гладкая в полосе ΠT функция с не более
чем счётным числом линий разрыва Γn, являющихся графиками функций γn ∈ C1(0, T ),
где n ∈ N ⊆ N0 = N
⋃ {0}; пусть эти линии попарно не пересекаются и существуют
односторонние пределы
u-n(t) =
lim
u(τ, ξ), u+n(t) =
lim
u(τ, ξ)
(τ,ξ)→(t,γn(t)-0)
(τ,ξ)→(t,γn(t)+0)
функции u(·) при подходе к каждой линии разрыва Γn. Тогда u(·) является обобщённым
энтропийным решением уравнения (1) в том и только в том случае, когда выполнены сле-
дующие условия:
1) функция u(·) в области своей гладкости удовлетворяет уравнению (1) в классическом
смысле;
2) на каждой линии разрыва Γn при любом t ∈ (0,T) имеет место условие Ранкина-
Гюгонио:
f (u+n(t)) - f(u-n(t))
γn(t) =
;
(4)
un(t) - un(t)
3) для любого n ∈ N и всех t ∈ (0, T ) выполнено условие допустимости разрыва: при
u+n(t) > u-n(t) (u+n(t) < u-n(t)) график функции f лежит не ниже (соответственно, не
выше) хорды, соединяющей точки этого графика с абсциссами u-n(t), u+n(t).
Замечание 1. Первые два условия предложения 1 эквивалентны тому, что функция u(·)
является обобщённым решением (в смысле распределений) уравнения (1), а последнее являет-
ся условием возрастания энтропии для кусочно-гладких решений и эквивалентно E-условию
О.А. Олейник [6].
Приведём основные результаты некоторых работ, имеющих непосредственное отношение к
рассматриваемой в данной статье задаче.
В работах [4, 7, 8] рассматривалась задача Коши (1), (2) со степенной функцией потока
f (u) = |u|α-1u/α, α > 1, и степенным начальным условием u0(x) = |x|β , β(α - 1) > 1.
Оказалось, что у такой задачи Коши существует кусочно-гладкое обобщённое энтропийное
решение, которое определено во всей полуплоскости t > 0, имеет счётное число линий разрыва
и меняет знак при переходе через каждую ударную волну. Кроме того, рассматриваемая задача
не имеет положительных решений ни в какой полосе ΠT .
В работах [9, 10] изучалась задача Коши (1), (2) со степенной функцией потока f(u) =
= |u|α-1u/α, α > 1, и экспоненциальным начальным условием u0(x) = exp(-x/(α - 1)).
Оказалось, что у такой задачи Коши существует решение, обладающее теми же, что и выше,
свойствами: оно определено во всей полуплоскости t > 0, имеет счётное число линий разрыва
и меняет знак при переходе через каждую ударную волну (линию сильного разрыва). Однако
более быстрый рост начального условия на бесконечности дал неожиданный эффект: постро-
енное в этих работах решение оказалось ограниченным в области t ≥ δ > 0, в то время как
в случае степенных начальных данных решение имеет рост порядка |x|1/(α-1) при x → ±∞
и не зависит от показателя степени β начального условия. Кроме того, решение является
односторонне периодическим по пространственной переменной. Эта задача также не имеет
положительного решения ни в какой полосе ΠT , что доказано в [11].
Решения, построенные в работах [4, 7-10], имеют одинаковую структуру. Полуплоскость
t > 0 делится гладкими попарно непересекающимися кривыми Γn, n ∈ N0, являющими-
ся графиками гладких функций γn : R+ → R, на счётное число областей (R+ = (0, +∞)).
Функциональная последовательность γn(t) является неограниченно монотонно убывающей.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
О ЗАДАЧЕ КОШИ ДЛЯ ОДНОМЕРНОГО ЗАКОНА СОХРАНЕНИЯ
311
В областях Dn = {(t, x) : γn(t) < x < γn-1(t)}, n ∈ N, между этими кривыми и в области
D0 = {(t,x) : x > γ0(t)} решение является классическим, а каждая из кривых Γn является
линией сильного разрыва (ударной волной), причём со стороны x > γn(t) кривая Γn является
огибающей семейства характеристик из области Dn. В работе [12] предложен единый способ
описания таких решений, основанный на преобразовании Лежандра.
В настоящей работе в пп. 3 и 4 доказано, что у задач Коши для уравнения (1) с функцией
потока f(u) = |u|α-1u/α, α > 1, и положительными начальными условиями, совпадающи-
ми со степенной или экспоненциальной функцией на минус бесконечности, существуют зна-
кочередующиеся энтропийные решения со счётным числом ударных волн. Причём в случае
экспоненциального роста начального условия существует знакочередующееся односторонне
периодическое по пространственной переменной энтропийнoе решение. Тем самым доказано,
что для существования решений с теми же свойствами, что и у решений из работ [4, 7-10], до-
статочно наличия степенного или экспоненциального поведения начального условия на минус
бесконечности. Все построенные в настоящей работе решения имеют структуру, описанную вы-
ше. Принципиальное отличие от ранее построенных примеров заключается в том, что ударная
волна Γ0 образована как огибающая семейства характеристик, идущих из начальной плоско-
сти t = 0, лишь при t ≤ t0 < +∞. Кроме того, в области D0 решение является непрерывным,
но, вообще говоря, не гладким. В п. 5 доказывается, что рассматриваемые задачи Коши не
имеют положительных решений ни в какой полосе ΠT .
2. Вспомогательные утверждения. Предпошлём формулировке основных результатов
ряд вспомогательных определений и утверждений.
Определение 2. Преобразованием Лежандра гладкой выпуклой вверх функции g : R → R
называется функция γ, задаваемая для каждого t ∈ R равенством
γ(t) = L(g)(t) := inf (kt - g(k)).
k∈R
Преобразование Лежандра функции g(k) легко записать параметрически, где роль пара-
метра выполняет переменная k, а именно
t = g′(k), γ(t) = kg′(k) - g(k).
(5)
Непосредственно из определения следует, что для всякого C ∈ R выполнены соотношения
L(g + C) = L(g) - C и L(Cg)(t) = CL(g)(t/C).
Отметим, что огибающая семейства прямых на плоскости определяется преобразованием
Лежандра (см. [13, с. 33]).
В дальнейшем будем рассматривать уравнение (1) со степенной функцией потока f(u) =
= |u|α-1u/α, α > 1.
Лемма. Пусть функция u: R+ × R → R удовлетворяет условиям предложения 1, и для
некоторого n ∈ N при всех t ∈ R+ справедливо равенство
γn(t) = f′(u+n(t)) ≡ |u+n(t)|α-1.
(6)
Тогда на линии разрыва Γn выполнено условие Ранкина-Гюгонио (4) в том и только том
случае, когда для всех t > 0 справедливо соотношение u-n(t) = -wu+n(t), где -w - корень
уравнения
|v|α-1v - αv + α - 1 = 0,
(7)
отличный от единицы.
Доказательство. В силу равенства (6) условие Ранкина-Гюгонио (4) на линии разрыва Γn
имеет вид
f (u+n(t)) - f(u-n(t))
f′(u+n(t)) =
,
t > 0.
un(t) - un(t)
Рассмотрим это равенство при фиксированном t как уравнение относительно u-n(t). Так
как функция потока является степенной, это уравнение является однородным. Сделав замену
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
312
ГАРГЯНЦ
u-n(t) = u+n(t)v, получим уравнение (7). Анализ функции h: R → R, h(v) = |v|α-1v - αv +
+ α - 1, показывает, что это уравнение имеет единственный корень, отличный от единицы,
причём он отрицателен и меньше -1. Лемма доказана.
В дальнейшем через -w, как и в формулировке леммы, обозначаем отличный от единицы
корень уравнения (7).
3. Энтропийное решение задачи Коши с начальным условием, совпадающим со
степенной функцией на бесконечности. Будем решать задачу Коши (1), (2) в полуплоско-
сти t > 0 с f(u) = |u|α-1u/α, α > 1, и кусочно-гладким начальным условием, совпадающим
со степенной функцией на минус бесконечности, т.е.
ut + |u|α-1ux = 0, t ∈ R+, x ∈ R,
(8)
{
|x|β,
если x ∈ (-∞, m),
u0(x) =
(9)
ũ0(x),
если x ∈ [m, +∞),
где β(α - 1) > 1, m ∈ R \ R+, ũ0(x) - произвольная положительная нестрого возрастающая
кусочно-гладкая функция, причём ũ0(m) ≥ |m|β.
Теорема 1. У задачи Коши (8), (9) существует кусочно-гладкое обобщённое энтропийное
решение u(·), которое определено во всей полуплоскости t > 0, обладает счётным числом
ударных волн Γn, n ∈ N0, являющихся графиками функций
1
γn(t) = -Cntη, η =
< 0, Cn = Cn(α, β) > 0,
1 - β(α - 1)
где Cn - строго возрастающая последовательность, при этом функция u(·) меняет знак
при переходе через каждую ударную волну.
Доказательство. Построим в явном виде кусочно-гладкое обобщённое энтропийное реше-
ние задачи (8), (9), удовлетворяющее условиям теоремы. Это решение будет иметь следующую
структуру: в областях гладкости Dn = {(t, x) : γn(t) < x < γn-1(t)}, n ∈ N, и в области D0 =
= {(t, x) : x > γ0(t)} решение строится методом характеристик, причём со стороны x > γn(t)
кривая Γn является огибающей семейства характеристик из области Dn. В каждой из об-
ластей Dn, n ∈ N0, проекции этих характеристик на плоскость (t, x) образуют семейство
прямых
x = kt - gn(k),
(10)
параметризованных своим наклоном k.
В окрестности любой точки прямой t = 0 классическое решение задачи (8), (9) существует
и единственно. Для его построения следует продолжить начальное условие u0 константой
вдоль характеристик. Характеристическая система для уравнения (8) имеет вид
˙t = 1,
x = f′(u),
u = 0.
(11)
Характеристикой, выходящей из точки (t0, x0, u0(x0)) = (0, s, u0(s)), где s ∈ R - параметр
на графике начального условия u0, является прямая
{(t, x, u) ∈ R3 : u ≡ u0(s), x = |u|α-1t + s}.
(12)
Проекция на плоскость (t, x) этой прямой имеет вид
x = |ũ0(s)|α-1t + s, если s ≥ m, и x = (-s)β(α-1)t + s, если s < m.
Сделав в последнем уравнении замену k = (-s)β(α-1), k > |m|1/(β(α-1)), и обозначив
g0(k) = k1/(β(α-1)), получим семейство прямых
x = kt - g0(k),
(13)
зависящих от параметра k > |m|1/(β(α-1)).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
О ЗАДАЧЕ КОШИ ДЛЯ ОДНОМЕРНОГО ЗАКОНА СОХРАНЕНИЯ
313
Доопределим функцию g0(k) той же формулой при всех k > 0. Тогда семейство пря-
мых (13) будет иметь огибающую γ0(t) = L(g0)(t), определённую при всех t ∈ R+. После
перехода от параметрического представления (5) к явному получим, что
1
γ0(t) = -C0tη, где C0 = C0(α,β) > 0, η =
< 0.
(14)
1 - β(α - 1)
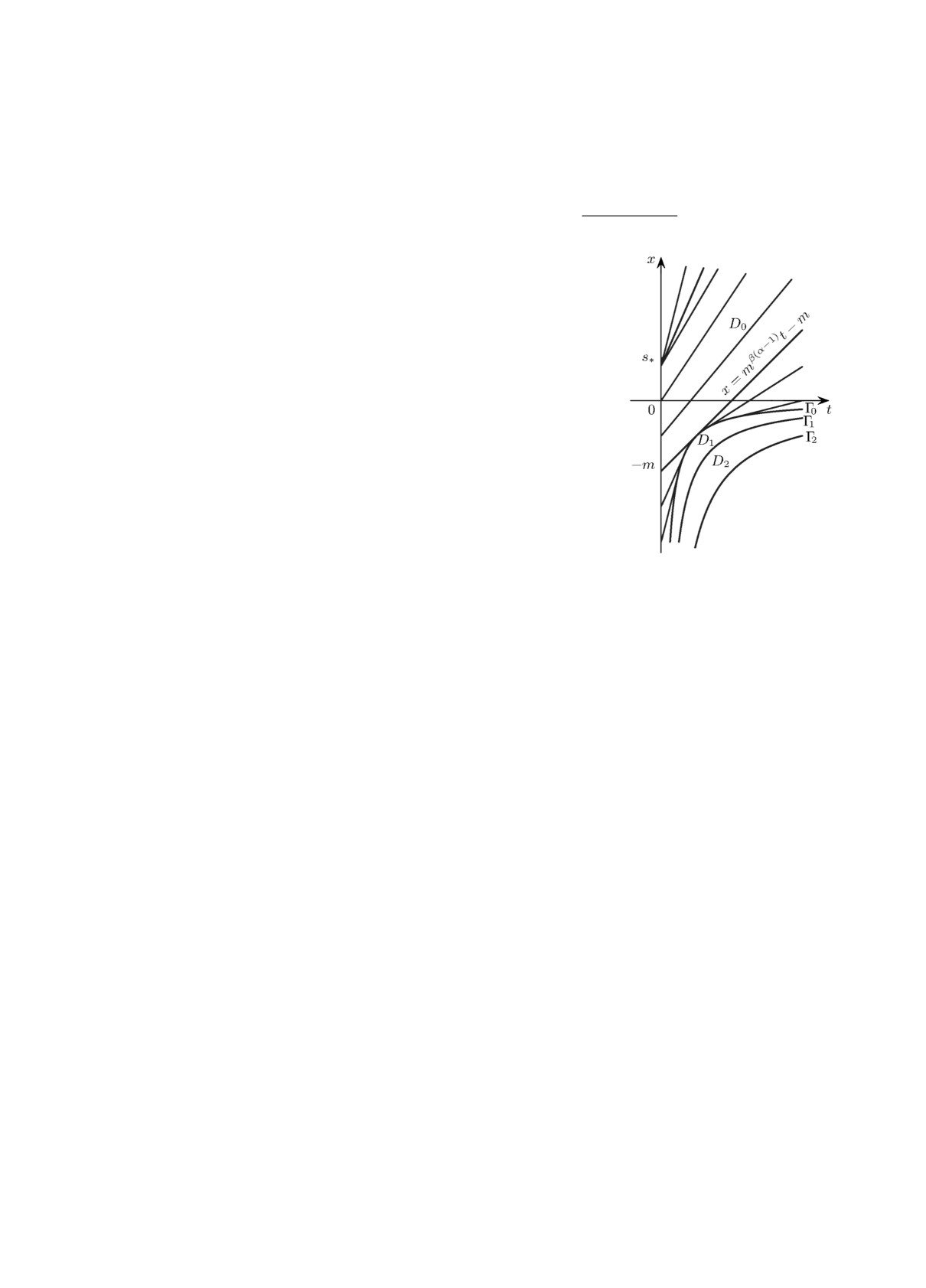
Определим решение в области D0 следующим образом
(рис. 1).
1) Если s ≥ m, то характеристики x = |ũ0(s)|α-1t + s име-
ют наклон, равный |ũ0(s)|β(α-1). Так как функция f′(ũ0(s)) =
= |ũ0(s)|α-1 не убывает, соответствующие характеристики не пе-
ресекаются. На каждой характеристике решение определяется
соотношением u ≡ ũ0(s).
Если монотонная функция ũ0 имеет разрыв (первого рода) в
точке s∗, то внутри угла f′(ũ0(s∗-0)) < (x-s∗)/t < f′(ũ0(s∗+0))
решение представляет собой волну разрежения (см. [5, с. 83-
87]), определяемую соотношением f′(u(t, x)) = (x - s∗)/t. Если
ũ0(m) = |m|β, то такой же волной разрежения f′(u(t,x)) = (x -
- m)/t заполняется и угол |m|β(α-1) < (x - m)/t < f′(ũ0(m)).
Построенное так решение u(t, x) является непрерывным в облас-
ти s ≥ m (см. [5, с. 83-87]).
2) Если s < m, то характеристики в соответствующей об-
Рис. 1. Характеристики и ли-
ласти x < |m|β(α-1)t + m начинают пересекаться, образовывая
нии разрыва для начального
условия степенного вида.
огибающую γ0(t) = -C0tη, 0 < t ≤ t0 (точка t0 = (|m|β(α-1) ×
× (-C0η)-1)1/(η-1) - это абсцисса точки касания графика функ-
ции γ0 с характеристикой x = |m|β(α-1)t + m). До этой огибающей решение определяет-
ся стандартным образом. Определим предел решения u+0(t) на огибающей из соотношения
γ0(t) = f′(u+0(t)) ≡ |u+0(t)|α-1.
3) В область {(t, x) : t > t0, γ0(t) < x < |m|β(α-1)t + m} характеристики не привносят
никакой информации из начального условия. В точках кривой γ0(t), t > t0, определим предел
решения u+0(t) из соотношения γ0(t) = f′(u+0(t)) ≡ |u+0(t)|α-1. Выпустим из каждой точки
кривой γ0(t), t > t0, касательную вправо. Продолжим решение с кривой γ0(t) вдоль всех
таких касательных соответствующей константой.
Опишем рекуррентную процедуру построения классического решения в областях Dn, n ∈
∈ N0. Итак, пусть решение в области Dn уже построено, причём кривая Γn является огибаю-
щей семейства характеристик из области Dn. Решение в области Dn+1 строится следующим
образом. В качестве “начального условия” выбирается условие
u|x=γn(t) = un(t),
которое находится из соотношения u-n(t) = -wu+n(t) (см. лемму). Далее решение продолжа-
ется константой вдоль характеристик, которые снова образуют огибающую.
Действительно, пусть x = k+nt - gn(k+n), (t, x) ∈ Dn, и x = k-nt - gn+1(k-n), (t, x) ∈ Dn+1, -
два семейства характеристик, параметризованные своим наклоном. В точке (t, γn(t)) кривой
разрыва Γn имеем равенства
t = g′n(k+n ), k+n t - gn(k+n ) = k-n t - gn+1(k-n ), k-n = wα-1k+n ,
из которых следует, что
gn+1(wα-1k+n) = gn(k+n) + g′n(k+n)(wα-1k+n - k+n).
Переобозначив k+n = k, получим следующую связь между соседними семействами характе-
ристик:
gn+1(wα-1k) = gn(k) + g′n(k)(wα-1k - k).
(15)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
314
ГАРГЯНЦ
Непосредственные вычисления показывают, что gn+1(k) = An+1g0(k) = An+1k1/(β(α-1)),
где An+1 = An+1(α, β), причём An+1 > An ≥ 1 для любого n ∈ N0. Учитывая свойства
преобразования Лежандра, а также формулу (14), получаем огибающую соответствующего
семейства характеристик γn+1(t) = L(gn+1)(t) = -Cn+1tη, где Cn+1 = C0(An+1)1-η > Cn.
Вследствие доказанной леммы построенное решение удовлетворяет условию Ранкина-Гю-
гонио. Энтропийность решения следует из того, что функция потока является выпуклой вниз
на положительной полуоси и выпуклой вверх на отрицательной полуоси. Теорема доказана.
4. Энтропийное решение задачи Коши с начальным условием, совпадающим
с экспоненциальной функцией на бесконечности. Рассмотрим задачу Коши для урав-
нения (8) с начальным условием
{
exp (-x/(α - 1)), если x ∈ (-∞, m),
u0(x) =
(16)
ũ0(x),
если x ∈ [m, +∞),
где
ũ0(x) - произвольная положительная нестрого возрастающая кусочно-гладкая функция,
причём ũ0(m) ≥ exp(-m/(α - 1)), m ∈ R.
Теорема 2. У задачи Коши (8), (16) существует обобщённое энтропийное решение u(·),
которое определено во всей полуплоскости t > 0, обладает счётным числом ударных волн Γn,
n ∈ N0, являющихся графиками функций
γn(t) = lnt + 1 - nC, C = C(α) > 0;
при этом функция u(·) удовлетворяет соотношениям
u(t, x) = (-1)n-1U(t, x + (n - 1)C), (t, x) ∈ Dn, n ∈ N,
(17)
где Dn = {(t, x) : γn(t) < x < γn-1(t)} и U = u|D1 .
Доказательство. Построим в явном виде кусочно-гладкое обобщённое энтропийное ре-
шение задачи (8), (16), удовлетворяющее условиям теоремы. Это решение будет иметь следу-
ющую структуру: в областях гладкости Dn, n ∈ N, и в области D0 = {(t, x) : x > γ0(t)}
решение строится методом характеристик, причём со стороны x > γn(t) кривая Γn являет-
ся огибающей семейства характеристик из области Dn. В каждой из областей Dn, n ∈ N0,
проекции этих характеристик на плоскость (t, x) образуют семейство прямых (10), парамет-
ризованных своим наклоном.
В окрестности любой точки прямой t = 0 классическое решение задачи (8), (16) существу-
ет и единственно. Для его построения следует продолжить начальное условие u0 константой
вдоль характеристик. Характеристическая система для уравнения (8) имеет вид (11). Характе-
ристикой, выходящей из точки (t0, x0, u0(x0)) = (0, s, u0(s)), где s ∈ R - параметр на графике
начального условия u0, является прямая (12). Проекция на плоскость (t, x) этой прямой
имеет вид
x = |ũ0(s)|α-1t + s, если s ≥ m, и x = e-st + s, если s < m.
Сделав в последнем уравнении замену k = e-s, k > e-m, и обозначив g0(k) = ln k,
получим семейство прямых (13), зависящих от параметра k > e-m.
Доопределим функцию g0(k) той же формулой при всех k > 0. Тогда семейство пря-
мых (13) будет иметь огибающую γ0(t) = L(g0)(t), определённую при всех t ∈ R+. После
перехода от параметрического представления (5) к явному получим, что
γ0(t) = 1 + ln t.
(18)
Решение в области D0 определяется аналогично тому, как это сделано в пп. 1)-3) доказа-
тельства теоремы 1. Именно, определим его следующим образом (рис. 2).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
О ЗАДАЧЕ КОШИ ДЛЯ ОДНОМЕРНОГО ЗАКОНА СОХРАНЕНИЯ
315
1′) Если s ≥ m, то характеристики в соответствующей
области имеют наклон, равный
|ũ0(s)|α-1. Так как функция
f′(ũ0(s)) = |ũ0(s)|α-1 не убывает, соответствующие характери-
стики не пересекаются. На каждой характеристике решение опре-
деляется соотношением u ≡ ũ0(s).
Если монотонная функция ũ0 имеет разрыв (первого рода) в
точке s∗, то внутри угла f′(ũ0(s∗ - 0)) < (x - s∗)/t < f′(ũ0(s∗ +
+0)) решение представляет собой волну разрежения (см. [5, с. 83-
87]), определяемую соотношением f′(u(t, x)) = (x - s∗)/t. Если
ũ0(m) = e-m/(α-1), то такой же волной разрежения f′(u(t,x)) =
= (x - m)/t заполняется и угол e-m < (x - m)/t < f′(ũ0(m)).
Построенное так решение u(t, x) является непрерывным в облас-
ти s ≥ m (см. [5, с. 83-87]).
2′) Если s < m, то характеристики в соответствующей об-
ласти x < e-mt + m начинают пересекаться, образовывая оги-
Рис. 2. Характеристики и ли-
бающую γ0(t) = 1 + ln t,
0 < t ≤ t0 (точка t0 = em - это
нии разрыва для начально-
с характеристи- го условия экспоненциального
абсцисса точки касания графика функции γ0
вида.
кой x = e-mt + m). До этой огибающей решение определяется
стандартным образом. Определим предел решения u+0(t) на оги-
бающей из соотношения γ0(t) = f′(u+0(t)) ≡ |u+0(t)|α-1.
3′) В область {(t,x) : t > t0, γ0(t) < x < e-mt+m} характеристики не привносят никакой
информации из начального условия. В точках кривой γ0(t), t > t0, определим предел решения
u+0(t) из соотношения γ0(t) = f′(u+0(t)) ≡ |u+0(t)|α-1. Выпустим из каждой точки кривой γ0(t),
t > t0, касательную вправо. Продолжим решение с кривой γ0(t) вдоль всех таких касательных
соответствующей константой.
Итак, построено решение задачи (8), (16) в области D0. Процедура построения решения
в областях Dn, n ∈ N, такая же, как и в теореме 1. Связь между функциями gn и gn+1,
которые задают семейства характеристик в областях Dn и Dn+1, описывается соотношени-
ем (15).
Непосредственные вычисления показывают, что gn+1(k) = gn(k) + C = g0(k) + (n + 1)C
для любого n ∈ N0, где C = C(α) > 0. Учитывая свойства преобразования Лежандра, а
также представление (18), получаем огибающую соответствующего семейства характеристик
γn+1(t) = L(gn+1)(t) = ln t - (n + 1)C.
Докажем, что построенное решение удовлетворяет соотношению (17). Действительно, со-
гласно доказанному выше, характеристики уравнения (8) имеют вид
x = kt - g1(k), (t,x) ∈ D1,
x = kt - (g1(k) + (n - 1)C), (t,x) ∈ Dn, n ∈ N.
Так как x = f′(u) = |u|α-1, то в точках области Dn имеем u(t, x) = |U(t, x + (n - 1)C)|.
Поэтому, поскольку при переходе через линию разрыва решение меняет знак, получаем соот-
ношение (17).
Вследствие доказанной леммы построенное решение удовлетворяет условию Ранкина-Гю-
гонио. Энтропийность решения следует из того, что функция потока является выпуклой вниз
на положительной полуоси и выпуклой вверх на отрицательной полуоси. Теорема доказана.
5. Несуществование положительного энтропийного решения. Покажем, что зада-
чи Коши для уравнения (8) с начальными условиями (9) и (16) не имеют положительных
решений ни в какой полосе. Для доказательства этого утверждения нам потребуются понятия
обобщённых энтропийных суб- и суперрешений этой задачи.
Обозначим f+ = max(f, 0); f- = max(-f, 0); sign+(f) = sign (f+); sign-(f) = -sign+(-f).
Приводимые ниже определения даны в работах [14, 15] (см. также [3, c. 328-329]).
Определение 3. Функция u: ΠT → R, u ∈ L∞loc(ΠT ), называется обобщённым энтропий-
ным субрешением задачи (1), (2), если выполняются следующие условия:
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
316
ГАРГЯНЦ
1) для любого k ∈ R имеет место неравенство
((u - k)+)t + (sign+(u - k)(f(u) - f(k)))x ≤ 0 в D′(ΠT );
2) esslim((u(t, x) - u0(x))+ = 0 в L1loc(R).
t→0+
Определение 4. Функция u: ΠT → R, u ∈ L∞loc(ΠT ), называется обобщённым энтропий-
ным суперрешением задачи (1), (2), если выполняются следующие условия:
1) для любого k ∈ R имеет место неравенство
((u - k)-)t + (sign-(u - k)(f(u) - f(k)))x ≤ 0 в D′(ΠT );
2) esslim((u(t, x) - u0(x))- = 0 в L1loc(R).
t→0+
Замечание 2. Несложно видеть, что функция u(·) является обобщённым энтропийным
решением задачи (1), (2) тогда и только тогда, когда она является обобщённым энтропийным
суб- и суперрешением одновременно.
В работах [14, 15] установлен следующий принцип сравнения для ограниченных обобщён-
ных энтропийных суб- и суперрешений.
Предложение 2. Если u: ΠT → R и v : ΠT → R, u, v ∈ L∞(ΠT ), - обобщённое эн-
тропийное субрешение и обобщённое энтропийное суперрешение задачи (1), (2) с начальны-
ми условиями u0 и v0 соответственно, u0,v0 ∈ L∞(R), и u0(x) ≤ v0(x) п.в. на R, то
u(t, x) ≤ v(t, x) п.в. на ΠT .
В работе [16] доказано, что максимум (минимум) конечного множества обобщённых энтро-
пийных субрешений (суперрешений) задачи (1), (2) также является обобщённым энтропийным
субрешением (суперрешением) этой задачи, откуда вытекает доказанное в работе [8]
Предложение 3. 1. Пусть u - обобщённое энтропийное субрешение задачи (1), (2) и
c ∈ R. Тогда функция v: ΠT
→ R, v(t,x) = max(u(t,x),c) также является обобщён-
ным энтропийным субрешением этой задачи с начальной функцией v0 : R → R, v0(x) =
= max(u0(x),c).
2. Пусть u - обобщённое энтропийное суперрешение задачи (1), (2) и c ∈ R. Тогда функ-
ция w : ΠT → R, w(t, x) = min(u(t, x), c) также является обобщённым энтропийным супер-
решением этой задачи с начальной функцией w0 : R → R, w0(x) = min(u0(x),c).
Теорема 3. Пусть f ∈ C1(R), функция h(x) = (f(x) - f(0))/x возрастает при x > 0
и для некоторого m ∈ R кусочно-гладкая функция u0 : R → R+ убывает при x < m, при-
чём lim
u0(x) = +∞. Пусть также выполнено соотношение∗)
-u-10(x) = o(h(x)) при
x→-∞
x → +∞. Тогда не существует неотрицательного обобщённого энтропийного решения зада-
чи (1), (2) ни в какой полосе ΠT .
Доказательство. Рассмотрим задачу Коши для уравнения (1) с начальным условием (2),
а также задачи Коши для этого же уравнения со следующими начальными условиями:
{
N, x < u-10(N),
(uN )t + f(uN )x = 0, uN |t=0 =
(19)
0, x ≥ u-10(N),
(UN )t + f(UN )x = 0, UN |t=0 = min (N, u0(x))
(20)
при фиксированном N ∈ N, N ≥ u0(m).
Заметим, что справедливы неравенства uN |t=0 ≤ UN |t=0 ≤ u|t=0.
Задача (19) представляет собой задачу Римана о распаде разрыва. Её единственным огра-
ниченным обобщённым энтропийным (энтропийность следует из определения функции h) ре-
шением uN ∈ L∞(ΠT ) является [5] функция
{
N, x < u-10(N) + h(N)t,
uN (t,x) =
0,
x ≥ u-10(N) + h(N)t.
∗) Здесь и ниже в доказательстве под u-10 подразумевается обратная функция к ограничению функции u0
на промежуток (-∞, m). На этом промежутке функция u0 монотонна, а значит, имеет обратную.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
О ЗАДАЧЕ КОШИ ДЛЯ ОДНОМЕРНОГО ЗАКОНА СОХРАНЕНИЯ
317
Отметим, что для любой фиксированной точки (t, x) ∈ R+ × R имеет место сходимость
uN (t,x) → +∞ при N → +∞, поскольку -u-10(x) = o(h(x)) при x → +∞.
Пусть u ∈ L∞loc(ΠT ) - неотрицательное обобщённое энтропийное решение (а значит, и обоб-
щённое энтропийное суперрешение) задачи (1), (2). Тогда в силу предложения 3 функция
UN : ΠT → R, UN (t,x) = min(u(t,x),N), также является обобщённым энтропийным суперре-
шением задачи (20), причём для всех (t, x) ∈ ΠT выполнено неравенство 0 ≤ UN (t, x) ≤ N в
силу неотрицательности функции u.
Таким образом, вследствие предложения 2 и определения функции UN почти всюду в
полосе ΠT справедливы неравенства uN (t, x) ≤ UN (t, x) ≤ u(t, x), но это противоречит тому,
что uN (t, x) → +∞ при N → +∞.
Следствие 1. Не существует неотрицательного обобщённого энтропийного решения за-
дачи Коши (8), (9) ни в какой полосе ΠT .
Доказательство. Заметим, что функции f(u) = |u|α-1u/α, h(x) = |x|α-1/α, α > 1, и
начальное условие u0, определённое равенством (9), удовлетворяют всем условиям теоремы 3.
Действительно, f ∈ C1(R), причём h - возрастающая при x > 0 функция, а неотрицательная
кусочно-гладкая функция u0 убывает на интервале
(-∞, m), причём lim
u0(x) = +∞.
x→-∞
Кроме того, x1/β = o(|x|α-1/α) при x → +∞, поскольку β(α - 1) > 1. Следовательно,
-u-10(x) = o(h(x)) при x → +∞. Следствие доказано.
Следствие 2. Не существует неотрицательного обобщённого энтропийного решения за-
дачи Коши (8), (16) ни в какой полосе ΠT .
Доказательство. Согласно доказательству следствия 1 определённые в нём функции f
и h удовлетворяют условиям теоремы 3. Условиям этой теоремы удовлетворяет и начальное
условие u0, определённое равенством (16). Действительно, неотрицательная кусочно-гладкая
функция u0 убывает на интервале (-∞, m), причём lim
u0(x) = +∞. Кроме того, имеет
x→-∞
место соотношение (α - 1) ln x = o(|x|α-1/α) при x → +∞, поэтому -u-10(x) = o(h(x)) при
x → +∞. Следствие доказано.
Работа выполнена при финансовой поддержке гранта Президента Российской Федерации
(проект МК-1204.2020.1), а также при финансовой поддержке Министерства науки и высшего
образования Российской Федерации (проект 0705-2020-0047).
СПИСОК ЛИТЕРАТУРЫ
1. Кружков С.Н. Обобщённые решения задачи Коши в целом для нелинейных уравнений первого
порядка // Докл. АН СССР. 1969. Т. 187. № 1. С. 29-32.
2. Кружков С.Н. Квазилинейные уравнения первого порядка со многими независимыми переменными
// Мат. сб. 1970. Т. 81. № 2. С. 228-255.
3. Труды С.Н. Кружкова: сб. ст. / Под ред. С.Н. Бахвалова. М., 2000.
4. Панов Е.Ю. О классах корректности локально ограниченных обобщённых энтропийных решений
задачи Коши для квазилинейных уравнений первого порядка // Фунд. и прикл. математика. 2006.
Т. 12. № 5. С. 175-188.
5. Горицкий А.Ю., Кружков С.Н., Чечкин Г.А. Уравнения с частными производными первого поряд-
ка. М., 1999.
6. Олейник О.А. О единственности и устойчивости обобщённого решения задачи Коши для квазили-
нейного уравнения // Успехи мат. наук. 1959. Т. 14. № 2. С. 165-170.
7. Горицкий А.Ю. Построение неограниченного энтропийного решения задачи Коши со счётнымм
числом ударных волн // Вестн. Моск. ун-та. Сер. 1. Математика, механика. 1999. № 2. С. 3-6.
8. Горицкий А.Ю., Панов Е.Ю. О локально ограниченных обобщённых энтропийных решениях задачи
Коши для квазилинейного уравнения первого порядка // Тр. Мат. Ин-та им. В.А. Стеклова РАН.
2002. Т. 236. № 5. С. 120-133.
9. Гаргянц Л.В. Локально ограниченные решения одномерных законов сохранения // Дифференц.
уравнения. 2016. Т. 52. № 4. С. 481-489.
10. Гаргянц Л.В. О локально ограниченных решениях задачи Коши для квазилинейного уравнения
первого порядка со степенной функцией потока // Мат. заметки. 2018. Т. 104. № 2. С. 191-199.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022
318
ГАРГЯНЦ
11. Gargyants L.V. Example of nonexistence of a positive generalized entropy solution of a Cauchy problem
with unbounded positive initial data // Russian J. of Math. Phys. 2017. V. 24. № 3. P. 412-414.
12. Гаргянц Л.В., Горицкий А.Ю., Панов Е.Ю. Построение неограниченных разрывных решений ска-
лярных законов сохранения при помощи преобразования Лежандра // Мат. сб. 2021. Т. 212. № 4.
С. 29-44.
13. Арнольд В.И. Геометрические методы в теории обыкновенных дифференциальных уравнений. М.,
2012.
14. Бенилан Ф., Кружков С.Н. Квазилинейные уравнения первого порядка с непрерывными нелиней-
ностями // Докл. РАН. 1994. Т. 339. № 2. С. 151-154.
15. Benilan Ph., Kruzhkov S.N. Conservation laws with continuous flux functions // Nonlin. Differ. Equat.
and Appl. 1996. V. 3. P. 395-419.
16. Панов Е.Ю. К теории обобщенных энтропийных суб- и суперрешений задачи Коши для квазили-
нейного уравнения первого порядка // Дифференц. уравнения. 2001. Т. 37. № 2. С. 252-259.
Московский государственный технический университет
Поступила в редакцию 24.11.2020 г.
им. Н.Э. Баумана
После доработки 24.11.2020 г.
Принята к публикации 09.03.2022 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№3
2022