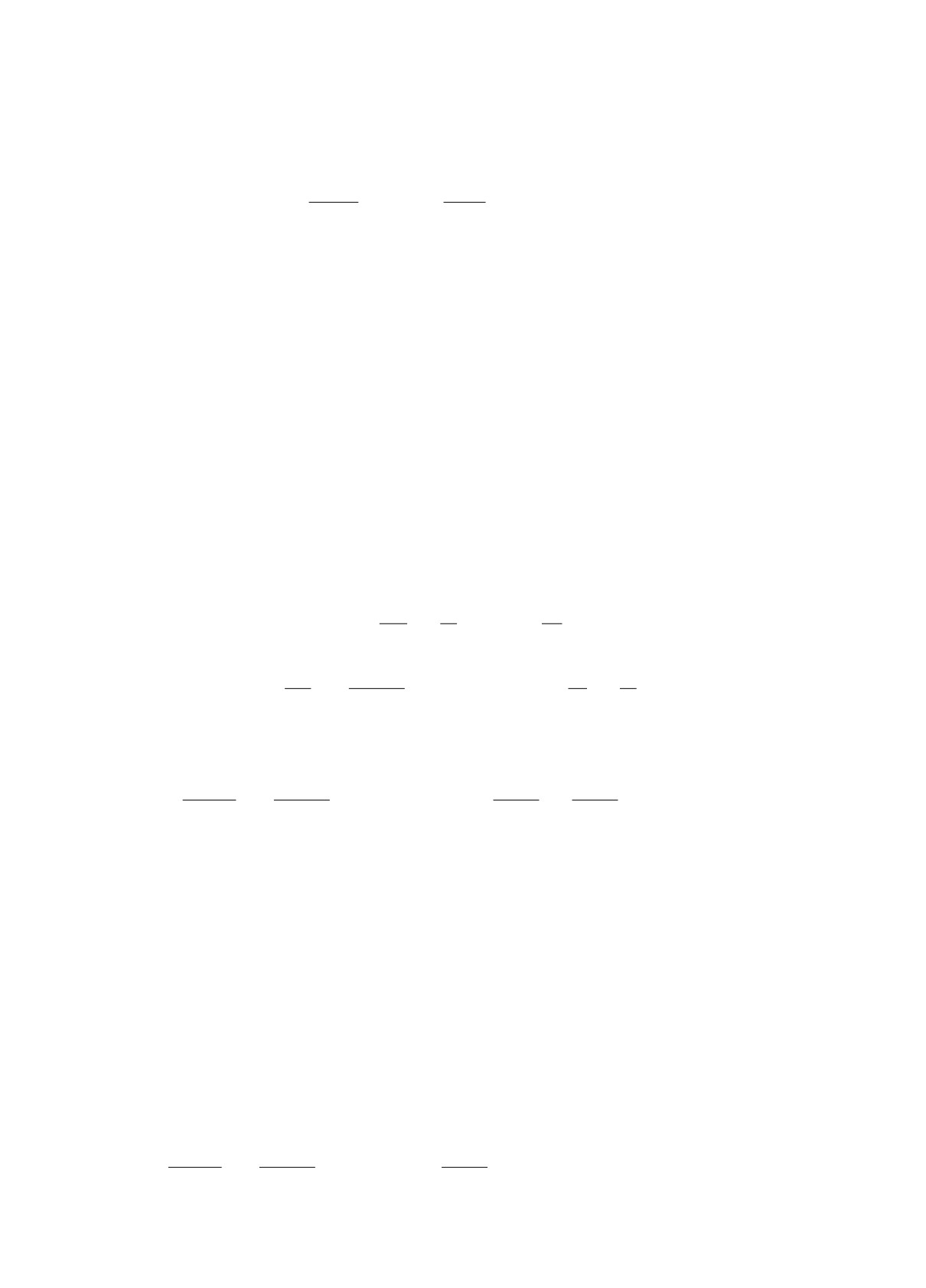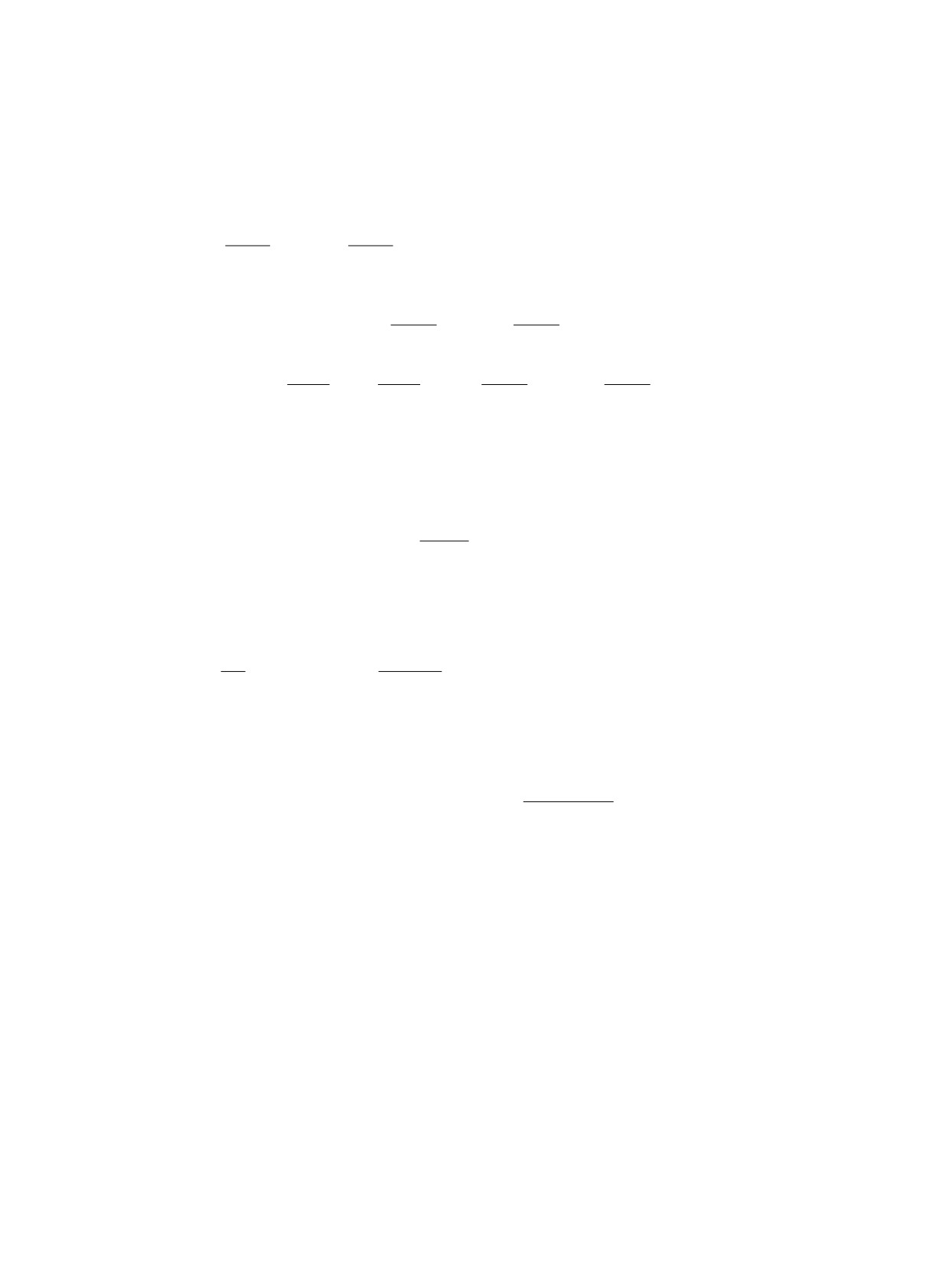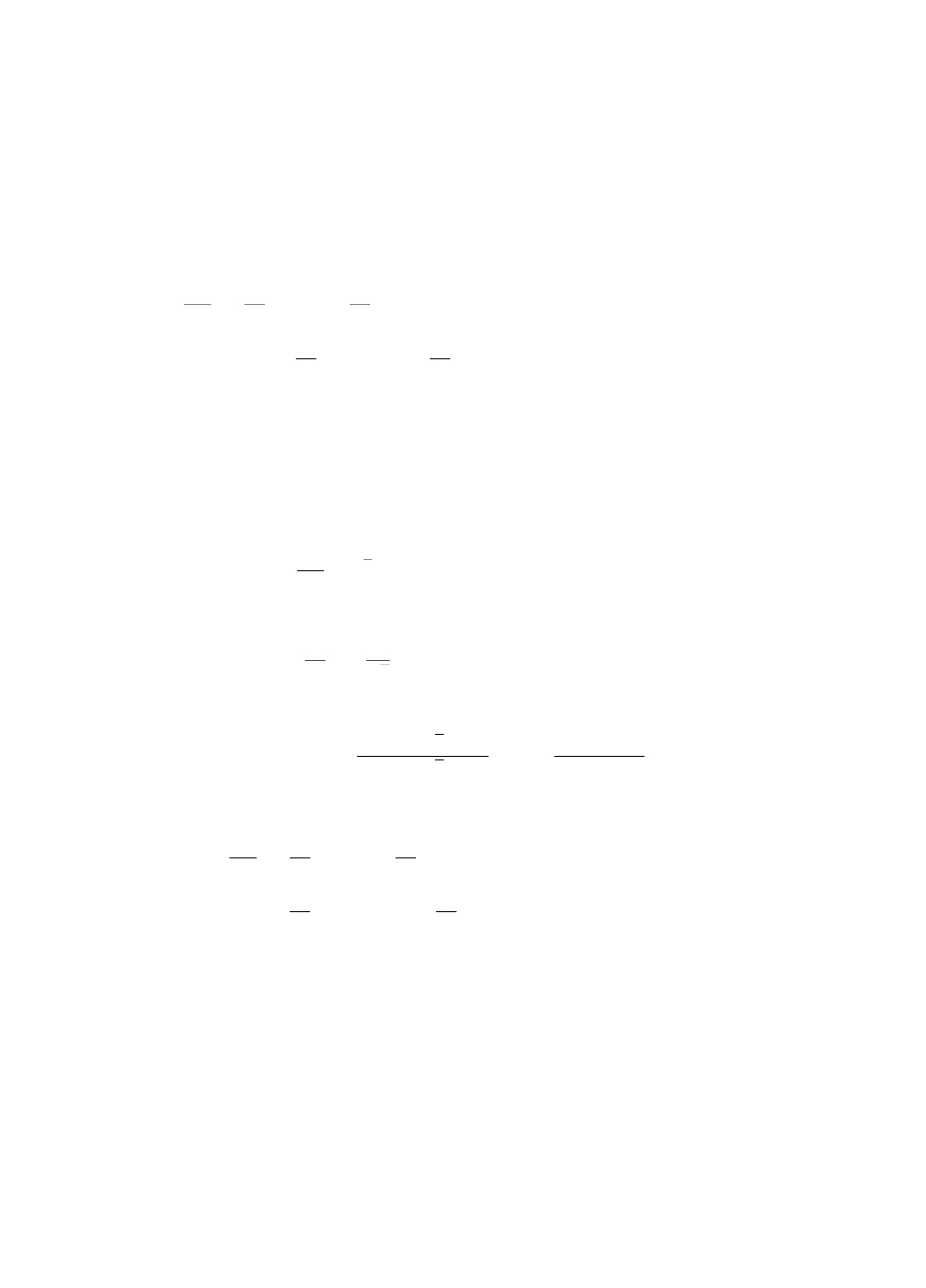ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 6, с.763-776
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
УДК 519.624.2
ДВИЖЕНИЕ ФРОНТА В ЗАДАЧЕ СО СЛАБОЙ
АДВЕКЦИЕЙ В СЛУЧАЕ НЕПРЕРЫВНОГО ИСТОЧНИКА
И ИСТОЧНИКА МОДУЛЬНОГО ТИПА
© 2022 г. Н. Н. Нефедов, Е. И. Никулин, А. О. Орлов
Получено асимптотическое приближение решения, имеющего вид движущегося внутрен-
него слоя (фронта), начально-краевой задачи для сингулярно возмущённого параболиче-
ского уравнения реакция-адвекция-диффузия с малой адвекцией. Отдельно рассмотрены
случай непрерывного источника (нелинейности, описывающей взаимодействие, реакцию)
и случай разрыва источника при некотором значении искомой функции, возникающий в
ряде актуальных приложений. Для каждой задачи построено асимптотическое приближе-
ние решения и доказаны теоремы существования и единственности такого решения.
DOI: 10.31857/S037406412206005X, EDN: CDARNG
1. Введение. Постановка задачи. Рассмотрим сингулярно возмущённую начально-кра-
евую задачу
∂2u
∂u
∂u
ε2
-ε
- εA(x, ε)
- f(u,x,ε) = 0, x ∈ (-1,1), t ∈ (0,T],
∂x2
∂t
∂x
∂u
∂u
(-1, t, ε) = 0,
(1, t, ε) = 0, t ∈ [0, T ],
∂x
∂x
u(x, 0, ε) = uinit(x, ε), x ∈ [-1, 1],
(1)
где ε ∈ (0, ε0] - малый параметр. В работе получено асимптотическое приближение решения
этой задачи, имеющего вид движущегося внутреннего слоя (фронта). Исследование формиро-
вания и движения фронтов в задачах для уравнений реакция-адвекция-диффузия обуслов-
лено важными приложениями, использующими для математических моделей такие задачи, в
частности в теории нелинейных волн (см. статьи [1, 2]), при изучении автоволновых процессов
в урбоэкологии (см. работы [3, 4]) и многих других приложениях.
Стационарные решения задачи (1) c пограничными и внутренними слоями изучены в [5].
Периодические решения задачи (1) рассматривались в [6, 7].
Результаты, полученные в данной работе, развивают результаты статьи [8], где рассмотрено
движение фронта при отсутствии адвекции (A(x, ε) = 0 в уравнении в (1)), на новые классы
задач, включающие так называемые модульные источники и адвекцию.
В обсуждаемых ниже задачах предполагается, что в начальный момент времени фронт
уже сформирован. Это означает, что функция uinit(x, ε) имеет внутренний переходный слой
в окрестности некоторой точки x00 ∈ (-1, 1), т.е. близка к некоторому корню ϕ(-)(x) вы-
рожденного уравнения f(u, x, 0) = 0 левее точки x00 и к корню ϕ(+)(x) правее этой точки.
В окрестности x00 происходит резкий переход от ϕ(-)(x) к ϕ(+)(x). Доказано существова-
ние решения вида движущегося фронта, т.е. такого решения, которое имеет внутренний пе-
реходный слой, в каждый момент времени локализованный в окрестности движущейся точки
x(t, ε) ∈ (-1, 1), асимптотическое приближение которой получено ниже.
В п. 2 будет разобран случай непрерывного источника кубического типа. Поскольку пове-
дение решения и его асимптотика в случае разрывной при некотором значении u функции
f (u, x, ε) в значительной мере аналогичны случаю, рассмотренному в п. 2, в п. 3 остановимся
лишь на отличительных особенностях. Полученные результаты проиллюстрированы примера-
ми, которые могут быть использованы для разработки эффективных численных методов для
исследуемых классов задач.
763
764
НЕФЕДОВ и др.
2. Случай непрерывного источника. Предполагаем, что выполнены следующие ус-
ловия:
Условие 1. Функции A(x, ε), f(u, x, ε) являются достаточно гладкими в своих областях
определения.
Условие 2. Пусть вырожденное уравнение f(u, x, 0) = 0 имеет ровно три решения u =
= ϕ(±,0)(x), причём
ϕ(-)(x) < ϕ(0)(x) < ϕ(+)(x), x ∈ [-1, 1],
а также выполнены неравенства
fu(ϕ(±)(x),x,0) > 0, fu(ϕ(0)(x),x,0) < 0, x ∈ [-1,1].
2.1. Построение формальной асимптотики решения. Асимптотика решения задачи
(1) строится методом пограничных функций (см. [9]) отдельно в каждой из областей [-1, x] ×
×[0, T ] и [x, 1]×[0, T ] с подвижной границей (см. [10]) с использованием развиваемого в наших
работах эффективного метода построения асимптотики локализации внутреннего слоя:
{
U(-)(x,t,ε), (x,t,ε) ∈ [-1, x] × [0,T] × (0,ε0],
U (x, ε) =
U(+)(x,t,ε), (x,t,ε) ∈ [x,1] × [0,T] × (0,ε0].
Каждую из функций U(±)(x, ε) будем представлять в виде суммы трёх слагаемых:
U(±)(x,t,ε) = u(±)(x,ε) + Q(±)(ξ,t,ε) + R(±)(η(±),ε).
(2)
Здесь u(±)(x, ε) = u(±)0(x) + εu(±)1(x) + . . . - регулярная часть разложения, функции
Q(±)(ξ,t,ε) = Q(±)0(ξ,t,ε) + εQ(±)1(ξ,t,ε) + ...
описывают поведение решения в окрестности точки перехода x(t, ε), ξ = (x - x(t, ε))/ε - пе-
ременная переходного слоя: ξ ≤ 0 для функций с индексом (-) и ξ ≥ 0 для функций с
индексом (+); функции R(η(±), ε) = R0(η(±)) + εR1(η(±)) + . . . описывают поведение решения
в окрестностях граничных точек отрезка [-1, 1], η(±) = (x ∓ 1)/ε - растянутые переменные,
соответственно, вблизи точек x = ±1. В настоящей работе не будем описывать процеду-
ру построения функций Ri(η(±)), поскольку они определяются стандартным образом (см.,
например, [5]). Отметим, что данные функции не зависят от переменной t и тем самым не
участвуют в описании движущегося переходного слоя, а функции R0(η(±)) = 0 в силу краевых
условий Неймана.
Положение внутреннего переходного слоя определяется из условия C1-сшивания асимпто-
тических представлений U(-)(x, t, ε) и U(+)(x, t, ε) в точке перехода
x(t, ε):
U(-)(x(t,ε),t,ε) = U(+)(x(t,ε),t,ε) = ϕ(0)(x(t,ε)),
(3)
∂
∂
ε
U(-)(x(t,ε),t,ε) = ε
U(+)(x(t,ε),t,ε).
(4)
∂x
∂x
Точку перехода x = x(t, ε) будем искать в виде разложения по степеням малого параметра ε:
x(t, ε) = x0(t) + εx1(t) + . . .
(5)
Коэффициенты данного разложения будут определены в процессе построения асимптотики.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
ДВИЖЕНИЕ ФРОНТА В ЗАДАЧЕ СО СЛАБОЙ АДВЕКЦИЕЙ
765
Регулярная часть асимптотики определяется после подстановки представления слагае-
мого u(±)(x, ε) в уравнение
(±)
∂2u
∂u(±)
ε2
- εA(x, ε)
- f(u(±),x,ε) = 0.
∂x2
∂x
Стандартным образом (см. статью [5]) получим алгебраические уравнения для определения
функций регулярной части u(±)k(x), k ∈ N0 ≡ N
⊔ {0}.
C учётом условия 2 регулярные функции нулевого порядка определяются как
u(±)0(x) = ϕ(±)(x).
Для сокращения записей введём обозначения
f(±)u(x) := fu(ϕ(±)(x),x,0).
Функции u(±)k(x) при k ∈ N определяются из уравнений
f(±)u(x)u(±)k(x) =h(±)k(x),
где функцииh(±)k(x) известны на каждом k-м шаге и выражаются рекуррентно через функции
u(±)k(x) с индексами 0, 1, . . . , k - 1. Разрешимость уравнений следует из условия 2.
Для того чтобы получить уравнения, которым удовлетворяют функции переходного слоя
Q(±)(ξ,t,ε), запишем дифференциальный оператор задачи в переменных (ξ,t). Оператор
2
∂
∂
∂
ε2
-ε
- εA(x, ε)
∂x2
∂t
∂x
принимает вид
)
∂2
(∂x(t,ε)
∂
∂
+
- A(εξ + x(t, ε), ε)
-ε
∂ξ2
∂t
∂ξ
∂t
Уравнения для функций Q(±)k(ξ, t, ε), k ∈ N0, определяются стандартным способом путём
приравнивания коэффициентов при одинаковых степенях ε в обеих частях равенств:
∂2Q(±)
(∂x(t,ε)
)∂Q(±)
∂Q(±)
+
- A(εξ + x(t, ε), ε)
-ε
= Qf(±)(ξ,t,ε),
(6)
∂ξ2
∂t
∂ξ
∂t
где
Qf(±)(ξ,t,ε) = f(u(±)(εξ + x(t,ε),ε) + Q(±)(ξ,t,ε),εξ + x(t,ε),ε) -
- f(u(±)(εξ + x(t,ε),ε),εξ + x(t,ε),ε).
Не будем раскладывать по степеням ε точку перехода x(t, ε), в отличие от подхода, изложен-
ного в работе [8]. Это упростит алгоритм построения асимптотики.
Потребуем, чтобы функции переходного слоя Q(±)k(ξ, t, ε), k ∈ N0, удовлетворяли услови-
ям равенства нулю на бесконечности:
Q(-)k(ξ,t,ε) → 0 при ξ → -∞,
Q(+)k(ξ,t,ε) → 0 при ξ → +∞, k ∈ N0, t ∈ [0,T].
Приравняв коэффициенты при ε0 в правой и левой частях равенств (6), получим уравне-
ния для функции Q(-)0(ξ, t, ε) при ξ ≤ 0 и функции Q(+)0(ξ, t, ε) при ξ ≥ 0:
∂2Q(±)0
(∂x(t,ε)
)∂Q(±)0
+
- A(x(t, ε), 0)
= f(ϕ(±)(x(t,ε)) + Q(±)0, x(t,ε),0).
(7)
∂ξ2
∂t
∂ξ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
766
НЕФЕДОВ и др.
Дополнительные условия при ξ = 0 получим из условия непрерывного сшивания (3), запи-
санного в нулевом порядке по ε:
Q(-)0(0,t,ε) + ϕ(-)(x(t,ε)) = Q(+)0(0,t,ε) + ϕ(+)(x(t,ε)) = ϕ(0)(x(t,ε)).
Добавим также условия на бесконечности Q(-)0(ξ, t, ε) → 0 при ξ → -∞, Q(+)0(ξ, t, ε) → 0
при ξ → +∞, t ∈ [0, T ].
Введём оператор D :
∂x(t,ε)
Dx :=
- A(x(t, ε), 0).
(8)
∂t
Введём функции
ũ(±)(ξ, x) = ϕ(±)(x(t,ε)) + Q(±)0(ξ,t,ε),
{
(-)
ϕ(-)(x(t, ε)) + Q
(ξ, t, ε), если ξ ≤ 0;
0
ũ(ξ, x) =
ϕ(+)(x(t, ε)) + Q(+)0(ξ, t, ε), если ξ ≥ 0;
∂ũ
∂ũ
v(-)(ξ, x) =
(ξ, x), ξ ≤ 0,
v(+)(ξ, x) =
(ξ, x), ξ ≥ 0.
(9)
∂ξ
∂ξ
Запишем уравнения (7), а также дополнительные условия с использованием (9):
∂2ũ(±)
∂ũ(±)
+Dx
= f(ũ(±), x,0),
ũ(±)(0, x) = ϕ(0)(x),
ũ(±)(±∞, x) = ϕ(±)(x).
(10)
∂ξ2
∂ξ
Вместе с задачами (10) рассмотрим задачу
∂2û
∂û
+W
= f(û, x,0),
û(0, x) = ϕ(0)(x),
û(±∞, x) = ϕ(±)(x).
(11)
∂ξ2
∂ξ
Задача (11) подробно изучена в статье [11]. Приведём необходимый нам результат в виде
леммы.
Лемма 1. Для каждого x ∈ (-1, 1) существует единственная величина W такая, что
задача (11) имеет единственное гладкое монотонное решение û(ξ, x), удовлетворяющее оцен-
ке
|û(ξ, x) - ϕ(±)(x)| < C exp(-κ|ξ|),
где C и κ - некоторые положительные постоянные. При этом зависимость W (x) опреде-
ляется следующим выражением:
∫
(
)2
)-1
∫
∂û
W(x) =
(ξ, x) dξ
f (u, x, 0) du.
∂ξ
−∞
ϕ(-)(x)
Гладкость функции W (x) совпадает с гладкостью функции f(û, x, 0).
Потребуем выполнения следующего условия.
Условие 3. Пусть задача
dx
= W(x) + A(x,0), x(0) = x00
(12)
dt
имеет решение x = x0(t):
-1 < x0(t) < 1 при t ∈ [0,T].
Потребуем также, чтобы
W (x0) + A(x0, 0) > 0 для всех x0 ∈ [-1, 1].
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
ДВИЖЕНИЕ ФРОНТА В ЗАДАЧЕ СО СЛАБОЙ АДВЕКЦИЕЙ
767
Неравенство в условии 3 гарантирует отсутствие стационарных решений у задачи (12).
Обозначим через (10а) задачи (10), в которых везде x заменено на x0(t), или, другими сло-
вами, в которых положили ε = 0. Из леммы 1 и условия 3 следует единственная разрешимость
задач (10а), так как выполнено условие Dx0 = W (x0). При этом
∂ũ(+)
∂ũ(-)
(0, x0(t)) -
(0, x0(t)) = 0.
∂ξ
∂ξ
В силу предполагаемой гладкости функций f, A (см. условие 1) задачи (10) являются
регулярным возмущением задач (10а), а потому также единственно разрешимы. Отметим,
что в силу представления (5) имеем теперь
∂ũ(+)
∂ũ(-)
(0, x(t, ε)) -
(0, x(t, ε)) = O(ε).
∂ξ
∂ξ
Таким образом, построение функции переходного слоя в нулевом порядке завершено.
Функции переходного слоя первого порядка находятся из следующих задач:
∂2Q(±)1
∂Q(±)1
+Dx
-f˜u(ξ,t)Q(±)1 = r(±)1(ξ,t,ε),
∂ξ2
∂ξ
Q(±)1(0,t,ε) + u(±)1(x) = 0,
Q(±)1(±∞,t,ε) = 0,
(13)
где введены обозначения
fu(ξ,t) = fu(ũ(ξ, x), x,0)
(14)
и
(
)
(
)
(±)
∂A
∂A
r(±)1(ξ,t,ε) =∂Q0
(x,0)ξ +
(x,0)
+
u(±)1(x) + ξdϕ(±)(x)
fu(ξ,t) +
∂ξ
∂x
∂ε
dx
(±)
dϕ
+
fx(ξ,t)
fε(ξ,t) + A(x,0)
(x).
dx
Здесь производные
fx(ξ,t),
fε(ξ,t) вычисляются в той же точке, что и производная
fu(ξ,t)
в (14). Задачу для функции Q(-)1(ξ, t, ε) будем решать на полупрямой ξ ≤ 0, а для функции
Q(+)1(ξ,t,ε) - на полупрямой ξ ≥ 0. Решения задач (13) записываются в явном виде:
Q(±)1(ξ,t,ε) = -u(±)1(x)v(±)(ξ,x)
+
v(±)(0, x)
∫
ξ
∫
η
+ v(±)(ξ, x)
(v(±)(η, x))-2e-(Dx)η
v(±)(σ, x)e(Dx)σr(±)1(σ, t, ε) dσ dη.
(15)
0
±∞
Из выражений для функций r(±)1(ξ, t, ε) следует, что они имеют экспоненциальные оценки, а
из (15) стандартным образом следует, что аналогичные оценки справедливы и для функций
Q(±)1(ξ,t,ε). Аналогично первому приближению можно определить функции переходного слоя
Q(±)k(ξ,t,ε) для любого k = 2,3...
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
768
НЕФЕДОВ и др.
2.2. Асимптотическое приближение положения фронта. В силу важности этого
раздела построения асимптотики выделим его в отдельный пункт.
Неизвестные коэффициенты xi(t), i ∈ N, разложения (5) определяются из условий сши-
вания (4) производных асимптотических разложений. Введём функцию
)
(+)
( dU
dU(-)
H(ε, t) := ε
(x,t,ε) -
(x,t,ε)
= H0(ε,t) + εH1(ε,t) + ε2H2(ε,t) + ... ,
(16)
dx
dx
где
(+)
∂Q
∂Q(-)0
0
H0(ε,t) =
(0, t, ε) -
(0, t, ε),
∂ξ
∂ξ
)
(+)
dϕ
dϕ(-)
(∂Q(+)1
∂Q(-)
1
H1(ε,t) =
(x) -
(x) +
(0, t, ε) -
(0, t, ε)
,
dx
dx
∂ξ
∂ξ
и т.д.
Условие C1-сшивания (4) выражается равенством H(x, t, ε) = 0. В силу леммы 1 и усло-
вия 3 с учётом разложения точки перехода (5) это равенство выполнено в порядке ε0.
Анализ задач (10), (11) показывает, что функция H0 может быть представлена в виде
∫
1
H0(ε,t) = (Dx - W(x))
v2(ξ, x)e(Dx)ξ dξ + O(ε2).
(17)
v(0, x)
−∞
Как следует из разложения (16) и представления (17), члены xi(t), i ≥ 1, высших поряд-
ков в (5) могут быть найдены из следующих задач Коши:
(
)
dxi
∂A(x, 0)
+ W′(x0(t)) +
xi(t) = Gi(t), xi(0) = 0,
(18)
dt
∂x
x=x0(t)
где Gi(t) - известные функции.
2.3. Обоснование формальной асимптотики. Положим
∑
x - Xn(t,ε)
Xn(t,ε) =
εixi(t), ξ =
ε
i=0
Кривая Xn(t, ε) разделяет область
D : (x,t) ∈ [-1,1] × [0,T] на две подобласти:
D(-)
D(+)
n
: (x, t) ∈ [-1, Xn(t, ε)] × [0, T ] и
n
: (x, t) ∈ [Xn(t, ε), 1] × [0, T ].
Определим функции
∑
U(-)n(x,t,ε) =
εi(u(-)i(x) + Q(-)i(ξ,t,ε) + R(-)i(η(-))), (x,t) ∈D(-)n,
i=0
∑
U(+)n(x,t,ε) =
εi(u(+)i(x) + Q(+)i(ξ,t,ε) + R(+)i(η(+))), (x,t) ∈D(+)n,
i=0
где x(t, ε), входящие в выражения для функций переходного слоя, заменены на Xn(t, ε), и
обозначим
{
n (x, t, ε), (x, t) ∈Dn-),
Un(x,t,ε) =
(19)
n (x, t, ε), (x, t) ∈Dn+).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
ДВИЖЕНИЕ ФРОНТА В ЗАДАЧЕ СО СЛАБОЙ АДВЕКЦИЕЙ
769
Для доказательства существования решения вида движущегося фронта используем асимп-
тотический метод дифференциальных неравенств [12]. Построим непрерывные функции
α(x, t, ε), β(x, t, ε) таким образом, чтобы они удовлетворяли условиям:
1) условие упорядоченности:
α(x, t, ε) ≤ β(x, t, ε), x ∈ [-1, 1], t ∈ [0, T ], ε ∈ (0, ε0];
2) действие дифференциального оператора на верхнее и нижнее решения:
∂2β
∂β
∂β
∂2α
∂α
∂α
ε2
-ε
- εA(x, ε)
- f(β,x,ε) ≤ 0 ≤ ε2
-ε
- εA(x, ε)
- f(α,x,ε)
∂x2
∂t
∂x
∂x2
∂t
∂x
для всех x ∈ (-1, 1), t ∈ [0, T ] за исключением тех x(t), в которых функции α(x, t, ε),
β(x, t, ε) являются негладкими;
3) условия на границе:
dα
∂β
∂α
∂β
(-1, t, ε) ≥ 0 ≥
(-1, t, ε),
(+1, t, ε) ≤ 0 ≤
(+1, t, ε), t ∈ [0, T ], ε ∈ (0, ε0];
dx
∂x
∂x
∂x
4) условия на начальную функцию:
α(x, 0, ε) ≤ uinit(x, ε) ≤ β(x, 0, ε), x ∈ [-1, 1], ε ∈ (0, ε0];
5) условия на скачок производных:
∂β
∂β
(x(t) - 0, t, ε) ≥
(x(t) + 0, t, ε),
dx
dx
где x(t) - точка, в которой верхнее решение является негладким;
∂α
∂α
(x(t) - 0, t, ε) ≤
(x(t) + 0, t, ε),
dx
dx
где x(t) - точка, в которой нижнее решение является негладким.
Известно (см. [13, 14]), что при выполнении условий 1)-5) существует решение задачи (1),
для которого выполняются неравенства
α(x, t, ε) ≤ u(x, t, ε) ≤ β(x, t, ε), (x, t) ∈ [-1, 1] × [0, T ].
Верхнее и нижнее решения задачи будем строить как модификацию асимптотических рядов
(19). Зададим функцию
xβ(t,ε) = Xn+1(t,ε) - εn+1δ(t),
где положительная функция δ(t) > 0 будет определена ниже. Будем строить верхнее решение
задачи в каждой из областей
D(-)
D(+)
: (x, t) ∈ [-1, xβ (t, ε)] × [0, T ] и
: (x, t) ∈ [xβ(t, ε), 1] × [0, T ],
β
β
{
(-)
β(-)(x,t,ε), (x,t) ∈Dβ
,
β(x, t, ε) =
β(+)(x,t,ε), (x,t) ∈D(+)β.
Будем сшивать функции β(-)(x, t, ε) и β(+)(x, t, ε) на xβ(t, ε) таким образом, чтобы вы-
полнялось равенство
β(-)(xβ(t,ε),t,ε) = β(+)(xβ(t,ε),t,ε) = ϕ(0)(xβ(t,ε)).
4
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
770
НЕФЕДОВ и др.
Отметим, что функция β(x, t, ε) не является гладкой. Введём растянутую переменную
x - xβ(t,ε)
ξβ =
ε
Построим функции β(±)(x, t, ε) как модификации формальной асимптотики (19):
β(-)(x,t,ε) = U(-)n+1|ξ
+ εn+1(μ + q(-)(ξβ,t,ε)) +
β
+ εn+1R(-)β(η(-)), (x,t) ∈ D(-)β, ξβ ≤ 0, η(-) ≥ 0;
β(+)(x,t,ε) = U(+)n+1|ξ
+ εn+1(μ + q(+)(ξβ,t,ε)) +
β
+ εn+1R(+)β(η(+)), (x,t) ∈ D(+)β, ξβ ≥ 0, η(+) ≤ 0.
Здесь под обозначениями U(±)n+1|ξ
мы понимаем функции из (19), в которых заменён аргумент
β
ξ у функций переходного слоя на ξβ, а Xn+1 - на xβ.
Положительная величина μ выбирается так, чтобы были выполнены условия 1) и 2). Функ-
ции R(±)β(η(±)) подбираются так, чтобы было выполнено условие 3). Их построение в данной
работе не рассматривается. Функции q(±)(ξβ, t, ε) нужны для устранения невязок, которые
возникают при действии оператора на верхнее решение. Определим их из следующих задач:
∂2q(±)
∂q(±)
+ Dxβ
-f˜u(ξβ,t)q(±)(ξβ,t,ε) - qf(±)(ξβ,t,ε) = 0,
2
∂ξβ
∂ξβ
q(±)(0,t,ε) + μ = 0; q(±)(±∞,t,ε) = 0,
(20)
где
qf(±)(ξ,t,ε) = μ
fu(ξ,t)
f(±)u(xβ)).
Для данных функций можно получить явные выражения
v(±)(ξ, xβ )
q(±)(ξβ,t,ε) = -μ
+
v(±)(0, xβ )
ξβ
η
∫
∫
+ v(±)(ξ,xβ)
(v(±)(η,xβ))
-2e-(Dxβ)η
v(±)(σ, xβ )e(Dxβ )σqf(±)(σ, t, ε) dσ dη.
(21)
0
±∞
Функции q(±)(ξβ, t, ε) имеют экспоненциальные оценки.
Можно упростить выражения (21):
ξβ
η
∫
∫
q(±)(ξβ,t,ε) = -μ -
f(±)u(xβ)
(v(±)(η,xβ))
-2e-(Dxβ)η
v(±)(σ, xβ )e(Dxβ )σ dσ dη.
0
±∞
По аналогичному алгоритму построим нижнее решение. Зададим функцию
xα(t,ε) = Xn+1(t,ε) + εn+1δ(t),
где δ(t) - та же самая функция, что и при построении верхнего решения.
Построим нижнее решение
{
α(-)(x,t,ε), (x,t) ∈Dα-),
α(x, t, ε) =
α(+)(x,t,ε), (x,t) ∈Dα+)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
ДВИЖЕНИЕ ФРОНТА В ЗАДАЧЕ СО СЛАБОЙ АДВЕКЦИЕЙ
771
задачи в каждой из областей
D(-)
D(+)
α
: (x, t) ∈ [-1, xα(t, ε)] × [0, T ] и
α
: (x, t) ∈ [xα(t, ε), 1] × [0, T ].
Будем сшивать функции α(-)(x, t, ε) и α(+)(x, t, ε) в точке xα(t, ε) таким образом, чтобы
было выполнено равенство
α(-)(xα(t,ε),t,ε) = α(+)(xα(t,ε),t,ε) = ϕ(0)(xα(t,ε)).
Отметим, что функция α(x, t, ε) не является гладкой. Введём растянутую переменную
x - xα(t,ε)
ξα =
ε
Построим функции α(±)(x, t, ε) как модификации формальной асимптотики (19):
α(-)(x,t,ε) = U(-)n+1|ξα + εn+1(μ + q(-)(ξα,t,ε)) +
+ εn+1R(-)α(η(-)), (x,t) ∈ D(-)β, ξα ≤ 0, η(-) ≥ 0;
α(+)(x,t,ε) = U(+)n+1|ξα + εn+1(μ + q(+)(ξα,t,ε)) +
+ εn+1R(+)α(η(+)), (x,t) ∈ D(+)α, ξα ≥ 0, η(+) ≤ 0.
Здесь μ > 0 - та же величина, что и в выражении для верхнего решения, а q(±)(ξα, t, ε)
определяются из задач (20), в которых растянутая переменная ξβ заменена на ξα.
Проверим, что построенные функции α(x, t, ε) и β(x, t, ε) удовлетворяют дифференци-
альным неравенствам 1)-5). Условие упорядоченности можно проверить аналогично тому, как
это было сделано в работе [8].
Покажем выполнение неравенства 2). Из способа построения верхнего и нижнего решений
следуют равенства
L[α(±)] = εn+1f¯(±)u(xα)μ + O(εn+2), L[β(±)] = -εn+1f¯(±)u(xβ )μ + O(εn+2).
Неравенства вблизи границы 3) выполняются за счёт модификации погранслойных функ-
ций и в данной работе не проверяются.
Проверим условие скачка производной
)
(+)
(∂β
∂β(-)
ε
-
=
∂x
∂x
x=xβ
x=xβ
(
(
)
)
1
dδ
∂A(x, 0)
= -εn+1
L(x0)
+ L(x0) W′(x0(t)) +
δ(t) + F (x0)
+ O(εn+2),
v(0, x0)
dt
∂x
x=x0(t)
где
[
∫
0
]+
∫
F (x0) = μ
f(±)u(x0)
v(±)(σ, x0)e(Dx0)σ dσ
,
L(x0) =
v2(ξ,x0)e(Dx0)ξ dξ > 0.
-
±∞
-∞
Определим функцию δ(t) как решение задачи
(
)
dδ
∂A(x, 0)
L(x0)
+ L(x0) W′(x0(t)) +
δ(t) + F (x0) = σ, δ(0) = δ0,
dt
∂x
x=x0(t)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
4∗
772
НЕФЕДОВ и др.
где σ - достаточно большая положительная величина, а δ0 > 0. В этом случае решение задачи
δ(t) - положительная функция. Таким образом, имеем
)
(+)
(∂β
∂β(-)
σ
ε
-
= -εn+1
+ O(εn+2).
∂x
∂x
v(0, x0)
x=xβ
x=xβ
Выражение в правой части отрицательно за счёт σ > 0. При том же выборе функции δ(t)
будет выполнено неравенство скачка производной для нижнего решения α(x, t, ε). Таким об-
разом, верна
Теорема 1. При выполнении условий 1-3 для любой достаточно гладкой начальной функ-
ции uinit(x, ε), лежащей между верхним и нижним решениями
α(x, 0, ε) ≤ uinit(x, ε) ≤ β(x, 0, ε),
существует решение u(x,t,ε) задачи (1), которое при любом t ∈ [0,T] заключено между
этими верхним и нижним решениями, и для которого функция Un(x,t,ε) является равно-
мерным в области [-1,1] × [0,T] асимптотическим приближением с точностью O(εn+1).
3. Случай модульно-кубичной правой части. Сформулируем основные отличия слу-
чая модульно-кубичной нелинейности от кубической нелинейности, рассмотренной в п. 2. Мо-
дульно-кубичной нелинейностью называем функцию, имеющую разрыв по искомой функции
следующего вида:
{
f(+)(u,x,ε), если u ≥ 0, x ∈ [-1,1];
f (u, x, ε) =
f(-)(u,x,ε), если u < 0, x ∈ [-1,1],
имеющую в областях u > 0 и u < 0 корни, отвечающие за точки покоя типа седла у соответ-
ствующих присоединённых систем (см. условие 2* ниже).
Отметим, что нелинейности модульно-кубичного типа находят своё применение в популя-
ционной динамике при построении модели перколяционной решётки фиксации мутаций [15],
а также в климатологии при изучении изменений температуры на поверхности Земли под
влиянием солнечной радиации [16, 17].
Сформулируем необходимые нам условия.
Условие 1*. Функции A(x, ε), f(±)(u, x, ε) являются достаточно гладкими в своих обла-
стях определения.
Условие 2*. Пусть вырожденное уравнение f(+)(u, x, 0) = 0 - единственное решение u =
= ϕ(+)(x), а уравнение f(-)(u,x,0) = 0 имеет единственное решение u = ϕ(-)(x), причём
ϕ(-)(x) < 0 < ϕ(+)(x), x ∈ [-1, 1],
а также выполнены неравенства
f(±)u(ϕ(±)(x),x,0) > 0, x ∈ [-1,1].
Определим решение (1) в этом случае следующим образом.
Определение. Функция
u(x, t, ε) ∈ C1,0([-1, 1] × [0, T ])
⋂C1,1([-1,1] × (0,T])⋂ C2,1((-1, x) × (0,T]⋃ (x,1) × (0,T])
называется решением задачи (1), если она удовлетворяет уравнению (1) в каждой из областей
(-1, x) × (0, T ] и (x, 1) × (0, T ], а также начальному и граничному условиям.
Асимптотику решения задачи (1) будем строить аналогично тому, как это делалось в п. 2.
Положение внутреннего переходного слоя определяется из условия C1-сшивания асимптоти-
ческих представлений U(-)(x, t, ε) и U(+)(x, t, ε), выражения которых имеют вид (2), в точке
перехода x(t, ε):
U(-)(x(t,ε),t,ε) = U(+)(x(t,ε),t,ε) = 0,
∂
∂
ε
U(-)(x(t,ε),t,ε) = ε
U(+)(x(t,ε),t,ε).
∂x
∂x
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
ДВИЖЕНИЕ ФРОНТА В ЗАДАЧЕ СО СЛАБОЙ АДВЕКЦИЕЙ
773
Регулярные члены асимптотических разложений (2) можно получить из уравнений
(±)
∂2u
∂u(±)
ε2
- εA(x, ε)
- f(±)(u(±),x,ε) = 0.
∂x2
∂x
В частности, согласно условию 2*, получим
u(±)0 = ϕ(±)(x), x ∈ [-1,1].
Функции переходного слоя нулевого приближения Q(±)0(ξ, t, ε) строятся из задач, анало-
гичных случаю гладкой правой части. Запишем их c использованием функции ũ(ξ, x):
∂2ũ(±)
∂ũ(±)
+Dx
= f(±)(ũ(±), x,0),
ũ(±)(0, x) = 0,
ũ(±)(±∞, x) = ϕ(±)(x).
(22)
∂ξ2
∂ξ
Наряду с задачей (22), рассмотрим задачу
∂2û
∂û
+W
= f(û, x,0),
û(0, x) = ϕ(0)(x),
û(±∞, x) = ϕ(±)(x).
(23)
∂ξ2
∂ξ
Задача (23) в теории бегущих волн для разрывных нелинейностей изучена в работе [18].
Точка разрыва нелинейности в рассматриваемом нами случае является неустойчивой сингу-
лярной точкой. Мы приведём здесь результат из [18], сформулировав его в виде леммы.
Лемма 2. Для каждого x ∈ (-1, 1) существует величина W такая, что задача (23)
имеет гладкое монотонное решение û(ξ, x) из класса решений определения (см. выше), удо-
влетворяющее оценке
|û(ξ, x) - ϕ(±)(x)| < C exp(-κ|ξ|),
где C и κ - некоторые положительные постоянные. При этом зависимость W (x) опреде-
ляется следующим выражением:
∫
(
)2
)-1
∫
∂ũ
W(x) =
(ξ, x) dξ
f (u, x, 0) du.
∂ξ
−∞
ϕ(-)(x)
Условие отсутствия стационарных решений у задачи (12) аналогично используемому в п. 2.
Условие 3*. Пусть задача (12) имеет решение x = x0(t) :
-1 < x0(t) < 1 при t ∈ [0,T].
Потребуем также, чтобы W (x0) + A(x0, 0) > 0 для всех x0 ∈ [-1, 1].
Разрешимость задач (22) следует из леммы 2 и условия 3* (аналогично случаю с непре-
рывной правой частью).
Действуя по алгоритму А.Б. Васильевой, можно определить функции Q(±)k(ξ, t, ε), k ∈ N,
аналогично тому, как это делалось в п. 2.1.
Коэффициенты в разложении точки перехода
x(t, ε) в случае разрывной правой части
определяются по алгоритму, описанному в п. 2.2. Главный член ряда x0(t) точки перехода, а
также старшие порядки xi(t), i ∈ N, определяются из задач (12) и (18), в которых использу-
ется функция W (x) из леммы 2.
Алгоритм построения верхнего β∗(x, t, ε) и нижнего α∗(x, t, ε) решений для случая мо-
дульно-кубичной нелинейности аналогичен изложенному в п. 2.3. Таким образом, верна
Теорема 2. При выполнении условий 1*-3* для любой достаточно гладкой начальной
функции uinit(x, ε), лежащей между верхним и нижним решениями
α∗(x,0,ε) ≤ uinit(x,ε) ≤ β∗(x,0,ε),
существует решение u(x,t,ε) из класса решений определения (см. выше) задачи (1) с модуль-
но-кубичной нелинейностью, которое при любом t ∈ [0,T] заключено между этими верхним
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
774
НЕФЕДОВ и др.
и нижним решениями, и для которого функция Un(x,t,ε) является равномерным в области
[-1, 1] × [0, T ] асимптотическим приближением с точностью O(εn+1).
Для доказательства теоремы используется асимптотический метод дифференциальных
неравенств [19], основанный на теоремах сравнения для параболических уравнений в случае
разрывных источников [20].
4. Примеры.
4.1. Случай непрерывной правой части. Рассмотрим начально-краевую задачу
∂2u
∂u
∂u
ε2
-ε
- εA(x, ε)
= (u2 - 1)(u - ϕ(0)(x)), x ∈ (-1, 1), t ∈ (0, T ],
∂x2
∂t
∂x
∂u
∂u
(-1, t, ε) = 0,
(1, t, ε) = 0, t ∈ [0, T ],
∂x
∂x
u(x, 0, ε) = uinit(x, ε), x ∈ [-1, 1].
Будем считать, что при всех x ∈ [-1, 1] выполнено неравенство
-1 < ϕ(0)(x) < 1.
Члены регулярной части нулевого порядка легко определяются: u(±)0(x) = ±1.
Начальная задача для определения положения фронта в нулевом приближении имеет вид
dx0
√
=
2ϕ(0)(x0) + A(x0, 0), x0(0) = x00.
dt
Определим теперь функцию ũ(ξ, x0) из начальной задачи
∂ũ
1
=-√
(ũ2 - 1),
ũ(0, x0) = ϕ(0)(x0).
∂ξ
2
Нетрудно получить выражения
√
C exp(-
2ξ) - 1
1 + ϕ(0)(x0)
ũ(ξ, x0) =
√
,
C =
C exp(-
2ξ) + 1
1 - ϕ(0)(x0)
4.2. Случай модульно-кубичной правой части. Рассмотрим начально-краевую задачу
∂2u
∂u
∂u
ε2
-ε
- εA(x, ε)
= f(u,x,ε), x ∈ (-1,1), t ∈ (0,T],
∂x2
∂t
∂x
∂u
∂u
(-1, t, ε) = 0,
(1, t, ε) = 0, t ∈ [0, T ],
∂x
∂x
u(x, 0, ε) = uinit(x, ε), x ∈ [-1, 1],
где
{
u - ϕ(-)(x), u < 0,
f (u, x, ε) =
u - ϕ(+)(x), u ≥ 0.
Будем считать, что при всех x ∈ [-1, 1] выполнены неравенства
ϕ(-)(x) < 0 < ϕ(+)(x) и ϕ(+)(x) > |ϕ(-)(x)|.
Члены регулярной части нулевого порядка легко определяются:
u(±)0(x) = ϕ(±)(x).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
ДВИЖЕНИЕ ФРОНТА В ЗАДАЧЕ СО СЛАБОЙ АДВЕКЦИЕЙ
775
Запишем задачи для функций переходного слоя нулевого порядка
∂2Q(±)0
∂Q(±)0
+W
=Q(±)0,
∂ξ2
∂ξ
Q(±)0(0,t,ε) + ϕ(±)(x(t,ε)) = 0,
Q(±)0(±∞,t,ε) = 0.
(24)
Нетрудно получить решения задач (24) в явном виде:
)
√
(1
Q(±)0(ξ,t,ε) = -ϕ(±)(x(t,ε))exp
(-W ±
W2 + 4)ξ
2
Тогда
v(+)(0,x0) - v(-)(0,x0) =
√
√
ϕ(+)(x0)
ϕ(-)(x0)
-
(-W -
W2 + 4) +
(-W +
W2 + 4) = 0,
2
2
и выражение для W (x0) имеет вид
|ϕ(+)(x0) + ϕ(-)(x0)|
W (x0) = -
√
ϕ(+)(x0)|ϕ(-)(x0)|
Работа выполнена при финансовой поддержке Российского фонда фундаментальных ис-
следований (проект 18-11-00042).
СПИСОК ЛИТЕРАТУРЫ
1. Руденко О.В. Неоднородное уравнение Бюргерса с модульной нелинейностью: возбуждение и эво-
люция интенсивных волн // Докл. РАН. 2017. Т. 474. № 6. С. 671-674.
2. Нефедов Н.Н., Руденко О.В. О движении фронта в уравнении типа Бюргерса с квадратичной и
модульной нелинейностью при нелинейном усилении // Докл. РАН. 2018. Т. 478. № 3. С. 274-279.
3. Olchev A., Radler K., Sogachev A., Panferov O., Gravenhorst G. Application of a three-dimensional
model for assessing effects of small clear-cuttings on radiation and soil temperature // Ecological
Modelling. 2009. V. 220. № 21. P. 3046-3056.
4. Levashova N., Sidorova A., Semina A., Ni M. A spatio-temporal autowave model of shanghai territory
development // Sustainability. 2019. V. 11. P. 3658-1-3658-13.
5. Васильева А.Б., Давыдова М.А. О контрастной структуре типа ступеньки для одного класса нели-
нейных сингулярно возмущённых уравнений второго порядка // Журн. вычислит. математики и
мат. физики. 1998. Т. 38. № 6. С. 938-947.
6. Нефедов Н.Н., Давыдова М.А. Периодические контрастные структуры в системах типа реакция-
диффузия-адвекция // Дифференц. уравнения. 2010. Т. 46. № 9. С. 1300-1312.
7. Нефедов Н.Н., Никулин Е.И. Существование и асимптотическая устойчивость периодического ре-
шения с внутренним переходным слоем в задаче со слабой линейной адвекцией // Модел. и анализ
информ. систем. 2018. Т. 25. № 1. С. 125-132.
8. Нефедов Н.Н., Божевольнов Ю.В. Движение фронта в параболической задаче реакция-диффузия
// Журн. вычислит. математики и мат. физики. 2010. Т. 50. № 2. С. 276-285.
9. Васильева А.Б., Бутузов В.Ф. Асимптотические методы в теории сингулярных возмущений. М.,
1990.
10. Нефедов Н.Н. Развитие методов асимптотического анализа переходных слоев в уравнениях реак-
ция-диффузия-адвекция: теория и применение // Журн. вычислит. математики и мат. физики.
2021. Т. 61. № 22. С. 2074-2094.
11. Fife C.P., Hsiao L. The generation and propogation of internal layers // Nonlin. Anal., Theory, Methods
and Appl. 1998. V. 12. № 1. P. 19-41.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022
776
НЕФЕДОВ и др.
12. Нефедов Н.Н. Метод дифференциальных неравенств для некоторых сингулярно возмущённых задач
в частных производных // Дифференц. уравнения. 1995. Т. 31. № 4. С. 719-722.
13. Sattinger D.H. Monotone methods in elliptic and parabolic boundary value problems // Indiana Univ.
Math. J. 1972. V. 21. № 11. P. 979-1001.
14. Pao C.V. Nonlinear Parabolic and Elliptic Equations. New York, 1992.
15. Гараева А.Я., Сидорова А.Э., Твердислов В.А., Левашова Н.Т. Модель предпосылок видообразова-
ния в представлениях теорий перколяций и самоорганизованной критичности // Биофизика. 2020.
Т. 65. № 5. С. 932-948.
16. Budyko M.I. The effect of solar radiation variations on the climate of the Earth // Tellus. 1968. V. 21.
№ 5. P. 611-619.
17. Diaz J. I. Mathematical analysis of some diffusive energy balance models in climatology mathematics
// Climate and Environment. 1993. P. 28-56.
18. Volpert A.I., Volpert V.A. Traveling-wave solutions of parabolic systems with discontinuous nonlinear
terms // Nonlin. Anal., Theory, Methods and Appl. 2002. V. 49. № 1. P. 113-139.
19. Нефедов Н.Н., Никулин Е.И., Орлов А.О. О периодическом внутреннем слое в задаче реакция-
диффузия с источником модульно-кубичного типа // Журн. вычислит. математики и мат. физики.
2020. Т. 60. № 9. С. 1513-1532.
20. Павленко В. Н. Сильные решения периодических параболических задач с разрывными нелинейно-
стями // Дифференц. уравнения 2016. Т. 52. № 4. С. 528-539.
Московский государственный университет
Поступила в редакцию 31.01.2022 г.
имени М.В. Ломоносова
После доработки 31.01.2022 г.
Принята к публикации 09.03.2022 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№6
2022