ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 6, с.813-833

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.622

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ,

РЕШЕНИЕ КОТОРЫХ ИМЕЕТ ПОЛЮСЫ ЦЕЛОГО

ПОРЯДКА НА ВЕЩЕСТВЕННОЙ ОСИ

Предложен эффективный метод решения задачи Коши для обыкновенного дифференци-

ального уравнения с кратными полюсами целого порядка, который позволяет проводить

сквозной расчёт через полюс как для единичного полюса, так и в случае цепочки полюсов.

В методе используется специальный алгоритм нахождения кратности каждого полюса.

По этой кратности определяется обобщённая инверсная функция, для которой K-крат-

ный полюс исходной функции является простым нулём. Расчёт такого нуля не представля-

ет трудности, поэтому предложенный метод позволяет получать высокую точность даже

вблизи полюсов. После прохождения этого нуля возобновляется расчёт исходной функ-

ции. Применение данного метода на последовательности полюсов даёт возможность найти

численное решение одновременно с апостериорной оценкой его погрешности. Метод про-

иллюстрирован на тестовых примерах.

DOI: 10.31857/S0374064122060085, EDN: CDFTQQ

Введение. Существует немало задач Коши для обыкновенных дифференциальных урав-

нений, решения которых имеют особые точки. Эти особые точки могут быть полюсами, в том

числе кратными. Кроме того, при численном расчёте серьёзную проблему представляют точки,

в которых обращается в нуль первая производная или одновременно несколько последователь-

ных производных, начиная с первой. Столь же проблематичны точки, в которых сама функция

конечна, но обращается в бесконечность её первая производная и, возможно, несколько после-

дующих. Подавляющее большинство таких задач являются нелинейными. Много подобных

задач возникает в квантовой механике. Другими примерами являются гамма-функция, эл-

липтические интегралы и др. В таких решениях особые точки оказываются, как правило, не

единственными, а образуют последовательности.

Такие задачи, за редкими исключениями, не решаются в элементарных функциях. Решения

многих задач являются специальными функциями математической физики. Для практическо-

го применения они требуют тщательного исследования их свойств, но даже в этом случае ре-

шение редко удаётся довести до числа. Положение усугубляется тем, что каждый узкий класс

задач требует введения своей специальной функции. Это большое поле деятельности для ма-

тематиков, однако практический выход для решения прикладных задач оказывается зачастую

недостаточным. Поэтому необходима разработка универсальных численных методов, позволя-

ющих единообразно решать задачи Коши с самыми разными типами особенностей. Численные

методы должны находить не только приближённое решение, но и одновременно конструктив-

ную оценку его погрешности. При этом желательно иметь не мажорантные интервальные

оценки (которые могут быть сильно завышенными), а асимптотически точные.

Данная работа посвящена построению таких методов. Для простейших случаев (например,

для полюсов кратности K = 1) предложен метод инверсной функции. Для полюсов целого

порядка K ≥ 1 разработан алгоритм, который для каждого полюса определяет его крат-

ность, и строится обобщённая инверсная функция, ориентированная на прохождение данного

полюса. В обоих случаях решение продолжается за полюс. Это позволяет вычислить решение,

содержащее цепочку полюсов с произвольными целыми кратностями.

Эти методы позволяют не только находить решение, но и оценивать погрешность реше-

ния. Для этого расчёты проводятся на последовательности равномерных сеток, сгущающихся

вдвое. К решениям на каждой паре соседних сеток применяется метод Ричардсона, дающий

асимптотически точное значение погрешности.

813

814

БЕЛОВ, КАЛИТКИН

1. Задачи с разрушением решения. Задачи с полюсами можно разделить на две кате-

гории.

1.1. Решение с единственной сингулярностью. Первая категория включает задачи

для уравнений в частных производных и обыкновенных дифференциальных уравнений, опи-

сывающие реальные физические процессы. Примерами являются различные режимы горения

термоядерных мишеней, процессы пробоя в полупроводниках, задачи нелинейной лазерной

оптики и акустики, гравитационный коллапс и др. В некоторый момент времени в решении

возникает сингулярность. В ряде случаев (например, если сингулярность является полюсом

целого порядка) возможно формально-математическое продолжение решения за полюс. Од-

нако это не имеет практического смысла, поскольку с физической точки зрения в момент

сингулярности исходное уравнение перестаёт описывать физическое явление. Поэтому в за-

дачах данного типа ставится вопрос о расчёте решения вплоть до ближайшей сингулярности

и численном исследовании последней. В литературе рассмотрены многие подобные задачи.

Наиболее хорошо изучены задачи, сводящиеся к параболическому уравнению с нелинейной

правой частью и в некоторых случаях - с нелинейным пространственным оператором (см.,

например, [1]).

Для расчёта таких задач обычно используют разностные схемы. Однако вблизи сингуляр-

ности решение разностных уравнений быстро теряет точность. Чтобы преодолеть эту труд-

ность, предлагались разные подходы, основанные на адаптировании сеток к решению по мере

приближения к сингулярности. Примерами таких подходов являются метод масштабирова-

ния [2], метод движущихся сеток [3], выбор очередного шага по времени по норме численного

решения на текущем временном слое [4] и ряд других. Отметим также работы [5, 6], в которых

для некоторых конкретных задач было найдено преобразование, которое переводит решение

в несингулярное.

Наиболее универсальным является подход, основанный на методе сгущения сеток. Он при-

меним как к системам обыкновенных дифференциальных уравнений, так и к уравнениям в

частных производных. Подробная методология такого подхода изложена в монографии [7].

Вкратце приведём её.

Пусть исходная задача описывается нестационарным уравнением в частных производных.

Вводится пространственная сетка, а пространственные операторы заменяются разностными

соотношениями. Тогда задача сводится к задаче Коши для системы большого числа обыкно-

венных дифференциальных уравнений. Интегрирование такой системы по времени проводится

с помощью некоторой независимой схемы, не связанной с пространственной схемой.

Неограниченное нарастание численного решения такой системы при приближении к неко-

торому моменту времени трактуется как сингулярность численного решения. Для расчёта

положения сингулярности используются специальные процедуры (см. работы [8-10]). Затем

одновременно проводится сгущение шагов по пространству и времени. Число обыкновенных

дифференциальных уравнений при этом соответственно увеличивается. Снова проводится чис-

ленный расчёт и определяется его момент сингулярности. Такое сгущение сеток проводится

столько раз, сколько позволяют вычислительные мощности.

Последовательность полученных решений и моментов их сингулярностей, согласно теоре-

мам Рябенького-Филиппова, стремится к точному решению и его моменту разрушения. Этот

метод позволил единообразно решить ряд различных задач. Дальнейшее усовершенствование

метода предполагает переход от временной переменной t к длине дуги интегральной кривой

l в многомерном пространстве [11, 12]. Это позволяет ещё повысить надёжность метода, рас-

считывать момент разрушения с хорошей точностью и во многих случаях определять его тип.

Метод сгущения сеток имеет строгое теоретическое обоснование в работах Л.Ф. Ричардсо-

на [13], В.С. Рябенького и А.Ф. Филлипова [14], П. Лакса [15]. Поскольку данный метод важен

для дальнейшего изложения, кратко напомним смысл этих работ.

Л.Ф. Ричардсон (см. [13]) обратил внимание, что погрешность вычисления квадратур обыч-

но имеет вид Ch^p, где h - шаг сетки, p - порядок точности разностной формулы. Поэтому

если сгущать сетку в q раз и сравнивать численные расчёты на двух сетках, то по разности

этих расчётов нетрудно вычислить асимптотически точную оценку погрешности расчёта на

каждой сетке. Позднее этот метод применялся рядом исследователей к решению дифферен-

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

815

циальных уравнений (там обычно удобно брать q = 2 для поточечного сравнения решений на

соседних сетках).

В книге [14] для разностных схем сформулированы четыре фундаментальные теоремы.

Для упрощения приведём их наглядные, но нестрогие формулировки.

Теорема. Из аппроксимации и устойчивости следует сходимость.

Эта теорема доказана для произвольных нелинейных схем.

Теорема. Для линейных разностных схем порядок сходимости равен порядку аппрокси-

мации.

Теорема. Для линейных задач с достаточно гладкими решениями применим метод Ри-

чардсона.

Теорема. Пусть разностная схема устойчива и аппроксимирует исходную задачу, а при

сгущении сеток численное решение сходится к предельной функции. Тогда точная задача

имеет решение, которым является данная предельная функция.

К аналогичным выводам пришел П. Лакс [15]. По-видимому, только совокупность описан-

ных теорем позволяет строить методы, в которых одновременно вычисляются решение и его

асимптотически точная величина погрешности.

1.2. Решение с цепочкой сингулярностей. Существует вторая категория задач, кото-

рые не описывают реальный физический процесс, а являются вспомогательными математиче-

скими проблемами. Примерами являются уравнения специальных функций (гипергеометри-

ческая функция, эллиптические функции, цилиндрические функции, гамма-функция и т.д.).

Решение таких задач может иметь множественные сингулярности. Эти функции широко ис-

пользуются в математической физике, причём в конкретных приложениях требуются значения

специальной функции не только до ближайшего полюса, но и между парой соседних полю-

сов. Поэтому в таких задачах требуется не только рассчитать решение вплоть до ближайшей

сингулярности, но и продолжить решение за неё и рассчитать последующие сингулярности.

Для составления таблиц специальных функций [16] и для стандартных программ прямо-

го расчёта [17] широко применяют численные методы. Стандартные схемы (например, схемы

Рунге-Кутты) позволяют рассчитать гладкие участки решения с хорошей точностью. Одна-

ко вблизи сингулярности ошибка таких схем катастрофически нарастает. Прямое продолже-

ние решения за полюс, как правило, невозможно. Поэтому решение продолжается за полюс

какими-то искусственными приёмами. Прохождение ряда полюсов представляет ещё большую

проблему и требует разработки специальных процедур. Насколько известно, универсальные

численные методы, единообразно решающие широкие классы таких задач, отсутствуют. На-

стоящая работа посвящена построению общих методов решения подобных задач.

2. Расчёт задач с сингулярностями.

2.1. Продолжение за полюс. Решения задач Коши с сингулярностями выходят за рам-

ки известных теорем о разрешимости. Сначала определим, что понимается под продолжением

решения за полюс. Для наглядности рассмотрим задачу Коши для одного автономного обык-

новенного дифференциального уравнения (ОДУ)

du/dt = f(u), t > 0; u(0) = u₀.

(2.1)

Случай систем рассматривается аналогично. Неавтономные задачи сводятся к системе ОДУ с

помощью процедур автономизации.

Пусть решение (2.1) имеет произвольное число изолированных особых точек на веществен-

ной оси. Будем считать, что функция u(t) аналитична в некоторых проколотых окрестностях

этих точек. Тогда можно использовать классическую классификацию особых точек по Пен-

леве [18]. Напомним, что особая точка t_∗ называется полюсом, если при обходе вокруг этой

точки значение u(t) не меняется и решение представимо рядом Пюизе (см. работы [19, 20]):

u(t) = a_-m(t - t_∗)^-m + . . . + a-1(t - t_∗)-1 + a₀ + . . .

В остальной части комплексной плоскости t будем предполагать, что решение имеет столько

непрерывных производных, сколько требуется для конкретной схемы интегрирования ОДУ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

816

БЕЛОВ, КАЛИТКИН

В реальных задачах положение полюсов неизвестно априори. Точку ближайшего полюса

обозначим через t = t_∗.

Перейдём к комплексным значениям аргумента t. Тогда полюс на вещественной оси можно

обойти по контуру на комплексной плоскости и, вернувшись на вещественную ось, продолжить

решение. При этом не возникает никаких особенностей. Такой подход позволяет продолжить

решение через любое число полюсов. Однако на практике такой подход неконструктивен, так

как требует существенно более трудоемкого численного интегрирования в комплексной плос-

кости.

Правее точки t = t_∗ формально существует бесконечно много точных решений диффе-

ренциального уравнения (2.1). Какое из них соответствует начальному условию u₀? При сде-

ланных предположениях относительно точного решения применима классическая процедура

аналитического продолжения. Наличие полюса первого порядка в точке t_∗ означает, что точ-

ное решение разлагается в этой точке в следующий ряд Пюизе с остаточным членом в форме

Пеано:

∑

a-1

+ a_p(t - t_∗)^p + o((t - t_∗)P+1).

(2.2)

t-t_∗

p=0

Коэффициенты a_p этого ряда зависят от начального условия u₀. Ряд (2.2) справедлив в

проколотом круге, радиус которого определяется положением ближайшей сингулярности либо

точки, в которой нарушается гладкость решения. Поэтому при t > t_∗ он выбирает то же самое

решение дифференциального уравнения (2.1), что и при t < t_∗. Именно оно соответствует

начальному условию u₀. Аналогично осуществляется продолжение решения за последующие

полюсы.

Заметим, что описанная процедура продолжения применима к задачам, в которых решение

имеет полюсы либо существенно особые точки (при этом предполагается, что все особые точки

являются изолированными). В этом случае ряд (2.2) содержит только целые степени (t - t_∗).

Если особая точка является точкой ветвления, то для продолжения нужно выбрать одну из

ветвей. При этом ряд (2.2) будет содержать дробные степени.

2.2. Трудности. Напомним типичные трудности, встречающиеся при численном решении

подобных задач. Рассмотрим любую явную схему. Пусть для упрощения шаг τ является посто-

янным. Формально численное решение существует на каждом шаге t_n = Nτ. Однако вблизи

первого полюса значения u(t_n) быстро нарастают и происходит переполнение. При исполь-

зовании переменного шага τ_n, уменьшающегося в соответствии с ростом решения, описанная

картина сохраняется.

Если взять неявную схему, то описанная картина сохраняется. Кроме того, возникает ещё

одна трудность. Решение на новом шаге находится из нелинейного алгебраического уравнения.

Для конечного временного шага τ_n это уравнение может не иметь вещественного решения. В

обоих случаях расчёт положения полюса затруднён и продолжение решения по той же схеме

невозможно.

3. Метод инверсной функции. Рассмотрим сначала задачу для одного ОДУ. Случай

систем будет рассмотрен далее.

3.1. Инверсная функция. Введём инверсную функцию v(t) = [u(t)]-1. Из (2.1) следует,

что эта функция удовлетворяет уравнению

dv/dt = ϕ(v), ϕ(v) = -v²f(v-1).

(3.1)

Это уравнение будем называть инверсным. Все полюсы функции u(t) становятся нулями

функции v(t) и, наоборот, нули функции u(t) становятся полюсами функции v(t).

Выберем точку t∈ (0, t_∗) такую, что на отрезке t ∈ (t, t_∗) точное решение u(t) сохраняет

знак. Для уравнения (3.1) выберем начальное условие v(t) = 1/u(t). Инверсное уравнение

с таким начальным условием будем называть инверсной задачей. Справедливы следующие

утверждения.

Теорема 1. Пусть решение u(t) задачи (2.1) обращается в бесконечность в точке t_∗,

аналитично в проколотой окрестности этой точки и имеет P +1 непрерывную производную

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

817

вне указанной окрестности. Особая точка t_∗ является полюсом первого порядка тогда и

только тогда, когда f(u)/u² имеет конечный ненулевой предел при u → ∞.

Доказательство. Необходимость. Пусть u(t) - некоторое решение дифференциального

уравнения в задаче (2.1), имеющее полюс первого порядка в точке t_∗. Тогда функция u(t)

представима рядом Пюизе (2.2). Продифференцировав его, получим ряд Пюизе для сложной

функции f(u(t)):

a-1

∑

f (u(t)) =

+ pa_p(t - t_∗)p-1 + o((t - t_∗)^P ).

(3.2)

(t - t_∗)²

p=1

Найдём разложение в ряд Пюизе для отношения f/u² :

∑

f (u(t))

= b_p(t - t_∗)^p + o((t - t_∗)^P),

u(t)²

p=0

b₀ = -1/a-1, b₁ = 2a₀/a2-1, b₂ = 3(a₁a-1 - a²⁰)/a3-1,...

(3.3)

Разложения (2.2), (3.2), (3.3) справедливы в некоторой малой окрестности точки t_∗. Однако

t → t∗ как раз соответствует u → ∞. Из (3.3) непосредственно видно, что в этом случае

отношение f/u² → -1/a-1. Необходимость доказана.

Достаточность. Сделаем формальную замену неизвестной функции u = 1/v. Новая

функция удовлетворяет инверсному уравнению (3.1), причём ϕ(v) = -v²f(v-1) → C = 0.

Это означает, что при любом ε > 0 найдётся такое δ > 0, что при достаточно малом |v| < δ

выполнено неравенство

C - ε < |ϕ(v)| < C + ε.

(3.4)

Выберем ε так, что |ε| < C. Тогда величины C + ε и C - ε имеют одинаковый знак, сле-

довательно, в указанной окрестности dv/dt остаётся знакоопределённой. Если функция u(t)

обращается в бесконечность в точке t_∗, то в этой точке v(t) обращается в нуль. Из неравенств

(3.4) следует, что этот нуль может быть только простым. Тогда в точке t_∗ функция u(t) имеет

полюс первого порядка. Теорема доказана.

Замечание 1. В доказательстве необходимости коэффициенты ряда (2.2) могут быть про-

извольными. Иными словами, рассматривается не одна интегральная кривая, а семейство ин-

тегральных кривых, имеющих полюс в точке t_∗. Это семейство интегральных кривых можно

трактовать как окрестность точного решения задачи (2.1).

Теорема 2. Пусть выполнены условия теоремы 1 и f(u)/u² → C = 0 при u → ∞.

Тогда найдётся такая окрестность особой точки t_∗ и окрестность начального условия u₀, в

которых решение v(t) инверсной задачи существует, единственно и равномерно непрерывно

зависит от начального условия u₀.

Доказательство. 1. Из условий теоремы следует, что в указанной окрестности ϕ(v) непре-

рывна и ограничена, причём ϕ(v) → -C при v → 0. Тогда, согласно классическим теоре-

мам [21], решение инверсной задачи v(t) существует и единственно.

2. Покажем, что оно равномерно непрерывно зависит от начального условия u₀. Расчёт

исходной задачи ведётся до момента t, который является начальным для инверсной задачи.

Согласно условиям на гладкость правой части f решение u(t) на отрезке (0, t), и в частности

его значение u(t), равномерно непрерывно зависит от u₀.

Покажем, что ϕ_v непрерывна. Из условий теоремы следует, что решение u(t) задачи (2.1)

имеет полюс первого порядка на отрезке интегрирования. Рассмотрим семейство интегральных

кривых, задаваемых рядом (2.2) с произвольным коэффициентами a_p,

-1 ≤ p ≤ P + 1.

Найдём соответствующее семейство интегральных кривых инверсного уравнения (3.1):

∑

v(t) =

= c_p(t - t_∗)^p + o((t - t_∗)P+1),

(3.5)

u(t)

p=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

818

БЕЛОВ, КАЛИТКИН

c₁ = 1/a-1, c₂ = -a₀/a2-1, c₃ = (a²⁰ - a₁a-1)/a3-1, ...

(3.6)

В силу произвольности коэффициентов a_i равенства (3.5), (3.6) задают не конкретное решение

инверсной задачи, а некоторую его окрестность. Дифференцированием нетрудно найти

∑

ϕ(v(t)) =

= pc_p(t - t_∗)p-1 + o((t - t_∗)^P ).

(3.7)

p=1

Вычислим ϕ_v из (3.5) и (3.7) как производную параметрической функции

]-1

[P-1∑

][_P∑

ϕt(v(t))

ϕv(v(t)) =

c_pp(p - 1)(t - t_∗)p-2

c_pp(t - t_∗)p-1

v_t(t)

p=2

∑

= d_p(t - t_∗)^p + o((t - t_∗)P-1),

(3.8)

p=0

d₀ = -2a₀/a₁, d₁ = 2(a²⁰ - 3a₁a-1)/a2-1, d₂ = 2(3a₀a₁a-1 - a³⁰ - 6a₂a2-1)/a3-1, ...

(3.9)

В силу оценки (3.4) ϕ(v) не обращается в нуль в некоторой окрестности v = 0. Поэтому ϕ_v

непрерывна и ряд (3.8) сходится.

Таким образом, согласно классическим теоремам [21], решение инверсной задачи (3.1) рав-

номерно непрерывно зависит от начального условия v(t). Последнее равномерно непрерывно

зависит от u₀. Это завершает доказательство теоремы.

Следствие 1. Построенная функция v(t) является решением инверсного уравнения (3.1)

как при t < t_∗, так и при t > t_∗. Тем самым она однозначно определяет продолжение

решения u(t) за полюс по правилу u(t) = [v(t)]-1.

Следствие 2. После прохождения полюса необходимо вернуться от инверсной задачи к

исходной. Обозначим точку перехода через

T. Примем эту точку за начальную для функции

u(t), зададим в ней начальное значение u

T)=[v

T )]-1 и продолжим расчёт исходного урав-

нения при t

T. Согласнодоказаннымтеоремамзначение u

T) зависит от u₀ равномерно

непрерывно. Поэтому то же справедливо для всего решения u(t) при t

Тем самым, если исходная задача (2.1) имеет не один полюс, а последовательность полюсов,

то к каждому из них применимы теоремы 1 и 2.

Следствие 3. Из следствия 2 непосредственно вытекает, что метод инверсной функции

применим к задачам с последовательностями полюсов первого порядка.

Следствие 4. Условия гладкости в теоремах 1 и 2 обеспечивают применимость раз-

ностных схем порядка точности до P-го и нахождение асимптотически точного значения

погрешности по методу Ричардсона.

Замечание 2. Проведённые доказательства являются локальными, т.е. относятся к неко-

торой окрестности точки t_∗. Если точка

t оказалась слишком далеко от точки t_∗, то её

необходимо передвинуть в сторону t_∗.

Алгоритм. В численном расчёте нахождение окрестностей точки t_∗, указанных в теоре-

мах 1 и 2, достаточно проблематично. Будем использовать следующий более простой алгоритм.

Выберем некоторую равномерную сетку t_n = nτ, n = 0, N . Здесь τ = T/N - шаг сетки.

Введём некоторое пороговое значение U > 0. Будем вести на этой сетке расчёт задачи (2.1) по

некоторой явной схеме до тех пор, пока для очередного сеточного значения u_n не выполнится

условие |un| > U. Обозначим этот номер узла через n∗. Далее с этого момента численно

решаем задачу (3.1) на той же сетке, выбирая в качестве начального условия v_n∗ = 1/u_n∗ .

При этом во всех последующих узлах сетки восстанавливаем численное значение u(t) по

соотношению u_n = 1/v_n.

Если в ходе этого расчёта функция v_n изменила знак, то это означает переход v(t) че-

рез нуль, что соответствует полюсу функции u(t). Таким образом мы находим решение по обе

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

819

стороны полюса и можем продолжать расчёт за полюс. Если при дальнейшем решении уравне-

ния (3.1) выполнится условие |v_n| > 1/U, то снова возвращаемся к решению уравнения (2.1).

Такой переход можно выполнять неограниченное количество раз. Этот способ позволяет про-

водить сквозной расчёт через полюс или через последовательность полюсов кратности 1. При

этом не происходит никакой потери точности, поскольку уравнение (3.1) в окрестности t_∗ не

имеет никаких особенностей.

3.2. Схемы. В любом узле сетки может произойти переход от функции u(t) к инверс-

ной функции v(t). Поэтому многошаговые схемы для такого расчёта непригодны. Следует

использовать только одношаговые схемы. В наших расчётах хорошие результаты дали:

- явные схемы Рунге-Кутты;

- явно-неявные одностадийные схемы Розенброка [22], из которых особенно надёжной была

вещественная схема точности O(τ)

un+1 = u_n + τw, (E - τf_u)w = f(u_n),

здесь E - единичная матрица; несколько уступала ей в надёжности, но имела точность O(τ²)

одностадийная схема с комплексным коэффициентом (CROS)

un+1 = u_n + τ Re w, (E - 0.5(1 + i)τf_u)w = f(u_n);

(3.10)

– диагонально-неявные схемы Рунге-Кутты BORK [23], из которых упомянем общеизвест-

ную обратную схему Эйлера точности O(τ)

un+1 = u_n + τf(un+1)

(3.11)

и рекурсивную схему точности O(τ²)

un+1 = u_n + τf(un+1 - 0.5τf(un+1)).

(3.12)

3.3. Положения полюсов. Пусть использована численная схема точности O(h^p). Най-

дём интервал [t_n, tn+1], на концах которого значения v_n и vn+1 имеют разные знаки. На

этом интервале лежит расчётное приближение к полюсу T. В окрестности точки смены знака

выберем p точек сетки t_j. Очевидно, для p = 2 это будут точки t_n и tn+1, для p = 4 -

точки tn-1, t_n, tn+1, tn+2.

Рассмотрим значения v_j в выбранных узлах как аргумент, а соответствующие значения

tj - как функцию этого аргумента. Проведём ньютоновскую (или иную) интерполяцию по

этим значениям v_j функции t(v) и вычислим значение t_∗ при v^∗ = 0. Это и будет расчётное

положение полюса.

3.4. Погрешность. Вычисление погрешности как традиционной нормы (C, L₂ или по-

добных им) от разности численного и точного решений неконструктивно на задачах с сингу-

лярностями. Причина в том, что расчётное положение полюса заведомо отличается от точного,

и поэтому погрешности вблизи полюса оказываются огромными.

В статье [24] было предложено использовать метрику Хаусдорфа для оценки близости ре-

шений, имеющих участки быстрого изменения. Опишем процедуру вычисления расстояния в

такой метрике. Возьмём точное решение u(t) на участке до первого полюса или на участ-

ке между двумя соседними полюсами. Возьмём сеточное решение u_n, относящееся к этому

участку; оно состоит из точек с координатами (t_n, u_n). При этом часть значений u_n вы-

числяется непосредственно решением уравнения (2.1), а лежащие вблизи полюсов значения

восстанавливаются по расчётным величинам v_n.

Опустим из каждой точки (t_n, u_n) перпендикуляр на кривую u(t). Длина этого перпен-

дикуляра d_n есть расстояние от точки до кривой. Выбрав d = max d_n, получим метрику

Хаусдорфа. Очевидно, она аналогична норме C.

На практике более выгодно построить аналог нормы L₂. Для этого возьмём среднеквад-

ратичную величину d_n в расчёте на одну точку:

)1/2

∑

⁽1

d²

(3.13)

n=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

7^∗

820

БЕЛОВ, КАЛИТКИН

где N - полное число точек на выбранном участке. Далее будем пользоваться определени-

ем (3.13).

4. Пример расчёта для одного ОДУ.

4.1. Автономный тест. Рассмотрим следующую задачу Коши:

(

)₂

=1+ u-

t > 0; u(0) =

(4.1)

Приведём точное решение (показано на

рис. 1) и его полюсы:

u(t) = π/4 + tg t, (t_∗)_m = π(m - 1/2), (4.2)

а также уравнение для функции v(t):

(

)₂

= -v² -

1-v

Расчёты проводились с разными констан-

тами перехода U. Оказалось, что большое

значение U приводит к худшей точности.

Значение U

≥ 100 давало неудовлетвори-

тельные результаты. Для иллюстративных

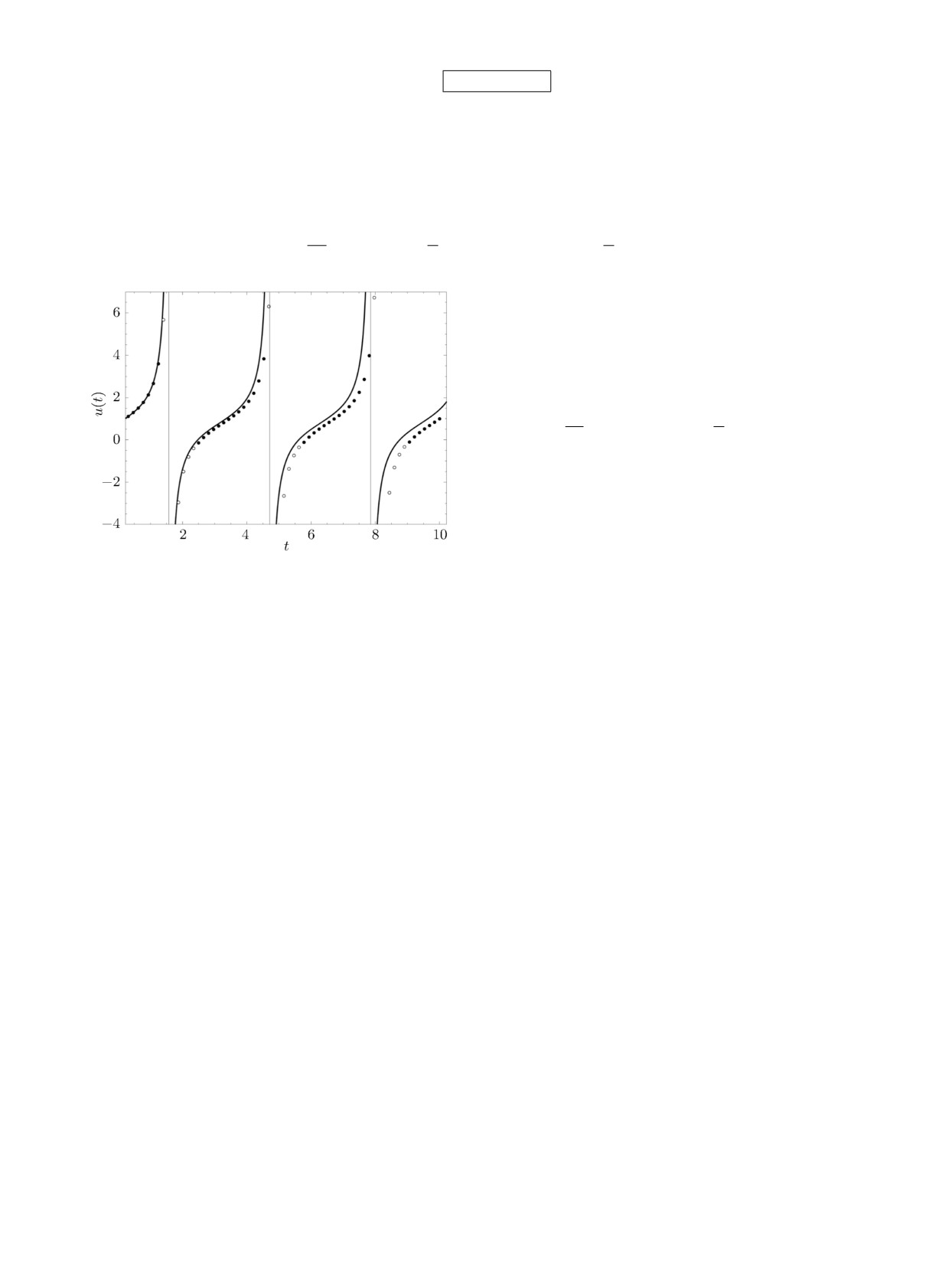
Рис. 1. Расчёт теста (4.1) с шагом τ = 0.157 по схеме

расчётов было выбрано U = 5. В общем слу-

ERK2: сплошная кривая - точное решение; тёмные

чае U должно служить настроечным пара-

точки - расчёт по u(t), светлые - по v(t).

метром программы.

4.2. Результаты. Для численной реализации были выбраны явные схемы Рунге-Кутты

второго и четвёртого порядков (ERK2 и ERK4) и схема CROS (3.10). Мы пользовались их ре-

ализацией в пакете GEABORK (см. [25]). Схемы ERK2 и CROS имеют аппроксимацию O(τ²),

а схема ERK4 - O(τ⁴). Все расчёты проводились до момента T = 10, что требовало прохож-

дения трёх полюсов. Опишем качественные и количественные результаты.

На рис. 1 показано численное решение по схеме ERK2 с шагом τ = 0.157. Шаг демонстра-

ционного расчёта выбран так, чтобы он был: а) несоизмерим с расстоянием между полюсами

(тогда узел сетки заведомо не попадает в полюс), б) достаточно велик, чтобы можно было

видеть отличие численного решения от точного. Видно, что расчёт хорошо проходит через по-

люсы. Ошибка накапливается с увеличением t_n, однако даже при таком крупном шаге можно

успешно пройти довольно много полюсов.

На рис. 2 для всех схем показана зависимость погрешности в метрике Хаусдорфа от вели-

чины шага. Для схем ERK2 и CROS кривые практически совпадают. График дан в двойном

логарифмическом масштабе. Линии графика прямые, начиная уже со второй сетки. Следова-

тельно, зависимость погрешности от шага является степенной. Тангенсы угла наклона этих

прямых равны -2 для схем ERK2 и CROS и -4 для ERK4. Таким образом, даже на задаче с

полюсами эти схемы реализуют свой теоретический порядок точности. Это свидетельствует о

высокой надёжности метода инверсной функции и о применимости метода Ричардсона даже

на задачах с сингулярностями.

Заметим, что для такого количественного определения точности необходим использован-

ный здесь среднеквадратичный аналог метрики Хаусдорфа. Обычные нормы L₂ или C и

даже традиционная метрика Хаусдорфа (являющаяся аналогом нормы C) не дают конструк-

тивного ответа. Для иллюстрации на рис. 2 показаны также погрешности в норме L₂. Сами эти

погрешности намного больше погрешностей в метрике Хаусдорфа. Кривые в традиционных

нормах имеют очень длинные нерегулярные участки: теоретическая сходимость начинается

только при чрезмерно малом шаге, который нечасто используется в практических расчётах.

На рис. 3 показана зависимость погрешности определения положения третьего полюса от

шага для всех схем. График дан в двойном логарифмическом масштабе. Картина полностью

аналогична рис. 2 - положение полюса вычисляется с точностью O(τ^p).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

821

Рис. 2. Зависимость погрешности решения от шага:

Рис. 3. Зависимость погрешности положения третье-

жирные линии - в метрике Хаусдорфа, тонкие - в нор-

го полюса от шага: тёмные точки - схемы ERK2 и

ме L2, тёмные точки - схемы ERK2 и CROS, свет-

CROS, светлые - схема ERK4.

лые - схема ERK4.

Обсудим некоторые следствия из этого. На грубой сетке расчётный и точный полюсы могут

отстоять на несколько интервалов сетки. Если p = 1 (схемы первого порядка точности), то

при сгущении сеток такое взаимное расположение расчётного и точного полюсов сохраняется.

Но если p ≥ 2, то после нескольких сгущений расчётный и точный полюсы попадут в один

и тот же интервал сетки. С этого момента на кривой погрешности в традиционной норме

начинается регулярный участок.

4.3. Неавтономный тест. Тест (4.1) был описан автономным уравнением. Однако к та-

кому же точному решению (4.2) приводит задача для неавтономного уравнения

(

)

= u-

(tg t + ctg t).

(4.3)

В этом случае уравнение для инверсной функции имеет следующий вид:

(

)

=- v-v²

(tg t + ctg t).

(4.4)

Расчёт неавтономной задачи (4.3) являет-

ся существенно более серьёзной проблемой,

чем решение автономной задачи. Поясним

причину этого на данном конкретном при-

мере. Правая часть уравнения (4.4) оказыва-

ется произведением двух сомножителей: пер-

вый зависит только от v, второй - только

от t. Второй сомножитель показывает, что

v должно менять знак (т.е. проходить через

нуль) точно при t_∗. Первый же сомножитель

приводит к изменению знака в точке, смещён-

ной на один или несколько шагов τ. Поэтому

вблизи t_∗ эти сомножители попеременно ме-

няют знак v_n и численное решение принима-

Рис. 4. Расчётная инверсная функция в неавтоном-

ет пилообразный вид, показанный на рис. 4.

ной задаче (4.4).

Этот эффект наблюдается на грубых сет-

ках. Он снижает точность расчёта и даже может привести к срыву расчёта. Однако на до-

статочно подробных сетках этот эффект обычно пропадает, т.е. качественный вид и точность

решения оказываются хорошими. Поэтому при возникновении подобных явлений в расчётах

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

822

БЕЛОВ, КАЛИТКИН

можно порекомендовать пользователю существенно уменьшать шаг сетки. Целесообразно так-

же увеличить разрядность вычислений.

4.4. Решение с ограниченной гладкостью. Выше было отмечено, что для работоспо-

собности метода инверсной функции достаточно аналитичности решения в некоторой проколо-

той окрестности полюса. Вне этой окрестности решение может иметь ограниченную гладкость

(но достаточную для применения той или иной разностной схемы). Этот случай не вызывает

ни теоретических, ни практических затруднений. Чтобы проиллюстрировать это, рассмотрим

следующую задачу:

{

(1 - t₀)-2,

0 ≤ t ≤ t₀ < 1,

1 - 2t₀

u(0) =

(4.5)

u²,

t₀ < t < 1,

(1 - t₀)²

Здесь t₀ ∈ [0, 1] - некоторое фиксированное число. Нетрудно убедиться, что точное решение

этой задачи имеет вид

{

(1 - t₀)-2(t - t₀) + (1 - t₀)-1,

0 ≤ t ≤ t₀ < 1,

u(t) =

(4.6)

(1 - t)-1,

t₀ < t < 1.

Решение (4.6) представляет собой линейную функцию, “склеенную” с гиперболой, и имеет вер-

тикальную асимптоту в точке t_∗ = 1. Это решение показано на рис. 5. Полное время расчёта T

выбирается так, чтобы выполнялось неравенство T > t_∗. Очевидно, что решение аналитично

в круге 0 < |t - t_∗| < t_∗ - t₀ на комплексной плоскости. При t = t₀ аналитичность наруша-

ется: в этой точке u(t) непрерывно вместе с первой производной, но уже вторая производная

претерпевает разрыв.

Положим t₀ = 0.5, T = π. Расчёт этой задачи проводился по методу инверсной функции с

использованием схем ERK1, ERK2 и ERK4. При указанной гладкости решения теоретическую

сходимость может обеспечить только первая из них. Остальные две использовались лишь с ил-

люстративной целью. На рис. 6 показаны погрешности в зависимости от шага сетки. Масштаб

графика двойной логарифмический. Погрешности решения вычислялись в среднеквадратич-

ном аналоге метрики Хаусдорфа. Видно, что для схемы ERK1 кривая погрешности стремится

к прямой с наклоном -1, что соответствует теоретическому порядку точности схемы. Анало-

гичное поведение имеет кривая погрешности расчёта положения полюса.

Рис. 5. Решение (4.6) задачи (4.5): жирная линия -

Рис. 6. Зависимость погрешности от шага сетки в

u, тонкая линия - вертикальная асимптота t = t∗.

тесте (4.5): сплошная линия - ERK1, штриховая -

Штриховой линией показана граница области анали-

ERK2, пунктирная - ERK4; кружки - погрешности

тичности решения t = t0.

решения, треугольники - погрешность расчёта поло-

жения полюса.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

823

Кривая погрешности решения для схемы ERK2 имеет вид “дрожащей” прямой, средний

наклон которой близок к -2. Это не вполне соответствует теоретическому характеру убыва-

ния погрешности, однако даже за рамками формальной применимости эта схема обеспечивает

хорошую количественную точность.

Кривая погрешности для схемы ERK4 резко отличается от прямой с наклоном -4. Это

неудивительно, поскольку для применимости данной схемы решение должно иметь пять непре-

рывных производных. Тем не менее, фактическая точность оказывается очень высокой (вплоть

до ошибок компьютерного округления ∼10-12).

Таким образом, проведённые расчёты показывают, что высокие требования к гладкости

решения (а именно, аналитичность) целесообразны лишь в непосредственной близости к по-

люсу. Вдали от полюса требования к гладкости могут быть существенно ниже, и достаточно

наличия нескольких непрерывных производных. Требование аналитичности в области, содер-

жащей положительную полуось t > 0, является избыточным.

5. Системы ОДУ. Рассмотрим автономную задачу Коши для системы ОДУ с полюсами

первого порядка

= f(u), t > 0, u(0) = u₀;

u = {u¹,u²,...,u^J}, f = {f¹,f²,...,f^J}.

(5.1)

Неавтономный случай как для одного уравнения, так и для систем сводится к автономной

задаче с помощью процедуры автономизации. Эта процедура будет описана далее.

Будем считать, что полюсы различных компонент не совпадают. Совпадение полюсов яв-

ляется вырожденным случаем, он будет рассмотрен отдельно. С формальной точки зрения

расстояние между соседними несовпадающими полюсами может быть любым. Однако для на-

дёжности численного расчёта нужно, чтобы это расстояние было существенно больше шага

сетки. Будем считать это условие выполненным (в противном случае шаг нужно уменьшить).

Таким образом, полюсы различных компонент можно рассматривать последовательно один за

другим.

5.1. Инверсный вектор. Пусть первым возникает полюс в компоненте u^k, соответству-

ющий момент времени обозначим через t^k∗. В некоторой окрестности этой точки справедливы

следующие разложения:

∑

ak-1

u^k =

a^kp(t - t^k∗)^p + o((t - t^k∗)P+1),

t-t^k

∗

p=0

∑

u^j =

a^jp(t - t^k∗)^p + o((t - t^k∗)P+1),

1 ≤ j ≤ J, j = k.

p=0

Компонента, имеющая полюс, разлагается в ряд Пюизе, а все прочие компоненты разлагаются

в ряды Тейлора. Верхние пределы сумм выбраны из предположения, что правые части явля-

ются P раз непрерывно дифференцируемыми, соответственно, компоненты решения имеют

P +1 непрерывную производную. Левую границу рассматриваемой окрестности по-прежнему

будем обозначать через t.

Введём k-ю инверсную функцию v^k(t) = [u^k(t)]-1 (её можно рассматривать как компонен-

ту инверсного вектора). Для неё в окрестности точки t^k∗ справедливо разложение, аналогичное

(3.5). Инверсная система имеет следующий вид:

dv^k

= (v^k)²f^k(u¹, u², . . . , uk-1, [v^k]-1, uk+1, . . . , u^J ) ≡

≡ ϕ^k(u¹,u²,... ,uk-1,[v^k]-1,uk+1,...,u^J),

du^j

= f^j(u¹,u²,... ,uk-1,[v^k]-1,uk+1,...,u^J),

1 ≤ j ≤ J, j = k.

(5.2)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

824

БЕЛОВ, КАЛИТКИН

Дифференцированием рядов для u^j (t), j = k, и v^k(t) нетрудно получить разложения правых

частей (5.2), аналогичные (3.7).

Рассмотрим инверсную систему в указанной окрестности точки t^k∗, принимая точку t за

начальную. Для компоненты v^k начальное условие имеет вид v^k(t) = [u^k(t)]-1, для про-

чих компонент оно записывается тривиально. Систему (5.2) вместе с указанным начальным

условием будем называть инверсной задачей.

Теорема 3. Пусть компонента u^k(t) обращается в бесконечность в точке t^k∗, анали-

тична в проколотой окрестности этой точки и имеет P +1 непрерывную производную вне

указанной окрестности. Особая точка t^k∗ является полюсом первого порядка тогда и только

тогда, когда f^k(u¹(t), u²(t), . . . u^J (t))/(u^k)² имеет конечный ненулевой предел при t → t^k∗.

Здесь подразумевается, что аргументами f^k являются ряды Пюизе для компонент u¹, u²,

..., u^J.

Доказательство практически дословно повторяет доказательство теоремы 1.

Теорема 4. Пусть выполнены условия теоремы 3 и f^k(u¹(t), u¹(2), u^J (t))/(u^k)² имеет

конечный ненулевой предел при t → t^k∗. Тогда найдётся такая окрестность особой точки t^k∗

и окрестность начального условия u₀, в которых решение инверсной задачи существует,

единственно и равномерно непрерывно зависит от начального условия u₀.

Доказательство во многом аналогично доказательству теоремы 2.

1. По условию правые части инверсной системы (5.2) непрерывны и ограничены. В силу

классических теорем разрешимости задач Коши для систем ОДУ решение инверсной системы

существует и единственно.

2. Покажем, что зависимость решения инверсной задачи от u₀ является равномерно непре-

рывной. Легко видеть, что начальное условие в точке t зависит от u₀ равномерно непрерывно.

Поэтому достаточно обосновать равномерно непрерывную зависимость решения инверсной за-

дачи от условия в точке t. Для этого достаточно показать, что компоненты якобиана системы

(5.2) непрерывны.

В самом деле, в якобиан системы (5.2) входят производные вида

∂ϕ^k

∂fⁱ

∂v^k

∂u^j

∂v^k

∂u^j

здесь всюду i, j = k. Производные вида ∂ϕk/∂uj и ∂fi/∂uj непрерывны в силу условий

гладкости на f (поскольку ϕ^k зависит от u^j точно так же, как f^k).

Выражения для ∂ϕ^k/∂v^k полностью аналогичны (3.8), (3.9). Тем же способом можно найти

∂fⁱ/∂v^k. Приведём для них несколько первых коэффициентов ряда (3.8):

d₀ = 2ai2ak-1, d₁ = 4ai2ak0 + 6ai3ak-1,

d₂ = 2[ai2(ak0)² + 3ai2ak1ak-1 + 6ai3ak0ak-1 + 6ai4(ak-1)²]/ak-1, ...

Видно, что производные ∂ϕk/∂vk и ∂fi/∂vk непрерывны, поскольку ϕk не обращается в

нуль в окрестности особой точки.

Таким образом, все компоненты якобиана непрерывны и решение инверсной задачи зависит

от u₀ равномерно непрерывно. Теорема доказана.

Следствие 5. Инверсная компонента v^k(t) однозначно определяет продолжение за полюс

для компоненты u^k(t) и тем самым для всей системы (5.1).

Следствие 6. После прохождения полюса следует вернуться от инверсной системы к

исходной. Это делается так же, как в случае одного уравнения. При этом зависимость

решения за полюсом от начального условия u₀ является равномерно непрерывной.

Последующий полюс может быть как в той же компоненте u^k, так и в какой-то другой.

В обоих случаях для него справедливы теоремы 3 и 4.

Следствие 7. Метод инверсной функции применим к системам со множественными

полюсами первого порядка.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

825

Следствие 8. Условие на гладкость f(u) позволяет применять разностные схемы по-

рядка точности до P -го и вычислять асимптотически точное значение погрешности по

Ричардсону.

5.2. Совпадение полюсов. Рассмотрим случай, когда полюсы нескольких компонент

совпадают. Пусть, для упрощения, таких компонент две. Если совпадают полюсы большего

числа компонент, то рассмотрение проводится полностью аналогично.

Пусть компоненты u^k и u^l имеют полюсы первого порядка, находящиеся в одной и той же

точке t^k∗ = t^l∗ ≡ t_∗. Пусть прочие компоненты не имеют особенностей в некоторой окрестности

этой точки. Тогда в этой окрестности точки t_∗ уже две компоненты разлагаются в ряд Пюизе:

∑

u^j =

−1 +

a^jp(t - t_∗)^p + o((t - t_∗)P+1), j = k,l,

t-t

∗

p=0

∑

u^j =

a^jp(t - t_∗)^p + o((t - t_∗)P+1), j = k,l.

p=0

В этом случае вводится не одна инверсная компонента, а две:

v^j(t) = [u^j(t)]-1, j = k,l.

Инверсная система имеет следующий вид:

dv^j

= (v^j )²f^j(u¹, u², . . . , uk-1, [v^k]-1, uk+1, . . . , ul-1, [v^l]-1, ul+1, . . . , u^J ) ≡

≡ ϕ^j(u¹,u²,... ,uk-1,[v^k]-1,uk+1,...,ul-1,[v^l]-1,ul+1,... ,u^J), j = k,l,

du^j

= f^j(u¹,u²,... ,uk-1,[v^k]-1,uk+1,...,ul-1,[v^l]-1,ul+1,... ,u^J), j = k,l.

Начальное условие в точке t выбирается очевидным образом.

Нетрудно показать, что для такой инверсной задачи справедлив аналог теоремы 4, в ко-

тором необходимо оговорить наличие конечного ненулевого предела для f^k(u(t))/(u^k (t))² и

f^l(u(t))/(u^l(t))² при t → t_∗. Напомним, что эти условия эквивалентны наличию полюсов

первого порядка в этих компонентах.

5.3. Автономизация. Неавтономная задача сводится к автономной с помощью процедуры

автономизации. Напомним эту процедуру. Пусть исходная задача имеет вид

du/dt = f(t, u), u(0) = u₀.

(5.3)

Введём новую компоненту решения u⁰ ≡ t. Для неё f⁰ = 1. Тогда неавтономная система (5.3)

переходит в автономную систему

du/dt = F(u⁰, u¹, . . . , u^J ), u⁰(0) = 0, u^j (0) = uj0,

1 ≤ j ≤ J,

F⁰ = 1, F^j = f^j,

1 ≤ j ≤ J.

(5.4)

Если f ∈ C^P (R_J), то такую же гладкость имеют правые части F. Поэтому для системы (5.4)

также справедливы теоремы 3 и 4.

Алгоритм. Описанный выше алгоритм расчёта легко обобщается на случай систем ОДУ.

Подчеркнём, что для каждой компоненты u^k(t) вектор-функции u(t) необходимо вводить

отдельную инверсную функцию v^k(t) = [u^k(t)]-1 (т.е. компоненту инверсного вектора). Пара-

метр A^k также следует выбирать отдельно для каждой компоненты.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

826

БЕЛОВ, КАЛИТКИН

6. Пример для системы ОДУ.

6.1. Тест. Для иллюстрации рассмотрим следующую систему ОДУ:

du₁

du₂

= u₁(u₁ + u₂),

= -u₂(u₁ + u₂), u₁(0) = u₂(0) = 2-1/2.

(6.1)

Точное решение (6.1) имеет вид

u₁ = tg (t - π/4), u₂ = ctg (t - π/4).

(6.2)

В моменты T1k = π/4+π(k-1/2) компоненты u₁ и u₂ имеют простые полюсы и простые нули

соответственно. В моменты T2k = π/4 + πk u₁ имеет простые нули, а u₂ - простые полюсы.

Это решение показано на рис. 7.

Для разных компонент переход к соответствующей инверсной функции может происхо-

дить в различные моменты времени. Поэтому необходимо рассмотреть следующие случаи.

Во-первых, пусть условие перехода выполнено только для функции u₁, т.е. |u₁| > A₁ и |u₂| <

< A₂. Тогда от (6.1) перейдём к системе

dv₁

du₂

u₂

= -1 - v₁u₂,

-u²².

(6.3)

v₁

Во-вторых, если |u₁| < A₁ и |u₂| > A₂, рассмотрим систему

du₁

u₁

dv₂

=u²¹ +

= v₂u₁ + 1.

(6.4)

v₂

Наконец, если условия |u1| > A1,

|u₂| > A2 выполнены для обеих компонент, то следует

решать систему

dv₁

v₁

dv₂

v₂

= -1 -

+ 1.

(6.5)

v₂

v₁

Очевидно, системы (6.3)-(6.5) являются нелинейными. Они не содержат малых параметров,

допускающих линеаризацию. Поэтому тест (6.1) достаточно представителен. Его важным пре-

имуществом является то, что точное решение (6.2) выражается в элементарных функциях.

6.2. Результаты. Мы проводили расчёты по схеме ERK4. Промежуток t ≤ T = 15 вклю-

чал пять полюсов для каждой компоненты решения. На рис. 8 показана точность нахождения

всего решения и положения пятого полюса для каждой из компонент. Обе компоненты вы-

числены с примерно одинаковой точностью. То же справедливо для положения всех полюсов

каждой из компонент.

Рис. 7. Решение задачи (6.1): сплошная линия - u1,

Рис. 8. Зависимость погрешности от шага сетки в те-

пунктирная - u2, вертикальные линии - положения

сте (6.1): кружки - решения для обеих компонент, тре-

полюсов.

угольники - положение пятого полюса в обеих компо-

нентах.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

827

Видно, что даже на достаточно грубой сетке с шагом τ = 0.075 получена отличная точ-

ность ∼3 · 10-6. Точность ∼10-13, соответствующая ошибкам округления, достигнута при

τ ∼ 10-3. Скорость убывания ошибки при уменьшении шага сетки соответствует теоретиче-

скому четвёртому порядку точности. Это подтверждает высокую надёжность предложенного

метода.

7. Кратные полюсы.

7.1. Трудности. Если полюс u(t) имеет кратность k > 1, то в точке t_∗ инверсная функ-

ция v(t) имеет нуль кратности k. Следовательно, в этой точке обращается в нуль не только

v(t), но и её производные до (k - 1)-й включительно.

Это представляет серьёзную проблему для численного решения. В самом деле, явные схе-

мы порядка точности p ≤ k передают p первых производных решения. В точке t_∗ все эти

производные обращаются в нуль, поэтому при t > t_∗ численное решение оказывается триви-

альным v ≡ 0. Такие явные схемы позволяют дойти до полюса t_∗, но не позволяют вести из

него дальнейший расчёт.

На практике ни один из узлов сетки не будет точно совпадать с точкой t_∗. Поэтому фор-

мальное продолжение решения за полюс возможно. Но при этом значения v(t) в районе полю-

са очень малы и существенно возрастает роль ошибок округления. Поэтому после сквозного

прохождения каждого полюса точность решения существенно ухудшается тем сильнее, чем

больше кратность полюса k. Найти много полюсов высокой кратности с 64-битовыми чис-

лами не удаётся, и требуется существенно увеличивать разрядность вычислений. Изложим

способ преодоления этой трудности.

7.2. Обобщённая инверсная функция. По скорости убывания функции v(t) при при-

ближении к полюсу можно определить кратность нуля k, который равен кратности полюса

функции u(t). Эффективные алгоритмы, позволяющие определить эту кратность, будут опи-

саны позже. Пока будем предполагать, что кратность k ближайшего полюса найдена (мы

допускаем, что разные полюсы могут иметь различную кратность). Тогда вместо инверсной

функции v(t) перейдём к обобщённой инверсной функции w(t). Для нечётного k она имеет

следующий вид:

w(t) = v1/k.

(7.1)

Дробная степень 1/k имеет k комплексных значений. При нечётном k одно из них веще-

ственно. В формуле (7.1) подразумевается выбор вещественной ветви корня.

При чётном k надо различать два случая. Если v > 0, то имеются два вещественных

значения корня, различающихся знаками. Для наших целей выбор знака безразличен. По-

этому также можно пользоваться записью (7.1). Если v < 0, то среди значений корней нет

вещественных. Для наших целей можно воспользоваться следующим обобщением:

w(t) = sgn (v)|v|1/k .

(7.2)

Формулой (7.2) можно пользоваться при любом знаке v. Заметим, что для нечётных k эта

формула также даёт правильный результат.

У обобщённой инверсной функции t_∗ есть простой корень. Сама функция w(t) удовле-

творяет уравнению

= -k-1w1+kf(w^-k).

(7.3)

Сквозное прохождение нуля w(t) является достаточно простой задачей по сравнению с зада-

чей о сквозном прохождении кратного нуля.

Для задачи (7.3) нетрудно доказать аналоги теорем 1 и 2 для случая одного уравнения и

теорем 3 и 4 для случая системы ОДУ. При этом в теоремах 1 и 3 следует заменить f/u² на

f /u1+1/k.

7.3. Определение кратности полюса. Диагностика кратности полюса проводится в тех

случаях, когда v_n становится достаточно малым. В этом случае можно принять гипотезу о

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

828

БЕЛОВ, КАЛИТКИН

том, что t_n достаточно близко к полюсу t_∗, а само поведение функции приближённо описы-

вается формулой v_n ≈ const · (t_∗ - t_n)^k. Одновременно с v_n продолжается расчёт величины

u_n = 1/v_n, и поведение функции u имеет вид u_n ≈ A(t_∗ -t_n)^-k, где A - некоторая константа.

Рассмотрим два соседних шага сетки t_n, tn+1. В них вычислено значение u_n, un+1 и

правые части f_n = f(u_n, t_n), fn+1 = f(un+1, tn+1). Очевидно, вблизи полюса можно считать,

что выполняются следующие приближённые соотношения:

u_n ≈ A(t_∗ - t_n)^-k, un+1 ≈ A(t_∗ - tn+1)^-k,

f_n ≈ Ak(t_∗ - t_n)-k-1, fn+1 ≈ Ak(t_∗ - tn+1)-k-1.

(7.4)

Это система четырёх уравнений с тремя неизвестными A, t_∗, k. Очевидно, система несов-

местна, но можно отыскать её приближённое решение. Важное требование к этому решению -

простота и надёжность расчётных формул.

Опустив промежуточные выкладки, приведём два приближённых решения для k :

k ≈ (tn+1 - t_n)(u_n/f_n - un+1/fn+1)-1, k ≈ (1 - ln(f_n/fn+1)/ln(v_n/vn+1))-1.

(7.5)

Отметим, что для применимости этих формул необходимо (но не достаточно) выполнение

следующих условий:

v_nvn+1 > 0, f_nfn+1 > 0, v_nf_n < 0,

|v_n| > |vn+1|.

Поэтому вычислять значения k (7.5) следует только при выполнении этих неравенств.

В наших расчётах формулы (7.5) давали совпадающие результаты. Разумеется, расчётное

значение q оказывалось нецелым. Но если несколько шагов подряд оно было достаточно близ-

ко к одному и тому же целому числу, то это целое число принималось за кратность полюса

теста. Расчёты показали, что найденное таким образом значение практически всегда совпа-

дало с реальной кратностью полюса. Поэтому данный алгоритм определения кратности был

принят в наших расчётах.

8. Теоретические аспекты построения тестов. Построение представительных тестов

для задач с кратными полюсами оказалось нетривиальной проблемой. Хороший тест должен

иметь точное решение, содержать цепочку кратных полюсов, не содержать особенности других

типов. Обсудим этот вопрос.

8.1. Несингулярные особенности. Тривиальным обобщением теста (4.1) является сле-

дующая задача:

= k(u - u₀)[(u - u₀)1/k + (u - u₀)-1/k] при нечётных k .

Точное решение этой задачи имеет вид

u(t) = u₀ + tg^kt.

Однако у такого теста имеется специфическая трудность, которая не свойственна общим за-

дачам с сингулярностями. В точном решении имеются точки t = πm, m = 0, 1, . . . В них

производные точного решения u(q)(t) = 0 для q = 1, k - 1. Такие точки назовём несингуляр-

ными особенностями. Прохождение такой особенности эквивалентно расчёту задачи с началом

в особой точке высокого порядка. Начало расчёта в особой точке является самостоятельной

трудной проблемой численных методов. В данной задаче эта трудность возникает многократ-

но, т.е. при прохождении каждой несингулярной особенности. Этот вопрос выходит за рамки

данной работы.

Сформулируем следующие очевидные условия.

1. Для отсутствия несингулярных особых точек необходимо, чтобы на интегральной кривой

между любой парой соседних полюсов выполнялось условие f(u, t) = 0.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

829

2. Для отсутствия несингулярных особых точек достаточно, чтобы f(u, t) = 0 ни в одной

полосе плоскости u, t, расположенной между соседними полюсами.

8.2. Единственный полюс. Можно сконструировать тест, не содержащий несингулярной

особенности. Например, это задача

= u^ν, ν > 1, u(0) = u₀.

Точное решение

u(t) = u₀(1 - t/t_∗)-1/(ν-1)

имеет полюс порядка k = (ν - 1)-1 в точке t_∗ = u1-ν0 /(ν - 1). Однако такой тест достаточно

прост, так как в нем имеется только один полюс, а не цепочка полюсов.

8.3. Полюсы чётного порядка. Задачи с полюсами чётного порядка имеют один суще-

ственный недостаток. Они в принципе не могут быть автономными. Справедлива

Теорема 5. Если решение имеет полюс чётной кратности и описывается дифференци-

альным уравнением первого порядка, то это уравнение не может быть автономным.

В самом деле, вблизи полюса чётной кратности левая и правая ветви решения имеют раз-

ные знаки производных при одном и том же значении решения u. Если задача автономна,

то правая часть f(u) есть однозначная функция u, и она не может иметь разные знаки при

одном и том же значении u. Это противоречие доказывает теорему.

8.4. Неавтономность. В п. 2 было замечено, что для простого полюса при неавтоном-

ной записи задачи могут возникать нежелательные осцилляции численного решения вблизи

полюса. Подобная трудность возникает и с кратными полюсами. Способа преодоления этой

трудности найти пока не удаётся. Поэтому целесообразно строить тесты с автономной записью

правой части.

9. Представительные тесты.

9.1. Цепочка полюсов третьего порядка. Нам удалось построить тест, отвечающий

сформулированным выше требованиям. В нем точное решение имеет следующий вид:

u = u₀ + tg³(t - t₀) + tg(t - t₀).

(9.1)

Наличие члена tg³(t - t₀) обеспечивает наличие полюса третьего порядка. В то же время

член tg (t-t₀) гарантирует отсутствие несингулярных особенностей. Уравнение (9.1) является

приведённым кубическим уравнением относительно tg (t-t₀). Из трёх корней этого уравнения

только один вещественный. Он имеет следующий вид:

√

tg (t - t₀) = -(2/

27)S sh ϕ, S = sgn (u - u₀), ϕ = (1/3) arcsh |(

27/2)(u - u₀)|.

(9.2)

Это решение можно записать и в другой форме:

√

tg (t - t₀) =³

u/2 + r +³

u/2 - r, r =

u²/4 + 1/27.

(9.3)

Продифференцировав точное решение по t, получим неавтономную запись дифференци-

ального уравнения:

= (1 + 3 tg²(t - t₀)) cos-2(t - t₀) = (1 + 3 tg²(t - t₀))(1 + tg²(t - t₀)).

Подставив сюда tg (t - t₀) из (9.2) или (9.3), получим автономное уравнение вида

√

= [1 + 3(2/

27 sgn (u - u₀) sh ϕ)²][1 + (2/

27 sgn (u - u₀) sh ϕ)²]

(9.4)

или

= 3[(u/2 + r)4/3 + (u/2 - r)4/3 + 1/9].

(9.5)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

830

БЕЛОВ, КАЛИТКИН

К сожалению, построить аналогичный автономный тест для полюсов произвольного нечёт-

ного порядка k не удалось. Если взять точное решение

u = u₀ + tg(t - t₀) + tg^k(t - t₀),

то дифференциальное уравнение в неавтономной форме записывается без труда:

1 + ktgk-1(t - t₀)

cos²(t - t₀)

Однако алгебраическое уравнение относительно tg (t - t₀) имеет k-ю степень, а при k ≥ 5

оно неразрешимо в радикалах.

9.2. Цепочка полюсов второго порядка. В этом случае задача может быть только

неавтономной. Мы построили следующий тест. Пусть точное решение имеет вид

u(t) = u₀ + sin(t - t₀) cos-2(t - t₀) = [1 + tg²(t - t₀)] sin(t - t₀).

(9.6)

Оно имеет полюсы порядка k = 2 при (t_∗)_m = π/2 + πm.

Продифференцировав (9.6), получим

= (1 + 2 tg²(t - t₀)) cos-1(t - t₀) = [1 + 2 tg²(t - t₀)][1 + tg²(t - t₀)] cos(t - t₀).

(9.7)

Выразим tg (t - t₀) из (9.6) и подставим в (9.7):

√

= (1/2 +

1/4 + (u - u₀)² + 2(u - u₀)²) cos(t - t₀).

(9.8)

Заметим, что одному и тому же точному решению могут соответствовать разные неавто-

номные формы записи задачи. Например, функция (9.6) является точным решением диффе-

ренциального уравнения

= cos-1(t - t₀) + 2 sin²(t - t₀) cos-3(t - t₀).

Однако все попытки расчёта указанного уравнения различными квадратурными формулами

оказались безуспешными - счёт разваливался.

Поэтому сконструированные здесь тесты (9.4), (9.5) и (9.8) представляют самостоятельную

ценность: решения имеют цепочки полюсов указанных порядков, отсутствуют особые точки

других типов, минимизировано влияние неавтономности. Эти задачи рекомендуются при те-

стировании других методов сквозного расчёта полюсов.

10. Апробация.

10.1. Цепочка полюсов третьего порядка. Из предыдущего обсуждения видно, что

тест (9.4) является представительным тестом, описывающим цепочку кратных полюсов, при-

чём полюсы являются единственными особенностями решения. В нем отсутствуют несингуляр-

ные особые точки. Поэтому апробация метода обобщённой инверсной функции была проведена

на этом тесте. В расчётах использована схема ERK4.

Были выполнены две серии расчётов теста (9.4) на последовательности равномерных сгу-

щающихся вдвое сеток. Расчёт проводился на отрезке 0 ≤ t ≤ T = 15, содержащем пять

полюсов. В первой серии во входных данных программы принудительно задавалась крат-

ность полюса k = 3. В этой серии при выполнении условия |u_n| > U выполнялся переход не

к простой, а сразу к обобщённой инверсной функции w, соответствующей данному k. Для

первой сетки задавался шаг τ = 0.15. Далее сетки последовательно сгущались вдвое, пока

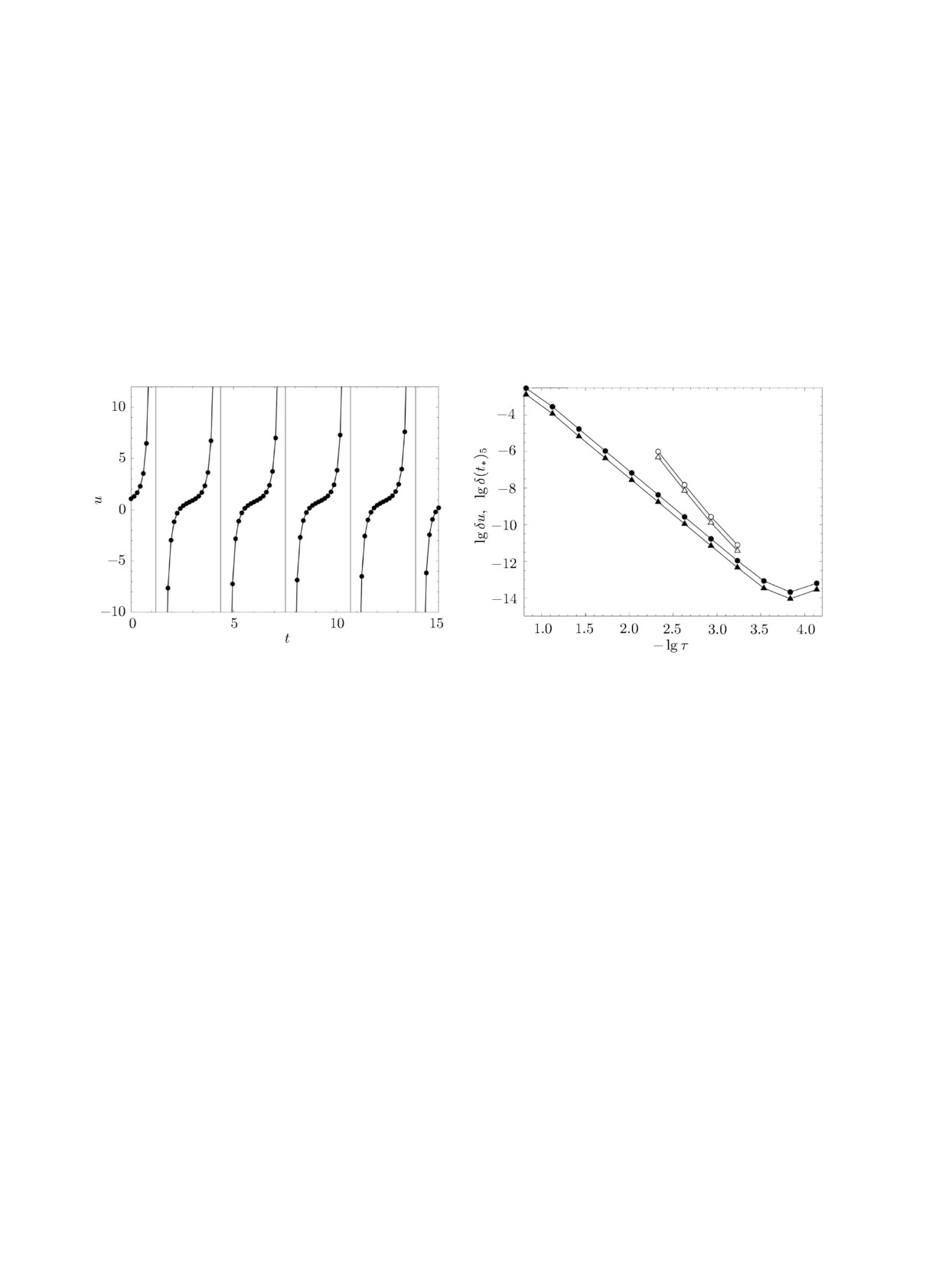
погрешности не достигали ошибок округления. На рис. 9 показан график решения на самой

грубой сетке. Видно, что при сквозном прохождении всех пяти полюсов третьего порядка чис-

ленное решение визуально совпадает с точным. Это свидетельствует о высокой надёжности

метода обобщённой инверсной функции.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

831

На рис. 10 показана зависимость погрешностей от шага сетки в двойном логарифмическом

масштабе. Каждая сетка отмечена значком. Для удобства эти значки соединены между собой

тонкими линиями. Линия с темными кружками показывает погрешность решения в средне-

квадратичном аналоге метрики Хаусдорфа.

Видно, что начальный участок линии слегка искривлен, но быстро происходит выход на

регулярный прямолинейный участок. Его наклон точно соответствует теоретическому поряд-

ку сходимости p = 4 схемы ERK4. Погрешность убывает до ∼10-14, затем перестаёт убы-

вать при дальнейшем сгущении сетки. Этот предел показывает, что ошибки округления всего

лишь в ∼100 раз превышают ошибку единичного округления компьютера 10-16. Это так-

же подтверждает высокую надёжность метода. Линия с темными треугольниками показывает

погрешность определения положения самого далекого пятого полюса. Для неё также справед-

ливо перечисленное выше.

Рис. 9. Расчёт теста (9.4) с шагом τ = 0.15 по схеме

Рис. 10. Зависимость погрешности решения и поло-

ERK4: сплошная линия - точное решение (9.1), точ-

жения пятого полюса от шага в тесте (9.4).

ки - численное решение.

Во второй серии расчётов кратность полюса не задавалась. Программа автоматически

определяла кратность по критерию (7.5). При этом сначала происходил переход от основ-

ной функции u к простой инверсной функции v. Когда для простой инверсной функции

устанавливался критерий (7.5), то производился переход к обобщённой инверсной функции.

На практике этот критерий не срабатывал как на грубых сетках, так и на слишком подроб-

ных. В этом случае счёт разваливался. Расчёты удалось провести на сетках с числами узлов

N = 400,800,1600,3200. Погрешность решения на всём отрезке [0,T] и ошибка положения

пятого полюса показаны на рис. 10 светлыми точками.

Видно, что на первой из этих четырёх сеток погрешности решения и пятого полюса в ∼100

раз превышают соответствующие значения, полученные при априорном задании правильного

k. При дальнейшем сгущении сеток расхождение быстро уменьшается. Кривые стремятся к

линиям, полученным при априорно заданном k. Таким образом, программа с автоматическим

выбором k по точности и надёжности уступает программе с априорно заданной кратностью

полюса. Однако видно, что она позволяет рассчитывать цепочки полюсов, о природе которых

заранее ничего неизвестно.

Сравнение двух серий расчётов показывает, что критерий определения кратности полюса

существенно менее надёжен, чем сам метод обобщённой инверсной функции.

10.2. Цепочка полюсов второго порядка. Расчёты теста (9.8) проводились по схеме

ERK4. На рис. 11 приведены численное решение при τ = 0.15 и точное решение (обозначения

соответствуют рис. 9). Численный расчёт успешно проходит через 5 полюсов.

На рис. 12 показана зависимость погрешности самого решения и положения пятого полю-

са от шага сетки (обозначения соответствуют рис. 10). Видно, что расчётные точки несколько

разбросаны вокруг усреднённой прямой. Это и есть проявление трудностей, связанных с ре-

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

832

БЕЛОВ, КАЛИТКИН

шением неавтономных задач. Однако средний наклон прямой соответствует теоретическому

порядку точности p = 4, и на умеренных сетках достигается очень высокая точность, близкая

к ошибкам единичного округления.

Рис. 11. Расчёт теста (9.8) с шагом τ = 0.15 по схеме Рис. 12. Зависимость погрешности решения и поло-

ERK4.

жения пятого полюса от шага в тесте (9.8).

Заключение. Предложенный в данной работе алгоритм сквозного прохождения полю-

сов высокой заранее неизвестной кратности оказался достаточно надёжным. Он обеспечивает

высокую точность сквозного расчёта не только единичного полюса, но и цепочки полюсов,

причём на автономных и неавтономных задачах.

Публикация выполнена при поддержке Программы стратегического академического ли-

дерства РУДН.

СПИСОК ЛИТЕРАТУРЫ

1. Самарский А.А., Галактионов В.А., Курдюмов С.П., Михайлов А.П. Режимы с обострением в

задачах для квазилинейных параболических уравнений. М., 1987.

2. Berger M., Kohn R.V. A rescaling algorithm for the numerical calculation of blowing-up solutions

// Comm. Pure Appl. Math. 1988. V. 41. № 6. P. 841-863.

3. Huang W., Ren Y., Russell R.D. Moving mesh methods based on moving mesh partial differential

equations // J. Comp. Phys. 1994. V. 113. P. 279-290.

4. Nakagawa T. Blowing up of a finite difference solution to u_t = u_xx + u2 // Appl. Math. Optimization.

1976. V. 2. P. 337-350.

5. McLaughlin D.W., Papanicolaou G.C., Sulem C., Sulem P.L. Focusing singularity of the cubic

Schrodinger equation // Phys. Rev. A. 1986. V. 34. P. 1200-1210.

6. Haynes R., Turner C. A numerical and theoretical study of blow-up for a system of ordinary differential

equations using the Sundman transformation // Atlantic Electr. J. Math. 2007. V. 2. № 1. P. 1-13.

7. Калиткин Н.Н. Численные методы. М., 1978.

8. Альшина Е.А., Калиткин Н.Н., Корякин П.В. Диагностика особенностей точного решения методом

сгущения сеток // Докл. РАН. 2005. Т. 404. № 3. С. 295-299.

9. Альшина Е.А., Калиткин Н.Н., Корякин П.В. Диагностика особенностей точного решения при

расчётах с контролем точности // Журн. вычислит. математики и мат. физики. 2005. Т. 45. № 10.

С. 1837-1847.

10. Свешников А.Г., Альшин А.Б., Корпусов М.О., Плетнер Ю.Д. Линейные и нелинейные уравнения

соболевского типа. М., 2007.

11. Белов А.А. Численное обнаружение и исследование сингулярностей решения дифференциальных

уравнений // Докл. РАН. 2016. Т. 468. № 1. С. 21-25.

12. Белов А.А. Численная диагностика разрушения решений дифференциальных уравнений // Журн.

вычислит. математики и мат. физики. 2017. Т. 57. № 1. С. 91-102.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ЗАДАЧ КОШИ

833

13. Richardson L.F., Gaunt J.A. The deferred approach to the limit // Phil. Trans. A. 1927. V. 226. P. 299-

349.

14. Рябенький В.С., Филлипов А.Ф. Об устойчивости разностных уравнений. М., 1956.

15. Lax P. On the stability of difference approximations to solutions of hyperbolic equations with variable

coefficients // Comm. Pure Appl. Math. 1961. V. 14. P. 497-520.

16. Janke E., Emde F., Lösch F. Taffeln hörere Functionen. Stuttgart, 1960.

17. NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov.

18. Painlevé P. Leçons sur la theorie analytique des equations differentielles. Paris, 1973.

19. Голубев В.В. Лекции по аналитической теории дифференциальных уравнений. М.-Л., 1941.

20. Кудряшов Н.А. Аналитическая теория нелинейных дифференциальных уравнений. М., 2004.

21. Хайрер Э., Нерсет С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежёст-

кие задачи. М., 1990.

22. Rosenbrock H.H. Some general implicit processes for the numerical solution of differential equations

// Comp. J. 1963. V. 5. № 4. P. 329-330.

23. Калиткин Н.Н., Пошивайло И.П. Обратные Ls-устойчивые схемы Рунге-Кутты // Докл. РАН.

2012. Т. 442. № 2. С. 175-180.

24. Белов А.А., Калиткин Н.Н. Экономичные методы численного интегрирования задачи Коши для

жёстких систем ОДУ // Дифференц. уравнения. 2019. Т. 55. № 7. С. 907-918.

25. Пошивайло И.П. Жесткие и плохо обусловленные нелинейные модели и методы их расчёта: дис

канд. физ.-мат. наук. М., 2015.

Московский государственный университет

Поступила в редакцию 17.01.2021 г.

имени М.В. Ломоносова,

После доработки 27.06.2021 г.

Российский университет дружбы народов,

Принята к публикации 09.03.2022 г.

г. Москва,

Институт прикладной математики

имени М.В. Келдыша РАН, г. Москва

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№6

2022