ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 7, с.867-881

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.929

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО

МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСКИХ СИНАПСОВ

Вводится в рассмотрение новая математическая модель нейронной сети с электрически-

ми связями, представляющая собой сингулярно возмущённую систему дифференциально-

разностных уравнений с запаздыванием. Излагаются некоторые методы исследования во-

просов о существовании и устойчивости в этой системе релаксационных периодических

движений. В случае диффузионных и симметричных полносвязных нейронных сетей уста-

навливается реализуемость в соответствующих математических моделях известного фено-

мена буферности.

DOI: 10.31857/S0374064122070019, EDN: CDXLYG

1. Постановка задачи. Остановимся сначала на выборе базовой математической моде-

ли функционирования отдельного нейрона. Следуя работам [1, 2], в качестве такой возьмём

скалярное нелинейное дифференциально-разностное уравнение вида

u = λf(u(t - 1))u

(1.1)

для мембранного потенциала u = u(t) > 0. Здесь параметр λ > 0, характеризующий скорость

протекания электрических процессов в системе, предполагается большим, точка означает диф-

ференцирование по t, а функция f(u) ∈ C²(R₊), R₊ = {u ∈ R : u ≥ 0}, обладает свойствами

f (0) = 1; f(u) + a, uf^′(u), u²f^′′(u) = O(1/u) при u → +∞,

(1.2)

где a = const > 0. Примером такой функции является

f (u) = (1 - u)/(1 + u/a).

(1.3)

Уравнение (1.1), представляющее собой некоторую модификацию известного уравнения

Хатчинсона [3], было предложено и исследовано в статье [4]. В ней показано, что при всех

λ ≫ 1 оно допускает экспоненциально орбитально устойчивый релаксационный цикл u_∗(t,λ)>

> 0, u_∗(0, λ) ≡ 1 периода T_∗(λ), удовлетворяющий предельным соотношениям

lim

T_∗(λ) = T₀,

max

|x_∗(t, λ) - x₀(t)| = O(1/λ), λ → ∞,

(1.4)

λ→∞

0≤t≤T∗(λ)

где T₀ = (1+a)t₀, t₀ = 1+1/a, x_∗(t, λ) = (1/λ) ln(u_∗(t, λ)), а T₀-периодическая функция x₀(t)

задаётся равенствами

⎧

⎨t

при 0 ≤ t ≤ 1,

x₀(t) =

1 - a(t - 1)

при 1 ≤ t ≤ t₀ + 1, x₀(t + T₀) ≡ x₀(t).

(1.5)

^⎩t - T₀

при t₀ + 1 ≤ t ≤ T₀,

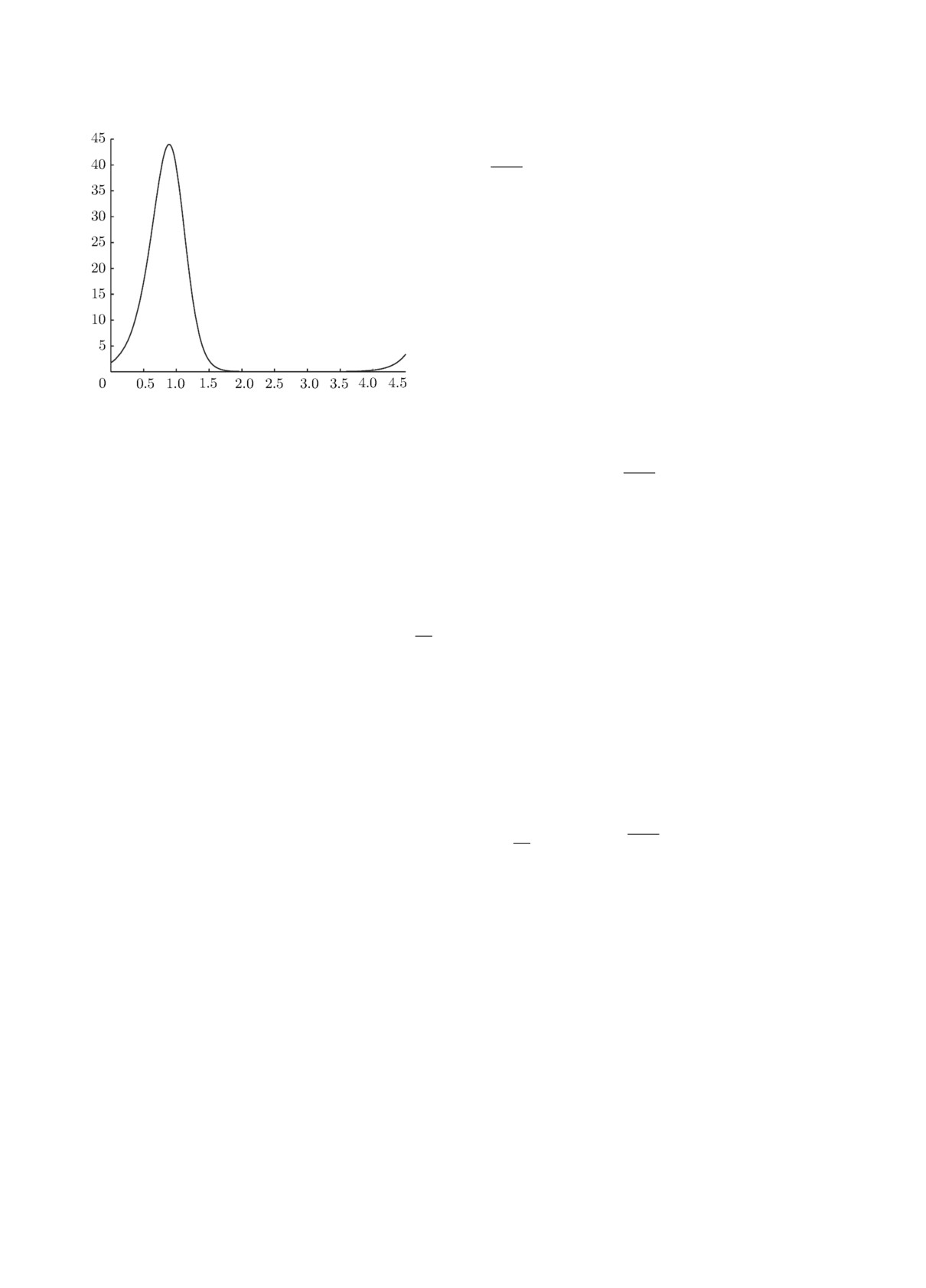
Наглядное представление о релаксационных свойствах этого цикла даёт его график на плоско-

сти (t, u), построенный численно для случая (1.1), (1.3) при λ = 5, a = 2 (рис. 1). Отметим,

что в дальнейшем под релаксационными колебаниями вслед за работами [2, 5] будем пони-

мать колебательные режимы исследуемых моделей, которые сочетают быстрые и медленные

движения.

867

868

ГЛЫЗИН, КОЛЕСОВ

Предположим теперь, что имеется сеть из

m ≥ 2 нейронов с потенциалами u_j

= u_j(t),

= 1, m. Будем считать, что они электриче-

ски взаимодействуют между собой по принципу

“каждый со всеми”. Тогда согласно общеприня-

тым представлениям о природе электрических си-

напсов (см., например, монографии [6, с. 39-40; 7,

с. 60-65] и статьи [8-10]) связь между нейронами

с номерами j и s, j = s, осуществляется посред-

ством соответствующего тока проводимости Isynj,s.

Последний, в свою очередь, в силу закона Ома

задаётся равенством

Isynj,s = d_j,s(u_s - u_j), d_j,s = const ∈ R.

(1.6)

Рис. 1. График u∗(t, λ) при a = 2, λ = 5.

Тем самым, приходим к системе вида

∑

u_j = λf(u_j(t - 1))u_j +

d_j,s(u_s - u_j), j = 1,m,

(1.7)

s=1

s=j

которая, собственно, и является одной из возможных математических моделей электрических

синапсов. Однако, на наш взгляд, модель (1.7) нуждается в некоторой модификации.

Суть упомянутой модификации состоит в том, чтобы заменить равенство (1.6) соотноше-

нием

⁽u_s)

Isynj,s = d_j,s g

u_j, d_j,s = const ∈ R,

(1.8)

u_j

где функция g(u) ∈ C³(R₊) удовлетворяет требованиям

g(u) < 0

при u ∈ [0, 1), g(0) = -1, g(u) > 0 при u > 1, g(1) = 0, g^′(1) > 0,

(1.9)

g(u) - b, ug^′(u), u²g^′′(u), u³g^′′′(u) = O(1/u) при u → +∞, b = const > 0.

(1.10)

Что же касается соответствующей модели электрических синапсов, то в данном случае она

приобретает вид

[

∑

⁽u_s)]u

u_j = λf(u_j(t - 1)) +

d_j,s g

j = 1,m.

(1.11)

u_j

s=1

s=j

Следует отметить, что между прежним законом (1.6) и модифицированной омической ги-

потезой (1.8) имеется определённая согласованность. Действительно, в силу условий (1.9) свой-

ства функции g(u) из (1.8) максимально близки к свойствам функции g(u) = u - 1 в слу-

чае (1.6). В частности, как и система (1.7) новая модель (1.11) в силу свойства g(1) = 0

допускает так называемый однородный цикл

u₁ = u₂ = ... = u_m = u_∗(t,λ),

(1.12)

где u_∗(t, λ) - периодическое решение уравнения (1.1), о котором говорилось выше (см. (1.4),

(1.5)). Что же касается отличий нового подхода к моделированию электрических синапсов от

общепринятого, то их два. Во-первых, при переходе от отдельного нейрона к соответствующей

сети сохраняется вольтерровская структура уравнений; во-вторых, соблюдён так называемый

закон насыщающих проводимостей, суть которого - выполнение условий вида (1.2), (1.10)

для всех входящих в систему нелинейностей. Тем самым наши модели (как отдельного ней-

рона (1.1), так и нейронной сети (1.11)) базируются на одних и тех же общих принципах,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

869

сформулированных в работе [2]. Под вольтерровской структурой уравнений (1.11) подразуме-

вается возможность записи их правых частей в виде произведения соответствующей зависимой

переменной и некоторой неособой в нуле функции. Это свойство гарантирует положительность

решений с положительными начальными условиями.

Вопрос о возможных периодических режимах системы (1.11) достаточно сложен. Поэто-

му, не претендуя на полноту анализа, ниже ограничимся рассмотрением лишь тех из них,

которые располагаются в некоторой окрестности её однородного цикла (1.12). Как оказывает-

ся, при нахождении таких режимов можно применить специальные асимптотические методы,

разработанные ранее в статье [11] для аналогичных (1.7) диффузионных систем

u_j = λf(u_j(t - 1))u_j + d(uj+1 - 2u_j + uj-1), j = 1,m,

(1.13)

где u₀ = u₁, um+1 = u_m, d = const > 0. Описание упомянутых методов приводится ниже.

2. Базовые теоремы. Прежде всего перейдём в системе (1.11) к новым переменным x,

y₁, ..., ym-1 по правилу

( j-1_∑

)

u₁ = exp(x/ε), u_j = exp

+ y_k , j = 2,m, ε = 1/λ.

k=1

В результате получим релаксационную систему вида

))

∑

( (s-1∑

x = F(x(t - 1),ε) + ε

d1,sg exp

y_r

(2.1)

s=2

r=1

))

∑

( (_j∑

))_m∑

( (s-1∑

))j-1∑

( (j-1∑

y_j =

dj+1,s g exp

- y_r

+ dj+1,s g exp

y_r

- dj,s g exp

- y_r

s=1

r=s

s=j+2

r=j+1

s=1

r=s

))

∑

( (s-1∑

−

d_j,s g exp

y_r

+ G_j(x(t - 1),y₁(t - 1),...,y_j(t - 1),ε), j = 1,m - 1,

(2.2)

s=j+1

r=j

где нелинейности F (x, ε), G_j (x, y₁, . . . , y_j , ε) задаются равенствами

F (x, ε) = f(exp(x/ε)),

{ ( (

))

( (

∑

∑ ))}

Gj (x, y1, . . . , yj, ε) =

f exp x/ε + y_k

- f exp x/ε + y_k

j = 1,m - 1.

k=1

Далее, фиксируем постоянную σ₀ : 0 < σ₀ < min(1, a) и на отрезке -σ0 ≤ t ≤ T0 + σ0

обозначим через

y⁰¹(t,z),... ,y0m-1(t,z), z = (z₁,... ,zm-1) ∈ Rm-1

компоненты решения импульсной задачи Коши

))

∑

( (_j∑

))_m∑

( (s-1∑

y_j =

dj+1,s g exp

- y_r

dj+1,s g exp

y_r

s=1

r=s

s=j+2

r=j+1

))

∑

( (j-1∑

))_m∑

( (s-1∑

− dj,s g exp

- y_r

d_j,s g exp

y_r

j = 1,m - 1,

(2.3)

s=1

r=s

s=j+1

r=j

y_j(1 + 0) = y_j(1 - 0) - (1 + a)y_j(0),

y_j(t₀ + 1 + 0) = y_j(t₀ + 1 - 0) - (1 + 1/a)y_j(t₀), j = 1,m - 1,

(2.4)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

870

ГЛЫЗИН, КОЛЕСОВ

(y₁, . . . , ym-1)|t=0 = z,

(2.5)

где T₀, t₀ - величины из (1.5). Рассмотрим затем отображение

= (y⁰¹(t, z), . . . , y0m-1(t, z))|t=T0 ,

(2.6)

действующее из Rm-1 в Rm-1. Справедливо следующее утверждение.

Теорема 1. Любой гиперболической неподвижной точке z = z_∗ отображения (2.6) в

системе (2.1), (2.2) при всех достаточно малых ε > 0 соответствует релаксационный цикл

(x(t, ε), y₁(t, ε), . . . , ym-1(t, ε)), x(0, ε) ≡ 0

(2.7)

периода T(ε), устойчивое и неустойчивое многообразия которого определяются соответ-

ствующими многообразиями этой точки. Кроме того, справедливы соотношения

lim

T (ε) = T₀,

max

|x(t, ε) - x₀(t)| = O(ε), ε → 0,

(2.8)

ε→0

−σ₀≤t≤T₀+σ₀

lim

max

|y_j(t, ε) - y0j(t, z_∗)| = 0,

max

|y_j (t, ε)| ≤ M, j = 1, m - 1,

(2.9)

ε→0

t∈Σ(ε)

−σ₀≤t≤T₀+σ₀

где x₀(t) - функция (1.5), M = const > 0, а множество Σ(ε) представляет собой отрезок

[-σ₀, T₀ + σ₀] с выброшенными интервалами

(1 - ε^δ, 1 + ε^δ), (t₀ + 1 - ε^δ, t₀ + 1 + ε^δ), δ = const ∈ (0, 1).

Доказательство данной теоремы опустим, поскольку в аналогичных ситуациях оно подроб-

но изложено в уже упоминавшейся работе [11], а также в статьях [12, 13].

Теорема 1 носит базовый характер, так как сводит интересующую нас проблему нахож-

дения устойчивых периодических решений системы (2.1), (2.2) к поиску устойчивых непо-

движных точек отображения (2.6). Однако достаточно очевидно, что в общем случае записать

и проанализировать это отображение не представляется возможным. Поэтому сделаем одно

упрощающее предположение, а именно будем считать, что коэффициенты синаптических свя-

зей малы, т.е.

d_j,s = νd0j,s,

0 < ν ≪ 1, d0j,s = const ∈ R.

(2.10)

Это обстоятельство в совокупности с имеющимся минимальным запасом гладкости функ-

ции g(u) (см. (1.10)) позволяет асимптотически проинтегрировать систему (2.3), (2.4) на от-

резке времени 0 ≤ t ≤ T₀.

Действительно, дополнив указанную систему начальным условием (2.5) и учтя гладкость

зависимости правых частей (2.3), (2.4) от параметров, приходим к выводу, что компонен-

ты y0j(t, z, ν), j = 1, m - 1, решения получившейся задачи Коши допускают при ν → 0

следующие асимптотические представления:

y0j(t,z,ν) = z_j + νψ_j(z)t + O(ν²), j = 1,m - 1,

0 ≤ t < 1;

(2.11)

y0j(t,z,ν) = -az_j + νψ_j(z) + νψ_j(-az)(t - 1) + O(ν²), j = 1,m - 1,

1 < t < t₀ + 1;

(2.12)

(

)

y0j(t,z,ν) = z_j -

ψ_j(z) + ν

ψ_j(-az) +

a²

+ νψ_j(z)(t - t₀ - 1) + O(ν²), j = 1,m - 1, t₀ + 1 < t ≤ T₀,

(2.13)

где

))

∑

( (_j∑

))_m∑

( (s-1∑

ψ_j(z) =

d⁰

g exp

- z_r

d⁰

g exp

z_r

j+1,s

s=1

r=s

s=j+2

r=j+1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

871

))

∑

( (j-1∑

))_m∑

( (s-1∑

− d⁰

j,s

g exp

- z_r

d⁰

j,s

g exp

z_r

j = 1,m - 1.

(2.14)

s=1

r=s

s=j+1

r=j

Добавим ещё, что остатки в (2.11)-(2.13) имеют указанный порядок малости равномерно по t

из соответствующих промежутков и по z ∈ Ω, где Ω ⊂ Rm-1 - произвольно фиксированный

компакт. Кроме того, формулы (2.11)-(2.13) сохраняют силу (вместе с порядками остатков)

при дифференцировании по компонентам z_k, k = 1, m - 1, вектора z.

Соотношения (2.11)-(2.14) свидетельствуют о том, что в случае (2.10) отображение (2.6)

асимптотически близко (в C¹-метрике) к тождественному, а точнее говоря, имеет вид

(

)

z_j → z_j + ν

(aψ_j (z) + ψ_j (-az)) + O(ν²), j = 1, m - 1.

(2.15)

a²

В свою очередь, опираясь на асимптотику (2.15), нетрудно заметить, что в рассматриваемой

ситуации интересующее нас отображение с точностью до величин порядка ν² совпадает с

оператором сдвига за время t = 1 по траекториям системы дифференциальных уравнений

(

)

Ż_j = ν

(aψ_j (z) + ψ_j(-az)), j = 1, m - 1.

(2.16)

a²

Справедливость данного факта следует из непосредственного асимптотического интегрирова-

ния системы (2.16) и сравнения получившихся формул с соотношениями (2.15). А это означает

справедливость следующего утверждения.

Теорема 2. Предположим, что выполнено неравенство

a>1

(2.17)

и модельная система

dz_j

= aψ_j (z) + ψ_j (-az), j = 1, m - 1,

(2.18)

dτ

получающаяся из (2.16) при замене времени τ = ν(1 - 1/a²)t, допускает гиперболическое

состояние равновесия

z_∗ = (z∗1,... ,z∗m-1).

(2.19)

Тогда при всех достаточно малых ν > 0 исходное отображение (2.15) имеет асимптоти-

чески близкую к (2.19) гиперболическую неподвижную точку

z_∗(ν) = (z∗1(ν),... ,z∗m-1(ν)): z^∗j(ν) = z^∗j + O(ν), j = 1,m - 1, ν → 0

(2.20)

с теми же свойствами устойчивости.

Предположим далее, что выполнено неравенство (2.17) и удалось найти требуемое состо-

яние равновесия (2.19) модельной системы (2.18). Тогда согласно теореме 1 для любых до-

статочно малых 0 < ν₁ < ν₂ найдётся такое ε₀ = ε₀(ν₁, ν₂) > 0, что при всех 0 < ε ≤ ε₀,

ν₁ ≤ ν ≤ ν₂ и при условии (2.10) система (2.1), (2.2) допускает гиперболический цикл

(x(t, ε, ν), y₁(t, ε, ν), . . . , ym-1(t, ε, ν)), x(0, ε, ν) ≡ 0

(2.21)

периода T (ε, ν), свойства устойчивости которого совпадают с аналогичными свойствами непо-

движной точки (2.20). Кроме того, справедливы аналогичные (2.8), (2.9) соотношения

lim

T (ε, ν) = T₀,

max

|x(t, ε, ν) - x₀(t)| = O(ε), ε → 0,

(2.22)

ε→0

−σ₀≤t≤T₀+σ₀

lim

max

|y_j (t, ε, ν) - y0j(t, z_∗(ν))| = 0,

max

|y_j (t, ε, ν)| ≤ M, j = 1, m - 1.

(2.23)

ε→0

t∈Σ(ε)

−σ₀≤t≤T₀+σ₀

Интересно отметить, что приведённый выше результат может быть усилен, а именно най-

дутся такие достаточно малые ε₀, ν₀ > 0, что цикл (2.21) существует и гиперболичен при

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

872

ГЛЫЗИН, КОЛЕСОВ

всех 0 < ε ≤ ε0,

0 < ν ≤ ν₀. Что же касается свойств (2.22), (2.23), то они выполняются

равномерно по ν ∈ (0, ν₀] и, в частности, постоянная M из (2.23) не зависит от ε, ν.

Справедливость перечисленных фактов обусловлена тем обстоятельством, что в силу (2.10)

система (2.1), (2.2) регулярна по параметру ν. Поэтому при независимом стремлении ε → 0,

ν → 0 цикл (2.21) сохраняется, а его начальные условия в фазовом пространстве C([-1,0];R^m)

имеют пределы x = t, y_j = z^∗j, j = 1, m - 1, -1 ≤ t ≤ 0, где z^∗j - компоненты вектора (2.19).

Ниже применимость базовых теорем 1, 2 иллюстрируется на двух наиболее популярных

нейронных сетях - диффузионной и симметричной полносвязной.

3. Существование и устойчивость дискретных автоволн. Аналогом диффузионной

модели (1.13) в нашем случае является система

[

(

)

⁽uj+1

⁽uj-1))]u

u_j = λf(u_j(t - 1)) + d g

j = 1,m,

(3.1)

u_j

где u₀ = u₁, um+1 = u_m, d = const > 0. Исследование аттракторов этой системы начнём с

вопроса об устойчивости её однородного цикла (1.12).

Заметим, что для сети (3.1), в отличие от общего случая (1.11), соответствующая импульс-

ная система (2.3), (2.4) приобретает более простой вид

y_j = d[g(exp yj+1)+g(exp(-y_j))-g(exp y_j)-g(exp(-yj-1))], j = 1,m - 1, y₀ = y_m = 0, (3.2)

y_j(1 + 0) = y_j(1 - 0) - (1 + a)y_j(0),

y_j(t₀ + 1 + 0) = y_j(t₀ + 1 - 0) - (1 + 1/a)y_j(t₀), j = 1,m - 1.

(3.3)

Это обстоятельство позволяет разобраться с устойчивостью нулевой неподвижной точки

отображения (2.6), которая в силу свойств (1.9) функции g(u) заведомо существует.

Теорема 3. Нулевая неподвижная точка отображения (2.6), порождённого системой

(3.2), (3.3), экспоненциально устойчива при любом d > 0.

Доказательство. Для нахождения матрицы Якоби Φ^′(0), отвечающей точке z = 0, необ-

ходимо линеаризовать систему (3.2) и учесть импульсные условия (3.3). В результате получаем,

что матрица Φ^′(0) представляет собой оператор сдвига по решениям импульсной системы

h_j = dg^′(1)(hj+1 - 2h_j + hj-1), h_j(1 + 0) = h_j(1 - 0) - (1 + a)h_j(0),

h_j(t₀ + 1 + 0) = h_j(t₀ + 1 - 0) - (1 + 1/a)h_j(t₀), j = 1,m - 1, h₀ = h_m = 0

(3.4)

за время от t = 0 до t = T₀. Далее, применим к (3.4) метод Фурье по собственным векторам

разностного оператора Лапласа, а точнее говоря, положим

(

)

∑

πk

h_j =

g_k(t)sin

j = 1,m - 1.

(3.5)

k=1

В результате убеждаемся в том, что компоненты g_k(t), k = 1, m - 1, из (3.5) являются реше-

ниями импульсной системы

ġ = -σg, g(1+0) = g(1-0)-(1+a)g(0), g(t0 +1+0) = g(t0 +1-0)-(1+1/a)g(t₀) (3.6)

при 0 ≤ t ≤ T₀, σ = σ_k, где в силу (1.9) имеем

)

⁽ πk

σ_k = 4dg^′(1)sin²

> 0, k = 1, m - 1.

(3.7)

На завершающем этапе дополним систему (3.6) начальным условием g = 1 при t = 0,

проинтегрируем получившуюся задачу Коши и положим μ_k = g|t=T0,σ=σ_k , где σk - дискретные

значения (3.7) параметра σ. В итоге получаем набор чисел μ_k, k = 1, m - 1, который, как

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

873

нетрудно увидеть, образует спектр интересующей нас матрицы Φ^′(0). Более того, справедливы

соотношения μ_k = μ(σ)|σ=σk , k = 1, m - 1, где

μ(σ) = ((1 + a) exp σ - 1)((1 + 1/a) exp σ - 1) exp(-σT₀), μ(0) = 1,

μ^′(σ) = ((2 - T₀)exp(2σ) + (T₀ - 1)exp σ - 1)T₀ exp(-σT₀) < 0 при σ ∈ (0,+∞),

μ(σ) → 0

при σ → +∞.

Отсюда очевидным образом следует, что μ_k ∈ (0, 1), k = 1, m - 1. Теорема 3 доказана.

В аналогичной (2.1), (2.2) системе, записанной для диффузионного случая, неподвижной

точке z = 0 отвечает цикл вида (2.7) с компонентами y₁ = . . . = ym-1 = 0, а в исходной диф-

фузионной цепочке (3.1) - однородный цикл (1.12). Теоремы 1, 3 приводят к выводу, что этот

цикл является экспоненциально орбитально устойчивым при любом фиксированном значении

параметра d > 0 и при всех достаточно больших λ.

Перейдём теперь к другим аттракторам диффузионной системы (3.1). По аналогии с непре-

рывным случаем дискретной автоволной или просто автоволной назовём любой её стационар-

ный режим, отличный от однородного цикла (1.12).

Нахождение автоволн будем проводить при аналогичном (2.10) предположении

d=ν,

0 < ν ≪ 1.

(3.8)

Напомним, что в случае (2.17), (3.8) в силу базовых теорем 1, 2 интересующий нас вопрос сво-

дится к поиску устойчивых состояний равновесия соответствующей модельной системы (2.18).

В свою очередь, несложный подсчёт показывает, что для диффузионной сети (3.1) упомянутая

система приобретает вид

dz_j

= Δ(-z_j) - Δ(z_j) + Δ(zj+1) - Δ(-zj-1), j = 1,m - 1, z₀ = z_m = 0,

(3.9)

dτ

где

Δ(z) = ag(exp z) + g(exp(-az)), z ∈ R.

(3.10)

Исследование автоволн начнём с простейшего случая m = 2, когда имеем дело с так

называемой билокальной моделью

)

⁽u₂

⁽u₁)

u₁ = λf(u₁(t - 1))u₁ + dg

u₁,

u₂ = λf(u₂(t - 1))u₂ + dg

u₂.

(3.11)

u₁

u₂

Для того чтобы в случае (2.17), (3.8) применить теоремы 1, 2, обратимся к системе (3.9),

которая при m = 2 состоит из одного скалярного уравнения

= Δ(-z) - Δ(z).

(3.12)

dτ

Анализ уравнения (3.12) требует некоторой информации о его правой части Ψ(z). Для

получения этой информации объединим факт нечётности Ψ(z) с формулой (3.10) и свойства-

ми (1.9), (1.10) функции g(u). В результате приходим к выводу, что

Ψ(0) = Ψ^′(0) = Ψ^′′(0) = 0, Ψ^′′′(0) = 2a(a² - 1)(g^′(1) + 3g^′′(1) + g^′′′(1)),

(3.13)

lim Ψ(z) = -(b + 1)(a - 1).

(3.14)

z→+∞

Предположим теперь, что наряду с неравенством (2.17) выполнено условие

g^′(1) + 3g^′′(1) + g^′′′(1) > 0.

(3.15)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

874

ГЛЫЗИН, КОЛЕСОВ

Тогда в силу свойств (3.13), (3.14) для функции Ψ(z) уравнение (3.12) имеет хотя бы одну

пару состояний равновесия z = ±z_∗, z_∗ > 0, таких, что Ψ^′(z_∗) = Ψ^′(-z_∗) ≤ 0. В общем же

случае справедливо строгое неравенство

Ψ^′(z_∗) < 0,

(3.16)

а значит, эти состояния равновесия экспоненциально устойчивы. Добавим, что в силу тео-

рем 1, 2 при условии (3.16) данной паре состояний равновесия в исходной модели (3.11) при

λ ≫ 1 и при надлежащем уменьшении параметра d соответствует пара устойчивых автовол-

новых периодических движений. Отметим ещё, что упомянутые циклы переходят друг в друга

при замене переменных u₁ → u₂, u₂ → u₁.

Вопрос о реализуемости ограничений (3.15), (3.16) требует отдельного рассмотрения. Для

этого привлечем конкретный пример функции связи g(u), а именно всюду ниже считаем, что

g(u) = (u - 1)/(1 + u/b), b = const > 0.

(3.17)

Тогда, как нетрудно увидеть,

g^′(1) =

g^′′(1) = -

g^′′′(1) =

b+1

(b + 1)²

(b + 1)³

а значит, неравенство (3.15) эквивалентно включению

√

b ∈ (0,2 -

^⋃ (2 +^√3, +∞).

(3.18)

В случае условия устойчивости (3.16) ситуация несколько сложнее. Получить для него

явные ограничения на параметры a, b, подобные (3.18), не удаётся. Однако, как показывает

численный анализ, оно заведомо справедливо, например, при значениях a = 2.5, b = 15 (на

рис. 2 изображён соответствующий этим параметрам график функции Ψ(z)). Что же касается

пары устойчивых циклов системы (3.11), существующих у неё согласно нашей теории, то для

конкретных нелинейностей (1.3), (3.17) и при a = 2.5, b = 15, d = 0.005, λ = 6 графики

на плоскости (t, u) компонент u = u₁(t), u = u₂(t) одного из них представлены на рис. 3

(сплошной линией показан график u₁(t), а пунктирной - график u₂(t)).

Рис. 3. Графики u1(t), u2(t) при a = 2.5,

Рис. 2. График Ψ(z) при a = 2.5, b = 15.

b = 15, d = 0.005, λ = 6.

Особого внимания заслуживает случай фиксированного a > 1 и достаточно больших зна-

чений параметра b, когда условие (3.16) всё же удаётся проверить аналитически. Для того

чтобы убедиться в этом, сделаем в уравнении (3.12) замены переменных

z = lnb + z, bτ → τ

(3.19)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

875

и учтём в его правой части вытекающие из формул (3.10), (3.17) асимптотические представ-

ления

[

]

[

]

a exp z

Δ(z)|z=lnb+z = b

+ O(1/b) , Δ^′(z)|z=lnb+z = b

+ O(1/b) ,

(3.20)

1 + exp z

(1 + exp z)²

Δ(z)|z=-lnb-z = b[1 + O(b-min(1,a-1))],

a exp(az)

Δ^′(z)|z=-lnb-z =

[a exp(-z) + O(1/b)] -

[1 + O(b-min(1,a-1))],

(3.21)

ba-2

справедливые при условии (2.17) и при b → +∞ равномерно по z из любого фиксирован-

ного компакта. В результате после отбрасывания асимптотически малых добавок приходим к

уравнению

a exp z

=1-

(3.22)

dτ

1 + exp z

допускающему экспоненциально устойчивое состояние равновесия

z = ln

(3.23)

a-1

Остаётся добавить, что в исходном уравнении (3.12) состоянию равновесия (3.23) отвечает

состояние равновесия z = z_∗(b) с асимптотикой

z_∗(b) = ln b + ln

+ O(b-min(1,a-1)), b → +∞,

a-1

удовлетворяющее требуемому условию устойчивости (3.16).

Обратимся теперь к диффузионной цепочке (3.1) при m ≥ 3, считая по-прежнему, что

нелинейность g(u) в ней задана равенством (3.17). Далее, фиксируем произвольно индекс j₀

из множества 1 ≤ j₀ ≤ m - 2, выполним во вспомогательной системе (3.9) аналогичные (3.19)

замены переменных

z_j = ln b + z_j, j = 1,j₀; z_j = - ln b + z_j, j = j₀ + 1,m - 1; bτ → τ,

(3.24)

и при условии (2.17) устремим параметр b к бесконечности. В результате, опираясь на асимп-

тотические равенства (3.20), (3.21), для новых переменных

zj , j = 1, m - 1, приходим к

некоторой предельной системе, которая в зависимости от индексов j₀ и m записывается по-

разному, а именно все возможные здесь ситуации исчерпываются следующими четырьмя слу-

чаями:

1) индекс j₀ = 1, при этом m ≥ 4;

2) средние значения индекса j₀ такие, что 2 ≤ j₀ ≤ m - 3, а m ≥ 5;

3) максимальное значение индекса j₀ = m - 2, причём m ≥ 4;

4) наконец, m = 3, j₀ = 1.

Рассмотрим подробнее случай 1). Учитывая, что j₀ = 1, для перехода от переменной z₁

к z₁ используется первая формула из замены (3.24), а для всех остальных значений индекса

j - вторая. Непосредственная подстановка асимптотических представлений (3.20), (3.21) в

формулы (3.9), (3.10) приводит к следующей предельной системе:

dz₁

a exp z₁

dz₂

a exp(-z₂)

=2-

- 1,

dτ

1 + exp z₁

dτ

1 + exp(-z₂)

dz_j

a exp(-z_j )

a exp(-zj-1)

3 ≤ j ≤ m - 2,

dτ

1 + exp(-z_j)

1 + exp(-zj-1)

dzm-1

a exp(-zm-1)

a exp(-zm-2)

-1-

(3.25)

dτ

1 + exp(-zm-1)

1 + exp(-zm-2)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

876

ГЛЫЗИН, КОЛЕСОВ

В случае 2) (2 ≤ j₀ ≤ m - 3, m ≥ 5) предельная система приобретает вид

dz₁

a exp z₁

a exp z₂

dz_j

a exp z_j

a exp zj+1

=1-

j = 2,j₀ - 1,

dτ

1 + exp z₁

1 + exp z₂

dτ

1 + exp z_j

1 + exp zj+1

dzj0

a exp zj0

dzj0+1

a exp(-zj0+1)

=1-

- 1,

dτ

1 + exp zj0

dτ

1 + exp(-zj0+1)

dz_j

a exp(-z_j )

a exp(-zj-1)

j₀ + 2 ≤ j ≤ m - 2,

dτ

1 + exp(-z_j)

1 + exp(-zj-1)

dzm-1

a exp(-zm-1)

a exp(-zm-2)

- 1;

(3.26)

dτ

1 + exp(-zm-1)

1 + exp(-zm-2)

в случае 3) (j₀ = m - 2, m ≥ 4) имеем дело с системой

dz₁

a exp z₁

a exp z₂

dz_j

a exp z_j

a exp zj+1

=1-

2 ≤ j ≤ m - 3,

dτ

1 + exp z₁

1 + exp z₂

dτ

1 + exp z_j

1 + exp zj+1

dzm-2

a exp zm-2

dzm-1

a exp(-zm-1)

=1-

- 2;

(3.27)

dτ

1 + exp zm-2

dτ

1 + exp(-zm-1)

в случае 4) (m = 3, j₀ = 1) получаем

dz₁

a exp z₁

dz₂

a exp(-z₂)

=2-

- 2.

(3.28)

dτ

1 + exp z₁

dτ

1 + exp(-z₂)

Несложный анализ каждого из вариантов (3.25)-(3.28) показывает, что при любых фикси-

рованных m ≥ 3, 1 ≤ j₀ ≤ m - 2 и при дополнительном условии

a>2

(3.29)

соответствующая предельная система для z_j , j = 1, m - 1, допускает единственное экспонен-

циально устойчивое состояние равновесия

(

)

z(j₀) = ln

, ln

,...,ln

,-ln

,...,-ln

,-ln

(3.30)

a-2

a-1

a-2

j₀-1

m-2-j₀

Что же касается системы (3.9), то в силу формул (3.20), (3.21), (3.24), (3.30) при условии (3.29)

и при всех b ≫ 1 она имеет m - 2 экспоненциально устойчивых состояния равновесия

z(j₀)(b) = (ln b, . . . , ln b, - ln b, . . . , - ln b) + z(j₀) + O(1/b), b → +∞, j0 = 1, m - 2.

(3.31)

j₀

m-1-j₀

Согласно теоремам 1, 2 в диффузионной цепочке (3.1) с нелинейностью (3.17) состояни-

ям равновесия (3.31) соответствуют экспоненциально орбитально устойчивые автоволновые

периодические режимы. Отсюда в силу произвольности m заключаем, что в рамках моде-

ли (3.1), (3.17) реализуется известное явление буферности. Суть этого явления в том, что при

подходящем подборе параметров a, b, λ, d и при увеличении m можно гарантировать со-

существование в указанной модели любого наперёд заданного конечного числа устойчивых

циклов. Добавим ещё, что феномен буферности характерен именно для нейронных систем,

поскольку он отражает ситуацию, когда в неокортексе человеческого мозга различные идеи и

концепции соревнуются друг с другом в целях доминирования.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

877

4. Случай симметричной полносвязной сети. В максимально симметричном случае,

когда все связи равноправны, интересующая нас математическая модель нейронной сети при-

обретает вид

[

∑

⁽u_s)]u

u_j = λf(u_j(t - 1)) + d

j = 1,m,

(4.1)

u_j

s=1

s=j

где d = const > 0. Интересны вопросы существования и устойчивости специальных её перио-

дических решений - так называемых режимов двухкластерной синхронизации.

Для описания упомянутых режимов фиксируем произвольно натуральное k : 1 ≤ k ≤ m - 1

и предположим, что совокупность индексов 1 ≤ j ≤ m разбита на два непересекающихся

множества A и B, состоящих из k и m - k элементов соответственно, т.е.

{1, 2, . . . , m} = A

^⋃B.

(4.2)

Тогда, очевидно, система (4.1) допускает решения с компонентами

u_j = v(t) при j ∈ A, u_j = w(t) при j ∈ B,

(4.3)

где переменные v, w удовлетворяют вспомогательной системе

)

⁽w

⁽v⁾

v = λf(v(t - 1))v + (m - k)dg

w = λf(w(t - 1))w + kdg

(4.4)

Если же, в свою очередь, система (4.4) имеет непостоянное периодическое решение

v = v(k)(t), w = w(k)(t), v(k)(t) ≡ w(k)(t),

(4.5)

то отвечающее ему решение (4.2), (4.3) исходной системы (4.1) назовём периодическим режи-

мом двухкластерной синхронизации.

Нетрудно увидеть, что один и тот же цикл (4.5) порождает целое семейство U_k перио-

дических режимов двухкластерной синхронизации. Все циклы из этого семейства задаются

равенствами (4.2), (4.3) при

v = v(k)(t), w = w(k)(t),

а их количество очевидно равно C^km.

Остановимся сначала на вопросе о существовании семейства циклов U_k. В связи с этим при

условиях (2.17), (3.8) применим к системе (4.4) теоремы 1, 2. В результате убедимся в том, что

проблема существования и устойчивости её неоднородного цикла (4.5) сводится к отысканию

ненулевого устойчивого состояния равновесия аналогичного (3.12) скалярного нелинейного

уравнения

= kΔ(-z) - (m - k)Δ(z),

(4.6)

dτ

где Δ(z) - функция (3.10).

Как и ранее, всюду ниже считаем, что нелинейность g(u) в (4.1) задана равенством (3.17).

Тогда, выполнив в (4.6) замены (3.19) и устремив при фиксированном a > 1 параметр b к

бесконечности, для новой переменной z получим аналогичное (3.22) уравнение

exp z

= k - a(m - k)

(4.7)

dτ

1 + exp z

Заметим, что при условии

(

)

a > max 1,

(4.8)

m-k

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

878

ГЛЫЗИН, КОЛЕСОВ

уравнение (4.7) допускает экспоненциально устойчивое состояние равновесия

z∗(k) = ln

(4.9)

a(m - k) - k

Что же касается исходного уравнения (4.6), то при выполнении неравенства (4.8) оно имеет

экспоненциально устойчивое состояние равновесия z∗(k)(b) > 0 с асимптотикой

z∗(k)(b) = ln b + z∗(k) + O(b-min(1,a-1)), b → +∞,

(4.10)

где величина z∗(k) определяется в (4.9).

Итак, из наших построений следует, что при выполнении условия (3.8) при всех λ ≫ 1 и

при фиксированных параметрах a и b, первый из которых удовлетворяет неравенству (4.8),

а второй - достаточно большой, система (4.1) с нелинейностью (3.17) имеет искомое семейство

U_k периодических режимов двухкластерной синхронизации. Перейдём теперь к вопросу об

устойчивости данных циклов. В связи с этим сделаем два полезных наблюдения.

Во-первых, несложная проверка показывает, что система (4.1) инвариантна относительно

замен

(u₁, u₂, . . . , u_m) → (uj1 , uj2 , . . . , ujm ),

(4.11)

где (j₁, j₂, . . . , j_m) - произвольная перестановка набора индексов (1, 2, . . . , m). Во-вторых, пе-

риодические режимы из семейства U_k допускают кодирование с помощью бинарных векторов

(ϑ₁, ϑ₂, . . . , ϑ_m) : ϑ_j = 1 или

0, j = 1, m.

(4.12)

Точнее говоря, предполагаем, что j-я координата вектора (4.12) равна 1 или 0 при j ∈ A

или j ∈ B соответственно. В этом случае между векторами (4.12), содержащими k единиц

и m - k нулей, и циклами семейства U_k имеет место взаимно-однозначное соответствие.

Суммируя сказанное выше, убеждаемся в том, что любые два цикла из U_k переходят

друг в друга под действием замен (4.11), а значит имеют одинаковые свойства устойчивости.

Таким образом, проблема устойчивости всех режимов семейства U_k сводится к исследованию

устойчивости только одного цикла (4.2), (4.3), (4.5), соответствующего бинарному вектору

(1, . . . , 1, 0, . . . , 0).

(4.13)

m-k

Для решения поставленной проблемы обратимся к модельной системе (2.18), отвечающей

системе (4.1) при условиях (2.17), (3.8), (3.17). Характерная особенность этой системы сос-

тоит в том, что нелинейности ψ_j (z) в ней теперь задаются равенствами (2.14), в которых

все коэффициенты d0j,s равны единице. Учитывая данное обстоятельство, нетрудно увидеть,

что при достаточно большом фиксированном значении параметра b и при дополнительном

условии (4.8) циклу семейства U_k с кодировкой (4.13) соответствует состояние равновесия

указанной системы с компонентами

z_j = 0, j = 1,m - 1, j = k; z_k = z∗(k)(b),

(4.14)

где z∗(k)(b) - состояние равновесия (4.10) уравнения (4.6). Таким образом, свойства устойчи-

вости интересующего нас цикла совпадают с аналогичными свойствами состояния равнове-

сия (4.14).

Несложный подсчёт показывает, что система в вариациях, получающаяся при линеариза-

ции системы (2.18) на упомянутом выше состоянии равновесия, преобразуется к виду

dh_j

= -(m - k)Δ^′(z_k)h_j,

1 ≤ j ≤ k - 1,

(4.15)

dτ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

879

(∑k

)

∑

(s-1∑

dh_k

= -Δ^′(-z_k)

h_r

- Δ^′(z_k)

h_r

(4.16)

dτ

s=1

r=s

s=k+1

r=k

dh_j

= -kΔ^′(-z_k)h_j, k + 1 ≤ j ≤ m - 1,

(4.17)

dτ

где z_k = z∗(k)(b) (см. (4.10)), Δ^′(z), z ∈ R, - производная функции (3.10). В свою очередь, из

структуры уравнений (4.15)-(4.17) следует, что собственные значения матрицы этой системы

задаются равенствами

λ_j = -(m - k)Δ^′(z_k),

1 ≤ j ≤ k - 1; λ_k = -kΔ^′(-z_k) - (m - k)Δ^′(z_k);

λ_j = -kΔ^′(-z_k), k + 1 ≤ j ≤ m - 1.

(4.18)

При анализе знаков величин (4.18) будем считать выполненным неравенство

a > 3.

(4.19)

В этом случае в силу соотношений (3.20), (3.21), (4.10) имеем

]

[ aexpz^∗

(k)

λ_j = -(m - k)b

+ O(1/b)

< 0,

1≤j ≤k;

(1 + exp z∗(k))2

λ_j = -

exp(-z∗(k))[1 + O(b-min(1,a-3))] < 0, k + 1 ≤ j ≤ m - 1,

отсюда и из (4.8), (4.19), в свою очередь, следует, что при выполнении неравенства

(

)

a > max 3,

(4.20)

m-k

все циклы семейства U_k являются экспоненциально орбитально устойчивыми.

В итоге отметим, что, как и в предыдущем случае, в рамках модели (4.1) с нелинейностью

(3.17) наблюдается феномен буферности. Действительно, из условия (4.20) следует, что при

d ≪ 1, λ ≫ 1 при достаточно большом фиксированном b > 0 и при a > max(3,m - 1)

в указанной модели существуют все семейства U_k, k = 1,m - 1, периодических режимов

двухкластерной синхронизации и все режимы из этих семейств устойчивы. Отсюда в силу

произвольности m заключаем, что можно добиться сосуществования любого конечного числа

устойчивых циклов.

5. Заключение. Интересно отметить, что система (1.11) может иметь и другие аттракто-

ры, отличные от тех, которые описывает теорема 1. Для пояснения сути дела предположим,

что коэффициенты синаптических связей заданы равенствами

d_j,s = λd0j,s, d0j,s = const ∈ R.

(5.1)

Далее с учётом соотношения (5.1) произведём в (1.11) замены

u_j = exp(x_j/ε), j = 1,m, ε = 1/λ ≪ 1.

В результате приходим к системе вида

∑

x_j = F(x_j(t - 1),ε) +

d0j,sH(x_s - x_j,ε), j = 1,m,

(5.2)

s=1

s=j

где F (x, ε) - функция из (2.1), H(x, ε) = g(exp(x/ε)).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

880

ГЛЫЗИН, КОЛЕСОВ

Обратим внимание, что в силу свойств (1.2), (1.9), (1.10) справедливы предельные ра-

венства

⎧

⎨1

при x < 0,

⎨-1

при x < 0,

lim

f (1)

при x = 0,

lim

при x = 0,

ε→0

^⎩-a при x > 0,

^⎩b при x > 0.

Отсюда следует, что при ε → 0 исходная релаксационная система (5.2) переходит в релейную

систему

∑

x_j = R₀(x_j(t - 1)) +

d0j,sH₀(x_s - x_j), j = 1,m.

(5.3)

s=1

s=j

Наличие предельного объекта (5.3) представляет собой ещё одну характерную особенность

нашего подхода к математическому моделированию электрических синапсов. Опираясь на эту

особенность, для отыскания аттракторов системы (5.2) можем воспользоваться общими ре-

зультатами из статьи [5] о соответствии между устойчивыми циклами релейной и релаксаци-

онной систем. Однако для того чтобы применить эти результаты сначала необходимо изучить

свойства предельной релейной системы. К сожалению, пока имеется весьма скудная инфор-

мациия об её аттракторах.

В первую очередь отметим, что система (5.3) допускает однородный цикл

x₁ = x₂ = ... = x_m = x₀(t),

(5.4)

где x₀(t) - периодическая функция (1.5). Вопрос же о нахождении у неё циклов, отличных

от (5.4), представляет собой отдельную и пока не решённую проблему. Добавим только, что,

как показывают численные эксперименты, такие циклы могут существовать даже в простей-

шем случае m = 2.

Для того чтобы убедиться в этом, обратимся к системе

x₁ = R₀(x₁(t - 1)) + d₁H₀(x₂ - x₁),

x₂ = R₀(x₂(t - 1)) + d₂H₀(x₁ - x₂),

(5.5)

где d₁, d₂ = const > 0. Отметим сразу, что в симметричном случае d₁ = d₂ кроме одно-

родного цикла (5.4) никаких других аттракторов в ней обнаружить не удалось. Однако в

несимметричном случае численный анализ данной системы при значениях параметров a =

= 2.5, b = 0.07, d₁ = 1.5, d₂ = 0.1 и при начальных условиях x₁ = -1, x₂ = t, заданных на

отрезке -1 ≤ t ≤ 0, показал наличие у неё устойчивого неоднородного цикла. Характерная

особенность этого цикла состоит в том, что его компоненты x₁(t), x₂(t) имеют по четыре

переключения на промежутке времени длины периода.

Напомним (см. работы [5, 14]), что согласно об-

щепринятой в теории релейных систем терминологии

точками переключения компоненты x_j(t) системы

(5.5) называются моменты времени, при прохождении

через которые производная xj(t) претерпевает конеч-

ные скачки, а сама функция x_j(t) остаётся непрерыв-

ной. В случае найденного нами цикла у его компонент

x₁(t), x₂(t) на отрезке длины периода имеются по две

точки переключения, связанные с переменами знаков

запаздывающих компонент x₁(t - 1) и x₂(t - 1) со-

ответственно, и ещё две общие для обеих компонент

точки переключения, обусловленные переменами зна-

ков функции x₁(t) - x₂(t).

Проекция упомянутого устойчивого цикла на

плоскость (x₁, x₂) представлена на рис. 4. Вопрос

Рис. 4. График кривой (x1(t), x2(t)) при о его аналитическом построении пока остаётся от-

a = 2.5, b = 0.07, d1 = 1.5, d2 = 0.1.

крытым.

Исследование выполнено при поддержке Российского научного фонда (проект 22-11-00209).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОБ ОДНОМ СПОСОБЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

881

СПИСОК ЛИТЕРАТУРЫ

1. Глызин С.Д., Колесов А.Ю., Розов Н.Х. Об одном способе математического моделирования хими-

ческих синапсов // Дифференц. уравнения. 2013. Т. 49. № 10. С. 1227-1244.

2. Глызин С.Д., Колесов А.Ю., Розов Н.Х. Релаксационные автоколебания в сетях импульсных ней-

ронов // Успехи мат. наук. 2015. Т. 70. Вып. 3 (423). С. 3-76.

3. Hutchinson G.E. Circular causal systems in ecology // Ann. N.Y. Acad. of Sci. 1948. V. 50. P. 221-246.

4. Колесов А.Ю., Мищенко Е.Ф., Розов Н.Х. Об одной модификации уравнения Хатчинсона // Журн.

вычислит. математики и мат. физики. 2010. Т. 50. № 12. C. 2099-2112.

5. Колесов А.Ю., Мищенко Е.Ф., Розов Н.Х. Реле с запаздыванием и его C¹-аппроксимация // Тр.

Мат. ин-та им. В.А. Стеклова 1997. Т. 216. C. 126-153.

6. Scott A.C. Neuroscience: a Mathematical Primer. New York, 2002.

7. Кащенко С.А., Майоров В.В. Модели волновой памяти. М., 2013.

8. Абарбанель Г.Д.И., Рабинович М.И., Селверстон А., Баженов М.В., Хуэрта Р., Сущик М.М.,

Рубчинский Л.Л. Синхронизация в нейронных ансамблях // Успехи физ. наук. 1996. Т. 166. № 4.

C. 363-390.

9. Леванова Т.А., Казаков А.О., Коротков А.Г., Осипов Г.В. Влияние электрической связи на дина-

мику ансамбля нейроноподобных элементов с синаптическими тормозящими связями // Изв. вузов.

Прикл. нелин. динамика. 2018. Т. 26. № 5. C. 101-112.

10. Щапин Д.С., Некоркин В.И. Параметрически возбуждаемые хаотические спайковые последова-

тельности и информационные аспекты в ансамбле нейронов ФитцХью-Нагумо // Письма в Журн.

эксп. и теор. физики. 2021. Т. 113. Вып. 6. C. 415-420.

11. Колесов А.Ю., Розов Н.Х. Автоволновые процессы в цепочках диффузионно связанных уравнений

с запаздыванием // Успехи мат. наук. 2012. Т. 67. Вып. 2 (404). C. 109-156.

12. Глызин С.Д., Колесов А.Ю., Розов Н.Х. Релаксационные автоколебания в нейронных системах. II

// Дифференц. уравнения. 2011. Т. 47. № 12. C. 1675-1692.

13. Колесов А.Ю., Розов Н.Х. Дискретные автоволны в системах дифференциально-разностных урав-

нений с запаздыванием из экологии // Тр. Мат. ин-та им. В.А. Стеклова. 2012. Т. 277. C. 101-143.

14. Глызин С.Д., Колесов А.Ю., Розов Н.Х. Релаксационные автоколебания в нейронных системах. I

// Дифференц. уравнения. 2011. Т. 47. № 7. C. 919-932.

Ярославский государственный университет

Поступила в редакцию 16.11.2021 г.

имени П.Г. Демидова

После доработки 20.05.2022 г.

Принята к публикации 25.05.2022 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022