ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 7, с.890-911
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
УДК 517.95
ОБРАТНАЯ ЗАДАЧА
С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
ДЛЯ АБСТРАКТНОГО ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
© 2022 г. И. В. Тихонов, М. Алмохамед
В банаховом пространстве рассматривается линейная обратная задача для абстрактного
дифференциального уравнения второго порядка. Стационарное неоднородное слагаемое
в уравнении предполагается неизвестным. В начальный момент времени заданы стандарт-
ные условия Коши. К ним добавляется дополнительное условие - финальное переопре-
деление третьего рода. Оно содержит комбинацию значений эволюционной функции и её
производной в выбранный финальный момент времени. Для изучаемой задачи установлен
критерий единственности решения, выраженный в спектральных терминах - через нули
характеристической целой функции. Результат носит универсальный характер и не тре-
бует ограничений на тип дифференциального уравнения. Отдельно обсуждается вопрос
о распределении нулей характеристической функции. Посредством проведённого анализа
получен ряд эффективных достаточных признаков единственности (и неединственности)
решения. Все они просты и удобны на практике.
DOI: 10.31857/S0374064122070032, EDN: CECRGN
1. Постановка задачи. Пусть E - комплексное банахово пространство и A - линей-
ный замкнутый оператор в E с областью определения D(A) ⊂ E (не обязательно плотной
в E). Зафиксируем вещественное число T > 0. На интервале (0,T) рассмотрим абстрактное
дифференциальное уравнение второго порядка
u′′(t) = Au(t) + g,
0<t<T,
(1)
с неизвестным элементом g ∈ E.
Для одновременного нахождения функции u: [0, T ] → E и элемента g добавим условия
Коши
u(0) = u0, u′(0) = u1
(2)
и специальное переопределение
αu(T ) + βu′(T ) = u2.
(3)
Элементы u0, u1, u2 ∈ E и числовые значения α, β ∈ C \ {0} считаем заданными.
Условие (3) будем называть финальным переопределением третьего рода. Задача (1)-(3)
относится к классу обратных задач (см. [1, 2]). Модельная форма (1)-(3), простая по виду,
но общая по характеру, позволяет охватить единым методом широкий круг примеров из ма-
тематической физики. Главное, чтобы изучаемое дифференциальное уравнение имело второй
порядок по выделенной переменной t, неформально полагаемой временем. Цель нашей рабо-
ты - получить критерий единственности решения обратной задачи (1)-(3) без ограничений на
оператор A, кроме отмеченных линейности и замкнутости. Поясним понятие решения.
Пару (u(t), g) назовём ослабленным решением обратной задачи (1)-(3), если
u ∈ C2((0,T),E)
⋂C1([0,T],E), u(t) ∈ D(A) при 0<t<T, g∈E,
(4)
и все соотношения (1)-(3) выполнены. При этом автоматически Au ∈ C((0, T ), E).
Повышая требования, будем считать ослабленное решение (u(t), g) классическим, если
u ∈ C2([0,T],E), u(t) ∈ D(A) при
0≤t≤T, g∈E.
(5)
890
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
891
При этом уравнение (1) должно выполняться на отрезке [0, T ], а в соотношениях (2) для
согласования условий естественно выбирать элемент u0 из D(A).
В основном мы будем рассматривать именно ослабленные решения (4), называя их далее
просто решениями. Тогда, установив критерий единственности для ослабленных решений (4),
получим результат, пригодный и для классических решений (5).
По-видимому, поставленная обратная задача ещё не изучена с должной подробностью.
Нам известны лишь прежние результаты [2; п. 8.3], где для уравнений “эллиптического типа”
с позитивным оператором A (в смысле П.Е. Соболевского, см. [3; с. 275]) обсуждался аналог
обратной задачи (1)-(3) со значениями α, β ∈ R, α2 + β2 = 0.
Отметим ещё, что специальные случаи α = 0, β = 0 (финальное переопределение первого
рода) и α = 0, β = 0 (финальное переопределение второго рода) более известны, и общие
критерии единственности для них получены в работах [4] и [5] соответственно. Поэтому далее,
не снижая общности, ограничимся предположением α = 0, β = 0, как и было указано при
постановке задачи. Точнее, наша постановка задачи (1)-(3) зависит от трёх числовых пара-
метров α, β ∈ C \ {0} и T > 0. Как мы увидим в дальнейшем, картина с единственностью
решения по-сути обусловлена одним “безразмерным” параметром p ≡ 2β/(αT ).
Завершая этот вводный раздел, отметим роль А.И. Прилепко, интерес и настойчивость
которого во многом сформировали подходы к изучению подобных обратных задач. Первона-
чальный импульс развитию дал, возможно, обзор [6], где был намечен переход от обратных
задач теории потенциала к некоторым идейно близким обратным задачам для эволюционных
уравнений (см. также [7]). Кроме того, выделим работы [8-12], идейно повлиявшие на наше
исследование и посвящённые различным неклассическим задачам с теми или иными финаль-
ными условиями (см. также [13-15]).
Теперь, использовав методику работы [4] и некоторые факты из теории целых функций,
установим универсальный критерий единственности решения для обратной задачи (1)-(3),
действующий без ограничений на тип дифференциального уравнения (1).
2. Однородная обратная задача. Допустим, что обратная задача (1)-(3) с некоторыми
элементами u0, u1, u2 ∈ E разрешима. Поставим вопрос о единственности её ослабленного
решения. Он очевидно сводится к вопросу об отсутствии нетривиальных решений у однородной
обратной задачи для уравнения (1) с условиями
u(0) = 0, u′(0) = 0, αu(T ) + βu′(T ) = 0.
(6)
Как обычно, тривиальным решением однородной задачи (1), (6) считаем пару
u(t) ≡ 0, g = 0.
(7)
Все другие решения задачи (1), (6) (если они есть) называем тогда нетривиальными∗).
Укажем простой способ, позволяющий строить нетривиальные решения однородной об-
ратной задачи (1), (6). Рассмотрим её “операционный аналог”, состоящий из скалярной задачи
Коши
y′′(t) = λy(t) + 1,
0≤t≤T,
(8)
y(0) = 0, y′(0) = 0
(9)
и финального условия
αy(T ) + βy′(T ) = 0.
(10)
Здесь λ - спектральный параметр. Требуется найти значения λ ∈ C, при которых в скалярной
задаче (8)-(10) существуют решения y ∈ C2[0, T ].
∗) Очевидно, что у таких нетривиальных решений (u(t), g) функция u(t) не должна обращаться в тожде-
ственный нуль на [0, T ], в то время как возможность g = 0 изначально исключать нельзя. Эта возможность
действительно реализуется в некоторых специальных ситуациях, когда собственные значения оператора A за-
полняют всю комплексную плоскость, и не реализуется, если хотя бы одна точка из C не является собственным
значением оператора A (подробнее см. [16]).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
892
ТИХОНОВ, АЛМОХАМЕД
Нетрудно понять, что каждому такому λ отвечает лишь одно возможное решение y(t)
(причём последнее не будет тождественным нулём). Этим спектральная задача (8)-(10) от-
личается от привычных спектральных задач типа Штурма-Лиувилля, где есть естественное
свойство линейности, и собственные функции можно умножать на ненулевые константы.
Анализ спектральной задачи (8)-(10) не сложен. Решение задачи Коши (8), (9) может быть
записано в виде
√
ch (
λt) - 1
y(t) = y(t, λ) =
(y(t) = t2/2 при λ = 0).
(11)
λ
При этом
√
sh (
λt)
y′(t) = y′t(t,λ) =
√
(y′(t) = t при λ = 0).
(12)
λ
Последующая подстановка выражений (11), (12) в финальное условие (10) даёт уравнение
√
√
ch (
λT ) - 1
sh(
λT )
α
+β
√
= 0.
(13)
λ
λ
Именно корни λ ∈ C уравнения (13) служат спектральными значениями задачи (8)-(10).
Поясним одно обстоятельство. Функции (11), (12) представимы степенными рядами
√
ch (
λt) - 1
t2
t4
t6
t2n+2
=
+λ
+λ2
+...+λn
+...,
(14)
λ
2!
4!
6!
(2n + 2)!
√
sh (
λt)
t
t3
t5
t2n+1
√
=
+λ
+λ2
+...+λn
+...,
(15)
λ
1!
3!
5!
(2n + 1)!
т.е. они являются целыми как по переменной t, так и по параметру λ. Тем самым никакой
√
“многозначности”, связанной с присутствием
λ, в формулах (11)-(13) не возникает. Отметим
также связь разложений (14), (15) с теорией так называемых обобщённых экспонент и теорией
функций типа Миттаг-Лёффлера (подробнее см. [17]; см. также [18; с. 33]).
Для последующего использования удобно ввести целые функции∗)
√
√
ch (
λT) - 1
sh(
λT )
L1(λ) = L1(λ;T) ≡
,
L2(λ) = L2(λ;T) ≡
√
(16)
λ
λ
переменной λ ∈ C. Составим из функций (16) следующую характеристическую функцию
изучаемой обратной задачи:
L(λ) = L(λ; T, α, β) ≡ αL1(λ) + βL2(λ), λ ∈ C.
(17)
Здесь числа α, β те же, что в условии (3) (а также в последнем из соотношений (6) и в фор-
муле (10)). Нули функции (17) совпадают с корнями уравнения (13) и со спектральными зна-
чениями λ скалярной задачи (8)-(10).
Поскольку L(λ) есть целая функция нецелого порядка ρ = 1/2, то множество нулей
Λ = Λ(T,α,β) ≡ {λ ∈ C: L(λ) = 0}
(18)
должно быть бесконечным (см. [19; с. 38-41]). Ясно, что это счётное множество с единственной
предельной точкой на бесконечности. Структура множества Λ и вопрос о правильной индек-
сации нулей будут рассмотрены отдельно, в пп. 8, 9 ниже. Там, в частности, отмечено, что
∗) Это элементарные целые функции порядка ρ = 1/2 по переменной λ ∈ C. Все необходимые сведения из
теории целых функций см. в [19, 20].
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
893
нули функции (17) являются, как правило, простыми, и особых проблем с кратностью точек
в множестве (18) не возникает.
Выберем фиксированное значение λ из множества (18), обозначив его временно через λ0.
Поскольку это некоторый нуль функции L(λ) и, автоматически, спектральное значение ска-
лярной задачи (8)-(10), то при λ = λ0 задача (8)-(10) имеет решение
2
ch (√λ0t) - 1
t
t4
t2n+2
y(t) = y(t, λ0) =
≡
+λ0
+...+λn
+...,
0≤t≤T.
λ0
2!
4!
0 (2n + 2)!
Допустим, что то же число λ0 ∈ Λ оказалось собственным значением оператора A из урав-
нения (1), т.е. Af0 = λ0f0 с собственным вектором f0 ∈ D(A), f0 = 0. Тогда пара
ch (√λ0t) - 1
u(t) = y(t, λ0)f0 =
f0, g = f0
(19)
λ0
удовлетворяет всем соотношениям (1), (6), образуя нетривиальное решение этой задачи. Такие
решения (если они есть) будем называть элементарными решениями однородной обратной
задачи (1), (6). Зафиксируем точное утверждение.
Лемма 1. Пусть некоторый нуль λ0 характеристической функции (17) является соб-
ственным значением оператора A с собственным вектором f0 ∈ D(A), f0 = 0. Тогда од-
нородная обратная задача (1), (6) имеет нетривиальное элементарное решение вида (19).
Точнее, подобных решений будет бесконечно много, так как собственный вектор f0 можно
умножать на любую ненулевую константу.
Лемма проверяется непосредственно. Понятно, что в её условиях единственность решения
обратной задачи будет нарушаться, поскольку в однородной версии (1), (6) появятся нетриви-
альные решения вида (19). Эти решения оказываются даже классическими, так как для них
требования (5) очевидно выполнены и уравнение (1) действует на всём отрезке [0, T ].
Итак, для единственности решения в обратной задаче необходимо, чтобы ни один нуль
характеристической функции L(λ) из формулы (17) не совпадал с собственным значением
оператора A. Наработанный прежде опыт (см. [4, 5]) подсказывает, что такое условие может
быть ещё и достаточным, и результат - критерий единственности решения - не исключён
в максимальной общности. Покажем, что эта надежда вполне обоснована.
3. Формулировка главного результата. Рассматриваем задачу (1)-(3) в исходных пред-
положениях из п. 1. Главный результат работы состоит в следующем.
Теорема 1. Пусть A - линейный замкнутый оператор в E. Предположим, что при
некоторых u0,u1,u2 ∈ E обратная задача (1)-(3) имеет ослабленное решение (u(t),g). Для
того чтобы это решение было единственным необходимо и достаточно, чтобы ни один нуль
характеристической функции (17) не являлся собственным значением оператора A.
При выборе u0 = u1 = u2 = 0 теорема 1 приобретает следующий специальный вид.
Теорема 2. Пусть A - линейный замкнутый оператор в E. Для того чтобы одно-
родная обратная задача (1), (6) имела только тривиальное решение (7) и не имела других
ослабленных решений необходимо и достаточно, чтобы ни один нуль характеристической
функции (17) не являлся собственным значением оператора A.
Ввиду очевидной линейности изучаемой обратной задачи теоремы 1 и 2 эквивалентны,
и можно ограничиться доказательством только теоремы 2. При этом необходимость в ней
получается ссылкой на лемму 1 и элементарные решения вида (19). Итак, зафиксируем логику:
нужный критерий будет установлен, если обосновать достаточность условия из теоремы 2
для единственности решения однородной обратной задачи (1), (6).
Последующее довольно объёмное доказательство существенно использует соображения из
теории целых функций. Чтобы не прерывать изложение, удобно сразу обсудить несколько
технических фактов, связанных с функциями L1(λ), L2(λ) из формулы (16) и с образованной
из них характеристической функцией L(λ) вида (17).
4. Элементарные целые функции и их поведение на мнимой оси. Рассматриваем
целые функции L1(λ), L2(λ) из формулы (16). Нам нужно охарактеризовать их поведение
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
894
ТИХОНОВ, АЛМОХАМЕД
на мнимой оси. Заметим, что обе эти функции являются вещественными в том смысле, что
их тейлоровские разложения по переменной λ содержат только вещественные коэффициенты
(см. формулы (14), (15), взятые при t = T > 0). Поэтому для каждой из функций значения
в комплексно сопряжённых точках плоскости будут комплексно сопряжены. Как следствие
имеем |L1(+iτ)| = |L1(-iτ)| и |L2(+iτ)| = |L2(-iτ)| в симметричных точках ±iτ на мнимой
оси. Здесь и всюду далее обозначаем через i мнимую единицу.
Введём характеристики
V1(τ) ≡ |L1(iτ)|, V2(τ) ≡ |L2(iτ)|,
(20)
зависящие от переменной τ ∈ R или, точнее, от |τ| ≥ 0.
Прямой подсчёт показывает, что
√
√
√
ch(
iτT ) - 1
ch (
|τ|/2T ) - cos(
|τ|/2T )
V1(τ) ≡
,
(21)
=
iτ
|τ|
√
√
√
√
h(
iτ T )
ch2(
|τ|/2T ) - cos2(
|τ|/2T )
V2(τ) ≡s
√
(22)
=
iτ
|τ|
Затем, использовав формулы ch2a = (1 + ch 2a)/2 и cos2 a = (1 + cos 2a)/2, заметим связь
√
√
√
√
ch (
2|τ|T ) - cos(
2|τ|T )
V2(τ) =
=
2V1(4τ).
(23)
2|τ|
Отметим также степенное разложение
2
∑
T
τ2 T6
τ4 T10
τ2n
T4n+2
V1(τ) =
+
+
+...=
,
τ2n = |τ|2n,
(24)
2!
22 6!
24 10!
22n (4n + 2)!
n=0
элементарно получаемое из (21). Перечисленные соотношения дают такой результат.
Лемма 2. Пусть функции L1(λ), L2(λ) определены по формулам (16). Тогда их харак-
теристики V1(τ), V2(τ) вида (20) являются строго положительными при τ ∈ R и строго
возрастающими при возрастании |τ| ≥ 0. При |τ| → ∞ верны асимптотики
√
√
ch (
|τ|/2T )
ch (
|τ|/2T )
V1(τ) ∼
,
V2(τ) ∼
,
(25)
|τ|
|τ|1/2
откуда V1(τ) = o(V2(τ)) при |τ| → ∞.
Доказательство. То, что функция V1(τ) строго положительна при τ ∈ R и строго возрас-
тает при возрастании |τ|, очевидно следует из формулы (24). Затем, глядя на формулу (23),
делаем аналогичные выводы относительно V2(τ). И, наконец, асимптотики (25), действую-
щие при |τ| → ∞ вместе с соотношением V1(τ) = o(V2(τ)), без труда выводятся из явных
представлений (21), (22). Лемма доказана.
Обратимся теперь к характеристической функции L(λ) = αL1(λ) + βL2(λ), построенной
по правилу (17) с фиксированными значениями α, β ∈ C \ {0}. По аналогии с (20) введём
величину
V (τ) ≡ |L(iτ)| = |αL1(iτ) + βL2(iτ)|, τ ∈ R.
(26)
Так как коэффициенты α, β могут быть невещественными, то утверждать, что функция V (τ)
зависит лишь от |τ| здесь уже, конечно, нельзя. Кроме того, неотрицательная функция V (τ)
уже не обязательно строго положительна при τ ∈ R (ибо какие-то нули функции L(λ) могут
оказаться на мнимой оси). Но поведение V (τ) при |τ| → ∞ легко охарактеризовать.
Действительно, имеем оценку сверху
V (τ) = |αL1(iτ) + βL2(iτ)| ≤ |α||L1(iτ)| + |β||L2(iτ)| = |α|V1(τ) + |β|V2(τ), τ ∈ R,
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
895
и соответствующую оценку снизу
V (τ) = |αL1(iτ) + βL2(iτ)| ≥ |β||L2(iτ)| - |α||L1(iτ)| = |β|V2(τ) - |α|V1(τ), τ ∈ R.
Отсюда получаем, что
|α|V1(τ)
V (τ)
|α|V1(τ)
1-
≤
≤1+
,
τ ∈ R,
(27)
|β|V2(τ)
|β|V2(τ)
|β|V2(τ)
где V1(τ) = o(V2(τ)) при |τ| → ∞ согласно лемме 2. Поэтому, переходя к пределу в (27)
и используя вторую асимптотику (25), замечаем, что
√
ch (
|τ|/2T )
V (τ) ≡ |L(iτ)| = |αL1(iτ) + βL2(iτ)| ∼ |β|V2(τ) = |β||L2(iτ)| ∼ |β|
(28)
|τ|1/2
при |τ| → ∞. Зафиксируем нужный результат в следующей форме.
Лемма 3. Пусть функции L1(λ), L2(λ) определены по формуле (16) и неотрицательная
величина V (τ) определена по формуле (26) с фиксированными значениями α, β ∈ C \ {0}.
Тогда V (τ) строго положительна при достаточно больших |τ| > 0, и верно соотношение
|α|V1(τ) + |β|V2(τ)
|α||L1(iτ)| + |β||L2(iτ)|
lim
= lim
= 1.
(29)
|τ|→∞
V (τ)
|τ|→∞
|αL1(iτ) + βL2(iτ)|
Доказательство. Строгая положительность V (τ) при достаточно больших |τ| > 0 сле-
дует из асимптотики (28). Для вычисления предела (29) достаточно заметить, что числитель
и знаменатель фигурирующей там дроби образуют величины, эквивалентные при |τ| → ∞
(см. асимптотические формулы (25) и (28)). Лемма доказана.
Соотношение (29) играет важную роль в дальнейшем. Вернёмся теперь к обратной задаче.
5. Начало доказательства главного результата: операторное тождество. Критерий
единственности решения доказываем в форме теоремы 2. Напомним, что в силу леммы 1
осталось установить достаточность условия из этого критерия.
Итак, предположим, что ни один нуль характеристической функции (17) не является соб-
ственным значением оператора A. Возьмём произвольное ослабленное решение (u(t), g) од-
нородной обратной задачи (1), (6) и покажем, что u(t) ≡ 0 на [0, T ] и g = 0, т.е. что решение
может быть только тривиальным.
Для реализации нашего плана потребуется ряд вспомогательных функций. Их построение
должно быть согласовано с изучаемой задачей (1), (6). Это означает, что функции должны
зависеть от выбора значений α, β ∈ C\{0}. Поскольку в конкретной ситуации такие значения
можно считать фиксированными, мы не указываем на α и β в используемых далее обозна-
чениях. Другими словами, вместо Y (t, λ; α, β) или Z(t, λ; α, β) пишем просто Y (t, λ), Z(t, λ)
и т.п. Аналогично всюду в доказательстве считаем фиксированным значение T > 0.
Начнём с того, что, комбинируя выражения (11) и (12), составим функцию
√
√
ch (
λt) - 1
sh (
λt)
Y (t, λ) = α
+β
√
(30)
λ
λ
с аргументами t ∈ [0, T ] и λ ∈ C. Отметим, что
Y (0, λ) ≡ 0, Y (T, λ) = L(λ), λ ∈ C.
(31)
Первое соотношение в (31) очевидно следует из определения (30); второе получается сравне-
нием с формулами (16), (17), задающими характеристическую функцию L(λ).
Центральную роль в этом разделе играет даже не сама функция Y (t, λ), а её производная
по переменной t. Введём обозначение
√
sh(
λt)
√
Z(t, λ) ≡ Y′t(t, λ) = α
√
+ β ch(
λt).
(32)
λ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
896
ТИХОНОВ, АЛМОХАМЕД
Продифференцировав дальше, получим
√
√
√
Z′t(t,λ) = α ch (
λt) + β
λsh (
λt),
(33)
√
√
√
Z′′tt(t,λ) = α
λsh (
λt) + βλ ch (
λt) = λZ(t, λ).
(34)
Выделим значения
Z(0, λ) = β, Z′t(0, λ) = α, λ ∈ C.
(35)
Отметим также то, что все функции Y (t, λ), Z(t, λ), Z′t(t, λ), Z′′tt(t, λ) являются целыми по
переменным t и λ, разложимыми в степенные ряды наподобие (14), (15).
Теперь, сочетая функцию Z(t, λ) из формулы (32) и функцию u(t) - первый компонент
выбранного решения (u(t), g), определим векторную целую функцию
∫T
f (λ) = Z(t, λ)u(T - t) dt, λ ∈ C.
(36)
0
Поскольку поведение u(t) вблизи границ отрезка [0, T ] может в определённом смысле “пор-
титься” (см. условия (4)), возьмём малое ε > 0 и рассмотрим аппроксимацию
∫
fε(λ) =
Z(t, λ)u(T - t) dt, λ ∈ C.
(37)
ε
Тогда
∫
∫
T
fε(λ) =
Z(t, λ)u(T - t) dt → Z(t, λ)u(T - t) dt = f(λ)
(38)
ε
0
при ε → 0 + 0 для любого фиксированного λ ∈ C. В предельном переходе (38) используется
то, что u ∈ C([0, T ], E) по определению ослабленного решения (4).
Напомним также, что u(t) ∈ D(A) при 0 < t < T и Au ∈ C((0, T ), E) с линейным замкну-
тым оператором A. Поэтому, согласно известным свойствам векторного интеграла Римана,
получаем, что fε(λ) ∈ D(A) для любого λ ∈ C, и вычисление Afε(λ) можно проводить
внесением оператора A под знак интеграла в (37) (см. [21, теорема 3.3.2]).
С учётом уравнения (1) имеем
∫
∫
∫
Afε(λ) =
Z(t, λ)Au(T - t) dt =
Z(t, λ)u′′(T - t) dt - g
Z(t, λ) dt.
(39)
ε
ε
ε
Последний “скалярный” интеграл в (39) допускает предельный переход
∫
∫
Z(t, λ) dt =
Y ′t(t,λ)dt = Y (T - ε,λ) - Y (ε,λ) → L(λ)
(40)
ε
ε
при ε → 0 + 0 для любого фиксированного λ ∈ C. В выкладке (40) использована связь (32)
с соотношениями (31).
Предшествующий “нескалярный” интеграл в (39) обрабатывается чуть сложнее. Проинте-
грируем два раза по частям
∫
∫
ε
Z(t, λ)u′′(T - t) dt = (Z(t, λ)u′(T - t) + Z′t(t, λ)u(T - t))
+ Z′′tt(t,λ)u(T - t)dt.
T-ε
ε
ε
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
897
При ε → 0 + 0 внеинтегральное слагаемое обращается в нуль. Действительно, с учётом дей-
ствующих условий (6) и (35), а также того, что u ∈ C1([0, T ], E), имеем
Z(ε, λ)u′(T -ε)+Z′t(ε, λ)u(T -ε)-Z(T -ε, λ)u′(ε)-Z′t(T -ε, λ)u(ε) → βu′(T )+αu(T )-0-0 = 0.
Затем, принимая во внимание связь Z′′tt(t, λ) = λZ(t, λ) (см. (34)), замечаем, что
∫
∫
∫
T
Z′′tt(t,λ)u(T - t)dt = λ
Z(t, λ)u(T - t) dt = λfε(λ) → λf(λ) = λ Z(t, λ)u(T - t) dt
ε
ε
0
при ε → 0 + 0 для любого фиксированного λ ∈ C (здесь f(λ), fε(λ) - векторные целые
функции из формул (36), (37) соответственно). В результате имеем соотношение
T
∫
∫
Z(t, λ)u′′(T - t) dt → 0 + λ Z(t, λ)u(T - t) dt = λf(λ)
(41)
ε
0
при ε → 0 + 0 для любого фиксированного λ ∈ C.
Теперь можем положить ε → 0 + 0 в формуле (39). Учитывая замкнутость оператора A,
а также соотношения (38), (40), (41), выводим из (39), что f(λ) ∈ D(A) при всех λ ∈ C и
Af(λ) = λf(λ) - L(λ)g, λ ∈ C.
(42)
Это основное операторное тождество для функции f(λ) из формулы (36). Напомним, что
векторная целая функция f(λ) определяется первым компонентом u(t) решения (u(t), g)
однородной обратной задачи (1), (6). Второй компонент g ∈ E, умноженный на характери-
стическую функцию L(λ) из формулы (17), входит в правую часть (42).
Равенство (42) можно дифференцировать по λ, внося производные под знак линейного
замкнутого оператора A. Последовательное дифференцирование приводит к тождествам
Af(m)(λ) = λf(m)(λ) + mf(m-1)(λ) - L(m)(λ)g, λ ∈ C,
(43)
верным при всех m ∈ N. При m = 0 формула (43) вновь обращается в тождество (42).
Воспользуемся теперь нашим базовым предположением о том, что ни один нуль характе-
ристической функции L(λ) не является собственным значением оператора A.
Допустим, например, что L(λ0) = 0 в точке λ0 ∈ C. Тогда подстановка λ = λ0 в тождест-
во (42) даёт результат Af(λ0) = λ0f(λ0). Отсюда, в силу упомянутого базового предположе-
ния, выводим, что f(λ0) = 0. Это означает, что в действующих условиях всякий нуль харак-
теристической функции L(λ) из формулы (17) будет нулём векторной целой функции f(λ),
определённой по формуле (36). Более того, если λ = λ0 - нуль кратности k ≥ 2 для L(λ),
то L(m)(λ0) = 0 при m = 0, . . . , k - 1, и последовательное применение формулы (43) показы-
вает, что f(m)(λ0) = 0 при m = 0, . . . , k - 1.
Зафиксируем установленный факт: при сделанном предположении всякий нуль характе-
ристической функции L(λ) из формулы (17) является нулём не меньшей кратности∗) для
векторной целой функции f(λ) из формулы (36). Другими словами, отношение
T
∫
f (λ)
1
=
Z(t, λ)u(T - t) dt
(44)
L(λ)
L(λ)
0
определяет векторную целую функцию переменной λ ∈ C.
∗) Как станет ясно в дальнейшем (см. п. 8 ниже), обычно все нули функции L(λ) являются простыми,
и лишь при некоторых специальных сочетаниях параметров α, β ∈ C \ {0} и T > 0 характеристическая
функция (17) имеет также один нуль кратности два. Иначе говоря, хотя кратных нулей у L(λ) почти никогда
не бывает, их потенциальную возможность всё же приходится учитывать.
3
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
898
ТИХОНОВ, АЛМОХАМЕД
Выведем отсюда, что u(t) ≡ 0 при 0 ≤ t ≤ T. Неформальную идею последующих рас-
суждений дал нам пример 200 из известного задачника [22; отд. 4, гл. 3, § 5]. Этот пример
был разобран в [22] со ссылкой на Карлемана. Для применения идеи в нашей ситуации схему
Карлемана пришлось видоизменить.
6. Продолжение доказательства: принцип Фрагмена-Линделёфа. Поскольку пред-
стоит активная работа с целыми функциями, удобно перейти полностью к скалярному случаю.
Возьмём линейный непрерывный функционал f∗ из сопряжённого банахова пространства E∗
и подействуем им на векторные компоненты в (44).
Обозначим F (λ) ≡ f∗(f(λ)) при λ ∈ C и ψ(t) ≡ f∗(u(t)) при 0 ≤ t ≤ T. Тогда, согласно
формуле (36), имеем
∫T
F (λ) = Z(t, λ)ψ(T - t) dt, λ ∈ C.
(45)
0
При взятии функционала f∗ нули функции f(λ) не исчезают, а их кратности не уменьшаются.
Отсюда заключаем, что отношение
F (λ)
f∗(f(λ))
Q(λ) ≡
=
(46)
L(λ)
L(λ)
определяет целую функцию переменной λ ∈ C (ср. (46) с прежним отношением (44)). Для
нужных оценок дроби (46) перепишем её числитель F (λ) в виде, отличном от (45).
Вспомним сначала, что Z(t, λ) = Y′t(t, λ), где Y (0, λ) ≡ 0 (см. формулу (32), а затем (31)).
Для функции ψ(t) ≡ f∗(u(t)) отметим соотношения
ψ ∈ C1[0,T], ψ(0) = 0,
(47)
выполненные согласно (4) и (6). (Из (6) также следует, что ψ′(0) = 0 и αψ(T ) + βψ′(T ) = 0,
но эти равенства уже не понадобятся.) Применив сказанное к интегралу (45), получаем, что
∫T
∫
T
F (λ) = Y′t(t, λ)ψ(T - t) dt = Y (t, λ)ψ′(T - t) dt, λ ∈ C,
(48)
0
0
где Y (T, λ)ψ(0) - Y (0, λ)ψ(T ) ≡ 0 из-за значений ψ(0) = 0 и Y (0, λ) ≡ 0.
Теперь преобразуем запись функции Y (t, λ). Исходя из определения (30), имеем
( t )2ch(√(t/T)2λT) - 1
(t
)sh(√(t/T)2λT)
Y (t, λ) = α
+β
√
T
(t/T )2λ
T
(t/T )2λ
Последующее сравнение с элементарными функциями (16) даёт выражение
Y (t, λ) = α(t/T )2L1((t/T )2λ) + β(t/T )L2((t/T )2λ),
0 ≤ t ≤ T, λ ∈ C.
(49)
Подставим (49) в интеграл (48) и сделаем там замену s = t/T. Получим представление
∫1
F (λ) = (αs2L1(λs2) + βsL2(λs2))η′(1 - s) ds, λ ∈ C,
(50)
0
где η(s) ≡ ψ(T s), η′(s) = T ψ′(T s) и η′(1 - s) = T ψ′(T - T s) при 0 ≤ s ≤ 1. Из (47)
следует, что
η ∈ C1[0,1], η(0) = 0.
(51)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
899
Представление (50) с функцией η(s) типа (51) используем при анализе отношения (46), со-
ставленного из функций F (λ) и L(λ) = αL1(λ) + βL2(λ).
Напомним (см. [19, 20]), что монотонные при r > 0 характеристики
M (F ; r) ≡ max|F (λ)|, M(L1; r) ≡ max|L1(λ)|, M(L2; r) ≡ max |L2(λ)|
|λ|=r
|λ|=r
|λ|=r
отражают рост целых функций F (λ), L1(λ), L2(λ) на плоскости C. Основываясь на (50),
запишем оценку
M (F ; r) ≤ Cη(|α|M(L1; r) + |β|M(L2; r)), r > 0,
(52)
с константой
∫1
Cη ≡
|η′(s)| ds = Var {η(s)}|10.
(53)
0
Элементарные функции (16), т.е. функции L1(λ), L2(λ), имеют порядок ρ = 1/2, а их ха-
рактеристики M(L1; r), M(L2; r) при r ≥ 1 оцениваются сверху через exp(√rT). Подставив
данную мажоранту в (52), получим, что и F (λ) не может расти быстрее, чем целая функция
порядка ρ = 1/2. Тот же характер роста имеет целая функция L(λ) = αL1(λ) + βL2(λ).
Но тогда по теореме о категориях (см. [19; с. 37]) рост целой функции Q(λ), задаваемой
отношением (46), не может быть выше, чем у функции порядка ρ = 1/2. В частности, заведо-
мо можем утверждать, что Q(λ) есть целая функция нулевого экспоненциального типа, т.е.
такая, что ln M(Q; r) = o(r) при r → +∞.
Оценим Q(λ) ≡ F (λ)/L(λ) на мнимой оси. Обозначим λ = iτ, где τ ∈ R, и используем
характеристики V1(τ), V2(τ) из формулы (20). Учитывая их строгую монотоность, действу-
ющую при возрастании |τ| ≥ 0 (см. лемму 2), выводим из (50), что
|F (iτ)| ≤ Cη(|α|V1(τ) + |β|V2(τ)), τ ∈ R,
(54)
с той же константой Cη вида (53). Согласно лемме 3 величина V (τ) ≡ |L(iτ)| строго поло-
жительна при достаточно больших |τ| > 0. Поэтому с учётом (54) можем корректно оценить
|F (iτ)|
|α|V1(τ) + |β|V2(τ)
|Q(iτ)| =
≤Cη
(55)
|L(iτ)|
V (τ)
при тех же достаточно больших |τ| > 0. Снова по лемме 3, если |τ| → ∞, то дробь в пра-
вой части (55) стремится к единице. Следовательно, непрерывная величина |Q(iτ)| является
ограниченной при τ ∈ R, или, другими словами, целая функция нулевого экспоненциального
типа Q(λ) оказывается ограниченной на мнимой оси. В силу известного варианта теоремы
Фрагмена-Линделёфа (см. [19; с. 71]) такая функция может быть только константой.
Итак, получили, что Q(λ) ≡ C в плоскости C. Но тогда F (λ) = CL(λ) при всех λ ∈ C
с некоторой константой C ∈ C. Используя представление (50), запишем
1
∫
(αs2L1(λs2) + βsL2(λs2))η′(1 - s) ds = C(αL1(λ) + βL2(λ)), λ ∈ C.
(56)
0
Покажем, что тождество (56) с функцией η(s), удовлетворяющей требованиям (51), возможно,
только если C = 0 и η(s) ≡ 0 при 0 ≤ s ≤ 1.
7. Завершение доказательства: теорема Мюнца. Проанализируем тождество (56),
выполненное при всех λ ∈ C с некоторой константой C ∈ C. Используя явные формулы (16)
(см. также (14) и (15)), разложим в степенные ряды
(
)
(
)
∑
∑
T2n+2
T2n+1
αT
T2n+1
αL1(λ) + βL2(λ) =
α
+β
λn =
+β
λn,
(2n + 2)!
(2n + 1)!
2n + 2
(2n + 1)!
n=0
n=0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
3∗
900
ТИХОНОВ, АЛМОХАМЕД
(
)
∑
s2n+2 T2n+2
s2n+1 T2n+1
αs2L1(λs2) + βsL2(λs2) =
α
+β
λn =
(2n + 2)!
(2n + 1)!
n=0
(
)
∑
s2n+2
T2n+1
=
αT
+ βs2n+1
λn.
2n + 2
(2n + 1)!
n=0
Подставим эти разложения в (56) и приравняем коэффициенты при одинаковых степенях λ.
С учётом очевидных сокращений на T2n+1/(2n+1)! получим счётный набор соотношений
∫
1
(
)
(
)
s2n+2
αT
αT
+ βs2n+1 η′(1 - s)ds = C
+ β , n = 0,1,2,...
(57)
2n + 2
2n + 2
0
Модуль интеграла в равенстве (57) мажорируется величиной
(
)
1
1
|α|T
+ |β|
max |η′(s)|,
(2n + 2)(2n + 3)
2n + 2
0≤s≤1
стремящейся к нулю при n → ∞. Но тогда и сам интеграл стремится к нулю при n → ∞.
Тем самым, переходя к пределу в (57), получаем при n → ∞ что 0 = Cβ. Здесь β = 0 по
условию. Поэтому C = 0.
Подставив найденное значение C в (57), получим соотношения
∫
1
(
)
s2n+2
αT
+ βs2n+1 η′(1 - s)ds = 0, n = 0,1,2,...
(58)
2n + 2
0
Заметим, что
∫
1
∫
1
∫
1
s2n+2
s2n+2
0
η′(1 - s)ds =
η(1 - s)
+ s2n+1η(1 - s)ds = s2n+1η(1 - s)ds
2n + 2
2n + 2
1
0
0
0
с учётом значения η(0) = 0 (см. (51)). Такое преобразование в (58) даёт результат
1
∫
(αT η(1 - s) + βη′(1 - s))s2n+1 ds = 0, n = 0, 1, 2, . . .
(59)
0
Полученное возможно, только если
αT η(1 - s) + βη′(1 - s) ≡ 0,
0 ≤ s ≤ 1.
(60)
Факт (60) выводится из (59) разными способами, но проще сразу воспользоваться теоремой
Мюнца, утверждающей в своей слабой редакции∗), что если непрерывная функция ортого-
∑∞
нальна на [0, 1] системе степеней {san }∞n=0, где 0 < a0 < a1 < . . . < +∞ и
a-1n = +∞,
n=0
то функция тождественно равна нулю на [0, 1] (см. номер 198 в [22; с. 44] или [23; с. 304-305];
см. также [24; с. 109] и [25; с. 116, 122-124]).
Итак, установлено соотношение (60). Оно очевидно эквивалентно обыкновенному диффе-
ренциальному уравнению η′(s) + (αT/β)η(s) = 0 при 0 ≤ s ≤ 1, к которому, согласно (51),
∗) Более известна сильная версия теоремы Мюнца о плотности линейных комбинаций степеней в простран-
ствах типа C[0, 1] или Lp[0, 1]. Отметим для точности, что в оригинальной работе Мюнца [23] рассматривался
лишь классический вариант пространства C[0, 1]. Но случай Lp оказался идейно близок, и перенесённый туда
результат тоже стали называть теоремой Мюнца (см., например, [24; гл. 3, § 6]).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
901
надо добавить начальное условие η(0) = 0. Отсюда следует, что η(s) ≡ 0 при 0 ≤ s ≤ 1.
Вспомнив связь η(s) ≡ ψ(T s) при 0 ≤ s ≤ 1, заключаем, что функция ψ(t) ≡ f∗(u(t))
тождественно равна нулю всюду на [0, T ]. Выбор функционала f∗ ∈ E∗ был произвольным,
поэтому на основании известного следствия теоремы Хана-Банаха (см. [21; теорема 2.7.4]) мо-
жем утверждать, что u(t) ≡ 0 при 0 ≤ t ≤ T. Подстановка такой функции в уравнение (1)
показывает, что g = 0.
Подведём итог: при сделанном предположении (о том, что ни один нуль характеристиче-
ской функции (17) не является собственным значением оператора A) неизбежно получаем,
что решение (u(t), g) однородной обратной задачи (1), (6) может быть только тривиальным.
Критерий единственности решения в форме теоремы 2 полностью доказан. Отсюда автомати-
чески следует теорема 1. Обоснование главного результата завершено.
8. Нули характеристической функции: общие сведения. Теперь для применения
установленного критерия требуется информация о распределении нулей характеристической
функции L(λ) = L(λ; T, α, β) из формулы (17). Уделим этому вопросу особое внимание.
Как и в формуле (18), рассматриваем множество Λ = Λ(T, α, β) ≡ {λ ∈ C: L(λ) = 0}.
Опишем его состав в зависимости от выбора параметров T > 0 и α, β ∈ C \ {0}. Специально
подчеркнём, что соглашение α = 0, β = 0 действует далее без оговорок - при обращении
в нуль одного из коэффициентов ситуация сразу упрощается и конкретный вид множества Λ
находится элементарным образом.
Действительно, если взять α = 0, β = 0 (как для финального переопределения первого
рода), то L(λ) = αL1(λ) с функцией L1(λ) = L1(λ; T ) из формулы (16) и
Λ(T, α, 0) = Λ(T, 1, 0) ≡ {λ ∈ C: L1(λ) = 0} = {-4k2π2/T2}k∈N,
(61)
причём все нули в множестве (61) имеют кратность два (см. также [4]). В свою очередь если
взять α = 0, β = 0 (как для финального переопределения второго рода), то L(λ) = βL2(λ)
с функцией L2(λ) = L2(λ; T ) из формулы (16) и
Λ(T, 0, β) = Λ(T, 0, 1) ≡ {λ ∈ C: L2(λ) = 0} = {-m2π2/T2}m∈N,
(62)
причём все нули в множестве (62) являются простыми (см. также [5]). Любопытная особен-
ность - присутствие в обоих множествах (61) и (62) общей серии нулей (-4k2π2/T2), взятых
при k ∈ N, сохранится и при рассмотрении финального переопределения третьего рода со
значениями α = 0, β = 0. Сосредоточимся сейчас именно на этом случае.
Используем элементарные формулы ch a - 1 = 2 sh2(a/2) и sh a = 2 sh (a/2) ch (a/2). С их
помощью для функций (16) запишем
√
√
√
√
L1(λ) = (2/λ)sh2(
λT/2), L2(λ) = (2/
λ) sh (
λT/2) ch (
λT/2).
Отсюда видно, что характеристическая функция (17) допускает альтернативное представление
√
(
√
√
)
2
λT
α
λT
λT
L(λ) =
√
sh
√
sh
+ β ch
= G1(λ)G2(λ),
(63)
λ
2
λ
2
2
т.е. функция L(λ) = αL1(λ) + βL2(λ) распадается в произведение двух целых функций
√
2
λT
G1(λ) = G1(λ;T) ≡
√
sh
,
(64)
λ
2
√
√
α
λT
λT
G2(λ) = G2(λ;T,α,β) ≡
√
sh
+ β ch
(65)
λ
2
2
переменной λ ∈ C. Тем самым множество нулей характеристической функции L(λ) оказыва-
ется составленным из множества нулей функции (64) и множества нулей функции (65).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
902
ТИХОНОВ, АЛМОХАМЕД
Удобно сократить число параметров и ввести стандартизированные функции
2
√ζ
H1(ζ) ≡
,
(66)
√ζsh
2
2
√ζ
√ζ
H2(ζ) = H2(ζ;p) ≡
+ pch
(67)
√ζsh
2
2
переменной ζ ∈ C. В записи (67) остался единственный параметр p ∈ C \ {0}. Очевидно, что
G1(λ;T) = TH1(λT2), G2(λ;T,α,β) = (αT/2)H2(λT2;2β/(αT)).
(68)
Поэтому характеристическая функция (17) представима в виде
L(λ) = L(λ; T, α, β) = cH1(λT2)H2(λT2; p),
(69)
где
c = αT2/2, p = 2β/(αT).
(70)
Условия (70) обеспечивают эквивалентность представлений (63) и (69) для L(λ).
Формулы перехода (68) показывают, что нули функций G1(λ), G2(λ) связаны с нулями
соответствующих функций H1(ζ), H2(ζ) преобразованием подобия λ = ζ/T2, сохраняющим
не только все геометрические соотношения нулей, но и их кратности.
Завершим этот первичный разбор ситуации следующим базовым утверждением.
Теорема 3. Множество нулей характеристической функции L(λ) вида (17) или, что
эквивалентно, вида (63) состоит из двух счётных серий. Первая универсальная серия нулей
λ(1)k = -4k2π2/T2, k ∈ N,
(71)
отвечает множителю (64) и не зависит от выбора значений α,β ∈ C \ {0}. Вторая серия
нулей отвечает множителю (65) и может быть записана в виде
λ(2)k = ζk/T2, k ∈ J,
(72)
где ζk = ζk(p) - нули элементарной целой функции (67) с параметром p = 2β/(αT ). Нуме-
рация k ∈ J = J(p) ⊂ Z в (72) может зависеть от значения p ∈ C \ {0}. Множества (71)
и (72) не пересекаются, т.е. ни один нуль функции (64) не является нулём функции (65).
Доказательство. Все корни уравнения sh (a/2) = 0 на плоскости C выражаются фор-
мулой ak = 2kπi, где k ∈ Z. При этом ch (ak/2) = cos kπ = 0. Отсюда, во-первых, следует,
что все нули функции (64) имеют вид (71) с указанной там нумерацией k ∈ N, а, во-вторых,
что ни один такой нуль λ(1)k не может быть нулём функции (65).
В то же время функция G2(λ) = G2(λ; T, α, β) вида (65) как целая функция нецелого
порядка ρ = 1/2 имеет бесконечное (счётное) множество нулей. Эти нули, учитывая вто-
рую связь в (68), можно формально записать в виде (72) через нули стандартизированной
функции (67). Вопрос о наиболее удобной нумерации k ∈ J в множестве таких нулей должен
уточняться отдельно. Теорема доказана.
√
√
Как видим, наличие общего множителя (2/
λ) sh (
λT/2) приводит к тому, что серия ну-
лей (71) оказывается общей для всех трёх функций L1(λ), L2(λ) и L(λ) = αL1(λ) + βL2(λ).
Тем самым (см. теорему 1) отсутствие среди чисел (71) собственных значений оператора A
есть необходимое условие единственности решения изучаемой обратной задачи (1)-(3) с фик-
сированным T > 0 при любом выборе параметров α, β ∈ C\{0} (см. также работы [4] и [5] про
случаи α = 0, β = 0 и α = 0, β = 0 соответственно). Эта особенность изучаемой обратной
задачи представляется весьма оригинальной.
Обсудим теперь вопрос о кратности нулей характеристической функции L(λ). Использу-
ем представление L(λ) = G1(λ)G2(λ) с функциями (64), (65). Поскольку, согласно теореме 3,
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
903
множества нулей указанных сомножителей не пересекаются, вопрос о кратных нулях доста-
точно рассмотреть отдельно для G1(λ) и G2(λ), точнее даже, для их регуляризированных
аналогов - функций H1(ζ) и H2(ζ) из формул (66) и (67) соответственно.
Вопрос об отсутствии кратных нулей у функции H1(ζ) решается просто. Имеем
(
2
√ζ
1
√ζ
2
√ζ)
H1(ζ) ≡
,
H′1(ζ) ≡
ch
-
√ζsh
2
2ζ
2
√ζsh
2
Как уже отмечалось при доказательстве теоремы 3, величины sh (a/2) и ch (a/2) никогда
одновременно не обращаются в нуль. Отсюда следует, что соотношение H1(ζ) = H′1(ζ) = 0
невозможно ни в какой точке ζ ∈ C.
Рассмотрим теперь функцию H2(ζ) = H2(ζ; p) с параметром p ∈ C \ {0}. Картина с её
кратными нулями оказывается довольно неожиданной. В решении поставленной задачи важ-
ную роль играют комплексно сопряжённые корни уравнения
sh z = z,
(73)
расположенные в полуплоскости Re z > 0. Множество таких корней запишем в виде
z = zn, n ∈ Z \ {0}, z-n = zn.
(74)
Считаем, что основная серия корней z = zn при n ∈ N расположена в первом координатном
угле Re z > 0, Im z > 0 и занумерована в порядке возрастания модулей.
Следующий результат получен авторами совместно с В.Б. Шерстюковым.
Теорема 4. Рассматриваем функцию H2(ζ; p) вида (67) с параметром p ∈ C \ {0}. Опре-
делим счётное множество значений
2
pn = -
,
n ∈ Z \ {0}, p-n = pn,
(75)
1 + chzn
где zn - корни (74) трансцендентного уравнения (73), попадающие в полуплоскость Re z > 0.
Тогда справедливы утверждения:
1. При каждом p ∈ C \ {0}, не входящем в множество (75), функция H2(ζ; p) имеет
только простые нули.
2. При p = pn из множества (75) функция H2(ζ; pn) помимо бесконечного числа простых
нулей имеет ровно один кратный нуль кратности два, который находится по формуле
ζ =z2n
(76)
с тем же zn из множества (74), что и при выборе параметра pn = -2/(1 + ch zn).
Добавим ещё, что при n ∈ N значения pn из формулы (75) попадают в область
-2 < Re p < 0,
0 < Imp < 1,
(77)
причём pn → 0 при n → ∞. Как следствие, при всех номерах n ∈ Z \ {0} значения pn не
могут быть вещественными.
Подробное доказательство теоремы 4 и обсуждение сопутствующих обстоятельств будет
дано отдельно (см. также [26, 27]). Сейчас отметим лишь, что все величины из теоремы 4
допускают эффективное исследование с выводом необходимых оценок, представляющих инте-
рес как для математической физики, так и для теории функций. В частности, уравнение (73)
посредством замены z = iξ с переменной ξ ∈ C приводится к виду
sin ξ = ξ.
(78)
Последнее встречается в спектральной теории при рассмотрении ряда задач механики сплош-
ной среды (см., например, [28-30]). С аналитической точки зрения уравнение (78) рассмат-
ривал ещё Харди [31]. Простой и понятный разбор ситуации, связанной с корнями подобных
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
904
ТИХОНОВ, АЛМОХАМЕД
уравнений, дал Маркушевич [32; c. 64-68]. Основываясь на его изложении, получаем прибли-
жённую формулу
(
)
1
π
1
zn ≈ ln(4nπ) +
+i
2nπ +
-
ln(4nπ)
(79)
4n
2
2nπ
для основной серии корней “нашего” уравнения (73). Родственный вариант, восходящий к ра-
боте Харди [31], имеет вид (см. [29; с. 392])
(
)
π
2
zn = ln((4n + 1)π) + δn + i
2nπ +
-
ln((4n + 1)π) + εn
(80)
2
(4n + 1)π
Отдельно показывается, что приближения (79) и (80) согласованы с нумерацией n∈N (см. [31]).
Высокую точность таких соотношений подтверждают следующие оценки В.Б. Шерстюкова:
2
4
0<δn <
ln2((4n + 1)π),
|εn| <
ln3((4n + 1)π),
(4n + 1)2π2
(4n + 1)3π3
действующие при всех номерах n ∈ N для остатков δn, εn ∈ R в формуле (80). Используя
информацию о корнях уравнения (73), можно весьма точно оценить величины (75), (76) из
теоремы 4 и указать для них ряд полезных аналитических соотношений. Здесь применимы
также методы компьютерной математики.
Упомянем, к примеру, что область (77), где локализуются значения pn при n ∈ N, по-
лучена из общих соображений, связанных с действием отображения pn = -2/(1 + ch zn) на
корни уравнения (73), расположенные в первом координатном угле. Однако, как показывает
численный расчёт, можно, не погрешив против истины, заменить множество (77) гораздо более
точным прямоугольником -0.11 < Re p < 0, 0 < Imp < 0.22.
Вернёмся к рассмотрению характеристической функции L(λ) = L(λ; T, α, β). Используем
представление (69) с параметром p = 2β/(αT ), заданным согласно (70). Проделанный анализ
позволяет утверждать, что в большинстве ситуаций, т.е. в случае общего положения, все нули
функции L(λ) = L(λ; T, α, β) являются простыми. Исключение составляют редкие примеры,
когда параметры α, β ∈ C \ {0} и T > 0 связаны специальным соотношением
αT + (1 + ch zn)β = 0
(81)
с некоторым корнем zn из множества (74) (ср. (81) с формулой (75) из теоремы 4). При
таком условии функция L(λ) = L(λ; T, α, β) помимо бесконечного числа простых нулей имеет
единственный нуль кратности два, и он находится по формуле λ = z2n/T2 с тем же значением
zn, что и в (81) (ср. формулу (72) с формулой (76) из теоремы 4).
Согласно теореме 4 значения 1 + ch zn = -2/pn не могут быть вещественными. Поэтому
соотношение (81) невозможно, если α, β ∈ R \ {0}. Отсюда получаем такое утверждение.
Теорема 5. При любом выборе параметров α, β ∈ R \ {0} и T > 0 все нули характери-
стической функции L(λ) = L(λ; T, α, β) из формулы (17) являются простыми.
Выбор вещественных параметров α и β в условии (3) является, безусловно, приоритет-
ным. Сосредоточимся именно на этом случае. Дополним теорему 5 следующим результатом.
Теорема 6. При любом выборе параметров α, β ∈ R \ {0} и T > 0 все нули характери-
стической функции L(λ) = L(λ; T, α, β) из формулы (17) являются вещественными.
Доказательство. С учётом основной теоремы 3 достаточно установить, что все нули ζk
стандартизированной функции (67) при любом выборе параметра p ∈ R \ {0} являются веще-
ственными. Зафиксируем значение p ∈ R \ {0} и рассмотрим скалярную задачу
4y′′(τ) - ζy(τ) = 0,
0 ≤ τ ≤ 1, y(0) = 0, y(1) + py′(1) = 0
(82)
со спектральным параметром ζ ∈ C. С точностью до умножения на константу решение диф-
ференциального уравнения из системы (82), удовлетворяющее первому условию y(0) = 0,
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
905
имеет вид y(τ) = (2/√ζ)sh (√ζτ/2). После подстановки данной функции во второе краевое
условие y(1) + py′(1) = 0 приходим к уравнению
2
√ζ
√ζ
+ pch
=0
(83)
√ζsh
2
2
относительно неизвестной ζ ∈ C. Корни уравнения (83) те же, что нули целой функции (67) -
они совпадают со спектральными значениями задачи (82). Но спектр в задаче (82) может быть
только вещественным.
Действительно, исходя из (82), введём оператор B = 4d2/dτ2 в линейном вещественном
пространстве C[0, 1] на области определения Dp ≡ {y ∈ C2[0, 1]: y(0) = 0, y(1) + py′(1) = 0}.
Используем в C[0, 1] скалярное произведение
∫1
(y1, y2) = y1(τ)y2(τ) dτ, (y, y) ≡ ∥y∥2.
0
Стандартное интегрирование по частям показывает симметричность оператора B в том смыс-
ле, что (By1, y2) = (y1, By2) для любых y1, y2 ∈ Dp. Как известно, такой оператор не может
иметь комплексных собственных значений ζ = γ1 + iγ2, γ1, γ2 ∈ R, γ2 = 0.
В самом деле, предположим, что B(y1 +iy2) = (γ1 +iγ2)(y1 +iy2) с некоторыми y1, y2 ∈ Dp,
т.е. By1 = γ1y1 - γ2y2 и By2 = γ1y2 + γ2y1. Тогда вычисление числа (By1, y2) = (y1, By2) даёт
равенство
γ1(y1,y2) - γ2(y2,y2) = γ1(y1,y2) + γ2(y1,y1) ∼ γ2(∥y1∥2 + ∥y2∥2) = 0.
Но если γ2 = 0, то y1(τ) ≡ 0 и y2(τ) ≡ 0 всюду на [0, 1].
Итак, ни сам оператор B, ни ассоциированная с ним спектральная задача (82) не могут
иметь комплексных (невещественных) собственных значений. Следовательно, корни уравне-
ния (83) и совпадающие с ними нули целой функции (67) будут исключительно веществен-
ными. Возвращаясь к исходной характеристической функции (17) (и учитывая теорему 3),
получаем утверждение теоремы 6. Доказательство завершено.
Подытожим: при любом выборе значений α, β ∈ R \ {0} все без исключения нули харак-
теристической функции L(λ) = L(λ; T, α, β) являются вещественными и простыми. Для того
чтобы завершить описание таких нулей, осталось, согласно теореме 3, в зависимости от пара-
метра p = 2β/(αT ) ∈ R \ {0} указать зоны локализации чисел ζk из формулы (72), или, что
то же самое, зоны локализации нулей ζk = ζk(p) ∈ R стандартизированной функции H2(ζ; p)
из формулы (67).
9. Подробно про зоны локализации. Разбор начнём в эквивалентных терминах - на
языке корней уравнения (83). При этом для лучшего понимания динамики корней в зависи-
мости от параметра p рассмотрим все значения p ∈ R, включая p = 0.
Случай p = 0 является особым, так как тогда корни уравнения (83) совпадают с нулями
(простыми нулями) функции H1(ζ) из формулы (66) и имеют вид ζk = -4k2π2 при k ∈ N.
Ещё один особый случай связан с возможным корнем ζ = 0. Подстановка такого числа
в уравнение (83) даёт соотношение 1 + p · 1 = 0, откуда очевидно, что ζ = 0 является корнем
для (83) тогда и только тогда, когда p = -1.
Приступим к изучению случая “общего положения”. Поскольку при p ∈ R корни урав-
нения (83) могут быть только вещественными, всюду в данном пункте считаем, что ζ ∈ R.
Используем замену
{
4μ2,
μ ≥ 0,
ζ =
(84)
−4μ2,
μ < 0.
Формула (84) задаёт биекцию, точнее, сохраняющий порядок изотонный гомеоморфизм между
прямой μ ∈ R и прямой ζ ∈ R. Уравнение (83) перейдёт в эквивалентную совокупность
[
(1/μ) sh μ + p ch μ = 0, μ ≥ 0,
(85)
(1/μ) sin μ + p cos μ = 0, μ < 0.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
906
ТИХОНОВ, АЛМОХАМЕД
Вновь видим, что корень μ = 0, соответствующий прежнему ζ = 0, возникает в (85) лишь
при p = -1. Временно исключим μ = 0 из рассмотрения. Тогда при μ ∈ (-∞, 0)
⋃ (0, +∞)
совокупность (85) приводится к следующему эквивалентному виду:
[
pμ = -th μ, μ > 0,
(86)
pμ = -tg μ, μ < 0.
Полученные уравнения проанализируем графически (рисунок).
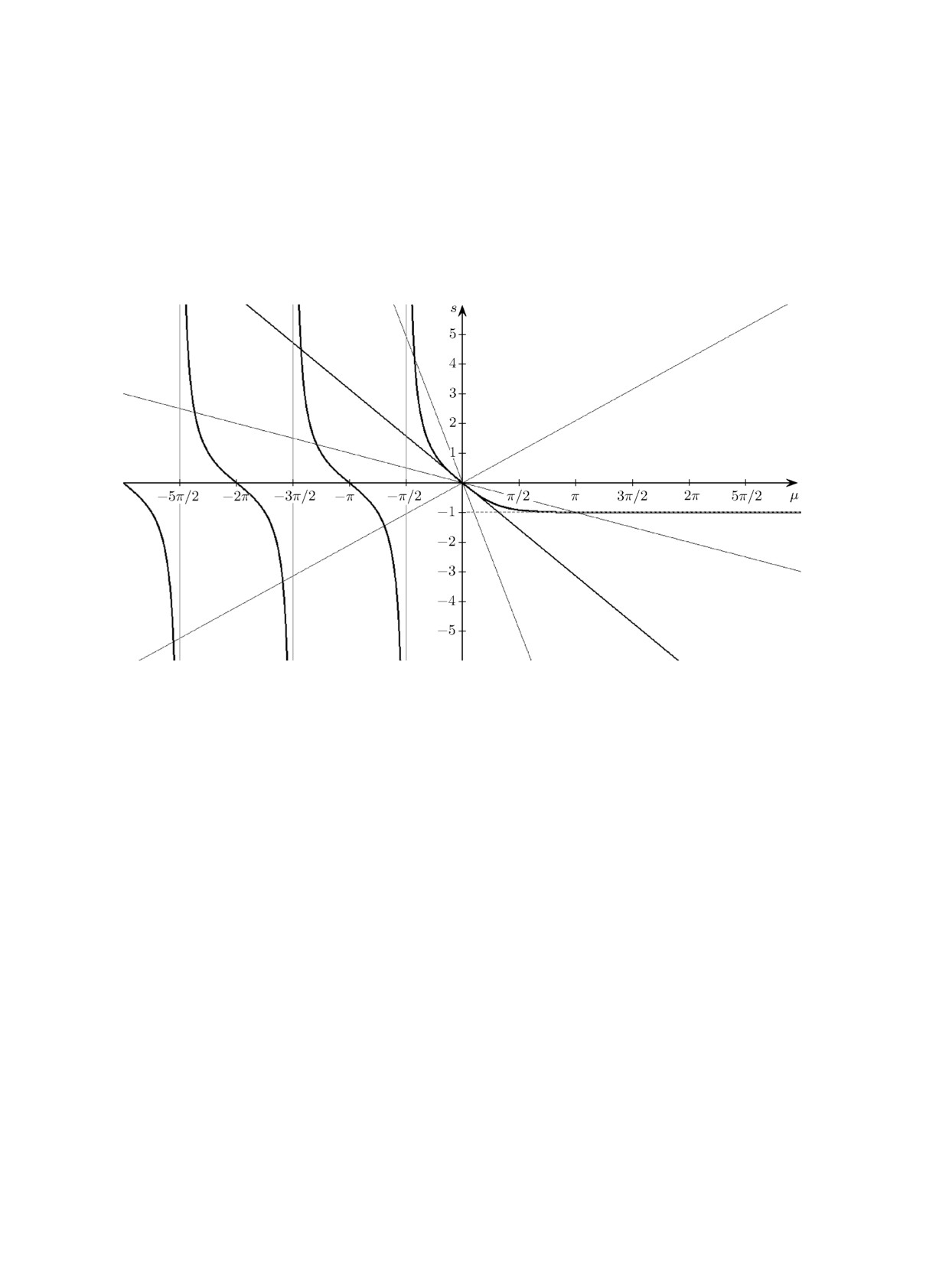
Рисунок. Геометрический анализ совокупности уравнений (86).
Введём вспомогательную функцию Φ(μ), составленную из счётного числа ветвей ϕk(μ)
следующим образом. Особая нулевая ветвь ϕ0(μ) определяется на множестве (-π/2, +∞) по
формулам ϕ0(μ) = -tg μ при μ ∈ (-π/2, 0) и ϕ0(μ) = -th μ при μ ∈ [0, +∞). Ясно, что
это непрерывная (точнее, непрерывно дифференцируемая), строго убывающая, выпуклая вниз
функция на (-π/2, +∞). Затем, при k ∈ N, положим ϕk(μ) = -tg μ на соответствующих
промежутках μ ∈ (-(2k + 1)π/2, -(2k - 1)π/2).
Рассмотрим графики функций s = Φ(μ) и s = pμ. Абсциссы их точек пересечения на мно-
жестве μ ∈ (-∞, 0)
⋃ (0, +∞) как раз дадут все корни, возникающие в (86). Для того чтобы
вернуться к исходной совокупности (85), добавим корень μ = 0, отвечающий единственно-
му значению параметра p = -1. При таком p секущая s = pμ к нулевой ветви s = ϕ0(μ)
перейдет в прямую s = -μ, касающуюся этой ветви в точке μ = 0.
В результате получаем счётное множество корней μk = μk(p), непрерывно зависящих от
параметра p ∈ R. Точнее, особый корень μ0 = μ0(p) определён лишь при p ∈ (-∞, 0) - он
соответствует ветви ϕ0(μ) и непрерывно возрастает с ростом p. Так, при p ∈ (-∞, -1) этот
корень μ0 = μ0(p) изменяется в промежутке (-π/2, 0) как корень уравнения pμ = -tg μ.
Затем при p = -1 возникает промежуточное значение μ0(0) = 0. Наконец, при p ∈ (-1, 0)
корень μ0 = μ0(p) изменяется в промежутке (0, +∞) уже как корень уравнения pμ = -th μ
с асимптотикой
μ0(p) ∼ -1/p, p → 0 - 0.
(87)
Асимптотика (87) устанавливается из простых соображений и даёт отличное приближение уже
при p ≥ -1/π. Действительно, при таких p точка пересечения графиков s = pμ и s = -th μ
будет расположена очень близко к асимптоте s = -1 графика s = -th μ. Следовательно,
уравнение pμ = -th μ с высокой точностью выражается как pμ = -1.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
907
Остальные “регулярные” корни μk = μk(p) с индексом k ∈ N определены при всех p ∈ R.
Точнее, при фиксированном k ∈ N каждый такой корень соответствует ветви ϕk(μ) = -tg μ и
непрерывно возрастает с ростом p в пределах от -(2k + 1)π/2 до -(2k - 1)π/2. В частности,
при p = 0 получаем элементарные значения μk(0) = -kπ, разделяющие основные нужные
нам случаи μk(p) ∈ (-(2k + 1)π/2, -kπ) при -∞ < p < 0 и μk(p) ∈ (-kπ, -(2k - 1)π/2) при
0 < p < +∞ (см. рисунок).
Таким образом, описание корней для совокупности (85) получено. Теперь, чтобы вернуть-
ся к исходному уравнению (83), используем замену (84). Следующий результат есть прямое
следствие проведённых выше рассуждений.
Теорема 7. Пусть p ∈ R. Тогда все корни уравнения (83) принадлежат R и при анализе
их расположения на прямой надо различать три случая.
1. Если p < 0, то корни уравнения (83) представимы в виде
-∞ < ... < ζk+1 < ζk < ... < ζ1 < ζ0.
(88)
При любом фиксированном k ∈ N корень ζk = ζk(p) строго возрастает с ростом p ∈ (-∞, 0),
непрерывно двигаясь от левой до правой границы в интервале (-(2k + 1)2π2,-4k2π2). Кроме
того, имеется особый корень ζ0 = ζ0(p), который строго возрастает в интервале (-π2,+∞),
непрерывно двигаясь от левой до правой границы так, что
-π2 < ζ0(p) < 0 при p ∈ (-∞,-1), ζ0(p) = 0 при p = -1, ζ0(p) > 0 при p ∈ (-1,0)
с асимптотикой ζ0(p) ∼ 4/p2 при p → 0 - 0.
2. Если p = 0, то корни уравнения (83) принимают вид ζk = -4k2π2 при k ∈ N.
3. Если p > 0, то корни уравнения (83) представимы в виде
-∞ < ... < ζk+1 < ζk < ... < ζ1.
(89)
При любом фиксированном k ∈ N корень ζk = ζk(p) строго возрастает с ростом p ∈ (0, +∞),
непрерывно двигаясь от левой до правой границы в интервале (-4k2π2,-(2k - 1)2π2). Как
следствие отсюда получаем, что при всех p > 0 корни (89) будут отрицательными, строго
меньшими числа (-π2).
Для того чтобы завершить картину и получить нули серии (72) для характеристической
функции (17) остаётся разделить на T2 числа (88) при p < 0 или числа (89) при p > 0 с их
описанием, указанным в теореме 7. Нетрудно убедиться при этом, что нули (71) и нули (72)
в теореме 3 при фиксированном p ∈ (-∞, 0)
⋃ (0, +∞) обладают следующим свойством пе-
ремежаемости: между двумя любыми последовательными нулями серии (72) находится ровно
один нуль серии (71). Точнее, при p < 0 имеем
λ(2)k = ζk/T2 < λ(1)k = -4k2π2/T2 < λ(2)k-1 = ζk-1/T2, k ∈ N,
а при p > 0 имеем
λ(2)k+1 = ζk+1/T2 < λ(1)k = -4k2π2/T2 < λ(2)k = ζk/T2, k ∈ N,
с учётом нумерации, введённой в теореме 7.
Отметим ещё несколько следствий, важных с практической точки зрения. Напомним, что
переход от параметра p к изначальным α, β и T происходит по формуле p = 2β/(αT )
(см. (70)). Утверждая, что нули функции (17) локализуются в каких-то интервалах, мы имеем
в виду, что вне этих интервалов нулей нет совсем, но в каждый из интервалов попадает хотя
бы один или даже два таких нуля. Слово “интервал” понимаем здесь в расширенном смысле -
как любой связный промежуток вещественной оси.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
908
ТИХОНОВ, АЛМОХАМЕД
Теорема 8. Для характеристической функции L(λ) = L(λ; T, α, β) из формулы (17) вы-
делим следующие типичные возможности.
1. При любом выборе параметров α > 0, β > 0 и T > 0 все нули функции (17) являются
вещественными и отрицательными, строго меньшими числа (-π2/T2). Точнее, эти нули
локализуются в интервалах [-4k2π2/T2, -(2k - 1)2π2/T2) при k ∈ N.
2. Также отрицательными будут все нули функции (17), если параметры α, β ∈ R \ {0}
и T > 0 связаны условием
-∞ < β/α < -T/2.
(90)
Точнее, тогда нули локализуются в интервалах (-π2/T2, 0) и (-(2k + 1)2π2/T2, -4k2π2/T2]
при k ∈ N.
3. Далее, если параметры α, β ∈ R \ {0} и T > 0 связаны специальным условием
β/α = -T/2
∼ αT + 2β = 0,
(91)
то характеристическая функция (17) имеет простой нуль в точке λ = 0 и остальные нули,
локализованные в интервалах (-(2k + 1)2π2/T2, -4k2π2/T2] при k ∈ N.
4. Если, наконец, параметры α, β ∈ R \ {0} и T > 0 связаны условием
-T/2 < β/α < 0,
(92)
то характеристическая функция (17) имеет один простой нуль на луче (0,+∞) и осталь-
ные нули, локализованные в интервалах (-(2k + 1)2π2/T2,-4k2π2/T2] при k ∈ N.
Доказательство. Перечисленные результаты получаются простым сравнением базовой
теоремы 3 и теоремы 7 (c учётом также теорем 5 и 6). Условия (90)-(92) соответствуют случаям
p ∈ (-∞,-1), p = -1, p ∈ (-1,0), разобранным в теореме 7 и отнесённым сейчас к параметру
p = 2β/(αT). Других обоснований не требуется.
Информацию, заложенную в теорему 8, можно уточнять ad infinitum путём дополнительно-
го изучения корней трансцендентных уравнений (86). Подобные уравнения известны в анализе,
начиная с Эйлера [33; с. 300-301] (см. также [34; с. 170-171]); ряд результатов представлен да-
же в учебной литературе (см. [35; с. 218, 453]). Полученного, впрочем, достаточно для многих
содержательных выводов, связанных c исходной обратной задачей (1)-(3).
10. Признаки единственности и неединственности решения. Для сокращения фор-
мулировок рассматриваем обратную задачу (1)-(3) в её однородной версии (1), (6). Оператор A
по-прежнему считаем линейным и замкнутым. Начнём с результатов абсолютного характера,
когда единственность ослабленного решения обратной задачи гарантирована независимо от
выбора значения T > 0.
Теорема 9. Пусть у оператора A нет вещественных собственных значений. Тогда при
любом выборе параметров α, β ∈ R \ {0} и T > 0 однородная обратная задача (1), (6) имеет
только тривиальное решение u(t) ≡ 0, g = 0.
Доказательство непосредственно следует из теорем 2 и 6.
Теорема 10. Пусть у оператора A нет собственных значений на луче (-∞, 0) ⊂ R. Тог-
да при любом выборе параметров α > 0, β > 0 и T > 0 однородная обратная задача (1), (6)
имеет только тривиальное решение u(t) ≡ 0, g = 0.
Доказательство следует из теоремы 2 и части 1 теоремы 8.
Теоремы 9 и 10 охватывают множество ситуаций. Так, под действие теоремы 10 можно
подвести линейные обратные задачи о нахождении источника для эллиптических уравнений
в цилиндрических областях, как в работах [7, 36, 37].
Укажем теперь два результата условного характера - когда единственность решения об-
ратной задачи зависит от выбора финального значения T > 0.
Теорема 11. Пусть у оператора A нет собственных значений на луче (-∞, -b) ⊂ R
√
с некоторым b > 0. Тогда при любом выборе параметров α > 0, β > 0 и T ∈ (0,π/
b]
однородная обратная задача (1), (6) имеет только тривиальное решение u(t) ≡ 0, g = 0.
√
Доказательство. Так как T ∈ (0, π/
b ], то -π2/T2 ≤ -b. Тем самым, по теореме 8,
часть 1, все нули характеристической функции (17) попадают на луч (-∞, -b), где нет соб-
ственных значений оператора A. Применяя теорему 2, получаем нужный результат.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
909
Теорема 12. Пусть у оператора A нет собственных значений на луче (-∞, 0) ⊂ R.
Пусть параметры α,β ∈ R \ {0} взяты разных знаков. Тогда при любом T из интервала
0 < T < -2β/α
(93)
однородная обратная задача (1), (6) имеет только тривиальное решение u(t) ≡ 0, g = 0.
Доказательство. Из условия (93) следует условие (90). Поэтому, применяя часть 2 теоре-
мы 8, заключаем, что нули характеристической функции (17) попадают на луч (-∞, 0), где
нет собственных значений оператора A. В итоге по теореме 2 получаем нужный результат.
Можно дать много других, более специальных, утверждений, связанных с непопаданием
собственных значений оператора A на интервалы локализации нулей из теоремы 8. Не будем
перегружать работу такими формулировками. Отметим ещё два результата противоположного
характера, когда единственность решения обратной задачи заведомо нарушается.
Теорема 13. Пусть оператор A имеет отрицательное собственное значение λ0 = -γ2,
где γ > 0. Пусть T = 2kπ/γ > 0 с некоторым k ∈ N. Тогда при всех α, β ∈ C \ {0}
однородная обратная задача (1), (6) имеет нетривиальное решение
(
)
2
T
2kπt
u(t) =
1 - cos
f0, g = f0
(94)
4k2π2
T
с собственным вектором f0 = 0 таким, что f0 ∈ D(A) и Af0 = -γ2f0 = -(4k2π2/T2)f0.
Доказательство. По теореме 3 собственное значение λ0 = -γ2 = -4k2π2/T2 попадает
в серию (71) и является нулём характеристической функции (17). Но тогда, согласно лемме 1,
нетривиальное решение задачи (1), (6) можно построить по формуле (19). Конкретная реали-
зация этой формулы даёт пару (94). Непосредственная подстановка в задачу подтверждает,
что соотношения (1), (6) выполнены при всех α, β ∈ C \ {0}. Теорема доказана.
В простых “гиперболических” примерах для уравнения колебаний струны оператор A об-
ладает серией собственных значений λm = -(mπ/l)2 при m ∈ N, где l > 0 - длина струны.
Тогда, как следует из теоремы 13, обратная задача (1), (6) имеет нетривиальные решения ви-
да (94) в любой момент времени T = Tk,m ≡ 2l(k/m), где k, m ∈ N. Указанные моменты
образуют счётное всюду плотное множество на луче 0 < T < ∞, т.е. этот “гиперболический”
случай в обратных задачах подобен по своей некорректности так называемой задаче Дирихле
для уравнения колебаний струны (см. [38]; ср. с [1; с. 140-143] и [15; с. 1619-1620]).
Завершим следующим обособленным результатом.
Теорема 14. Пусть оператор A имеет собственное значение λ0 = 0, и Af0 = 0 с эле-
ментом f0 ∈ D(A), f0 = 0. Предположим, что параметры α,β ∈ R \ {0} и T > 0 связаны
условием αT + 2β = 0. Тогда однородная обратная задача (1), (6) имеет нетривиальное
решение вида
u(t) = (t2/2)f0, g = f0.
(95)
Доказательство. По теореме 8 с условием (91) собственное значение λ0 = 0 является
нулём характеристической функции (17). Воспользуемся формулой (19) вместе с уточнением,
указанным в (11) для λ = 0. Получим пару (95). Проверка соотношений (1), (6) здесь не
представляет труда. Теорема доказана.
Ясно, что когда много собственных значений оператора A совпадает с нулями характери-
стической функции (17), мы можем комбинировать возникающие пары вида (19), осуществляя
синтез все более сложных решений однородной обратной задачи (1), (6). В совсем уже специ-
альных случаях, когда характеристическая функция (17) имеет кратный нуль кратности два
(см. теорему 4), возможны примеры, где кроме элементарных решений вида (19) появляются
присоединённые элементарные решения (u(t),g), учитывающие наличие у оператора A не
только собственных векторов из D(A), но и присоединённых векторов из D(A2) (см. [26]).
Авторы признательны А.Б. Костину, А.И. Прилепко и Ю.С. Эйдельману за проявленный
интерес и поддержку наших исследований. Особые благодарности А.Ю. Попову - за ценные
консультации по теории целых функций и В.Б. Шерстюкову - за научные контакты.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
910
ТИХОНОВ, АЛМОХАМЕД
СПИСОК ЛИТЕРАТУРЫ
1. Денисов А.М. Введение в теорию обратных задач. М., 1994.
2. Prilepko A.I., Orlovsky D.G., Vasin I.A. Methods for Solving Inverse Problems in Mathematical Physics.
New York; Basel, 2000.
3. Красносельский М.А., Забрейко П.П., Пустыльник Е.И., Соболевский П.Е. Интегральные операто-
ры в пространствах суммируемых функций. М., 1966.
4. Тихонов И.В., Эйдельман Ю.С. Обратная задача для дифференциального уравнения в банаховом
пространстве и распределение нулей целой функции типа Миттаг-Лёффлера // Дифференц. урав-
нения. 2002. Т. 38. № 5. С. 637-644.
5. Алмохамед М. Критерий единственности решения в линейной обратной задаче с финальным пе-
реопределением второго рода // Вестн. Воронежского гос. ун-та. Сер. Физика. Математика. 2019.
№ 3. С. 50-58.
6. Прилепко А.И. Обратные задачи теории потенциала (эллиптические, параболические, гиперболи-
ческие уравнения и уравнение переноса) // Мат. заметки. 1973. Т. 14. № 5. С. 755-767.
7. Прилепко А.И. Избранные вопросы в обратных задачах математической физики // Условно-кор-
ректные задачи мат. физики и анализа. Новосибирск, 1992. С. 151-162.
8. Искендеров А.Д., Тагиев Р.Г. Обратная задача об определении правых частей эволюционных урав-
нений в банаховом пространстве // Вопросы прикл. мат. и киберн. Науч. тр. Азербайджанского
ун-та. 1979. № 1. С. 51-56.
9. Эйдельман Ю.С. Единственность решения обратной задачи для дифференциального уравнения в
банаховом пространстве // Дифференц. уравнения. 1987. Т. 23. № 9. С. 1647-1649.
10. Тихонов И.В., Эйдельман Ю.С. Единственность решения двухточечной обратной задачи для аб-
страктного дифференциального уравнения с неизвестным параметром // Дифференц. уравнения.
2000. Т. 36. № 8. С. 1132-1133.
11. Тихонов И.В. Обобщённая задача Уорда для абстрактных дифференциальных уравнений // Диф-
ференц. уравнения. 2005. Т. 41. № 3. С. 325-336.
12. Тихонов И.В., Алмохамед М. Об одной обратной задаче для дифференциального уравнения высоко-
го порядка в банаховом пространстве // Некоторые актуальные проблемы современной математики
и математического образования. СПб., 2019. С. 91-95.
13. Амиров А.Х. О разрешимости обратных задач для уравнения второго порядка // Функц. анализ и
его прил. 1986. Т. 20. Вып. 3. C. 80-81.
14. Орловский Д.Г. Об одной обратной задаче для дифференциального уравнения второго порядка
в банаховом пространстве // Дифференц. уравнения. 1989. Т. 25. № 6. С. 1000-1009.
15. Орловский Д.Г. К задаче определения параметра эволюционного уравнения // Дифференц. урав-
нения. 1990. Т. 26. № 9. С. 1614-1621.
16. Тихонов И.В. Структурные свойства нуль-решений абстрактной задачи Коши // Интегральные
преобразования и специальные функции. Информ. бюллетень. 2002. Т. 3. № 1. С. 22-38.
17. Тихонов И.В., Алмохамед М. Обобщённые экспоненты и их применение в теории дифференциаль-
ных уравнений // Системы компьютерной математики и их приложения. Вып. 21. Смоленск, 2020.
С. 345-353.
18. Попов А.Ю., Седлецкий А.М. Распределение корней функций Миттаг-Леффлера // Совр. матема-
тика. Фунд. направления. 2011. Т. 40. С. 3-171.
19. Левин Б.Я. Распределение корней целых функций. М., 1956.
20. Леонтьев А.Ф. Целые функции. Ряды экспонент. М., 1983.
21. Хилле Э., Филлипс Р. Функциональный анализ и полугруппы. М., 1962.
22. Полиа Г., Сеге Г. Задачи и теоремы из анализа. Часть 2. Теория функций. Распределение нулей.
Полиномы. Определители. Теория чисел. М., 1978.
23. Müntz Ch.H.
Über den Approximationssatz von Weierstraß // Mathematische Abhandlungen Hermann
Amandus Schwarz zu seinem Fünfzigjährigen Doctorjubiläum. Berlin; Heidelberg, 1914. S. 303-312.
24. Качмаж С., Штейнгауз Г. Теория ортогональных рядов. М., 1958.
25. Masayoshi Hata. Problems and Solutions in Real Analysis. Series on Number Theory and Its Applications.
V. 4. New Jersey; London; Singapore, 2007.
26. Алмохамед М., Тихонов И.В. О некоторых спектральных исследованиях, связанных с теорией об-
ратных задач // Совр. проблемы теории функций и их приложения: материалы 21-й междунар.
Саратовской зимней школы. Саратов, 2022. C. 20-26.
27. Тихонов И.В., Шерстюков В.Б., Алмохамед М. О некоторых трансцендентных уравнениях, важ-
ных для математической физики // Совр. проблемы теории функций и их приложения: материа-
лы 21-й междунар. Саратовской зимней школы. Саратов, 2022. C. 294-299.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022
ОБРАТНАЯ ЗАДАЧА С ПЕРЕОПРЕДЕЛЕНИЕМ ТРЕТЬЕГО РОДА
911
28. Fadle J. Die Selbstspannungs-Eigenwertfunktionen der quadratischen Scheibe // Ingenieur-Archiv (≡
Archive of Applied Mechanics). 1940. Bd. 11. S. 125-149.
29. Buchwald V.T. Eigenfunctions of plane elastostatics. I. The strip // Proceedings of the Royal Society of
London. Ser. A. Math. and Phys. Sci. 1964. V. 277. № 1370. P. 385-400.
30. Katopodes F.V., Davis A.M.J., Stone H.A. Piston flow in two-dimensional channel // Physics of Fluids.
2000. V. 12. № 5. P. 1240-1243.
∑∞
31. Hardy G.H. On the zeroes of integral function x-sinx =
// The Messenger of Math.
1
n+1!
1902. V. 31. № 11. P. 161-165.
32. Маркушевич А.И. Целые функции. Элементарный очерк. М., 1975.
33. Эйлер Л. Введение в анализ бесконечных. Т. 2. М., 1961.
34. Comtet L. Advanced Combinatorics. The Art of Finite and Infinite Expansions. Dordrecht; Holland, 1974.
35. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому
анализу. Т. 1. Предел. Непрерывность. Дифференцируемость. М., 2003.
36. Соловьев В.В. Разрешимость обратных задач для эллиптического уравнения в цилиндре // Вестн.
Московского гос. обл. ун-та. Сер. Физика. Математика. 2012. № 1. С. 27-38.
37. Алмохамед М. Восстановление правой части в уравнении Пуассона при помощи специальных кра-
евых условий // Совр. проблемы теории функций и их приложения: материалы 20-й междунар.
Саратовской зимней школы. Саратов, 2020. С. 30-32.
38. Bourgin D.G., Duffin R. The Dirichlet problem for the vibrating string equation // Bull. of the Amer.
Math. Soc. 1939. V. 45. № 12. Part 1. P. 851-858.
Московский государственный университет
Поступила в редакцию 15.02.2022 г.
имени М.В. Ломоносова,
После доработки 15.02.2022 г.
Московский педагогический государственный
Принята к публикации 25.05.2022 г.
университет,
Университет Алеппо,
г. Алеппо, Сирия
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№7
2022