ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 7, с.921-929

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.632+519.633

О РЕШЕНИИ УРАВНЕНИЯ СМЕШАННОГО ТИПА

В НЕОГРАНИЧЕННОЙ ОБЛАСТИ

Разработаны способы численного решения задачи для уравнения смешанного типа в

неограниченной области. Предложен способ задания искусственных граничных условий,

позволяющий проводить расчёты в ограниченной области такой, что численное решение

сходится к проекции точного решения на эту область. Подробно рассмотрен случай, когда

решение удовлетворяет волновому уравнению в ограниченной области и уравнению Лапла-

са в оставшейся части пространства. Приведён алгоритм для случая, когда в ограниченной

области процесс описывается уравнением теплопроводности. Приведены примеры решений

в двумерном случае. Исследована скорость сходимости итерационного алгоритма.

DOI: 10.31857/S0374064122070056, EDN: CEFVXE

Введение. В работе рассмотрены задачи, описываемые гиперболическими или параболи-

ческими уравнениями во внутренней подобласти и уравнением Лапласа - во внешней, причём

внутренняя подобласть конечных размеров со всех сторон окружена внешней бесконечной

подобластью. Построены алгоритмы численного решения таких задач.

Алгоритмы базируются на основной интегральной формуле Грина для оператора Лапла-

са. Суть методов состоит во введении расчётной области конечных размеров, построении ис-

кусственных граничных условий и итерационного алгоритма для реализации этих условий.

Подобные алгоритмы использованы в работе [1] для решения внешних задач для оператора

Лапласа.

В п. 1 приведена постановка задачи, построен вычислительный алгоритм, исследована ско-

рость его сходимости. C помощью интегро-интерполяционного метода в п. 2 построена раз-

ностная схема. В п. 3 приведены примеры решения задачи с помощью алгоритма, проведено

сравнение теоретической и экспериментальной оценок скоростей сходимости.

1. Постановка задачи. Построение итерационного алгоритма. Пусть в ограничен-

ной области D (рис. 1) некоторый процесс описывается волновым уравнением, вне этой об-

ласти - уравнением Лапласа. На границе ∂D решение непрерывно вместе с нормальной про-

изводной, а также является ограниченным на бесконечности и в нуле:

∂²u

= c²Δu, r ∈ D, t > 0;

∂t²

Δu = 0, r ∈ Rⁿ \ D, n = 1,2,3;

u|t=0 = α(r), r ∈ D;

u_t|t=0 = β(r), r ∈ D;

]

^[∂u

[u] = 0,

на ∂D ;

∂n

|u| < +∞.

(1)

Здесь [ · ] - знак скачка величины, указанной в скобках, c - константа.

Целью работы является построение алгоритма численного решения задачи в ограниченной

области D₂ : D ⊂ D₂ (рис. 1) такого, что проекция решения (1) на указанную ограниченную

область будет совпадать с решением задачи в ограниченной области.

921

922

ГАЛАНИН и др.

Без потери общности под D₂ будем понимать шар в прост-

ранстве соответствующей размерности радиуса R₂. Введём

обозначение R - радиус шара, полностью включающего в се-

бя область D (R < R₂). Форма области D может быть

сложной, что не позволяет задать для соответствующей за-

дачи функцию Грина. Поэтому для такого случая в статье [1]

рассмотрена дополнительная граница ∂D₁ в области D₂ \ D,

представляющая собой сферу радиуса R₁ : R < R₁ < R₂

(рис. 1).

Для нахождения решения в ограниченной области будем

использовать условие

u||r|=R2 = Su||r|=R1 .

(2)

Рис. 1. Рассматриваемая область. Здесь S - линейный оператор. В двумерном или трёхмерном

случаях S - это интеграл Пуассона (приведён далее).

В одномерном плоском (декартовом, n = 1) случае потребуем выполнения условия



∂u



= 0.

(3)



∂r

|r|=0

В одномерном сферически симметричном и трёхмерном случаях от решения (1) будем требо-

вать регулярности на бесконечности:

|u| → 0,

|r| → ∞.

Введённых условий достаточно для существования и единственности решений рассматри-

ваемых задач. Не возникает сомнений, что при должной аппроксимации задачи (1)-(3) в огра-

ниченной области D₂ будет получено искомое (приближённое к точному) решение.

Рассмотрим итерационный вариант решения, при котором значение функции u на каждой

итерации находится при заданном значении приближения граничного условия на границе |r| =

= R₂, а затем по полученному решению пересчитывается по (2), и решение в области ищется

снова.

В одномерных плоском (декартовом) и цилиндрически симметричном случаях справедливо

равенство

Su||r|=R1 = u||r|=R1 ,

а в одномерном сферически симметричном случае

R₁

Su||r|=R1 =

u||r|=R1 .

R₂

Исследуем сходимость итерационного процесса в одномерном случае.

Ограничимся исследованием дифференциально-разностной задачи. Для этого заменим

производные по времени на конечно-разностные с шагом τ. Пусть разыскивается решение на

новом временном слое в соответствии с задачей

y = c²Δy + f, r ∈ D;

τ²

Δy = 0, r ∈ Rⁿ \ D, n = 1,2,3;

]

^[∂y

[y] = 0,

на ∂D;

∂n

|u| < +∞;

y||r|=R2 = Sy||r|=R1.

(4)

Здесь правая часть f определяется решением с предыдущих временных слоёв.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О РЕШЕНИИ УРАВНЕНИЯ СМЕШАННОГО ТИПА

923

Устроим итерационный процесс: ищем решение на k-й итерации путём нахождения реше-

ния (4) с граничным условием

y^k||r|=R

=μk-1,

после нахождения которого пересчитаем условие по правилу

μ^k = Sy^k||r|=R

Сходимость итераций будет иметь место, если

|δμ^k| ≤ q|δμk-1| с 0 < q < 1. Здесь

δμ^k = μ - μ^k, μ = y||r|=R2.

Утверждение 1. В одномерных случаях описанный итерационный процесс сходится со

скоростью геометрической прогрессии с показателем q, равным

cτ cth (R/(cτ)) + (R₁ - R)

cτ cth (R/(cτ)) + (R₂ - R₁)

в плоском (декартовом) случае,

cτ I₀(R/(cτ))/I₁(R/(cτ)) + R(ln R₁ - ln R)

cτ I₀(R/(cτ))/I₁(R/(cτ)) + R(ln R₂ - ln R)

в цилиндрически симметричном случае,

cτ th (R/(cτ)) + (R₁ - R)

cτ th (R/(cτ)) + (R₂ - R)

в сферически симметричном случае.

В данном утверждении I₀ и I₁ - функции Инфельда (Бесселя комплексного аргумента).

Доказательство предложения состоит в прямом решении задачи (4) для δy^k = y - y^k и

анализе граничного условия.

Как видно, во всех случаях показатели q < 1 и в основном при малых τ определяются сла-

гаемыми, которые не зависят от τ. В значительной степени данные показатели соответствуют

аналогичным коэффициентам задачи для уравнения Лапласа в пространстве (см. [1]).

Рассмотрим также задачу, аналогичную (1), но с заменой волнового уравнения на уравне-

ние теплопроводности с постоянной температуропроводностью a² :

∂u

= a²Δu, r ∈ D, t > 0,

(5)

∂t

с очевидными изменениями начальных условий (1).

Будем решать эту задачу также итерационным способом, который исследуем, ограничив-

шись дифференциально-разностным приближением.

Утверждение 2. Для задачи с уравнением теплопроводности (5) итерационный процесс

сходится с показателем геометрической прогрессии q из утверждения 1, в котором коэф-

фициент c заменён на a, а τ - на

√τ.

Сходимость подобного итерационного процесса в одномерном случае исследована в рабо-

те [2]. В статье [3] приведены результаты численного моделирования в двумерном случае.

Замечание. В общем трёхмерном случае для решения задачи справедлив принцип макси-

мума, поэтому сходимость итераций также имеет место, как и для уравнения Лапласа [1, 2, 4].

2. Построение разностной схемы. Положим далее значение скорости c = 1. Рассмот-

рим пространственно двумерный случай. Задачу будем решать в цилиндрических коорди-

натах.

Решение внешней задачи для уравнения Лапласа для круга известно и задаётся интегралом

Пуассона [5, с. 314, 6, с. 157]. В двумерном случае он имеет вид

2π

∫

r² - R²¹

u(r, ϕ) = Su||r|=R1 =

u(R₁, ψ)

dψ, r > R₁.

(6)

2π

r² - 2rR₁ cos(ϕ - ψ) + R²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

924

ГАЛАНИН и др.

Вычислив интеграл Пуассона от значений искомой функции на границе ∂D₁, можно по-

лучить значения функции на границе области D₂.

Тогда исходная задача (1), (2) в области уравнения Лапласа примет вид

Δu = 0,

r∈D₂ \D;

∫

2π

R²² - R²¹

u|∂D2 =

u(R₁, ψ)

dψ.

2π

R²² - 2R₁R₂ cos(ϕ - ψ) + R²

Построим итерационный алгоритм для учёта интегрального граничного условия (6). Зна-

чение u^s на границе области D₂ на каждой новой итерации будет вычисляться через уже

известные значения us-1 на предыдущей итерации. Для нахождения u^s имеем задачу с усло-

виями Дирихле на внешней границе ограниченной области:

u^s|∂D2 = Sus-1|∂D1 .

Схожий алгоритм применён в работах [1-3].

Для численного расчёта введём равномерную сетку в

Ω = {0 ≤ r ≤ R₂,

0 ≤ ϕ ≤ 2π,

0≤t≤T}

с шагом h_r по координате r, шагом h_ϕ по координате ϕ и шагом τ по времени. Выберем

шаг так, чтобы узлы сетки N, N₁, N₂ попадали на границы областей радиусов R, R₁ и R₂

соответственно.

Построим разностную схему для волнового уравнения интегро-интерполяционным мето-

дом (см. [7, с. 215]). Она имеет вид

ytt =

(ri+1/2y_r - ri-1/2y_r)(σ) +

y(σ)¯ϕϕ.

(7)

r_ih^r

r²

Здесь y(σ) = σŷ + (1 - 2σ)y + σy, где y - сеточная функция, приближающая решение u,

σ - вес. Неизвестной является функция ŷ. Обозначения разностных производных и сеточных

функций на разных временных слоях соответствуют обозначениям в работах [7, с. 210; 8, гл. 1].

Полученная схема является трёхслойной, для нахождения неизвестного значения ŷ_ij необ-

ходимо знать значения решения с двух предыдущих слоёв. Значения u на нулевом слое из-

вестны из начального условия u|t=0 = α(r, ϕ), на первом слое можно вычислить решение

из условия u_t|t=0 = β(r, ϕ). Схема (7) имеет второй порядок по пространству и времени,

поэтому аппроксимируем второе начальное условие тоже со вторым порядком. Для этого вос-

пользуемся формулой Тейлора.

Отсюда значение решения на первом временном слое имеет вид

(

)

y1ij = α + τβ +

(ri+1/2α_r - ri-1/2α_r) +

ϕϕ

r_ih^r

r²

Аналогично (7) построим разностную схему для уравнения Лапласа:

(ri+1/2y_r - ri-1/2y_r)(σ) +

y(σ)¯ϕϕ = 0.

r_ih^r

r²

Для приближённого вычисления интеграла Пуассона (6) воспользуемся квадратурной фор-

мулой трапеций

(

h_ϕ(R²² - R²¹)

0.5yN1,0

0.5yN1,Nϕ

yN2,j =

2π

R²¹ - 2R₁R₂ cos(ϕ_j - ϕ₀) + R²²

R²¹ - 2R₁R₂ cos(ϕ_j - ϕNϕ ) + R²

)

∑

yN1,m

R²¹ - 2R₁R₂ cos(ϕ_j - ϕ_m) + R²

m=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О РЕШЕНИИ УРАВНЕНИЯ СМЕШАННОГО ТИПА

925

Здесь N₁, N₂ - номера узлов сетки по радиусу, соответствующие r = R₁ и r = R₂. Число

узлов сетки по углу ϕ равно N_ϕ + 1. По углу аппроксимированы периодические граничные

условия.

Решение задачи должно быть ограничено в нуле по радиусу. Аппроксимируем уравнение

(1) в нуле так, как это описано в работах [7, с. 313; 8, с. 434].

На границе области D поставлены условия сопряжения. Для аппроксимации условия ра-

венства потоков рассмотрим ячейки [rN-1/2, r_N ]×[ϕj-1/2, ϕj+1/2] и[r_N , rN+1/2]×[ϕj-1/2, ϕj+1/2].

В первой ячейке проинтегрируем волновое уравнение, а во второй - уравнение Лапласа. Из дан-

ных равенств выразим поток u в точке r_N , приравняем и получим аппроксимацию условия

сопряжения

ytt =

(rN1+1/2yr - rN₁-1/2yr)(σ) +

y(σ)¯ϕϕ.

h^rirN1

r²

N₁

Если границей области D является не окружность, то возникает необходимость постановки

условий сопряжения на границе, например, вида ϕ = const, которое построим также путём

интегрирования уравнений по ячейке [ri-1/2, ri+1/2] × [ϕ_Np

,ϕ_Np

], где N^ϕ - номер узла

ϕ-1/2

ϕ+1/2

по ϕ, попадающего на границу D :

ytt =

(ri+1/2y_r - ri-1/2y_r)(σ) +

y(σ)¯ϕϕ.

h^rir_i

r²

Для проверки итерационного алгоритма (получения эталонного решения в отсутствии ана-

литического) рассмотрим вспомогательную задачу. Вместо условия (6) на внешней границе

поставим условие равенства нулю производной решения по r, а радиус внешней области R₂

увеличим, чтобы уменьшить влияние данного граничного условия на решение в исходной об-

ласти. Таким образом, необходимо решить задачу в области D′2 радиуса R′2 = QR₂, Q > 0 -

некоторый коэффициент, с другим граничным условием, которое аппроксимируем интегро-

интерполяционным методом, проинтегрировав уравнение Лапласа в ячейке

[rN2-1/2, rN2]×

× [ϕj-1/2, ϕj+1/2]:

2rN2-1/2

y(σ)¯r +

y(σ)¯ϕϕ = 0,

rN2h_r

r²

N₂

где N₂ - узел, попадающий на границу ∂D′2.

3. Построение разностной схемы. Рассмотрим четыре варианта задачи: пример 1 -

одномерная цилиндрически симметричная задача, примеры 2 и 3 - двумерная задача с обла-

стью D в виде круга, при этом в примере 2 аналитическое решение известно, а для примера 3

особым способом найдено “эталонное” решение, в примере 4 область D представляет собой по-

ловину круга. Во всех расчётах будем использовать σ = 0.5. Для решения системы линейных

алгебраических уравнений используем решатель BiCGStab - стабилизированный метод бисо-

пряжённых градиентов для задач с разреженными матрицами, реализованный в библиотеке

Eigen. Для оценки норм ошибок используется равномерная норма.

Пример 1. Пусть R - корень уравнений J₁(R) = 0, J₁ - функция Бесселя первого рода,

граница области D совпадает с кругом радиуса R, T = 0.5 - время протекания процесса.

Начальные условия при r < R :

u(r, ϕ, 0) = J₀(r), u_t(r, ϕ, 0) = 0.

Точное решение задаётся выражением

{

J₀(r)cos t,

0≤r≤R;

u(r, ϕ, t) =

J₀(R)cos t,

r>R.

Для нахождения решения итерационным способом на каждом временном слое воспользуемся

разностными схемами, построенными ранее.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

926

ГАЛАНИН и др.

Согласно результатам вычислительных экспериментов (табл. 1) разностная схема позволя-

ет получить решение одномерной задачи, при этом наблюдается второй порядок сходимости.

Таблица 1. Сравнение численного решения одномерной

задачи (пример 1) с точным. R1 = 2R, R2 = 4R. На-

чальный шаг h = (hr , hϕ, τ ) = (0.383171, π/4, 0.05)

Шаг Относительная ошибка Отношение ошибок

4.92 · 10-3

h/2

7.53 · 10-4

6.54

h/4

1.88 · 10-4

3.99

h/8

3.94 · 10-5

4.78

Рассмотрим влияние положения границы области D₁ на сходимость. Зафиксируем грани-

цы областей D, D₂, а положение ∂D₁ будем менять.

Согласно утверждению 1 должна наблюдаться сходимость со скоростью геометрической

прогрессии с коэффициентом q. Тогда число итераций можно оценить по формуле

ln ε

(8)

ln q

где ε - убывание ошибки, ∥y^s - y^∗∥/∥y⁰ - y^∗∥ < ε.

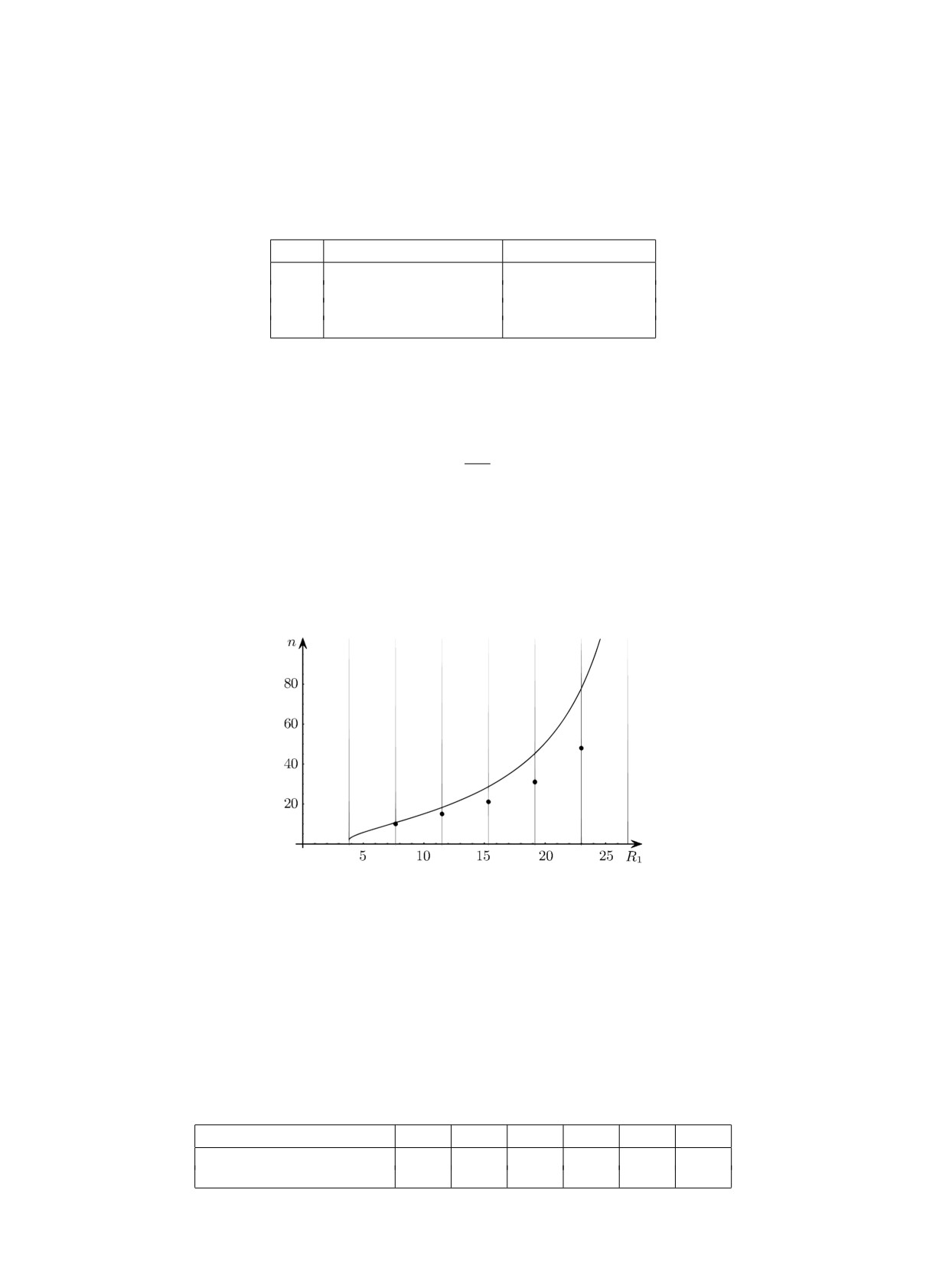
На рис. 2 приведены два графика: сплошная линия - график зависимости априорной оцен-

ки необходимого числа итераций до сходимости по формуле (8), а точками отмечен результат

вычислительных экспериментов. Видим, что качественно и количественно графики близки.

График оценки числа итераций мажорирует график результатов вычислительного экспери-

мента.

Рис. 2. Зависимость числа итераций от положения

границы R1 при решении одномерной задачи (при-

мер 1) R2 = 8R.

Зависимость коэффициента геометрической прогрессии от R₁ в расчётах вычислим как

log_q 10-5 = n(R₁).

(9)

По результатам, представленным в табл. 2, можно сделать вывод, что погрешность в опре-

делении коэффициента q составляет около 10 % и связана с тем, что разностная задача лишь

аппроксимирует исходную.

Таблица 2. Сравнение коэффициентов геометрической прогрессии, предска-

занных в утверждении 1 и полученных в ходе вычислительных экспериментов

q согласно утверждению 1

0.338

0.531

0.669

0.775

0.863

0.936

q по (9)

0.316

0.464

0.578

0.690

0.787

0.940

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О РЕШЕНИИ УРАВНЕНИЯ СМЕШАННОГО ТИПА

927

Пример 2. Пусть внутренняя область D имеет форму круга радиуса R = 2.40483. Необ-

ходимо решить задачу (1) с начальными условиями

u|t=0 = 0, u_t|t=0 = J₁(r) sin ϕ.

Точное решение задаётся выражением

{

J₁(r)sin tsinϕ,

0≤r≤R;

u(r, ϕ, t) =

1.24846r-1 sin t sin ϕ,

r>R.

Результаты серии расчётов (табл. 3) показывают, что построенный метод сходится к точному

решению в области D₂ со вторым порядком.

Можно предположить, что наихудшая скорость сходимости в двумерном случае должна

наблюдаться на задачах типа примера 1, решения которых построены на основной гармонике.

Результаты решения примеров 1 и 2 с разным положением границы R₁ это подтверждают

(табл. 4).

Таблица 3. Сравнение численного решения двумерной

Таблица 4. Зависимость числа итераций до схо-

задачи (пример 2) с точным R1 = 2R, R2 = 4R. На-

димости от положения границы ∂D1

чальный шаг h = (hr , hϕ, τ ) = (0.229031, π/16, 0.1)

Шаг Относительная ошибка Отношение ошибок

n (пример 1)

3.03 · 10-3

n (пример 2)

h/2

7.63 · 10-4

3.97

h/4

1.92 · 10-4

3.98

h/8

4.79 · 10-5

4.00

Пример 3. Пусть внутренняя область D имеет форму круга радиуса R = 1.

Необходимо решить задачу (1) с начальными условиями

u|t=0 = 0, u_t|t=0 = r sin ϕ.

(10)

В силу того, что аналитическое решение достаточно сложно, воспользуемся методом рас-

ширения расчётной области для получения эталонного решения.

Результаты серии расчётов (табл. 6) показывают, что норма отклонения (для двух после-

довательных значений Q) численного решения в области D₂ уменьшается с увеличением Q,

что соответствует ожиданиям. Для вычисления нормы отклонения численного решения ис-

пользована равномерная норма.

Также проведена серия расчётов (табл. 6), которая демонстрирует, что измельчение сет-

ки позволяет получить более точное решение, но измельчение сетки более чем в 4 раза при

неизменном Q не позволяет получить более точного решения.

Таблица 5. Зависимость отклонения решения

Таблица 6. Зависимость нормы ошибки чис-

примера 3 в D2 от размера расчётной области

ленного решения примера 3 от шага сетки.

h = (hr,hϕ,τ) = (0.1,0.25π,0.1) - шаги по

Норма отклонения

пространству и времени, Q = 5

3.05 · 10-3

Шаг

Норма ошибки

1.69 · 10-3

3.26 · 10-3

1.37 · 10-3

h/2

3.05 · 10-3

1.12 · 10-3

h/4

2.78 · 10-3

Пример 4. Рассмотрим задачу, в которой внутренняя область D имеет форму полукруга

радиуса R = 1 (рис. 3). В этой области будем решать задачу (1) с начальными условиями (10).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

928

ГАЛАНИН и др.

Для данного примера также проблематично записать аналитическое решение и приме-

нён метод расширения расчётной области. Результаты расчётов свидетельствуют о том, что

ошибка уменьшается с увеличением параметра Q и с уменьшением шагов по времени и прост-

ранству (табл. 7 и 8).

Таблица 7. Зависимость отклонения решения

Таблица 8. Зависимость нормы ошибки чис-

в D2 примера 4 от размера расчётной области

ленного решения примера 4 от шага сетки.

h = (hr,hϕ,τ) = (0.1,0.25π,0.1) - шаги по

Норма отклонения

пространству и времени, Q = 5

4.77 · 10-3

Шаг

Норма ошибки

1.92 · 10-3

4.77 · 10-3

1.12 · 10-3

h/2

1.92 · 10-3

1.13 · 10-3

h/4

1.77 · 10-3

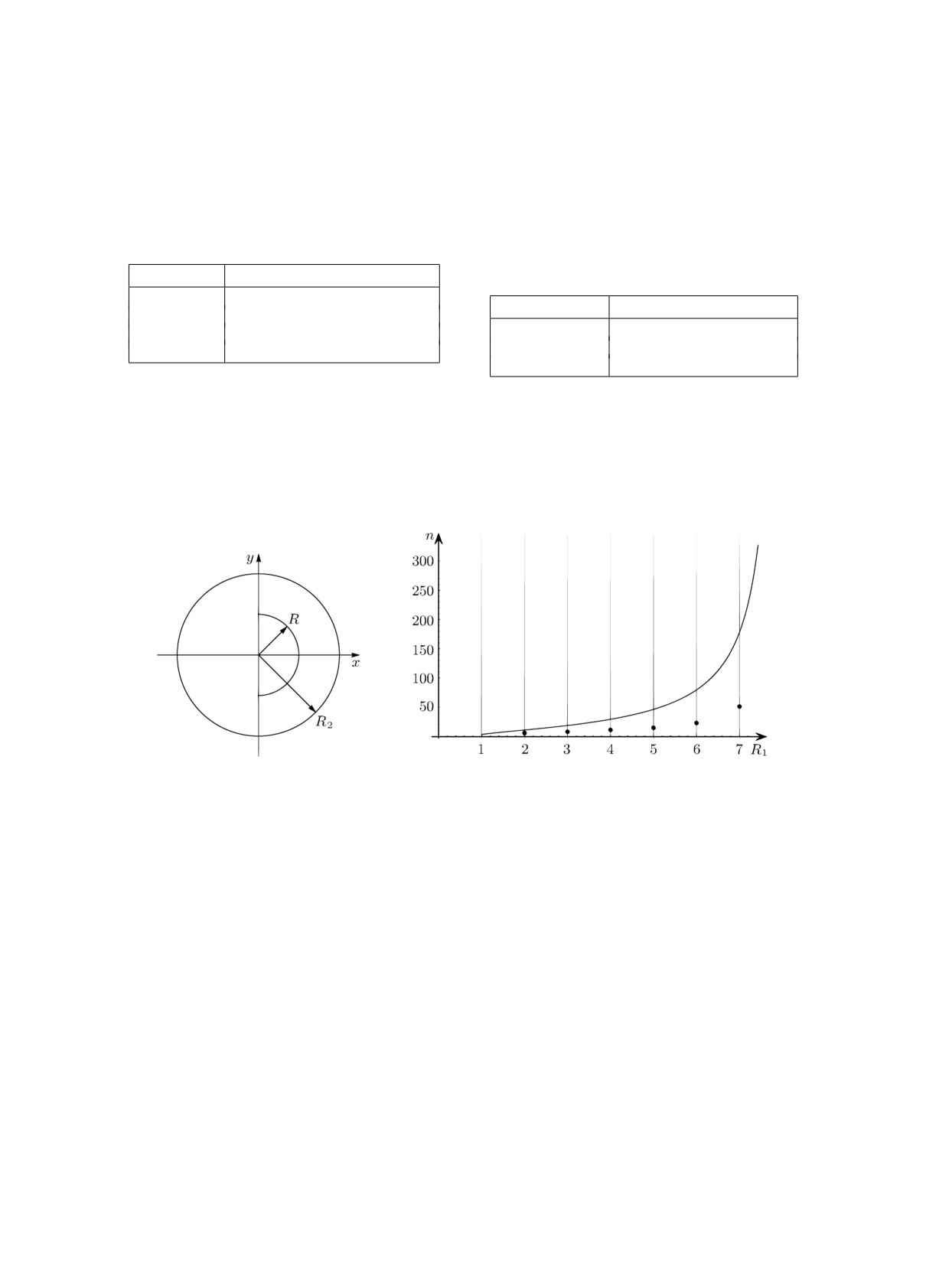
Для примеров 3 и 4 получены оценки зависимости числа итераций до сходимости от раз-

мера R₁. Результаты вычислительных экспериментов представлены на рис. 4. Графики для

примеров 3 и 4 идентичны. В этих случаях R = 1 - радиус внутренней области D, R₁ -

радиус дополнительной области D₁ (варьировался), R₂ = 3 - радиус внешней области D₂.

С увеличением радиуса дополнительной области количество итераций увеличивается, значит

чем ближе эта граница к границе внутренней области, тем выше скорость сходимости.

Рис. 3. Структура расчётной

Рис. 4. Графики зависимости числа итераций от по-

области в примере 4.

ложения границы R1 (для примеров 3 и 4).

Заключение. Разработан алгоритм решения задач для уравнений смешанного типа в

неограниченной области в случае, когда в некоторой финитной области процесс описывает-

ся уравнением гиперболического (или параболического) типа, а вне - эллиптического. Иссле-

дована скорость сходимости построенного вычислительного алгоритма. Проведено сравнение

оценки скорости сходимости алгоритма с результатами вычислительных экспериментов в дву-

мерном случае. Данный алгоритм может быть легко обобщён на трёхмерный случай. Даже

в двумерном случае вычислительные затраты при применении метода меньше, чем при ис-

пользовании расширения расчётной области, но могут уступать методу задания интегрально-

го граничного условия. В трёхмерном же случае ожидается, что итерационный метод будет

наиболее эффективен среди перечисленных.

Исследование выполнено за счёт Российского научного фонда (грант 22-21-00260).

СПИСОК ЛИТЕРАТУРЫ

1. Галанин М.П., Сорокин Д.Л. О решении внешних краевых задач для уравнения Лапласа // Диф-

ференц. уравнения. 2020. Т. 56. № 7. С. 918-926.

2. Галанин М.П., Сорокин Д.Л., Ухова А.Р. Методы численного решения дифференциального уравне-

ния смешанного типа в неограниченной области // Мат. моделирование и численные методы. 2021.

№ 1. С. 91-109.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О РЕШЕНИИ УРАВНЕНИЯ СМЕШАННОГО ТИПА

929

3. Galanin M.P., Sorokin D.L. Numerical solution tasks with mixed operator in unlimited area // CEUR

Workshop Proceedings. 2020. V. 2543. P. 370-376.

4. Савченко А.О., Ильин В.П., Бутюгин Д.С. Метод решения внешней трёхмерной краевой задачи

для уравнения Лапласа // Сиб. журн. индустр. мат. 2016. Т. 19. № 2. С. 88-99.

5. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1972.

6. Свешников А.Г., Боголюбов А.Н., Кравцов В.В. Лекции по математической физике. М., 1993.

7. Галанин М.П., Савенков Е.Б. Методы численного анализа математических моделей. М., 2010.

8. Самарский А.А. Введение в теорию разностных схем. М., 1971.

Институт прикладной математики

Поступила в редакцию 18.02.2022 г.

имени М.В. Келдыша РАН, г. Москва,

После доработки 18.02.2022 г.

Московский государственный технический

Принята к публикации 25.05.2022 г.

университет имени Н.Э. Баумана

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022