ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 7, с.930-946

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.633+517.962.2+517.958

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

РЕШЕНИЯ ДВУХФАЗНОЙ ЗАДАЧИ СТЕФАНА

Исследуются свойства разностного метода решения двухфазной задачи Стефана на сетке,

согласованной с формой границы раздела фаз. Математическая модель учитывает конвек-

тивное движение, возникающее в жидкости, теплоперенос в твёрдой и жидкой фазах, на

границе раздела фаз - условие баланса внутренней энергии. Фазовый переход происходит

при постоянной температуре. Положение межфазной границы определяется с помощью

метода выпрямления фронта. Показано, что предложенная вычислительная схема являет-

ся консервативной и энергетически нейтральной.

DOI: 10.31857/S0374064122070068, EDN: CEIGQC

Введение. Накопленный опыт применения метода конечных разностей для решения слож-

ных прикладных задач показывает, что при конструировании вычислительного алгоритма

недостаточно опираться только на такие свойства разностных схем как аппроксимация, устой-

чивость и сходимость. Необходимо также учитывать конкретные физические свойства исследу-

емого явления. Одним из основных критериев качества вычислительной процедуры является

выполнение разностных аналогов законов сохранения, т.е. консервативность. Для построения

консервативных разностных схем используется интегро-интерполяционный метод [1-3]. При-

менение неконсервативных разностных схем может существенно понизить точность результа-

тов расчётов, а в ряде случаев привести к неверным результатам. А.Н. Тихонов и А.А. Самар-

ский, изучив способы аппроксимации уравнений с разрывными коэффициентами, показали,

что разностная схема, обеспечивающая второй порядок точности в классе достаточно гладких

коэффициентов, не сходится в классе разрывных коэффициентов [1, 4-7].

В работе А.А. Самарского и Ю.П. Попова [3] сформулирован принцип полной консерватив-

ности разностных схем. Он состоит в выполнении на разностном уровне не только аналогов

основных законов сохранения, присущих тому или иному явлению, но и дополнительных соот-

ношений, свойственных дифференциальной задаче (наличие дивергентной и недивергентной

формы записи законов сохранения, выполнение балансов отдельных видов энергии и т.п.). Та-

ким образом, в надёжной дискретной модели различные формы записи законов сохранения

должны переходить друг в друга с помощью тождественных преобразований, аналогичных

тем, которые имеют место в дифференциальном случае.

Принцип полной консервативности был первоначально сформулирован для уравнений га-

зовой динамики и магнитной гидродинамики, а затем применён к другим классам задач ма-

тематической физики. В работе [8] в одномерном приближении были рассмотрены некоторые

особенности применения принципа полной консервативности при решении эволюционных за-

дач с подвижными границами. Для задачи о кристаллизации многокомпонентного раствора

на подвижной и фиксированной сетках были построены дивергентные и недивергентные раз-

ностные схемы, гарантирующие выполнение балансов внутренней энергии и массы. Как и в

дифференциальном случае, разностные уравнения переходят друг в друга с помощью замены

переменных.

В статье [9] рассмотрена задача Стефана в цилиндрической системе координат в осесиммет-

ричном приближении. Основу математической модели составляют уравнения Навье-Стокса в

переменных функции тока-вихрь, уравнения тепло- и массопереноса в твёрдой и жидкой фа-

зах, условия термодинамического равновесия на границе раздела фаз. Для определения поло-

жения границы раздела фаз используется метод выпрямления фронта [10]. Задача решается

в системе координат, полученной в результате замены переменных специального вида. В этой

системе координат положение границы раздела фиксировано. Разностная схема построена в

930

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

931

новой системе координат на неподвижной сетке. Получены дивергентная и недивергентная

формы записи, аппроксимирующие соответствующие формы записи исходной дифференци-

альной задачи, при этом на разностном уровне выполняются законы сохранения кинетической

и внутренней энергии, балансы масс для компонентов. В работе [11] показано, что в разностной

схеме, построенной с помощью метода выпрямления фронта, можно выполнить дискретный

аналог преобразования системы координат и получить алгебраически эквивалентную вычис-

лительную схему на подвижной сетке, согласованной с формой границы раздела фаз.

В данной работе продолжены исследования свойств разностной схемы, предложенной в ста-

тьях [9, 11]. Доказано, что разностный оператор, аппроксимирующий диссипативные члены в

уравнениях движения жидкости и теплопереноса в расчётной системе координат, самосопря-

жён и отрицательно определён. Показано, что вычислительная схема, полученная с помощью

метода выпрямления фронта, является энергетически нейтральной. Рассмотрены граничные

условия для вихря, обеспечивающие выполнение закона сохранения завихрённости на раз-

ностном уровне. Результаты, полученные ниже и в работах [9, 11], позволяют утверждать, что

построенный класс схем наследует основные свойства исходной дифференциальной задачи о

фазовом переходе.

1. Постановка задачи. Задача о фазовом переходе рассматривается в рамках следу-

ющих предположений. Твёрдая и жидкая фазы имеют одинаковые плотности ρ^s = ρ^lq и

удельные теплоёмкости c^sp = c^pq, но различные коэффициенты теплопроводности - k^s и k^lq

соответственно. Жидкая фаза является вязкой несжимаемой жидкостью с кинематической

вязкостью ν. Поля температуры T (t, r, z) и скоростей V(t, r, z) жидкости предполагают-

ся осесимметричными. Моделирование осуществляется в цилиндрической системе координат

Orz в области Ω(r,z) = [0,R] × [0,Z]. В подобласти Ω^s(t,r,z) = {(r,z) : r ∈ [0,R], z ∈

∈ [0, ζ(t, r)]} находится твёрдая фаза, жидкая фаза располагается в подобласти Ω^lq(t, r, z) =

= {(r, z) : r ∈ [0, R], z ∈ [ζ(t, r), Z]}. Здесь z = ζ(t, r) - граница раздела фаз, положение

которой изменяется в ходе процесса.

Движение жидкости описывается уравнениями Навье-Стокса в переменных функции то-

ка-завихрённости. Компоненты вектора скорости V = (V^r, 0, V^z) записаны в виде

1 ∂ψ

Vr =

Vz =-

(1)

r ∂z

r ∂r

где ψ - функция тока. Завихрённость ω = rot V определяется следующим образом:

ω = (0,ω_ϕ,0), ω_ϕ = ∂_zV ^r - ∂_rV ^z,

где ∂r = ∂/∂r,

∂z = ∂/∂z. Для удобства в качестве неизвестной функции в уравнениях

движения будем использовать ω = -ω_ϕ/r. Конвективный перенос в жидкости описывается с

помощью уравнения переноса завихрённости

∂ω

1 ∂T

K(r,z)(ω,ψ) =

D(r,z)(r²ω) + β_T g

∂t

r ∂r

уравнения, связывающего завихрённость и функцию тока

-ω =

D(r,z)(ψ),

и уравнения конвективного теплопереноса

∂T

K(r,z)(T,ψ) =

D(r,z)(T).

∂t

Здесь βT - коэффициент температурного расширения, g - ускорение свободного падения,

K(r,z)/r - оператор, описывающий конвективный перенос

K(r,z)(f,ψ) = ∂_rH^r + ∂_zH^z, f = ω,T,

(2)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

5^∗

932

ГУСЕВ и др.

где компоненты конвективного потока H(r,z) = (H^r, H^z) имеют вид

H^r(f) = rV^rf = [∂_zψ]f, H^z(f) = rV^zf = -[∂_rψ]f,

D(r,z)/r - эллиптический оператор, описывающий диссипативные процессы в уравнениях пе-

реноса завихрённости и конвективной теплопроводности:

D(r,z)(r^βf) = ∂_rW^r + ∂_zW^z, f = ω,ψ,T,

(3)

компоненты потока W(r,z) = (W^r, W^z) вычисляются

Таблица. Параметры диссипативного

следующим образом:

потока

W^r(r^βf) = κr^α∂_r(r^βf), W^z(r^βf) = κr^α∂_z(r^βf),

-1

значения параметров κ, α, β приведены в таблице.

-1

Распределение температуры в твёрдой фазе описы-

k/(cpρ)

вается уравнением теплопроводности

∂T

D(r,z)(T).

∂t

На межфазной границе температура равна температуре фазового перехода

T|z=ζ(t,r) =T_ph

и выполняется закон сохранения энергии (условие Стефана):

[[(k∇T · N)]] = λρv_n.

(4)

Здесь [[q]] = q^s -q^lq - скачок величины q на фронте кристаллизации, ∇ = (∂_r, ∂_z), λ - скрытая

теплота плавления, v_n = v_ph(e_z · N), v_ph = v_ph(t, r) = dζ/dt - скорость движения границы

раздела фаз, N - единичная нормаль к межфазной границе, направленная в жидкую фазу,

e_z - единичный вектор в направлении оси z.

Граничные условия для температуры имеют вид

T|z=0 = T_bot(t,r), T|z=Z = T_top(t,r), T|r=R = T_wall(t,z).

Условия для функции тока и температуры на оси ампулы вытекают из условий симметрии

ψ = 0, ω_ϕ = 0,

∂_rT = 0.

Краевые условия для функции тока на фронте кристаллизации, верхней и боковой границах

жидкой фазы:

ψ = 0,

∂_nψ = 0.

Здесь ∂_n - производная по направлению внешней нормали к соответствующей границе.

2. Метод выпрямления фронта. Для решения задачи с внутренней подвижной гра-

ницей, положение которой необходимо определять в ходе решения задачи, применяется метод

выпрямления фронта (см. [10]). Физическая область Ω(r, z) отображается в расчётную область

S(ξ, η) так, что в новой системе координат положение границы раздела фаз фиксировано и

совпадает с координатной линией η = const.

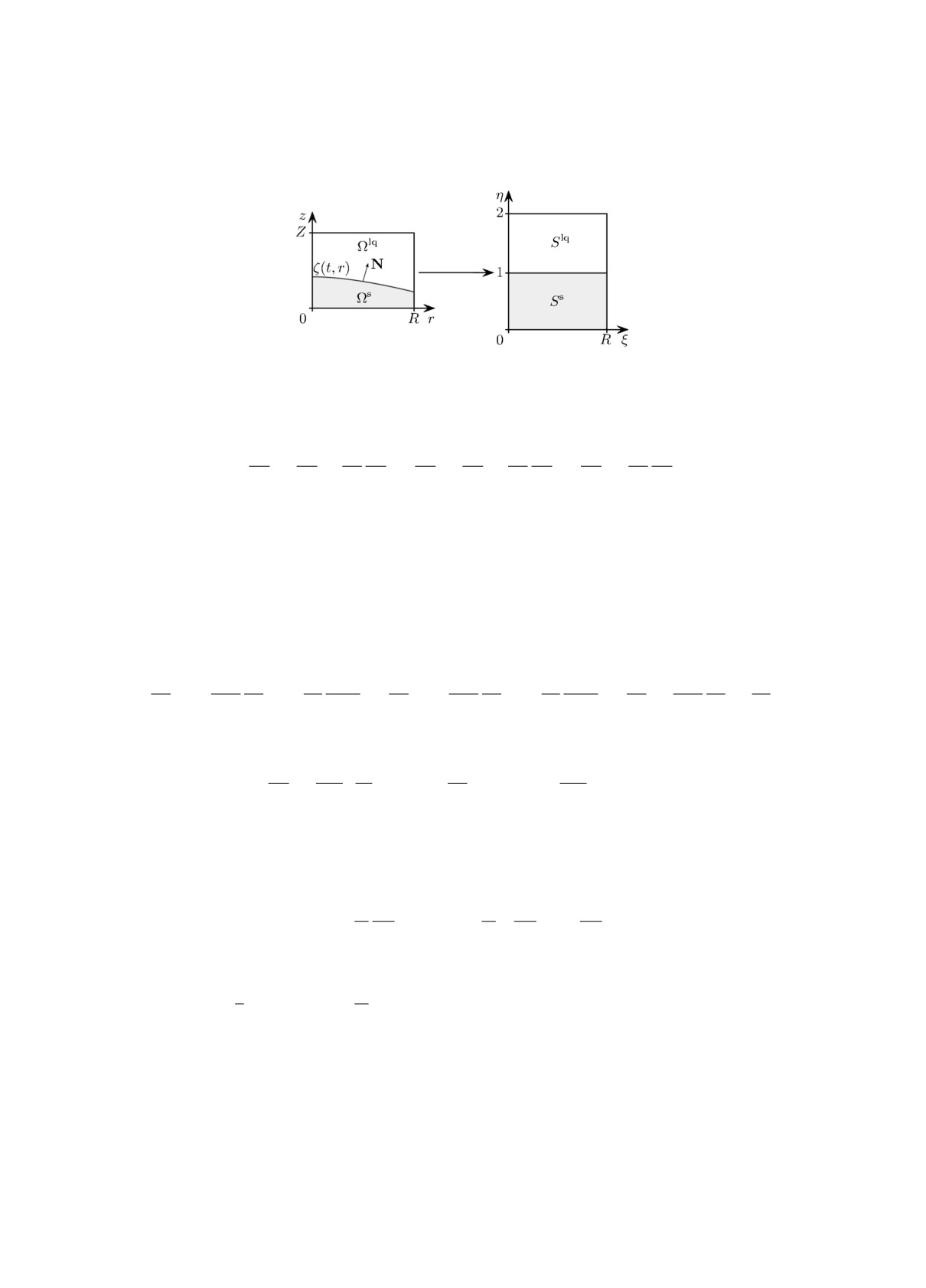
2.1. Преобразование системы координат. В данной работе используется замена пере-

менных, при которой области Ω^s, Ω^lq в новой системе координат становятся прямоугольни-

ками S^s и S^lq (рис. 1), а границы областей z = 0 , z = ζ(t, r) , z = Z переходят в прямые

η = 0, η = 1, η = 2 соответственно. Связь между системами координат имеет вид

{

z ∈ [0,ζ(t,r)],

t=t,ξ=r,η=z/ls,

(5)

1 + (z - ζ)/l^lq, z ∈ [ζ(t,r),Z],

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

933

где l^s = l^s(t, ξ) = ζ(t, ξ), l^lq = l^lq(t, ξ) = Z - ζ(t, ξ) - толщины зон Ω^s и Ω^lq соответственно.

Якобиан преобразования (5): J_m = ∂(t, ξ, η)/∂(t, r, z) = 1/l^m, m = s, lq.

Рис. 1. Преобразование системы координат.

Запишем задачу в новой системе координат (t, ξ, η). Частные производные неизвестных

функций f = T, ω, ψ преобразуются следующим образом:

∂f

∂η ∂f

∂f

∂η ∂f

∂f

∂η ∂f

∂t

∂t ∂η

∂r

∂ξ

∂r ∂η

∂z

∂z ∂η

Для вычисления производных ∂η/∂t,

∂η/∂r,

∂η/∂z воспользуемся обратным для (5) преоб-

разованием координат

{

t = t, r = ξ, z =ϕs(t,ξ,η) = Z1 + ls(η - ¹⁾,η ∈ [0,1],

(6)

ϕlq(t, ξ, η) = Z₂ + l^lq(η - 2), η ∈ [1, 2].

Якобиан этого преобразования равен J-1m = ∂(t, r, z)/∂(t, ξ, η) = l^m. Нетрудно показать, что

элементы матрицы Якоби вычисляются по формулам [12, 13]

∂η

∂z

1 ∂ϕ^m

∂η

∂z

1 ∂ϕ^m

∂η

∂r

∂t

Jm1

∂t

l^m

∂t

∂r

Jm1

lm ∂ξ

∂z

Jm1

∂ξ

l^m

Для производной по времени получим

[

]

∂f

∂

(ξl^mf) -

(ξϕm˜f)

T (ξ,η)(f).

∂t

ξl^m

∂t

∂η

ξl^m

В дальнейшем для краткости будем опускать волну над t и верхний индекс m у функций

l^m, ϕ^m, ϕ^mt = ∂ϕ^m/∂t, ϕ^mξ = ∂ϕ^m/∂ξ.

Формулы для вычисления скорости движения жидкости (1) преобразуются следующим

образом:

[

]

1 ∂ψ

∂ψ

Vr =

Vz =-

-ϕ_ξ

(7)

ξl ∂η

ξl

∂ξ

∂η

Тогда для конвективных членов (2) имеем

K(r,z)(f,ψ) =

K(ξ,η)(f,ψ), K(ξ,η)(f,ψ) = ∂_ξH^ξ + ∂_ηH^η.

(8)

ξl

Компоненты конвективного потока H(ξ,η) = (H^ξ, H^η) в расчётной области имеют вид

H^ξ = ξlU^ξf = [∂_ηψ]f, H^η = ξlU^ηf = -[∂_ξψ]f.

(9)

Здесь величины U^ξ и U^η равны скоростям переноса f вдоль соответствующих координатных

направлений и вычисляются по формулам

U^ξ = ∂_ηψ/(ξl), U^η = -∂_ξψ/(ξl).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

934

ГУСЕВ и др.

Важно отметить, что выражения (8), (9), полученные в расчётной системе координат (t, ξ, η)

для конвективных членов, с точностью до якобиана совпадают с записью соответствующего

оператора в физической области Ω^lq(t, r, z).

Оператор (3) преобразуется следующим образом:

D(r,z)(r^βf) =

D(ξ,η)(ξ^βf), D(ξ,η)(ξ^βf) = ∂_ξW^ξ + ∂_ηW^η,

ξl

где компоненты потока W(ξ,η) = (W^ξ , W^η) в расчётной системе координат имеют вид

W^ξ(ξ^βf) = κξ^α[L^ξξ∂_ξ(ξ^βf) + L^ξη∂_η(ξ^βf)],

(10)

W^η(ξ^βf) = κξ^α[L^ηξ∂_ξ(ξ^βf) + L^ηη∂_η(ξ^βf)].

(11)

Коэффициенты L^ξξ, L^ξη, L^ηξ, L^ηη вычисляются по формулам

L^ξξ = l, L^ξη = L^ηξ = -ϕ_ξ, L^ηη = (1 + ϕ2ξ)/l.

Таким образом, уравнения Навье-Стокса в расчётной системе координат имеют вид

[

]

∂

T (ξ,η)(ω) +

K(ξ,η)(ω,ψ) =

D(ξ,η)(ξ²ω) + β_T g

(ξlT ) -

(ξϕ_ξ T ) ,

(12)

ξl

∂ξ

∂η

−ω =

D(ξ,η)(ψ).

(13)

ξl

Для уравнения теплопереноса получим

T (ξ,η)(T) +

K(ξ,η)(T,ψ) =

D(ξ,η)(T).

(14)

ξl

Здесь и далее предполагается, что в твёрдой фазе конвективные члены тождественно равны

нулю.

Граничные условия и условия на фронте преобразуются аналогично. Для условия Стефана

(4) имеем (см. [9])

[[ (

)]]

∂T

k L^ηξ

+L^ηη

= λρv_ph.

(15)

∂ξ

∂η

Определим скалярное произведение функций f, g, интегрируемых с квадратом в области

S(ξ, η), следующим образом:

∫

(f, g)_S = fgξl dS.

Здесь и далее dS = dξ dη.

2.2. Свойства модели в расчётной системе координат. Система уравнений (12)-(15)

обладает следующими свойствами.

Закон сохранения завихрённости. Запишем уравнение (13), связывающее функцию

тока и завихрённость в неподвижной системе координат:

-ω = [∂_ξ(lV^z) - ∂_η(V^r + ϕ_ξV^z)]/(ξl).

(16)

Здесь мы воспользовались выражением (7) для скорости жидкости и равенством l_ξ = ϕ_ξη.

Применив теорему Остроградского-Гаусса, из уравнения (16) в силу условий прилипания по-

лучим закон сохранения завихрённости

∫

− ωξl dS =

[∂_ξ(lV^z) - ∂_η(V^r + ϕ_ξV^z)] dS = (lV^z)|ξ=0 dη.

(17)

S^lq

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

935

Закон сохранения кинетической энергии. Конвективные члены в уравнении переноса

завихрённости (12) не вносят вклад в баланс кинетической энергии [14], т.е.

)

∫

⁽K(ξ,η)

(ω, ψ)

,ψ

K(ξ,η)(ω,ψ)ψ dS = 0.

(18)

ξl

S^lq

Закон сохранения внутренней энергии. В рассматриваемой системе выполняется за-

кон сохранения теплоты. При этом для конвективных членов в уравнениях теплопереноса (14)

имеем

)

⁽K(ξ,η)

(T, ψ)

⁽K(ξ,η)

(T, ψ)

= 0,

= 0.

(19)

ξl

S^lq

D(ξ,η)(f)

Свойства эллиптического оператора. Оператор

, f = ξ2ω,ψ,T, является

ξl

самосопряжённым и отрицательно определённым в пространстве функций D(S^′) = {f ∈

∈ C²(S^′) : f|_∂S′ = 0}.

Покажем самосопряжённость оператора. Воспользуемся тем, что на границе области функ-

ции f и g обращаются в нуль; проинтегрировав дважды, получим

)

∫

⁽D(ξ,η)

(f)

[∂_ξ (κξ^αL^ξξ∂_ξf + κξ^αL^ξη∂_ηf) + ∂_η(κξ^αL^ηη∂_ηf + κξ^αL^ηξ∂_ξf)]g dS =

ξl

S^′

∫

(

)

D(ξ,η)(g)

[∂_ξ(κξ^αL^ξξ∂_ξ g + κξ^αL^ηξ∂_ηg) + ∂_η(κξ^αL^ηη∂_ηg + κξ^αL^ξη∂_ξg)]f dS = f,

(20)

ξl

S^′

Самосопряжённость оператора имеет место в силу того, что L^ξη = L^ηξ.

Покажем отрицательную определённость оператора:

)

∫

⁽D(ξ,η)

(f)

D(ξ,η)(f)f dS =

ξl

S^′

∫

[κξ^αL^ξξ(∂_ξ f)² + 2κξ^αL^ξη∂_ξf∂_ηf + κξ^αL^ηη(∂_ηf)²] dS.

(21)

S^′

В силу критерия Сильвестра подынтегральное выражение является положительно определён-

D(ξ,η)(f)

ной квадратичной формой, поэтому оператор

- отрицательно определённый.

ξl

Численный метод решения задачи будем строить таким образом, чтобы на разностном

уровне выполнялись дискретные аналоги свойств (17)-(21).

3. Разностная задача.

3.1. Сетка и сеточные функции. В расчётной области S(ξ,η) введём прямоугольную

сетку ω(ξ,η)h = ω^ξh × ω^ηh : ω^ξh = {ξ_i, i = 0, M, ξ₀ = 0, ξ_M = R}, ω^ηh = {η_j , j = 0, N, η₀ = 0,

η_j∗ = 1, η_N = 2} таким образом, чтобы фронт кристаллизации располагался в узлах сетки

c координатами (ξ_i, η_j∗ ), i = 0, M; шаги сетки ω(ξ,η)h: hξi+1/2 = ξi+1 - ξ_i, hηj+1/2 = ηj+1 - η_j .

Введём также потоковые узлы: ξi+1/2 = (ξi+1+ξ_i)/2, ηj+1/2 = (ηj+1+η_j)/2. Расчётную область

S(ξ, η) разобьём на прямоугольные ячейки S(ξ,η)ij = [ξi-1/2, ξi+1/2]×[ηj-1/2, ηj+1/2] с границами

∂S(ξ,η)i+1/2,j,

∂S(ξ,η)i,j-1/2,

∂S(ξ,η)i-1/2,j,

∂S(ξ,η)i,j+1/2; длины границ ячейки S(ξ,η)ij равны ℏ^ξi = 0.5(hξi+1/2 +

+ hξi-1/2) и ℏ^ηj = 0.5(hηj+1/2 + hηj-1/2), её площадь dS(ξ,η)ij = ℏ^ξiℏ^ηj. Также рассмотрим ячейки

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

936

ГУСЕВ и др.

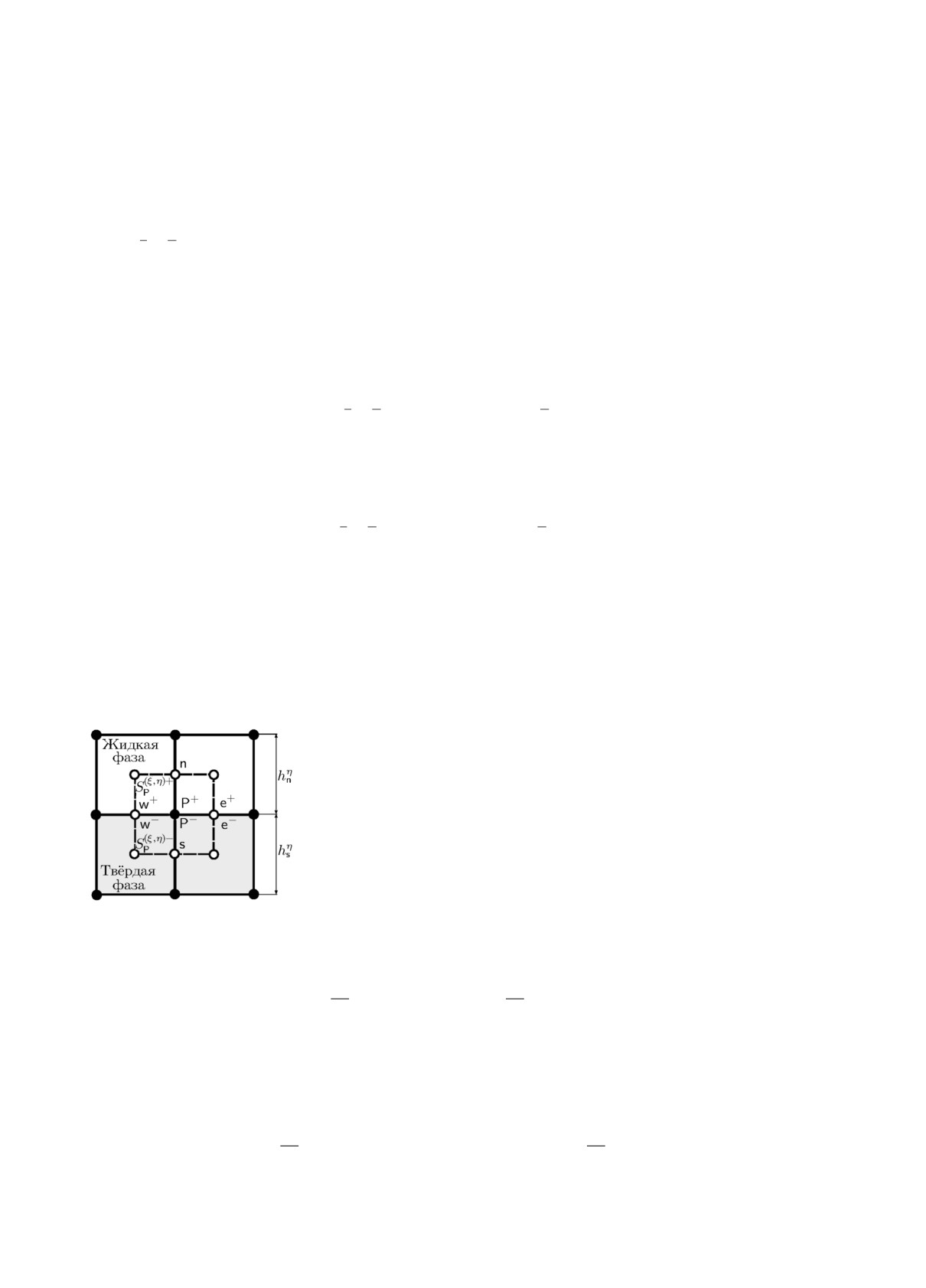
S(ξ,η)i+1/2j+1/2 с центрами в точках (ξi+1/2,ηj+1/2) (рис. 2). Сетка по времени ωτ = {t0 = 0,

tk+1 = t_k + τ, k = 0,1,...}, где τ - шаг по времени.

Рис. 2. Сетка и сеточные функции.

Сеточные функции f^kij = f(t_k, ξ_i, η_j ), f = T,ψ,ω, будем относить к узлам сетки. До-

определим эти функции внутри расчётных ячеек: f(t_k, ξ, η) = f^kij при (ξ, η) ∈ S(ξ,η)ij. Длины

фаз lij+1/2 задаются в серединах горизонтальных границ ячеек S(ξ,η)ij. Длина фазы в центре

ячейки вычисляется с помощью линейной интерполяции

l_ij

= (lij+1/2hηj+1/2 + lij-1/2hηj-1/2)/(2ℏ^ηj ).

Таким образом, l_ij = lsi в твёрдой фазе, l_ij = llqi в жидкой фазе,

l_ij∗ = (llqihηj∗+1/2+lih^j∗-1/2)/(2ℏj∗⁾

на фронте кристаллизации. Физические параметры областей κ и метрические коэффициенты

L^ξξ, L^ξη, L^ηη относятся к центрам ячеек S(ξ,η)i+1/2j+1/2 (см. рис. 2).

Подмножество узлов сетки ω(ξ,η)h, принадлежащих жидкой фазе, обозначим через ω(ξ,η)lq.

Введём множество индексов узлов сетки ωγξ,η) : (I_γ × J_γ ), γ = h, lq, а также множество

индексов внутренних узлов сетки ωγξ,η) : (I_γ × J_γ ). Для проверки выполнения интеграль-

ных свойств сеточного решения определим скалярное произведение для сеточных функций,

заданных в центрах ячеек S(ξ,η)ij, следующим образом:

∑

(f, g)_γ =

f_ijg_ijξ_il_ij dS(ξ,η)ij, γ = h,lq.

(22)

(i,j)∈(Iγ ×Jγ )

Для обозначения узлов сетки введём также локальную географическую нотацию [2] (см.

рис. 2). Определим сеточные операторы разностного дифференцирования. Для пространствен-

ных производных в направлении оси ξ имеем fP,ξ = (f_E - f_P)/h^e, fP,¯_ξ = fW,ξ; разностные

аппроксимации пространственных производных в направлении оси η : fP,η = (f_N - f_P)/hⁿ,

fP,η = fS,η, fP,η = (f_n - f_P)/(0.5hⁿ), fP,̃η = fS,̃η. Разностную производную по времени обозна-

чим через f_t =

f_P - f_P)/τ, где

f_P = f(t_k + τ,ξ_P,η_P).

3.2. Разностная схема. С помощью интегро-интерполяционного метода построим кон-

сервативную разностную схему. Проинтегрируем уравнения (12)-(14) по ячейке S(ξ,η)P. В ре-

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

937

гулярных точках сетки для эволюционных уравнений (12), (14) получим

∫

T (ξ,η)(f)dS +

K(ξ,η)(f,ψ)dS -

D(ξ,η)(ξ^βf)dS = 0.

(23)

(ξ,η)

S(ξ,η)P

S_P

(Аппроксимация подъемной силы в уравнении переноса завихрённости строится стандартным

образом.)

Построим сначала аппроксимации для второго и третьего интегралов в уравнении (23).

Перейдём с помощью теоремы Остроградского-Гаусса к интегралам по границе ячейки и по-

лучим

∫

K(ξ,η)(f, ψ) dS ≈ K(ξ,η)(f, ψ)ℏξℏη =

[H^ξN^ξ + H^ηN^η] dγ,

(24)

S(ξ,η)

∂S(ξ,η)

∫

(ξ,η)(ξ^βf) dS ≈ D(ξ,η)(ξβ f)ℏξℏη =

[W^ξN^ξ + W^ηN^η] dγ.

(25)

S(ξ,η)

∂S(ξ,η)

Здесь N^ξ, N^η - компоненты вектора внешней нормали к границе ячейки S(ξ,η)P.

Процесс построения аппроксимаций для операторов K(ξ,η) и D(ξ,η) сводится к вычисле-

нию значений соответствующих потоков в центрах границ ячейки S(ξ,η)P. При этом требуется

вычислять значения сеточных функций, а также их производных в узлах, в которых они не

определены. Переинтерполяцию соответствующих величин можно осуществлять различными

способами, однако предпочтение следует отдавать аппроксимациям, обеспечивающим на раз-

ностном уровне выполнение дискретных аналогов свойств (17)-(21) дифференциальной зада-

чи (12)-(15). В дальнейшем при выборе интерполяционных формул будем руководствоваться

данным принципом.

3.2.1. Аппроксимация конвективных членов. Для конвективных членов имеем

∫

[H^ξN^ξ + H^ηN^η] dγ =

H^ξ dη -

H^ξ dη +

H^η dξ -

H^η dξ.

∂S(ξ,η)

∂Seξ,η)

∂Swξ,η)

∂Snξ,η)

∂Ssξ,η)

Отсюда следует, что выражение (24) можно представить в виде

K(ξ,η)h(f,ψ)ℏ^ξℏ^η = (Hξe - Hξw)ℏ^η + (Hηn - Hηs)ℏ^ξ.

В уравнении переноса завихрённости (12) конвективный поток в центрах границ ячейки

будем аппроксимировать следующим образом:

Hξe = 0.5[ψ

◦

ω_E + ψ

◦

ω_P], Hηn = 0.5[ψ

◦

ω_N + ψ

◦

ω_P].

E,η

P,η

N,ξ

P,ξ

Потоки через “западную” и “южную” границы вычисляются аналогично. Таким образом, ап-

проксимация конвективных членов в уравнениях Навье-Стокса имеет вид

K(ξ,η)h(ω,ψ) = (ψ

◦

(26)

P,η

ω_P)◦η^.

Выражение (26) совпадает с соотношением, предложенным А. Аракавой в работе [14], для

аппроксимации конвективных членов в уравнении Навье-Стокса в декартовой системе коор-

динат. В работе [14] доказано следующее утверждение.

Утверждение 1. Конвективные члены, записанные в форме (26), не вносят вклад в ба-

ланс кинетической энергии, т.е.

)

⁽K(ξ,η)

(ω, ψ)

,ψ

= 0.

ξl

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

938

ГУСЕВ и др.

В уравнении теплопереноса (14) компоненты конвективного потока в центрах границ ячеек

вычисляются следующим образом:

Hξe(T) = ψ

◦

T_e, Hηn(T) = ψ

◦

T_n,

e,η

n,ξ

а конвективные члены записываются в виде

K(ξ,η)h(T,ψ) = (ψ

◦

T_e)˜ξ - (ψ

◦

T_n)_η.

(27)

e,η

n,ξ

Выражение (27) также предложено в работе [14] для аппроксимации конвективных членов в

уравнении теплопереноса в декартовой системе координат. Там же доказано ещё одно утвер-

ждение.

Утверждение 2. Конвективные члены, записанные в форме (27), не влияют на баланс

теплоты, а также на среднее по области значение квадрата температуры, т.е.

)

⁽K(ξ,η)

(T, ψ)

⁽K(ξ,η)

(T, ψ)

= 0,

= 0.

ξl

Таким образом, использование выражений (26), (27) для аппроксимации конвективных чле-

нов в уравнениях переноса завихрённости и теплопереноса позволяет построить энергетически

нейтральную вычислительную схему.

3.2.2. Аппроксимация эллиптического оператора. Для оператора D(ξ,η) из соотно-

шения (25) получим

D(ξ,η)h(ξ^βf)ℏ^ξℏ^η = (Wξe - Wξw)ℏ^η + (Wηn - Wηs)ℏ^ξ.

(28)

Аппроксимируем потоки в выражении (28) на границе ячейки S(ξ,η)P. Рассмотрим для опре-

делённости “восточную” границу

∫

Wξeℏ^η =

W^ξ(ξ^βf)dη =

[L^ξξ∂_ξ(ξ^βf) + L^ξη∂_η(ξ^β f)] dη.

(29)

∂Seξ,η)

Здесь L^ξξ = ξ^ακL^ξξ, L^ξη = ξ^ακL^ξη и L^ηη = ξ^ακL^ηη, L^ηξ = ξ^ακL^ηξ. Для интегралов по

границе ячейки в (29) имеем

∫

L^ξξ∂_ξ(ξ^βf)dη ≈ Lξξe(ξ^βf)_ξℏ^η,

∂Seξ,η)

∫

L^ξη∂_η(ξ^βf)dη ≈ 0.5[hηnLξηne(ξ^βf)e,η + hηsLξηse(ξ^βf)e,η].

(30)

∂Seξ,η)

Для вычисления метрических коэффициентов и разностных производных в центре границы

∂Seξ,η) будем использовать следующие интерполяционные формулы:

Lξξe = [hηnLξξne + hηsLξξse]/(2ℏ^η), (ξ^βf)e,η = 0.5[(ξ^βf)P,η + (ξ^βf)E,η],

(ξ^β f)e,η = 0.5[(ξ^β f)P,η + (ξ^βf)E,η].

Поток через “северную” границу ∂Snξ,η) вычисляется по формуле

∫

Wηnℏ^ξ =

W^η(ξ^βf)dξ ≈ Lηηn(ξ^βf)_ηℏ^ξ + 0.5[hξeLηξne(ξ^βf)n,ξ + hξwLηξnw(ξ^βf)n,¯_ξ],

∂Snξ,η)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

939

а в центре границы имеем

Lηηn = [hξeLηηne + hξwLηηnw]/(2ℏ^ξ), (ξ^βf)n,ξ = 0.5[(ξ^βf)P,ξ + (ξ^βf)N,ξ],

(ξ^β f)n,¯_ξ = 0.5[(ξ^β f)P,¯_ξ + (ξ^β f)N,¯_ξ].

Выражения для потоков через “западную” и “южную” границы вычисляются аналогичным

образом.

Рассмотрим пространство сеточных функций D_h(ωγξ,η)) = {f_ij , (i, j) ∈ (I_γ×J_γ ) : f_ij = 0,

(i, j) ∈ (I_γ×J_γ ) \ (I_γ ×J_γ )}. Докажем следующие утверждения.

Утверждение 3. Для сеточных функций из пространства D_h(ωγξ,η)) разностный опера-

тор D(ξ,η)h(f_ij)/(ξ_il_ij) является отрицательно определённым относительно сеточного ска-

лярного произведения (22):

)

⁽D(ξ,η)

(f)

< 0, γ = h, lq.

(31)

ξl

Доказательство. Левую часть неравенства (31) запишем в виде

)

⁽D(ξ,η)

(f)

∑

(Wξi+j/2 - Wξi-j/2)f_ijℏ^ηj +

(Wηij+1/2 - Wηij-1/2)f_ij ℏ^ξi. (32)

ξl

(i,j)∈(Iγ ×Jγ )

Рассмотрим первую сумму в правой части (32). Преобразуем в ней члены, содержащие

коэффициент L^ξξ. Представим эти члены в виде полусуммы разностных производных назад

и вперед в направлении ξ :

∑

[Lξξi+j/2f_ξ - Lξξi-j/2f¯_ξ]fijℏ^j =

(i,j)∈(Iγ ×Jγ )

∑

[hξi-1/2(Lξξi+j/2f_ξ)¯_ξ + hξi+1/2(Lξξi-j/2f¯_ξ)ξ]fij ℏ^j.

(33)

(i,j)∈(Iγ ×Jγ )

Используем в правой части равенства (33) формулу суммирования по частям [15, с. 46] по

индексу i. С учётом условий на границе области имеем

∑

1^∑

[hξi-1/2(Lξξi+j/2f_ξ)¯_ξ + hξi+1/2(Lξξi-j/2f¯_ξ)ξ]fijℏ^j =

j∈Jγ i∈Iγ

∑

[hξi+1/2Lξξi+j/2(f_ξ)² + hξi-1/2Lξξi-j/2(f¯_ξ)²]ℏ^ηj.

(34)

j∈Jγ i∈Iγ

Запишем члены, содержащие смешанные производные, в виде

∑

S₁ =

hξi-1/2hηj+1/2(Lξηi+j/2+1/2f_η)¯_ξfij +1

hξi+1/2hηj+1/2(Lξηi-j/2+1/2f_η)_ξf_ij +

(i,j)∈(Iγ ×Jγ )

∑

hξi-1/2hηj-1/2(Lξηi+j/2-1/2f_η)¯_ξfij +1

hξi+1/2hηj-1/2(Lξηi-j/2-1/2f_η)_ξf_ij. (35)

(i,j)∈(Iγ ×Jγ )

Применим к первому слагаемому в (35) формулу суммирования по частям по индексу i:

∑

1^∑

ξη

hξi-1/2hηj+1/2(Lξηi+j/2+1/2f_η)¯_ξfij = -1∑

hξi+1/2hηj+1/2L

f_ξf_η.

i+j/2+1/2

j∈Jγ i∈Iγ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

940

ГУСЕВ и др.

Преобразуем второе, третье и четвертое слагаемые в (35) аналогичным образом и получим

∑

S₁ = -

[hξi+1/2hηj+1/2Lξηi+j/2+1/2f_ξf_η + hξi-1/2hηj+1/2Lξηi-j/2+1/2f¯_ξfη] -

(i,j)∈(Iγ ×Jγ )

∑

[hξi-1/2hηj-1/2Lξηi-j/2-1/2f¯_ξfη + hξi+1/2hηj-1/2Lξηi+j/2-1/2fξfη].

(36)

(i,j)∈(Iγ ×Jγ )

Рассмотрим вторую сумму в правой части выражения (32). Для членов, содержащих ко-

эффициент L^ηη, имеем

∑

[Lηηij+1/2f_η - Lηηij-1/2f_η]f_ijℏ^ξi =

(i,j)∈(Iγ ×Jγ )

∑

[hηj+1/2Lηηij+1/2(f_η)² + hηj-1/2Lηηij-1/2(f_η)²]ℏ^ξi.

(37)

(i,j)∈(Iγ ×Jγ )

Члены, содержащие смешанные производные, запишем в виде

∑

S₂ = -

[h^ξ

h^η

L^ηξ

f_ξf_η + h^ξ

h^η

L^ηξ

f_ξf_η] -

i+1/2

j+1/2

i+j/2+1/2

i+1/2

j-1/2

i+j/2-1/2

(i,j)∈(Iγ ×Jγ )

∑

[h^ξ

h^η

L^ηξ

f_η + h^ξ

h^η

L^ηξ

f_η].

(38)

i-1/2

j+1/2

i-j/2+1/2

i-1/2

j-1/2

i-j/2-1/2

(i,j)∈(Iγ ×Jγ )

В силу того, что L^ξη = L^ηξ, выражение (38) совпадает c (36), т.е. S₁ = S₂.

Заменив в правой части соотношения (32) потоки их представлениями (34), (36)-(38), по-

лучим

)

∑

⁽D(ξ,η)

(f)

hξi+1/2hηj+1/2[Lξξi+j/2+1/2(f_ξ)² +2Lξηi+j/2+1/2f_ξf_η +Lηηi+j/2+1/2(f_η)²]-

ξl

(i,j)∈(Iγ ×Jγ )

∑

hξi-1/2hηj+1/2[Lξξi-j/2+1/2(f¯_ξ)² + 2Lηξi-j/2+1/2f¯_ξfη + Lηηi-j/2+1/2(fη)²] -

(i,j)∈(Iγ ×Jγ )

∑

hξi+1/2hηj-1/2[Lξξi+j/2-1/2(f_ξ)² + 2Lξηi+j/2-1/2f_ξf_η + Lηηi+j/2+1/2(f_η)²] -

(i,j)∈(Iγ ×Jγ )

∑

hξi-1/2hηj-1/2[Lξξi-j/2-1/2(f¯_ξ)² + 2Lξηi-j/2-1/2f¯_ξfη + Lηηi-j/2-1/2(fη)²].

(i,j)∈(Iγ ×Jγ )

В силу критерия Сильвестра квадратичные формы, находящиеся под знаками сумм, явля-

ются положительно определёнными:

L^ξξpq = l_pq > 0, L^ξξpqL^ηηpq - (L^ξηpq)² = 1 > 0, p = i ± 1/2, q = j ± 1/2,

откуда

)

⁽D(ξ,η)

(f)

< 0, γ = h, lq.

ξl

Утверждение доказано.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

941

Утверждение 4. Для сеточных функций из пространства D_h(ωγξ,η)) разностный опера-

тор D(ξ,η)h(f_ij)/(ξ_il_ij) является самосопряжённым относительно сеточного скалярного про-

изведения (22):

)

(

⁽D(ξ,η)

(f)

D(ξ,η)h(g)⁾

= f,

γ = h,lq.

(39)

ξl

Доказательство. Запишем левую часть равенства (39) следующим образом:

)

⁽D(ξ,η)

(f)

∑

D(ξ,η)h(f_ij)g_ijℏ^ξiℏ^ηj =

ξl

(i,j)∈(Iγ ×Jγ )

∑

(Wξi+j/2 - Wξi-j/2)g_ij ℏ^ηj +

(Wηij+1/2 - Wηij-1/2)g_ij ℏ^ξi.

(40)

(i,j)∈(Iγ ×Jγ )

Рассмотрим первую сумму в правой части (40). Преобразуем в ней члены, содержащие

коэффициент L^ξξ. Для этого дважды воспользуемся формулой суммирования по частям по

индексу i:

∑

hξi-1/2(Lξξi+j/2f_ξ)¯_ξgijℏ^j = -

hξi+1/2Lξξi+j/2f_ξg_ξℏ^ηj =

(i,j)∈(Iγ ×Jγ )

∑

hξi-1/2(Lξξi+j/2g_ξ)¯_ξfijℏ^j.

(41)

(i,j)∈(Iγ ×Jγ )

Применив последовательно формулу суммирования по частям по индексам i и j, запишем

члены, содержащие смешанные производные, в виде

∑

hξi-1/2hηj+1/2(Lξηi+j/2+1/2f_η)¯_ξgij +1

hξi+1/2hηj+1/2(Lξηi-j/2+1/2f_η)_ξg_ij +

(i,j)∈(Iγ ×Jγ )

∑

hξi-1/2hηj-1/2(Lξηi+j/2-1/2f_η)¯_ξgij +1

hξi+1/2hηj-1/2(Lξηi-j/2-1/2f_η)_ξg_ij =

(i,j)∈(Iγ ×Jγ )

∑

hξi+1/2hηj-1/2(Lξηi+j/2+1/2g_ξ)_ηf_ij +1

hξi-1/2hηj-1/2(Lξηi-j/2+1/2g¯_ξ)ηfij +

(i,j)∈(Iγ ×Jγ )

∑

hξi+1/2hηj+1/2(Lξηi+j/2-1/2g_ξ)_ηf_ij +1

hξi-1/2hηj+1/2(Lξηi-j/2-1/2g¯_ξ)ηfij. (42)

(i,j)∈(Iγ ×Jγ )

Здесь воспользовались тем, что

∑

hξi-1/2hηj+1/2(Lξηi+j/2+1/2f_η)¯_ξgij =

(i,j)∈(Iγ ×Jγ )

∑

hξi+1/2hηj+1/2Lξηi+j/2+1/2f_ηg_ξ =1

hξi+1/2hηj-1/2(Lξηi+j/2+1/2g_ξ)_ηf_ij,

(i,j)∈(Iγ ×Jγ )

оставшиеся слагаемые в левой части равенства (42) преобразованы аналогично.

Рассмотрим вторую сумму в правой части (40). Для членов, содержащих коэффициент

L^ηη, получим

∑

hηj-1/2(Lηηj+1/2f_η)_ηg_ijℏ^ξi =

hηj-1/2(Lηηij+1/2g_η)_ηf_ijℏ^ξi.

(43)

(i,j)∈(Iγ ×Jγ )

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

942

ГУСЕВ и др.

Аналогично (42) запишем

∑

hξi+1/2hηj-1/2(Lηξi+j/2+1/2f_ξ)_ηg_ij +1

hξi+1/2hηj+1/2(Lηξi+j/2-1/2f_ξ)_ηg_ij +

(i,j)∈(Iγ ×Jγ )

∑

hξi-1/2hηj-1/2(Lηξi-j/2+1/2f¯_ξ)ηgij +1

hξi-1/2hηj+1/2(Lηξi-j/2-1/2f¯_ξ)ηgij =

(i,j)∈(Iγ ×Jγ )

∑

hξi-1/2hηj+1/2(Lηξi+j/2+1/2g_η)¯_ξfij +1

hξi-1/2hηj-1/2(Lηξi+j/2-1/2g_η)¯_ξfij +

(i,j)∈(Iγ ×Jγ )

∑

hξi+1/2hηj+1/2(Lηξi-j/2+1/2g_η)_ξf_ij +1

hξi+1/2hηj-1/2(Lηξi-j/2-1/2g_η)_ξf_ij. (44)

(i,j)∈(Iγ ×Jγ )

Подставим правые части выражений (41)-(44) в правую часть равенства (40). В силу того,

что L^ξη = L^ηξ , имеем

)

(

⁽D(ξ,η)

(f)

D(ξ,η)h(g)⁾

= f,

γ = h,lq.

ξl

Утверждение доказано.

Возможны и другие способы переинтерполяции искомых функций в потоковые точки. Со-

ответствующие разностные выражения могут иметь тот же порядок аппроксимации, что и

операторы (26)-(28). Однако построенные на их основе разностные уравнения не будут обла-

дать свойствами, аналогичными свойствам исходной дифференциальной задачи. В работе [16]

предложена следующая аппроксимация оператора D(ξ,η) :

D(ξ,η)(ξβf)ℏξℏη = (Wξe -Wξw)ℏη + (Wηn -Wηs)ℏξ,

Wξ

= Lξξe (ξ^βf)_ξ + Lξηe[(ξ^βf)_ne - (ξ^βf)_se]/ℏ^η,

Wη

= Lηηn(ξ^βf)_η + Lηξn [(ξ^βf)_ne - (ξ^βf)_nw]/ℏ^ξ.

D(ξ,η)

Нетрудно показать, что разностный оператор

(f_ij)/(ξ_il_ij ) не является самосопряжённым

относительно сеточного скалярного произведения (22). При этом выражения, использующиеся

в статье [16] для аппроксимации конвективных членов, не обеспечивают выполнение разност-

ных аналогов законов сохранения кинетической энергии, массы и теплоты.

3.2.3. Аппроксимация производной по времени. Для оператора T(ξ,η)(f) получим

∫

T (ξ,η)(f)dξ dη ≈ T (ξ,η)h(f)ℏ^ξℏ^η = ∂_t(l_Pf_P)ξ_Pℏ^ξℏ^η - [(ϕ_tf)_n - (ϕ_tf)_s]ξ_Pℏ^ξ.

(45)

S(ξ,η)P

Здесь (ϕ_tf)_n = ϕn,tf_n, (ϕ_tf)_s = ϕs,tf_s. Значения функции f в центрах горизонтальных граней

ячейки вычисляется по формулам f_n = (f_P + f_N)/2, f_s = (f_P + f_S)/2. Проинтегрируем (45)

по отрезку [t_k, tk+1], полученное выражение разделим на шаг τ и площадь ячейки dS(ξ,η)P :

T(ξ,η)h,τ(f) = (l_Pf_P)_t - [(ϕ_t

f)_n -(ϕ_tf)s]/ℏη.

(46)

ξ_P

Аппроксимация (46) содержит нелинейный член

PfP, для удобства запишем её в недивер-

гентной форме:

T(ξ,η)h,τ(f) = (l_Pf_P)_t - [(ϕ_t

f)_ηhηn + (ϕ_tf)˜¯ηhηs]/(2ℏη).

ξ_P

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

943

Воспользуемся формулами разностного дифференцирования произведения [15, с. 51]:

(l_Pf_P)_t = lP,tfP + lPfP,t = [ln,thηn + ls,thηs]/(2ℏη

f_P + [l_nhηn + l_shηs]/(2ℏ^η)fP,t,

[(ϕ_t

f)_ηhηn + (ϕ_tf)˜¯ηhηs]/(2ℏη) = [(ϕtηfP + ϕt,nfη)hηn + (ϕt˜¯ηfP + ϕt,sf˜¯η)hηs]/(2ℏη).

Отсюда с учётом того, что ln,t = ϕ_tη, ls,t = ϕtη, получаем недивергентную форму записи

производной по времени:

T(ξ,η)h,τ(f) = l_PfP,t - [ϕt,nfηhηn + ϕt,s

f˜¯ηhηs]/(2ℏ^η).

(47)

ξ_P

3.2.4. Аппроксимация уравнения, связывающего значения функции тока и за-

вихрённости. Аппроксимация уравнения (13) во внутренних точках области имеет вид

-ω_Pl_Pξ_P dS(ξ,η)P = D(ξ,η)h(ψ)dS(ξ,η)P.

(48)

Граничные условия для завихрённости строятся следующим образом: уравнение (13) интегри-

руется по приграничным ячейкам с учётом условий прилипания и непротекания. Рассмотрим

для определённости ячейку на вертикальной границе области. Получим

h^w

-ω_Pr_Pl_P

ℏ^η = [WξP(ψ) - Wξw(ψ)]ℏ^η + [Wηn(ψ) - Wηs(ψ)]hw

В силу условия прилипания на границе жидкой фазы имеем ψ = 0, WξP(ψ) = 0, ψP,ξ = ψN,ξ =

= ψS,ξ = 0, откуда

h^w

L^nwhⁿ + L^swh^s

L^nw

L^sw

-ω_Pr_Pl^lq

ℏ^η =

ψ_W -

ψ_NW +

ψ_SW.

(49)

2h^w

В декартовой системе координат L^ξξ = 1, L^ξη = L^ηξ = 0 и условие (49) преобразуется в

известное условие А. Тома [17]. Уравнения для завихрённости на других участках границы

жидкой фазы аппроксимируются аналогичным образом.

Утверждение 5. Пусть сеточная функция ω_ij удовлетворяет уравнению (48). Тогда

выполнен разностный аналог закона сохранения завихрённости в форме

∑

−

ω_ijl_ijξ_i dS(ξ,η)ij =

(V^zl)1/2j ℏ^ηj.

(i,j)∈(I_lq×J_lq)

j∈J_lq

Доказательство. Из уравнения (48) следует, что

∑

−

ω_ijl_ijξ_i dS(ξ,η)ij =

[(Wξi+j/2 - Wξi-j/2)ℏ^ηj + (Wηij+1/2 - Wηij-1/2)ℏ^ξi] -

(i,j)∈(I_lq×J_lq)

∑

−

[ω0jl0j ξ₀ dS(ξ,η)0j + ω_Njl_Nj ξ_N dS(ξ,η)Nj] -

[ω_ij∗ l0j∗₊₀ξ_i dS(ξ,η)ij∗ + ωiM liM ξi dS(ξ,η)iM].

(50)

j∈J_lq

i∈I_lq

Сумму потоков, протекающих через грани внутренних ячеек сетки, можно свести к следу-

ющей сумме по граничным контрольным объёмам:

∑

[(Wξi+j/2 - Wξi-j/2)ℏ^ηj + (Wηij+1/2 - Wηij-1/2)ℏ^ξi ] =

(i,j)∈(I_lq×J_lq)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

944

ГУСЕВ и др.

∑

[WξN-j/2 - Wξj/2]ℏ^ηj +

(51)

[WηiM-1/2 - Wηij∗+1/2]ℏi.

j∈J_lq

i∈I_lq

Подставив (50) в (51), получим

∑

−

ω_ijl_ijξ_i dS(ξ,η)ij = -

[ω0j l0j ξ₀ dS(ξ,η)0j + Wξj/2ℏ^ηj] -

[ω_Njl_Nj ξ_N dS(ξ,η)Nj - WξN-j/2ℏ^ηj] -

(i,j)∈(I_lq×J_lq)

j∈J_lq

∑

−

[ω_ij∗ l_ij∗₊₀ξ_i dS(ξ,η)ij∗ + W^ηij∗+1/2ℏⁱ] -

[ω_iM l_iM ξ_i dS(ξ,η)iM - WηiM-1/2ℏ^ξi].

(52)

i∈I_lq

Завихрённость на оси ω0j = 0, и в силу граничных условий (49) вторая, третья и четвёртая

суммы в правой части (52) также обращаются в нуль. Тогда

∑

−

ω_ijl_ijξ_i dS(ξ,η)ij =

-Wξ1/2jℏ^ηj.

(i,j)∈(I_lq×Jω)

j∈J_lq

Сравнив выражение (7) для скорости V^z и соотношение (10) для потока W^ξ, получим, что

V zl = -W^ξ(ψ), откуда

∑

−

ω_ijl_ijξ_i dS(ξ,η)ij =

(V^zl)1/2j ℏ^ηj.

(i,j)∈(I_lq×J_lq)

j∈J_lq

Утверждение доказано.

Заменим в уравнениях (12), (13) дифференциальные операторы их разностными аппрок-

симациями (26)-(28) и (47). Таким образом, неявная разностная схема для уравнений Навье-

Стокса имеет вид

T(ξ,η)h,τ(ω) dS(ξ,η)P + K(ξ,η)h(ω

ψ)dS(ξ,η)P = D(ξ,η)h(ω)dS(ξ,η)P - F(ξ,η)h(T) dS(ξ,η)P,

-ωlPξ_PdS(ξ,η)P = D(ξ,η)h

ψ) dS(ξ,η)P.

Функция тока и завихрённость в граничных условиях (49) также

отнесены к верхнему временному слою.

3.2.5. Аппроксимация условия Стефана. Для аппрокси-

мации условия Стефана (15) проинтегрируем уравнение теплопе-

реноса (14) по ячейке S(ξ,η)P, содержащей границу раздела фаз.

Область интегрирования разобьём на две подобласти: S(ξ,η)+P -

расположенную в жидкости и S(ξ,η)-P - лежащую в твёрдой фазе

(рис. 3). Аппроксимация T(ξ,η)(T ) на межфазной границе зада-

ётся формулой (45). Однако стоить помнить, что l_n, ϕt,n и l_s,

Рис. 3. Ячейка на фронте

кристаллизации.

ϕt,s относятся к жидкой и твёрдой фазам соответственно. Про-

интегрировав конвективные члены по области S(ξ,η)+P, получим

hⁿ

K(ξ,η)h(f,ψ)ℏ^ξ hⁿ

= [Hξe(T ) - Hξw(T )]

+ [Hηn(T ) - HηP(T )]ℏ^ξ .

Для вычисления H^w(T ), H^e(T ) используются следующие выражения: H^w(T ) = ψw,ηT_w,

H^e(T) = ψe,ηT_e; при этом компонента HηP(T) = 0, так как ψ

◦ = 0. Проинтегрировав дисси-

P,ξ

пативные члены по областям S(ξ,η)+P и S(ξ,η)-P, имеем

∫

hⁿ

D(ξ,η)+h(T)ℏ^ξ hⁿ

≈

D(ξ,η)(T)dΩ = [W^ξ

-W^ξ

]

+ [Wηn - W^η

]ℏ^ξ,

(53)

e⁺

w⁺

P⁺

S(ξ,η)+

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

О СВОЙСТВАХ ОДНОГО РАЗНОСТНОГО МЕТОДА

945

∫

h^s

D(ξ,η)-h(T)ℏ^ξ h^s

≈

D(ξ,η)(T)dΩ = [W^ξ

-W^ξ

]

+ [W^η

- Wηs ]ℏ^ξ.

(54)

e^-

w^-

P^-

S(ξ,η)-

Здесь величины с индексами P⁺, e⁺, w⁺ принадлежат S(ξ,η)+P, а с индексами P^-, e^-, w^-

располагаются в S(ξ,η)-P. Просуммировав (53) и (54), получим следующую аппроксимацию:

D(ξ,η)h(T)ℏ^ξℏ^η = [Wξe - Wξw]ℏ^η + [Wηn - Wηs]ℏ^ξ + [W^η

-W^η

]ℏ^ξ .

P^-

P⁺

Из условия Стефана (15) следует, что

W^η

-W^η

= λρξ_Pv_ph.

P^-

P⁺

Таким образом на границе раздела фаз аппроксимация диссипативных членов (28) дополняет-

ся слагаемым, описывающим выделение/поглощение теплоты при смене агрегатного состояния

вещества.

Во внутренних точках сетки неявная разностная схема для уравнений теплопереноса име-

ет вид

T(ξ,η)h,τ(T)dS(ξ,η)P + K(ξ,η)h

T)dS(ξ,η)P =D(ξ,η)h

T)dS(ξ,η)P.

Благодаря тому, что аппроксимации условий на границе раздела фаз и границах областей

согласованы с аппроксимациями соответствующих уравнений во внутренних узлах сетки, на

разностном уровне выполнен закон сохранения энергии. Из выполнения дискретного аналога

закона сохранения для квадрата искомой величины следует, что температура на протяжении

всего расчёта ограничена в любой точке сетки. Данное обстоятельство исключает возможность

возникновения в расчёте нелинейной вычислительной неустойчивости (nonlinear computational

instability [14, 18]).

Заключение. Для двухфазной задачи Стефана в цилиндрической системе координат по-

строена энергетически нейтральная консервативная разностная схема, в которой на разност-

ном уровне выполняются дискретные аналоги законов сохранения завихрённости, кинетиче-

ской и внутренней энергии. Показано, что разностный оператор, аппроксимирующий дисси-

пативные члены в уравнениях Навье-Стокса и теплопереноса, является самосопряжённым

и отрицательно определённым. В работе [11] показано, что преобразование системы коорди-

нат, выполненное на дискретном уровне в построенной разностной схеме, позволяет получить

консервативную разностную схему для задачи Стефана на подвижной сетке, согласованной с

формой фронта кристаллизации. Таким образом, предложенная разностная схема наследует

основные свойства исходной дифференциальной задачи как в неподвижной, так и в физиче-

ской системе координат. Важно отметить, что рассмотренная разностная схема естественным

образом обобщается на случай численного моделирования процесса кристаллизации много-

компонентного соединения [9].

СПИСОК ЛИТЕРАТУРЫ

1. Самарский А.А. Введение в теорию разностных схем. М., 1971.

2. Patankar S. Numerical Heat Transfer and Fluid Flow. London, 1981.

3. Cамарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М., 1971.

4. Тихонов А.Н., Самарский А.А. О разностных схемах для уравнений с разрывными коэффициента-

ми // Докл. АН СССР. 1956. Т. 108. № 3. С. 393-396.

5. Тихонов А.Н., Самарский А.А. О сходимости разностных схем в классе разрывных коэффициентов

// Докл. АН СССР. 1959. Т. 124. № 3. С. 529-532.

6. Тихонов А.Н., Самарский А.А. Об однородных разностных схемах // Журн. вычислит. математики

и мат. физики. 1961. Т. 1. № 1. С. 5-63.

7. Тихонов А.Н., Самарский А.А. Об однородных разностных схемах // Докл. АН СССР. 1958. Т. 122.

№ 4. С. 562-566.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

946

ГУСЕВ и др.

8. Мажорова О.С., Попов Ю.П., Щерица О.В. Консервативные разностные схемы для термодиффу-

зионной задачи Стефана // Дифференц. уравнения. 2013. Т. 49. № 7. С. 897-905.

9. Gusev A.O., Shcheritsa O.V., Mazhorova O.S. Conservative finite volume strategy for investigation of

solution crystal growth techniques // Computers & Fluids. 2020. V. 202. P. 104501.

10. Landau H.G. Heat conduction in a melting solid // J. of Appl. Math. 1950. V. 8. P. 81-94.

11. Гусев А.О., Щерица О.В., Мажорова О.С. К вопросу об эквивалентности разностных методов ре-

шения задачи Стефана на подвижных и фиксированных сетках // Дифференц. уравнения. 2021.

Т. 57. № 7. С. 907-921.

12. Флетчер К. Вычислительные методы в динамике жидкости. Т. 2. М., 1991.

13. Steger J. Implicit finite-difference simulation of flow about arbitrary two-dimensional geometries // Amer.

Inst. of Aeronaut. Astronaut. J. 1978. V. 16. № 7. P. 679-686.

14. Arakawa A. Computational design for long-term numerical integration of the equation of fluid motion:

two dimensional incompressible flow // J. Comput. Phys. 1966. V. 1. P. 119-143.

15. Самарский А.А. Теория разностных схем. М., 1989.

16. Lan C.W. Newton’s method for solving heat transfer, fluid flow and interface shapes in a floating molten

zone // Int. J. Numer. Methods Fluids. 1994. V. 19. P. 41-65.

17. Thom A. The flow past circular cylinders at low speeds // Proc. Roy. Soc. London. Ser. A. 1933. V. 141.

№ 4. P. 651-669.

18. Phillips N. An Example of Non-linear Computational Instability. The Atmosphere and the Sea in Motion.

New York, 1959. P. 501-504.

Институт прикладной математики

Поступила в редакцию 10.03.2022 г.

имени М.В. Келдыша РАН, г. Москва,

После доработки 10.03.2022 г.

Принята к публикации 25.05.2022 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022