ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 7, с.962-976

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.622.2+681.5.015

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ

ДИНАМИЧЕСКИХ СИСТЕМ

Представлен подход к решению задач параметрической идентификации динамических сис-

тем, целью которого является нахождение такой интервальной оценки параметров моде-

ли, при которой решение соответствующей задачи моделирования содержало бы исходные

(экспериментальные) данные или минимизировало бы отклонение от них. В основе под-

хода лежит ранее разработанный, апробированный и обоснованный алгоритм адаптивной

интерполяции для моделирования динамических систем с интервальными параметрами.

Сформулирована задача минимизации расстояния между решением интервальной задачи и

экспериментальными значениями фазовых переменных в пространстве границ интерваль-

ных оценок параметров модели. Получено выражение градиента минимизируемой целевой

функции для дальнейшего применения методов оптимизации первого порядка. Выполнена

апробация предложенного подхода на представительном ряде задач.

DOI: 10.31857/S0374064122070081, EDN: CEMWGM

Введение. Обратные задачи играют очень важную роль во многих областях. Определение

закономерностей по имеющимся экспериментальным данным является ключевым моментом в

построении математических моделей. Задача параметрической идентификации возникает на

этапе, когда модель того или иного физического процесса уже определена, но неизвестными

остаются параметры этой модели. Классический подход к определению параметров заключа-

ется в построении и минимизации некоторой целевой функции, которая характеризует откло-

нение модельного решения от экспериментальных данных.

Важной особенностью обратных задач является то, что они часто бывают некорректны-

ми. К признакам некорректности относятся: отсутствие решения, наличие более одного реше-

ния, сильная зависимость решения от погрешности входных данных (важность этого фактора

связана с тем, что информация о фазовых переменных, как правило, поступает с некоторой

погрешностью).

Существует ряд работ, посвящённых рассматриваемому классу задач [1-4]. В статьях [5,

6] предлагаются методы решения обратной коэффициентной задачи для уравнений в частных

производных. В [7] решается обратная задача по определению плотности тепловых источни-

ков для уравнения субдиффузии. В работе [8] исследуется параметрическая идентификация

в обратных задачах теплопроводности в условиях интервальной неопределённости на основе

нейронных сетей, а в [9] предлагается структурно-параметрическая идентификация динами-

ческих объектов по интервальным исходным данным. В [10] представлен итеративный интер-

вальный метод для прогнозирования границ параметров модели в условиях неопределённости

в измеренных данных. Отметим важную роль обратных задач в аэрокосмической отрасли [11],

вычислительной астрофизике [12] и электронике [13].

Применение интервального аппарата [14-16] в задачах параметрической идентификации

связано с предположением, что параметры модели могут быть интервальными. Преимуще-

ство в использовании интервальных моделей заключается в том, что они дают ограничение

сверху и снизу на интересующие величины, в отличие от классических моделей, которые их

аппроксимируют.

При описании динамики различных объектов и процессов наиболее часто используются

математические модели в виде систем обыкновенных дифференциальных уравнений (ОДУ),

поэтому далее рассматриваются именно они.

962

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

963

В работе сформулирована задача минимизации расстояния между решением интервальной

задачи и исходными значениями фазовых переменных в пространстве границ интервальных

оценок параметров модели. Для дальнейшего применения методов оптимизации первого по-

рядка получено выражение градиента соответствующей минимизируемой целевой функции.

В процессе определения границ интервальных оценок необходимо многократно решать пря-

мую интервальную задачу, для этого применяется ранее разработанный алгоритм адаптивной

интерполяции (см. [17]).

Алгоритм адаптивной интерполяции относится к группе методов, определяющих явную

зависимость решения задачи от значений интервальных параметров. В данной группе можно

выделить две подгруппы: методы, оперирующие символьными выражениями [18-20], и методы,

представляющие решение в виде полинома относительно интервальных параметров [17, 21, 22].

Алгоритм адаптивной интерполяции входит во вторую подгруппу.

Алгоритм имеет теоретическое обоснование [17, 23, 24]. Его идея заключается в построении

для каждого момента времени полинома, который интерполирует зависимость решения задачи

от значений параметров в заданной области неопределённости. Интерполяционный полином

строится по определённому набору узлов, которые образуют сетку. На каждом шаге алгоритма

сначала выполняется обновление значений, хранящихся в узлах сетки, а далее в зависимости

от погрешности интерполяции происходит адаптация. В тех местах сетки, где погрешность

большая, происходит добавление новых узлов, а в тех местах, где погрешность маленькая, -

разрежение сетки. В классической версии алгоритма используется интерполяция на полных

сетках, и из-за экспоненциального роста числа узлов при увеличении размерности области

неопределённостей он может применяться только к системам с небольшим числом (6-7) ин-

тервальных параметров. В работах [25-27] рассмотрены два подхода, позволяющих расширить

область применения на динамические системы с большим количеством интервальных парамет-

ров: разреженные сетки [28-30] и тензорные поезда [31, 32]. С использованием данных подходов

были промоделированы системы, содержащие до 18 интервальных параметров.

Схематично процесс решения задачи параметрической идентификации можно представить

следующим образом. Сначала выполняется инициализация неизвестных параметров некото-

рыми произвольными интервалами и решается прямая задача. В каждом моменте времени,

в котором известна информация о значении фазовых переменных, решается задача миними-

зации расстояния между параметрическим множеством, полученным в процессе работы алго-

ритма адаптивной интерполяции, и исходными (экспериментальными) данными. Если точка

минимума лежит на одной из границ области неопределённости, то граница соответствую-

щего интервала расширяется. Если точки минимума для всех моментов времени не лежат

на определённой границе области неопределённости, то граница соответствующего интервала

сужается. Далее снова решается прямая задача и т.д. до тех пор, пока интервальные оценки

параметров не сойдутся.

1. Постановка задачи. Рассматриваются математические модели, заданные в виде сис-

темы ОДУ c интервальными начальными условиями и параметрами:

dy_i(t)

= f_i(y₁(t),y₂(t),... ,y_n(t),θ₁,θ₂,... ,θ_m,t), i = 1,n,

y_i(t₀) ∈ [y0i,y0i], i = 1,n,

θ_i ∈ [θ_i,θ_i], i = 1,m, t ∈ [t₀,t_N],

(1)

где n - количество уравнений в системе, m - количество параметров, y0i, y0i, i = 1, n, θ_i,

θ_i, i = 1, m, - нижние и верхние границы интервальных неопределённостей. Отметим, что

интервальные неопределённости могут быть вырожденными, в этом случае границы будут

совпадать. Вектор-функция f = (f₁, f₂, . . . , f_n)^т удовлетворяет всем условиям, обеспечиваю-

щим единственность и существование решения при всех y_i(t₀) ∈ [y0i, y0i], i = 1, n, и θ_i ∈ [θ_i, θ_i],

i = 1,m.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

7^∗

964

МОРОЗОВ, РЕВИЗНИКОВ

Решение системы (1) в каждый момент времени t_k является параметрическим множе-

ством:

Y^k = {y^k(x₁,x₂,... ,x_n,z₁,z₂,... ,z_m) : x_i ∈ [y0i,y0i], i = 1,n, z_i ∈ [θ_i,θ_i], i = 1,m},

где y^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m) = (y₁(t_k), y₂(t_k), . . . , y_n(t_k))^т - решение следующей неинтер-

вальной системы ОДУ:

dy_i(t)

= f_i(y₁(t),y₂(t),... ,y_n(t),z₁,z₂,... ,z_m,t), i = 1,n,

y_i(t₀) = x_i, i = 1,n, t ∈ [t₀,t_k].

(2)

Пусть известны N экспериментальных точек в фазовом пространстве в различные момен-

ты времени:

ŷ(t_k) = (yˆ₁(t_k),yˆ₂(t_k), . . . ,yˆ_n(t_k))^т, k = 1, N .

(3)

Задача параметрической идентификации заключается в нахождении таких границ интервалов

y⁰¹, y⁰¹, y⁰², y⁰², ... , y0n, y0n, θ₁, θ₁, θ₂, θ₂, ... , θ_m, θ_m, что ŷ(tk) ∈ Yk, k = 1, N. В данной

постановке подразумевается, что для каждого ŷ(t_k) должны существовать такие значения x₁,

x₂, ..., x_n и z₁, z₂, ..., z_m, при которых y^k(x₁,x₂,... ,x_n,z₁,z₂,... ,z_m) = ŷ(t_k). Отметим,

что не всегда можно добиться того, чтобы любая точка принадлежала множеству решений Y^k,

но, как правило, в практических задачах это выполнимо.

Для нахождения соответствующих интервальных оценок начальных условий и параметров

выполняется переход к задаче минимизации отклонения модельного решения от эксперимен-

тальных данных. Минимизируется следующая целевая функция:

∑

J (y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m) =

ρ(Y^k, ŷ(t_k)),

(4)

k=1

где ρ(Y^k, ŷ(t_k)) = min

∥y^k - ŷ(t_k)∥² - квадрат расстояния между множеством Y^k и точ-

y^k∈Y^k

кой ŷ(t_k). Традиционно в качестве нормы вектора ∥ · ∥ используется взвешенная евклидова

норма

∑

∥a∥² =

w_ia2i,

i=1

где w_i - веса, которые позволяют учесть разную природу фазовых переменных (для удобства

изложения будем полагать, что w_i = 1, i = 1, n).

Как будет видно в дальнейшем, важную роль в предлагаемом подходе играет явное пред-

ставление y^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m), x_i ∈ [y0i, y0i], i = 1, n, z_i ∈ [θ_i, θ_i], i = 1, m, которое

возможно получить с помощью алгоритма адаптивной интерполяции. В этом случае при вы-

числении ρ(Y^k, ŷ(t_k)) минимизацию можно выполнять в пространстве начальных условий и

параметров без дополнительного интегрирования системы (2):

]

∑

ρ(Y^k, ŷ(t_k)) =

min

(y^ki(x₁, . . . , x_n, z₁, . . . , z_m) - ŷ_i(t_k))2 .

(5)

x_i∈[y0i,y0i], i=1,ni=1

z_i∈[θ_i,θ_i], i=1,m

При минимизации (4) предполагается, что получающиеся интервальные оценки являются

правильными:

y0i ≤ y0i, i = 1,n, θ_i ≤ θ_i, i = 1,m.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

965

Утверждение. Если y⁰¹,

y⁰¹, ... ,

y0n,

θ₁,

θ₁, ... ,

θm,

θm - набор значений, на

котором достигается минимум целевой функции (4), то на любом другом наборе y⁰¹, y⁰¹,

..., y0n, y0n, θ₁, θ₁, ..., θ_m, θ_m таком, что

y⁰¹ ≤ y⁰¹,

y⁰¹ ≤ y⁰¹, ... , y0n ≤ y0n,

y0n ≤ y0n,

θ₁ ≤θ1,

θ₁ ≤ θ₁, ... , θ_m ≤θm,

θm ≤ θm,

(6)

будет достигаться минимум.

Докажем от противного. Предположим, что существует такой набор y⁰¹, y⁰¹, . . . , y0n, y0n,

θ₁, θ₁, ..., θ_m, θ_m, удовлетворяющий условию (6), при котором минимум не достигается,

тогда

J (y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m) > J(y⁰¹, y⁰¹, . . . , y0n, y0n,θ1,θ1, . . . ,θm,θm).

Целевая функция (4) представляет собой сумму слагаемых, следовательно, существует такое

k-е слагаемое, для которого выполняется неравенство

]

∑

min

(y^ki(x, z) - ŷ_i(t_k))2

> min

(y^ki(x, z) - ŷ_i(t_k))2

x_i∈[y0i,y0i], i=1,ni=1

x_i∈[y0i,y0i], i=1,n

i=1

z_i∈[θ_i,θ_i], i=1,m

z_i∈[θi,θi], i=1,m

где x = (x₁, x₂, . . . , x_n) и z = (z₁, z₂, . . . , z_m). С учётом того, что [y0i, y0i] ⊆ [y0i, y0i] и [θ0i,θ0i] ⊆

⊆ [θ0i , θ0i ], получаем противоречие. Утверждение доказано.

Сформулированное утверждение можно рассматривать и в обратную сторону - в плане

возможности уменьшения найденных интервальных оценок, что является важным при прак-

тической реализации. Однако отметим, что целью предлагаемого подхода является не нахож-

дение минимальной интервальной оценки, а только определение таких значений y⁰¹, y⁰¹, ,

..., y0n, y0n, θ₁, θ₁, ..., θ_m, θ_m, при которых целевая функция (4) будет равна нулю или

минимальна. Тем не менее если очевидным образом можно уменьшить получаемые интерваль-

ные оценки начальных условий и параметров, то эта процедура выполняется.

2. Методы решения. Поиск минимума целевой функции (4) в аналитическом виде зача-

стую затруднителен, поэтому необходимо применять численные методы оптимизации [33, 34].

Наиболее широко использующимися являются градиентные методы, которые, хотя и требуют

знания градиента целевой функции, обладают высокой скоростью сходимости, компенсирую-

щей затраты на вычисления градиента.

Одна итерация метода градиентного спуска записывается следующим образом:

u(j+1) = u(j) - λ(j)∇F(u(j)),

где u - вектор переменных, ∇F - градиент минимизируемой функции F, λ(j) - скорость

градиентного спуска. Данный класс методов является хорошо изученным и исследованным,

поэтому подробно рассматриваться в данной работе не будет.

Для того чтобы вычислить градиент целевой функции (4), необходимо продифференциро-

вать (5) по границе области поиска минимума. Обозначим через (xk1, . . . , x^kn, zk1, . . . , z^km) точку

минимума (5):

(xk1,...,x^kn,zk1,...,z^km)=

arg min

J^k(x₁,... ,x_n,z₁,... ,z_m),

(7)

x_i∈[y0i,y0i], i=1,n

z_i∈[θ_i,θ_i], i=1,m

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

966

МОРОЗОВ, РЕВИЗНИКОВ

где

∑

J^k(x₁,... ,x_n,z₁,... ,z_m) =

(y^ki(x₁, . . . , x_n, z₁, . . . , z_m) - ŷ_i(t_k))².

i=1

Дополнительно запишем компоненты градиента J^k :

dJ^k(x₁, . . . , x_n, z₁, . . . , z_m)

dx_j

∑

dy^ki(x₁, . . . , x_n, z₁, . . . , z_m)

(y^ki(x₁, . . . , x_n, z₁, . . . , z_m) - ŷ_i(t_k))

j = 1,n,

dx_j

i=1

dJ^k(x₁, . . . , x_n, z₁, . . . , z_m)

dz_j

∑

dy^ki(x₁, . . . , x_n, z₁, . . . , z_m)

(y^ki(x₁, . . . , x_n, z₁, . . . , z_m) - ŷ_i(t_k))

j = 1,m.

(8)

dz_j

i=1

Очевидно, что если точка минимума лежит не на границе рассматриваемой области, то

изменение границы никак не будет на неё влиять, т.е. производная по границе будет равна

нулю. А если точка лежит на границе, то производная равна частной производной в этой

точке. В результате компоненты градиента (4) имеют следующий вид:

⎧

⎨0,

x^kj = y0j,

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

dy⁰

⎩

x^kj = y0j,

k=1

dx_j

⎧

⎨0,

x^kj = y0j,

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(x

,...,x^kn,zk1,...,z^km)

dy⁰

⎩

x^kj = y0j,

k=1

dx_j

j = 1,n,

⎧

⎨0,

zkj = θ_j,

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

dθ_j

⎩

zkj = θ_j,

k=1

dz_j

⎧

⎨0,

zkj = θ_j,

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

dθ_j

⎩

zkj = θ_j,

k=1

dz_j

j = 1,m.

(9)

Проанализируем (8). Так как (xk1, . . . , x^kn, zk1, . . . , z^km) является точкой минимума, то гради-

ент (8) в этой точке будет равен нулю в случае, когда точка находится внутри рассматриваемой

области [y⁰¹, y⁰¹]×. . .×[y0n, y0n]×[θ₁, θ₁]×. . .×[θ_m, θ_m], или может быть направлен внутрь области

в случае, когда точка находится на границе. Отсюда

⎧

⎨≤ 0,

x^kj = y0j,

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

= 0,

y0j < x^kj < y0j,

j = 1,n,

dx_j

⎩

≥ 0,

x^kj = y0j,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

967

⎧

⎨≤ 0,

zkj = θ_j,

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

= 0,

θ_j < z^kj < θ_j,

j = 1,m,

dz_j

⎩

≥ 0,

zkj = θ_j,

и для (9) получаем

[

]

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

max 0,

dy⁰

dx_j

k=1

[

]

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

min 0,

j = 1,n,

dx_j

dy⁰

k=1

[

]

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

max 0,

dθ_j

dz_j

k=1

[

]

dJ(y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m)

∑

dJ^k(xk1, . . . , x^kn, zk1, . . . , z^km)

min 0,

j = 1,m.

dθ_j

dz_j

k=1

Следовательно, в процессе минимизации целевой функции (4) нижние границы интервалов не

будут увеличиваться, а верхние границы - уменьшаться, т.е. получающаяся область неопре-

делённости [y⁰¹, y⁰¹] × . . . × [y0n, y0n] × [θ₁, θ₁] × . . . × [θ_m, θ_m] не будет сужаться. Однако если ни

одна точка минимума (7) не лежит на определённой границе, то соответствующая производная

равна нулю и границу можно передвинуть, тем самым уменьшив рассматриваемую область.

Таким образом, получаем правила сужения:

y0i = min(xki), если

= 0, y0i = max(xki), если

= 0, i = 1, n,

dy0i

dy⁰

θ_i = min(zki), если

= 0, θ_i = max(zki), если

= 0, i = 1, m.

dθ_i

Это соответствует следствию из ранее сформулированного утверждения о том, что получаю-

щиеся интервальные оценки можно уменьшить. Отметим, что в контексте рассматриваемых

задач данный момент является ключевым, потому что позволяет исключить постоянное рас-

ширение интервальных оценок.

3. Алгоритм адаптивной интерполяции. Для решения задачи параметрической иден-

тификации требуется знать

y^k(x₁,x₂,... ,x_n,z₁,z₂,... ,z_m), k = 1,N, x_i ∈ [y0i,y0i], i = 1,n, z_i ∈ [θ_i,θ_i], i = 1,m.

В свою очередь, для этого необходимо решить прямую задачу (1).

В данном пункте приводится краткое описание алгоритма адаптивной интерполяции для

интегрирования систем ОДУ с интервальными начальными условиями и параметрами в соот-

ветствии с работами [17, 25, 26].

Цель алгоритма - для каждого момента времени t_k построить вектор-функцию

Pk(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m),

интерполирующую y^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m) с контролируемой точностью.

В начальный момент времени t₀ вектор-функция P⁰ определяется тривиальным образом:

P⁰(x₁,x₂,... ,x_n,z₁,z₂,... ,z_m) = (x₁,x₂,... ,x_n)^т.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

968

МОРОЗОВ, РЕВИЗНИКОВ

Построим с помощью индукции решение для произвольного момента времени. Пусть в

момент времени t_k известна P^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m). Получение

Pk⁺¹(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m)

сводится к интерполяции неявной функции

F(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m) = (y₁(tk+1), y₂(tk+1), . . . , y_n(tk+1))^т,

заданной в виде системы ОДУ

dy_i(t)

= f_i(y₁(t),y₂(t),... ,y_n(t),z₁,z₂,... ,z_m,t), i = 1,n,

y_i(t_k) = P^ki(x₁,x₂,... ,x_n,z₁,z₂,... ,z_m), i = 1,n, t ∈ [t_k,tk+1].

Традиционно интерполяционный полином P^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m)строится по опре-

делённому набору узлов, которые образуют сетку. Поэтому сначала выполняется перенос ре-

шений, которые соответствуют узлам, на (k + 1)-й временной слой, а далее в зависимости

от значения погрешности интерполяции происходит адаптация. В тех местах сетки, где по-

грешность большая, происходит добавление новых узлов, а в тех местах, где погрешность ма-

ленькая, - разрежение сетки. Интерполяционный полином P может быть любым, необходимо

только, чтобы была возможность контролировать погрешность интерполяции.

При решении задачи параметрической идентификации y^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m) за-

меняется полученным интерполяционным полиномом P^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m). Отме-

тим, что так как полином представляет собой явную функцию, то требуемые в процессе вы-

числений частные производные можно вычислить аналитически.

4. Результаты. Далее решены несколько задач параметрической идентификации. В ка-

честве критерия остановки градиентного спуска применялось ограничение на значение мини-

мизируемой целевой функции J < 10-12. Во всех примерах вместо экспериментальных точек

использовались квазиреальные экспериментальные точки, полученные следующим образом.

Параметры и начальные условия задавались интервально и решалась прямая задача. В рав-

номерно распределённые в интервале интегрирования моменты времени t_k в найденное реше-

ние P^k(x₁, x₂, . . . , x_n, z₁, z₂, . . . , z_m) подставлялись случайные значения из соответствующих

интервалов:

x₁ = xk1 ∼ U(y⁰¹,y⁰¹), x₂ = xk2 ∼ U(y⁰²,y⁰²), ... , x_n = x^kn ∼ U(y0n,y0n),

z₁ = zk1 ∼ U(θ₁,θ₁), z₂ = zk2 ∼ U(θ₂,θ₂), ... , z_m = z^km ∼ U(θ_m,θ_m),

(10)

где U(a, b) - непрерывное равномерное распределение на отрезке [a, b]. Таким образом,

ŷ(t_k) = P^k(xk1, xk2, . . . , x^kn, zk1, zk2, . . . , z^km).

Исходные интервальные оценки начальных условий и параметров:

[

]

[

]

min(xki),max(xki) ,

i = 1,n,

min(zki),max(zki) ,

i = 1,m.

Вначале рассматривается система ОДУ с двумя неизвестными параметрами, которая со-

ответствует модели Лотки-Вольтерры [35]:

u^′ = αu - 2uv, v^′ = -v + βuv,

u(0) = 1, v(0) = 3, t ∈ [0, 5.3].

(11)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

969

Из интервала интегрирования были взяты 20 равномерно расположенных точек с шагом

по времени 0.265. Квазиреальные экспериментальные точки на фазовой плоскости получены

при следующих интервальных оценках параметров: α ∈ [1.95, 2.035] и β ∈ [0.9652, 1.045].

Начальное приближение в методе градиентного спуска: α⁽⁰⁾ ∈ [1.5, 1.51] и β⁽⁰⁾ ∈ [0.6, 0.61].

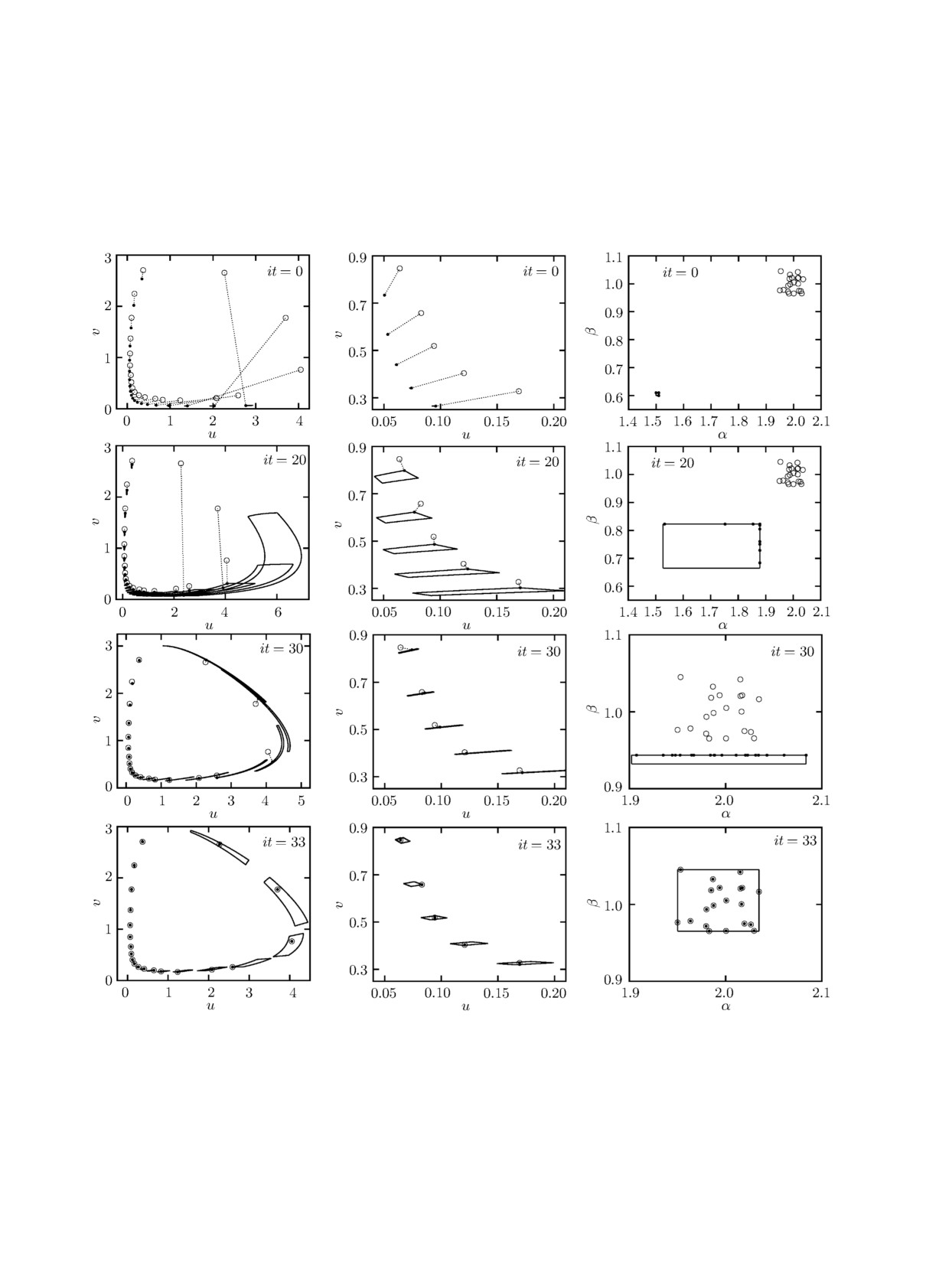
На рис. 1 проиллюстрирован процесс параметрической идентификации системы.

Рис. 1. Результаты решения задачи параметрической идентификации для системы (11).

На рис. 1 и на всех рисунках далее сплошными линиями показаны множества решений

прямой задачи в различные моменты времени (первая и вторая колонка на рис. 1), светлые

кружки - экспериментальные данные. Жирная точка обозначает ближайшую точку к экспе-

риментальной точке в множестве решений прямой задачи, а пунктирная линия - расстояние

между ними. Сумма квадратов расстояний фактически определяет значение минимизируемой

целевой функции (4).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

970

МОРОЗОВ, РЕВИЗНИКОВ

Каждая строка рис. 1 соответствует определённой итерации градиентного спуска. Слева по-

казана фазовая плоскость, а по центру - её увеличенная часть (u ∈ [0.04, 0.21] и v ∈ [0.25, 0.9]).

На рисунках справа продемонстрировано решение задачи в пространстве параметров. Здесь

светлыми кружками показаны полученные случайным образом значения параметров (10) при

генерации экспериментальных точек; жирными точками - решение соответствующей задачи

(7); сплошной линией - интервальная оценка параметров (получающаяся область неопреде-

лённости).

В процессе минимизации множества решений прямой задачи стремятся покрыть экспери-

ментальные точки, о чем свидетельствует уменьшение расстояний между ними. При it = 30

наблюдается, что все жирные точки принадлежат верхней границе интервальной оценки пара-

метра β. Это говорит о том, что исходные значения параметров (10) расположились с одной

стороны относительно текущей области неопределённости. На последней итерации видно, что

полученные множества решений полностью покрыли экспериментальные точки, кроме того,

определены соответствующие значения параметров, о чем свидетельствует совпадение жир-

ных точек со светлыми кружками на рисунке справа.

Далее рассматривается система ОДУ, в которой неизвестными являются начальные

условия:

u^′ = 4u -

uv +

u², v^′ = -2v +

uv +

v²,

u(0) = u₀, v(0) = v₀, t ∈ [0, 4].

(12)

Аналогично предыдущему примеру из интервала интегрирования были взяты 20 равно-

мерно расположенных точек с шагом по времени 0.2. Исходные интервальные оценки началь-

ных условий: u₀ ∈ [4.301, 4.639] и v₀ ∈ [2.861, 3.180]. Начальное приближение: u⁽⁰⁾⁰ ∈ [3.3, 3.7]

и v⁽⁰⁾⁰ ∈ [3.8,4.2]. На рис. 2 показан процесс решения задачи.

Рис. 2. Иллюстрация решения задачи параметрической идентификации для системы (12).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

971

Траектория решения прямой задачи имеет спиралевидную структуру, что является осо-

бенностью рассматриваемой системы ОДУ. С каждой итерацией градиентного спуска получа-

ющиеся множества решений приближаются к экспериментальным точкам, уменьшается сум-

марная длина пунктирных линий. На 37-й итерации все экспериментальные точки содержатся

в соответствующих множествах решений прямой задачи. Полученные интервальные оценки

начальных условий u⁽³⁷⁾⁰ ∈ [4.301, 4.639] и v⁽³⁷⁾⁰ ∈ [2.861, 3.180] совпадают с исходными. Одна-

ко такая ситуация имеет место не всегда, далее будут рассмотрены примеры, где количество

фазовых переменных отличается от количества неизвестных величин.

Отметим, что решение задачи (12) можно получить, выполнив интегрирование в обратную

сторону для каждой экспериментальной точки, тем самым найдя соответствующие прообразы

в пространстве начальных условий, по которым можно построить интервальную оценку.

Рассмотрим задачу (11) с увеличенным количеством неизвестных величин. Из системы

исключим информацию о начальных условиях:

u^′ = αu - 2uv, v^′ = -v + βuv,

u(0) = u₀, v(0) = v₀, t ∈ [0, 5.3].

(13)

Исходные интервальные оценки начальных условий и параметров, по которым генериро-

вались экспериментальные точки на фазовой плоскости:

u₀ ∈ [0.9505,1.046], v₀ ∈ [2.952,3.050], α ∈ [1.959,2.041], β ∈ [0.9732,1.048].

Начальное приближение:

u⁽⁰⁾⁰ ∈ [0.8,0.81], v⁽⁰⁾⁰ ∈ [2.8,2.81], α⁽⁰⁾ ∈ [1.8,1.81], β⁽⁰⁾ ∈ [0.6,0.61].

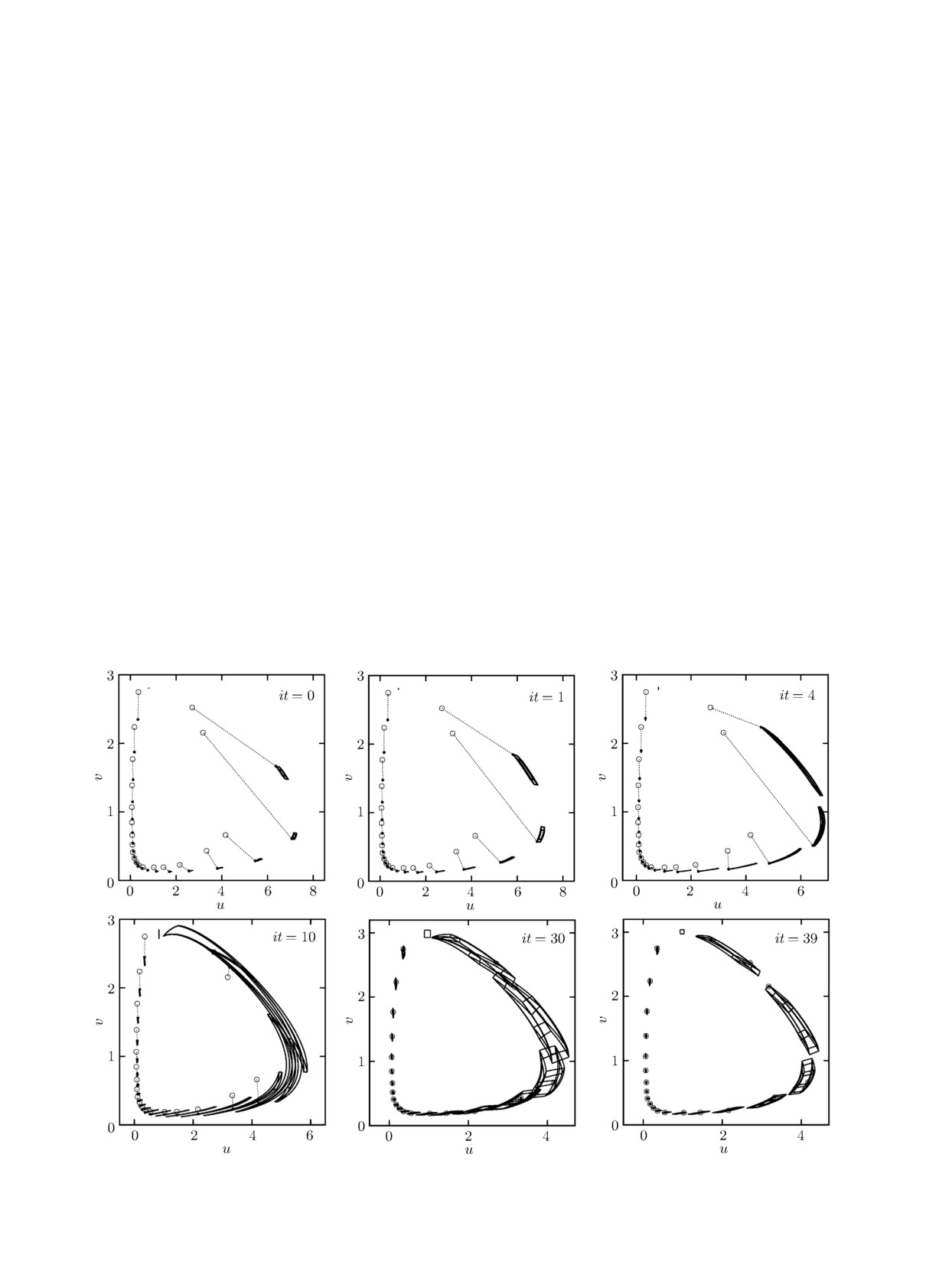
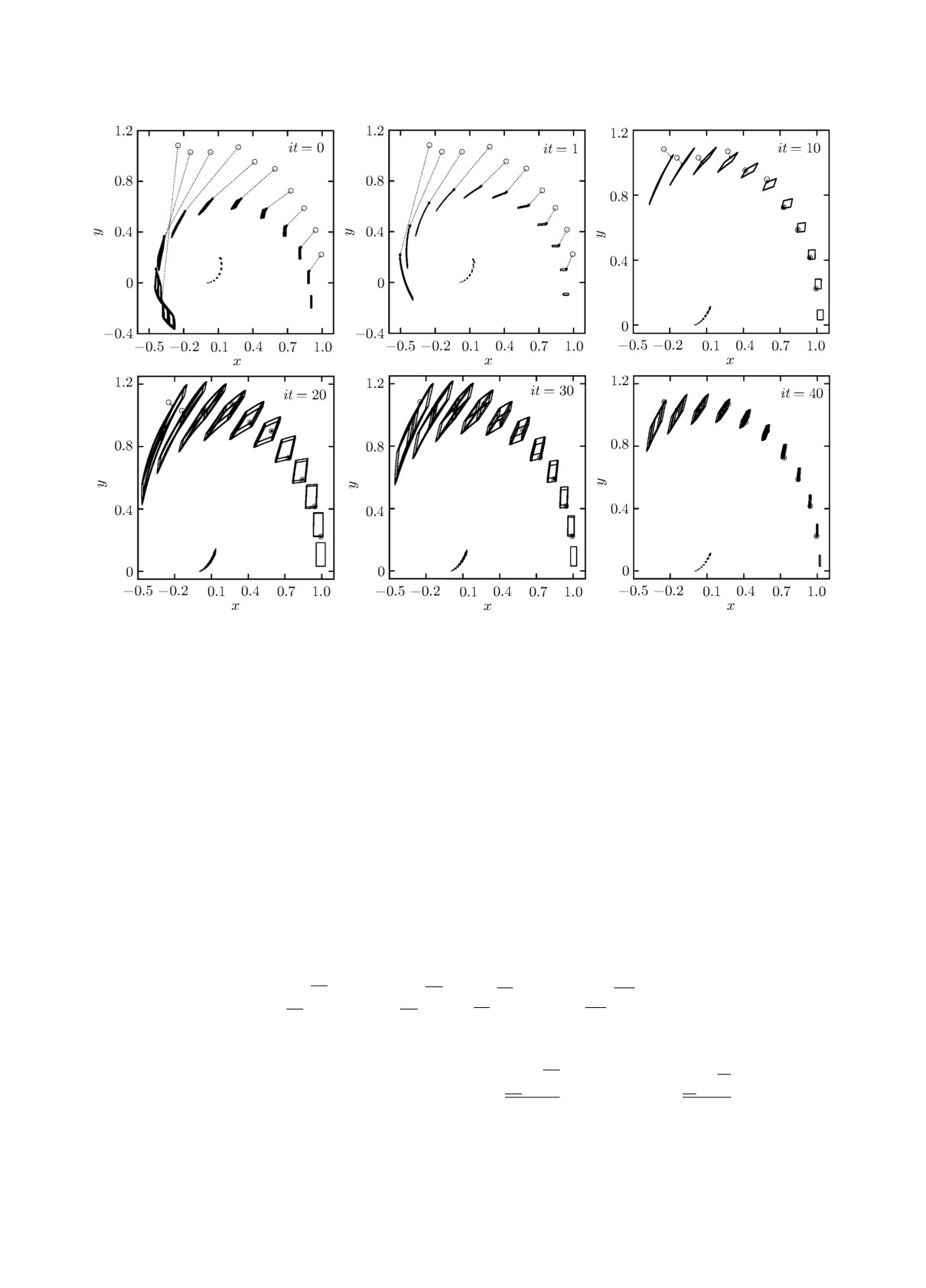
На рис. 3 показан процесс поиска интервальных оценок параметров и начальных условий.

Множество решений прямой задачи в каждый момент времени представляет собой проекцию

деформирующегося четырёхмерного прямоугольного параллелепипеда.

Рис. 3. Процесс решения задачи параметрической идентификации для системы (13).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

972

МОРОЗОВ, РЕВИЗНИКОВ

На последней итерации получены следующие интервальные оценки: u⁽³⁹⁾⁰ ∈ [0.9393, 1.033],

v(39)0 ∈ [2.972, 3.037], α(39) ∈ [1.970, 2.035] и β(39) ∈ [0.9749, 1.033]. Они отличаются от ис-

ходных оценок, но при этом все экспериментальные точки содержатся в соответствующих

множествах решений прямой задачи. Отметим, что результат зависит от выбора начального

приближения, так как минимизируемая целевая функция является многоэкстремальной.

В заключение рассмотрим модельную задачу: движение тела с неизвестным начальным

положением, неизвестными начальными скоростями и неизвестной массой под действием сил

гравитации вокруг массивного тела. Система ОДУ в безразмерных переменных имеет следу-

ющий вид:

x′1 = vx₁, y′1 = vy₁,

x₂ - x₁

y₂ - y₁

vx^′

=m₂

vy^′

=m₂

((x₂ - x₁)² + (y₂ - y₁)²)3/2

x′2 = vx₂, y′2 = vy₂,

x₁ - x₂

y₁ - y₂

vx^′

=m₁

vy^′

=m₁

((x₂ - x₁)² + (y₂ - y₁)²)3/2

x₁(0) = x1,0, y₁(0) = y1,0,

vx₁(0) = vx1,0, vy₁(0) = vy1,0,

x₂(0) = y₂(0) = 0, vx₂(0) = vy₂(0) = 0,

m₂ = 10², t ∈ [0,0.2].

(14)

В отличие от предыдущих примеров здесь с шагом по времени 0.02 было взято меньше то-

чек - 10. Кроме того, экспериментальные данные содержали информацию только о фазовых

переменных, соответствующих положению первого тела (x₁, y₁). Подобные задачи возникают

в астрофизике, когда об исследуемом космическом объекте кроме его положения на небес-

ной сфере ничего не известно. Исходные интервальные оценки начальных условий и массы

тела: x1,0 ∈ [1.000, 1.018], y1,0 ∈ [3.583 · 10-3, 1.956 · 10-2], vx1,0 ∈ [8.183 · 10-3, 3.794 · 10-1],

vy1,0 ∈ [10.04,10.48] и m₁ ∈ [10.07,10.45]. Начальное приближение: x(0)1,0 ∈ [0.9,0.91], y(0)1,0 ∈

∈ [-0.2, -0.1], vx(0)1,0 ∈ [0.0, 0.1], vy(0)1,0 ∈ [9.5, 9.6] и m⁽⁰⁾¹ ∈ [9.5, 9.6]. На рис. 4 продемонстри-

ровано изменение множеств решений прямой задачи в процессе параметрической идентифи-

кации.

Здесь показаны две последовательности множеств, которые соответствуют положению двух

тел в пространстве в различные моменты времени. Так как второе тело более массивное и

изначально находится в состоянии покоя, его перемещение в пространстве незначительно по

сравнению с первым телом.

На 40-й итерации градиентного спуска получены следующие интервальные оценки началь-

ного положения, скорости и массы первого тела, при которых решение прямой задачи полно-

стью содержит экспериментальные точки:

x(40)1,0 ∈ [1.016,1.027], y(40)1,0 ∈ [3.042 · 10-2,1.011 · 10-1],

vx(40)1,0 ∈ [-0.2047,-0.1264], vy(40)1,0 ∈ [9.721,10.10], m⁽⁴⁰⁾¹ ∈ [9.480,9.483].

Отметим, что в процессе параметрической идентификации данной системы выполнялась

минимизация целевой функции в десятимерном пространстве (пять интервальных неопреде-

лённостей, в каждой по две границы).

Таким образом, с помощью предложенного подхода успешно была решена задача интер-

вальной параметрической идентификации для различных систем ОДУ с разным количеством

неизвестных значений.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

973

Рис. 4. Параметрическая идентификация системы (14).

5. Обсуждение. В общем случае задача (7) может иметь множество решений. В частно-

сти, данная ситуация возникает, когда точка

ŷ(t_k) принадлежит множеству Y^k, тогда (7)

превращается в систему

yk1(x₁,... ,x_n,z₁,... ,z_m) = ŷ₁(t_k), yk2(x₁,... ,x_n,z₁,... ,z_m) = ŷ₂(t_k),

...,

y^kn(x₁,... ,x_n,z₁,... ,z_m) = ŷ_n(t_k),

(15)

в которой n уравнений и (n + m) неизвестных. На рис. 3 видно, что множество решений

системы ОДУ (13) представляет собой проекцию четырёхмерного деформирующегося пря-

моугольного параллелепипеда. Здесь каждой точке на фазовой плоскости соответствует дву-

мерная поверхность в пространстве параметров и начальных условий, которая определяется

решением соответствующей системы (15).

В качестве (xk1, . . . , x^kn, zk1, . . . , z^km) имеет смысл брать любую точку, наиболее близкую к

центру рассматриваемой области

[y⁰¹, y⁰¹] × . . . × [y0n, y0n] × [θ₁, θ₁] × . . . × [θ_m, θ_m],

т.е.

)2]

∑

⁽y0i +y0i

∑

⁽θ_i +θ_i

(xk1,...,x^kn,zk1,...,z^km)=

arg min

-x_i

-z_i

(x₁,...,xn,z1,...,zm)∈χi=1

i=1

где χ - множество решений (15). Выбор точки таким образом дополнительно способствует

сужению получаемых интервальных оценок.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

974

МОРОЗОВ, РЕВИЗНИКОВ

Представленный в работе подход также применим, когда в один и тот же момент t_k из-

вестно несколько экспериментальных точек. В этом случае целевая функция (4) примет сле-

дующий вид:

∑∑

J (y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m) =

ρ(Y^k, ŷ^j (t_k)),

k=1 j=1

где N_k - количество экспериментальных точек в момент t_k,

ŷ^j(t_k) - j-я экспериментальная

точка.

Кроме того, рассматриваемый подход обобщается на случай, когда вместо эксперименталь-

ных точек известны интервальные оценки фазовых переменных:

(

)т

Ŷ^k =

[ŷk0, ŷk0],[ŷk1, ŷk1],... ,[ŷ^kn, ŷ^kn]

k = 1,N.

Целевая функция (4) запишется следующим образом:

∑

J (y⁰¹, y⁰¹, . . . , y0n, y0n, θ₁, θ₁, . . . , θ_m, θ_m) =

ρ(Y^k,Ŷk),

(16)

k=1

где ρ(Y^k,Ŷk) характеризует степень непересечения множеств Y^k иŶk. В частности, величи-

на ρ(Y^k,Ŷk) может соответствовать расстоянию между множеством Y^k и самой удалённой

от него точкой множества

Ŷ^k :

]

∑

ρ(Y^k,Ŷk) = max

min

(y^ki(x₁, . . . , x_n, z₁, . . . , z_m) - ŷ^ki)2

ŷki∈[ŷ^ki,ŷ^ki]

x_i∈[y0i,y0i], i=1,ni=1

i=1,n z_i∈[θ_i,θ_i], i=1,m

или, например, являться интегральной характеристикой:

ŷk₁

ŷk₂

ŷkn

∫

]

∑

ρ(Y^k,Ŷk) =

···

min

(y^ki(x₁, . . . , x_n, z₁, . . . , z_m) - ŷ^ki)2

dŷ^kndŷkn-1···dŷk1.

x_i∈[y

,y0i], i=1,n

i=1

ŷk

ⁿ z_i∈[θ_i,θ_i], i=1,m

Решение задачи параметрической идентификации при наличии интервальных оценок фа-

зовых переменных (минимизация (16)) требует применения специального математического ап-

парата. Данное направление является предметом дальнейших исследований.

Заключение. В работе представлен интервальный подход к решению задачи интерваль-

ной параметрической идентификации. Цель подхода заключается в нахождении такой интер-

вальной оценки начальных условий и параметров системы ОДУ, при которой решение содер-

жало бы экспериментальные данные или минимизировало бы отклонение от них. Приведена

целевая функция, зависящая от границ соответствующих интервальных неопределённостей,

минимизация которой эквивалентна решению исходной задачи параметрической идентифика-

ции. Выполнен анализ целевой функции и получено выражение градиента для дальнейшего

применения методов оптимизации первого порядка. Сформулировано и доказано утвержде-

ние о том, что если минимум целевой функции достигается на определённых интервальных

оценках, то и на более широких оценках он тоже будет достигаться. При вычислении значения

целевой функции и градиента необходимо решать прямую интервальную задачу, для который

применяется ранее разработанный алгоритм адаптивной интерполяции. Выполнена апробация

предложенного подхода на нескольких системах ОДУ, содержащих разное количество неиз-

вестных параметров. Продемонстрирована эффективность подхода: для всех задач успешно

получены интервальные оценки параметров, при которых решение содержит эксперименталь-

ные точки.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ИНТЕРВАЛЬНЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ

975

СПИСОК ЛИТЕРАТУРЫ

1. Самарский А.А., Вабищевич П.Н. Численные методы решения обратных задач математической

физики. М., 2009.

2. Денисов А.М. Введение в теорию обратных задач. М., 1994.

3. Марчук Г.И. Сопряженные уравнения и анализ сложных систем. М., 1992.

4. Ватульян А.О. Математические модели и обратные задачи // Соросовский образоват. журн. 1998.

№ 11. С. 143-148.

5. Денисов А.М. Итерационный метод решения обратной коэффициентной задачи для гиперболиче-

ского уравнения // Дифференц. уравнения. 2017. Т. 53. № 7. С. 943.

6. Гаврилов С.В., Денисов А.М. Численные методы решения нелинейного операторного уравнения,

возникающего в обратной коэффициентной задаче // Дифференц. уравнения. 2021. Т. 57. № 7.

С. 900-906.

7. Ашуров Р.Р., Мухиддинова А.Т. Обратная задача по определению плотности тепловых источников

для уравнения субдиффузии // Дифференц. уравнения. 2020. Т. 56. № 12. С. 1596-1609.

8. Дилигенская А.Н., Самокиш А.В. Параметрическая идентификация в обратных задачах теплопро-

водности в условиях интервальной неопределённости на основе нейронных сетей // Вестн. Самарск.

гос. техн. ун-та. 2020. Т. 28. № 4 (68). С. 6-18.

9. Петрикевич Я.И. Структурно-параметрическая идентификация динамических объектов по интер-

вальным исходным данным: дис

канд. техн. наук. М., 2006.

10. Xiao N., Fedele F., Muhanna R.L. Inverse problems under uncertainties-an interval solution for the beam

finite element // Conf. Paper: 11th Intern. Conf. on Structural Safety & Reliability. New York, 2013.

(https://www.researchgate.net/publication/269518192).

11. Nenarokomov A.V., Alifanov O.M., Krainova I.V., Titov D.M., Morzhukhina A.V. Estimation of

environmental influence on spacecraft materials radiative properties by inverse problems technique

// Acta Astronautica. 2019. V. 160. P. 323-330.

12. Кабанихин С.И., Куликов И.М., Шишленин М.А. Алгоритм восстановления характеристик началь-

ного состояния сверхновой звезды // Журн. вычислит. математики и мат. физики. 2020. Т. 60. № 6.

С. 1035-1044.

13. Абгарян К.К., Носков Р.Г., Ревизников Д.Л. Обратная коэффициентная задача теплопереноса в

слоистых наноструктурах // Изв. вузов. Материалы электронной техники. 2017. Т. 20. № 3. С. 213-

219.

14. Moore R. Interval Analysis. New Jersey, 1966.

15. Moore R.E., Kearfott R.B., Cloud M.J. Introduction to Interval Analysis. Philadelphia, 2009.

16. Шарый С.П. Конечномерный интервальный анализ. Новосибирск, 2019.

17. Морозов А.Ю., Ревизников Д.Л. Алгоритм адаптивной интерполяции на основе kd-дерева для чис-

ленного интегрирования систем обыкновенных дифференциальных уравнений с интервальными

начальными условиями // Дифференц. уравнения. 2018. Т. 54. № 7. С. 963-974.

18. Makino K., Berz M. Models and Their Applications // Numerical Software Verification 2017: conf. July

22-23, 2017. Germany, Heidelberg, 2017. P. 3-13.

19. Nataraj P.S.V., Sondur S. The extrapolated Taylor model // Reliable Computing. July, 2011. P. 251-278.

20. Рогалев А.Н. Гарантированные методы решения систем обыкновенных дифференциальных урав-

нений на основе преобразования символьных формул // Вычислит. технологии. 2003. Т. 8. № 5.

С. 102-116.

21. Fu C., Ren X., Yang Y.-F., Lu K., Qin W. Steady-state response analysis of cracked rotors with uncertain

but bounded parameters using a polynomial surrogate method // Commun. Nonlin. Sci. Numer. Simul.

2019. V. 68. P. 240-256.

22. Fu C., Xu Y., Yang Y., Lu K., Gu F., Ball A. Response analysis of an accelerating unbalanced rotating

system with both random and interval variables // J. Sound Vibrat. 2020. V. 466. P. 115047.

23. Морозов А.Ю., Ревизников Д.Л., Гидаспов В.Ю. Алгоритм адаптивной интерполяции на основе

kd-дерева для решения задач химической кинетики с интервальными параметрами // Мат. моде-

лирование. 2018. Т. 30. № 12. С. 129-144.

24. Морозов А.Ю., Журавлев А.А., Ревизников Д.Л. Анализ и оптимизация алгоритма адаптивной

интерполяции численного решения систем обыкновенных дифференциальных уравнений с интер-

вальными параметрами // Дифференц. уравнения. 2020. Т. 56. № 7. С. 960-974.

25. Гидаспов В.Ю., Морозов А.Ю., Ревизников Д.Л. Алгоритм адаптивной интерполяции с использо-

ванием TT-разложения для моделирования динамических систем с интервальными параметрами

// Журн. вычислит. математики и мат. физики. 2021. Т. 61. № 9. С. 1416-1430.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

976

МОРОЗОВ, РЕВИЗНИКОВ

26. Morozov A.Yu., Zhuravlev A.A., Reviznikov D.L. Sparse grid adaptive interpolation in problems of

modeling dynamic systems with interval parameters // Math. 2021. V. 9. P. 298.

27. Морозов А.Ю., Ревизников Д.Л. Алгоритм адаптивной интерполяции на разреженных сетках для

численного интегрирования систем обыкновенных дифференциальных уравнений с интервальными

неопределённостями // Дифференц. уравнения. 2021. Т. 57. № 7. С. 976-987.

28. Смоляк С.А. Квадратурные и интерполяционные формулы на тензорных произведениях некоторых

классов функций // Докл. АН СССР. 1963. Т. 148. № 5. С. 1042-1045.

29. Bungatrz H-J., Griebel M. Sparse grids // Acta Numerica. 2004. V. 13. № 1. P. 147-269.

30. Gerstner T., Griebel M. Sparse grids // Encycl. of Quantitat. Finance / Ed. R. Cont. New York, 2010.

31. Oseledets I.V. Tensor-train decomposition // SIAM J. on Sci. Comput. 2011. V. 33. № 5. P. 2295-2317.

32. Oseledets I., Tyrtyshnikov E. TT-cross approximation for multidimensional arrays // Linear Algebra and

its Appl. 2010. V. 432. № 1. P. 70-88.

33. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М., 1985.

34. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. М., 2005.

35. Арнольд В.И. Обыкновенные дифференциальные уравнения. Ижевск, 2000.

Федеральный исследовательский центр

Поступила в редакцию 20.02.2022 г.

“Информатика и управление” РАН, г. Москва,

После доработки 20.02.2022 г.

Московский авиационный институт

Принята к публикации 25.05.2022 г.

(национальный исследовательский университет)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022