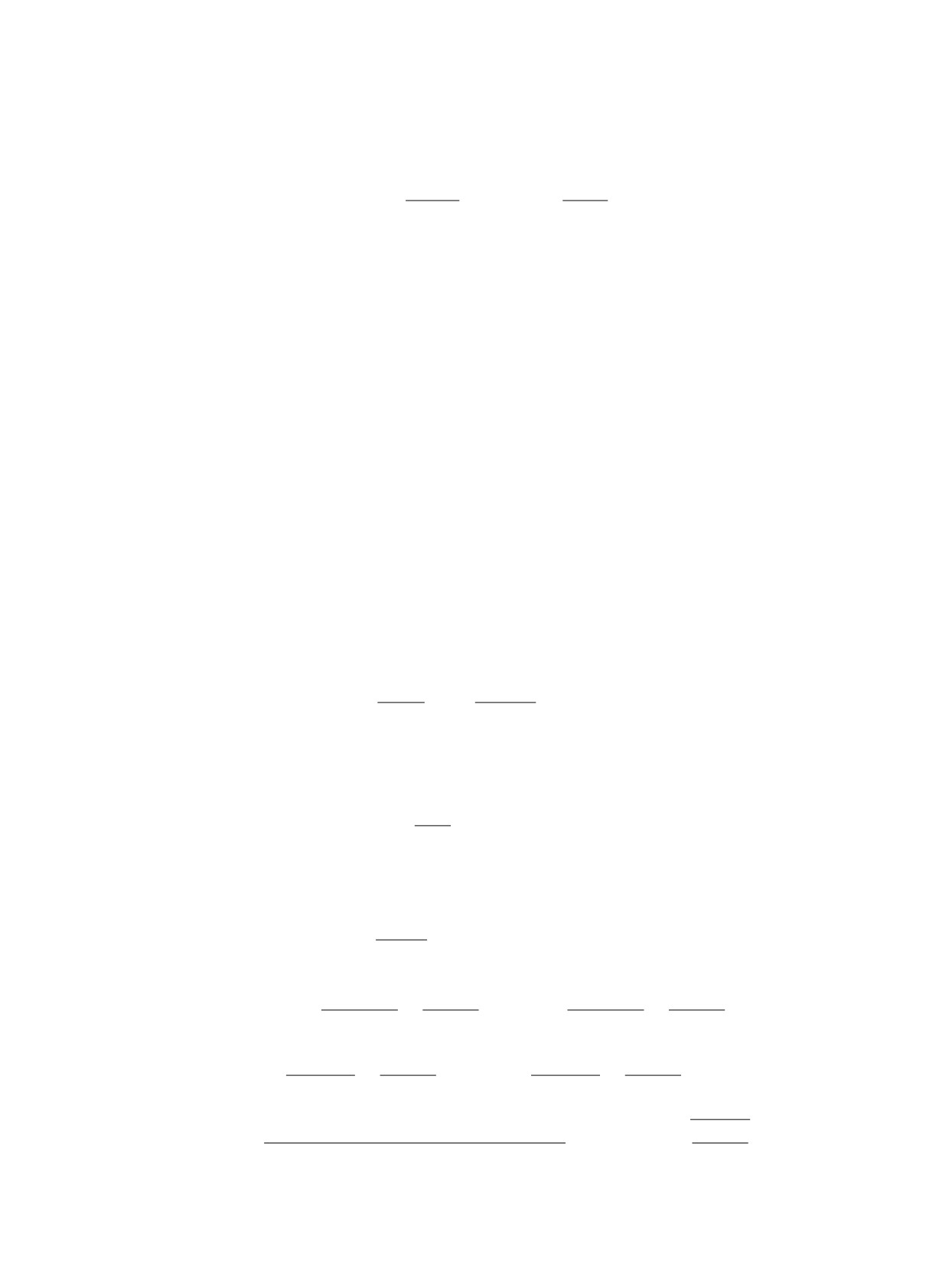ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 7, с.977-994

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.63+517.958:532.5

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

НА ОСНОВЕ РАЗРЫВНОГО МЕТОДА ГАЛЁРКИНА

ДЛЯ РЕЛАКСАЦИОННОЙ МОДЕЛИ БАЕРА-НУНИЦАТО

Для моделирования динамики двухфазных сред в рамках полностью неравновесной моде-

ли Баера-Нунциато с учётом жёсткой механической релаксации рассматривается разрыв-

ный метод Галёркина/Рунге-Кутты. Для монотонизации решения используются лимитер

WENO-S, который применяется непосредственно к консервативным переменным модели.

Релаксационные процессы моделируются с использованием неявного метода Гира шестого

порядка с адаптивным выбором шага интегрирования. Для построения численного пото-

ка применяется подход на основе теории DLM, позволяющей обобщить методы годунов-

ского типа на случай неконсервативных гиперболических систем уравнений. С помощью

разработанного метода проводится расчёт одномерных и двумерных задач, даётся анализ

результатов расчётов. В двумерном случае данные расчётов сравниваются с результатами

лабораторных экспериментов.

DOI: 10.31857/S0374064122070093, EDN: CEQMHD

Введение. Настоящая работа посвящена численному решению двухфазной полностью

неравновесной модели Баера-Нунциато (БН) с релаксационными слагаемыми. Данная модель

впервые предложена в работе [1] для анализа процесса перехода дефлаграции в детонацию

при моделировании динамики горения гранулированных взрывчатых веществ. В дальнейшем

она применялась для решения широкого спектра задач и в настоящее время может рассмат-

риваться как базовая модель для целого ряда обобщений [2-6].

Математическая формулировка модели приведена в п. 1 настоящей работы. Укажем здесь

ряд её свойств, которые усложняют задачу построения вычислительных алгоритмов для её

решения:

(а) система уравнений БН является гиперболической системой первого порядка и включает

в себя члены как в дивергентной, так и в квазилинейной форме. Она не может быть записана

полностью в дивергентном виде;

(б) модель включает в себя релаксационные члены, которые описывают процесс релаксации

механических и термодинамических параметров фаз к равновесному значению. По крайней

мере в ряде приложений характерные времена релаксации могут быть значительно меньше

характерных времён протекания других газодинамических процессов. В этом смысле система

уравнений БН является “жёсткой”.

В связи с этим численное решение уравнений БН является сложной задачей, решению

которой посвящено значительное число работ (см., например, [7-11]). Большая их часть на-

правлена на рассмотрение указанных выше трудностей.

Для построения аппроксимации задачи в настоящей работе используется разрывный ме-

тод Галёркина/Рунге-Кутты (RK/DG, Runge-Kutta/Discontinuous Galerkin method) [12]. Его

использование предполагает построение слабой постановки задачи. Для неконсервативных

систем такая постановка может быть построена с помощью так называемой теории DLM

(DalMaso-LeFloch-Murat) [13]. Этот подход позволяет обобщить традиционные методы го-

дуновского типа на случай неконсервативных систем уравнений. Теория DLM основана на

понятии пути - гладкого отображения, которое интерполирует между состояниями решения

на разрыве и определяет структуры ударной волны. При этом различным путям соответству-

ют различные решения задачи Римана. В связи с этим выбор пути однозначно определяет вид

решения задачи. Обоснование того или иного способа выбора пути для конкретной постановки

задачи является открытым вопросом (см. [14]).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

978

ПОЛЕХИНА и др.

Целью настоящей работы является реализация и исследование возможностей вычисли-

тельного алгоритма решения уравнений модели БН, основанного на совместном применении

сравнительно простых компонент, которые включают в себя:

- применение разрывного метода Галёркина для построения пространственных аппрокси-

маций уравнений модели;

- лимитирование консервативных переменных с использованием геометрического лимитера

WENO-S;

- применение теории DLM для формулировки слабой постановки задачи;

- использование простейшего расщепления по физическим процессам для учёта жёстких

релаксационных слагаемых;

- применение неявного метода Гира для интегрирования правых частей модели.

Эффективность предложенной методики иллюстрируется результатами численных экспе-

риментов. Рассмотренные тесты соответствуют физической постановке задачи, в которой сре-

да эффективно является двухфазной и гетерогенной с прямым разрешением границы раздела

фаз. Распределение фаз описывается в рамках так называемой диффузной границы. В этом

случае обе фазы формально присутствуют в каждой точке пространства, но в области одно-

родности фазы одна из двух объёмных долей пренебрежимо мала. В рамках такой постановки

рассматриваются задачи прохождения ударной волны из лёгкого вещества в тяжёлое (в од-

номерной постановке) и взаимодействия ударной волны с пузырями более тяжёлого и более

лёгкого (по отношению к вмещающей среде) газа.

В первом случае сравнение результатов расчётов проводится с аналитическим решением в

рамках модели Капилы [5]. Последняя является равновесной по скоростям и давлениям фаз

и может быть получена как предел модели БН при исчезающе малых временах релаксации.

Для двумерных тестов результаты расчётов сравниваются с результатами лабораторных экс-

периментов.

Работа имеет следующую структуру. Математическая модель и её особенности представ-

лены в п. 1. Описанию и особенностям реализации вычислительного алгоритма посвящён п. 2.

В п. 3 описаны результаты моделирования и проводится их анализ. В заключении формули-

руются основные результаты работы.

1. Модель Баера-Нунциато с релаксацией. Модель БН описывает двухфазную среду

как совокупность двух взаимопроникающих континуумов, каждый из которых характеризу-

ется своей скоростью и совокупностью термодинамических параметров состояния. Скорости

и давления фаз в общем случае не равны между собой, и, таким образом, модель являет-

ся полностью неравновесной. Система уравнений модели БН в варианте, приведённом в [15],

имеет вид

∂α_k

+ u_I · ∇α_k = ν(P_k - P_k),

(1a)

∂t

∂α_kρ_k

+ ∇ · (α_kρ_ku_k) = 0,

(1b)

∂t

∂α_kρ_ku_k

+ ∇ · (α_kρ_ku_k

^⊗u_k) + ∇(α_kP_k) - P_I∇α_k = μ(u_k - u_k),

(1c)

∂t

∂α_kρ_kE_k

+ ∇ · (α_k(ρ_kE_k + P_k)u_k) - P_Iu_I∇α_k = μ(u_k - u_k) · u_I + ν(P_k - P_k)P_I.

(1d)

∂t

Здесь α_k, ρ_k, u_k, P_k, E_k - объёмная доля, плотность, поле скоростей, давление и полная

энергия фазы k = 1, 2 соответственно; k = {1, 2} \ {k}; величины ν, μ - релаксационные

параметры. Для объёмных долей выполнено условие нормировки α₁ +α₂ = 1. Полная энергия

k-й фазы определена равенством

E_k = U_k + u_k · u_k/2,

где U_k - внутренняя энергия фазы.

Уравнения модели включают в себя: уравнение динамики для объёмной доли (1a), законы

сохранения массы (1b), импульса (1c) и энергии (1d).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

979

Величины u_I и P_I являются так называемыми интерфейсными скоростью и давлением и

могут быть определены целым рядом способов (см. [1, 16-18]). В настоящей работе использу-

ется вариант, предложенный в оригинальной работе [1]:

u_I = u₁, P_I = P₂,

(2)

где u₁ - скорость более сжимаемой фазы, P₂ - давление менее сжимаемой фазы.

Термодинамические свойства фаз определяются уравнениями состояния (УрС) и имеют

вид U_k = U_k(P_k, ρ_k). В данной работе рассматриваются УрC двух видов. Первое - это хорошо

известное двучленное УрС

P_k + γ_kP_∞,k

U_k =

(3)

(γ_k - 1)ρ_k

где P_∞,k и γ_k - референсное давление и показатель адиабаты. Вторым является УрС Ми-

Грюнайзена [19, раздел 2.7.6, с. 81]

ρ_k

∫

P_k - Pxk(ρ_k)

Pxk(ρ_k)

U_k =

+ Uxk(ρ_k), Uxk =

dρ_k,

(γ_k - 1)ρ_k

ρ²

ρ⁰

)-E1,k

)-E2,k

⁽ρ0k

P^x(ρk) = A1,k

-A2,k

(4)

ρ_k

где A_k, E_k - параметры.

Правые части уравнений (1) описывают взаимодействие фаз и часто называются релакса-

ционными в силу того, что они обеспечивают релаксацию скоростей и давлений фаз к оди-

наковому значению. Численные эксперименты, описанные в настоящей работе, соответствуют

физической постановке с прямым разрешением межфазных границ. В постановках такого типа

характерные времена релаксации много меньше характерных времён протекания других газо-

динамических процессов. В этом случае параметры μ и ν велики, и в этом смысле система

уравнений (1) является “жёсткой”.

Отметим, что система уравнений (1) содержит “неконсервативные произведения” вида

P_I∇α_k, P_Iu_I∇α_k и не может быть записана в консервативной форме. Эта особенность явля-

ется типичной для целого ряда многофазных многоскоростных моделей (см. [20]). Обобщённое

решение и соответствующие соотношения Ранкина-Гюгонио (РГ) для неконсервативных сис-

тем уравнений позволяет сформулировать теория DLM [13, 21], которая в дальнейшем также

используется для построения численной схемы.

Для системы уравнений (1) может быть построен её предел при μ, ν → +∞. Соответству-

ющая модель является равновесной по скоростям и давлениям и носит название модели Капи-

лы [5]. Уравнения модели приведены в приложении. В силу того, что далее рассматривается

случай жёсткой релаксации, соответствующий большим значениям μ и ν, представляется

естественным сравнивать численные решения уравнений (1) с точным аналитическим реше-

нием модели Капилы. Точное решение задачи Римана о распаде разрыва для модели Капилы

строится в приложении.

2. Вычислительный алгоритм. Использованный алгоритм численного решения систе-

мы уравнений (1) основан на применении следующих подходов: расщеплении по физическим

процессам для расчёта релаксационных правых частей системы, разрывном методе Галёркина

для решения однородной системы (1) и неявном многошаговом методе Гира [22, гл. 3, с. 331]

для интегрирования “жёстких” правых частей системы (1). Далее в настоящем пункте описаны

основные компоненты полного алгоритма решения задачи.

2.1. Разрывный метод Галёркина. Рассмотрим трёхмерный вариант неоднородной не-

линейной гиперболической системы уравнений, записанной в декартовой системе координат:

∑

∂Q

∂F_ξ

∂Q

B_ξ(Q)

= S(Q),

(5)

∂t

∂x_ξ

ξ=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

8^∗

980

ПОЛЕХИНА и др.

где x = (x₁, x₂, x₃) ∈ Ω = [0, L₁] × [0, L₂] × [0, L₃] ⊂ R³, t ∈ [0, T ] ⊂ R⁺, Q = Q(x, t) =

(Q₁, . . . , Q_M ) ∈ Ω_q ⊂ R^M , M - общее число компонент вектора Q, Ω_q - фазовое пространство

вектора Q, F_ξ - вектор потока, B_ξ - матрица, отвечающая квазилинейной неконсервативной

части уравнений, S - источники, описывающие механическую релаксацию.

Введём разбиение {ω_ijk} (декартова сетка) области Ω и обозначим ячейку сетки (конеч-

ный элемент) ω_ijk = [x1,i, x1,i+1] × [x2,j , x2,j+1] × [x3,k, x3,k+1], где x1,i = iΔx₁

(0 ≤ i ≤ N₁),

x2,j = jΔx2

(0 ≤ j ≤ N₂), x3,k = kΔx₃

(0 ≤ k ≤ N₃). Пусть индекс α каким-либо об-

разом упорядочивает тройки индексов ( i, j, k). Обозначим через V^ph(Ω) подпространство

элементов из L¹(Ω), проекции которых на ячейки ω_α принадлежат векторному пространству

P^p(ω_α) полиномов степени p:

V^ph = {v ∈ L¹(Ω) : v|ωα ∈ P^p(ω_α), 1 ≤ α ≤ N}, N = N1N2N3.

Представим решение Q(x, t) в ячейке ω_α конечномерной аппроксимацией Q_h ∈ V^ph :

∑

Q_h(x,t)|ωα =

ψ(l)α(x)Q(l)α(t),

(6)

l=0

где ψαl) - полином Лежандра степени l. Для получения полудискретной системы уравнений

относительно приближённого решения Q_h(x, t) подставим представление (6) в систему (5),

затем умножим (5) на пробную функцию v_h ∈ V^ph и проинтегрируем получившееся тождество

по ячейке ω_α :

∫

[

]

∫

∑

∂Q

∂F_ξ

∂Q_h

v_h(x)dx +

B_ξ(Q_h)

v_h(x) =

S(Q_h)v_h(x) dx.

(7)

∂t

∂x

∂xξΨ

ξ=1ωα

ωα

Для определения обобщённого решения (7) в случае неконсервативных систем (B_ξ = 0)

в настоящей работе используется распространённый подход, основанный на применении тео-

рии DLM [13, 21]. В рамках этого подхода для корректного определения “неконсервативного

произведения” вводится липшицево отображение Ψ : [0, 1] × Ω_q × Ω_q → Ω_q (путь), которое

“соединяет” значения решения по разные стороны от разрыва в точке x_d по направлению

внешней единичной нормали n, Ψ(Q^-, Q⁺; 0) = Q^-, Ψ(Q^-, Q⁺; 1) = Q⁺, Ψ(Q, Q; η) = Q,

Q^± = lim

Q(x_d ± hn).

h→0

Третье слагаемое в левой части системы (5) имеет вид “неконсервативного” произведения

B_ξ(Q)∂Q/∂x_ξ. Его значения в слабом смысле могут быть определены следующим образом [13]:

∫

[

]

∫

∂Q

∂Q_h

B_ξ(Q_h)

v_h(x)dx +

∂xξΨ

∂x_ξ

ωα

ω0α

∫

(∫1

)

∂Ψ(Q^-,Q⁺;η)

B_ξ(Ψ(Q^-,Q⁺;s))

dη v_h(x) dσ,

(8)

∂η

∂ωα

где ω0α = ω_α \ ∂ω_α, n - внешняя единичная нормаль к ∂ω_α. Заметим, что данное определе-

ние существенно зависит от выбранного пути Ψ. В дальнейшем используется линейный путь

Ψ(Q^-, Q⁺; η) = Q^- + η(Q⁺ - Q^-). Выбор пути Ψ является важным компонентом численного

алгоритма - он определяет решение задачи Римана системы (1) (см. [13, 21]).

На основе сделанных выше построений численная схема для разрывного метода Галёркина

может быть записана в виде

∫

∑

∂Q_h(x,t)

∂v_h(x)

∂Q_h

v_h(x)dx -

F_ξ

dx +

B(Q_h)

v_h(x)dx +

∂t

∂x

ξ=1ωα

ξ=1

ωα

ω0α

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

981

∫

+ v_h(x)D_n(x)dσ = S(Q_h)v_h(x)dx.

(9)

∂ωα

ωα

В настоящей работе в качестве численного потока используется поток HLLEM [8]:

s_outF(Q_in) - s_inF(Q_out)

s_outs_in

D_n =

n+κ

(Q_out - Q_in) -

s_out - s_in

s_in

−κ

B(Q_out, Q_∗)(Q_∗ - Q_out)

B(Q_∗, Q_in)(Q_in - Q_∗)],

s_in - s_out

где κ = n₁ + n₂ + n₃, Q_in ∈ ω_α, Q_out ∈ ω_β, где ω_β - ячейка, смежная к ω_α через элемент

её поверхности. Скорость распространения волн в задаче Римана оценивается следующим

образом:

{

min / max(0, Λ(Qin/out), Λ(^Q)), если κ > 0,

sin/out =

Q₌₂-1(Qin + Q_out).

max / min(0, Λ(Qin/out), Λ(^Q)) в противном случае,

Рассматривая произвольное v_h ∈ V^ph, v_h(x)|ωα ∈ span {ψαl)}, получаем следующую полу-

дискретную систему уравнений относительно переменных {Qαl)}, определённых в (6):

dQα

= H( Qα) + I( Qα).

(10)

Здесь

Q_α = (Q(0)0,α,... ,Q(p)0,α,Q(0)1,α,... ,Q(0)M,α,... ,Q(p)M,α) - вектор неизвестных. Его компонен-

ты Qml),α в дальнейшем будем называть l-й гармоникой (l = 0, p) m-й компоненты век-

тора Q_α. Матрица M ∈ R(p+1)×(p+1) является матрицей Грама с компонентами [M]_ml =

∫

= ωαψαl)ψαm) dx,векторH(Qα^{)-аппроксимациядифференциальногооператоравлевой}

части системы (5), вектор I(Qα) соответствует аппроксимации правой части системы (5):

∫

I(l)m = S_m(Q_h)ψ(l)α dx.

(11)

ωα

Одна из наиболее простых стратегий решения системы (10) - расщепление по процессам

первого порядка. Разобьём временной интервал на части точками {tn}. Далее на каждом

временном шаге t ∈ [tⁿ, tn+1] сначала решается задача Коши для системы обыкновенных

дифференциальных уравнений (ОДУ)

dQα

= H( Qα), t ∈ (tⁿ,tn+1],

(12)

c начальными данными

= Q_α(tⁿ) для определения “промежуточного” решения

Qα,H =

= Q_α(tn+1). Затем решается задача Коши для системы ОДУ

dQα

= I( Qα), t ∈ (tⁿ,tn+1],

(13)

с начальными данными

Qα,H. Её решение

Q_α рассматривается как решение задачи (10).

Для интегрирования по времени однородной системы (12) далее используется вариант ме-

тода Рунге-Кутты TVD/RK3 [12] с лимитированием консервативных переменных на каждом

шаге метода. В настоящей работе используется многостадийный лимитер на основе лимите-

ра WENO-S и дополнительных лимитирующих процедур, обеспечивающих физическую кор-

ректность решения - положительность давления, внутренней энергии и объёмных долей фаз.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

982

ПОЛЕХИНА и др.

Процедура лимитирования будет описана в п. 2.3. Для интегрирования по пространству ис-

пользуется метод квадратур Гаусса-Лежандра.

Для интегрирования системы уравнений (13) используется неявный метод Гира с автома-

тическим выбором шага интегрирования, описанный в п. 2.2.

2.2. Алгоритм расчёта релаксационных слагаемых. Задача Коши для ОДУ (13)

решается неявным линейным многошаговым методом Гира [22, гл. 3, с. 331]. на временном

интервале t ∈ (tⁿ, tn+1]. Разобьём временной интервал на части точками tn0, tn1, . . . , tnχ-1,

где tnj+1 = t^nj + τ_j, tn0 = t_n, tnχ-1 = tn+1. Таким образом, Δt = tn+1 - tⁿ - шаг интегрирования

газодинамической части задачи, а τ_j - шаг интегрирования релаксационной части. Разностная

схема решения задачи Коши для (13) имеет следующий вид:

∑

= Q_α(tⁿ);

ζ_k Qj+1-kα = τ_jβ₀R(Qj+1α), j = 0,1,...

(14)

k=0

Здесь τ_j = const, R = M-1I. Аппроксимации релаксационных членов I, определённых в (11),

рассчитываются численно методом квадратур Гаусса-Лежандра.

В дальнейшем все численные расчёты проводятся методом Гира 6-го порядка (K = 6). Ко-

Q^j

эффициенты метода представлены в табл. 1. Для начала счёта требуется знать значения

α,

j = 1,K - 1. Для этого рекуррентно используется метод Гира, т.е. сначала для нахождения

используется метод Гира первого порядка, затем второго для

и т.д.

Таблица 1. Коэффициенты метода Гира до 6-го порядка, ζ0 = 1

ζ1

ζ2

ζ3

ζ4

ζ5

ζ6

-1

2/3

-4/3

1/3

6/11

-18/11

9/11

-2/11

12/25

-48/25

36/25

-16/25

3/25

60/137

-300/137

300/137

-200/137

75/137

-12/137

60/147

-360/147

450/147

-400/147

225/147

-72/147

10/147

Нелинейная система уравнений (14) решается численно методом Ньютона:



∂F (Qα+1)



(Qj+1,s+1α -Qj+1,sα) = -F (Qj+1,sα),

(15)



∂Qα+1

Qj+1,s

Qj+1,0

где индекс s обозначает номер итерации,

= Q^α соответствует s = 0. Функция F

имеет следующий вид:

∑

F(Qj+1α) = ζ₀ Qj+1α - τ_jβ₀R(Qj+1α) -

ζ_p Qj+1-kα.

k=1

Матрица Якоби ∂F (Qα+1)/∂Qα+1 в (15) вычисляется с применением численного дифференци-

рования или аналитически (для каждого численного расчёта ниже это указывается отдельно).

Итерации метода Ньютона продолжаются до тех пор, пока величина r = max|rm| не станет

меньше заданного значения. Здесь r_m определены следующим образом:

⎧

⎨

Qj+1,s+1

α,m

- Q^α

если |Qα

| > 1,

r_m =

Qj+1,s+1

(16)

α,m

⎩

Qj+1,s+1

α,m

- Q^α

в противном случае.

Шаг τ_j может быть переменным и определяется адаптивно. В начальный момент τ₀ =

= Δt/6, где Δt - шаг интегрирования задачи (12). В случае если превышено максимальное

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

983

число N_max ньютоновских итераций (далее N_max = 10) или если решение сходится к нефи-

зичным результатам (отрицательное давление или объёмная доля и т.д.), то шаг интегриро-

вания уменьшается. В случае когда число итераций меньше минимального значения N_min

(далее N_min = 3), шаг интегрирования увеличивается. При этом если шаг интегрирования

меняется, то необходимо вернуться к первому шагу метода Гира и рекуррентно пересчитать

Q^j

значения

α, j = 1,K - 1, для нового значения временного шага τ.

Коэффициенты релаксации μ и ν в системе (13) либо задаются постоянными, либо рассчи-

тываются в каждой точке пространства динамически таким образом, чтобы фазовые давления

и скорости релаксировали за один газодинамический временной шаг Δt. Соответствующая

оценка строится следующим образом. Релаксация давлений и скоростей в случае межфазных

соотношений (2) и УрС (3) может быть записана в виде

(

)

d(u₁ - u₂)

= -μ(u₁ - u₂)

α₁ρ₁

α₂ρ₂

)

d(P₁ - P₂)

⁽P_I +C1aP₁ +C1b

P_I + C2aP₁ + C2b

= -ν(P₁ - P₂)

(17)

α₁C1a

α₂C2a

где C_ka = 1/(γ_k - 1), C_kb = γ_kP_∞,k/(γ_k - 1). Здесь также предполагается, что релаксация

скоростей не влияет на релаксацию давлений. Другими словами, в первом уравнении в (17)

фиксировано давление. Тогда коэффициенты релаксации можно оценить следующим образом:

(

)-1

⁽P_I +C1aP₁ +C1b

P_I + C2aP₁ + C2b

μ=

ν =

(18)

Δt α₁ρ₁

α₂ρ₂

Δt

α₁C1a

α₂C2a

Такой выбор значений μ и ν обеспечивает релаксацию за один временной шаг Δt.

2.3. Алгоритм монотонизации решения. В качестве основного ограничителя для моно-

тонизации решения используется ограничитель WENO-S, предложенный в работе [23]. Однако

после его использования полученные значения компонент решения могут быть нефизичными -

особенно вблизи зоны резкого изменения объёмной доли. Для решения этой проблемы ис-

пользуется дополнительное лимитирование решения. Общая схема лимитирования выглядит

следующим образом.

1. Применение ограничителя, обеспечивающего положительность объёмных долей и плот-

ностей фаз. Данный ограничитель обозначим через Λ₁ [24].

2. Применение ограничителя WENO-S (обозначим его через Λ₂).

3. Применение ограничителя, обеспечивающего положительность давлений фаз (обозначим

его через Λ₃).

Рассмотрим подробнее каждый из этапов лимитирования.

Ограничитель Λ₁. Пусть имеется вектор Q(x,t) с компонентами Q_m(x,t). В ячейке ω_α

согласно представлению (6) величины Q_m(x, t) имеют вид

∑

(Q_m)_h(x, t)|ωα =

ψ(l)α(x)Q(l)m,α(t), m = 1,M.

l=1

Введём среднее значение Q_m(x, t) равенством

∫

Q_m =

(Q_m)_h(x, t)|ωα dx.

|ω_α|

ωα

Процесс лимитирования сводится к пересчёту всех величин по следующей формуле:

(Qm)_h(x,t) = Q_m + θ((Q_m)_h(x,t) - Q_m),

(19)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

984

ПОЛЕХИНА и др.

где θ - параметр. Если область значений Q_m лежит на интервале (a, b), то для этой величины

рассчитывается параметр θ_m по формуле

{

}

Q_m - (a + ε)

Q_m - (b - ε)

θ_m = min

Q_m - (Q_m)_min

Qm - (Qm)max

Если значения Q_m определены на (a, ∞), то

{

}

Q_m - (a + ε)

θ_m = min

Q_m - (Q_m)_min

где

(Q_m)_min = min(Qm)h(x, t)|ωα = min(Qm)h(xgp, t)|ωα ,

ωα

xgp

(Q_m)_max = max(Qm)h(x, t)|ωα = max(Qm)h(xgp, t)|ωα ,

ωα

xgp

x_gp - квадратурные точки конечного элемента ω_α, ε > 0 - малая величина (в данной работе

ε = 10-6).

Параметр θ_m рассчитывается для величин {α₁, α₂, α₁ρ₁, α₂ρ₂}, при этом значения α₁ и

α₂ определены на (0,1), значения ρ₁ и ρ₂ определены на (0,∞). Общий коэффициент ли-

митирования рассчитывается по формуле

θ = min{θm}.

Затем операция лимитирования Λ₁ с общим коэффициентом θ применяется ко всем компо-

нентам вектора Q по формуле (19).

Ограничитель Λ₂. Ограничитель WENO-S применяется в два шага.

Шаг 1. Идентификация ячеек, в которых решение подлежит лимитированию. В данной

работе используется TVB-индикатор [23].

Шаг 2. Применение ограничителя WENO-S для реконструкции решения в отмеченных

ячейках.

Рассмотрим лимитер WENO-S. Сначала опишем его одномерный вариант по направлению

оси Ox₁. Рассмотрим ячейки ω_ijk, где i = i₀ - 1, i₀, i₀ + 1, j = j₀, k = k₀, a индекс α их

локально упорядочивает как α = -1, 0, 1 соответственно. Реконструкция решения в централь-

ной ячейке α = 0 происходит в соответствии с выражением

Qnewm,0(x) = κ-1Qmodm,-1(x) + κ₀Qm,0(x) + κ₁Qmodm,1(x),

где

)-1

( ∑

γ_n

κ_j = κ_j

κ_n

κ_n =

n = -1,0,1.

(ε + β_n)^r

n=-1,0,1

Здесь γ_n - линейный вес, ε = 10-6 и r = 2. Линейные веса должны удовлетворять следующим

требованиям:

γ₀ ≫ γ±1, γ-1 + γ₀ + γ₊₁ = 1.

В настоящей работе γ₀ = 0.998, γ±1 = 0.001. Индикатор гладкости β_α рассчитывается по

формуле

∫

(

)₂

∑

∂^l

β_α =

Δx2l-1

Q_m,α(x) dx₁, α = -1,0,1.

∂x^l

l=1_ω

Здесь p - степень полинома Q_m,α(x).

Применение ограничителя может быть записано в операторном виде как Q^new0 = Λ2,ξQ₀

для направления вдоль оси Ox_newξ. Для многомерного случая и декартовых сеток Q^new0 =

= Λ₂Q₀, где Λ₂ = Λ2,3Λ2,2Λ2,1.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

985

Ограничитель Λ₃. На данном этапе лимитирования в каждой квадратурной точке ячей-

ки ω_α вычисляются давления фаз. Если давление какой-либо фазы отрицательно хотя бы в

одной точке, то в этой ячейке оставляются только средние величины консервативных пере-

менных.

3. Вычислительные эксперименты. Тесты, рассмотренные ниже, соответствуют физи-

ческой постановке с прямым разрешением межфазных границ. Напомним, что в постановках

такого типа предполагается, что все фазы одновременно присутствуют в каждой точке прост-

ранства, но объёмные доли всех фаз, кроме одной, пренебрежимо малы всюду за исключени-

ем “диффузных границ” - относительно тонких пространственных областей, соответствующих

границам раздела фаз среды.

Тесты 1 и 2, предложенные в [19] (разделы 2.7.5 и 2.7.6 соответственно), являются соот-

ветственно одномерной задачей Римана о распаде разрыва и задачей о прохождении ударной

волны (УВ) через контактную границу двух веществ при больших соотношениях плотностей

(из лёгкого в тяжёлое или из тяжёлого в лёгкое) и разных УрС. Эти тесты допускают анали-

тическое решение в рамках модели Капилы (см. приложение).

Тесты 3-5 исследуют в рамках пространственно двумерной постановки взаимодействие УВ

с пузырём криптона, азота или гелия в воздухе. Полученные численные расчёты сравниваются

с экспериментальными данными [25], а также с численными расчётами, полученными другими

авторами [26].

Численные эксперименты проводились с шагом интегрирования, рассчитанным из условия

Куранта:

(Δx_ξ,k)

min

ξ,k

Δt = CFL

(20)

λ_max

где CFL = 0.9 для p = 0 и CFL = 0.2 для p = 1 (здесь p - порядок полинома Лежандра

в (6)), λ_max - максимальное собственное значение системы уравнений (1).

Тест 1. Тест характеризуется тем, что распад разрыва происходит на контактной грани-

це при больших соотношениях давлений (×1000). Первая фаза представляет собой воду, а

вторая - воздух (ρ₁/ρ₂ ≈ 20). Начальные данные приведены в табл. 2. Контактный разрыв

(КР) в начальный момент времени задан в точке x₀ для всех переменных. Коэффициенты

релаксации оцениваются по формуле (18). Численные эксперименты проводились в расчётной

области [0, 1].

Таблица 2. Начальные данные 1D расчётов

Начальные данные

Тест

Тип УрС

Параметры

x < x0

x > x0

P1 = 10⁹, P2 = 10⁹,

P1 = 10⁶, P2 = 10⁶,

УрС (3)

γ1 = 4.4, π1 = 6·10⁸,

ρ1 = 1000, ρ2 = 50,

γ2 = 1.4, π2 = 0,

u1 = 0, u2 = 0,

x0 = 0.7

α1 = 1 - 10-4

α1

= 10-4

P1 = P2 = 10-5,

фаза 1: УрС (3)

γ1 = 1.4, π1 = 0,

ρ1 = 0.125, ρ2 = 7.82,

фаза 2: УрС (4)

γ2 = 4.54777,

u1 = u2 = 0

u1 = u2 = 0,

A1,2 = A2,2 = 62.6,

α1 = 1 - 10-4

α1 = 10-4

E1,2 = 4, E2,2 = 1,

x0 = 0.4

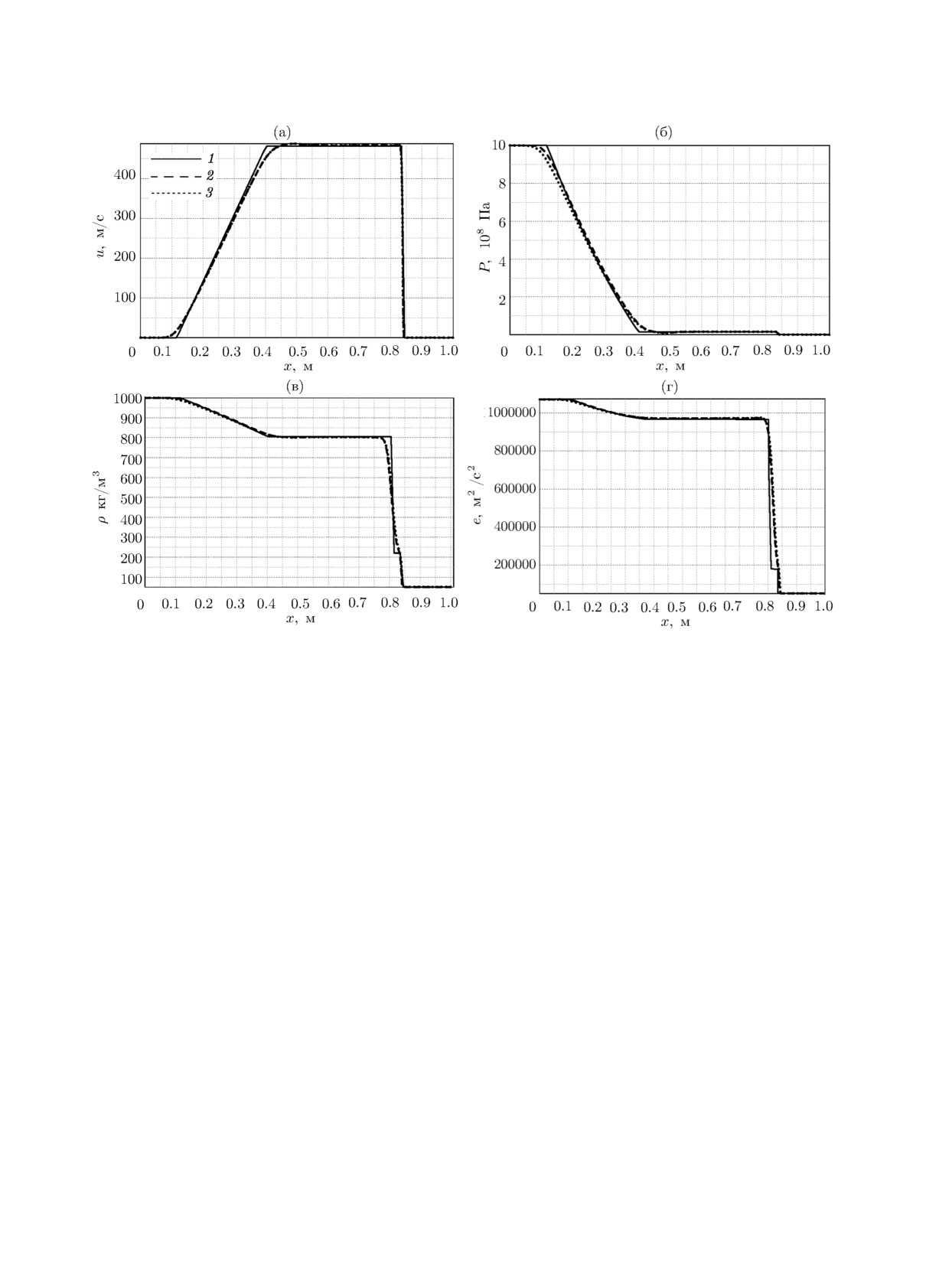
Удельная внутренняя энергия e, представленная на рис. 1 и рис. 2, рассчитывается сле-

дующим образом:

U₁α₁ρ₁ + U₂α₂ρ₂

α₁ρ₁ + α₂ρ₂

На рис. 1 показано сравнение результатов численных расчётов для N = 2500 с аналитиче-

ским решением, полученным в приложении, на момент времени t = 2.2 · 10-4 c (см. табл. 2).

Видно, что численные результаты достаточно хорошо воспроизводят аналитическое решение.

На кривой давления результаты с p = 1 менее диссипативны, чем результаты для p = 0.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

986

ПОЛЕХИНА и др.

Рис. 1. Распределения для всех переменных в тесте 1 (1 - аналитическое решение, 2 - численный расчёт с

p = 1, 3 - численный расчёт с p = 0).

Tecт 2. Тест характеризуется тем, что УВ формируется в первой фазе, менее плотной, а

затем проходит через КР из лёгкого вещества в тяжёлое. Таким образом, в отличие от преды-

дущего теста положения КР и скачка давления не совпадают в начальный момент времени.

В начальный момент времени КР задан в точке x₀ (см. табл. 2). Отношение плотностей сред

ρ₂/ρ₁ ≈ 60. Начальные данные представлены в табл. 2. На левой границе задаются следующие

краевые условия:

α₂ = 10-4, α₁ = 1 - α₂, α₁ρ₁ = 0.1249875, α₂ρ₂ = 0.000782,

α₁ρ₁u₁ = 0.288596, α₂ρ₂u₂ = 0.0018.

На правой границе устанавливаются условия симметрии. Численные эксперименты проводи-

лись в расчётной области [-1.4, 1], а результаты расчётов представлены для расчётной облас-

ти [0, 1]. Коэффициенты релаксации при расчёте на временном интервале (tⁿ, tn+1] задаются

равными λ = 5 · 10⁹ кг/(м · c), ν(n)k = α(n)1,kα(n)2,k · 10⁶ Па-1 · c-1, где α^pi,k - значение объёмной

доли фазы i = 1, 2 в ячейке с номером k на временном слое p.

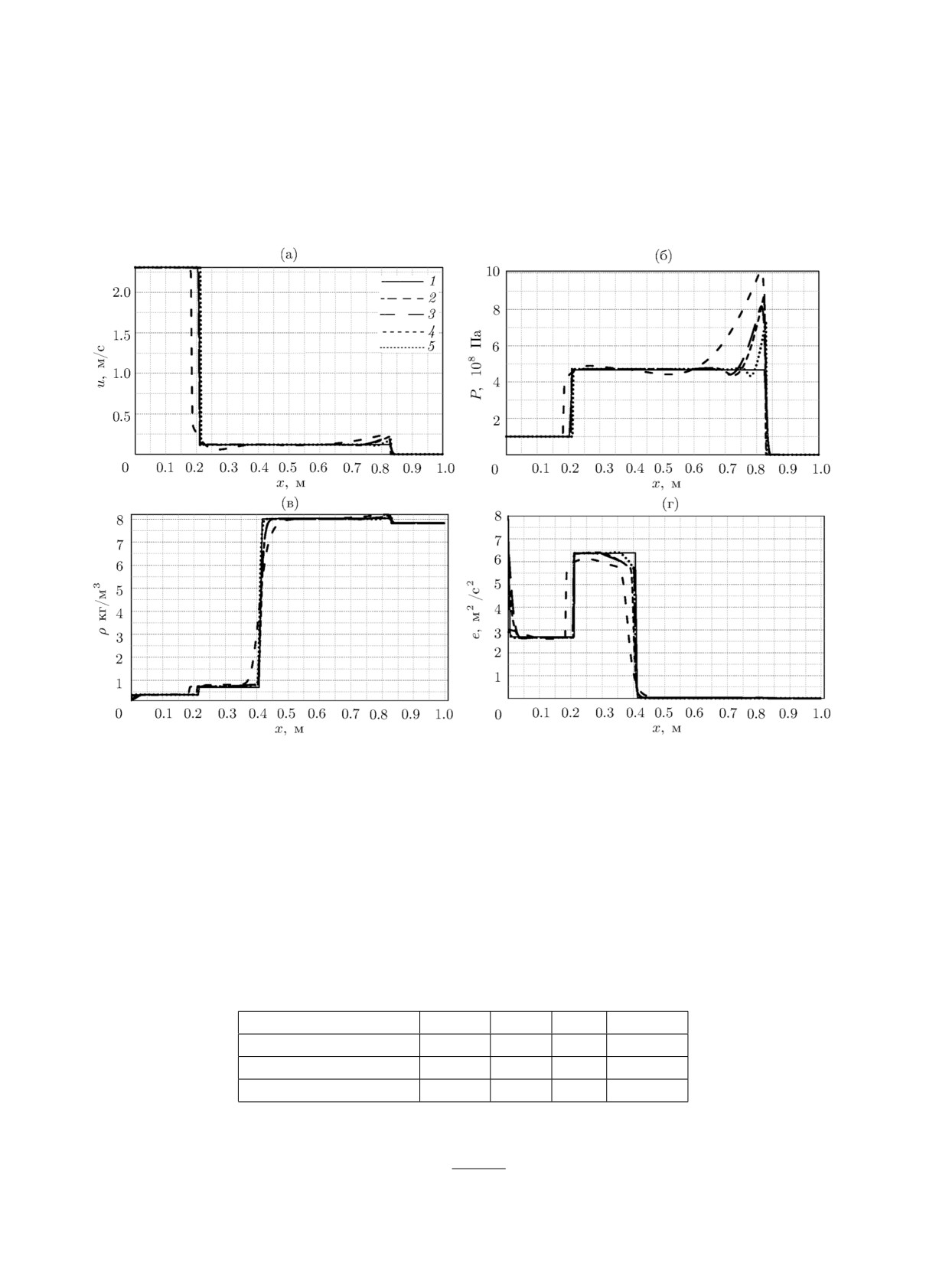
Результаты численных экспериментов представлены на рис. 2 на момент времени t =

= 0.606323 c для N = 5000 (p = 0, 1), N = 40000 (p = 0) и N = 160000 (p = 0). Обратим

внимание на пик в окрестности УВ, который возникает в результате взаимодействия УВ с КР.

Видно, что численное решение сходится к аналитическому решению, однако очень медленно.

Такие результаты связаны с наличием в системе (1) “неконсервативных произведений”.

Проблемы со сходимостью численного решения неконсервативной системы уравнений к

обобщённому решению хорошо известны [7, 8] и подробно обсуждаются в работе [14]. Связано

это с тем, что в отличие от консервативных систем соотношения РГ для неконсервативных

систем зависят от структуры разрыва, т.е. от производных высших порядков [14]. Задавая путь

в теории DLM, мы неявно задаём уравнение для определения структуры разрыва. С другой

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

987

стороны, первое дифференциальное приближение разностной схемы, описанной в п. 2, зави-

сит не только от заданного пути, но и от численной вязкости. Таким образом, уравнение для

определения структуры разрыва, которое используется для получения аналитического реше-

ния, не совпадает с первым дифференциальным приближением численной схемы. Системное

решение этой проблемы в настоящее время неизвестно.

Рис. 2. Распределения для всех переменных в тесте 2: 1 - аналитическое решение; 2 - N = 5000, p = 0; 3 -

N = 5000, p = 1; 4 - N = 40000, p = 0; 5 - N = 160000, p = 0.

Тест 3-5. В данной серии экспериментов исследуется прохождение УВ через пузырек ге-

лия, азота или криптона диаметром D₀ = 0.4 м, содержащийся в ударной трубе. Для фаз

используется УрС (3) с параметрами, указанными в табл. 3. Термодинамические параметры

пузырька и окружающего воздуха приведены в табл. 3 (pеференсное давление P_∞ = 0). Схе-

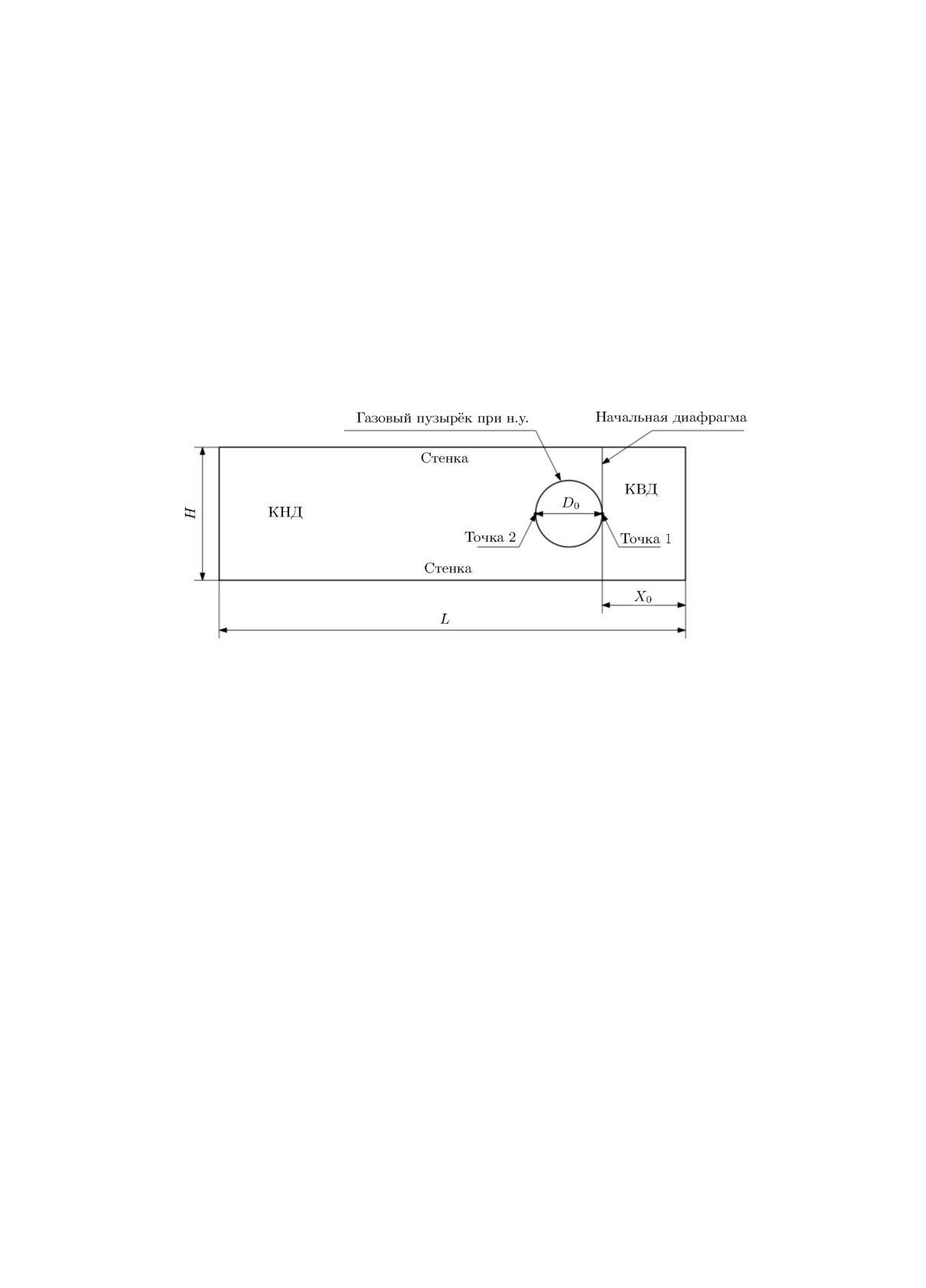
матическое представление расчётной области с размерами L = 0.3 м, H = 0.08 м, X₀ = 0.05 м

представлено на рис. 3. В камере низкого давления (КНД) задаются нормальные начальные

условия, а в камере высокого давления (КВД) - P₀ = 249 090 Па. На твердых стенках уста-

навливаются условия симметрии. Численные эксперименты проводились на расчётной сетке

для N₁ = 900, N₂ = 240 с p = 1. Коэффициенты релаксации оцениваются по формуле (18).

Таблица 3. Термодинамические свойства воздуха и пузырька

Физические свойства

Воздух Гелий Азот Криптон

Плотность ρ, кг/м³

1.29

0.167

1.25

3.506

Скорость звука c, м/c

340

1007

367

220

Показатель адиабаты γ

1.4

1.67

Динамика прохождения УВ через пузырёк зависит от числа Атвуда

ρ_b - ρ_s

ρ_b + ρ_s

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

988

ПОЛЕХИНА и др.

где ρ_b - плотность пузырька, ρ_s - плотность окружающей среды. После того как фронт УВ

достигает газового пузырька, он перестаёт быть плоским, так как одна часть волны взаи-

модействуют с пузырьком (в дальнейшем будем называть её проходящей УВ), а другая нет

(падающая УВ). Если плотность газового пузырька больше, чем плотность окружающей сре-

ды (A > 0), то УВ по газовому пузырьку распространяется медленнее. Соответственно, если

плотность газового пузырька меньше, чем плотность окружающий среды (A < 0), то УВ

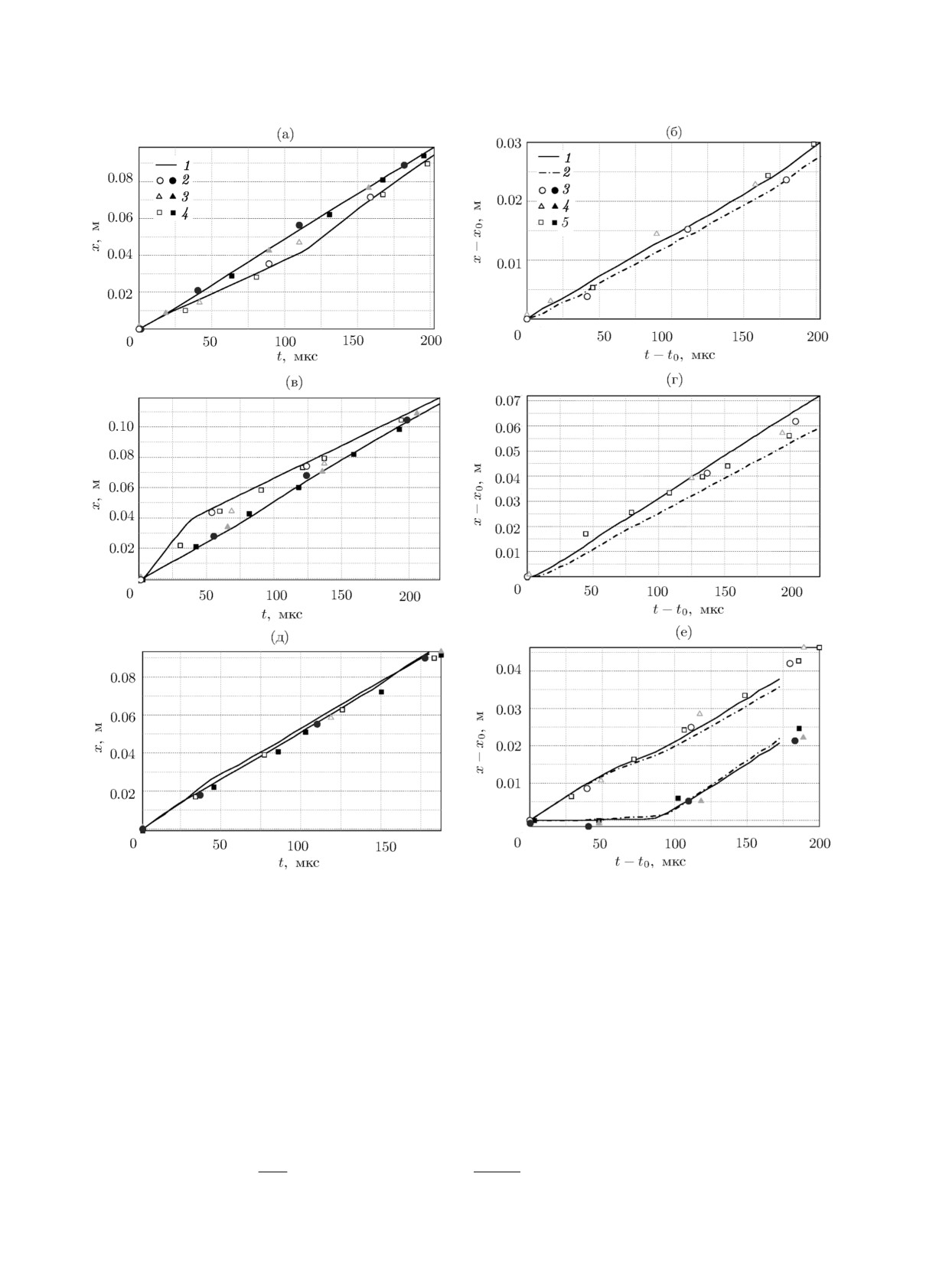
по газовому пузырьку распространяется быстрее. Результаты численных экспериментов по

скорости распространения падающей и проходящей УВ представлены на рис. 4, a (криптон),

рис. 4, в (гелий) и рис. 4, г (азот). Видно, что скорость проходящей УВ для криптона меньше,

чем скорость падающей УВ (A = 0.4621), выше для гелия (A = -0.7708) и практически

совпадают для азота (A = -0.0157). Наблюдается хорошее согласие полученных численных

результатов с экспериментальными данными по скорости распространения падающей и про-

ходящей УВ.

Рис. 3. Схематическое представление расчётной области для тестов 3-5.

Эволюция газового пузырька исследуется путём отслеживания значений решения в точ-

ках 1 и 2, связанных с межфазной границей пузырька (см. рис. 3). Экспериментальные данные

для точки 2 в [25] представлены только для азота. Для обработки результатов численных рас-

чётов по определению положения межфазной границы устанавливалось пороговое значение

α_cr. На рис. 4 представлены результаты с α_cr = 0.1 и α_cr = 0.3. Видно, что полученные

численные результаты хорошо согласуются с экспериментальными данными по описанию эво-

люции газового пузырька.

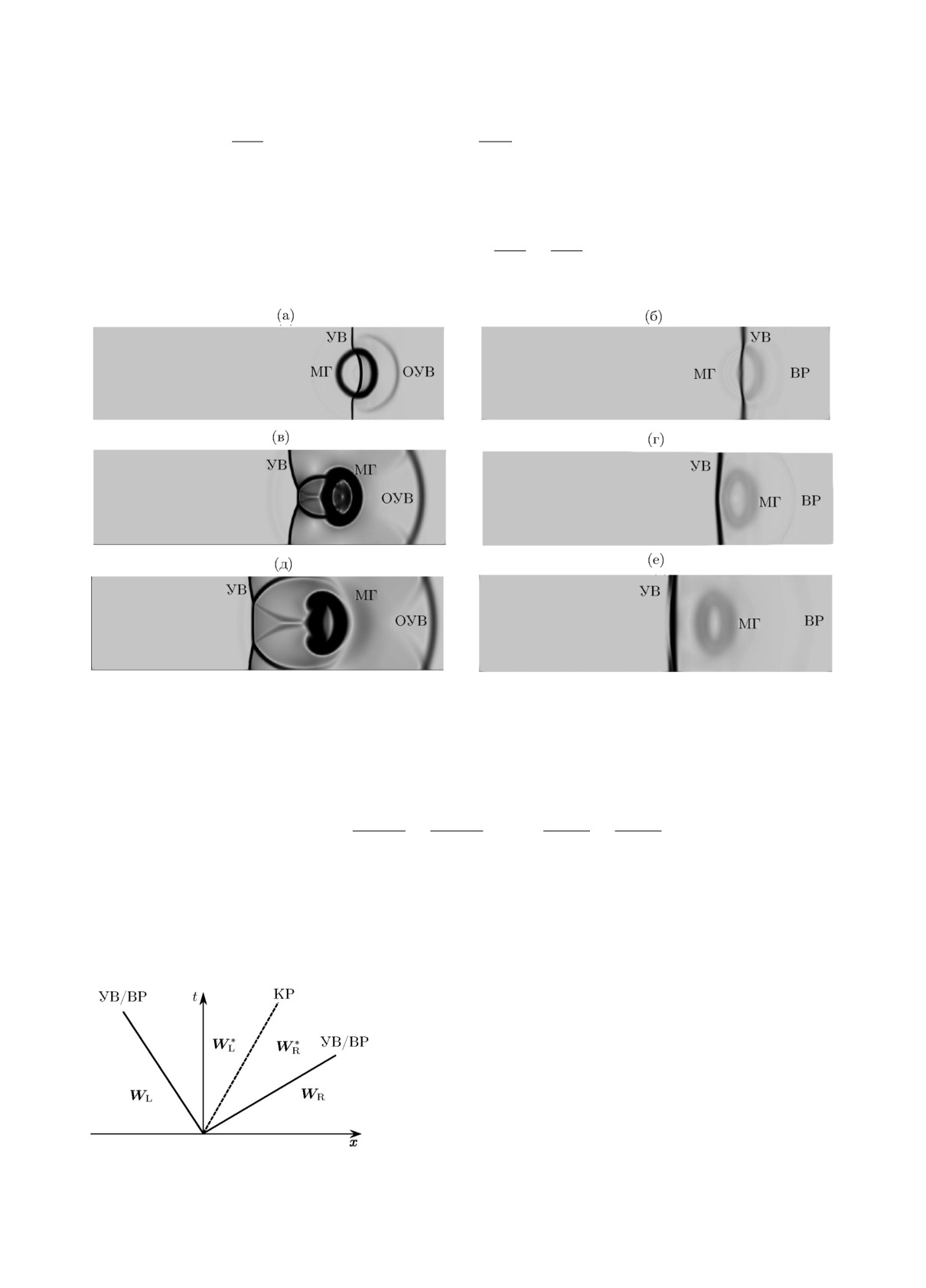
На рис. 5 представлена структура волн, которая формируется при взаимодействии пузырь-

ка азота и криптона с ударной волной (УВ). На pис. 5, а видно, что проходящая УВ медленнее

падающей УВ (случай A = 0.4621), а при прохождении УВ через пузырёк азота её фронт

практически не деформируется (случай A = -0.0157).

В работе [26] приведены также численные результаты для рассматриваемых постановок.

Указанная работа отличается от настоящей тем, что в ней рассматривается равновесная по

скорости модель [5]. Напомним, что в настоящей работе использовалась полностью неравно-

весная модель, а равновесие по скорости и давлению обеспечивается “жёсткой” механической

релаксацией. На рис. 4 также видно согласие полученных численных расчётов с результатами

численных расчётов, полученных в работе [26].

Заключение. В работе рассматривается полностью неравновесная модель Баера-Нунци-

ато с релаксационными слагаемыми. Вычислительный алгоритм для решения этой модели

включает в себя решение гиперболической части с помощью разрывного метода Галёркина с

использованием метода Рунге-Кутты для интегрирования по времени, вычисление релаксаци-

онных слагаемых, а также монотонизация решения с использованием ограничителя, обеспе-

чивающего положительность объёмных долей и плотностей, а также ограничителя WENO-S.

В работе показано, что полученный вычислительный алгоритм демонстрирует достаточно хо-

рошее совпадение рассчитанных данных с экспериментальными в ряде тестовых расчётов.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

989

Рис. 4. x - t диаграммы в тестах 3 (a, б), 4 (в,г) и 5 (д, е) для падающей и проходящей УВ - а, в, д: 1 -

численный расчёт; 2 - эксперимент 1 [25]; 3 - эксперимент 2 [25]; 4 - численные расчёты [26] (тёмные значки -

падающая УВ, светлые - проходящая УВ); x - t диаграммы для точки межфазной границы - б, г, е: 1 -

численный расчёт, αcr = 0.3; 2 - численный расчёт, αcr = 0.1; 3 - эксперимент 1 [25]; 4 - эксперимент 2 [25];

5 - численные расчёты [26] (тёмные значки - точка 1, светлые - точка 2).

Приложение. Задача Римана о распаде разрыва. В данном пункте динамика двух-

фазной среды в задаче Римана изучается на основе хорошо известной модели Капилы (которая

в дальнейшем обозначается как БН5 [5]). Эта модель получена из модели БН7 (1) в предпо-

ложении мгновенной механической релаксации [5]. Другими словами, скорости и давления

фаз в каждой точке пространства для модели БН5 равны. Решение модели БН5 может быть

использовано для валидации численных расчётов, полученных на основе модели БН7, для

физических постановок, которые соответствуют прямому разрешению межфазных границ.

В модели БН5 законы сохранения массы записываются для каждой фазы отдельно, а за-

коны сохранения импульса и энергии - для смеси в целом:

∂α₁

∂α_kρ_k

+ u · ∇α₁ = K∇ · u,

+ ∇ · (α_kρ_ku) = 0,

∂t

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

990

ПОЛЕХИНА и др.

∂ρu

∂ρE

+ ∇ · (ρu

^⊗u + P) = 0,

+ ∇ · ((ρE + P)u) = 0,

(21)

∂t

где u и P - скорость и давление смеси, ρ = α₁ρ₁ + α₂ρ₂ и E = e + u²/2 - плотность и полная

энергия смеси, коэффициент K определяет сжимаемость фаз [5]:

)

^∕(ρ₁c²¹

ρ₂c²²

K = (ρ₂c²² - ρ₁c²¹)

α₁

α₂

Рис. 5. Структура волн в тестах 3 (а,б), 4 (в, г), 5 (д,е) для пузырька криптона (а, в, д) и азота (б, г, е),

которая рассчитывалась как f(ρ2) = 1 - exp(-∥∇ρ2∥2/25) (МГ - межфазная граница, ОУВ - отражённая УВ,

ВР - волна разрежения): a - t = 60 мкс, б - t = 50, в - t = 171, г - t = 102, д - t = 240, е - t = 179.

Система уравнений (21) дополняется нормировочным соотношением α₁ + α₂ = 1, а также

уравнением состояния смеси, которое имеет вид

(

))∕(

)

⁽α₁γ₁π₁

α₂γ₂π₂

α₁

α₂

P = ρe -

(22)

γ₁ - 1

γ₂ - 1

в случае, если для описания фаз используется двучленное УрС вида (3). Начальные условия

имеют следующий вид:

{

W_L, x < 0,

W|t=0 =

WR, x > 0,

где W = (u, P, ρ₁, ρ₂, α₁) - вектор примитивных пере-

менных задачи.

С течением времени начальный разрыв распадается

на несколько. На каждом из них выполняются соотно-

шения РГ. Схематически автомодельная картина реше-

ния в одномерном случае на плоскости x-t представле-

на на рис. 6. Предполагается, что всего возможно пять

конфигураций, а именно: левая и правая линии разры-

Рис. 6. Расположение линий разрыва для

ва могут быть либо УВ, либо ВР, а центральная линия

задачи Римана.

разрыва, если она есть, является КР.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

991

Запишем соотношения РГ для модели БН5 вдоль некоторого пути Ψ (k = 1, 2):

∫1

∫

∂(α₁)_Ψ

∂(u)_Ψ

ξ[α₁] = (u)_Ψ

ds - (K)_Ψ

ds,

(23a)

∂s

ξ[α_kρ_k] = [α_kρ_ku],

(23b)

ξ[ρu] = [ρu² + P ],

(23c)

ξ[ρE] = [ρEu + P u],

(23d)

где скобки обозначают скачок на линии разрыва: [f] = f⁺ - f^-, верхний индекс “ + ” (“- ”)

указывает, что состояние вычисляется перед (за) разрывом, ξ - скорость разрыва.

В дальнейшем используем следующие обозначения. Невозмущённые области слева от раз-

рыва будем обозначать индексом “_L ”, невозмущённые области справа от него - индексом “_R ”.

Индекс 0 может обозначать как правое невозмущённое состояние, так и левое. Состояния

слева и справа от контактного разрыва обозначим W∗L и W∗R соответственно (см. рис. 6).

Утверждение. Решение задачи Римана (P^∗, v∗1,L, v∗1,R) для системы уравнений (21), (22)

вдоль линейного пути

Ψ(s; W_L, W_R) = (1 - s)W_L + sW_R

(24)

удовлетворяют системе уравнений

F₁(P^∗,v∗1,L,v∗1,R;W_L,W_R) = u_R - u_L + Φ(P^∗,v∗1,L;W_L) + Φ(P^∗,v∗1,R;W_R) = 0,

F₂(P^∗,v∗1,L;W_L) = 0, F₂(P^∗,v∗1,R;W_R) = 0,

где

⎧

⎨

⁽v⁰ +v⁾

⁽K⁰ +K⁾

(α⁰¹ - α₁)

(v⁰ - v) = 0, если P > P⁰,

F₂(P,v₁;W₀) =

⎩

если P ≤ P⁰,

⎧

⎪(P - P0)/m(P, v1), если P > P0,

⎨

∫

Φ(P, v₁; W₀) =

(25)

⎪

если P ≤ P⁰.

⎩

I(P )

P⁰

Здесь функции α₁(P, v₁), v(P, v₁), K(P, v₁) и m(P, v₁) определяются соотношениями

α⁰¹ρ⁰¹v₁

α₁(v₁,v) =

v(v₁, v₂) = Y⁰¹v₁ + Y⁰²v₂,

ρ⁰v

{

)

⁽P⁰ +γ₁π₁

P⁰ + P

⁽P⁰ +γ₂π₂

P⁰ + P

v₂(v₁,P) = Y⁰¹v⁰

+Y⁰²v⁰

γ₁ - 1

γ₂ - 1

)}∕{

)}

⁽P +γ₁π₁

P⁰ + P

⁽P +γ₂π₂

P⁰ + P

+Y⁰

v₁

Y⁰

γ₁ - 1

γ₂ - 1

√

P (γ₂ - γ₁) + γ₂π₂ - γ₁π₁

P -P

K(P, α₁) =

m(P, v) =

(26)

P (γ₁/α₁ + γ₂/α₂) + γ₁π₁/α₁ + γ₂π₂/α₂

v⁰ - v

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

992

ПОЛЕХИНА и др.

Доказательство. Преобразуем систему уравнений (23) c учётом пути (24) к следующему

виду:

[α₁]v = K[v],

(27a)

Y+k = Y^-k,

(27b)

ρ⁺(u⁺ - ξ) = ρ^-(u^- - ξ) = m,

(27c)

P⁺ - P^- + m(u⁺ - u^-) = 0,

(27d)

P⁺ - P^- + m²(v⁺ - v^-) = 0,

(27e)

p⁺ + p

e⁺ - e^- +

(v⁺ - v^-) = 0,

(27f)

где k = 1, 2, m - массовая скорость, Y_k = α_kρ_k/ρ - массовые доли, v_k = 1/ρ_k - удельный

объём k-й фазы, v = Y₁v₁ + Y₂v₂ - удельный объём смеси,

f = (f⁺ + f^-)/2. Отметим, что

уравнения (27b) и (27c) получены в результате сложения уравнений (23b) для k = 1, 2, а урав-

нения (27d) и (27e) эквиваленты друг другу (в дальнейшем используются оба соотношения).

Если m = 0, то разрыв является УВ, если m = 0, то КР. В последнем случае соответ-

ствующие соотношения (27) упрощаются до следующих:

u⁺ = u^- = ξ, P⁺ = P^-.

(28)

Соотношения в ВР для модели БН5 получены в работе [27]:

)1/γk

⁽P +π_k

ρ_k = ρ⁰

dP = ±I(P )du, Y_k = Y0k,

(29)

P⁰ + π_k

где волна разрежения распространяется со скоростью ξ = u ± c_w, k = 1, 2; знаки “ + ” и

“-” относятся к правой и левой волнам разрежения соответственно; индекс

обозначает

невозмущённое состояние, а I(P ) имеет следующий вид:

∕

(∑

I(P ) = ρc_w =

Y⁰

(ρ0kc0k)²

⁽P +π_k )(γk+1)/γk)-1/2.

P⁰ + π_k

k=1,2

Выражения (27)-(29) позволяют получить решение задачи Римана общего вида. В самом

деле, из соотношений (28) следует, что на КР давление и скорость непрерывны при переходе

через разрыв:

P^∗ = P∗L = P∗R, u^∗ = u∗L = u∗R.

(30)

Вид решения на разрыве (УВ или ВР) зависит только от P^∗. Если P^∗ > P⁰, то разрыв яв-

ляется УВ, если P^∗ ≤ P⁰, то ВР. Для скорости имеем u^∗ = u⁰ ±Φ(P, v₁; W₀), где Φ(P, v₁; W₀)

определяется равенством (25). Поэтому вне зависимости от конфигурации на линии разрыва

для скорости справедливы соотношения

u∗L = u_L - Φ(P^∗,v∗1,L;W_L), u∗R = u_R + Φ(P^∗,v∗1,R;W_R).

(31)

Далее из равенств (30) и (31) вытекает, что

F₁(P^∗,v∗1,L,v∗1,R;W_L,W_R) = u∗R - u∗L = u_R - u_L + Φ(P^∗,v∗1,L;W_L) + Φ(P^∗,v∗1,R;W_R) = 0.

Для определения v₁ используем уравнение (27a), которое запишем в виде

⎧

⎨

⁽v⁰ +v⁾

⁽K⁰ +K⁾

(α⁰¹ - α₁)

(v⁰ - v) = 0, если P > P⁰,

F₂(v₁,P;W₀) =

⎩

если P ≤ P⁰.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ВАЛИДАЦИЯ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА

993

Выражая переменные α₁, v, K через переменные P и v₁ и используя систему (27), получаем

α⁰¹ρ⁰¹v₁

α₁(v₁,v) =

v(v₁, v₂) = Y⁰¹v₁ + Y⁰²v₂,

ρ⁰v

{

)

⁽P⁰ +γ₁π₁

P⁰ + P

⁽P⁰ +γ₂π₂

P⁰ + P

v₂(v₁,P) = Y⁰¹v⁰

+Y⁰²v⁰

γ₁ - 1

γ₂ - 1

)}∕{

)}

⁽P +γ₁π₁

P⁰ + P

⁽P +γ₂π₂

P⁰ + P

+Y⁰v1

Y⁰

γ₁ - 1

γ₂ - 1

P (γ₂ - γ₁) + γ₂π₂ - γ₁π₁

K(P, α₁) =

P (γ₁/α₁ + γ₂/α₂) + γ₁π₁/α₁ + γ₂π₂/α₂

В итоге приходим относительно трёх неизвестных P^∗, v∗1,L, v∗1,R к системе трёх нелиней-

ных уравнений

F₁(P^∗,v∗1,L,v∗1,R;W_L,W_R) = 0, F₂(P^∗,v∗1,L;W_L) = 0, F₂(P^∗,v∗1,R;W_R) = 0,

(32)

что доказывает утверждение.

Система уравнений (32) относительно переменных (P^∗, v∗1,L, v∗1,R) может быть решена, на-

пример, методом Ньютона. Далее по любой из формул (31) определяется скорость, а оставши-

еся переменные находятся по формулам (26).

Исследование Полехиной (Тухватуллиной) Р.Р. (пп. 2.2, 3, приложение) выполнено при

финансовой поддержке Российского научного фонда (проект 19-71-30004). Исследование Са-

венкова Е.Б. и Алексеева М.В. (введение, пп. 2.1, 2.3, заключение) выполнено при поддержке

Московского центра фундаментальной и прикладной математики (соглашение с Министер-

ством науки и высшего образования Российской Федерации № 075-15-2019-1623).

СПИСОК ЛИТЕРАТУРЫ

1. Baer M.R., Nunziato J.W. A two-phase mixture theory for the deflagration-to-detonation transition (ddt)

in reactive granular materials// Int. J. of Multiphase Flow. 1986. V. 12. № 6. P. 861-889.

2. Drew D., Passman S. Theory of Multicomponent Fluids. New York, 2014.

3. Favrie N., Gavrilyuk S., Saurel R. Solid-fluid diffuse interface model in cases of extreme deformations

// J. Comput. Phys. 2009. V. 228. № 16. P. 6037-6077.

4. Kapila A., Son S., Bdzil J., Menikoff R. Two-phase modeling of DDT: structure of the velocity-relaxation

zone // Phys. Fluids. 1997. V. 9. № 12. P. 3885-3897.

5. Kapila A., Melnikoff R., Bdzil J., Son S., Stewart S. Two-phase modeling of deflagration-to-detonation

transition in granular materials: reduced equations // Phys. Fluids. 2001. V. 13. № 10. P. 3002-3024.

6. Murrone A., Guillard H. A five-equation reduced model for compressible two phase flow problems // J.

Comput. Phys. 2005. V. 202. № 2. P. 664-698.

7. De Lorenzo M., Pelanti M., Lafon P. HLLC-type and path-conservative schemes for a single-velocity

six-equation two-phase flow model: a comparative study // Appl. Math. and Comput. 2018. V. 333.

P. 95-117.

8. Dumbser M., Balsara D.S. A new efficient formulation of the hllem Riemann solver for general

conservative and non-conservative hyperbolic systems // J. of Comput. Phys. 2016. V. 304. P. 275-319.

9. Kemm F., Gaburro E., Thein F., Dumbser M. A simple diffuse interface approach for compressible flows

around moving solids of arbitrary shape based on a reduced Baer-Nunziato model // Computers &

Fluids. 2020. V. 204. P. 104536.

10. Chiocchetti S., Müller C. A solver for stiff finite-rate relaxation in Baer-Nunziato two-phase flow models

// Droplet Interactions and Spray Processes / Eds. G. Lamanna, S. Tonini, G.E. Cossali, B. Weigand.

Cham, 2020. P. 31-44.

11. Serezhkin A., Menshov I. On solving the Riemann problem for non-conservative hyperbolic systems of

partial differential equations // Computers & Fluids. 2020. V. 210. P. 104675.

12. Cockburn B., Shu C.-W. The Runge-Kutta local projection-discontinuous-Galerkin finite element

method for scalar conservation laws // ESAIM Math. Model. Numer. Anal. 1991. V. 25. № 3. P. 337-361.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

994

ПОЛЕХИНА и др.

13. Dal Maso G., Lefloch P.G., Murat F. Definition and weak stability of nonconservative products // J. de

Mathématiques Pures et Appliquées. 1995. V. 74. № 6. P. 483-548.

14. Castro M.J., LeFloc C.h P.G., Luz Muñoz-Ruiz M., Parés C. Why many theories of shock waves are

necessary: convergence error in formally path-consistent schemes // J. of Comput. Phys. 2008. V. 227.

№ 17. P. 8107-8129.

15. Bdzil J.B., Menikoff R., Son S.F., Kapila A.K., Scott Stewart D. Two-phase modeling of deflagration-to-

detonation transition in granular materials: A critical examination of modeling issues // Phys. of Fluids.

1999. V. 11. № 2. P. 378-402.

16. Andrianov N., Warnecke G. The Riemann problem for the Baer-Nunziato two-phase flow model // J. of

Comput. Phys. 2004. V. 195. № 2. P. 434-464.

17. Daude F., Berry R.A., Pascal Galon. A finite-volume method for compressible non-equilibrium two-phase

flows in networks of elastic pipelines using the Baer-Nunziato model // Comput. Meth. in Appl. Mech.

and Eng. 2019. V. 354. P. 820-849.

18. Saurel R., Abgrall R. A simple method for compressible multifluid flows // SIAM J. Sci. Comput. 1999.

V. 21. № 3. P. 1115-1145.

19. Янилкин Ю.В, Бондаренко Ю.А., Гончаров Е.А., Гужова А.Р., Колобянин В.Ю., Софронов В.Н.,

Стаценко В.П. Тесты для гидрокодов, моделирующих ударноволновые течения в многокомпонент-

ных средах. Саров, 2017.

20. Nigmatulin R. Dynamics of Multiphase Media. New York, 1990.

21. Le Floch P., Liu T.-P. Existence Theory for Nonlinear Hyperbolic Systems in Nonconservative Form.

V. 5. Berlin; New York, 1993. P. 261-280.

22. Ваннер Г., Хайрер Э., Нёрсетт С. Решение обыкновенных дифференциальных уравнений. Нежест-

кие задачи. М., 1990.

23. Zhong X., Shu C.-W. A simple weighted essentially nonoscillatory limiter for Runge-Kutta discontinuous

Galerkin methods // J. Comput. Phys. 2013. V. 232. № 1. P. 397-415.

24. Zhong X., Shu C.-W. On positivity-preserving high order discontinuous Galerkin schemes for compressible

Euler equations on rectangular meshes // J. Comput. Phys. 2010. V. 229. № 23. P. 8918-8934.

25. Layes G., Le Métayer O. Quantitative numerical and experimental studies of the shock accelerated

heterogeneous bubbles motion // Physics of Fluids. 2007. V. 19. № 4. P. 042105.

26. Nowakowski A.F., Ballil A., Nicolleau F.C.G.A. Passage of a shock wave through inhomogeneous media

and its impact on gas-bubble deformation // Phys. Rev. E. 2015. V. 92. № 2. P. 023028.

27. Petitpas F., Franquet E., Saurel R., Le Metayer O. A relaxation-projection method for compressible

flows. Part ii: Artificial heat exchanges for multiphase shocks // J. of Comput. Phys. 2007. V. 225. № 2.

P. 2214-2248.

Институт прикладной математики

Поступила в редакцию 04.03.2022 г.

имени М.В. Келдыша РАН, г. Москва

После доработки 04.03.2022 г.

Принята к публикации 25.05.2022 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022