ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 7, с.995-1008

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.6+517.9

ОЦЕНКИ ТОЧНОСТИ ПРОЕКЦИОННОГО МЕТОДА

СО СТАБИЛИЗАТОРОМ ДРОБНОЙ ГЛАДКОСТИ

В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА

ПО ЕГО НАКЛОНАМ

С. А. Турганбаев, Т. Е. Романенко

Рассматривается проекционный метод со стабилизатором дробной гладкости для аппрок-

симации задачи восстановления волнового фронта по его наклонам. Показана устойчивость

метода в шкале периодических функций двух аргументов. Найдены условия согласования

параметров стабилизатора с шагом сетки, позволяющие провести вывод согласованных с

гладкостью наклонов оценок скорости сходимости проекционного метода. С помощью тео-

рии интерполяции получены оценки точности метода при естественных требованиях на

гладкость наклонов из шкалы анизотропных пространств Соболева дробной гладкости.

DOI: 10.31857/S037406412207010X, EDN: CERLCH

Введение. Одной из важных задач адаптивной оптики является восстановление волново-

го фронта по данным об измерениях его локальных наклонов. Такие измерения проводятся с

помощью датчика Шака-Гартмана (см., например, [1]), который также с успехом применяется

для оценки параметров атмосферной турбулентности [2], при конструировании оптоэлектрон-

ных инструментов [3], в прикладных задачах медицинской физики [4] и в др. областях. По-

скольку на практике измерения наклонов сопровождаются искажениями различной природы,

то данные о наклонах обычно являются негладкими функциями координат. Кроме того, сами

волновые фронты зачастую являются негладкими и даже разрывными. Разработка устойчи-

вых методов восстановления волнового фронта в этих условиях является весьма актуальной

задачей (см. работы [5-10]).

Ранее в статьях [9, 10] было предложено семейство новых методов реконструкции волнового

фронта, в основе которых лежит вариационный подход в сочетании с проекционным методом

на основе билинейных сплайнов. Такая комбинация методов наилучшим образом подходит для

случая восстановления волнового фронта, не обладающего высокой гладкостью и не обяза-

тельно непрерывного. Отличительной особенностью схем работы [10] является использование

стабилизатора с разностными производными второго порядка в дробной степени, нацеленного

на улучшение пространственно-частотной характеристики (ПЧХ) метода, причём параметры

стабилизатора выбираются также на основе вариационного подхода. В сравнении с широко

используемым методом Симпсона [5] семейство методов в статье [10] позволяет достичь луч-

шего профиля ПЧХ в области высоких частот, а по сравнению с семейством кумулятивных

методов в работе [6] в практическом применении не приводит к накоплению погрешности и

устойчиво работает в случае потери данных о наклонах.

Представляемые в данной статье результаты посвящены исследованию точности проекци-

онного метода, описанного в [10], используемого для конечномерной аппроксимации вариаци-

онной задачи восстановления волнового фронта. Сложностью рассматриваемой задачи явля-

ется возможная негладкость волновых фронтов и, соответственно, необходимость развивать

такие способы исследования погрешности, которые позволяли бы получать оценки скорости

сходимости аппроксимаций в естественных функциональных классах исходных данных (на-

клонов) без априорных предположений об их дополнительной гладкости.

1. Вариационный метод восстановления волнового фронта по его наклонам. Опи-

шем и исследуем вариационный подход к восстановлению волнового фронта u(x, y) по изме-

рениям его наклонов g₁(x, y), g₂(x, y) вдоль соответствующих направлений x и y. Отметим,

995

9^∗

996

РАЗГУЛИН и др.

что непосредственное восстановление волнового фронта из условия равенства градиентов вол-

нового фронта (или их конечномерных аппроксимаций) измеряемым наклонам приводит к

операторному уравнению первого рода, которое представляет собой плохообусловленную за-

дачу (см. [7]), устойчивое решение которой строится на основе регуляризованного варианта

метода сингулярных разложений. Вместо операторного уравнения сформулируем задачу вос-

становления волнового фронта в пределах квадратной апертуры T² = [-π, π] × [-π, π] в виде

задачи минимизации функционала невязки J(u):

∫∫

J (u) =

((u_x(x, y) - g₁(x, y))² + (u_y(x, y) - g₂(x, y))²) dx dy.

(1)

T²

Функционал J(u) задаёт среднеквадратичное отклонение между наблюдаемыми наклонами

волнового фронта g₁(x, y), g₂(x, y) и соответствующими производными u_x = ∂u/∂x, u_y =

= ∂u/∂y искомого волнового фронта.

Для дальнейшего изложения

∫∫

верждения. Сокращения 〈u, φ〉 =T2 u(x, y)φ(x, y) dx dy и ∥u∥ = (〈u, u〉)1/2 обозначают стан-

дартные скалярное произведение и норму в L₂(T²). Для вектора наклонов g = (g₁, g₂) ∈

∈ L₂(T²) × L₂(T²) используется евклидова норма ∥g∥ = (∥g₁∥² + ∥g₂∥²)1/2. Для полной орто-

нормированной в L₂(T²) системы комплексных экспонент e_k,m(x, y) = (2π)-1 exp(i(kx + my)),

k,m ∈ Z, и коэффициентов û_k,m = 〈u,e^∗k,m〉, e^∗k,m = e_-k,-m разложения функции u ∈ L₂(T²)

∑

по этой системе в силу равенства Парсеваля имеем ∥u∥² =(k,m)∈Z2 |ûk,m|².

Будем использовать анизотропные пространства функций

∑

(1 + k2s + m2r)|û_k,m|² < +∞}, s, r > 0.

H^s,r(T²) = {u ∈ L₂(T²) : ∥u∥2Hs,r(T2)⁼

(k,m)∈Z²

Нетрудно видеть, что по теореме о следах [11, гл. 1, § 4] используемые далее пространст-

ва Hs,0(T²) (H0,r(T²)) при s > 0.5 (r > 0.5 соответственно) состоят из 2π-периодических

функций по переменной x (y соответственно), которые Гёльдер-непрерывны по x (y соот-

ветственно) со значениями в L₂(0, 2π) с показателем s - 0.5 (r - 0.5 соответственно).

Будем использовать изотропное пространство функций H^s(T²) = H^s,s(T²). В частности,

пространство H¹(T²) является замкнутым подпространством пространства Соболева H¹ на

множестве T² (см. [12, гл. 3]) с эквивалентными нормами

∑

∥u∥_H1 = (∥u∥² + ∥u_x∥² + ∥u_y∥²)1/2,

(1 + k² + m²)|û_k,m|².

∥u∥2H1(T2)⁼

(k,m)∈Z²

Для пространства Соболева второго порядка H² используется норма

∥u∥_H2 = (∥u∥² + ∥u_x∥² + ∥u_y∥² + ∥u_xx∥² + ∥u_xy∥² + ∥u_yy∥²)1/2.

Рассмотрим подпространство

H^θ(T²) функций с нулевым средним (или, что то же самое,

∫∫

û0,0 = 0), т.е.

H^θ(T²) = {u ∈ H^θ(T²) :T2 u(x,y)dxdy = 0}. Для функций из

H¹(T²) имеет

место неравенство Пуанкаре

∫∫

(|u_x|² + |u_y|²) dx dy ≥

|u|² dx dy,

(2)

T²

проверка которого в рассматриваемом случае легко проводится с помощью разложения по ком-

плексным экспонентам e_k,m(x, y). Отметим, что обзору современных результатов по точным

константам в неравенствах типа Пуанкаре посвящена работа [13].

В качестве допустимого множества функционала (1) будем использовать пространство

H¹(T²). Такой выбор допустимого множества функционала невязки представляется достаточ-

но естественным для рассматриваемой задачи восстановления волнового фронта, поскольку,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОЦЕНКИ ТОЧНОСТИ ПРОЕКЦИОННОГО МЕТОДА

997

во-первых, позволяет естественным образом вычислять его наклоны и, во-вторых, охватывает

широкий круг негладких поверхностей, в том числе разрывных (пример см. в [11, п. 9.4]).

Необходимое условие минимума функционала невязки (1) на

H¹(T²) получается из равен-

ства нулю его первой вариации и приводит к интегральному тождеству

〈u_x, φ_x〉 + 〈u_y, φ_y〉 = 〈g₁, φ_x〉 + 〈g₂, φ_y〉 для любых функций φ ∈H1(T²),

(3)

которому должен удовлетворять искомый волновой фронт u(x, y) ∈H1(T²).

Теорема 1. Пусть g₁, g₂ ∈ L₂(T²). Тогда вариационная задача (3) имеет единственное

решение u ∈H1(T²). Решение непрерывно зависит от вектора наклонов и справедлива оценка

√

∥u∥_H1(T2₎ ≤

2∥g∥.

(4)

Доказательство. Задача (3) может быть записана в стандартном для вариационных за-

дач виде

a(u, φ) = ℓ(φ) для любой φ ∈H1(T²),

(5)

где введены обозначения для билинейной формы a(u, φ) = 〈u_x, φ_x〉 + 〈u_y, φ_y〉 и линейного

функционала ℓ(φ) = 〈g₁, φ_x〉 + 〈g₂, φ_y〉. Непрерывность билинейной формы и функционала

вытекает из оценок

|a(u, φ)| ≤ ∥u_x∥∥φ_x∥ + ∥u_y∥∥φ_y ∥ ≤ ∥u∥_H1(T2₎∥φ∥_H1(T2₎,

|ℓ(φ)| ≤ ∥g∥∥φ∥_H1(T2₎.

(6)

Свойство коэрцитивности билинейной формы следует из неравенства Пуанкаре (2) и записы-

вается в виде

(7)

a(u, u) ≥ 0.5∥u∥2H1 (T2)длявсехфункцийu∈H1(T²).

Тогда существование и единственность решения вариационной задачи (5) следует из непрерыв-

ности функционала, непрерывности и коэрцитивности билинейной формы и теоремы Лакса-

Мильграма (см., например, [14, с. 19; 15, с. 43]). Оценка (4) является следствием неравенства

(2) и вытекающей из (5) и неравенства Коши-Буняковского оценки ∥u_x∥² + ∥u_y∥² ≤ ∥g∥².

Теорема доказана.

Исследуем гладкость решения вариационной задачи в зависимости от гладкости входных

данных g₁, g₂.

Теорема 2. Пусть g₁ ∈ Hs,0(T²), g₂ ∈ H0,s(T²), s ∈ (0, 1]. Тогда решение вариационной

H 1+s(T2)иимеетместооценка

задачи (3) принадлежит

∥u∥_H1+s(T2₎ ≤ C(∥g₁∥_Hs,0(T2₎ + ∥g₂∥_H0,s(T2₎).

(8)

∑

Доказательство. Рассмотрим разложение u =

û_n,me_n,m(x,y) полученного

(0,0)=(n,m)∈Z²

в теореме 1 решения задачи (3) (или, что то же самое, (5)). Возьмём в (5) пробную функцию

φ = e^∗k,l. Несложные вычисления показывают, что a(u,e^∗k,l) = (k²+l²)u_k,l и ℓ(e^∗k,l) = -i(kĝ1,k,l+

+ lĝ2,k,l), где

ĝj,k,l = 〈gj , e^k,l〉 - коэффициенты разложения наклонов, j = 1, 2. Получаем

kĝ1,k,l +lĝ2,k,l

û_k,l = -i

(0, 0) = (k, l) ∈ Z²,

û0,0 = 0.

(9)

k² + l²

Воспользуемся (9) и оценим норму

∑

(1 + k2(1+s) + l2(1+s))|û_k,l|² ≤

∥u∥2H1+s(T2)⁼

(0,0)=(k,l)∈Z²

∑

(1 + k2(1+s) + l2(1+s))(k²|ĝ1,k,l|² + l²|ĝ2,k,l|²)

≤2

(k² + l²)²

(0,0)=(k,l)∈Z²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

998

РАЗГУЛИН и др.

Заметим, что для всех индексов, по которым проводится суммирование, справедливо

(1 + k2(1+s) + l2(1+s))k²

(1 + k2(1+s) + l2(1+s))k2(1-s)

k2s ≤ 3k2s.

(k² + l²)²

Аналогично получаем

(1 + k2(1+s) + l2(1+s))l²

≤ 3l2s.

(k² + l²)²

С учётом этих оценок имеем

∑

∥u∥2H1+s(T2)≤C1

(k2s|ĝ1,k,l|² + l2s|ĝ2,k,l|²) = C₁(∥g₁∥2Hs,0(T2)+∥g2∥H0,s(T2)).

(0,0)=(k,l)∈Z²

Отсюда вытекают включение u ∈H1+s(T²) и искомая оценка (9). Теорема доказана.

2. Проекционная схема аппроксимации вариационной задачи. Для построения ко-

нечномерной аппроксимации вариационной задачи (3) на основе проекционного метода возь-

мём натуральное чётное N, введём множество индексов

I = {-N/2,-N/2 + 1,...,N/2 - 1}

и рассмотрим подпространство

S¹(T²) = Lin {φ_k,l(x,y)} ⊂ H¹(T²)

размерности N × N кусочно-линейных по каждому направлению сплайнов, являющихся ли-

нейными комбинациями функций φ_k,l(x, y) = φ_k(x)φ_l(y), (k, l) ∈ I², где φ_k(t) = max(0, 1 -

- |t - kh|h-1), k ∈ I\{-N/2}, φ-N/2(t) = φ1-N/2(t + h) + φ1-N/2(t + h - 2π), h = 2πN-1.

Обозначи

S¹(T²) = S¹(T²)

⋂ H1(T²). Представив далее аппроксимацию искомого волнового

∑

фронта в виде конечной суммы u^h(x, y) =(k,l)∈I2 u^hk,lφk,l(x, y)

S¹(T²) и ограничившись в

тождестве (3) пробными функциями из подпространства

S¹(T²), приходим к конечномерной

вариационной задаче

〈u^hx, φ_x〉 + 〈u^hy, φ_y〉 = 〈g₁, φ_x〉 + 〈g₂, φ_y〉 при всех φ

S¹(T²).

(10)

Условие принадлежности решения u^h пространству

S¹(T²) накладывает условие равенства

нулю среднего значения сеточной функции

∑

u^hk,l = 0.

(11)

(k,l)∈I²

Отметим, что поскольку в записи равенств (10) пробные функции φ

S¹(T²) участвуют

только под знаком производных, то фактически можно расширить класс пробных функций

до всего пространства S¹(T²). Тогда задача (10) допускает эквивалентную запись в виде опе-

раторного уравнения относительно матрицы искомых коэффициентов u^h = {u^hkl} (см. [10])

B₂Λ₁u^h + B₁Λ₂u^h = f, f = f¹ + f²

(12)

с дополнительным условием (11), где

x_k

∫

f1k,l = h-3

φ_l(y)

(g₁(x, y) - g₁(x + h, y)) dx dy,

yl-1

xk-1

y_l

∫

f2k,l = h-3

φ_k(x)

(g₂(x, y) - g₂(x, y + h)) dx dy.

xk-1

yl-1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОЦЕНКИ ТОЧНОСТИ ПРОЕКЦИОННОГО МЕТОДА

999

Операторы B_j , Λ_j задаются с помощью матриц Грама (см. монографию [16, гл. 2, § 2])

в L₂(-π,π) рассматриваемых одномерных сплайнов и их градиентов, B_j = E_j - h²Λ_j/6,

E_j - единичный оператор по соответствующему направлению, j = 1,2. Отметим особенность

записи слагаемых в уравнении (12): операторы с индексом j = 1 действуют по переменной x

(по строкам), операторы с индексом j = 2 действуют по переменной y (по столбцам). Таким

образом, например, запись B₂Λ₁ означает суперпозицию двух операторов, действующих по

разным переменным.

∑

Далее каждой функции u^h(x, y) =(k,l)∈I2 u^hk,lφk,l(x, y) из пространства сплайнов S¹(T²)

сопоставим заданную на I² сеточную функцию u^h = {u^hk,l}, составленную из коэффициентов

разложения по базисным сплайнам. Для сеточных функций будем использовать дискретное

скалярное произведение и соответствующую дискретную евклидову норму

√

∑

〈u^h, v^h〉_h =

u^hk,lv^hk,lh²,

∥u^h∥_h =

〈u^h, u^h〉_h.

(k,l)∈I²

Сеточные комплексные экспоненты

(

)

(

)

2πkj

2πml

e_k(x_j) =

√

exp i

e_m(y_l) =

√

exp i

2π

являются собственными функциями как операторов Λ₁, Λ₂ с собственными значениями

)

⁽kh

⁽mh⁾

λ_k =

sin²

λ_m =

sin²

k,m ∈ I,

(13)

h²

так и операторов B₁, B₂ с собственными значениями

h²

μ_k = 1 -

λ_k, μ_m = 1 -

λ_m, k,m ∈ I.

Собственные значения допускают известные двусторонние оценки

0≤λ_k ≤

k ∈ I,

(14)

h²

≤ μ_k ≤ 1, k ∈ I.

(15)

Сеточные комплексные экспоненты e_k,m(x_j , y_l) = e_k(x_j )e_m(y_l) представляют собой ортонор-

мированный базис в пространстве сеточных функций на I² : 〈e_k,m, e^∗p,q〉_h = δ_k,mδ_p,q, где δ_k,m -

символ Кронекера. Любая заданная на I² сеточная функция {z_j,l} однозначно раскладыва-

ется в сумму

∑

z_j,l =

zk,mek,m(xj , yl),

zk,m = 〈z, ek,m〉h.

(k,m)∈I²

Для функции u^h(x, y) из пространства сплайно

S¹(T²) и её сеточного варианта u^h спра-

ведливо соотношение ∥uh∥2 = 〈uh, uh〉 = 〈B1B2uh, uh〉h, где B1B2 означает суперпозицию

двух операторов по соответствующим переменным. Отсюда в силу (15) вытекает эквивалент-

ность норм для функций и

S¹(T²):

∥u^h∥_h ≤ ∥u^h∥ ≤ ∥u^h∥_h.

(16)

Задачу (10) можно записать в аналогичном задаче (5) виде:

a(u^h, v^h) = ℓ(v^h), u^h

S¹(T²) для любой функции v^h

S¹(T²).

(17)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

1000

РАЗГУЛИН и др.

Теорема 3. Пусть g₁, g₂ ∈ L₂(T²). Тогда задача (17) имеет единственное решение u^h ∈

∈

S¹(T²) и справедлива оценка

√

∥u^h∥_H1(T2₎ ≤

2∥g∥.

(18)

Доказательство аналогично доказательству теоремы 1.

Следующие теоремы дают оценки скорости сходимости u^h к функции u в различных

нормах и при различных требованиях к гладкости измеряемых наклонов g₁, g₂.

Теорема 4. Пусть g₁ ∈ H1,0(T²), g₂ ∈ H0,1(T²). Тогда имеют место оценки скорости

сходимости решения u^h задачи (17) к решению u задачи (3):

∥u^h - u∥_H1(T2₎ ≤ C₁h(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎),

(19)

∥u^h - u∥ ≤ C₂h²(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎).

(20)

Доказательство. В силу симметричности билинейной формы, оценок (6), (7) и замеча-

ния 2.3.1 к лемме Сеа [14, с. 109] имеем

√

∥u^h - u∥_H1(T2₎ ≤

inf

∥u - v^h∥_H1(T2₎.

v^h

S¹(T²)

Использовав аппроксимационные свойства тензорного произведения кусочно-линейных сплай-

нов [17, с. 37], приходим к оценке с независящей от решения u и шага сетки константой

C₁ > 0:

∥u^h - u∥_H1(T2₎ ≤ C₁h∥u∥_H2(T2₎.

(21)

Воспользовавшись далее оценкой (8) из теоремы 2, окончательно получаем (19). При тех же

требованиях к гладкости наклонов для получения оценки в норме L₂(T²) воспользуемся лем-

мой Обэна-Нитше (см., например, [14, с. 139]). Имеем

(

)

∥u^h - u∥ ≤ M∥u^h - u∥_H2(T2₎ × sup

inf

∥φ_q - φ^h∥_H1(T2) ,

(22)

q∈L₂(T²)

∥q∥

φ^h

S¹(T²)

где φ_q - единственное решение вариационной задачи

a(φ_q, v) = 〈q, v〉 для всех v ∈H1(T²).

(23)

Инфимум в (22) оценивается аналогично (21) и подобно доказательству оценки (8) теоремы 2

имеем

inf

∥φ_q - φ^h∥_H1(T2₎ ≤ C₁h∥φ_q∥_H2(T2₎ ≤ C₂h∥q∥.

(24)

φ^h

S¹(T²)

Подставив полученную оценку в (22) с учётом неравенства (19), окончательно получаем (20).

Теорема доказана.

Исследуем сходимость метода в норме L₂(T²) при негладких наклонах g₁, g₂ ∈ L₂(T²).

Теорема 5. Пусть g₁, g₂ ∈ L₂(T²). Тогда справедлива оценка скорости сходимости

∥u^h - u∥ ≤ C₃h∥g∥.

(25)

Доказательство. Обратимся снова к неравенству (22). Поскольку задача (23) не зави-

сит от наклонов g₁, g₂, то для оценки инфимума воспользуемся (24). В силу неравенства

треугольника и (4), (18) имеем

√

∥u^h - u∥_H1(T2₎ ≤ ∥u^h∥_H1(T2₎ + ∥u∥_H1(T2₎ ≤ 2

2∥g∥.

Подставив полученные оценки в (22), приходим к (25). Теорема доказана.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОЦЕНКИ ТОЧНОСТИ ПРОЕКЦИОННОГО МЕТОДА

1001

3. Проекционная схема со стабилизатором дробной гладкости. Рассмотрим следу-

ющую модификацию схемы (5):

B₂Λ₁w^h + B₁Λ₂w^h + γ(Λ₁Λ₂)^sw^h = f.

(26)

По сравнению с (5) схема (26) содержит зависящий от двух параметров γ > 0, s > 0 до-

полнительный стабилизатор γ(Λ₁Λ₂)^sw^h. Это слагаемое отвечает за выравнивание частотной

характеристики метода в области средних частот и привносит в уравнение смешанные произ-

водные дробного порядка. Различные способы выбора параметров стабилизатора обсуждаются

в работе [10].

Действие стабилизатора реализуется в пространстве фурье-коэффициентов разложения по

комплексным экспонентам e_m,n в виде мультипликатора γ(λ_mλ_n)^s, а для самих коэффици-

ентов

ŵ^hm,n разложения искомого решения задачи (26) имеет место формула

f_m,n

ŵ^hm,n =

0 = (m,n) ∈ I²,

μ_nλ_m + μ_mλ_n + γ(λ_mλ_n)^s

где

f_m,n - коэффициенты Фурье правой части f. Из (14), (15) вытекает корректность вычис-

лений по формуле (26).

Далее потребуется вариационный аналог операторного уравнения (26):

a_s(w^h,v^h) = ℓ(v^h), w^h

S¹(T²) при всех v^h

S¹(T²),

(27)

где отвечающая задаче (26) билинейная форма имеет вид

a_s(w^h,v^h) = 〈u^hx,v^hx〉 + 〈w^hy,v^hy〉 + γ〈B-11B-12(Λ₁Λ₂)^su^h,v^h〉.

(28)

Отметим, что в формуле (28) в скалярном произведении в четвертом слагаемом использовано

обозначение для восполнения сеточной функции

∑

B-11B-12(Λ₁Λ₂)^sw^h =

(B-11B-12(Λ₁Λ₂)^sw^h)_k,lφ_k,l(x, y)

S¹(T²).

(k,l)∈I²

Теорема 6. Пусть g₁, g₂ ∈ L₂(T²). Тогда задача (26) (задача (27)) имеет единственное

решение w^h

S¹(T²) и справедлива оценка

∥w^h∥_H1(T2₎ ≤ C₁∥g∥.

(29)

Пусть g₁ ∈ H1,0(T²), g₂ ∈ H0,1(T²). Тогда справедлива оценка

∥Λ_j w^h∥_h ≤ C₂(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎), j = 1, 2.

(30)

Доказательство проводится аналогично доказательству теоремы 1. Существование вы-

текает из (26), где знаменатель не обращается в нуль. Для вывода оценки (29) возьмём в (27)

v^h = w^h в качестве пробной функции. Имеем

a(w^h, w^h) + γ〈B-11B-12(Λ₁Λ₂)^sw^h, w^h〉 = ℓ(w^h).

Перейдём к дискретным функциям во втором слагаемом левой части и получим

a(w^h, w^h) + γ〈(Λ₁Λ₂)^sw^h, w^h〉_h = ℓ(w^h).

Воспользовавшись далее коэрцитивностью билинейной формы a(w^h, w^h) (оценка (7)), непре-

рывностью функционала ℓ(w^h) (оценка (6)), а также вытекающей из оценки (14) неотрица-

тельностью операторов Λ₁, Λ₂, приходим к неравенству (29).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

1002

РАЗГУЛИН и др.

Для доказательства оценки (30) воспользуемся (26), равенством Парсеваля и неравенства-

ми (15):

∑

λ2m

f_m,n|²

∥Λ₁w^h∥2h =

λ2m| ŵ^hm,n|² =

≤

(μ_nλ_m + μ_mλ_n + γ(λ_mλ_n)^s)²

(0,0)=(m,n)∈I²

∑

≤C₁

f_m,n|² = C₁∥f∥2h ≤ C₂(∥g₁∥2H1,0(T2)+∥g2∥H0,1(T2)).

(0,0)=(m,n)∈I²

Теорема доказана.

Исследуем близость решения w^h к точному решению u задачи (3).

Теорема 7. Пусть g₁, g₂ ∈ L₂(T²). Тогда справедлива оценка скорости сходимости

∥w^h - u∥ ≤ (C₃h + C₄γλσ(s)N/2)∥g∥, σ(s) = max{2s - 3/2, 0}.

(31)

Пусть g₁ ∈ H1,0(T²), g₂ ∈ H0,1(T²). Тогда при 0.25 ≤ s справедлива оценка скорости сходи-

мости

∥w^h - u∥_H1(T2₎ ≤ (C₅h + C₆γλσ(s)N/2)(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎).

(32)

При 0 < s < 0.25 оценка имеет вид

∥w^h - u∥_H1(T2₎ ≤ C₇h(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎) + C₈γ∥g∥.

(33)

Также справедлива оценка

∥w^h - u∥ ≤ (C₉h² + C₁₀γλη(s)N/2)(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎), η(s) = max{2s - 2, 0}.

(34)

Доказательство. В силу неравенства треугольника имеем

∥w^h - u∥ ≤ ∥w^h - u^h∥ + ∥u^h - u∥,

∥w^h - u∥_H1(T2₎ ≤ ∥w^h - u^h∥_H1(T2₎ + ∥u^h - u∥_H1(T2₎.

В правых частях этих неравенств нормы разности u^h - u оцениваются с помощью (19), (20)

и (25). Осталось оценить нормы разности z^h = w^h - u^h решения w^h задачи (26) и решения

u^h задачи (12). Вычитая почленно равенства (26) и (12), приходим к уравнению

B₂Λ₁z^h + B₁Λ₂z^h + γ(Λ₁Λ₂)^sw^h = 0

(35)

или, в эквивалентной вариационной форме,

a(z^h, v^h) + γ〈B-11B-12(Λ₁Λ₂)^sw^h, v^h〉 = 0 при каждой v^h

S¹(T²).

Полагая v^h = z^h и используя коэрцитивность билинейной формы, в случае 0.25 ≤ s имеем

0.5∥z^h∥2H1(T2)≤a(zh,zh)=-γ〈B11B²¹(Λ1^Λ2)sw^h,zh〉⁼

= -γ〈(Λ₁Λ₂)^sw^h,z^h〉_h = -γ〈(Λ₁Λ₂)s-1/4w^h,(Λ₁Λ₂)1/4z^h〉_h ≤

≤ γ∥(Λ₁Λ₂)s-1/4w^h∥_h∥(Λ₁Λ₂)1/4z^h∥_h ≤ C₁γ∥(Λ₁Λ₂)s-1/4w^h∥_h∥z^h∥_H1(T2₎.

Отсюда следуют неравенства

∥z^h∥_H1(T2₎ ≤ γC₂∥(Λ₁Λ₂)s-1/4w^h∥_h ≤ γλσ(s)N/2C₃∥(Λ₁Λ₂)1/2w^h∥_h.

C помощью оценки (30) имеем

∥(Λ₁Λ₂)1/2w^h∥_h ≤ C₃(∥Λ₁w^h∥_h + ∥Λ₂w^h∥_h) ≤ C₄(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОЦЕНКИ ТОЧНОСТИ ПРОЕКЦИОННОГО МЕТОДА

1003

Следовательно,

∥z^h∥_H1(T2₎ ≤ γλσ(s)N/2C₅(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎).

В более простом случае 0 < s < 0.25 воспользуемся оценкой (29):

0.5∥z^h∥2H1(T2)≤γC1∥wh∥h∥(Λ1^Λ2)1/4z^h∥h≤γC2∥wh∥H¹(T²)∥zh∥H¹(T²)≤γC3∥g∥∥zh∥H¹(T²)^,

в результате получим

∥z^h∥_H1(T2₎ ≤ γC₃∥g∥.

Применив далее оценку (19), приходим к (32) и (33).

Получим для z^h оценки дискретной нормы L₂. Из уравнения (35) вытекает выражение

для соответствующих коэффициентов Фурье

γ(λ_mλ_n)^s ŵ^hm,n

zhm,n = -

μ_nλ_m + μ_mλ_n

√

Отсюда в случае s > 0.75 с использованием (14), (15) и неравенства (λ_mλ_n)1/2 ≤ (λ_m +λ_n)/

имеем

∑

(λ_mλ_n)2s| ŵ^hm,n|²

∥z^h∥2h =

|z^hm,n|2 = γ2

≤

(μ_nλ_m + μ_mλ_n)²

(0,0)=(m,n)∈I²

∑

(λ_mλ_n)2s-1/2(μ_nλ_m + μ_mλ_n)| ŵ^hm,n

|²

≤C₅γ2

∥g∥².

≤C₅γ²λ4s-3N/2∥w^h∥2H1(T2)≤C6γ2λ^N

(μ_nλ_m + μ_mλ_n)²

(0,0)=(m,n)∈I²

Тогда с учётом (16) получаем

∥z^h∥ ≤ C₇γλ2s-3/2N/2∥g∥.

При 0 < s ≤ 0.75 имеем (λ_mλ_n)2s ≤ C₉(μ_nλ_m + μ_mλ_n)³ и оценка нормы принимает вид

∥z^h∥ ≤ C₉γ∥g∥.

Объединив полученные оценки с неравенством (25), заключаем, что при g ∈ L₂(T²) справед-

ливо неравенство

∥w^h - u∥ ≤ (C₃h + C₁₀γλσ(s)N/2)∥g∥.

Оценка (31) доказана.

При дополнительной гладкости наклонов g₁ ∈ H1,0(T²), g₂ ∈ H0,1(T²) воспользуемся

неравенством

(λ_mλ_n)2s ≤ C₁₂λ2η(s)N/2(μ_nλ_m + μ_mλ_n)²(λ_m + λ_n)², η(s) = max{2s - 2, 0}.

Тогда с учётом неравенств (30) имеем

∑

(λ_mλ_n)2s| ŵ^hm,n

|²

∥z^h∥2h

=γ²

≤

(μ_nλ_m + μ_mλ_n)²

(0,0)=(m,n)∈I²

∑

≤C₁₁γ²λ2η(s)N/2

(λ_m + λ_n)²| ŵ^hm,n|² ≤ C₁₂γ²λ2η(s)N/2(∥Λ₁w^h∥2h + ∥Λ₂w^h∥2h) ≤

(0,0)=(m,n)∈I²

≤ C₁₃γ²λ2η(s)N/2(∥g₁∥2H1,0(T2) + ∥g2∥H 0,1(T2)).

С помощью (20) получаем неравенство (34). Теорема доказана.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

1004

РАЗГУЛИН и др.

Обсудим согласование параметров в оценках теоремы 7. Полученные в теореме 7 оценки

показывают, что для сходимости проекционного метода выбор параметров γ и s необходимо

согласовывать с шагом сетки h в зависимости от гладкости наклонов и выбора нормы. Учтём,

что в силу (13) λN/2 = 4h-2. Тогда для случая g₁, g₂ ∈ L₂(T²) при согласовании 0 < γ <

< C₁₄h1+2σ(s) в силу (31) имеет место оценка

∥w^h - u∥ ≤ C₁₅h∥g∥.

(36)

Если же g₁ ∈ H1,0(T²), g₂ ∈ H0,1(T²), то при 0 < γ < C₁₆h2+2η(s) в силу (34) справедлива

оценка скорости сходимости

∥w^h - u∥ ≤ C₁₇h²(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎),

(37)

а при 0 < γ < C₁₈h1+2σ(s) в силу (32) имеем

∥w^h - u∥_H1(T2₎ ≤ C₁₉h(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎).

(38)

Таким образом, при выполнении вычислительных экспериментов для наилучшего исполь-

зования свойства выравнивания частотной характеристики схемы при одновременном сохра-

нении точности вычислений параметр γ следует брать достаточно малым. Результаты вы-

числительных экспериментов подтверждают справедливость сделанных теоретических оценок

точности с согласованным выбором параметров.

4. Оценки скорости сходимости в пространствах дробной гладкости. В данном

пункте с помощью интерполяции оператора погрешности выведем оценки скорости сходимости

в анизотропных пространствах дробной гладкости. Введём необходимые обозначения. Пусть

X и Y - гильбертовы пространства со скалярными произведениями 〈·,·〉_X,

〈·,·〉_Y и соот-

ветствующими евклидовыми нормами ∥ · ∥_X , ∥ · ∥_Y , причём X вложено в Y, всюду плотно и

непрерывно. Из [11, п. 2.1] известно, что существует Λ = Λ^∗ > 0 - некоторый, вообще говоря,

неограниченный оператор в Y с D(Λ) = X, причём норма в X эквивалентна норме графика

Λ. Следуя [11], для θ ∈ [0, 1] рассмотрим промежуточные пространства Лионса [X, Y ]θ =

= D(Λ1-θ) с нормой графика ∥u∥[X,Y]θ = (∥u∥2Y + ∥Λ1-θu∥2Y )1/2. Очевидно, что [X,Y ]₀ = X,

[X, Y ]₁ = Y, т.е. пространства [X, Y ]_θ непрерывно соединяют крайние пространства X и Y.

В частности, аналогично [11, гл. 1, пп. 9 и 13] с использованием теоремы об интерполяции

пересечений пространств проверяется, что для θ ∈ [0, 1] справедливы равенства

[H¹(T²), L₂(T²)]_θ = H1-θ(T²),

(39)

[H1,0(T²) × H0,1(T²), L₂(T²) × L₂(T²)]_θ = H1-θ,0(T²) × H0,1-θ(T²).

(40)

Также потребуются интерполяционные пространства, построенные с помощью К-метода.

Рассмотрим функционалы

K_p(t,a;X,Y ) =

inf

(∥a₀∥^pX + t^p∥a₁∥^pY )1/p, p ∈ {1, 2}.

a₀+a₁=a,a₀∈X,a₁∈Y

Согласно [18, п. 1.3.2] при θ ∈ (0, 1) определим интерполяционные пространства

{

∫

)1/2

}

(X, Y )θ,2 = a ∈ Y : ∥a∥(X,Y)θ,2 =

t-1-2θK²¹(t,a;X,Y )dt

< +∞ .

√

Поскольку K₂ ≤ K₁ ≤

2K₂, то использование функционала K₂ в предыдущем определении

даёт эквивалентную норму. Отсюда в силу [11, теорема 15.1] при каждом θ ∈ (0, 1) вытекает

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОЦЕНКИ ТОЧНОСТИ ПРОЕКЦИОННОГО МЕТОДА

1005

эквивалентность норм пространств [X, Y ]_θ и (X, Y )θ,2. Однако равномерной по параметру θ

эквивалентности нет в силу полученного в упомянутой теореме равенства

∫

t-1-2θK²²(t,a;X,Y )dt = C(θ)∥Λ1-θa∥2Y

(41)

с неограниченным при θ → 0 + 0, θ → 1 - 0 множителем

+∞

s1-2θ

C(θ) =

ds =

1+s²

2sin(πθ)

(см. также [19, с. 116]).

Если X и Y - другая пара пространств со свойствами, аналогичными свойствам пары X

и Y, то имеет место следующее утверждение (см., например, [18, теорема 1.3.3]).

Теорема 8. Пусть для двух пар пространств X, Y и X , Y задан линейный оператор

T ∈ L(X → X)

^⋂ L(Y → Y). Тогда T ∈ L((X,Y )θ,2 → (X,Y)θ,2) и справедлива оценка

Mθ1, M₀ = ∥T∥L(X→X), M₁ = ∥T∥L(Y→Y).

(42)

∥T ∥L((X,Y)θ,2→(X ,Y)θ,2) ≤

Нам потребуется следствие из этой теоремы для промежуточных пространств Лионса. Для

любого a ∈ [X, Y ]_θ в силу (42) имеем неравенство

∥T a∥(X,Y)θ,2 ≤ M1-θ0Mθ1∥a∥(X,Y)

(43)

θ,2

Поскольку при переходе от нормы пространства К-метода к норме пространства Лионса фи-

гурирующий в (41) множитель C(θ) входит в обе части неравенства (43), то после несложных

перенормировок получаем неравенство в пространствах Лионса с независящей от θ ∈ [0, 1]

константой C₂₀ > 0:

∥T a∥[X,Y]θ ≤ C₂₀M1-θ0Mθ1∥a∥[X,Y]

(44)

Теорема 9. Пусть выполнено условие согласования параметров схемы и шага сетки 0 <

<γ <C₂₁h1+2σ(s), 0 < h < 1. Тогда для любых α ∈ [0,1] справедливы следующие оценки:

∥w^h - u∥_Hα(T2₎ ≤ C₂₂h(∥g₁∥_Hα,0(T2₎ + ∥g₂∥_H0,α(T2₎),

(45)

∥w^h - u∥_L

(46)

2(T²) ≤^C23h1+α(^∥g1^∥Hα,0(T²)+∥g2^∥H0,α(T²)),

∥w^h - u∥_Hα(T2₎ ≤ C₂₄h2-α(∥g₁∥_H1,0(T2₎ + ∥g₂∥_H0,1(T2₎).

(47)

Доказательство. Рассмотрим оператор погрешности проекционной схемы

R : g = (g₁,g₂) → w^h - u

на разных сочетаниях пар пространств, участвующих в оценках (36)-(38).

Начнём с оценок(36), (38). Имеем R ∈ L(L₂(T²) × L₂(T²) → L₂(T²)) с операторной нормой

M₁ ≤ C₁₅h и R ∈ L(H1,0(T²) × H0,1(T²) → H¹(T²)) с операторной нормой M₀ ≤ C₁₉h.

Применим неравенство (44), в котором в роли T выступает оператор погрешности R на парах

пространств Y = L₂(T²)×L₂(T²), Y = L₂(T²) и X = H1,0(T²)×H0,1(T²), X = H¹(T²). Тогда

с учётом соотношений (39), (40) неравенство (44) принимает вид

∥w^h - u∥_H1-θ(T2₎ ≤ C₂₂h(∥g₁∥_H1-θ,0(T2₎ + ∥g₂∥_H0,1-θ(T2₎).

Обозначив α = 1 - θ, получим (45).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

1006

РАЗГУЛИН и др.

Из рассмотрения оценок (36), (37) вытекает возможность применить для оператора по-

грешности R неравенство (44) на парах пространств Y = L2(T2) × L2(T2), Y = L2(T2) с

операторной нормой M₁ ≤ C₁₅h и X = H1,0(T²) × H0,1(T²), X = L₂(T²) с операторной

нормой M₀ ≤ C₁₇h². Положив θ = 1 - α, приходим к оценке (46).

Наконец, оценки (37), (38) позволяют рассмотреть оператор погрешности на парах про-

странств Y = H1,0(T²) × H0,1(T²), Y = L₂(T²) с операторной нормой M₁ ≤ C₁₇h² и X =

= H1,0(T²) × H0,1(T²), X = H¹(T²) с операторной нормой M₀ ≤ C₁₉h. Положив θ = 1 - α и

применив (44), получим (47). Теорема доказана.

5. Пример восстановления негладкого волнового фронта по неточно заданным

наклонам. Качество восстановления негладкого волнового фронта продемонстрируем на при-

мере поверхности, задаваемой уравнением

u(x, y, n, κ) = u₀ + exp{-(r/a)2M }U(x, y, n, κ),

U (x, y, n, κ) =

⎧

[κr + 2n(ϕ - π/2) + π/6^]

⎪

⎨(κr + 2n(ϕ - π/2) + π/6) mod 2π,

если

нечётное;

2π

(48)

⎪

[κr + 2n(ϕ - π/2) + π/6^]

⎩2π-(κr+2n(ϕ-π/2)+π/6)mod2π,если

чётное,

2π

√

где ϕ = argctg(y/x), r =

x² + y², n ∈ N, κ ∈ R,

[·] - целая часть числа. Функция из

(48) описывает многолепестковую (при κ = 0) и спиральную (при κ = 0) структуры с n

рукавами, при этом параметр κ отвечает за степень закрученности спирали. Такая функция

служит адекватной моделью для кусочно-гладких фазовых фронтов, встречающихся при ра-

боте датчиков Шака-Гартмана. Константа u₀ выбирается из условия равенства нулю среднего

значения функции, 2π-периодичность рассматриваемой функции по переменным x, y обес-

печивалась приближённым равенством нулю самой функции и её производных при достаточно

большом M (в расчётах брались значения a = 0.7π, M = 4).

В приведённом примере для численного моделирования в качестве исходных данных бра-

лись дискретные значения точных наклонов волнового фронта (48), к которым далее добавлял-

ся 5 %-й гауссов шум для имитации искажений измерений наклонов на сетке 512 × 512. Далее

проводилось восполнение дискретных наклонов из пространства сплайнов S¹(T²) и находи-

лась правая часть в (12), которая в этом случае выражается через разностные производные

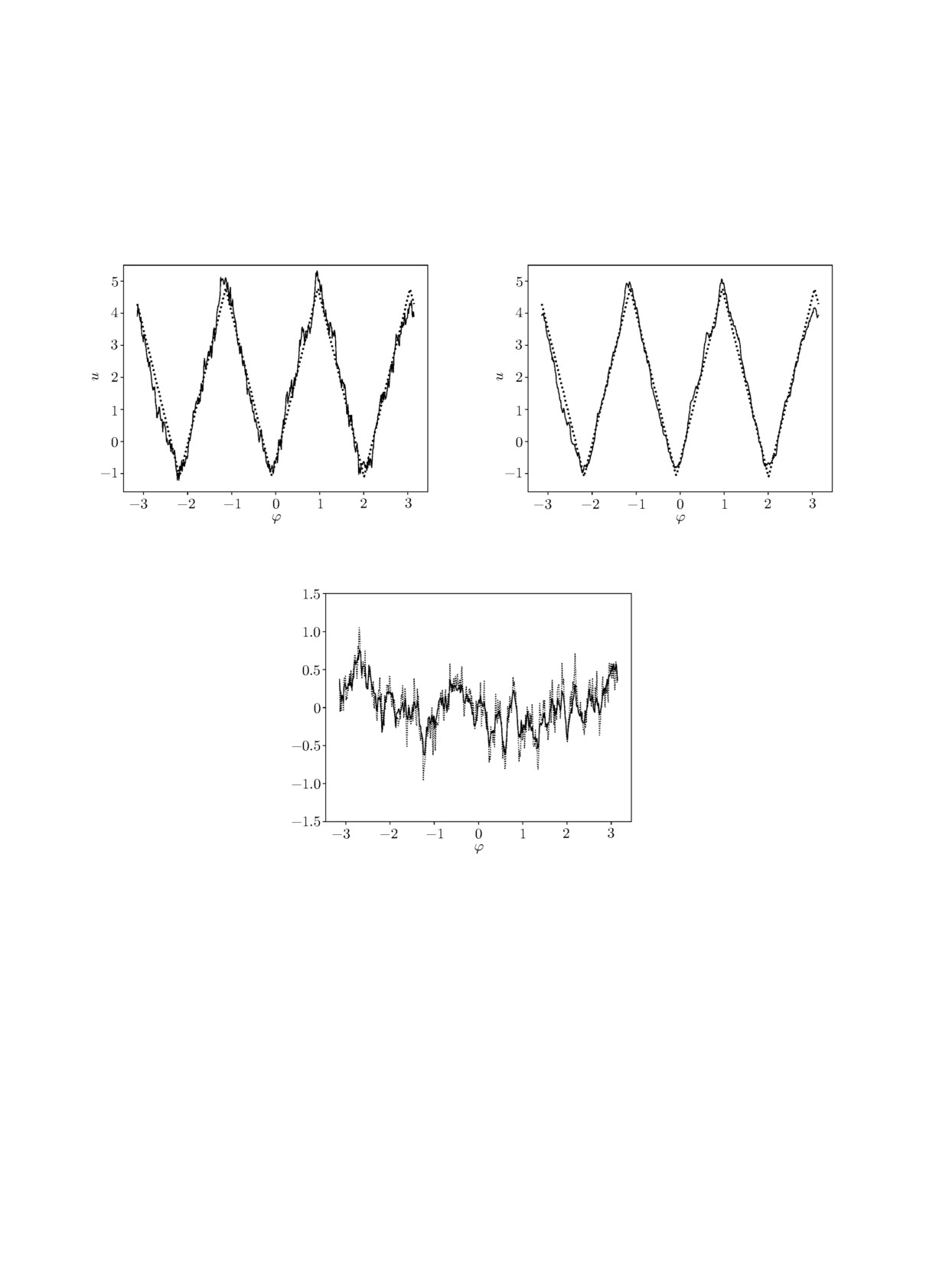
от дискретных наклонов (подробнее см. в [9]). Результаты вычислений на примере волнового

фронта (48) с параметрами κ = 2, n = 3 иллюстрируются на рис. 1, а для схемы без стабили-

затора (γ = 0) и на рис. 1, б для схемы со стабилизатором (γ = 0.03, s = 0.9) в виде сечений

волнового фронта окружностью r = π/2,

0 ≤ ϕ ≤ 2π. На рис. 2 приведены графики сече-

ний отклонений от искомого волнового фронта (48) полученного решения со стабилизатором и

без него. Сравнение показывает, что схема уверенно справляется с восстановлением кусочно-

гладких фаз. При этом линии разрывов производной точно локализуются и в областях вне раз-

рывов имеет место хорошее поточечное приближение. Как видно из графиков, использование

стабилизатора приводит к эффективному локальному сглаживанию паразитных искажений

волнового фронта, вызванных неточностью измерений наклонов.

Заключение. В работе рассмотрена проблема восстановления волнового фронта по его

наклонам, которая возникает в адаптивной оптике и связана с определением фазы световой

волны на основе датчика Шака-Гартмана. Вариационная постановка задачи приводит к урав-

нению Пуассона на подпространстве периодических функций с нулевым средним, при этом

свойство коэрцитивности задачи вытекает из неравенства Пуанкаре для таких функций. При

условии согласования шага сетки с параметрами стабилизатором дробного порядка получе-

ны оценки точности проекционного метода на основе билинейных сплайнов при естественных

требованиях к гладкости волнового фронта из анизотропных пространств Соболева с целыми

показателями гладкости. На основе выбора специальных анизотропных пространств с дробны-

ми показателями гладкости, составляющих непрерывную шкалу, соединяющую пространства

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

ОЦЕНКИ ТОЧНОСТИ ПРОЕКЦИОННОГО МЕТОДА

1007

с целыми показателями гладкости, и использования связанных с ними методов интерполя-

ции оператора погрешности проекционного метода получены шкалы оценок точности метода,

согласованные с дробной гладкостью наклонов. Теоретические оценки иллюстрируются ре-

зультатами численного эксперимента по эффективному восстановлению кусочно-негладких

спиральных волновых фронтов в условиях неточно заданных дискретных наклонов.

(а)

(б)

Рис. 1. Графики сечений при r = π/2 искомого фронта u(x, y, 3, 2) (пунктирная линия) и w^h (сплошная

линия) без стабилизатора (а) и со стабилизатором (б).

Рис. 2. Графики сечений при r = π/2 отклоне-

ний w^h от искомого фронта u(x, y,3, 2) без стаби-

лизатора (пунктирная линия) и со стабилизатором

(сплошная линия).

Работа выполнена при финансовой поддержке Российского фонда фундаментальных иссле-

дований (проект 18-29-02103) (А.В. Разгулин, Н.Г. Ирошников, А.В. Ларичев) и Министерства

образования и науки Российской Федерации в рамках реализации программы Московского

центра фундаментальной и прикладной математики (соглашение 075-15-2022-284) (А.В. Раз-

гулин, Т.Е. Романенко).

СПИСОК ЛИТЕРАТУРЫ

1. Platt B.C., Shack R. History and principles of Shack-Hartmann wavefront sensing // J. Refract. Surg.

2001. V. 17. № 5. P. S573-S577.

2. Andreeva M.S., Iroshnikov N.G., Koryabin A.B., Larichev A.V., Shmalgauzen V.I. Usage of wavefront

sensor for estimation of atmospheric turbulence parameters // Optoelectronics, Instrumentation and

Data Processing. 2012. V. 48. P. 197-204.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022

1008

РАЗГУЛИН и др.

3. Baryshnikov N.V., Denisov D.G., Dzhumamuratova A.A., Larichev A.V. Development and research of

an optoelectronic device based on a wavefront sensor to control the form parameters of intraocular lenses

// Measurement Techniques. 2019. V. 62. P. 31-35.

4. Goncharov A.S., Iroshnikov N.G., Larichev A.V., Nikolaev I.P. The impact of speckle on the measure-

ment of eye aberrations // J. of Modern Optics. 2015. V. 62. № 21. P. 1775-1780.

5. Bahk S.W. Highly accurate wavefront reconstruction algorithms over broad spatial-frequency bandwidth

// Optics Express. 2011. V. 19. № 20. P. 18997-19014.

6. Zhariy M., Neubauer A., Rosensteiner M., Ramlau R. Cumulative wavefront reconstructor for the Shack-

Hartmann sensor // Inverse Problems and Imaging. 2011. V. 5. № 4. P. 893-913.

7. Neubauer A. On the ill-posedness and convergence of the Shack-Hartmann based wavefront reconstruction

// J. of Inverse and Ill-posed Problems. 2010. V. 18. № 5. P. 551-576.

8. Kindermann S., Neubauer A., Ramlau R. A singular value decomposition for the Shack-Hartmann based

wavefront reconstruction // J. of Comput. and Appl. Math. 2012. V. 236. № 8. P. 2186-2199.

9. Razgulin A.V., Kuzhamaliyev Y.Z., Goncharov A.S., Larichev A.V. A variational method for wavefront

reconstruction from Shack-Hartman sensor measurements // Atmospheric and Oceanic Optics. 2017.

V. 30. № 4. P. 399-403.

10. Razgulin A.V., Kuzhamaliyev Y.Z., Iroshnikov N.G., Larichev A.V. A variational method of wavefront

reconstruction from local slope measurements using a fractional order of smoothness stabilizer // Comput.

Math. and Model. 2019. V. 30. № 2. P. 164-176.

11. Лионс Ж.-Л., Мадженес Э. Неоднородные граничные задачи и их приложения. М., 1971.

12. Adams R., Fournier J. Sobolev Spaces. Pure and Applied Mathematics. V. 140. Amsterdam, 2003.

13. Kuznetsov N., Nazarov A. Sharp constants in the Poincare, Steklov and related inequalities (a survey)

// Mathematika. 2015. V. 61. № 2. P. 328-344.

14. Сьярле Ф. Метод конечных элементов для эллиптических задач. М., 1980.

15. Обэн Ж.-П. Приближенное решение эллиптических краевых задач. М., 1977.

16. Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. М., 1981.

17. Варга Р. Функциональный анализ и теория аппроксимации в численном анализе. М., 1974.

18. Трибель Х. Теория интерполяции, функциональные пространства, дифференциальные операторы.

М., 1980.

19. Tartar L. An introduction to Sobolev spaces and interpolation spaces. Berlin; Heidelberg, 2007.

Московский государственный университет

Поступила в редакцию 18.02.2022 г.

имени М.В. Ломоносова,

После доработки 18.02.2022 г.

ООО “ВК Цифровые технологии”,

Принята к публикации 25.05.2022 г.

г. Москва

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58

№7

2022