ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2022, том 58, № 8, с.1112-1120
ЧИСЛЕННЫЕ МЕТОДЫ
УДК 519.63+517.958:533.9
ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ ДИНАМИКИ РАЗВИТИЯ
ДВУМЕРНЫХ ВОЗМУЩЕНИЙ
В МАГНИТНЫХ ЛОВУШКАХ-ГАЛАТЕЯХ
© 2022 г. К. В. Брушлинский, Е. В. Степин
Исследование устойчивости ловушек для магнитного удержания плазмы является одной
из главной задач в решении проблемы управляемого термоядерного синтеза. Основные
тенденции, качественные и количественные закономерности в этом вопросе могут быть
получены в терминах математического моделирования и вычислительного эксперимента.
Объектом моделирования в настоящей работе являются магнитоплазменные конфигура-
ции в распрямлённой в цилиндр тороидальной ловушке “Галатея-Пояс”, которые выводят-
ся из состояния равновесия малыми возмущениями. Математический аппарат исследова-
ния составляют задачи с двумерными нестационарными дифференциальными уравнения-
ми магнитной газодинамики для возмущений основных параметров плазмы и магнитного
поля, полученными в линейном приближении. В серии расчётов с различными начальными
данными в работе изучена картина развития возмущений с течением времени и описаны
её основные закономерности. Получено ограничение на максимальное давление плазмы,
выраженное в безразмерных единицах, в пределах которого возмущения не растут со вре-
менем, т.е. устойчивость обсуждаемых конфигураций сохраняется.
DOI: 10.31857/S0374064122080118, EDN: CGZSZO
Введение. Настоящая статья продолжает серию работ по численным исследованиям рав-
новесных плазменных конфигураций в магнитных ловушках, которые являются постоянным
объектом внимания в программах реализации управляемого термоядерного синтеза. Конкрет-
но рассматривается класс ловушек, в которых удерживающее плазму магнитное поле создаётся
токонесущими проводниками, погружёнными в плазменный объём, но не соприкасающимися
с горячей плазмой. Они инициированы А.И. Морозовым и названы “галатеями” [1]. Отличи-
тельной особенностью этих устройств является большое разнообразие геометрии магнитного
поля и, следовательно, богатый спектр возможных равновесных плазменных конфигураций
в них. С примерами технологической реализации галатей можно ознакомиться в работах [2-
4]. Работы предшествующих лет и общая идеология многосвязных ловушек обсуждаются в
монографии [5, с. 545]. Теория используемых математических моделей процессов в галате-
ях предполагает плазму достаточно плотной, допускающей приближения механики сплошной
среды. Математический аппарат моделей составляют задачи для дифференциальных уравне-
ний магнитной газодинамики (МГД), в приближённом решении которых значительную роль
играют численные методы и расчёты с применением современной высокопроизводительной
вычислительной техники.
Исследования магнитоплазменных конфигураций в ловушках направлены в основном на
решение двух групп вопросов. Во-первых, определяются геометрия и количественные характе-
ристики равновесных конфигураций. Рассматриваемые конфигурации в значительной части
установок обладают симметрией (плоской, осевой, винтовой) или допускают её, что существен-
но упрощает описание математических моделей и процесс их исследования. Система уравнений
плазмостатики, благодаря симметрии, сводится к одному скалярному дифференциальному
уравнению второго порядка для функции потока магнитного поля - хорошо известному урав-
нению Грэда-Шафранова [6, 7], двумерные краевые задачи для которой решаются численно
итерационными методами установления. Решения задач для этого уравнения в применении к
ловушкам-галатеям представлены в работах [8-14] и монографиях [15, 16]. Уравнение Грэда-
Шафранова хорошо описывает идеализированную ситуацию строгого равновесия, в котором
игнорируется высокая конечная проводимость плазмы и связанная с ней медленная диффузия
магнитного поля.
1112
ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ ДИНАМИКИ
1113
Во-вторых, существенным в проблеме удержания плазмы на протяжении необходимого
времени становится общий для современной физики плазмы вопрос об устойчивости рассмат-
риваемых равновесных конфигураций (см. [17-19]).
В применении к галатеям, а более конкретно - к галатее-поясу [3], в наших предшествую-
щих работах поставлены и частично решены следующие вопросы:
1) определено необходимое, но не достаточное условие “диффузионной устойчивости”, свя-
занное со сходимостью итерационных методов решения задач с уравнением Грэда-Шафранова
и, как выяснилось, со спектральным свойством дифференциального оператора линеаризован-
ной задачи [15, 16];
2) найдено условие устойчивости кольцевых одномерных конфигураций, окружающих один
прямой проводник с током - основной элемент конструкций всех галатей; условия устойчиво-
сти получены в терминах спектральных задач с линеаризованными МГД-уравнениями, сведён-
ными к одному уравнению второго порядка для вектора скорости [20-22], а именно, численно
найдена “граница устойчивости”, при которой дифференциальный оператор имеет нулевое соб-
ственное значение;
3) численно решена аналогичная двумерная задача с галатеей-поясом и показано, что эта
“граница устойчивости” усиливает ограничение на максимальное давление, отнесённое к маг-
нитным единицам, связанное с требованием “диффузионной устойчивости” [23].
В настоящей работе рассмотрена двумерная задача об устойчивости галатеи-пояса, рас-
прямлённой в цилиндр квадратного сечения, без перехода к двумерной линеаризованной зада-
че с возмущённым вектором скорости. Малые возмущения равновесной конфигурации описы-
ваются системой в общем случае семи линеаризованных МГД-уравнений, которая распадается
на две независимые друг от друга системы: одна содержит пять уравнений для возмущений
υ1x, υ1y, p1, H1x, H1y в плоскости (x,y), а другая - два уравнения для возмущения ско-
рости и магнитного поля в осевом направлении: υ1z и H1z. Основной интерес представляет
первая система, для которой ставится и численно решается начально-краевая задача в квад-
рате. Здесь не требуется искать спектр задачи, поскольку зависимость возмущений от времени
имеет вид exp(iωt), и устойчивость проявляется в том, что решение задачи не растёт со вре-
менем.
В результате серии расчётов качественно получен следующий результат: устойчивость име-
ет место только при обсуждаемом выше ограничении на отношение характерных значений
газового давления плазмы к её магнитному давлению, которое сильнее, чем условие “диф-
фузионной” устойчивости и практически не зависит от выбора начальных условий и других
деталей постановки задачи.
Сопоставление двух различных методов исследования и совпадение основного результата,
во-первых, подтверждает сам результат, во-вторых, представляет самодостаточный методиче-
ский интерес в вопросах численного моделирования актуальных задач современной физики.
1. Постановка задачи и метод решения. Математическая модель исследуемого объек-
та - распрямлённой в цилиндр квадратного сечения ловушки “Галатея-Пояс” с двумя прямыми
проводниками и равновесной конфигурации плазмы, магнитного поля и электрического тока
в ней получена ранее (см., например, [13, 23]) в процессе численного решения краевой задачи
с уравнением Грэда-Шафранова для функции магнитного потока ψ(x,y):
dp
Δψ +
+jex =0
(1)
dψ
в квадрате -2 < x,y < 2 с граничным условием ψ|Γ = 0. Здесь и ниже все величины
приведены к безразмерной форме, т.е. отнесены к естественным единицам, составленным из
размерных параметров задачи:
2Jc
c Hu
H2u
xu = yu = x0, Hu =
,
ju =
,
pu =
,
cxu
4π xu
4π
где x0 - расстояние от оси до центров токонесущих проводников, Jc - величина полного
электрического тока в каждом из них.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022
1114
БРУШЛИНСКИЙ, СТЕПИН
Равновесная конфигурация магнитного поля при этом может быть найдена с помощью
следующих соотношений:
∂ψ
∂ψ
Hx =
,
Hy = -
∂y
∂x
Предполагается, что давление плазмы между магнитными силовыми линиями ψ(x, y) =
= const задаётся в виде функции
(
)
(ψ - ψ0)2
p(ψ) = p0 exp
-
,
(2)
q2
где ψ0 = ψ(0, 0) - равенство, обеспечивающее сосредоточение плазмы в центре и на проходя-
щей через него сепаратрисе поля в соответствии с идеологией магнитного удержания плазмы,
без соприкосновения с конструкционными элементами ловушки. Величина p0 является одним
из основных параметров задачи и соответствует максимальному давлению плазмы, выражен-
ному в безразмерных единицах, которое достигается в ловушке.
Электрический ток в проводниках условного радиуса rc с центрами x1 = 1, x2 = -1,
погружённых в плазменный объём, моделируется с помощью функции jex в уравнении (1) в
следующем виде:
(
)
∑
(x - xk)2 + y2
2
jex = j0
exp
-
,
j0 =
r2c
r2c
k=1
Решение этой задачи существует, т.е. итерационный метод решения сходится, при ограни-
чении p0 < pdiff0 , которое названо условием “диффузионной” устойчивости. Этот тип соответ-
ствует устойчивости рассматриваемых двумерных конфигураций относительно возмущений
магнитного поля той же размерности.
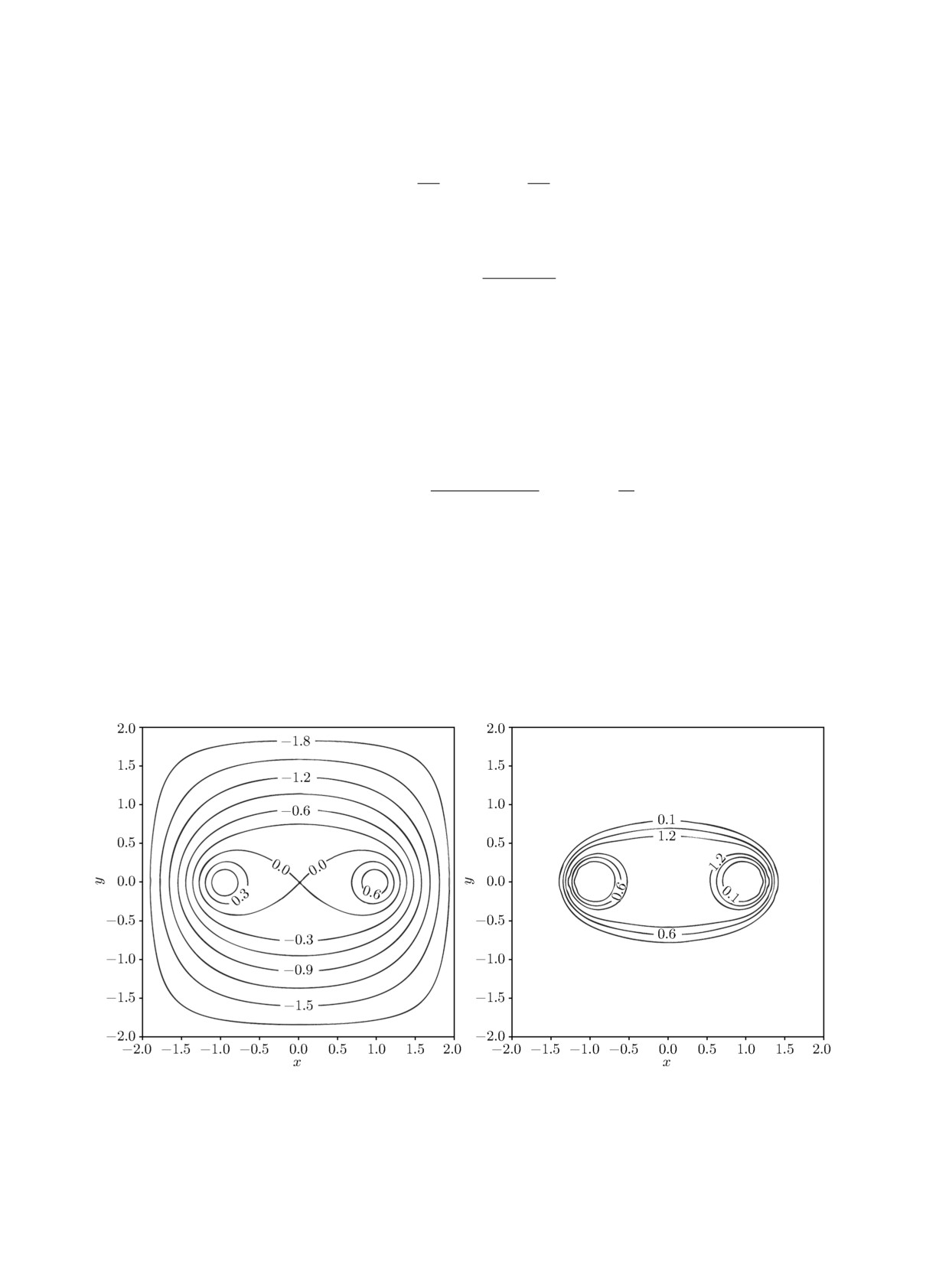
В качестве примера равновесной магнитоплазменной конфигурации, исследованию устой-
чивости которой посвящена настоящая работа, на рис. 1 представлен результат расчёта обсуж-
даемой задачи с уравнением (1) при максимальном значении безразмерного давления плазмы
p0 = 1.5.
(а)
(б)
Рис. 1. Равновесная магнитоплазменная конфигурация в цилиндрическом аналоге ловушки “Галатея-Пояс”
квадратного сечения при p0 = 1.5: (а) - линии уровня функции магнитного потока ψ(x, y); (б) - линии уровня
безразмерного давления плазмы p(x, y).
Как уже неоднократно обсуждалось в предыдущих работах, на рисунке видно, что ос-
новной объём плазмы сосредоточен в центре ловушки в окрестности сепаратрисы магнитного
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022
ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ ДИНАМИКИ
1115
поля в соответствии с видом функции (2), и плазма не соприкасается с внешней границей уста-
новки и токонесущими проводниками, создающими удерживающее магнитное поле. Отметим,
что здесь представлена конфигурация при значении давления p0 почти в два раза большим,
чем рассмотренным в работе [23], при этом плазменный объём приобрел выпуклый в сторо-
ну внешней границы ловушки вид. Изменение давления плазмы наиболее интенсивно вблизи
проводников и внешней границы равновесной конфигурации. Подробное исследование зависи-
мости свойств равновесных магнитоплазменных конфигураций в ловушке “Галатея-Пояс” от
основных параметров задачи, включая p0, rc и q, содержится в статье [24].
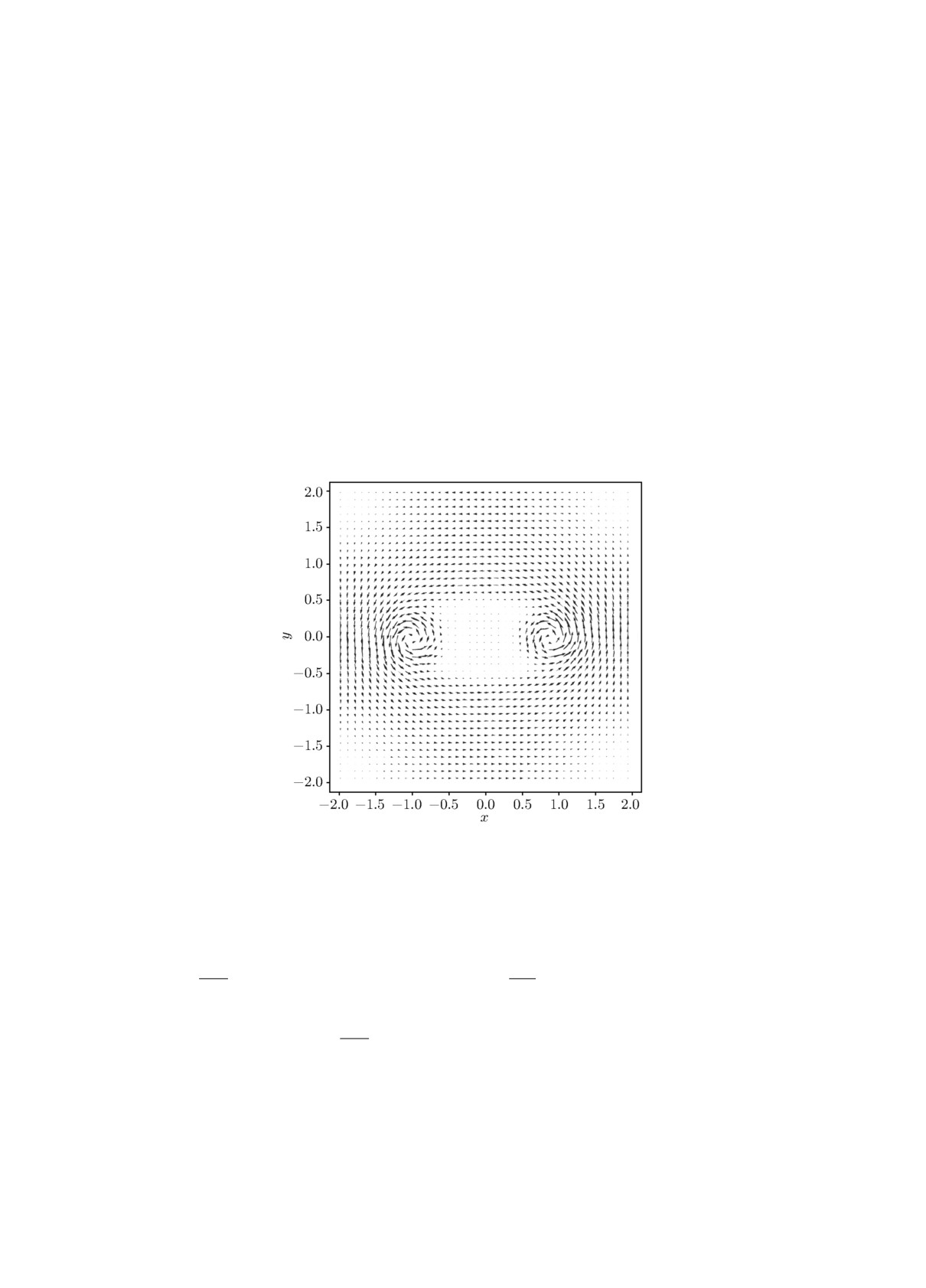
Отдельный интерес, в контексте проводимых в данной работе исследований устойчивости
равновесных конфигураций в галатее-поясе, представляет вид векторного поля напряжённо-
сти магнитного поля H = (Hx, Hy) в рассматриваемой системе, представленный на рис. 2.
Магнитное поле направлено против часовой стрелки вокруг плазменного объёма и на его
внешней границе. Такое же направление оно имеет и вокруг проводников с током. Именно
такая конфигурация магнитного поля обеспечивает условие несоприкосновения плазмы с кон-
струкционными элементами ловушки: результирующая амперова сила FA = j×H направлена
в сторону сепаратрисы магнитного поля в области, занимаемой плазмой, и при этом в окрест-
ности проводников изотропно обращена от них.
Рис. 2. Векторное поле напряжённости магнитного
поля H = (Hx, Hy) в равновесной магнитоплазмен-
ной конфигурации при p0 = 1.5.
Исследование устойчивости этих конфигураций ведётся в терминах линеаризованных на
состоянии покоя дифференциальных уравнений магнитной газодинамики
∂υ1
∂p1
ρ
+ ∇p1 = j1 × H + (j - jex) × H1,
+ υ1 · ∇p + γpdivυ1 = 0,
∂t
∂t
∂υ1
= rot(υ1 × H), j = rotH,
(3)
∂t
где величины без индекса соответствуют состоянию равновесия, а индексом “1” отмечены ма-
лые возмущения.
В отличие от предыдущих работ, уравнения (3) сводятся не к уравнениям второго порядка
только для скорости, а к полной системе семи уравнений первого порядка. В условиях симмет-
рии рассматриваемой задачи невозмущённые величины p, H, j зависят только от перемен-
ных x, y. Возмущения будем предполагать тоже двумерными, т.е. зависящими от (t, x, y).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022
1116
БРУШЛИНСКИЙ, СТЕПИН
В этих предположениях уравнения (3) распадаются на две независимые системы, одна из ко-
торых содержит пять уравнений для векторов возмущений в плоскости (x, y), а другая - два
уравнения только для z-компонент векторов υ1 и H1 :
)
∂u1
∂p1
(∂H1y
∂H1x
ρ
+
+Hy
-
+ jplH1y = 0,
∂t
∂x
∂x
∂y
)
∂υ1
∂p1
(∂H1y
∂H1x
ρ
+
-Hx
-
- jplH1x = 0,
∂t
∂y
∂x
∂y
)
∂p1
∂p
∂p
(∂u1
∂υ1
+
u1 +
υ1 + γp
+
= 0,
∂t
∂x
∂y
∂x
∂y
∂H1x
∂
∂H1y
∂
+
(Hxυ1 - Hyu1) = 0,
-
(Hxυ1 - Hyu1) = 0,
(4)
∂t
∂y
∂t
∂x
(
)
∂w1
∂H1z
∂H1z
∂H
1z
∂
∂
ρ
- Hx
+Hy
= 0,
-
(Hxw1) -
(Hyw1) = 0,
(5)
∂t
∂x
∂y
∂t
∂x
∂y
где (u1, υ1, w1) - компоненты вектора скорости возмущений υ1, jpl = jz - jex.
Система (5) фактически является вариантом хорошо известной системы уравнений акусти-
ки, решения которой не растут со временем. Поэтому для исследования эволюции двумерных
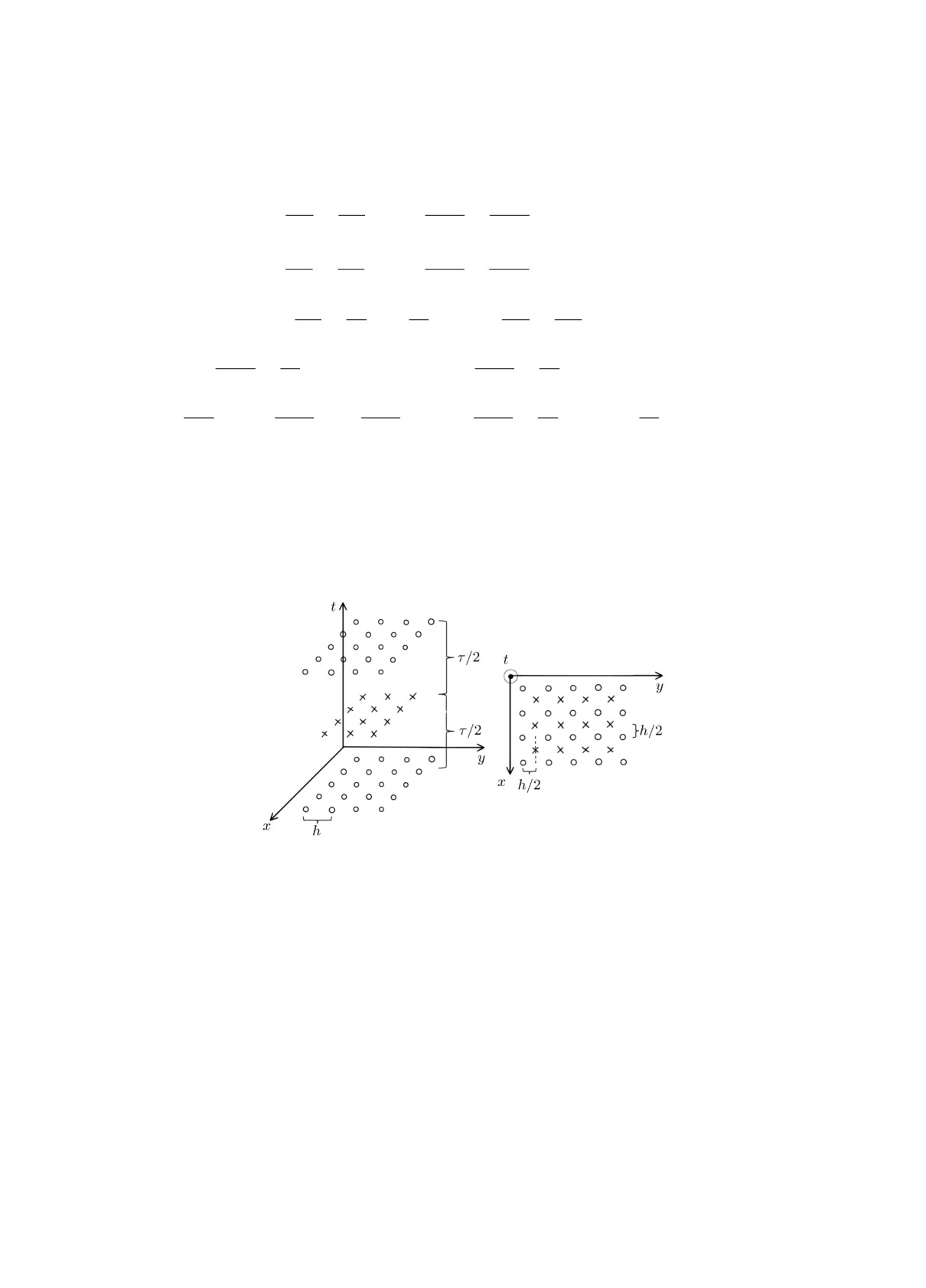
возмущений сосредоточимся на решении основной системы (4). Её разностный аналог лег-
ко построить с помощью разностной сетки “шахматного” типа (рис. 3), состоящей из целых
(кружки) и полуцелых (кресты) точек, смещённых друг относительно друга на полшага по x,
y и t. Расчёт ведётся в квадратной области -2 < x,y < 2 с граничным условием υ1n = 0.
Рис. 3. Равномерная разностная сетка “шахматного” типа.
h - шаг по пространственным координатам x и y, τ - шаг
по времени t.
Вопрос об устойчивости равновесия относительно двумерных возмущений здесь решается
напрямую, т.е. без спектрального анализа дифференциального оператора второго порядка в
уравнениях только для скорости возмущений. В расчётах основной интерес представляет пове-
дение возмущений со временем на качественном уровне: растут или не растут они со временем.
В результате этот подход, несмотря на кажущуюся внешне громоздкость (исследуется задача
для пяти уравнений вместо двух или трёх), оказался логически проще и легче реализуемым в
расчётах.
2. Результаты численного моделирования. В серии расчётов получены основные зако-
номерности, качественные и количественные выводы об устойчивости двумерных равновесных
магнитоплазменных конфигураций в распрямлённой в цилиндр квадратного сечения ловушке
“Галатея-Пояс” относительно малых возмущений параметров задачи, включая динамические,
той же размерности.
Отметим, что, в отличие от статьи [23], используемый в настоящем исследовании подход
позволяет напрямую проследить эволюцию параметров возмущений с ростом времени. В дан-
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022
ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ ДИНАМИКИ
1117
ной работе выбраны такие начальные условия задачи с уравнениями (4), которые отвечают
выводу из состояния равновесия самой среды кинематическим способом, т.е. эти условия со-
ответствуют начальному профилю возмущений скорости, но при этом предполагается, что в
начальный момент времени возмущения магнитного поля и давления плазмы отсутствуют.
Такая ситуация может возникать в реальных условиях, когда магнитная ловушка, например,
приводится в движение.
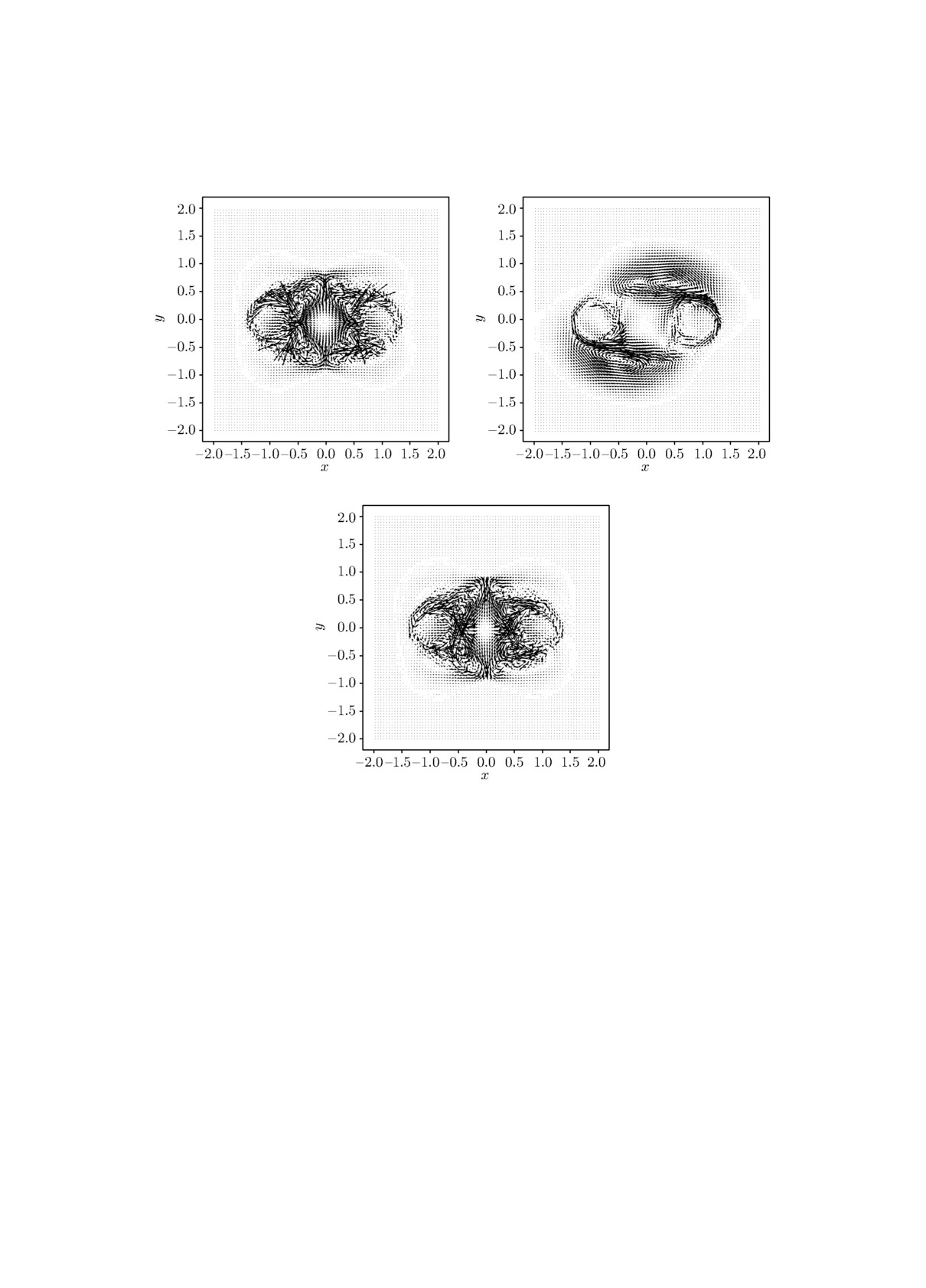
На рис. 4 на примере равновесной магнитоплазменной конфигурации с p0 = 1.5 (см. рис. 1,
2) представлены различные варианты начального профиля возмущений скорости плазмы, ко-
торые были использованы в расчётах. На рис. 4, а векторное поле скорости возмущений υ1
сонаправлено с магнитным полем равновесной конфигурации (см. рис. 2), на рис. 4, б плазма
приобретает начальный импульс в направлении верхнего правого угла ловушки, и, наконец,
на рис. 4, в скорость возмущений направлена по часовой стрелке, т.е. противоположно маг-
нитному полю.
(а)
(б)
(в)
Рис. 4. Начальные профили векторного поля возмущений скорости плазмы в магнитоплаз-
менной конфигурации с p0 = 1.5.
Расчёты показали, что динамика возмущений сильно зависит от начальных данных. От-
дельно стоит отметить, что, несмотря на отсутствие возмущений магнитного поля в началь-
ный момент времени, они появляются уже на первых итерациях численного решения задачи и
развиваются с течением времени. Этот результат согласуется с физической природой процес-
са: движение плазмы как электропроводной среды приводит к перераспределению магнитной
конфигурации ловушки.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022
1118
БРУШЛИНСКИЙ, СТЕПИН
На рис. 5 представлена картина возмущений магнитного поля при фиксированном значении
времени расчёта для начальных данных, соответствующих рис. 4.
(а)
(б)
(в)
Рис. 5. Развитие возмущений магнитного поля в конфигурации с p0 = 1.5 при различных
начальных условиях на возмущение скорости. Срез по времени T = 1.
В случае, когда начальный профиль возмущений скорости плазмы сонаправлен с маг-
нитным полем равновесной конфигурации, наблюдается “втекание” магнитного поля внутрь
ловушки в центр со стороны её верхней и нижней границ, при этом в центральной области
ловушки магнитное поле поворачивается в сторону проводников и приобретает тенденцию к
их огибанию (рис. 5, а). В расчётах также наблюдается образование на периферии плазменной
конфигурации симметрично расположенных в каждом из её квадрантов вихрей возмущений
магнитного поля. Если плазма начинает смещение вдоль диагонали ловушки (рис. 5, б), то кар-
тина относительно предыдущего случая качественно меняется. Вблизи правого проводника с
центром в точке x1 = 1 на верхней границе плазменного объёма наблюдается развитие вихря
возмущений магнитного поля, отвечающее, по всей видимости, суперпозиции влияния магнит-
ного поля равновесной конфигурации, направленного против часовой стрелки, и начального
профиля поля скорости возмущений. Такой же вихрь симметричным образом возникает в
области левого проводника на нижней границе ловушки. Наконец, характер развития воз-
мущений в случае, когда начальный профиль скорости имеет противоположное магнитному
полю равновесной конфигурации направление (рис. 5, в), с точностью да наоборот повторяет
картину, представленную на рис. 5, а: магнитное поле “вытекает” из плазменного объёма через
середину верхней и нижней границы ловушки, при этом в области проводников возмущения
магнитного поля направлены в центр плазменного объёма.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022
ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ ДИНАМИКИ
1119
В основе таких сложных картин развития возмущений магнитного поля лежит тенденция
магнитоплазменной конфигурации восстановить изначальное равновесие. Динамика развития
возмущений скорости имеет более простой характер, поэтому соответствующие графики в дан-
ной работе не приводятся. Отметим лишь, что плазма обтекает области, занятые проводни-
ками, не соприкасаясь с ними. Наибольшую скорость имеют возмущения на внешней границе
плазменного объёма, где давление плазмы интенсивно падает.
Очевидно, что картина развития возмущений будет уникальна для каждого конкретного
варианта начальных данных. Если учитывать также начальные возмущения магнитного поля
H1 и давления плазмы p1, то можно моделировать практически любые ситуации, при которых
магнитные ловушки подвергаются тому или иному воздействию.
В конечном итоге, как это уже было отмечено выше, устойчивость той или иной магнито-
плазменной конфигурации оказывается напрямую связанной с вопросом: растут ли обсужда-
емые возмущения со временем или нет? В настоящей работе результаты расчётов показали,
что возмущения параметров плазмы, какую бы сложную картину развития, связанную со спо-
собом задания начальных данных, они ни имели, не растут со временем, если максимальное
давление плазмы p0, выраженное в магнитных единицах, не превышает некоторого критиче-
ского значения pcr0. При этом обнаруженное критическое значение pcr0 оказалось меньше pdiff0 ,
соответствующего “диффузионной” устойчивости, т.е. устойчивости относительно возмущений
только магнитного поля той же размерности, что и изучаемые конфигурации. Этот результат
качественно совпадает с полученным ранее в работе [23], но совсем из других соображений, а
именно, из численного анализа спектральных свойств дифференциального оператора второго
порядка для вектора скорости возмущений. Совпадение результатов говорит о состоятельно-
сти обеих математических моделей устойчивости равновесных магнитоплазменных конфигу-
раций в ловушках, создаваемых для удержания плотной горячей плазмы. В расчётах значение
критического давления было уточнено до pcr0 ≈ 4. Важно также отметить, что неустойчи-
вость обсуждаемых конфигураций в ловушке “Галатея-Пояс” проявляется в неограниченном
росте амплитуды возмущений именно на периферии плазменного объёма, где давление плаз-
мы интенсивно убывает, и этот результат также подтверждается выводами из исследований
одномерных конфигураций, окружающих прямой проводник с током, опубликованных в ра-
ботах [20-22].
Утверждение. Для исследования малых двумерных возмущений равновесных магнито-
плазменных конфигураций в ловушке “Галатея-Пояс” сформулирована и численно реализована
в программном коде нестационарная МГД-модель, позволяющая проследить их развитие во
времени. Установлено, что возмущения не растут при более сильном ограничении на мак-
симальное давление плазмы, измеренное в магнитных единицах, чем для “диффузионной”
устойчивости, т.е. устойчивости относительно возмущений магнитного поля. Представ-
ленные выводы качественно совпадают и количественно уточняют предыдущие результаты,
полученные с помощью спектрального метода.
Заключение. В работе представлена двумерная нестационарная модель устойчивости
равновесных конфигураций в ловушках-галатеях - перспективных установках для магнит-
ного удержания плазмы, разрабатываемых в рамках решения проблемы управляемого тер-
моядерного синтеза. Модель позволяет проследить эволюцию возмущений параметров плаз-
мы и магнитного поля, а также качественно и количественно оценить критерии, способству-
ющие или препятствующие устойчивости рассматриваемых ловушек. На примере ловушки
“Галатея-Пояс” с двумя токонесущими проводниками, погружёнными в плазменный объём,
выполнена серия расчётов с различными способами задания начальных профилей скорости
возмущений и выявлены основные закономерности в характере их развития. Получен кри-
терий МГД-устойчивости, связанный с ограничением на максимальное давление плазмы в
ловушке, выраженное в безразмерных единицах. Эти результаты качественно совпадают и
количественно уточняют полученные раннее результаты в цикле исследований устойчивости
ловушек-галатей.
Работа выполнена при финансовой поддержке Министерства науки и высшего образования
Российской Федерации в рамках реализации программы Московского центра фундаменталь-
ной и прикладной математики по соглашению № 075-15-2022-283.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022
1120
БРУШЛИНСКИЙ, СТЕПИН
СПИСОК ЛИТЕРАТУРЫ
1. Морозов А.И. О галатеях - плазменных ловушках с омываемыми плазмой проводниками // Физика
плазмы. 1992. Т. 18. Вып. 3. С. 305-316.
2. Морозов А.И., Пустовитов В.Д. О стеллараторе с левитирующими обмотками // Физика плазмы.
1991. Т. 17. Вып. 10. С. 1276.
3. Морозов А.И., Франк А.Г. Тороидальная магнитная ловушка-галатея с азимутальным током // Фи-
зика плазмы. 1994. Т. 20. № 11. С. 982-989.
4. Морозов А.И., Бугрова А.И., Бишаев А.М., Липатов А.С., Козинцева М.В. Параметры плазмы в
модернизированной ловушке-галатее “Тримикс” // Журн. техн. физики. 2007. Т. 77. № 12. С. 15-20.
5. Морозов А.И. Введение в плазмодинамику. М., 2008.
6. Grad H., Rubin H. Hydrodynamic equilibria and force-free fields // Proc. 2nd United Nations Int. Conf.
on the Peaceful Uses of Atomic Energy. Geneva. 1958. V. 31. P. 190-197 / N.Y. Columbia Univ. Press,
1959.
7. Шафранов В.Д. Равновесие плазмы в магнитном поле // Вопросы теории плазмы / Под ред. М.А.
Леонтовича. М., 1963. Вып. 2. С. 92-131.
8. Брушлинский К.В., Зуева Н.М., Михайлова М.С., Морозов А.И., Пустовитов В.Д., Ту-
зова Н.Б. Численное моделирование прямых винтовых шнуров с проводниками, погруженными в
плазму // Физика плазмы. 1994. Т. 20. № 3. С. 284-292.
9. Брушлинский К.В., Морозов А.И., Петровская Н.Б. Численное моделирование винтовой равновес-
ной конфигурации с плазмой на сепаратрисе // Мат. моделирование. 1998. Т. 10. № 11. С. 29-36.
10. Морозов А.И., Савельев В.В. О галатеях-ловушках с погруженными в плазму проводниками
// Успехи физ. наук. 1998. Т. 168. № 11. С. 1153-1194.
11. Брушлинский К.В., Игнатов П.А. Плазмостатическая модель магнитной ловушки “Галатея-Пояс”
// Журн. вычислит. математики и мат. физики. 2010. Т. 50. № 12. С. 2184-2194.
12. Брушлинский К.В., Гольдич А.С., Десятова А.С. Плазмостатические модели магнитных ловушек-
галатей // Мат. моделирование. 2012. Т. 24. № 8. С. 81-86.
13. Брушлинский К.В., Кондратьев И.А. Сравнительный анализ расчётов равновесия плазмы в торои-
дальных и цилиндрических магнитных ловушках // Мат. моделирование. 2018. Т. 30. № 6. С. 76-94.
14. Tao B., Jin X., Li Z., Tong W. Equilibrium configuration reconstruction of multipole galatea magnetic
trap based on magnetic measurement // IEEE Transactions on Plasma Science. 2019. V. 47. № 7. P. 3114-
3123.
15. Брушлинский К.В. Математические и вычислительные задачи магнитной газодинамики. М., 2009.
16. Брушлинский К.В. Математические основы вычислительной механики жидкости, газа и плазмы.
М., 2017.
17. Кадомцев Б.Б. Гидромагнитная устойчивость плазмы // Вопросы теории плазмы / Под ред.
М.А. Леонтовича. М., 1963. Вып. 2. С. 132-176.
18. Соловьёв Л.С. Гидромагнитная устойчивость замкнутых плазменных конфигураций // Вопросы
теории плазмы / Под ред. М.А. Леонтовича. М., 1972. Вып. 6. С. 210-290.
19. Бейтман Г. МГД-неустойчивости. М., 1982.
20. Брушлинский К.В., Кривцов С.А., Степин Е.В. Об устойчивости равновесия плазмы в окрестности
прямого проводника с током // Журн. вычислит. математики и мат. физики. 2020. Т. 60. № 4.
С. 153-163.
21. Брушлинский К.В., Степин Е.В. Математические модели равновесных конфигураций плазмы,
окружающей проводники с током // Дифференц. уравнения. 2020. Т. 56. № 7. С. 901-909.
22. Brushlinskii K.V., Stepin E.V. Plasma equilibrium and stability in a current-carrying conductor vicinity
// J. Phys.: Conf. Ser. 2020. V. 1640. P. 012018.
23. Брушлинский К.В., Степин Е.В. Вопросы устойчивости в двумерных математических моделях
равновесия плазмы в магнитных ловушках-галатеях // Дифференц. уравнения. 2021. Т. 57. № 7.
С. 867-879.
24. Brushlinskii K.V., Stepin E.V. On equilibrium magnetoplasma configurations in “Galatea-Belt” magnetic
traps // J. Phys.: Conf. Ser. 2021. V. 2028. P. 012026.
Институт прикладной математики
Поступила в редакцию 22.02.2022 г.
имени М.В. Келдыша РАН, г. Москва,
После доработки 22.02.2022 г.
Национальный исследовательский ядерный
Принята к публикации 05.07.2022 г.
университет “МИФИ”, г. Москва,
Московский государственный университет
имени М.В. Ломоносова
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 58
№8
2022