ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 1, с.73-84
УРАВНЕНИЯ В КОНЕЧНЫХ РАЗНОСТЯХ
УДК 517.962.2
ПРОЕКТОРНЫЙ ПОДХОД К ПОСТРОЕНИЮ
АСИМПТОТИКИ РЕШЕНИЯ НАЧАЛЬНЫХ ЗАДАЧ
ДЛЯ СЛАБО НЕЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ
С МАЛЫМ ШАГОМ В КРИТИЧЕСКОМ СЛУЧАЕ
© 2023 г. Г. А. Курина, Нгуен Тхи Хоай
Алгоритм построения асимптотического решения начальной задачи, содержащего погра-
ничные функции, для слабо нелинейной системы дискретных уравнений с малым ша-
гом в критическом случае при некоторых условиях приведён в статье В.Ф. Бутузова и
А.Б. Васильевой (Дифференц. уравнения. 1970. Т. 6. № 4. С. 650-664). В настоящей работе
для построения асимптотики решения этой задачи используются ортогональные проекто-
ры. Такой проекторный подход существенно упрощает понимание алгоритма построения
асимптотики и позволяет записать в явном виде задачи, из которых можно найти члены
асимптотики решения любого порядка.
DOI: 10.31857/S0374064123010077, EDN: OCIIXC
Посвящается светлой памяти А.Б. Васильевой и В.Ф. Бутузова
Введение. Важным классом дискретных (разностных) уравнений, называемых также
уравнениями в конечных разностях, являются уравнения с малым шагом. Они возникают, в
частности, при дискретизации непрерывных уравнений для численного анализа. Начальные
задачи для таких уравнений с малым шагом ε являются сингулярно возмущёнными, посколь-
ку при нулевом значении ε происходит потеря начального условия. Наиболее сложным при
этом является так называемый критический случай, когда из вырожденного уравнения (с ну-
левым значением малого параметра) решение не определяется однозначно.
Асимптотическое решение начальных задач для слабо нелинейных дискретных систем с
малым шагом в критическом случае впервые было построено В.Ф. Бутузовым и А.Б. Василье-
вой в работе [1], результаты которой представлены также в монографии [2, с. 22-27]. Обзор
публикаций, посвящённых задачам управления дискретными системами с малым шагом, при-
ведён в [3].
В настоящей статье рассматривается задача из [2, с. 22] вида
x(t + ε) = B(t)x(t) + εf(x(t), t, ε), t = 0, ε, 2ε, . . . (t ≤ T ),
(1)
x(0) = x0,
(2)
где x(t) ∈ X, dim X = m, величина ε ≥ 0 означает малый параметр.
При некоторых условиях I-III в [2, с. 22-27] построено асимптотическое решение задачи
(1), (2), содержащее пограничные функции. Будем рассматривать задачу (1), (2) при тех же
условиях.
Условие I. Матрица B(t) при t ∈ [0, T ] имеет k-кратное собственное значение λ(t) ≡ 1,
которому при каждом t соответствует k линейно независимых собственных векторов v1(t),
v2(t), ..., vk(t), а остальные собственные значения удовлетворяют условию |λi(t)| < 1.
Условие II. Матрица B(t) и функция f(x, t, ε) достаточно гладкие по своим аргументам.
Будем использовать достаточно гладкие собственные векторы. В силу условия II существо-
вание таких собственных векторов следует из работы [4].
Отметим, что условие II из [2, с. 22] в нашем случае усилено предположением о гладкости
всюду, а не в некоторой области пространства переменных.
Условие III, связанное с разрешимостью некоторого уравнения, сформулируем позже.
73
74
КУРИНА, ХОАЙ
В отличие от работ [1, 2] здесь для построения асимптотики решения задачи (1), (2) ис-
пользуются ортогональные проекторы. Такой проекторный подход позволяет хорошо понять
суть алгоритма А.Б. Васильевой и В.Ф. Бутузова, основанного на методе пограничных функ-
ций, и представить явные выражения задач для отыскания членов асимптотического решения
любого порядка. Заметим, что в [1, 2] предложен алгоритм построения асимптотики реше-
ния любого порядка, но записаны явным образом только задачи для отыскания нескольких
первых членов асимптотики. Наличие явных формул полезно специалистам, применяющим
асимптотические методы для решения практических задач.
Проекторный подход уже использовался в [5, 6] для асимптотического решения начальных
задач для сингулярно возмущённых дифференциальных уравнений двух типов в критическом
случае, а также в [7] для построения асимптотического решения нулевого порядка для сингу-
лярно возмущённой линейно-квадратичной задачи управления в критическом случае.
В п. 1 настоящей статьи представлены соотношения для членов разложения решения за-
дачи (1), (2) по целым неотрицательным степеням ε в виде суммы функций, зависящих от t,
и пограничных функций, зависящих от аргумента t/ε. В п. 2 вводятся ортогональные проек-
торы, которые используются при нахождении членов разложения решения. В п. 3 приведён
алгоритм построения асимптотического решения задачи (1), (2) нулевого порядка, а в п. 4 -
n-го порядка, n ≥ 1. Таблицы в этих пунктах показывают последовательность нахождения
членов асимптотики. В п. 5 приводится иллюстративный пример построения асимптотического
приближения первого порядка для решения дискретной задачи с малым шагом, рассматрива-
емого в статье типа, с помощью проекторного подхода.
Далее штрих будет означать транспонирование, I - единичную матрицу.
1. Декомпозиция задачи. Следуя [1], будем искать асимптотическое решение задачи (1),
(2) в виде
x(t) = x(t, ε) + Πx(τ, ε),
(3)
где
∑
∑
x(t, ε) =
εjxj(t), Πx(τ,ε) =
εjΠjx(τ), τ = t/ε.
(4)
j≥0
j≥0
Функции Πj x(τ) будут определяться с помощью дополнительного условия
Πjx(τ) → 0 при τ → +∞.
∑
Рядj≥0 εj xj (t) с членами, зависящими от аргумента t, называется регулярным рядом
∑
(см., например, [2, с. 8]), в отличие от пограничного рядаj≥0 εj Πj x(τ), τ ≥ 0, состоящего из
так называемых пограничных функций, которые существенны только для аргументов вблизи
точек, где заданы дополнительные условия (в окрестности нуля в рассматриваемом случае).
Как принято в теории сингулярных возмущений, будем использовать представление
f (x(t, ε) + Πx(τ, ε), t, ε) ≡ f + Πf,
где
∑
f = f(x(t,ε),t,ε) =
εjfj(t),
j≥0
∑
Πf = f(x(ετ, ε) + Πx(τ, ε), ετ, ε) - f(x(ετ, ε), ετ, ε) =
εjΠjf(τ).
j≥0
Замечание 1. Как и в [2, с. 23], функции xj(t), j = 0, 1, 2, . . . , при построении асимптоти-
ки решения будут рассматриваться для всех t ∈ [0, T ]. В окончательном же асимптотическом
представлении (4) значения xj (t) используются только для t = 0, ε, 2ε, . . . в соответствии с
дискретным изменением t в системе (1).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
ПРОЕКТОРНЫЙ ПОДХОД К ПОСТРОЕНИЮ АСИМПТОТИКИ РЕШЕНИЯ
75
Подставляя разложение (3) в (1) и приравнивая коэффициенты при одинаковых степе-
нях ε, отдельно зависящие от t и τ, получаем следующие уравнения для членов рядов (4):
∑
1
dj-ixi(t)
xj(t) +
= B(t)xj(t) + fj-1(t),
(5)
(j - i)! dtj-i
i=0
∑
τj-i dj-iB
Πjx(τ + 1) = B(0)Πjx(τ) +
(0)Πix(τ) + Πj-1f(τ),
(6)
(j - i)! dtj-i
i=0
где j = 0, 1, 2, . . .
Чтобы записать уравнения (5), (6) в одинаковом виде для любого j ≥ 0, будем считать,
что члены разложений с отрицательными индексами равны нулю.
Подставив разложение (3) в (2) и приравняв коэффициенты при одинаковых степенях ε,
имеем равенства
x0(0) + Π0x(0) = x0,
(7)
xj(0) + Πjx(0) = 0, j > 0.
(8)
2. Декомпозиция пространства. Положим A(t) = B(t)-I. Разложим пространство X
в ортогональные суммы (см., например, [8, с. 24])
X = KerA(t)
⊕ Im A(t)′ = Ker A(t)′ ⊕Im A(t).
(9)
Ортогональные проекторы пространства X на подпространства Ker A(t) и Ker A(t)′ обо-
значим соответственно через P (t) и Q(t).
Определим n × k-матрицы V (t) и S(t) следующим образом: V (t) = (v1(t), . . . , vk(t)) и
S(t) = (s1(t), . . . , sk(t)), где s1(t), . . . , sk(t) - собственные векторы матрицы A(t)′, соот-
ветствующие собственному значению λ(t) = 0. В силу условия I (линейной независимости
собственных векторов) матрицы V (t)′V (t) и S(t)′S(t) размера k × k обратимы. Нетрудно
проверить, что P (t) = V (t)(V (t)′V (t))-1V (t)′ и Q(t) = S(t)(S(t)′S(t))-1S(t)′ являются орто-
гональными проекторами пространства X на подпространства Ker A(t) и Ker A(t)′, соответ-
ствующими разложениям (9) пространства X в ортогональные суммы.
Оператор
A(t) = (I - Q(t))A(t)(I - P (t)) : Im A(t)′ -→ Im A(t)
имеет обратный оператор, который будем обозначать через A(t)+ = (I - P (t))A(t)+(I - Q(t)).
Из условия I следует, что для каждого t ∈ [0, T ] модуль собственных значений оператора
B(t) = (I - P (t))B(t)(I - P (t)) : Im A(t)′ → Im A(t)′ меньше единицы, и матрица S(t)′V (t)
размера k × k обратима (см. [2, с. 12]).
Из последнего факта вытекает
Лемма 1. Оператор Q(t)P (t) : Ker A(t) → Ker A(t)′ обратим при всех t ∈ [0, T ].
Доказательство. Предположим противное. Тогда при некотором t существует элемент
x ∈ KerA(t) такой, что
Q(t)P (t)x = 0.
(10)
Элемент x представим в виде линейной комбинации векторов vj (t), j = 1, k, т.е. x = V (t)c,
где c = (c1, c2, . . . , ck)′. Применим к (10) слева оператор V (t)′. Учитывая вид проекторов P (t)
и Q(t), получаем равенство
V (t)′S(t)(S(t)′S(t))-1S(t)′V (t)c = 0.
Отсюда в силу обратимости оператора S(t)′V (t) получаем c = 0. Значит, x = 0, что доказы-
вает обратимость оператора Q(t)P (t).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
76
КУРИНА, ХОАЙ
3. Асимптотическое решение нулевого порядка. Используя введённые проекторы,
найдём члены асимптотики решения задачи (1), (2) нулевого порядка. Из (5) при j = 0 полу-
чаем уравнение для x0(t):
A(t)x0(t) = 0.
Следовательно,
(I - P (t))x0(t) = 0.
(11)
С учётом (11) находим из (7) начальное значение
(I - P (0))Π0x(0) = (I - P (0))x0.
(12)
Из (6) при j = 0 получаем уравнение для Π0x(τ):
Π0x(τ + 1) = B(0)Π0x(τ).
(13)
Замечание 2. Легко видеть, что B(t)|KerA(t) = I. Следовательно, (I - P (0))B(0)P (0) -
нулевой оператор, а P (0)B(0)P (0) - тождественный оператор в Ker A(0).
Ввиду этого замечания уравнение (13) эквивалентно двум уравнениям:
(I - P (0))Π0x(τ + 1)
B(0)(I - P (0))Π0x(τ),
(14)
P (0)Π0x(τ + 1) = P (0)Π0x(τ) + P (0)B(0)(I - P (0))Π0x(τ).
(15)
Будем использовать следующее легко доказываемое утверждение (см., например, [9, с. 20]).
Лемма 2. Решение задачи
y(t + 1) = Cy(t) + f(t), y(0) = y0, t = 0, 1, 2, . . . ,
определяется по формуле
∑
y(t) = Cty0 +
Ct-i-1f(i).
i=0
В силу этой леммы единственным решением начальной задачи (14), (12) является функция
(I - P (0))Π0x(τ)
B(0)τ (I - P (0))x0.
(16)
Поскольку спектральный радиус оператора
B(0) меньше единицы, то из лемм 5.6.10 [10,
с. 347] и 5.6.11 [10, с. 348] следует
Лемма 3. Существует норма оператора
B(0), меньшая единицы, и lim
B(0)τ = 0.
τ→+∞
Следовательно, (I - P (0))Π0x(τ) является пограничной функцией.
Используя лемму 2, запишем решение уравнения (15)
∑
P (0)Π0x(τ) = P (0)Π0x(0) +
P (0)B(0)(I - P (0))Π0x(i).
i=0
Так как P (0)Π0x(τ) должно стремиться к нулю при τ → +∞, то с учётом (16) из послед-
него равенства имеем
∑
P (0)Π0x(0) = - lim
P (0)B(0)(I - P (0))Π0x(i) =
τ→+∞
i=0
∑
= - lim
P (0)B(0)(I - P (0)
B(0)i(I - P (0))x0 =
τ→+∞
i=0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
ПРОЕКТОРНЫЙ ПОДХОД К ПОСТРОЕНИЮ АСИМПТОТИКИ РЕШЕНИЯ
77
∑
= -P(0)B(0)(I - P(0))
B(0)i(I - P (0))x0.
i=0
Ввиду леммы 3 последний ряд сходится. Итак,
∑
P (0)Π0x(τ) = -P (0)B(0)(I - P (0))
B(0)i(I - P (0))x0 +
i=0
∑
+ P(0)B(0)(I-P(0)
B(0)i(I - P (0))x0 =
i=0
∑
= -P(0)B(0)(I - P(0)
B(0)τ
B(0)i(I - P (0))x0.
(17)
i=0
В силу леммы 3 P (0)Π0x(τ) является пограничной функцией. Таким образом, пограничная
функция Π0x(τ) найдена. Тогда из (7) можно найти начальное значение
P (0)x0(0) = P (0)(x0 - Π0x(0)).
(18)
Из (5) при j = 1 получаем уравнение для x1(t) :
dx0(t)
A(t)x1(t) = -f0(t) +
,
dt
где f0(t) = f(x0(t), t, 0).
Принимая во внимание (11), запишем условие разрешимости последнего уравнения:
d(P (t)x0(t))
Q(t)
= Q(t)f(P(t)x0(t),t,0).
(19)
dt
Учитывая тождество
d(P (t)x(t))
d(P (t)2x(t))
dP (t)
d(P (t)x(t))
=
=
P (t)x(t) + P (t)
,
(20)
dt
dt
dt
dt
из (19) получаем нелинейное уравнение
(
)
d(P (t)x0(t))
dP (t)
= (Q(t)P (t))-1Q(t) -
P (t)x0(t) + f(P (t)x0(t), t, 0)
+
dt
dt
dP (t)
+ (I - P (t))
P (t)x0(t),
dt
совпадающее с (16) из работы [5].
Применив к (20) слева оператор P (t), имеем тождество
dP (t)
P (t)
P (t)x(t) = 0.
(21)
dt
Поэтому уравнение для P (t)x0(t) можно записать в виде
(
)
d(P (t)x0(t))
dP (t)
dP (t)
= (Q(t)P (t))-1Q(t) -
P (t)x0(t) + f(P (t)x0(t), t, 0)
+
P (t)x0(t). (22)
dt
dt
dt
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
78
КУРИНА, ХОАЙ
Если B(t) = B - постоянная матрица, то проекторы P (t) = P и Q(t) = Q тоже постоян-
ные, и последнее уравнение примет вид
d(P x0(t))
= (QP )-1Qf(P x0(t), t, 0).
(23)
dt
Предположим, что выполнено
Условие III. Задача (22), (18) имеет единственное решение на отрезке [0, T ].
Аналогичное предположение о разрешимости некоторой начальной задачи для нелинейного
уравнения меньшей размерности, чем исходное, было дано в [1] (см. также [2, с. 24]).
При этом условии функция x0(t) однозначно определяется. Следовательно, найдена асимп-
тотика нулевого порядка решения задачи (1), (2) (табл. 1).
Таблица 1. Последовательность нахождения
членов асимптотики нулевого порядка
Члены асимптотики
Формулы
(I - P(t))x0(t) = 0
(11)
(I - P(0))Π0x(τ)
(16)
P(0)Π0x(τ)
(17)
P(t)x0(t)
(22), (18)
4. Асимптотические решения высших порядков. Предположим, что члены xj(t) и
Πjx(τ) разложений (4), j = 0,n - 1, n ≥ 1, уже найдены. Определим xn(t) и Πnx(τ).
Из (5) при j = n получаем равенство
∑
1
dn-ixi(t)
A(t)xn(t) =
- fn-1(t),
(n - i)! dtn-i
i=0
где правая часть известна. Применив к этому уравнению оператор I - Q(t), имеем
)
(n-1∑
1
dn-ixi(t)
(I - Q(t))A(t)(I - P (t))xn(t) = (I - Q(t))
- fn-1(t)
(n - i)! dtn-i
i=0
Отсюда находим
)
(n-1∑
1
dn-ixi(t)
(I - P (t))xn(t) = A(t)+(I - Q(t))
- fn-1(t)
(24)
(n - i)! dtn-i
i=0
Тогда из (8) при j = n определяется начальное значение
(I - P (0))Πnx(0) = -(I - P (0))xn(0).
(25)
С обозначением
∑
τn-i dn-iB
Πζn-1(τ) =
(0)Πix(τ) + Πn-1f(τ)
(n - i)! dtn-i
i=0
уравнение (6) при j = n примет вид
Πnx(τ + 1) = B(0)Πnx(τ) + Πζn-1(τ).
Отметим, что Πζn-1(τ) → 0 при τ → +∞.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
ПРОЕКТОРНЫЙ ПОДХОД К ПОСТРОЕНИЮ АСИМПТОТИКИ РЕШЕНИЯ
79
Ввиду замечания 2 последнее уравнение эквивалентно двум уравнениям:
(I - P (0))Πnx(τ + 1)
B(0)(I - P (0))Πnx(τ) + (I - P (0))Πζn-1(τ),
(26)
P (0)Πnx(τ + 1) = P (0)Πnx(τ) + P (0)B(0)(I - P (0))Πnx(τ) + P (0)Πζn-1(τ).
(27)
Применяя лемму 2, получаем решение неоднородного линейного дискретного уравнения
(26) с заданным начальным условием (25), а именно,
∑
(I - P (0))Πnx(τ) = -B(0)τ (I - P (0))xn(0) +
B(0)τ-i-1(I - P (0))Πζn-1(i).
(28)
i=0
Из леммы 2 следует вид решения уравнения (27):
∑
P (0)Πnx(τ) = P (0)Πnx(0) + (P (0)B(0)(I - P (0))Πnx(i) + P (0)Πζn-1(i)).
i=0
Так как функция P (0)Πnx(τ) должна стремиться к нулю при τ → +∞, то из последнего
выражения получаем
∑
P (0)Πnx(0) = - (P (0)B(0)(I - P (0))Πnx(i) + P (0)Πζn-1(i)).
i=0
Следовательно,
∑
P (0)Πnx(τ) = - (P (0)B(0)(I - P (0))Πnx(i) + P (0)Πζn-1(i)).
(29)
i=τ
Итак, функция Πnx(τ) найдена. Тогда из (8) при j = n можно найти начальное значение
P (0)xn(0) = -P (0)Πnx(0).
(30)
Запишем условие разрешимости уравнения (5) при j = n + 1:
)
∑
1
dn+1-ixi(t)
Q(t)
- fn(t)
= 0.
(n + 1 - i)! dtn+1-i
i=0
Здесь fn(t) = fx(t)xn(t) + η(t), где fx(t) = fx(x0(t), t, 0), а η(t) - известная функция, зави-
сящая от xj (t) при j < n.
Учитывая, что (I - P (t))xn(t) уже известная функция, последнее уравнение можно запи-
сать в виде
d(P (t)xn(t))
Q(t)
= Q(t)(fx(t)P(t)xn(t) + ζ(t)),
dt
где
∑
1
dn+1-ixi(t)
d(I - P (t))xn(t)
ζ(t) = η(t) -
+ fx(t)(I - P(t))xn(t) -
(n + 1 - i)! dtn+1-i
dt
i=0
- известная функция.
Использовав тождества (20) и (21), последнее уравнение запишем следующим образом:
((
)
)
d(P (t)xn(t))
dP (t)
dP (t)
= (Q(t)P (t))-1Q(t) fx(t) -
P (t)xn(t) + ζ(t)
+
P (t)xn(t).
(31)
dt
dt
dt
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
80
КУРИНА, ХОАЙ
Сравнение (31) с (24) из [5] показывает, что, в отличие от приближения нулевого порядка,
уравнения для нахождения компоненты решения P (t)xn(t) при n ≥ 1 для рассматриваемой
здесь дискретной системы с малым шагом и сингулярно возмущённой системы дифференци-
альных уравнений из [5] различны. Заметим, что в [5] имеется опечатка, а именно, как следует
из предшествующего (24) уравнения, первый знак плюс в правой части уравнения (24) нужно
заменить на минус.
Функция P (t)xn(t) будет определяться однозначно из линейного дифференциального урав-
нения (31) с начальным условием (30).
Таким образом, функция xn(t) найдена. Следовательно, найдена асимптотика n-го поряд-
ка решения задачи (1), (2) (табл. 2).
Таблица 2. Последовательность нахождения
членов асимптотики n-го порядка, n ≥ 1
Члены асимптотики
Формулы
(I - P(t))xn(t)
(24)
(I - P(0))Πnx(τ)
(28)
P(0)Πnx(τ)
(29)
P(t)xn(t)
(31), (30)
Итак, доказана
Теорема. При выполнении условий I-III существуют явные представления для задач,
выраженные через ортогональные проекторы на Ker (B(t) - I) и Ker (B(t)′ - I), из которых
однозначно определяются члены асимптотического решения задачи (1), (2) вида (3), (4) лю-
бого порядка. При этом члены асимптотики находятся в следующей последовательности:
(I - P (t))xj(t), (I - P (0))Πj x(τ), P (0)Πj x(τ), P (t)xj(t), j ≥ 0.
5. Иллюстративный пример. Рассмотрим систему вида (1)
(
)
(
)(
)
(
)
x1(t + ε)
3/2
-1/2
x1(t)
x2(t) + t
=
+ε
,
t = 0,ε,2ε,... (t ≤ 0.3),
(32)
x2(t + ε)
1
0
x2(t)
0
с начальным условием
(
)
(
)
x1(0)
1
=
(33)
x2(0)
-1
5.1.Точное решение. Найдём решение задачи (32), (33).
Из второго уравнения в системе (32) следует, что x2(t) = x1(t - ε). Подставив это выра-
жение для x2(t) в первое уравнение системы (32), получим
x1(t + ε) = 3/2x1(t) - (1/2 - ε)x1(t - ε) + εt.
(34)
Из (32) и (33) имеем два условия для переменной x1 :
x1(0) = 1, x1(ε) = 2 - ε.
(35)
Так как t = εk, k = 0, 1, 2, . . . , то из (34), (35) получаем для y(k) = x1(εk) начальную
задачу для дискретного неоднородного уравнения второго порядка с постоянными коэффици-
ентами
y(k + 1) = 3/2y(k) - (1/2 - ε)y(k - 1) + ε2k, y(0) = 1, y(1) = 2 - ε.
Стандартным методом находим общее решение последнего уравнения
y(k) = x1(εk) = c1λk1 + c2λk2 - εk - 1/2 - ε,
где λ1 = (3 +
√1 + 16ε)/4 и λ2 = (3 -√1 + 16ε)/4 являются корнями характеристического
уравнения, а -(εk + 1/2 + ε) - частным решением неоднородного уравнения.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
ПРОЕКТОРНЫЙ ПОДХОД К ПОСТРОЕНИЮ АСИМПТОТИКИ РЕШЕНИЯ
81
Используя значения y(0) и y(1), получаем
5 + 2ε - (3 + 2ε)λ2
3
c1 =
,
c2 =
+ε-c1.
√1 + 16ε
2
5.2. Проекторы и вспомогательные операторы. В этом примере
(
)
(
)
3/2
-1/2
1/2
-1/2
B=
,
A=B-I =
,
1
0
1
-1
(
)
(
)(
)
(
)
(
)
x2(t) + t
0
1
x1(t)
t
1
f (x(t), t, ε) =
=
+
,
x0 =
0
0
0
x2(t)
0
-1
Поскольку матрица B постоянная, будем опускать аргумент t в обозначениях матриц, их
собственных векторов и проекторов.
Собственные значения матрицы B равны 1 и 0.5, Ker A = {(a, a)′}, V = (1, 1)′, Ker A′ =
= {(-2a, a)′}, S = (-2, 1)′, Im A = {(a, 2a)′}, Im A′ = {(a, -a)′}, где a - любое действитель-
ное число, и согласно формулам для ортогональных проекторов из п. 2 имеем
(
)
(
)
(
)
(
)
1/2
1/2
4/5
-2/5
1/2
-1/2
1/5
2/5
P =
,
Q=
,
I-P =
,
I-Q=
1/2
1/2
-2/5
1/5
-1/2
1/2
2/5
4/5
Оператор
(
)
-1/4
1/4
′
A = (I - P)A(I - P) =
: Im A′ → ImA
1/4
-1/4
имеет отрицательное собственное значение, равное -1/2.
Оператор
(
)
1/4
-1/4
′
B = (I - P)B(I - P) =
: Im A′ → Im A
-1/4
1/4
имеет собственное значение 1/2, модуль которого меньше 1.
Также получаем
(
)
(
)
-1
1
1/2τ+1
-1/2τ+1
A+ =
: Im A → ImA′,
Bτ =
,
τ ≥ 1,
1
-1
-1/2τ+1
1/2τ+1
(
)
(
)
1
1/5
1/5
(I - P )x0 =
,
QP =
: Ker A → Ker A′,
-1
-1/10
-1/10
(
)
(
)
5/2
0
5/4
-1/4
(QP )-1 =
: KerA′ → Ker A, PB =
,
5/2
0
5/4
-1/4
(
)
3/4
-3/4
PB(I - P) =
: Im A′ → Ker A.
3/4
-3/4
5.3. Асимптотика нулевого порядка. Из (11) имеем
x10(t) - x20(t) = 0.
(36)
Из (16) и (17) с учётом выражений из п. 5.2 получаем, что
(
)
(
)
τ
1/2
-3/2τ
(I - P )Π0x(τ) =
и PΠ0x(τ) =
-1/2τ
-3/2τ
Значит,
(
)
τ-1
-1/2
Π0x(τ) =
-1/2τ-2
6
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
82
КУРИНА, ХОАЙ
Из (18) следует равенство
(
)
3
Px0(0) =
,
3
т.е.
x10(0) + x20(0) = 6.
(37)
Из (23) получаем уравнение
d
(x10(t) + x20(t)) = 2(x10(t) + x20(t)) + 4t.
(38)
dt
Решение задачи (38), (37) определяется по формуле
x10(t) + x20(t) = 7e2t - 2t - 1,
отсюда и из (36) имеем
7
1
x10(t) = x20(t) =
e2t - t -
2
2
Таким образом, получено асимптотическое приближение нулевого порядка решения задачи
(32), (33)
(
)
1-t/ε
7e2t/2 - t - 1/2 - 2
x0(t,ε) =
,
t = kε, k = 0,1,2,...
7e2t/2 - t - 1/2 - 22-t/ε
5.4. Асимптотика первого порядка. Из (24) при n = 1 имеем равенство
x11(t) - x21(t) = 7e2t - 1.
(39)
Поскольку Πζ0(τ) = Π0f(τ),
(
)
(
)
Π20x(τ)
-1/2τ-2
Π0f(τ) = f(x0(0) + Π0x(τ),0,0) - f(x0(0),0,0) =
=
,
0
0
то из (28) при n = 1 с учётом (39) и выражений из п. 5.2 получаем
(
)
τ-2
-3/2τ - τ/2
(I - P )Π1x(τ) =
3/2τ + τ/2τ-2
Из (29) при n = 1 находим
(
)
(
∑∞
)
∑
(13 + 12i)/2i+1
13/2τ + 6
i/2i
∑
i=τ
PΠ1x(τ) =
=
∞
(13 + 12i)/2i+1
13/2τ + 6
i/2i
i=τ
i=τ
Для вычисления последнего ряда понадобится
Лемма 4. Имеет место равенство
∑i
τ+1
=
2i
2τ-1
i=τ
∑∞
Доказательство. Сначала найдём сумму ряда
ixi при x ∈ (-1, 1). Представим
∑∞
∑∞
i=1
∑∞
этот ряд в виде
(i + 1)xi -
xi. Введём обозначение S(x) =
(i + 1)xi. После
i=1
i=1
i=1
интегрирования имеем
x
∫
∑
∑
x2
S(t) dt =
xi+1 = x2
xi =
,
1-x
i=1
i=0
0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
ПРОЕКТОРНЫЙ ПОДХОД К ПОСТРОЕНИЮ АСИМПТОТИКИ РЕШЕНИЯ
83
отсюда получаем
(
)
2
d
x
2x - x2
S(x) =
=
dt
1-x
(1 - x)2
∑∞
∑∞
Значит,
ixi = (2x - x2)/(1 - x)2 - x/(1 - x) = x/(1 - x)2 и
i/2i = 2.
i=1
i=1
Следовательно, сумма рассматриваемого ряда при τ = 1 вычисляется по доказываемой
формуле. Справедливость этой формулы при всех τ легко доказывается методом математи-
ческой индукции.
Использование этой леммы для вычисления ряда в выражении для P Π1x(τ) даёт
(
)
τ
(25 + 12τ)/2
PΠ1x(τ) =
(25 + 12τ)/2τ
Следовательно,
(
)
τ-1
(11 + 4τ)/2
Π1x(τ) =
(7 + 4τ)/2τ-2
Используя (30) при n = 1, получаем
x11(0) + x21(0) = -50.
(40)
Уравнение (31) при n = 1 имеет вид
(
)
d
d
1d2x0
Px1 = (QP)-1Q fx(t)Px1 + fx(t)(I - P)x1 + fε(t) -
(I - P )x1 -
dt
dt
2 dt2
С учётом найденных значений запишем равенство для одной компоненты последнего
уравнения
d
(x11 + x21) = 2(x11 + x21) - 70e2t + 2.
(41)
dt
Решение задачи (41), (40) определяется по формуле
x11(t) + x21(t) = -49e2t - 70te2t - 1.
Из последнего соотношения и равенства (39) получаем
x11(t) = -(21 + 35t)e2t - 1, x21(t) = -(28 + 35t)e2t.
Таким образом, получено асимптотическое приближение первого порядка решения задачи
(32), (33):
(
)
1-t/ε
-(21 + 35t)e2t - 1 + (11 + 4t/ε)2
x1(t,ε) = x0(t,ε) + ε
,
t = kε, k = 0,1,2,...
-(28 + 35t)e2t + (7 + 4t/ε)22-t/ε
Если разложить точное решение x(kε) в ряд по целым неотрицательным степеням ε, то
получим совпадение членов, не зависящих от ε и порядка ε в этом разложении, с соответ-
ствующими членами в x1(kε, ε) и x2(kε, ε).
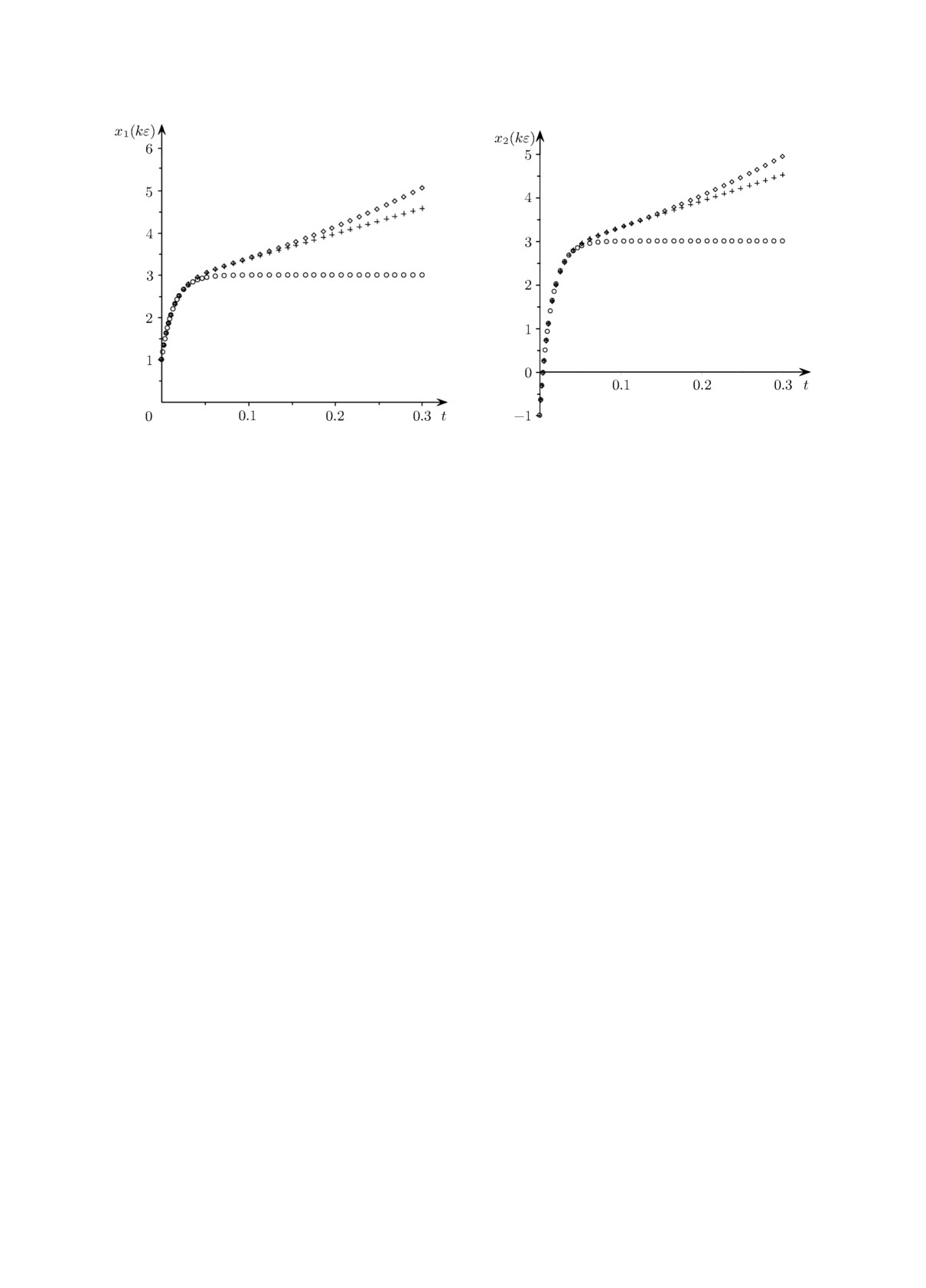
Графики точного и приближённых решений для задачи (32), (33) при ε = 0.01 представ-
лены на рис. 1 и 2.
Заключение. В статье предложен новый подход к построению асимптотики решения на-
чальных задач для слабо нелинейных дискретных систем с малым шагом в критическом случае
с использованием ортогональных проекторов. Такой подход помогает понять суть алгоритма
А.Б. Васильевой и В.Ф. Бутузова из работы [1] и получить в явном виде задачи для нахожде-
ния асимптотики решения любого порядка.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023
6∗
84
КУРИНА, ХОАЙ
Рис. 1. Точное решение
(⋄) и приближённые
Рис. 2. Точное решение (⋄) и приближённые
решения нулевого (◦) и первого (+) порядков
решения нулевого (◦) и первого (+) порядков
для x1(kε).
для x2(kε).
Авторы выражают глубокую благодарность О.Б. Цехан за полезные обсуждения.
Работа первого автора выполнена при поддержке Российского научного фонда (проект
21-11-00202). Работа второго автора поддержана Научным университетом Вьетнамского наци-
онального университета, г. Ханой (проект TN.22.01).
СПИСОК ЛИТЕРАТУРЫ
1. Бутузов В.Ф., Васильева А.Б. Дифференциальные и разностные системы уравнений с малым па-
раметром в случае, когда невозмущённая (вырожденная) система расположена на спектре // Диф-
ференц. уравнения. 1970. T. 6. № 4. С. 650-664.
2. Васильева А.Б., Бутузов В.Ф. Сингулярно возмущенные уравнения в критических случаях. М.,
1978.
3. Kurina G.A., Dmitriev M.G., Naidu D.S. Discrete singularly perturbed control problems (a survey)
// Dyn. Contin. Discrete Impuls. Syst. Ser. B: Appl. Algorithms. 2017. V. 24. P. 335-370.
4. Sibuya Y. Some global properties of matrices of functions of one variable // Math. Ann. 1965. V. 161.
P. 67-77.
5. Kurina G. Projector approach to constructing asymptotic solution of initial value problems for singularly
perturbed systems in critical case // Axioms. 2019. V. 8. № 2. P. 56-60.
6. Курина Г.А., Хоай Н.Т. Проекторный подход к алгоритму Бутузова-Нефедова асимптотического
решения одного класса сингулярно возмущённых задач в критическом случае // Журн. вычислит.
математики и мат. физики. 2020. Т. 60. № 12. С. 2073-2084.
7. Kurina G.A., Hoai N.T. Projector approach for constructing the zero order asymptotic solution for the
singularly perturbed linear-quadratic control problem in a critical case // AIP Conf. Proc. Int. Conf.
Analysis and Applied Mathematics (ICAAM 2018). 2018. V. 1997. P. 430-436.
8. Каto T. Perturbation Theory for Linear Operators. Berlin, Heidelberg, 1966.
9. Гайшун И.В. Системы с дискретным временем. Минск, 2001.
10. Horn R.A., Johnson C.R. Matrix Analysis. Cambridge, 2013.
Воронежский государственный университет,
Поступила в редакцию 24.08.2022 г.
Федеральный исследовательский центр
После доработки 02.10.2022 г.
“Информатика и управление” РАН, г. Москва,
Принята к публикации 21.10.2022 г.
Научный университет Вьетнамского
национального университета, г. Ханой
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№1
2023