ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 10, с. 1335-1356
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
УДК 517.957
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
ДЛЯ УРАВНЕНИЙ ОДНОМЕРНОЙ ИОНИЗАЦИИ
В СЛУЧАЕ ПОСТОЯННЫХ СКОРОСТЕЙ
АТОМОВ И ИОНОВ
© 2023 г. М. Б. Гавриков, А. А. Таюрский
Рассмотрены основные начально-краевые (смешанные) задачи для нелинейной системы
уравнений одномерной ионизации газа в случае постоянных скоростей атомов газа и воз-
никающих в результате ионизации ионов. Неизвестными в этой системе являются концен-
трации атомов и ионов. Найдена общая формула достаточно гладкого решения системы.
Показано, что смешанные задачи для системы уравнений одномерной ионизации допуска-
ют интеграцию в виде явных аналитических выражений. В случае смешанной задачи для
конечного отрезка аналитическое решение строится посредством рекуррентных формул,
каждая из которых определена в треугольнике, принадлежащем некоторой указанной в
работе триангуляции области определения неизвестных функций.
DOI: 10.31857/S0374064123100035, EDN: ONCTCE
Введение. В работе рассмотрено аналитическое решение основных начально-краевых за-
дач для системы уравнений одномерной ионизации [1, с. 304; 2]
∂na
∂vana
∂ni
∂vini
+
= -kInani,
+
=kInani,
(1)
∂t
∂z
∂t
∂z
где t ∈ R - время, z ∈ R - пространственная координата, na, ni - подлежащие нахождению
концентрации атомов и ионов, va, vi - заданные скорости движения атомов и ионов, kI > 0 -
известный коэффициент ионизации. Ниже система уравнений ионизации решается аналитиче-
ски в случае va = const, vi = const. Система (1) относится к полулинейным гиперболическим
системам [3, с. 17], а в случае va = const, vi = const она записана в инвариантах [3, с. 28]. При
vi = va = const характеристики системы (1) совпадают, и она легко по ним интегрируется
(см. п. 1). В случае vi = va характеристические векторы (1, va),
(1, vi) линейно независимы
и, разлагая вектор (t, z) по базису из характеристических векторов и принимая координа-
ты разложения за новые независимые переменные в (1), эта система, как показано в п. 1,
сводится к виду, когда в новых переменных дифференциальный оператор левой части (1) рас-
щепляется на два независимых оператора, что позволяет проинтегрировать систему уравнений
ионизации. Указанный приём позволяет решать и некоторые другие задачи, например, задачу
о поглощении (сорбции) газа поглощающим веществом [4, с. 165].
В п. 1 поставлены основные начально-краевые задачи для системы (1) в случае постоянных
скоростей в неограниченных областях переменной z и на отрезке [0, L], L > 0. Предложенное
в работе решение смешанных задач, основанное на формулах, выведенных в п. 1, намного про-
ще и принципиально отличается от известных приёмов решения преимущественно линейных
начально-краевых задач, базирующихся либо на методе Фурье, либо на применении преоб-
разования Лапласа к неизвестным функциям. На основе результатов, полученных в п. 1, в
пп. 2-4 дано аналитическое решение поставленных краевых задач в неограниченных областях
переменной z, а в п. 5 на их основе решена начально-краевая задача на отрезке [0, L]. Приве-
денные в пп. 2-5 формулы доказывают, в частности, существование и единственность решений
начально-краевых задач для системы (1). С другой стороны, они позволяют искать различные
асимптотики решений рассмотренных задач (например, при t → +∞ или при неограничен-
ном удалении от границы области ионизации). Однако в настоящей работе эти результаты не
рассматриваются.
1335
1336
ГАВРИКОВ, ТАЮРСКИЙ
Представляет значительный интерес обобщение предложенного в работе метода решения
системы (1) для постоянных скоростей va, vi на практически важный случай [5], когда va =
= const > 0, vi = vi(z) - заданная непрерывно дифференцируемая функция, имеющая по-
ложительную производную и единственный нуль внутри заданного отрезка [0, L] (обычно
полагают vi(z) = a(z - z0), a > 0, z0 ∈ (0, L) [6]). Начально-краевая задача для таких vi(z)
сводится к задаче Гурса [3, с. 96], когда краевые условия ставятся на характеристике z = z0
системы (1). Численное решение показывает [7, 8], что в этом случае система (1) допускает
периодические по времени решения, которые применительно к стационарному плазменному
двигателю [1, с. 316; 9; 10] длины L описывают низкочастотные ионизационные колебания,
наблюдаемые в эксперименте и называемые бривинг модами [11, 12]. Тем самым проведённые
в настоящей работе исследования являются первым важным шагом в математическом анализе
бривинг мод.
1. Решения уравнений ионизации в случае постоянных скоростей. Решим систему
(1) в случае, когда va = const, vi = const.
Рассмотрим основной случай va = vi. Проведём замену (t, z) ↔ (α, β) независимых пере-
менных:
(t, z) = α(1, va) + β(1, vi),
или в координатном виде
t = α + β, z = αva + βvi,
α = (tvi - z)(vi - va)-1, β = (z - tva)(vi - va)-1, (α,β) = φ(t,z).
(2)
Отсюда для дифференциальных операторов получим соотношения
∂
vi
∂
va
∂
∂
1
∂
1
∂
=
-
,
=-
+
∂t
vi - va ∂α
vi - va ∂β
∂z
vi - va ∂α
vi - va ∂β
Подставив эти выражения в систему (1), сведём её к эквивалентному виду
∂na
∂ni
= -kInani,
=kInani.
(3)
∂α
∂β
Итак, задача нахождения непрерывно дифференцируемых решений системы (1) в области
D переменных (t, z) равносильна задаче нахождения непрерывно дифференцируемых реше-
ний системы (3) в области φ(D) переменных (α, β). Отображение φ линейное, невырожден-
ное, с определителем det φ = 1/(vi - va) = 0. В частности, оно переводит прямые в прямые,
многоугольники - в многоугольники, выпуклые множества - в выпуклые множества и т.д. По-
строим сначала элементарную теорию решений системы (3) в прямоугольнике Π = [α0, α1] ×
× [β0, β1], α0 < α1, β0 < β1.
Теорема 1. 1. Пусть A(α), B(β) - дважды непрерывно дифференцируемые функции на
отрезках [α0,α1],
[β0, β1] соответственно, причём A(α) = B(β) для любых α ∈ [α0, α1],
β ∈ [β0,β1]. Тогда функции
B′(β)
A′(α)
=
,
=
(4)
kI(A(α) - B(β))
kI(A(α) - B(β))
составляют непрерывно дифференцируемое решение системы (3) в прямоугольнике Π.
2. Если непрерывно дифференцируемые решения na, ni систем (3) таковы, что множе-
ство нулей каждой из этих функций в Π имеет пустую внутренность и
A(α),
B(β) -
ещё пара функций на [α0, α1], [β0, β1] соответственно, удовлетворяющих условиям части 1
теоремы и восстанавливающих по формулам (4) те же самые функции na, ni в Π, то
найдутся константы R = 0 и C, для которых справедливы равенства
A(α) = RA(α) + C, α ∈ [α0, α1],
B(β) = RB(β) + C, β ∈ [β0, β1].
(5)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1337
Обратно, если функции
A(α),
B(β) вычисляются по A(α), B(β) посредством формул (5)
для некоторых констант R = 0 и C, то они удовлетворяют условиям части 1 теоремы и
по формулам (4) восстанавливают те же функции na, ni, что и для A(α), B(β).
3. В условиях части 1 теоремы функции na, ni, вычисляемые по формулам (4), удовле-
творяют всюду в Π неравенствам na ≥ 0, ni ≥ 0 тогда и только тогда, когда либо A(α),
B(β) монотонно не убывают на отрезках [α0, α1],
[β0, β1] соответственно и
inf
A(α) > sup B(β)
α∈[α0,α1]
β∈[β0,β1]
(что равносильно A(α0) > B(β1)), либо A(α), B(β) монотонно не возрастают соответ-
ственно на [α0,α1],
[β0, β1] и
sup
A(α) < inf B(β)
α∈[α0,α1]
β∈[β0,β1]
(что равносильно A(α0) < B(β1)).
Доказательство. Поскольку A(α) = B(β) для любых α ∈ [α0, α1], β ∈ [β0, β1], то
правые части равенств (4) определены корректно в Π и, очевидно, являются непрерывно
дифференцируемыми в прямоугольнике Π функциями. По правилам дифференцирования
находим
∂na
B′(β)A′(α)
∂ni
A′(α)B′(β)
=-
,
=
∂α
kI(A(α) - B(β))2
∂β
kI(A(α) - B(β))2
Отсюда и из (4) следует тождественная справедливость равенств (3).
2. Пусть
A(α),
B(β) - ещё пара функций, удовлетворяющих части 1 теоремы. Тогда всюду
в Π выполнены тождества
B′(β)k-1I(A(α) - B(β))-1 = na(α,β) =B′(β)k-1I
A(α) -B(β))-1,
A′(α)k-1I(A(α) - B(β))-1 = ni(α,β)
A′(α)k-1I
A(α) -B(β))-1.
(6)
Обозначим
=
A(α) -B(β))(A(α) - B(β))-1.
Тогда функция R непрерывна и отлична от нуля всюду в Π и
B′(β) = B′(β)R(α,β),
A′(α) =
= A′(α)R(α,β) для всех (α,β) ∈ Π. Отсюда следует, что множества нулей функций
B′(β) и
B′(β) совпадают и, по условию, имеют пустую внутренность. Аналогично множества нулей
функций
A′(α) и A′(α) совпадают и имеют пустую внутренность. Кроме того, указанные
множества замкнуты и нигде не плотны в соответствующих отрезках [β0, β1] и [α1, α1]. Пусть
U ⊆ [β0,β1], V ⊆ [α0,α1] - дополнения указанных множеств, тогда
U= [β0,β1],
V = [α0,α1],
и для любой точки (α, β) ∈ V × U имеем
B′(β)/B′(β) = R(α,β)
A′(α)/A′(α) ⇒ R(α,β) ≡ R = const на V × U.
Поскольку R - непрерывная функция и V × U
V ×U = Π, то R(α,β) ≡ R всюду в Π.
Но тогда (B(β) - RB(β))′ = 0,
A(α) - RA(α))′ = 0 и, значит, найдутся константы C и D,
для которых
B(β) - RB(β) ≡ C,
A(α) - RA(α) ≡ D всюду на отрезках [β0, β1],
[α1, α1]
соответственно. Подставляя равенства
B = RB +C,
A = RA + D в соотношения (6) и
учитывая R = 0, получаем
B′(β)(D - C)/R = B′(β), A′(α)(D - C)/R = A′(α).
Поскольку по условию A′(α) и B′(β) не равны тождественно нулю, то D - C = 0, что
доказывает прямое утверждение. Обратное утверждение очевидно.
3. Пусть na ≥ 0, ni ≥ 0 в Π и выполнены условия части 1 теоремы, в частности, имеют
место равенства (4). Из непрерывности ненулевой функции двух переменных A(α) - B(β) в
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1338
ГАВРИКОВ, ТАЮРСКИЙ
Π и связности Π следует, что либо A(α)-B(β) > 0 всюду в Π, либо A(α)-B(β) < 0 всюду
в Π. Поэтому из равенств (4) вытекает, что либо A(α) - B(β) > 0 всюду в Π и A′(α) ≥ 0,
B′(β) ≥ 0 всюду на [α0,α1],
[β0, β1] соответственно, либо A(α) - B(β) < 0 всюду в Π и
A′(α) ≤ 0, B′(β) ≤ 0 всюду на [α0,α1], [β0, β1] соответственно. В первом случае функции
A(α), B(β) монотонно не убывают в своих областях определения и inf A(α) > sup B(β).
Во втором случае A(α), B(β) монотонно не возрастают в своих областях определения и
supA(α) < inf B(β), где инфимум и супремум по α берутся на отрезке [α0,α1], а по β - на
[β0, β1]. Остальные утверждения очевидны. Теорема доказана.
Если A(α), B(β) удовлетворяют условиям части 1 теоремы 1, то na, ni, вычисляемые
по формулам (4), непрерывно дифференцируемы в Π и существуют непрерывные в Π сме-
шанные производные ∂2na/(∂α ∂β), ∂2na/(∂β ∂α) и ∂2ni/(∂α ∂β), ∂2ni/(∂β ∂α). Это обсто-
ятельство позволяет сформулировать обратное утверждение.
Теорема 2. Пусть na > 0, ni > 0 - непрерывно дифференцируемое решение (3) в прямо-
угольнике Π, для которого существуют непрерывные в Π смешанные частные производные
∂2na/(∂α ∂β),
∂2na/(∂β ∂α) и ∂2ni/(∂α ∂β),
∂2ni/(∂β ∂α). Тогда найдутся дважды непре-
рывно дифференцируемые функции A(α), B(β), определённые на сторонах прямоугольника,
соответственно, [α0,α1] и [β,β1], для которых A(α) = B(β) при всех α ∈ [α0,α1], β ∈
∈ [β0, β1], и всюду в Π выполнены равенства (4).
Замечание. Таким образом, для класса положительных непрерывно дифференцируемых
решений системы (3), для которых в Π существуют обе непрерывные смешанные частные
производные, формулы (4) задают общий вид решений этого класса.
Доказательство теоремы 2. Пусть X = ln na, Y
= ln ni. Очевидно, что функции
X(α, β), Y (α, β) непрерывно дифференцируемые в Π и существуют в Π непрерывные сме-
шанные частные производные ∂2X/(∂α ∂β), ∂2X/(∂β ∂α) и ∂2Y/(∂α ∂β), ∂2Y/(∂β ∂α). От-
носительно неизвестных X, Y система (3) записывается в виде
∂X
∂Y
= -kIeY ,
= kIeX, (α,β) ∈ Π.
∂α
∂β
Отсюда следуют равенства
∂2X
∂eY
∂Y
∂2Y
∂eX
∂X
= -kI
= -kIeY
= -k2IeX+Y ,
=kI
=kIeX
= -k2IeX+Y .
∂β ∂α
∂β
∂β
∂α ∂β
∂α
∂α
По теореме Шварца ∂2Y/(∂α ∂β) = ∂2Y/(∂β ∂α), поэтому из проведённых вычислений сле-
дует тождество ∂2(X - Y )/(∂β ∂α) ≡ 0 всюду в Π. Отсюда элементарным интегрированием
получается, что ∂(X - Y )/∂α = a0(α) - непрерывная на [α0, α1] функция и, значит, X - Y =
∫
∫
=
=
a0(α)dα, очевидно, непрерывно дифференцируема,
и тогда из равенства X - Y = a(α) + b(β) следует непрерывная дифференцируемость b(β)
на отрезке [β0, β1]. Итак, X - Y = a(α) + b(β) и na/ni = ea(α)eb(β) = C(α)D(β), где C(α),
D(β) - положительные непрерывно дифференцируемые функции соответственно на [α0, α1]
и [β0, β1].
Подставив выражение na = niC(α)D(β) в первое уравнение системы (3), получим соотно-
шение
∂(niC(α))
= -kIn2i C(α)D(β),
∂αD(β)
равносильное равенству
n-2i∂ni
+ C′(α)C-1(α)n-1i = -kI.
∂α
Пусть Z = 1/ni, тогда относительно Z получается линейное обыкновенное дифференци-
альное уравнение первого порядка
∂Z
- C′(α)C-1(α)Z = kI.
(7)
∂α
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1339
Решим уравнение (7) при каждом фиксированном β ∈ [β0, β1] на отрезке [α0, α1] методом
вариации произвольной постоянной. Однородное уравнение имеет решение
Zодн = Γ(β)C(α).
Варьируя по α произвольную постоянную Γ(β), получаем
∂Γ
C(α) = kI ,
∂α
откуда
∫
Γ(α, β) = kI C-1(α) dα + kI K(β),
=
∫
def=
= -K(β). Из равенства Z = Γ(α,β)C(α) вытекает положительность и
непрерывная дифференцируемость Γ(α, β) в Π. Из равенства Γ(α, β) = kI (A(α) - B(β)) и
двукратной непрерывной дифференцируемости A(α) следует непрерывная дифференцируе-
мость функции B(β). Из положительности Γ(α, β) всюду в Π вытекает A(α) = B(β) для
любых α ∈ [α0, α1], [β0, β1]. Наконец, из равенства A′(α) = 1/C(α) следует тождество
ni = Z-1 = Γ-1(α,β)C-1(α) = A′(α)k-1I(A(α) - B(β))-1,
(8)
совпадающее со вторым равенством (4). Чтобы получить первое равенство (4) и установить
двукратную непрерывную дифференцируемость функции B(β) на [β0, β1], подставим соот-
ношение (8) во второе уравнение системы (3):
A′(α)B′(β)
(A′(α))2
=kI
C(α)D(β),
kI(A(α) - B(β))2
k2I(A(α) - B(β))2
где было использовано равенство na = niC(α)D(β). Учитывая тождества A′(α)C(α) = 1 и
A′(α) > 0, получаем B′(β) = D(β). Значит, функция B(β) дважды непрерывно дифферен-
цируема по β. Кроме того, с учётом (8) имеем
A′(α)C(α)D(β)
B′(β)
na = niC(α)D(β) =
=
,
kI(A(α) - B(β))
kI(A(α) - B(β))
что совпадает с первым равенством (4). Итак, мы указали функции A(α), B(β), удовлетво-
ряющие условиям 1 теоремы 1, для которых выполнены равенства (4). Теорема доказана.
Из части 2 теоремы 1 следует, что в формулах (4) всегда можно считать A(α), B(β) мо-
нотонно неубывающими функциями на [α0, α1], [β0, β1] соответственно. Кроме того, стороны
прямоугольника Π могут быть интервалами или полуинтервалами, в том числе полубеско-
нечными или бесконечными. Соответствующие изменения формулировки части 3 теоремы 1
очевидны.
Из теорем 1, 2 следует, что в φ-1(Π) решение системы (1) задаётся формулами
B′(β)
A′(β)
tvi - z
z - tva
na(t,z) =
,
ni(t,z) =
,
α=
,
β=
,
(9)
kI(A(α) - B(β))
kI(A(α) - B(β))
vi - va
vi - va
где A(α), B(β) - произвольные функции, удовлетворяющие части 1 теоремы 1.
Доказательство теоремы 2 очевидным образом обобщается на случай, когда Π ⊆ R2 =
= {(α, β)} - замкнутое выпуклое множество с непустой внутренностью Int Π, причём Π =
= IntΠ, где черта означает замыкание множества. Тогда Π ⊆ [a0,α1] × [β0,β1], где [α0,α1] -
проекция Π на ось α, а [β0, β1] - на ось β (какие-то из величин α0, α1, β0, β1 при этом
могут быть бесконечными). В этом случае справедливость теоремы 2 (называемой ниже обоб-
щённой) вытекает из следующей легко проверяемой леммы.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1340
ГАВРИКОВ, ТАЮРСКИЙ
Лемма. Пусть Iλ = (aλ, bλ), aλ < bλ, λ ∈ Λ, - непустое семейство интервалов и
φλ(α) - непрерывно дифференцируемые функции на Iλ, причём для любых λ1 = λ2 имеем
⋂
φλ1 |Iλ
⋂Iλ
= φλ2|Iλ
Iλ2
+ const. Тогда найдётся непрерывно дифференцируемая функция
1
2
1
⋃
φ(α), заданная на открытом множестве I =λ∈Λ Iλ, для которой φ|Iλ = φλ + const для
всех λ ∈ Λ, где const зависит от λ.
Ниже в качестве Π рассматривается либо замкнутая полуплоскость, граница которой непа-
раллельна осям координат (пп. 2, 3), либо замкнутый тупой угол, ограниченный двумя луча-
ми, исходящими из начала координат (п. 4), либо замкнутая полуполоса, ограниченная двумя
параллельными прямыми (п. 5).
Формулы (9) справедливы для vi = va, при vi = va они теряют смысл. Для vi = va =
= v общее решение системы (1) получается напрямую, без введения новых координат α и
β, интегрированием уравнений этой системы вдоль характеристик. Характеристики системы
(1) имеют вид z(t) = vt + const и различаются значениями const. Пусть na(t) = na(t, z(t)),
ni(t) = ni(t,z(t)) - значения неизвестных функций na, ni вдоль фиксированной характери-
стики. Тогда из (1) следует, что функции na(t), ni(t) удовлетворяют системе обыкновенных
дифференциальных уравнений (ОДУ)
dna
dni
= -kInani,
=kInani.
(10)
dt
dt
Складывая почленно эти уравнения, получаем первый интеграл системы (10): d(na + ni)/dt ≡
≡ 0, откуда следует na + ni ≡ C = const. Поскольку na ≥ 0, ni ≥ 0, то C ≥ 0. При C = 0
имеем na(t) ≡ 0, ni(t) ≡ 0 - тривиальное решение системы (10), не имеющее смысла. Поэтому
ниже считаем C > 0. Тогда na = C - ni, и для нахождения ni имеем ОДУ
dni
= kIni(C - ni).
(11)
dt
Проинтегрировав, получим
∫
dni
= kIt + const,
ni(C - ni)
откуда
1
ni
ln
kIt + const.
=
C
C-ni
Поскольку ni ≥ 0, na = C - ni ≥ 0, то 0 ≤ ni ≤ C, и в последнем равенстве знак модуля
можно снять. В результате имеем
CDexp(CkIt)
C
ni =
,
na = C - ni =
,
D ≥ 0, C > 0.
(12)
1 + Dexp(CkIt)
1 + Dexp(CkIt)
В случае D = 0 получим одно из двух особых решений уравнения (11): ni ≡ 0. Другое
особое решение: ni ≡ C. Формулы (12) задают общее решение системы (10) на произвольной
характеристике. Константы C и D определяются значениями na, ni в произвольной точке
на рассматриваемой характеристике. В частности, при решении начально-краевых задач для
системы (1) значения C и D определяются начальными и граничными условиями (см. ниже).
Применим формулы (9), (12) для решения начально-краевых задач для системы (1), кото-
рые представляют основной практический интерес. Ограничимся следующими простейшими
задачами.
(I) Начальная задача (задача Коши). В полуплоскости z ∈ R, t ≥ 0 найти непре-
рывно дифференцируемое решение системы (1), для которого выполнены начальные условия
na(0,z) = n0a(z), ni(0,z) = n0i(z), z ∈ R, где n0a(z), n0i(z) - заданные неотрицательные непре-
рывно дифференцируемые функции на прямой.
(II) Краевая задача. Для va, vi ≥ 0 в полуплоскости z ≥ 0, t ∈ R найти непрерывно
дифференцируемое решение системы (1), для которого выполнены краевые условия na(t, 0) =
= na0(t), ni(t,0) = ni0(t), t ∈ R, где na0(t), ni0(t) - заданные неотрицательные непрерывно
дифференцируемые функции на прямой.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1341
(III) Начально-краевая (смешанная) задача. Для va, vi ≥ 0 в первом квадранте
z ≥ 0, t ≥ 0 найти непрерывно дифференцируемое решение системы (1), для которого вы-
полнены начальные условия na(0, z) = n0a(z), ni(0, z) = n0i(z), z ≥ 0, и краевые условия
na(t,0) = na0(t), ni(t,0) = ni0(t), t ≥ 0, где n0a(z), n0i(z), z ≥ 0, na0(t), ni0(t), t ≥ 0, -
заданные непрерывно дифференцируемые функции на полупрямых z ≥ 0 и t ≥ 0, подчиня-
ющиеся условиям согласования
na0(0) = n0a(0), ni0(0) = n0i(0), n′a0(0) + va(n0a)′(0) + kIna0(0)ni0(0) = 0,
n′i0(0) + vi(n0i)′(0) - kIna0(0)ni0(0) = 0.
(IV) Смешанная задача на отрезке. Для va > 0 > vi в полуполосе 0 ≤ z ≤ L,
t ≥ 0 найти непрерывно дифференцируемое решение системы (1), удовлетворяющее гранич-
ным условиям na(t, 0) = na0(t), ni(t, L) = ni0(t), t ≥ 0, и начальным условиям na(0, z) =
= n0a(z), ni(0,z) = n0i(z), 0 ≤ z ≤ L, где na0(t), ni0(t), t ≥ 0, n0a(z), n0i(z), 0 ≤ z ≤ L, -
заданные непрерывно дифференцируемые функции, удовлетворяющие условиям согласования
na0(0) = n0a(0), ni0(0) = n0i(L),
n′a0(0) + va(n0a)′(0) + kIn0a(0)n0i(0) = 0, n′i0(0) + vi(n0i)′(L) - kIn0a(L)n0i(L) = 0.
Более сложные начально-краевые задачи в этой работе не рассматриваются.
Сначала исследуем случай vi = va = v.
Задача Коши (I). Решим её методом характеристик. Пусть точка (z, t) лежит в полу-
плоскости t ≥ 0, z ∈ R. Через эту точку проходит единственная характеристика (vs+const, s)
для значения const = z -vt, и она имеет вид (z +v(s-t), s). На этой характеристике решение
системы (1) задаётся формулами (12), в которых t нужно заменить на s. С другой стороны,
эта характеристика пересекает ось z при s = 0 в единственной точке z - vt, где известны
значения n0a(z - vt) и n0i(z - vt). Поэтому в формулах (12) с s вместо t константы C и D
находятся из условий na(0) = n0a(z - vt), ni(0) = n0i(z - vt). В результате получаем
C = n0a(z - vt) + n0i (z - vt), D = n0i (z - vt)/n0a(z - vt),
C(y)D(y) exp(C(y)kI t)
C(y)
ni(z,t) =
,
na(z,t) =
,
y = z - vt.
1 + D(y)exp(C(y)kIt)
1 + D(y)exp(C(y)kIt)
Нетрудно прямой подстановкой в (3) убедиться в том, что полученные формулы задают ре-
шение задачи Коши в классе непрерывно дифференцируемых функций.
Краевая задача (II). Единственная характеристика, проходящая через точку (z, t) по-
луплоскости z ≥ 0, пересекает ось t в точке s = t - z/v, являющейся решением уравнения
z + v(s - t) = 0, где известны значения na и ni. Поэтому при вычислении констант C и D
из формулы (12) с s вместо t нужно в этих формулах положить s = t - z/v и вычислять
правые части (12) по формулам ni = ni0(t - z/v), na = na0(t - z/v). В итоге получим
ni0(t - z/v)
C = na0(t - z/v) + ni0(t - z/v), D =
exp(-CkI (t - z/v)),
na0(t - z/v)
C(y)D(y) exp(C(y)kI t)
C(y)
ni(z,t) =
,
na(z,t) =
,
y = t - z/v.
1 + D(y)exp(C(y)kIt)
1 + D(y)exp(C(y)kIt)
Нетрудно прямой подстановкой в (3) проверить, что полученные формулы задают решение
краевой задачи (II) в классе непрерывно дифференцируемых функций.
Смешанная задача (III). Пусть z ≥ 0, t ≥ 0. Единственная характеристика, проходя-
щая через точку (z, t) при z < tv, пересекает полуось t ≥ 0 в точке s = t - z/v, где na, ni
известны и задаются краевыми условиями, но не пересекают полуось z ≥ 0. При z > tv эта
характеристика пересекает полуось z ≥ 0 в точке z - vt, где na, ni известны и задаются на-
чальными условиями, но не пересекают полуось t ≥ 0. При z = tv указанная характеристика
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1342
ГАВРИКОВ, ТАЮРСКИЙ
пересекает обе полуоси z ≥ 0 и t ≥ 0 в нулевых точках, где начальные и краевые условия
совпадают. Поэтому константы C = C(y), D = D(y) и функции ni(z, t), na(z, t) находятся
по формулам
{
n0a(z - vt) + n0i(z - vt),
z ≥ tv,
C(y) =
na0(t - zv-1) + ni0(t - zv-1),
z ≤ tv,
⎧
⎪n0i(z - vt)
{
⎨
,
z ≥ tv,
n0a(z - tv)
z - vt,
z ≥ tv,
D(y) =
y=
⎪
ni0(t - zv-1)
t-zv-1,
z ≤ tv.
⎩
exp(-CkI (t - z/v)), z ≤ tv,
na0(t - zv-1)
Условия согласования в нуле гарантируют, что функции C(z, t), D(z, t) будут непрерывны
и непрерывно дифференцируемы в первом квадранте.
В случае v = 0 краевая и смешанная задачи теряют смысл, ионизация в различных точках
пространства происходит независимо и определяется только временем. Формулы для na и ni
получаются из приведённых выше формул решения задачи Коши (I), если в них положить
v = 0. Если v ≤ 0, то краевая задача ставится в полуплоскости z ≤ 0, t ∈ R, а смешанная
задача - во втором квадранте z ≤ 0, t ≥ 0.
2. Решение задачи Коши (I). Рассмотрим задачу Коши (I) в случае va = vi. В пере-
менных (α, β) задача состоит в поиске непрерывно дифференцируемого решения системы (3)
= {α + β ≥ 0}, которое на границе α + β = 0 этой полуплоскости имеет
заданные значения
na(α,β) = na(-β,β) = n0a(αva + βvi) = n0a(β(vi - va)), α + β = 0,
ni(α,β) = ni(-β,β) = n0i(αva + βvi) = n0i(β(vi - va)) α + β = 0.
Выше был изложен способ решения системы (3) в произвольном прямоугольнике Π. Построим
решение системы (3) в бесконечном прямоугольнике Π∞ = R × R ⊇ P, которое на прямой α +
+β = 0 совпадает с заданными функциями,
na|α+β=0 = n0a(β(vi - va)), ni|α+β=0 = n0i(β(vi - va)).
Если такое решение существует, то его сужение на P даёт, очевидно, искомое решение за-
дачи Коши в переменных (α, β). Согласно теореме 1 решение системы (3) в прямоугольнике
Π∞ определяется двумя дважды непрерывно дифференцируемыми функциями A(α), B(β),
α, β ∈ R, и вычисляется по этим функциям посредством формул (4). При этом, согласно
теореме 1, A(α), B(β) должны удовлетворять двум условиям:
1) области значений функций A(α), B(β) не пересекаются: A(R)
⋂B(R) = ∅, и тогда,
учитывая связность прямой R, либо A(R) < B(R), либо B(R) < A(R),
2) если A(R) < B(R), то A(α), B(β) - монотонно невозрастающие на R функции, если
B(R) < A(R), то A(α), B(β) - монотонно неубывающие на R функции.
Функции A(α), B(β) определяются по известным значениям na и ni на прямой α+β = 0
(т.е. из начальных условий). Из тождеств (4) получим
n0a(β(vi - va)) = na(-β,β) = B′(β)k-1I(A(-β) - B(β))-1,
n0i(β(vi - va)) = ni(-β,β) = A′(-β)k-1I(A(-β) - B(β))-1, β ∈ R.
(13)
Обозначим na(β) = kI n0a(β(vi - va)), ni(β) = kI n0i(β(vi - va)), A0(β) = A(-β). Тогда na и
ni - неотрицательные функции, а условия (13) дают линейную систему ОДУ с переменными
коэффициентами для нахождения функций A0(β), B(β) на прямой R:
B′ = na(β)(A0 - B), A′0 = -ni(β)(A0 - B).
(14)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1343
Поскольку na(β), ni(β) непрерывно дифференцируемы по β, то любое решение системы (14)
дважды непрерывно дифференцируемо всюду на прямой. Кроме того, для любых C, D ∈ R
существует, и притом единственное, решение системы (14), для которого A0(0) = C, B(0) =
= D. Если C = D, то из теоремы единственности для системы (14) следует, что решение с
такими начальными условиями: A0(β) ≡ C, B(β) ≡ D. Поэтому далее считается, что C = D.
Из теоремы единственности решения задачи Коши для системы (14) следует, что решение (14)
с начальными условиями A0(0) = C, B(0) = D имеет вид
β
∫
B(β) = D + (C - D) na(β)e-N(β) dβ,
0
β
β
∫
∫
= (na(β) + ni(β)) dβ.
(15)
0
0
Действительно, обозначим правые части равенств (15) через
B(β) и
A0(β). Очевидно,
B(0) =
= D = B(0),
A0(0) = C = A0(0). Кроме того,
B(β),
A0(β) - решение системы (14). Прове-
рим, например, справедливость первого уравнения (14). Левая его часть равна
B′(β) = (C -
−D)nae-N , а правая имеет вид
(
∫
β
∫
β
)
na
A0 -B) = na C - D + (D - C) nie-N dβ - (C - D) nae-N dβ
=
0
0
( ∫β
∫
β
)
( ∫β
)
= na(C - D) 1 - nie-N dβ - nae-N dβ
= na(C - D) 1 - (ni + na)e-N dβ
=
0
0
0
( ∫β
)
= na(C-D) 1- N′e-N dβ
= na(C-D)(1+e-N|β0) = na(C-D)(1+e-N -1) = na(C-D)e-N.
0
Тем самым справедливость первого уравнения системы (14) установлена. Аналогично доказы-
вается второе равенство (14). Итак,
A0(β),
B(β) - решение (14), удовлетворяющее начальным
условиям
A0(0) = C,
B(0) = D. Осталось воспользоваться теоремой единственности.
Из равенств (15) вытекает справедливость условия 1). Пусть D > C, тогда A0(α) < B(β)
(что равносильно A(α) < B(β)) для любых α, β ∈ R. В самом деле, это неравенство с учётом
тождеств (15) равносильно соотношению
α
β
∫
∫
nie-N dα + nae-N dβ < 1.
(16)
0
0
Пусть γ > 0 - любая верхняя граница чисел α, β. Учитывая неотрицательность функций
ni, na, левая часть (16), очевидно, не превосходит единицы:
∫
γ
∫
γ
∫
γ
∫
γ
nie-N dβ + nae-N dβ = (ni + na)e-N dβ = N′e-N dβ = -e-N|γ0 = 1 - e-N(γ) < 1,
0
0
0
0
что и доказывает (16). Если C > D, то B(β) < A0(α) для любых α, β ∈ R. Последнее
неравенство (его несложно проверить с учётом тождеств (15)), тоже равносильно соотноше-
нию (16). Тем самым справедливость условия 1) установлена. Если A(R) < B(R), то правая
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1344
ГАВРИКОВ, ТАЮРСКИЙ
часть первого равенства (14) неположительна, а второго равенства - неотрицательна. Поэто-
му B(β) монотонно не возрастает, A0(β) монотонно не убывает на R, и значит, функция
A(β) = A0(-β) тоже монотонно не возрастает на R. Аналогично устанавливается, что при
B(R) < A(R) функции B(β) и A(β) монотонно не убывают на R. Тем самым доказана
справедливость условия 2).
Итак, согласно теореме 1, формулы (4) с учётом (15) дают решение задачи Коши в пере-
менных (α, β) ∈ P :
(
∫
∫
β
)-1
na(α,β) = k-1Ina(β)e-N(β)
1 - nie-N dα - nae-N dβ
,
0
0
(
∫
∫
β
)-1
ni(α,β) = k-1Ini(α)e-N(α)
1 - nie-N dα - nae-N dβ
0
0
В переменных (z, t) получаем следующие формулы:
[
∫
∫
)]-1
kI
na(z,t) = n0a(z - vat)e-N(z-vat) 1-
n0i(p)e-N(p) dp +
n0a(p)e-N(p) dp
,
vi - va
0
0
[
∫
∫
)]-1
kI
ni(z,t) = n0i(z - vit)e-N(z-vit) 1-
n0i(p)e-N(p) dp +
n0a(p)e-N(p) dp
,
vi - va
0
0
p
∫
kI
N (p) =
[n0a(q) + n0i(q)] dq, z ∈ R, t ≥ 0,
(17)
vi - va
0
где n0i(p) ≥ 0, n0a(p) ≥ 0 - произвольные непрерывно дифференцируемые функции, и зна-
менатель в формулах (17) заведомо положителен. Итак, формулы (17) дают аналитическое
решение системы (1) при t ≥ 0, удовлетворяющее начальному условию
na(z,0) = n0a(z), ni(z,0) = n0i(z), z ∈ R.
Итоговые формулы (17) для решения задачи Коши в координатах (α, β) не зависят от
констант C и D, C = D, определявших функции A0(β), B(β). Это не случайно. Если
A0(β),
B(β) - другие решения системы (14) с начальными условиями
A0(0)
C,
B(0) =D,
D=
C =D, то однозначно определяются константы R = 0, S, для которых
C = RC + S,
= RD + S. Рассмотрим функции RA0(y) + S, RB(y) + S, которые удовлетворяют системе
(14) и начальному условию
C,
D, поэтому, по теореме единственности решения задачи Коши
для линейной системы (14),
A0(β) ≡ RA0(β) + S,
B(β) ≡ RB(β) + S, в частности,
A(α) =
=A¯0(-α) ≡ RA(α) + S. Но для таких пар функций
A(α),
B(β) и A(α), B(β) формулы (4)
дают одни и те же значения na, ni.
3. Краевая задача (II). Рассмотрим краевую задачу (II) в случае vi = va. Анализ это-
го случая проходит по той же схеме, что и решение задачи Коши выше. Выделим основные
моменты. В переменных (α, β) ищем непрерывно дифференцируемое решение системы (3) в
полуплоскости P0 = {αva +βvi ≥ 0}, для которого функции na, ni на границе полуплоскости
P0,
∂P0 = {αva + βvi = 0} принимают заданные значения na(α,β) = na0(α + β), ni(α,β) =
= ni0(α+β), αva +βvi = 0. Построим такое непрерывно дифференцируемое решение системы
(3) в бесконечном прямоугольнике Π∞ = R × R ⊇ P0, которое на границе полуплоскости P0,
т.е. на прямой αva + βvi = 0, совпадает с заданными функциями na0(α + β), ni0(α + β).
Тогда, очевидно, сужение этого решения на P0 будет искомым решением краевой задачи в
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1345
координатах (α, β). Согласно теореме 1 искомое решение определяется двумя непрерывно
дифференцируемыми функциями A(α), B(β) и вычисляется по этим функциям посредством
формул (4). При этом функции A(α), B(β) должны удовлетворять условиям 1) и 2), сфор-
мулированным в п. 2. Функции A(α), B(β) определяются по известным значениям na, ni
на границе P0. На этой границе β = -αva/vi, и значит, согласно (4) имеем
na0(α(vi - va)/vi) = B′(-αva/vi)k-1I[A(α) - B(-αva/vi)]-1,
ni0(α(vi - va)/vi) = A′(α)k-1I[A(α) - B(-αva/vi)]-1, α ∈ R.
(18)
Обозначим
na(α) = kI(va/vi)na0(α(vi - va)/vi), ni(α) = kIni0(α(vi - va)/vi), B0(α) = B(-αva/vi).
Тогда краевое условие (18) даёт линейную систему ОДУ на прямой с переменными коэффи-
циентами для нахождения функций A(α), B0(α):
B′0 = -na(α)(A - B0), A′ = ni(α)(A - B0).
(19)
Поскольку функции na(α), ni(α) непрерывно дифференцируемы, то любое решение системы
(19) дважды непрерывно дифференцируемо и определено на всей прямой. Рассмотрим решение
задачи Коши для системы (19) с начальными условиями A(0) = C = B0(0) = D. Несложно
проверить, что это решение вычисляется по формулам (см. выше)
∫α
∫
α
∫
α
= (na + ni) dα. (20)
0
0
0
С помощью формул (20) обосновывается (см. выше) справедливость условий 1) и 2) для функ-
ций A(α), B(β) = B0(-βvi/va). Условие (16) при этом заменяется на следующее:
∫α
∫
β
1 + nieN dα + naeN dβ > 0, α,β ∈ R.
(21)
0
0
И если C > D, то A(α) > B(β), а при C < D имеем A(α) < B(β) для всех α, β ∈ R.
По формулам (4) с учётом выражений (20) получим решение краевой задачи в координатах
(α, β) ∈ P0 :
[
∫
α
∫
]-1
vi
1
na(α,β) =
na(-βvi/va)eN(-βvi/va)
1+
nieN dα +
naeN dβ
,
va
kI
0
0
[
∫
α
∫
]-1
1
ni(α,β) = ni(α)eN(α)
1+
nieN dα +
naeN dβ
kI
0
0
Подставляя в эти формулы α = (tvi - z)/(vi - va), β = (z - tva)/(vi - va), получаем после
несложных преобразований решение краевой задачи в переменных (z, t):
[
∫
∫
)]-1
kI
na(z,t) = na0(t - z/va)eN(t-z/va) 1+
vini0(p)eN(p) dp +
vana0(p)eN(p) dp
,
vi - va
0
0
4
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1346
ГАВРИКОВ, ТАЮРСКИЙ
[
∫
∫
)]-1
kI
ni(z,t) = ni0(t - z/vi)eN(t-z/vi) 1+
vini0(p)eN(p) dp +
vana0(p)eN(p) dp
,
vi - va
0
0
p
∫
kI
N (p) =
[vana0(q) + vini0(q)] dq,
(22)
vi - va
0
где na0(p) ≥ 0, ni0(p) ≥ 0 - произвольные непрерывно дифференцируемые функции, и зна-
менатель в (22), согласно неравенству (21), заведомо положителен. Итак, формулы (22) дают
аналитическое решение системы (1) в полуплоскости z ≥ 0, удовлетворяющее краевому усло-
вию na(0, t) = na0(t), ni(0, t) = ni0(t) для всех t ∈ R.
4. Решение смешанной задачи (III). Рассмотрим смешанную задачу (III) в случае
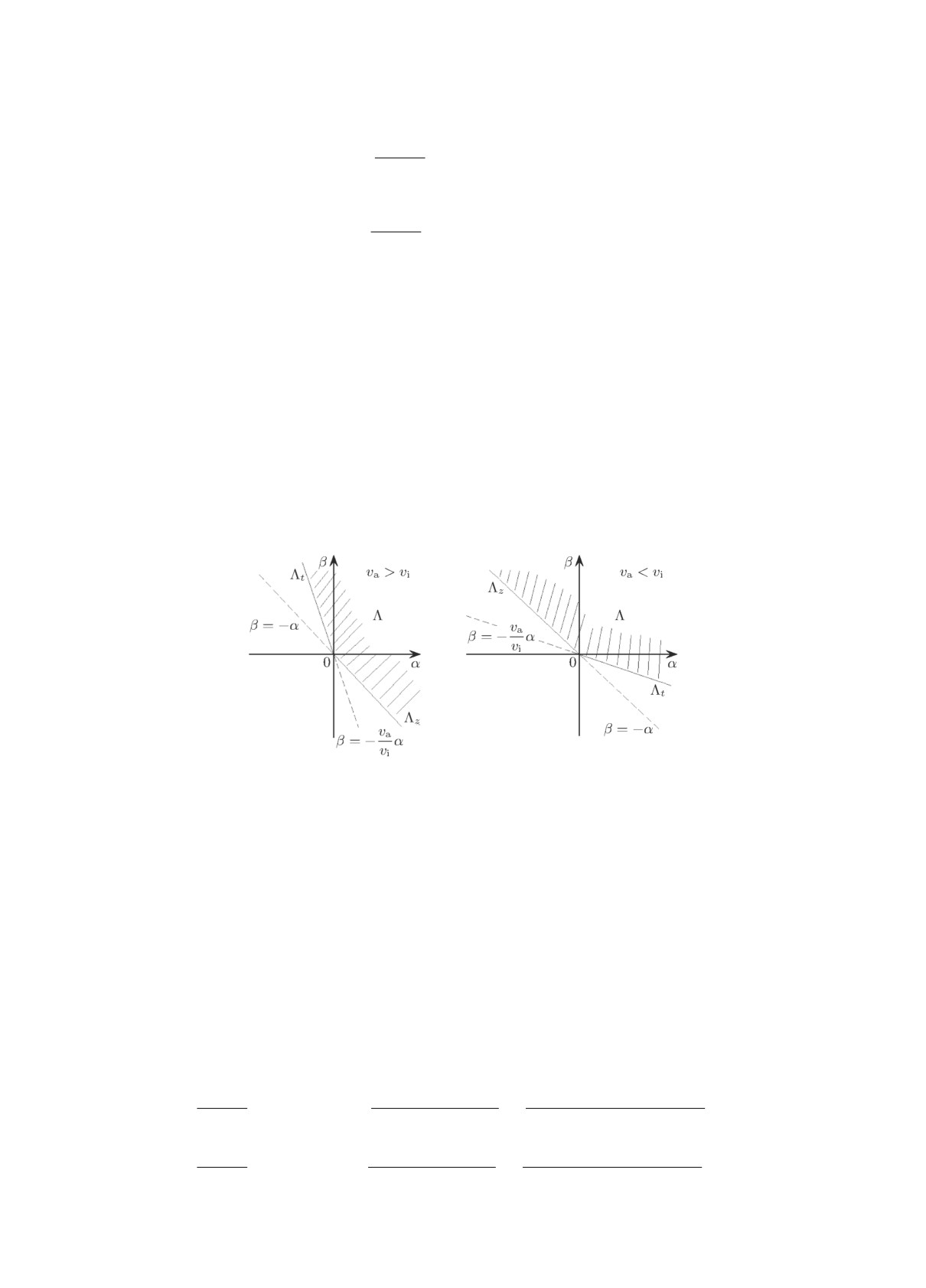
va > 0, vi > 0, va = vi. В координатах (α,β) её решение сводится к поиску в тупом угле
= {(α, β) : α + β ≥ 0, αva + βvi ≥ 0} непрерывно дифференцируемых функций na(α, β),
ni(α,β), удовлетворяющих системе (3) и имеющих заданные значения на границе угла ∂Λ.
Последнее множество состоит из двух лучей, которые обозначим Λt и Λz :
∂Λ = Λt
⋃Λz, Λt ⋂Λz = {(0,0)}, Λt = φ{(t,0) : t ≥ 0}, Λz = φ{(0,z) : z ≥ 0}.
В зависимости от vi, va угол Λ и лучи Λt, Λz показаны на рис. 1.
Рис. 1. Угол Λ и лучи Λt, Λz в зависимости от vi, va.
Значения искомого решения на лучах Λt, Λz определяются равенствами
na(α,β) = na0(α + β), ni(α,β) = ni0(α + β), (α,β) ∈ Λt, αva + βvi = 0, α + β ≥ 0;
na(α,β) = n0a(αva + βvi), ni(α,β) = n0i(αva + βvi), (α,β) ∈ Λz, α + β = 0, αva + βvi ≥ 0.
Проведём построение искомого решения для случая vi > va. Для нахождения решения в угле
Λ построим непрерывно дифференцируемое решение системы (3) в бесконечном прямоуголь-
нике Π∞ = R × R ⊇ Λ, которое на лучах Λt и Λz совпадает с указанными выше значениями.
Тогда сужение построенного решения в прямоугольнике Π∞ на угле Λ даст решение сме-
шанной задачи. Решение системы (3) в Π∞, согласно теореме 1, определяется двумя дважды
непрерывно дифференцируемыми в R функциями A(α), B(β) и вычисляется по этим функ-
циям посредством формул (4). Покажем, что функции A(α), B(β) однозначно определяются
значениями искомого решения на лучах Λt и Λz. На луче Λt (β = -αva/vi) имеем
(
)
vi - va
B′(β)
B′(-αva/vi)
na0
α
= na(α,β)
(4)=
=
,
α ≥ 0,
vi
kI(A(α) - B(β))
kI(A(α) - B(-αva/vi))
(
)
vi - va
A′(α)
A′(α)
ni0
α
= ni(α,β)
(4)=
=
,
α ≥ 0,
vi
kI(A(α) - B(β))
kI(A(α) - B(-αva/vi))
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1347
а на луче Λz (β = -α)
B′(β)
B′(β)
na0(β(vi - va)) = na(α,β)
(4)=
=
,
β ≥ 0,
kI(A(α) - B(β))
kI(A(-β) - B(β))
A′(α)
A′(-β)
ni0(β(vi - va)) = ni(α,β)
(4)=
=
,
β ≥ 0.
(23)
kI(A(α) - B(β))
kI(A(-β) - B(β))
= A(-β), α ≥ 0, β ≥ 0. Тогда на полу-
прямой α ≥ 0 функции B0(α), A(α), согласно (23), удовлетворяют линейной системе ОДУ с
переменными коэффициентами:
B′0 = -na0(α)(A - B0), A′ = ni0(α)(A - B0), α ≥ 0,
(
)
(
)
vi - va
vi - va
=kI
na0
α
,
ni0(α)=
kIni0
α
,
(24)
vi
vi
vi
а на полупрямой β ≥ 0 функции B(β), A0(β), согласно (23), удовлетворяют линейной системе
ОДУ с переменными коэффициентами:
B′ = n0a(β)(A0 - B), A′0 = -n0i(β)(A0 - B), β ≥ 0,
= kIn0a(β(vi - va)),
= kIn0i (β(vi - va)).
(25)
Решив системы (24), (25), найдём функции B0(α), A(α), α ≥ 0, и B(β), A0(β), β ≥ 0, после
чего доопределим A и B в областях отрицательных значений аргументов равенствами
= B0(-βvi/va), β ≥ 0, A(α) = A0(-α), α ≤ 0.
(26)
Полученные функции A и B на прямой являются искомыми, если выбрать решения систем
(24) и (25) с одинаковыми начальными условиями A(0) = C, B0(0) = D и A0(0) = C, B(0) =
= D, где C = D. Тогда функции A(α), B(β) будут непрерывны на R, а из (26) следует их
непрерывная дифференцируемость в нуле:
= kIni0(0)(A(0) - B0(0)) = kIni0(0)(C - D),
= kIn0i (0)(A0(0) - B(0)) = kIn0i (0)(C - D),
= kIn0a(0)(A0(0) - B(0)) = kIn0a(0)(C - D),
= kIna0(0)(A(0) - B0(0)) = kIna0(0)(C - D).
Из этих вычислений и условий согласования ni0(0) = n0i(0), na0(0) = n0a(0) следует, что
A′(0+) = A′(0-), B′(0+) = B′(0-), поэтому A и B непрерывно дифференцируемы в нуле
и, значит, на R. Покажем, что при выполнении условий согласования
n′a0(0) + va(n0a)′(0) + kIna0(0)ni0(0) = 0, n′i0(0) + vi(n0i)′(0) - kIna0(0)ni0(0) = 0
(27)
вторые производные в нуле для A и B слева и справа совпадают: A′′(0+)=A′′(0-), B′′(0+)=
= B′′(0-). Тогда из (24), (25) следует двукратная непрерывная дифференцируемость функ-
ций A и B на R. Например, покажем равенство A′′(0+) = A′′(0-); B′′(0+) = B′′(0-)
проверяется аналогично. Имеем
=
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
4∗
1348
ГАВРИКОВ, ТАЮРСКИЙ
(24)= n′i0(0)kI ((vi - va)/vi)(C - D) + ni0(0)kI (ni0kI (C - D) + na0(0)kI (va/vi)(C - D)) =
= kI(C - D){n′i0(0)(vi - va)/vi + kIni0(0)(ni0(0) + na0(0)va/vi)},
=
(25)= -(n0i)′(0)(vi - va)kI (C - D) - n0i(0)kI (-n0i(0)kI (C - D) - n0a(0)kI (C - D)) =
= kI(C - D){-(n0i )′(0)(vi - va) + kIn0i (0)(n0i (0) + n0a(0))}.
Учитывая условия согласования ni0(0) = n0i(0), na0(0) = n0a(0) и второе равенство (27), за-
ключаем, что A′′(0+) = A′′(0-).
Чтобы проверить условия 1) и 2) и преобразовать к удобному для анализа виду формулы
(4), воспользуемся явными выражениями решений задач Коши для систем (25), (24). Несложно
проверить (см. аналогичное рассуждение выше), что для этих решений справедливы тож-
дества
β
β
∫
∫
B(β) = D + (C - D)
n0ae-N dβ, A0(β) = C + (D - C)
n0ie-N dβ, β ≥ 0,
(28)
0
0
α
∫α
∫
B0(α) = D + (D - C)
na0eM dα, A(α) = C + (C - D)
ni0eM dα, α ≥ 0,
(29)
0
0
β
α
∫
∫
N (β) =
(n0a + n0a)dβ, M(α) =
(na0 + ni0)dα.
0
0
Значит, согласно (26), функции A(α) и B(β) вычисляются по формулам
⎧
⎧
∫
⎪
∫
⎪
⎪
⎪
⎪C + (D - C)
n0ie-N dα, α ≤ 0,
⎪D + (D - C)
na0eM dβ, β ≤ 0,
⎨
⎨
0
A(α)=
B(β)=
(30)
∫
β
⎪
⎪
∫
⎪
⎪
⎪C + (C - D)
ni0eM dα, α ≥ 0,
⎪
+ (C - D)
n0ae-N dβ, β ≥ 0.
⎩
⎩D
0
0
Пусть D > C, тогда выполнено неравенство A(α) < B(β) для любых α, β ∈ R. Действи-
тельно, указанное неравенство, с учётом (30), сводится к следующему эквивалентному виду в
каждом из четырёх логически возможных случаев:
β
∫
∫
n0ie-N dα +
n0ae-N dβ < 1, α ≤ 0, β ≥ 0,
0
0
∫
∫
n0ie-N dα -
na0eM dβ < 1, α ≤ 0, β ≤ 0,
0
0
β
∫α
∫
−
ni0eM dα +
n0ae-N dβ < 1, α ≥ 0, β ≥ 0,
0
0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1349
∫α
∫
−
ni0eM dα -
na0eM dβ < 1, α ≥ 0, β ≤ 0.
(31)
0
0
Справедливость неравенств (31) в случаях α ≤ 0, β ≥ 0 (см. (16)) и α ≥ 0, β ≤ 0 (см.
(21)) была установлена выше. В случае α ≤ 0, β ≤ 0, учитывая неотрицательность всех
подынтегральных функций, имеем цепочку оценок:
∫
∫
∫
∫
∫
n0ie-N dα -
na0eM dβ ≤
n0ie-N dα ≤
(n0i + n0a)e-N dα = N′e-N dα =
0
0
0
0
0
= -e-N|N(-α)0 < 1.
Аналогично в случае α ≥ 0, β ≥ 0 имеем оценки
β
β
β
β
∫α
∫
∫
∫
∫
−
ni0eM dα +
n0ae-N dβ ≤
n0ae-N dβ ≤
(n0a + n0i)e-N dβ = N′e-N dβ =
0
0
0
0
0
= -e-N|N(β)0 < 1.
Итак, соотношения (31) установлены и, значит, установлена справедливость неравенства
A(α) < B(β) для всех α, β. Если D < C, то точно так же проверяется неравенство B(β) <
< A(α) для всех α, β ∈ R. Далее, если A(α) < B(β) для всех α, β, то из второго уравнения
(24) и равенств (26) следует, что A′(α) ≤ 0 для α ≥ 0, а из второго уравнения (25) и равенств
(26) следует A′0(β) ≥ 0 для β ≥ 0, но тогда из (26) вытекает неравенство A′(α) ≤ 0 для
α ≤ 0. Итак, при всех α ∈ R имеем A′(α) ≤ 0. Аналогично устанавливается, что B′(β) ≤ 0
для всех β ∈ R. Если A(α) > B(β) для всех α, β ∈ R, то точно так же проверяется, что
A′(α) ≥ 0, B′(β) ≥ 0 для всех α, β. Тем самым условие 2) установлено.
Наконец, преобразуем формулы (4), задающие решение системы (3) в прямоугольнике
Π∞ ⊇ Λ, в каждом из четырёх квадрантов плоскости (α,β). При этом ограничимся толь-
ко квадрантами I, II, IV, квадрант III (α ≤ 0, β ≤ 0), исключим из рассмотрения, поскольку
тупой угол Λ, согласно рис. 1, лежит в объединении квадрантов I, II, IV, а с квадрантом III
пересекается только по нулевой точке. Для удобства введём в рассмотрение функции
∫
p
∫
p
kI
kI
=
=
(vana0(q) + vini0(q)) dq.
(32)
vi - va
vi - va
0
0
Тогда N(β) = N∗(β(vi - va)), M(α) = M∗(α(vi - va)/vi) для любых α, β ∈ R.
Для α ≥ 0, β ≥ 0 имеем
B′(β)
na(α,β)
(4)=
(30)=
kI[A(α) - B(β)]
[
∫
α
∫
β
]-1
(30)=(C - D)n0a(β)e-N(β) 1 (C - D) + (C - D)
ni0(α)eM(α) dα-(C -D)
n0a(β)e-N(β) dβ
=
kI
0
0
= n0a(β(vi - va))e-N∗(β(vi-va)) ×
[
∫
α
∫
β
]-1
× 1 + kI ni0(α(vi - va)/vi)eM∗(α(vi-va)/vi)
dα - kI n0a(β(vi - va))e-N∗(β(vi-va)) dβ
=
0
0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1350
ГАВРИКОВ, ТАЮРСКИЙ
= n0a(β(vi - va))e-N∗(β(vi-va)) ×
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp -
n0a(p)e-N∗(p) dp
vi - va
0
0
Аналогично
A′(β)
ni(α,β)
(4)=
(30)=
kI[A(α) - B(β)]
[
∫
α
∫
β
]
-1
(30)= (C - D)ni0(α)eM(α) 1 (C - D) + (C - D)
ni0(α)eM(α) dα-(C -D)
n0a(β)e-N(β) dβ
=
kI
0
0
= ni0(α(vi - va)/vi)eM∗(α(vi-va)/vi) ×
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp -
n0a(p)e-N∗(p) dp
vi - va
0
0
Для двух других квадрантов аналогичные подсчёты с использованием формул (4), (30) дают
для α ≥ 0, β ≤ 0
na(α,β) = ni0(-β(vi - va)/vi)eM∗(-β(vi-va)/va) ×
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp +
vana0(p)eM∗(p) dp
,
vi - va
0
0
ni(α,β) = ni0(α(vi - va)/vi)eM∗(α(vi-va)/vi) ×
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp +
vana0(p)eM∗(p) dp
;
vi - va
0
0
для α ≤ 0, β ≥ 0
na(α,β) = n0a(β(vi - va))e-N∗(β(vi-va)) ×
[
∫
∫
)]-1
kI
× 1-
n0i(p)e-N∗(p) dp +
n0a(p)e-N∗(p) dp
,
vi - va
0
0
ni(α,β) = n0i(-α(vi - va))e-N∗(-α(vi-va)) ×
[
∫
∫
)]-1
kI
× 1-
n0i(p)e-N∗(p) dp +
n0a(p)e-N∗(p) dp
vi - va
0
0
Осталось перейти в полученных формулах от координат (α, β)
к координатам (z, t), учитывая преобразование (2). При этом
β(vi -va) = z-vat, -α(vi -va) = z-vit, α(vi -va)/vi = t-z/vi,
−β(vi - va)/va = t - z/va. В итоге первый квадрант плоскости
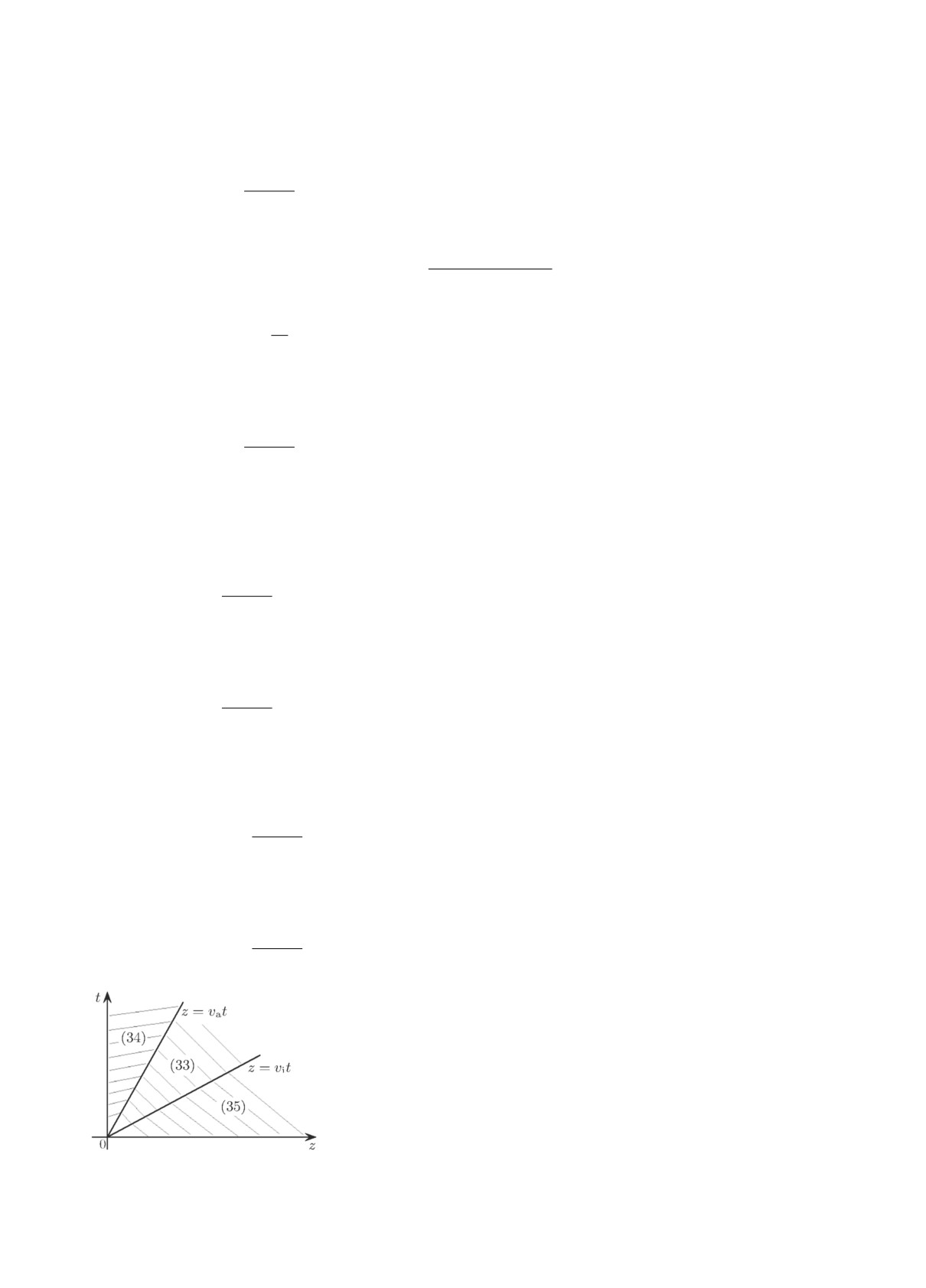
(z, t), где ищется решение смешанной задачи для системы (1),
прямыми z = vat, z = vit делится на три области (показаны
на рис. 2), в каждой из которых решение задаётся одной из
групп формул:
Рис. 2. Области нахождения ре-
na(z,t) = n0a(z - vat)e-N∗(z-vat) ×
шения смешанной задачи.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1351
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp -
n0a(p)e-N∗(p) dp
,
vi - va
0
0
ni(z,t) = ni0(t - z/vi)eM∗(t-z/vi) ×
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp -
n0a(p)e-N∗(p) dp
;
(33)
vi - va
0
0
M∗(t-z/va)
na0(t - z/va)e
na(z,t) =
×
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp +
vana0(p)eM∗(p) dp
,
vi - va
0
0
ni(z,t) = ni0(t - z/vi)eM∗(t-z/vi) ×
[
∫
∫
)]-1
kI
× 1+
vini0(p)eM∗(p) dp +
vana0(p)eM∗(p) dp
;
(34)
vi - va
0
0
na(z,t) = n0a(z - vat)e-N∗(z-vat) ×
[
∫
∫
)]-1
kI
× 1-
n0i(p)e-N∗(p) dp +
n0a(p)e-N∗(p) dp
,
vi - va
0
0
ni(z,t) = n0i(z - vit)e-N∗(z-vit) ×
[
∫
∫
)]-1
kI
× 1-
n0i(p)e-N∗(p) dp +
n0a(p)e-N∗(p) dp
(35)
vi - va
0
0
Формулы (33) и (34) на луче z = vat, t ≥ 0, и формулы (33) и (35) на луче z = vit, t ≥ 0,
очевидно, совпадают. При z = 0 формула (34) даёт краевые условия na0(t), ni0(t), t ≥ 0,
а при t = 0 формула (35) даёт начальные условия n0a(z), n0i(z), z ≥ 0. Итак, формулы
(33)-(35), с учётом выражений (32), полностью определяют решение смешанной задачи для
системы (1) по известным граничным na0(t), ni0(t), t ≥ 0, и начальным n0a(z), n0i(z), z ≥ 0
условиям.
5. Начально-краевая задача на отрезке (IV). Решение задачи (IV) в переменных
(α, β) сводится к решению системы (3) в полуполосе
Π = {(α,β) : α + β ≥ 0,
0 ≤ αva + βvi ≤ L}.
Множество Π является замкнутым выпуклым подмножеством R2, причём Π = Int Π, а
проекции Π на координатные оси α и β равны, соответственно, [0, +∞) и [β0, +∞), где
β0 = L/Δ, Δ = vi -va < 0. Согласно обобщённой теореме 2 решение системы (3) в замкнутой
области Π определяется двумя дважды непрерывно дифференцируемыми функциями A(α),
α ≥ 0, B(β), β ≥ β0, для которых A(α) = B(β), α,β ∈ Π, и оно задаётся формулами (4).
Эти функции определяются однозначно начальными и граничными условиями задачи (IV),
которые в переменных (α, β) примут вид
na(α,-α) = n0a(-αΔ), ni(α,-α) = n0i(-αΔ),
0 ≤ α ≤ α0 = -β0,
(36)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1352
ГАВРИКОВ, ТАЮРСКИЙ
na(α,-αva/vi) = na0(αΔ/vi), α ≥ 0,
na(α,-αva/vi + L/vi) = na0(αΔ/vi + L/vi), α ≥ α0.
(37)
Граница ∂Π множества Π состоит из замкнутого отрезка [a, b], a = (0, 0), b = (α0, β0), и двух
замкнутых параллельных лучей [a, ∞) и [b, ∞), являющихся графиками функций α(β) =
= -βvi/va и β(α) = -αva/vi +L/vi соответственно. Условия (36), (37) означают, что известны
значения функции na на части границы ∂Π, состоящей из объединения [a, b]
⋃ [a, ∞), а функ-
ции ni - на границе [a, b]
⋃ [b, ∞). Для определения функций A(α), α ≥ 0, B(β), β ≥ β0,
построим рекуррентно их сужения на отрезках [0, α0],
[α0, α1],
[α1, α2], . . . (для A(α)) и
отрезках [β0, β1], [β1, β2], [β2, β3], . . . (для B(β)), имеющие непересекающиеся внутренности
и дающие разбиение областей определения этих функций: [0, +∞] = [0, α0]
⋃ (⋃∞k=1[αk-1,αk]),
⋃∞
[β0, +∞] =
[βk-1, βk]. Здесь βk = L/Δ - kL/vi, αk = kL/va - L/Δ, k ∈ N
⋃{0}. Обозна-
k=1
чим A0 = A|[0,α0], Ak = A|[αk-1,αk], k ≥ 1, Bk = B|[βk-1,βk], k ≥ 1, B0 = B|[β0,0] = B1|[β0,0],
B∗ = B|[0,β1] = B1|[0,β1].
Из формул (4) и начальных условий (36) следует, что функции A0(α), B0(β) являются
решениями задачи Коши для линейной системы уравнений
A′0(α) = kI ni(α)[A0(α) - B0(-α)],
0≤α≤α0,
B′0(β) = kI na(α)[A0(-β) - B0(β)], β0 ≤ β ≤ 0,
A0(0) = C, B0(0) = D,
ni(α) = n0i(-αΔ),
na(β) = n0a(βΔ),
(38)
где C и D, C = D, - произвольные константы. Нетрудно указать явный вид решения системы
(38):
∫α
A0(α) = C + (C - D) kI ni(α)eN(α) dα,
0≤α≤α0,
0
∫
B0(β) = D + (D - C) kI na(-α)eN(α) dα, β0 ≤ β ≤ 0,
0
∫α
N (α) = kI
[ni(α) + na(-α)]dα, α ≥ 0.
0
Функция B∗(β), 0 ≤ β ≤ β1, в силу (4) и граничного условия (37) ищется как решение задачи
Коши для линейного уравнения
B′∗(β) = kIna(β)[A0(α(β)) - B∗(β)], B∗(0) = D,
0≤β ≤β1,
(39)
где α(β) определена выше, na(β) = na0(β + α(β)) = na0(-βΔ/va).
Теперь B1 однозначно определяется из условий B1|[β0,0] = B0, B1|[0,β1] = B∗. Зная функ-
цию B1 на [β0, β1], последовательно находим функции B1 → A1 → B2 → A2 → B3 →
... → Bk → Ak → Bk+1 → ... на основании формулы (4) и граничного условия (37) следую-
щим способом.
По Bk(β) функция Ak(α), k ≥ 1, находится из решения задачи Коши для линейного
уравнения на отрезке [αk-1, αk]:
A′(α) = kIni(α)[A(α) - Bk(β(α))], A(αk-1) = Ak-1(αk-1),
(40)
где β(α) = -αva/vi + L/vi, ni(α) = ni0(α + β(α)) = ni0(αΔ/vi + L/vi).
По Ak(α) функция Bk+1(β), k ≥ 1, определяется из решения задачи Коши для линейного
уравнения на отрезке [βk, βk+1]:
B′(β) = kIna(β)[Ak(α(β)) - B(β)], B(βk) = Bk(βk),
(41)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1353
где α(β) = -βvi/va, na(β) = na0(α(β) + β) = na0(-βΔ/va). В этом построении используются
очевидные равенства α(βk+1) = αk, β(αk) = βk, k ≥ 0.
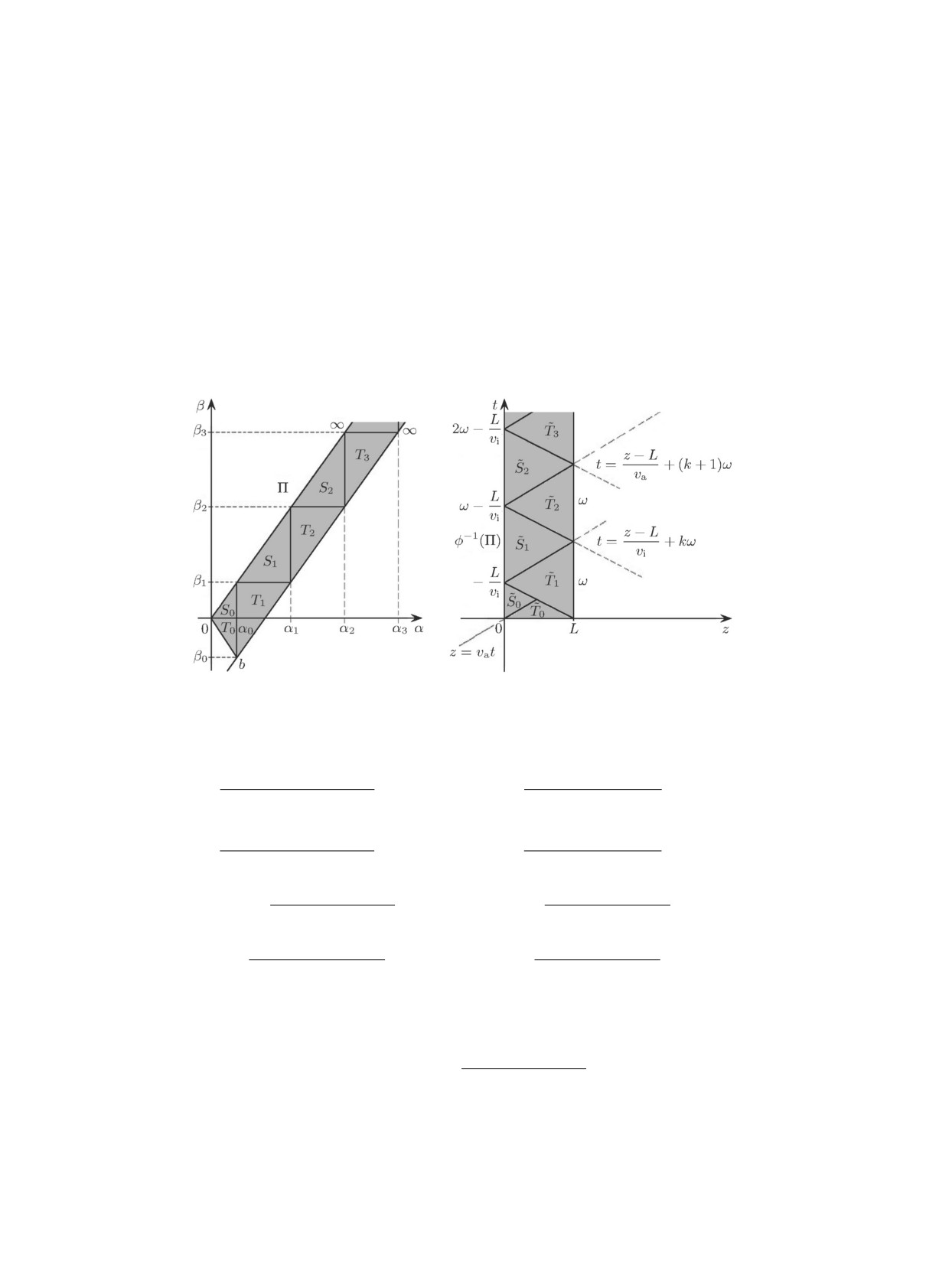
Используя соотношения (38)-(41) и формулы (4), можно построить решение системы (3)
в полуполосе Π, удовлетворяющее начальным и граничным условиям (36), (37). Для этого
разобьём полуполосу Π на треугольники Tk, Sk, k ≥ 0, как указано на рис. 3. Формально
имеем
Tk = {(α,β) : αk-1 ≤ α ≤ αk, β(α) ≤ β ≤ βk}, k ≥ 1,
Sk = {(α,β) : βk ≤ β ≤ βk+1, α(β) ≤ α ≤ αk}, k ≥ 1,
T0 = {(α,β) : 0 ≤ α ≤ α0,
-α ≤ β ≤ 0}, S0 = {(α,β) : 0 ≤ β ≤ β1, α(β) ≤ α ≤ α0}.
Нетрудно проверить, что внутренности всех треугольников попарно не пересекаются, а в сумме
треугольники дают полуполосу Π.
Рис. 3. Триангуляции полуполос Π и φ-1(Π) в переменных (α, β) и (z, t).
Тогда для точки (α, β) ∈ Π имеем
Ak-1(α(β)) - Bk(β)
Ak(α) - Bk(β(α))
na(α,β) = na(β)
,
ni(α,β) = ni(α)
,
(α, β)∈Tk , k ≥ 2,
Ak(α) - Bk(β)
Ak(α) - Bk(β)
Ak(α(β)) - Bk+1(β)
Ak(α) - Bk(β(α))
na(α,β) = na(β)
,
ni(α,β) = ni(α)
,
(α, β)∈Sk, k ≥ 1,
Ak(α) - Bk+1(β)
Ak(α) - Bk+1(β)
A0(-β) - B0(β)
A0(α) - B0(-α)
na(α,β) = na(β)
,
ni(α,β) = ni(α)
,
(α, β) ∈ T0,
A0(α) - B0(β)
A0(α) - B0(β)
A0(α(β)) - B1(β)
A0(α) - B0(-α)
na(α,β) = na(β)
,
ni(α,β) = ni(α)
,
(α, β) ∈ S0.
(42)
A0(α) - B1(β)
A0(α) - B1(β)
Если (α, β) ∈ T1, то формула для ni(α, β) справедлива, а для na(α, β) верна только при
β ≥ 0. Для β ≤ 0 она видоизменяется:
A0(-β) - B0(β)
na(α,β) = na(β)
A1(α) - B1(β)
Это следствие того, что B1 вычисляется по-разному для β ≥ 0 и β ≤ 0. Легко проверить,
что в пересечении любых двух треугольников приведённые формулы (42) дают одни и те же
значения. Прямой подстановкой с учётом формул (38)-(41) легко проверить, что функции (42)
являются решением системы (3).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1354
ГАВРИКОВ, ТАЮРСКИЙ
Решив уравнения (40), (41) методом вариации произвольной постоянной, приходим к следу-
ющим рекуррентным соотношениям, позволяющим вычислить функции Ak(α), k ≥ 1, Bk(β),
k≥2:
β
[
∫
]
vi
Bk+1(β) = Ak(α(β)) + ef(βk)-f(β) Bk(βk) - Ak(αk+1) +
ef(β)-f(βk)A′k(α(β))dβ
=
va
βk
[
∫
β
[
(
)]
]
vi
L
= Ak(β)+ef(βk)-f(β) Bk(βk)-Ak(αk+1)+
ef(β)-f(βk)
kIni(α(β)) Ak(α(β))-Bk β+
dβ ,
va
vi
βk
β
∫
vi
f (β) = kI na(β) dβ, α(β) = -
β, βk ≤ β ≤ βk+1, k ∈ N,
(43)
va
0
[
∫
α
]
va
Ak(α) = Bk(β(α)) + eg(a)-g(αk-1) Ak-1(αk-1) - Bk(βk-1) +
eg(αk-1)-g(α)B′k(β(α))dβ
=
vi
αk
[
∫
α
va
= Bk(β(α)) + eg(α)-g(αk-1) Ak-1(αk-1) - Bk(βk-1) +
eg(αk-1)-g(α)kIna(β(α)) ×
vi
αk-1
[
(
)
]
]
L
× Ak-1 α-
− Bk(β(α)) dα ,
va
∫α
va
g(β) = kI ni(β) dα, β(α) = -
α+
L, αk-1 ≤ α ≤ αk, k = 2,3,...
(44)
vi
vi
0
При k = 1 первое равенство в (44) справедливо, а второе верно, если интегральное слагаемое
в фигурной скобке скорректировать в зависимости от α следующим образом. При α0 ≤ α ≤
≤ L/va интегральное слагаемое в фигурной скобке нужно заменить на I(α), где
α
∫
va
I(α) =
eg(α0)-g(α)kIna(β(α))[A0(-β(α)) - B0(β(α))]dα.
vi
α0
При L/va ≤ α ≤ α1 интегральное слагаемое заменяется на выражение
∫α
I(L/va) + (va/vi)
eg(α0)-g(α)kIna(β(α))[A0(α - L/va) - B1(β(α))]dα.
L/va
Итак, зная A0(α), B0(β) и B1(β) (при β ≤ 0 B1(β) = B0(β), а при β ≥ 0 B1(β) является
решением уравнения (39):
β
∫
vi
B1(β) = A0(α(β)) + e-f(β)(D - C) + e-f(β)
ef(β)kI ni(α(β))[A0(α(β)) - B0(-α(β))]dβ,
va
0
где 0 ≤ β ≤ β1), по формулам (43), (44) последовательно находим функции A1, B2, A2, B3,
..., а затем по формулам (42) вычисляем na, ni в полуполосе Π в переменных (α,β).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ
1355
Сделаем несколько заключительных замечаний.
1. Проведённое построение зависит от констант C и D, но итоговые формулы (42) от C
и D не зависят (зависимости от C и D числителя и знаменателя в этих формулах взаимно
уничтожаются).
2. При C > D из (43), (44) индукцией по k нетрудно вывести, что функции A(α) и B(β)
монотонно возрастают и A(α) > B(β) для (α, β) ∈ Π, а при C < D функции A(α) и B(β)
монотонно убывают и A(α) < B(β) для (α, β) ∈ Π. В частности, числитель и знаменатель
формул (42) имеют одинаковые знаки и все знаменатели отличны от нуля.
3. По построению функции A(α), B(β) непрерывны. Если начальные и граничные усло-
вия непрерывно дифференцируемы, то с учётом условий согласования нетрудно установить
двукратную непрерывную дифференцируемость функций A(α) и B(β).
4. Переходя в формулах (42) к переменным t = α + β, z = αva + βvi, получаем решение
начально-краевой задачи на отрезке [0, L] в полуполосе φ-1(Π) : t ≥ 0,
0 ≤ z ≤ L. По-
скольку преобразование независимых переменных (α, β) = φ(z, t) линейное и невырожденное,
то полные прообразы
Sk = φ-1(Sk),
Tk = φ-1(Tk), k ≥ 0, являются также треугольника-
ми с непересекающимися внутренностями, дающими разбиение полуполосы φ-1(Π) = {(z, t),
0 ≤ z ≤ L, t ≥ 0}, как это показано на рис. 3. Нетрудно проверить, что границы треугольни-
ков
Tk,
Sk, k ≥ 1, задаются прямыми t = (z - L)/vi + kω, k ∈ N
⋃{0}, t = (z - L)/va + kω,
k ∈ N, где ω = LΔ/(viva), и прямыми z = 0, z = L. Треугольники
S0,
T0 пересекают-
ся по границе t = z/va. Явные формулы (42) для решения в переменных (z, t) получаются
после подстановки в них выражений α = (tvi - z)/Δ, β = (z - tva)/Δ с учётом равенств
α(β) = (tvi - zvi/va)/Δ, β(α) = va(z - tvi)/(viΔ) + L/vi. Например, для (z, t)
Tk, k ≥ 2,
получим
na(z,t) = na0(zv-1a - t)[Ak-1((tvi - viv-1az)/Δ) - Bk((z - tva)/Δ)] ×
× [Ak-1((tvi - z)/Δ) - Bk((z - tva)/Δ)]-1,
ni(z,t) = ni0(t - zv-1i + Lv-1i)[Ak((tvi - z)/Δ) - Bk(Lv-1i + vav-1iΔ-1(z - tva))] ×
× [Ak-1((tvi - z)/Δ) - Bk((z - tva)/Δ)]-1.
Аналогично преобразуются и другие формулы (42).
Заключение. В работе рассмотрены основные начально-краевые (смешанные) задачи для
нелинейной системы уравнений одномерной ионизации газа в случае постоянных скоростей
атомов и ионов и указан общий вид решений этой системы.
Показано, что смешанные задачи для системы уравнений одномерной ионизации допускают
интеграцию в виде явных аналитических выражений. Особый интерес представляет смешан-
ная задача для конечного отрезка. В этом случае аналитическое решение строится посредством
рекуррентных формул, каждая из которых определена в треугольнике, принадлежащем неко-
торой триангуляции области определения неизвестных функций. Формулы для решения крае-
вой задачи на отрезке получены для случая va > 0 > vi. Для остальных случаев (va < 0 < vi;
va > 0, vi > 0; va < 0, vi < 0; va = 0, vi = 0; va = 0, vi = 0) решение строится аналогично.
В случае va = vi построение решения сильно упрощается интегрированием системы (1) по
общим характеристикам (подробности см. в [13]).
Полученные результаты доказывают существование и единственность решения поставлен-
ных начально-краевых задач и могут использоваться для построения различных асимптоти-
ческих формул для полученных решений.
Для исследования ионизационных колебаний представляет значительный интерес обобще-
ние предложенного в работе метода решения смешанной задачи на отрезке на практически
важный случай, когда скорость атомов постоянна и положительна, а скорость ионов линейна,
имеет положительную производную и обращается в нуль внутри рассматриваемого отрезка.
Работа выполнена при финансовой поддержке Министерства науки и высшего образования
Российской Федерации в рамках реализации программы Московского центра фундаменталь-
ной и прикладной математики по соглашению № 075-15-2022-283.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023
1356
ГАВРИКОВ, ТАЮРСКИЙ
СПИСОК ЛИТЕРАТУРЫ
1. Морозов А.И. Введение в плазмодинамику. М., 2006.
2. Baranov V.I., Nazarenko Y.S., Petrosov V.A., Vasin A.I., Yashnov Y.M. Theory of oscillations and
conductivity for Hall thrusters // 32nd Joint Propulsion Conf. 1996. AIAA 96-3192.
3. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой
динамике. М., 1978.
4. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1977.
5. Бишаев A.M., Ким В. Исследование локальных параметров плазмы в ускорителе с замкнутым
дрейфом электронов и протяжённой зоной ускорения // Журн. техн. физики. 1978. Т. 48. № 9.
С. 1853-1857.
6. Chapurin O., Smolyakov A.I., Hagelaar G., Raitses Y. On the mechanism of ionization oscillations in
Hall thrusters // J. Appl. Phys. 2021. V. 129. P. 233307.
7. Гавриков М.Б., Таюрский А.А. Некоторые математические вопросы ионизации плазмы // Преприн-
ты ИПМ им. М.В. Келдыша. 2021. № 94.
8. Гавриков М.Б., Таюрский А.А. Стационарные и осциллирующие решения уравнений ионизации
// Журн. вычислит. математики и мат. физики. 2022. Т. 62. № 7. С. 1158-1179.
9. Fife J., Martinez-Sanchez M., Szabo J. A numerical study of low-frequency discharge oscillations in Hall
thrusters // 33rd Joint Propulsion Conf. 1997. AIAA 97-3052.
10. Barral S., Ahedo E. On the origin of low frequency oscillations in Hall thrusters // AIP Conf. Proc. 2008.
V. 993. P. 439-442.
11. Dale E., Jorns B. Two-zone Hall thruster breathing mode mechanism. Part I: Theory // 36th Intern.
Electric Propulsion Conf. Vienna, 2019.
12. Boeuf J., Garrigues L. Low frequency oscillations in a stationary plasma thruster // J. Appl. Phys. 1998.
V. 84. P. 3541-3554.
13. Гавриков М.Б., Таюрский А.А. Аналитическое решение смешанных задач для уравнений одномер-
ной ионизации в случае постоянных скоростей атомов и ионов // Препринты ИПМ им. М.В. Кел-
дыша. 2023. № 30.
Институт прикладной математики
Поступила в редакцию 25.05.2023 г.
имени М.В. Келдыша РАН, г. Москва,
После доработки 25.05.2023 г.
Московский государственный технический
Принята к публикации 20.07.2023 г.
университет имени Н.Э. Баумана
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 10
2023