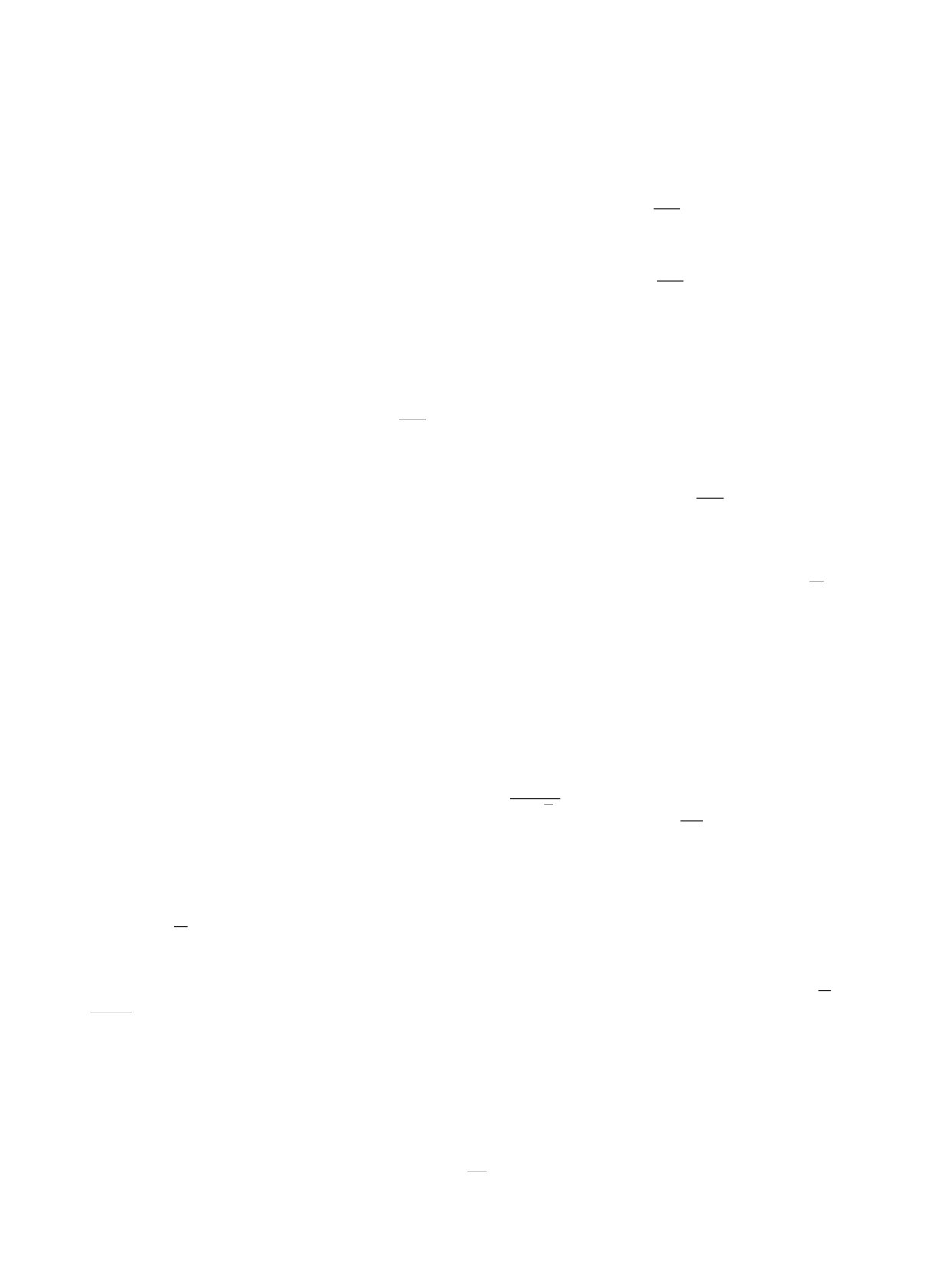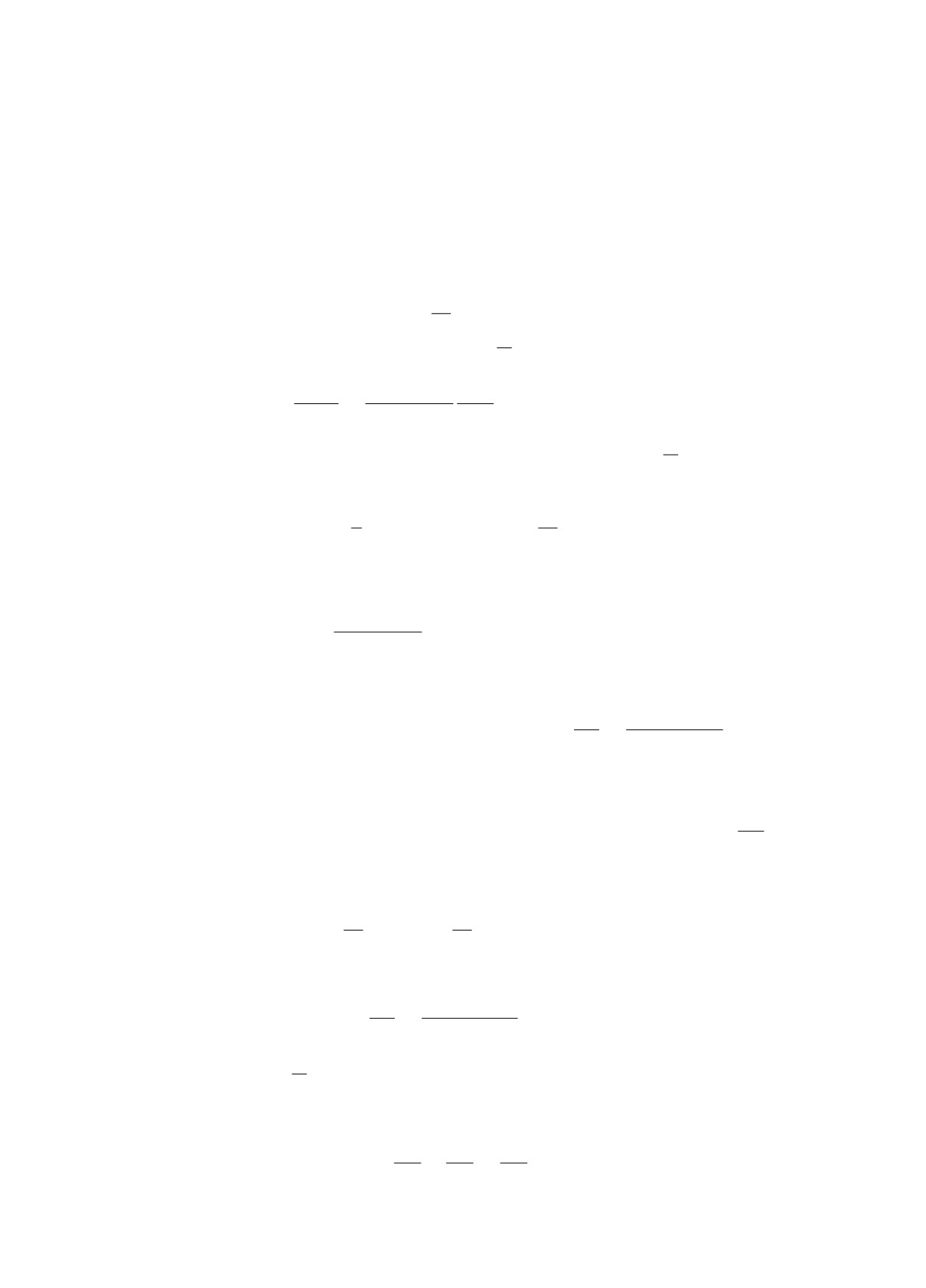ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 10, с. 1385-1396

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956.2

О ВЛИЯНИИ НЕИЗОЛИРОВАННЫХ ОСОБЕННОСТЕЙ

В МЛАДШЕМ КОЭФФИЦИЕНТЕ УРАВНЕНИЯ БИЦАДЗЕ

НА ПОСТАНОВКУ КРАЕВЫХ ЗАДАЧ

Изучено влияние неизолированных особенностей в младших коэффициентах (т.е. когда

младшие коэффициенты имеют особенности по замкнутым линиям, лежащим внутри об-

ласти) уравнения Бицадзе на постановку краевых задач. Обнаружено, что условия в задаче

Римана-Гильберта на границе области недостаточно для её решения, поэтому рассмотрена

задача, объединяющая элементы задач Римана-Гильберта на границе области и линейного

сопряжения на окружностях-носителях сингулярностей коэффициентов, лежащих внутри

области. С помощью надлежащего уточнения теоремы Келлога о конформном отображе-

нии этой области на круг исследован вопрос разрешимости этой задачи.

DOI: 10.31857/S0374064123100060, EDN: ONKXZI

Статья посвящается юбилеям моих учителей:

75-летию Александра Павловича Солдатова

и 85-летию Нусрата Раджабовича Раджабова

1. История вопроса. Классическая теорема Коши-Ковалевской гарантирует локальную

аналитичность решения линейного дифференциального уравнения, представленного в нор-

мальной форме, если его коэффициенты, правая часть и начальные данные аналитичны (в

случае вещественных переменных разлагаются в сходящиеся степенные ряды) или если ко-

эффициенты и правая часть эллиптического уравнения порядка m удовлетворяют условию

Гёльдера с показателем 0 < α < 1 (тогда производные порядка m любого решения этого

уравнения также удовлетворяют условию Гёльдера с тем же показателем).

Исследования вырождающихся эллиптических уравнений показали, что аналитичность

коэффициентов уравнения наследуется его решением. Фундаментальная система состоит из

функций, представляющих собой произведение голоморфной в окрестности точки (плоско-

сти) вырождения функции на функцию, которая может иметь особенность на указанном мно-

жестве. Эта особенность либо степенная, при этом показатель находится по коэффициентам

уравнения, либо логарифмическая, степенная и логарифмическая или экспоненциальная. Для

обоснования существования решения краевой задачи для вырождающихся уравнений, как пра-

вило, используют неявные методы построения решения (например, метод барьеров). При этом

затруднительно выяснить структуру решения и проследить, как аналитичность коэффициен-

тов и правой части уравнения отражается на решении задачи (см. работы [1-8]).

Как следует из исследований, посвящённых вырождающимся дифференциальным уравне-

ниям, на решения краевых задач может влиять особенность коэффициентов, содержащихся

в рассматриваемой области. Например, в статье [9] изучена разрешимость задачи Римана-

Гильберта для обобщённого уравнения Коши-Римана

Q(z)

w_z =

w(z) + a(z)w + b(z)w,

|z| < 1,

P (z)

где Q(z), P (z) - полиномы, причём P (z) внутри круга

|z| ≤ 1 имеет простые корни,

a(z), b(z) ∈ L^p(D) (здесь и дальше p > 2). Здесь и ниже используются стандартные обо-

значения 2∂_z = ∂_x + i∂_y,

2∂_z = ∂_x - i∂_y. Показано, что число непрерывных решений задачи

зависит не только от индекса, но и от места расположения и типа особенностей коэффициентов

уравнения.

1385

1386

РАСУЛОВ

В работе [10] для обобщённой системы Коши-Римана с сингулярной линией выявлено, что

для корректной постановки краевой задачи необходимо рассматривать задачу, объединяющую

элементы задач Римана-Гильберта (на границе области) и линейного сопряжения (на сингу-

лярном отрезке, содержащемся внутри области).

В теории эллиптических уравнений важное место занимает система уравнений Бицадзе [1,

с. 134]

u1xx - u1yy - 2u2xy = 0,

2u1xy + u2xx - u2yy = 0.

Как известно, любая эллиптическая система уравнений второго порядка с постоянными коэф-

фициентами и двумя неизвестными функциями от двух переменных приводится к одному из

уравнений [11]:

u_zz = 0

или u_zz = 0,

где u = u₁ + iu₂.

Класс задач для первого уравнения (уравнения Лапласа) хорошо изучен, в отличие от

задач для второго уравнения (уравнения Бицадзе).

С другой стороны, как следует из работ [12, 13], уравнение Бицадзе непосредственно свя-

зано с уравнением Стокса. Согласно [12] в плоском случае уравнение Стокса базируется на

функции потока u₁(x, y) и функции напряжения u₂(x, y) и имеет вид

u1xx - u1yy = -4ηu2xy,

-u1xy = η(u2yy - u2xx),

где η - материальная постоянная. Подстановка 2ηu₂ → u₂ переводит эту систему в систему

уравнений Бицадзе, поэтому исследование системы уравнений Бицадзе с младшими членами

представляет особый интерес.

Уравнение Бицадзе с младшими регулярными коэффициентами было исследовано в рабо-

тах [1, 14-18] и др. Важность изучения уравнения с главной частью u_zz и с особенностями

в младших коэффициентах была подчёркнута ещё в 80-х годах прошлого века А.В. Бицадзе.

Но эти исследования были связаны с некоторыми трудностями принципиального характера,

особенно когда коэффициенты сингулярны во внутренней точке рассматриваемой области. По-

нятие сверхсингулярных особенностей было введено Н.Р. Раджабовым [4]. В статье [19] для

уравнения Бицадзе с младшими коэффициентами, имеющими в одной внутренней точке рас-

сматриваемой области сильную особенность, найдено интегральное представление обобщён-

ного решения из класса непрерывных функций. В [20] для уравнения Бицадзе с младшими

коэффициентами, имеющими в конечном числе точек рассматриваемой области сильные осо-

бенности и интегрируемую особенность в начале координат, найдено обобщённое решение из

класса непрерывных функций задачи типа Римана-Гильберта.

В настоящей работе исследовано влияние неизолированных особенностей в младших коэф-

фициентах уравнения Бицадзе на постановку краевых задач.

2. Интегральное представление решений в явной форме. Пусть область D содер-

жит окружности γ_j = {z : |δ_j | = r_j }, где δ_j ≡ z - z_j , j = 1, n, и ограничена простым

ляпуновским контуром Γ, ориентированным против часовой стрелки, и пусть для краткости

ρ = ρ1 ...ρ_n, ρ_j(z) = δ-1j|δ_j|||z - z_j| - r_j|, j = 1,n.

∑_n

В открытом множестве D₀ = D \ γ, γ =

γ_j, рассмотрим уравнение Бицадзе с сингу-

j=1

лярными младшими коэффициентами следующего вида:

∑

a_j

a₀

u_zz +

u_z +

u=f,

(1)

ρ_j

j=1

∑_n

где a₀, a₁, . . . , an ∈ C(D), a0 = -ρ(ab + b2), a = -

a_jρ-1j и функция b(z) ∈ C(D)

j=1

аналитична в области D. Относительно правой части f уравнения предполагаем, что она

принадлежит пространству L^p(G₀), p > 2, в каждой подобласти G₀ ⊆ D₀.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

О ВЛИЯНИИ НЕИЗОЛИРОВАННЫХ ОСОБЕННОСТЕЙ

1387

В работе для уравнения Бицадзе (1) построено представление общего решения. Далее для

уравнения (1), коэффициенты которого допускают особенность первого порядка на окружно-

сти γ_j, исследована краевая задача, объединяющая элементы задач Римана-Гильберта на Γ

и линейного сопряжения на γ_j, j = 1, n.

Выбор таких коэффициентов уравнения объясняется тем, что левую часть (1) можно пред-

ставить в виде

(

)

∑

a_j

a₀

∂

u_zz +

u_z +

+ a + b (uz - bu)

(2)

ρ_j

∂z

j=1

и свести исследование к интегрированию уравнений первого порядка

U_z - (a + b)U = f, u_z + bu = U

(3)

с сингулярным коэффициентом

a₁

a_n

+...+

(4)

ρ₁

ρ_n

и регулярным коэффициентом b.

Заметим, что функция f принадлежит соболевскому пространству W1,p(D₀), если в лю-

бой подобласти G₀ ∈ D₀ её обобщённая производная f_z ∈ Lploc(G₀), p > 2.

Напомним некоторые известные факты из теории эллиптических систем, изложенные в

монографии [21] и в книге [8].

Пусть в некотором открытом множестве G на плоскости задана линейная эллиптическая

система первого порядка с постоянными старшими коэффициентами, младшие коэффициенты

и правая часть которой принадлежат Lploc(G), т.е. принадлежат W1,p(G₀) в любой ограни-

ченной области G₀, лежащей в множестве G вместе со своей границей. Тогда на основании

внутренней регулярности (см. [21]) любое слабое решение u уравнения регулярно в том смыс-

ле, что оно принадлежит классу W1,ploc(G) и удовлетворяет рассматриваемой системе. В силу

теоремы вложения функция u в действительности принадлежит классу C^μ(G₀) с показате-

лем μ ≤ (p - 2)/p. В соответствии с внутренней регулярностью решений и согласно свойству

левой части уравнения (2) в дальнейшем решение уравнения (1) предполагается регулярным

в открытом множестве D₀.

Более точно, под регулярным решением уравнения (1) в рассматриваемой области D₀ по-

нимается функция u, которая в любой замкнутой подобласти G₀ ⊆ D₀ имеет первую обоб-

щённую производную по z, принадлежащую классу L^p(G₀), и удовлетворяет этому уравне-

нию.

Уравнение (1), согласно (2), (3), сводится к интегрированию двух уравнений первого по-

рядка вида

U_z - CU = f.

(5)

Хорошо известно, что в его исследовании существенную роль играет интегральный оператор

Помпейу-Векуа [21, с. 31]

∫

f (ζ) d₂ζ

(T f)(z) = -

(6)

ζ-z

здесь и ниже d₂ζ означает элемент площади. Если f ∈ L^p(D), p > 2, то функция U =

= Tf принадлежит соболевскому пространству W1,p(D) и удовлетворяет уравнению U_z = f,

причём оператор (6) ограничен. Напомним, что имеет место следующее вложение [21, с. 39]

данных пространств в класс Гёльдера:

W1,p(D) ⊆ C^μ(D), μ = 1 -

в частности, оператор T компактен в пространствах L^p(D) и C(D). Всюду в дальнейшем

предполагается, что p > 2. Когда точное значение показателя Гёльдера μ несущественно,

вместо C^μ(D) используем обозначение H(D) [22, с. 31].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

1388

РАСУЛОВ

Пусть в уравнении (5) коэффициент C и правая часть f принадлежат классу L^p(D). Оче-

видно, что в этом случае для функции V = e^-TC U справедливо соотношение V_z = e^-TC U_z -

- Ce^-TCU = e^-TCf. Следовательно, общее решение этого уравнения определяется формулой

U = e^TCφ + (e^TCTe^-TC)f

(7)

с произвольной аналитической в области D функцией φ. Функции e^±TC рассматриваются

здесь как операторы умножения.

Теперь рассмотрим уравнение

∂u

- (a + b)u = f

(8)

∂z

с коэффициентом (4), который запишем в виде

∑

a^∗j(z - z_j)

a(z) =

+ a₀(z), a₀(z) ∈ L^p(D),

|z - z_j |(|z - z_j | - r_j )

j=1

где a^∗j ∈ C и функция b(z) ∈ C(D) аналитична в области D. В этом случае коэффициент

a имеет особенность на окружностях γ_j, j = 1, n, и решение уравнения предполагается

регулярным в множестве D₀.

Лемма 1. Пусть a₀(z) ∈ L^p(D), функция b(z) ∈ C(D) аналитична в области D и

∑_n

ω_∗ = 2

a^∗j ln ||z - z_j| - r_j|. Тогда функция

j=1

Ω(z) = ω_∗(z) + (T (a₀ + b))(z), z ∈ D₀,

(9)

удовлетворяет уравнению Ω_z = a + b.

∑_n

Доказательство проводится проверкой, что функция Ω(z) = 2

a^∗j ln ||z - z_j| - r_j| +

j=1

+(T (a₀ + b))(z) удовлетворяет уравнению Ω_z(z) = a + b с функцией

∑

a^∗j(z - z_j)

a(z) = -

+ a₀(z).

|z - z_j |(|z - z_j | - r_j)

j=1

С другой стороны, как было отмечено выше, для (a₀ + b) ∈ L^p функция T (a₀ + b) явля-

ется решением уравнения (T (a₀ + b))_z = a₀ + b. Отсюда следует, что функция Ω(z) в (9)

удовлетворяет уравнению Ω_z = a + b.

Теорема 1. Пусть функция Ω(z) определена формулой (9) и e-Ωf ∈ L^p(D). Тогда общее

решение уравнения (8) в классе C(D\γ) определяется формулой

u = e^Ω[φ + T(e-Ωf)],

где φ ∈ C(D\γ) аналитична в открытом множестве D\γ.

Из леммы 1 следует, что у функции

eΩ(z) = C₀(z)||z - z₁| - r₁|2a1 ··· ||z - z_n| - r_n|2an

C₀(z) непрерывна в замкнутой области D и всюду отлична от нуля. Поэтому, согласно тео-

реме 1, решение u(z) уравнения (9) ведет себя как

u(z) = O(1)(||z - z_j | - r_j|2aj ) при

|z - z_j | → r_j .

Заметим, что функция eΩ(z) при Re a^∗j < 0, j = 1, n (Re a^∗j > 0, j = 1, n), допускает в

окружности δ_j = r_j особенность (нуль) степенного порядка. При Re a^∗j ≥ 0, j = 1, k, эти

функции, очевидно, ограничены. Если Re a^∗j = 0, j = 1, n, т.е. a = a₀ ∈ L^p(D), то получим

обычное равенство T a = T a₀ ∈ W1,p(D).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

О ВЛИЯНИИ НЕИЗОЛИРОВАННЫХ ОСОБЕННОСТЕЙ

1389

Обратимся к уравнению (5). Пусть коэффициент C ∈ L^p(D₀), причём функция T C су-

ществует, принадлежит W1,p(D₀) и удовлетворяет уравнению (T C)_z = C. Тогда в предпо-

ложении e^-TC f ∈ L^p(D) представление (7) сохраняет свою силу по отношению к области

D₀. В частности, согласно теореме 1 оно справедливо для соответствующего уравнения с

∑_n

коэффициентом a =

a^∗jρ-1j, удовлетворяющим условию a₀(z) ∈ L^p(D). Совместно с

j=1

разложением (3) это обстоятельство позволяет описать общее решение уравнения (1).

Итак, на основании теоремы 1, приведённых выше рассуждений и при обозначениях

∑

ω_∗ = a^∗jω_j, φ ≡ φ₂

j=1

доказана следующая

Теорема 2. Пусть a₀(z) ∈ L^p(D) и Re a^∗j ≤ 0, j = 1, n. Тогда при eω∗ f ∈ L^p(D) любое

решение уравнения (1) в области D₀ определяется формулой

u = e^-Tbφ₁ + (e^-TbTeω∗+T(a0+2b))φ₂ + (e^-TbTeω∗+T(a0+2b)Te-ω∗-T(a0+b))f,

(10)

где функции φ₁, φ₂ аналитичны в области D₀, причём e-ω∗ φ₂ ∈ L^p(D), и определяются

однозначно по u.

Заметим, что согласно известному свойству интегралов типа Коши [22, с. 22] функция

h_k ∈ H(D), k = 0,1,2, где h₀ = -Tb, h₁ = T(a₀ + 2b), h₂ = T(a₀ + b).

В действительности можно утверждать больше, что показывает

Лемма 2. В условиях теоремы 2 функция h_k ∈ W1,p(D), k = 0, 1, 2.

Доказательство этой леммы содержится в статье [19].

Представление (10) после переобозначения с учётом леммы 2 можем записать в виде

u = eh0φ₁ + (eh0Teω∗+h1)φ₂ + (eh0Teω∗+h1Te-ω∗-h2)f

с некоторыми h_j ∈ W1,p(D), j = 0, 1, 2, или кратко

u=eh0φ₁ +T₀φ₂ +T₁f,

(11)

с соответствующими интегральными операторами T₀, T₁. Эти операторы действуют по фор-

мулам

∫

k₀(z,ζ)

(T₀ϕ)(z) = -

eω∗(ζ)ϕ(ζ)d₂ζ, z ∈ D,

ζ-z

где k₀(z, ζ) = eh0(z)-h1(ζ), и

∫

k₁(z,ζ)

(T₁ϕ)(z) = -

e-ω∗(ζ)ϕ(ζ)d₂ζ, z ∈ D,

ζ-z

где k₁(z, ζ) = eh0(z)-h1(ζ)[h(z) - h(ζ)] и h = T eh1+ω∗ ∈ W1,p(D).

Из (10) или (11) видно, что аналитические функции φ₁, φ₂ определяются по u однозначно

и восстанавливаются по формулам

φ₂ = e-ω∗+h0+^h(u_z - bu) + Te-ω∗+h0+^hf, φ₁ = e-h0(u - T₀φ₂ - T₁f).

(12)

3. Постановка краевой задачи. Полученное интегральное представление (10) позволя-

ет для уравнения (1) исследовать краевую задачу, объединяющую элементы задач Римана-

Гильберта на границе Γ и линейного сопряжения на окружностях γ_j , j = 1, n.

Задача R. Найти регулярное решение уравнения (1) в классе

u, e-ω∗ (u_z - bu) ∈ C^μ(D_j ), j = 1, n,

0 < μ < 1 - 2/p,

(13)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

1390

РАСУЛОВ

удовлетворяющее краевым условиям

ReG₁u|_Γ = g₁, Re G₂e-ω∗(u_z - bu)|_Γ = g₂, t ∈ Γ,

(14)

(e-Ωu)⁺(t) - G_j (t)(e-Ωu)^-(t) = g_j (t), t ∈ γ_j , j = 1, n,

(15)

(e-Ωu)⁺(t) - (e-Ωu)^-(t) = 0, t ∈ γ_k, k = 1, 2, . . . , j - 1, j + 1, . . . , n,

e-ω∗(u_z - bu)⁺(t) = e-ω∗(u_z - bu)^-(t), t ∈ γ_j, j = 1,n,

(16)

где знаки “ + ” и “ - ” указывают на граничные значения со стороны D+j и D^-j.

Эту задачу рассматриваем при следующих требованиях на её данные:

1) e-ω∗ f ∈ L^p(D);

2) функции G_k, g_k ∈ C^ν (Γ), k = 1, 2, j, причём G₁ и G₂ всюду отличны от нуля, G_j (t) ∈

∈ H(γ_j) также всюду отличны от нуля, причём lnG_j ∈ H(γ_j);

3) g(t) ∈ H(Γ), g_j (t) ∈ H(γ_j), j = 1, n.

Как следует из условий задачи, одна из окружностей γ_j , лежащих внутри Γ, является

носителем условий задачи линейного сопряжения (15), а остальные окружности, лежащие

внутри Γ, являются носителями условий сопряжения (16).

Замечание. Из постановки задачи R видно, что окружности γ_j , j = 1, n, являющиеся

носителями сингулярностей, разбивают область на части, на границах которых необходимо

дополнительно задавать граничные условия типа (15) и (16).

4. Классическая задача Римана-Гильберта. Напомним постановку классической за-

дачи Римана-Гильберта [22, 23]: найти аналитическую в области D функцию φ(z) ∈ H(D),

удовлетворяющую на границе Γ = ∂D условию

ReGφ|_Γ = g,

(17)

где функция G = G₁ + iG₂ ∈ H(Γ) всюду отлична от нуля, H - класс функций, удовлетворя-

ющих условию Гёльдера с некоторым показателем [22, с. 18, 145].

Далее воспользуемся компактным изложением А.П. Солдатова о решении задачи Римана-

Гильберта и приведём некоторые факты о разрешимости классической задачи Римана-Гиль-

берта (17) в случае единичного круга D с границей T = ∂D. C этой целью функцию φ

продолжим в область C \ D = {z : |z| > 1}, положив, что она удовлетворяет условию φ = φ_∗,

где φ_∗ определяется с помощью инверсии φ_∗(z) = φ(1/z). Операция φ → φ_∗, являющаяся

линейной, инволютивна над полем R, т.е. (φ_∗)_∗ = φ. Видно, что φ^±∗(t) = φ^∓, t ∈ T. Задачу

(17) с коэффициентом G можем представить в виде

φ⁺ -Gφ^- = g,

(18)

где

G₌ -G/G и g = 2g/G.

Последняя задача с коэффициентом

G исследуется с помощью так называемой

^G-канони-

ческой функции. По определению под ней понимается функция X(z), которая аналитична в

каждой связной компоненте D, C \ D и продолжается по непрерывности на её замыкание D,

C \ D; всюду отлична от нуля, включая её граничные значения X^±; вместе с X-1(z) имеет

конечный порядок на бесконечности и удовлетворяет соотношению

X⁺ =GX^-.

Определим индекс Коши [22, с. 125]

æ = Ind_ΓG =

arg G(t)|_Γ.

2π

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

О ВЛИЯНИИ НЕИЗОЛИРОВАННЫХ ОСОБЕННОСТЕЙ

1391

Лемма 3. Пусть æ = Ind_ΓG, так что функция θ(t) = arg G(t) - æarg t ∈ H(T), и пусть

{

∫

|z| < 1,

π - 2θ(t)

R(z) =

Θ(z) =

dt.

z^2æ,

|z| > 1,

2π

t-z

Тогда функция X(z) = R(z)eΘ(z)-Θ(0)/2 является

G-канонической и обладает свойством

X_∗(z) = X(z)z-2æ.

Теорема 3. В условиях леммы 3 все решения задачи (17) в классе H(D) описываются

формулой

φ(z) = Ig (z) + X(z)p(z), p ∈ P0-2æ,

(19)

где

∫

X(z)

g(t)

Ig (z) ≡

πi

G(t)X⁺(t) t - z

а функция g удовлетворяет условиям ортогональности

∫

g(t)

q(t) dt = 0, q ∈ P02æ-2,

(20)

G(t)X⁺(t)

где P0k - класс многочленов степени k.

Доказательство. Как уже отмечалось, при дополнительном условии φ = φ_∗ задача (17)

эквивалентна задаче (18). Последняя представляет собой задачу линейного сопряжения по

отношению к

G = -G/G и g = f/G.

Очевидно, что при æ ≤ 0 размерность пространства P0-2æ над полем R равна -2æ + 1,

а при æ ≥ 0 размерность пространства P02æ-2 равна 2æ - 1. Во всех случаях индекс задачи

(17) равен -2æ + 1 и, в частности, всегда отличен от нуля.

Рассмотрим функцию

A(z) = Θ(z) - Θ(0)/2, z ∈ D,

фигурирующую в представлении канонической функции X(z). В явном виде запишем

∫

πi

θ(t) dt

πi

A(z) =

θ(t) d₁t, A(0) =

θ(t) d₁t.

t-z

2π

По формуле Сохоцкого-Племеля отсюда имеем

∫

πi

θ(t) dt

A⁺(t₀) =

- ia(t₀) -

θ(t) d₁t.

t-t₀

2π

Полагая e2iβ = t₀/t, можем записать равенства

id₁t

i - ctgβ

d₁t,

t-t₀

1-e2iβ

так что

∫

πi

A⁺(t₀) =

- ia(t₀) +

θ(t) ctg β d₁t.

2π

Следовательно, функцию A(z) можем однозначно определить по условиям

∫

ImA⁺ =

- θ, ReA(0) = -

θ(t) d₁t.

(21)

2π

Теорема доказана.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

1392

РАСУЛОВ

Обратимся к общему случаю односвязной области D. Пусть простой контур Γ = ∂D

принадлежит классу C1,μ, тогда по теореме Келлога конформное отображение w = ω(z)

этой области на единичный круг D принадлежит классу C1,μ(D) или, что равносильно, его

производная ω^′ ∈ H(D). Зафиксируем точку z₀ ∈ D из условия ω(z₀) = 0.

Теорема 4. Пусть æ = Ind_ΓG, так что функция θ(t) = arg G(t)-æ arg t ∈ H(Γ), и пусть

X(z) = eΘ(z)-Θ(0)/2, где функция Θ ∈ H(D) определяется как решение задачи Дирихле

∫

Im Θ⁺ =

- θ, ReΘ(z₀) = -

θ(t)|ω^′(t)| d₁t.

2π

Тогда все решения задачи (17) в классе H(D) описываются формулой

∫

X(z)

g(t)

ω^′(t)dt

φ(z) =

+ X(z)p[ω(z)], p ∈ P0-2æ,

(22)

πi

G(t)X⁺(t) ω(t) - ω(z)

где функция g удовлетворяет условиям ортогональности

∫

g(t)

q[ω(t)]ω^′(t) dt = 0, q ∈ P02æ-2.

(23)

G(t)X⁺(t)

Доказательство почти очевидно. Пусть простой контур Γ = ∂D принадлежит классу

C1,μ, тогда по теореме Келлога конформное отображение w = ω(z) этой области на единич-

ный круг D принадлежит классу C1,μ(D). Рассмотрим в области D задачу

ReG₀φ|_Γ = g₀

(24)

с коэффициентом G₀ = G◦ω-1. Пусть A₀ ∈ H(D₀) есть решение задачи (21) по отношению к

соответствующей функции α₀ = arg G₀(t) - æarg t ∈ H(Γ), которая определяется аналогично

лемме 3, и пусть X₀ = eA0 . Тогда согласно (21) функция A = A₀ ◦ ω и аналогичным образом

связаны функции X и X₀. Применим теорему 4 к задаче (24), добавив к соответствующим

обозначениям в соотношениях (19), (20) индекс нуль. Тогда при подстановке ω они перейдут

в соотношения (22), (23), что и завершает доказательство теоремы.

5. Решение задачи R. Из (10) (или из (11)) видно, что аналитические функции φ₁, φ₂

определяются по u однозначно и восстанавливаются по формулам (12).

В рассматриваемом случае (p > 2) пространство W1,p(D) вложено в гёльдерово прост-

ранство H(D) (причём Cμ0 (D) ⊆ H(D) с показателем μ₀ = 1 - 2/p).

Следовательно, при μ < μ₀ соответствие между решением u по формуле (10) уравне-

ния (1) из класса (13) и парой аналитических в D функций φ₁, φ₂ ∈ H(D) будет взаимно-

однозначным.

Положив

G₁ = G₁e-h0-h|_Γ,

G₂ = G₂eh0 |_Γ,

условия (14) задачи R с ограниченными операторами R_j : H(D) → H(Γ), действующими по

формулам

R₀ϕ = ReG₁[T₀ϕ]|_Γ, R₁ϕ = Re G₁[T₁ϕ]|_Γ, R₂ϕ = Re G₂ϕ|_Γ,

примут вид

ReG2φ₂|_Γ = g₂ - R₂f ≡

g₂, ReG1φ₁|_Γ - R₀φ₂ = g₁ - R₁f ≡

g₁,

а условия (15) и (16) задачи R запишутся как

(φ⁺¹ - G_j φ-1)|γj = g^∗j, φ⁺²(t) = φ-2(t), t ∈ γ_k, k = 1, 2, . . . , j - 1, j + 1, . . . n,

где g^∗j = g_j - e-h0 (F⁺ - G_j F^-), F = T₀φ₂ + T₁f.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

О ВЛИЯНИИ НЕИЗОЛИРОВАННЫХ ОСОБЕННОСТЕЙ

1393

В результате задача R будет сведена к эквивалентной задаче

ReG2φ₂|_Γ = g₂ - R₂f ≡

g₂, ReG1φ₁|_Γ - R₀φ₂ = g₁ - R₁f ≡

g₁, (φ⁺¹ - G_jφ-1)|γj = g^∗j,

φ⁺²(t) = φ-2(t), t ∈ γ_k, k = 1,2,... ,j - 1,j + 1,... ,n.

Таким образом, задача R приводится к последовательному решению двух задач (см. ни-

же), в результате решения которых определим соответственно значения искомых функций

φ₁(z) и φ₂(z).

Решение задачи R рассмотрим в двух случаях: когда область D ≡ D - единичный круг и

когда область D - произвольная конечная область, ограниченная гладким замкнутым конту-

ром Γ.

Сперва рассмотрим задачу R в случае единичного круга, т.е. относительно области D =

= {z : |z| ≤ 1}. Тогда окружности γ_k = {z : |z - z_k| = r_k < 1}, k = 1, 2, . . . , j - 1, j + 1, . . . , n,

являются носителями граничных данных в силу условий (16).

Согласно второму условию (16) и первой формуле обращения для функции φ₂ в (12) при-

ходим к эквивалентной задаче

φ⁺²(t) = φ-2(t), t ∈ γ_j, j = 1,n,

(25)

где через φ⁺²(t) и φ-2(t) обозначены предельные значения функций φ⁺²(z) и φ-2(z) соот-

ветственно из внутренних частей областей D_k, k = 1, n, в их внешние части и наоборот. Отме-

тим, что мы воспользовались свойствами функций f₀ = e-ω∗+h0+^hf ∈ L^p, p > 2, (T f₀)^±(t) ∈

∈ H(D) и (h₀ + h)⁺ = (h₀ + h)^-, (Tf₀)⁺(t) = (Tf₀)^-(t), t ∈ γ_j, j = 1,n.

Следовательно, условия (25) определяют единую аналитическую функцию φ₂ во всей об-

ласти D, включая все окружности γ_j , j = 1, n. Этот факт позволяет нам изучить второе

условие в (14) и прийти к краевой задаче Гильберта со следующими данными:

ReG2φ₂|_T = g₂,

(26)

коэффициент

G₂ = G₂eh0+^h|_T, индекс

æ₂ =

argG2(t)|_T =

arg G₂(t)|_T

2π

и правая часть

g₂ = g₂ - Re [G₂eh0+^hTf₀|_T],

и сформулировать её решение на основе теорем 2 и 3.

Теорема 5. Пусть æ₂ = Ind_ΓG₂, так что функция θ₂(t) = arg G₂(t) - æ₂arg t ∈ H(T),

и пусть X₂(z) = eΘ2(z)-Θ2(0)/2, где функция Θ₂ ∈ H(D) определяется как решение задачи

Дирихле

∫

Im Θ⁺² =

- θ₂, ReΘ₂(z₀) = -

θ₂(t)d₁t.

2π

В условиях леммы 3 и теорем 2, 3 все решения задачи (26) в классе H(D) описываются

формулой

φ₂(z) = Ig₂ (z) + X₂(z)p(z), p ∈ P⁰

-2æ₂

где

∫

X₂(z)

g₂(t)

Ig₂ (z) ≡

πi

G₂(t)X⁺²(t) t - z

а функция g₂(z) удовлетворяет условиям ортогональности

∫

g₂(t)

q(t) dt = 0, q ∈ P^02æ

2-2

G₂(t)X⁺²(t)

где P0k - класс многочленов степени k.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

1394

РАСУЛОВ

Теперь, используя первое условие в (16), интегральное представление (10), формулу обра-

щения для функции φ₁ в (12) и условие (15), получаем для φ₁ краевую задачу

ReG₀φ₁|_Γ = g₀, (φ⁺¹ - G_jφ-1)|_l = g^∗j,

(27)

где G₀ = G₁(eh0 )|_Γ, g₀ = g₁ - Re [G₁F |_Γ], g^∗j = g_j - e-h0 (F⁺ - G_j F^-), F = T₀φ₂ + T₁f.

Теорема 6. При выполнении условий теоремы 1 фредгольмова задача (27) рассматрива-

ется в классе (13) и её индекс равен 1 - 2æ₁, где

æ₁ =

arg G₁(t)|_Γ.

2π

Более точно, все решения задачи (27) в классе H(D) описываются формулой

∫

X₁(z)

g∗1(t)

φ₁(z) =

+ X₁(z)p(z), p ∈ P0-2æ

πi

G₁(t)X⁺¹(t) t - z

где X₁(z) = eΘ1(z)-Θ1(0)/2 - каноническая функция, функция Θ₁ ∈ H(D) определяется как

решение задачи Дирихле

∫

Im Θ⁺¹ =

- θ₂, ReΘ₁(z₀) = -

θ₁(t)d₁t,

2π

в которой θ₁(t) = arg G₁(t) - æ₁arg t ∈ H(T) и функция g∗1 удовлетворяют условиям орто-

гональности

∫

g∗1(t)

p(t) dt = 0, p ∈ P^02æ

1-2

G₁(t)X⁺(t)

причём

∫

g^∗j(t)

g∗1 = g_j - Re [αe^Ω(Tf₀)|_T] - Re [GX₁ψ]|_T, ψ(z) =

dt,

2πi

X+j(t)(t - z)

g∗1 = g_j - e-h0 (F⁺ - G_jF^-), F = T₀φ₂ + T₁f.

Доказательство. По теореме 2 общее решение u уравнения (1) в классе (13) представимо

в виде (10) (или в краткой форме в виде (11)), где функция φ принадлежит H(D^±j). Кроме

того, в силу леммы 1 функция Ω ∈ H(Γ). Поэтому подставим данное представление в условия

(14), (15) и используем формулу обращения для искомой функции φ₁ из (12). Заметим, что

arg G₀|_Γ =

arg G₁|_Γ = æ₁.

(28)

2π

Согласно хорошо известным свойствам интеграла типа Коши [22], функция

(

∫

)

ln G_j (t)(t) dt

X_j(z) = exp

z∈D+j

^⋃D^-j,

(29)

2πi

t-z

γ_j

принадлежит классу H(D^±j), j = 1, 2, причём её граничное значение ln X^±j ∈ H(γ_j ) на

окружности γ_j удовлетворяет краевому условию X+j = G_j X^-j. Поэтому второе краевое усло-

вие в (27) можно записать в виде

φ⁺¹

φ-1

g^∗j

X+j

X^-j

X⁺

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

О ВЛИЯНИИ НЕИЗОЛИРОВАННЫХ ОСОБЕННОСТЕЙ

1395

Функция

∫

g^∗j(t)

ψ(z) =

2πi

X+j(t)(t - z)

γ_j

принадлежит классу H(D^±j) и удовлетворяет краевому условию

(t)

g^∗j

ψ⁺(t) - ψ^-(t) =

X+j(t)

Следовательно, разность

φ₁(z)

φ₀(z) =

- ψ(z)

(30)

X_j(z)

аналитична в области D и принадлежит классу H(D). Подстановка формул (29) и (30) в (27)

приводит к эквивалентной задаче Римана-Гильберта:

Re(α₀φ₀)|_T = g₀,

где α₀ = G₁X_j e-h0-h|_T и g₀ = g₁ - Re [G₁e-h0-hX_j ψ]|_T.

Равенство (28) сохраняется и для α₀, G_j .

Резюмируя результаты исследований, сформулированные для единичного круга в теоре-

мах 5 и 6, используя теорему Келлога, приходим к результату, представляющему решение

задачи R для области D₀. При этом сохраняем обозначения формул как в теоремах 1-6.

Теорема 7. Пусть выполнены условия теоремы 2 и æ_k = Ind_ΓG_k, k = 1, 2, так что

функция θ_k(t) = arg G_k(t)-æ_karg t ∈ H(Γ), и пусть X_k(z) = R_k(z)eΘk (z)-Θk(0)/2, где функция

Θ_k ∈ H(D) аналитична в области D и её мнимая часть определяется как решение задачи

Дирихле

∫

Im Θ+k =

- θ_k, Re Θ_k(z₀) = -

θ_k(t)|ω^′(t)|d₁t, k = 1,2.

2π

Тогда все решения задачи R в классе H(D) описываются формулой

u=eg0φ₂ +T₀φ₁ +T₁f,

в которой аналитические функции φ_k(z), k = 1, 2, определяются формулами

∫

X_k(z)

gk(t)

ω^′(t)dt

φ_k(z) =

+ X_k(z)p_k[ω(z)], p_k ∈ P⁰

k = 1,2,

−2æ_k

πi

Gk(t)X^k(t)ω(t)-ω(z)

где функция g_k удовлетворяет условиям ортогональности

∫

gk(t)

q[ω(t)]ω^′(t) dt = 0, q ∈ P^02æ

k = 1,2.

k-2

Gk(t)X_k

(t)

СПИСОК ЛИТЕРАТУРЫ

1. Бицадзе А.В. Некоторые классы уравнений в частных производных. М., 1981.

2. Смирнов М.М. Вырождающиеся гиперболические уравнения. Минск, 1997.

3. Солдатов А.П. Одномеpные сингуляpные опеpатоpы и кpаевые задачи теоpии функций. М., 1991.

4. Раджабов Н.Р. Введение в теорию дифференциальных уравнений в частных производных со сверх-

сингулярными коэффициентами. Душанбе, 1992.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023

7^∗

1396

РАСУЛОВ

5. Ломов С.А., Ломов И.С. Основы математической теории пограничного слоя. М., 2011.

6. Коровина М.В. Дифференциальные уравнения с коническим вырождением в пространствах с

асимптотиками // Дифференц. уравнения. 2009. Т. 45. № 9. С. 1249-1258.

7. Ломов И.С. Метод регуляризации сингулярных возмущений и исследование нерегулярно вырож-

дающихся эллиптических задач. Некоторые проблемы теории возмущений и метод регуляризации

// Сб. науч. тр., посвящ. 100-летию со дня рождения Сергея Александровича Ломова. М., 2023.

C. 105-122.

8. Берс Л., Джон Ф., Шехтер М. Уравнения с частными производными. М., 1966.

9. Begehr H., Dao-Qing Dai. On continuous solutions of a generalized Cauchy-Riemann system with more

than one singularity // J. Differ. Equat. 2004. V. 196. P. 67-90.

10. Расулов А.Б., Солдатов А.П. Краевая задача для обобщённого уравнения Коши-Римана с сингу-

лярными коэффициентами // Дифференц. уравнения. 2016. Т. 52. № 5. С. 637-650.

11. Фролов П.С. О компонентах связности вещественных эллиптических систем на плоскости // Докл.

АН СССР. 1968. Т. 181. № 6. С. 1350-1353.

12. Bochev P.B. Analysis of least-squares finite element methods Muhammad Tahir, A.R. Davies for the

Navier-Stokes equations // Siam J. Numer. Anal. 1997. V. 34. № 5. P. 1817-1844.

13. Tahir M., Davies A.R. Stokes-Bitsadze problem - I // Punjab University J. of Math. 2005. V. 32.

P. 77-90.

14. Солдатов А.П. Эллиптические системы второго порядка в полуплоскости // Изв. РАН. 2006. Т. 70.

№ 6. С. 161-192.

15. Сакс Р.С. Краевые задачи для эллиптических систем дифференциальных уравнений. Новосибирск,

1975.

16. Товмасян Н.Е. Эффективные методы решения задачи Дирихле для эллиптических систем диффе-

ренциальных уравнений второго порядка с постоянными коэффициентами в областях, ограничен-

ных эллипсом // Дифференц. уравнения. 1969. Т. 5. № 1. C. 60-71.

17. Tovmasyan N.E. Boundary Value Problems for Partial Differential Equations and Applications in

Electrodynamics. Singapore, 1994.

18. Бабаян А.О. Об одной краевой задаче для уравнения Бицадзе в единичном круге // Изв. HAH

Армении. Математика. 2007. Т. 42. № 4. C. 3-10.

19. Солдатов А.П., Расулов А.Б. Уравнение Бицадзе с сильными особенностями в младших коэффи-

циентах // Дифференц. уравнения. 2018. Т. 54. № 2. С. 238-248.

20. Rasulov A.B., Fedorov Yu.S., Sergeeva A.M. Integral representations of solutions for the Bitsadze equation

with the set of supersingular points in the lower coefficients // Proc. Intern. Conf. on Appl. and Eng.

Math. (ICAEM). August 27-29, 2019. Taxila, Pakistan. Danvers, 2019. P. 13-17.

21. Векуа И.Н. Обобщённые аналитические функции. М., 1959.

22. Мусхелишвили Н.И. Сингулярные интегральные уравнения. М., 1968.

23. Гахов Ф.Д. Краевые задачи. М., 1977.

Национальный исследовательский университет

Поступила в редакцию 11.05.2023 г.

“Московский энергетический институт”

После доработки 15.08.2023 г.

Принята к публикации 25.08.2023 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 10

2023