ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 11, с. 1500-1514

ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.968.48

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ НЕЛИНЕЙНЫХ

ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ТИПА СВЁРТКИ

НА ВСЕЙ ЧИСЛОВОЙ ПРЯМОЙ

Для специальной системы интегральных уравнений свёрточного типа с монотонной и вы-

пуклой нелинейностью, естественно возникающей при поиске стационарных или предель-

ных состояний в различных динамических моделях прикладного характера, например в

моделях распространения эпидемий, доказаны теоремы существования либо отсутствия

нетривиального ограниченного решения с пределами на ±∞ в зависимости от этих значе-

ний и структуры матричного ядра исследуемой системы. Также изучен вопрос единствен-

ности такого решения при его наличии. Приведены конкретные примеры систем, парамет-

ры которых удовлетворяют ограничениям сформулированных теорем.

DOI: 10.31857/S0374064123110055, EDN: PDZECG

Введение. В настоящей работе изучается существование нетривиального решения систе-

мы нелинейных интегральных уравнений типа свёртки

∞

∫

∑

f_i(x) =

λ_j(x)

K_ij(x - t)G_j(f_j(t))dt, i = 1,n, x ∈ R,

(1)

j=1

-∞

относительно искомой ограниченной на числовой прямой вектор-функции f = (f₁, . . . , f_n)^т,

имеющего конечные пределы на ±∞, где^т - знак транспонирования. При этом предполагает-

ся, что матричное ядро K := K(x) = (K_ij (x))ni,j=1 (здесь и далее, если не оговорено противное,

индексы i и j изменяются от 1 до n) обладает следующими свойствами:

a) симметрично K = K^т и чётно K(-x) = K(x);

b) элементы ядра положительны, непрерывны, ограничены∫и интегрируемы на всей пря-

∞

мой, при этом спектральный радиус матрицы A = (a_ij ), a_ij =

K_ij(x)dx, равен единице;

-∞

∫_∞

c) элементы ядра монотонно убывают при удалении от нуля, а

|x|K_ij (x) dx < +∞.

-∞

В силу свойств a), b) и теоремы Перрона (см. [1, с. 260]) у матрицы A существует положи-

тельный собственный вектор с собственным числом единица - спектральным радиусом этой

матрицы. Зафиксируем такой вектор и обозначим его через η.

Понятно, что разрешимость системы (1) может зависеть и от функций G_j и λ_j на прямой.

Относительно первых будем предполагать, что каждая из них:

A) непрерывная и монотонно возрастающая на всей прямой;

B) строго выпуклая вверх на положительной полуоси, G_i(η_i) = η_i;

C) нечетная.

И пусть каждая из функций λ_i :

I) непрерывна, положительна, не превосходит единицы и отделена от нуля;

II) имеет единичные пределы на ±∞ и интегрируема на прямой разностью 1 - λ_i.

Положим ϵ_i = inf

λ_i(x). В силу I) имеем ϵ_i > 0.

x∈R

При различных значениях параметров K, G_j и λ_j система (1) естественно возникает в

различных разделах математической физики, в эконометрике, в математической биологии.

Например, скалярные и векторные интегральные уравнения такого типа встречаются в ки-

нетической теории газов (при изучении нелинейного интегро-дифференциального уравнения

1500

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ

1501

Больцмана в рамках модифицированной модели Бхатнагара-Гросса-Крука), в теории нели-

нейного переноса излучения (в неоднородных средах и в спектральных линиях), в динамиче-

ской теории p-адических открытых, замкнутых и открыто-замкнутых струн (для скалярного

поля тахионов), в математической теории распределения дохода (в рамках модифицированной

нелинейной модели Саргана) и в математической теории распространения эпидемических за-

болеваний (в рамках модели Дикмана-Капера) (см. [2-12]). При единичных λ_i существование

и единственность ограниченного монотонно возрастающего нечётного непрерывного решения

системы (1) с граничными условиями lim

f_i(x) = ±η_i обсуждались в работах [13] и [14], а

x→±∞

при λ_i(x) ≥ 1 аналогичные вопросы изучались в [15]. Отметим также, что скалярные аналоги

системы (1) достаточно подробно исследованы в статьях [16-20] при различных ограничениях

на параметры системы.

Как отмечено выше, мы ищем решение системы (1) с конечными пределами на бесконеч-

ности. Обозначим

γ_i := lim

f_i(x), β_i := lim

f_i(x).

x→-∞

x→+∞

Сначала вопрос существования или отсутствия нетривиального решения этой системы бу-

дет исследован при единичных значениях λ_j в следующих случаях:

p₁) γ_i ≥ 0, β_i ≥ 0;

p₂) γ_i ≤ 0, β_i ≤ 0;

p₃) γ_i < 0, β_i > 0;

p₄) γ_i > 0, β_i < 0.

Покажем, что у системы (1) нет нетривиальных ограниченных решений в первых двух

случаях (и при единичных λ_i), есть монотонное решение в последних двух (где применим

результаты из [13] и [14])). Затем, при λ_i(x) ≡ 1, докажем существование и единственность

непрерывного положительного решения системы (1) с предельными условиями

lim

f_i(x) = η_i

x→±∞

и интегрируемыми разностями η_i - f_i.

Далее будут приведены параметры системы (1), имеющие прикладной характер и удовле-

творяющие всем условиям доказанных теорем.

1. Обозначения и вспомогательные факты.

1.1. Существование решения при λ_j ≡ 1. Наряду с системой (1), при единичных λ_j

рассмотрим следующую систему интегральных уравнений с суммарно-разностным ядром на

полупрямой R⁺ = [0, +∞):

∞

∫

∑

Q_i(ϕ_i(x)) =

(K_ij (x - t) - K_ij(x + t))ϕ_j (t) dt,

(2)

j=1 0

относительно неотрицательной ограниченной вектор-функции ϕ(x) = (ϕ₁(x), . . . , ϕ_n(x))^т, где

Q_i - обратная функция к G_i на R⁺. Согласно [13] система (2) имеет нетривиальное непре-

рывное неубывающее решение с нулевым значением в нуле, положительным вне нуля и пре-

дельным значением η на бесконечности и, кроме того, с интегрируемой разностью η - ϕ.

Прямые вычисления показывают, что функции

{

Q_i(ϕ_i(x)),

если x ≥ 0,

f_i(x) =

-Q_i(ϕ_i(-x)),

если x < 0,

являются решением исходной системы (1) при единичных λ_i. Это решение непрерывное,

нечётное, неубывающее с предельными значениями ±η и интегрируемыми разностями ±η -f

на ±∞ соответственно.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1502

ДАВЫДОВ и др.

В силу нечётности функций G_j решением системы (1) является и вектор-функция -f, а

также сдвиги f^c(x) = f(x + c), c ∈ R, найденного решения, в чем легко убедиться прямой

проверкой (напомним, что рассматривается случай единичных параметров λ_j ).

1.2. Априорная оценка ограниченного решения системы (1). Пусть f^∗ - ограни-

ченное решение системы (1) на всей прямой. Положим

α_i := sup|f^∗i(x)|.

x∈R

Имеет место

Лемма 1. При условиях a), b), A)-C) и I) имеет место следующая оценка сверху:

α_i ≤ η_i, i = 1,n.

Доказательство. В силу K_ij > 0, нечётности и монотонности функций G_j из (1) имеем

∫

∞

∫

∞

∑

|f^∗i(x)| ≤

K_ij(x - t)|G_j(f^∗j(t))|dt =

K_ij(x - t)G_j(|f^∗j(t)|)dt ≤

j=1_-∞

∫

∞

∑

Gj (αj )

≤ G_j(α_j) K_ij(y)dy =

a_ijη_j

≤ max

a_ijη_j,

η_j

1≤j≤n

j=1

-∞

откуда в силу определения супремума и равенства Aη = η получим

)

⁽G_j(α_j)

α_i ≤ Mη_i c M = max

(3)

1≤j≤n

η_j

Взяв в (3) вместо индекса i индекс j₀, при котором достигается максимум M, имеем

αj0 ≤ Gj0(αj0 ).

Так как αj0 ≥ 0, то в силу непрерывности и строгой выпуклости функции Gj0 вверх на R⁺

из соотношения Gj0 (ηj0 ) = ηj0 получаем, что последнее неравенство возможно только при

αj0 ≤ ηj0 . Отсюда, с учётом монотонности функции Gj0 и (3), находим

Gj₀ (ηj₀ )

α_i ≤ η_i

=η_i.

ηj0

Лемма доказана.

1.3. Разрешимость вспомогательной системы уравнений. Рассмотрим вспомога-

тельную систему уравнений

∑

ξ_i =

a_ijε_jG_j(ξ_j)

(4)

j=1

относительно неизвестного вектора ξ с неотрицательными компонентами, где

ε_j := inf

λ_j(x) ∈ (0,1),

(5)

x∈R

а матрица A = (a_ij ) описана выше. Имеет место

Лемма 2. Пусть матрица A симметрична, имеет положительные компоненты и еди-

ничный спектральный радиус. Тогда система уравнений (4) имеет не более одного неотрица-

тельного ненулевого решения, если выполнены условия A), B) и (5).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ

1503

Доказательство. Допустим противное, т.е. что система (4) имеет два различных таких

решения ξ

ξ, и пусть ξ_i∗

ξ_i∗. Отметим, что все компоненты этих решений положитель-

ны, поскольку все слагаемые в правой части системы неотрицательны в силу наложенных

условий, при этом слагаемое для положительной компоненты решения положительно. В силу

положительности чисел ε_j и a_ij из (4) имеем

∑

|ξ_i

ξ_i| ≤

a_ijε_j|G_j(ξ_j) - G_j

ξ_j)|.

(6)

j=1

Используя симметричность матрицы A, из (6) найдём

∑

ε_iG_i

ξ_i)|ξ_i

ξ_i| ≤

ε_iG_i

ξ_i)

a_ijε_j|G_j(ξ_j) - G_j

ξ_j)| =

i=1

j=1

∑

= ε_j|G_j(ξ_j)-G_j

ξ_j)|

a_jiε_iG_i

ξ_i) =

ε_j

ξ_j|G_j(ξ_j) - G_j

ξ_j)|

j=1

i=1

j=1

или

∑

ε_i(G_i

ξ_i)|ξ_i

ξ_i|

ξ_i|G_i(ξ_i) - G_i

ξ_i)|) ≤ 0.

i=1

Обозначим Π := {i ∈ {1, 2, . . . , n} : ξ_i

ξ_i}. Очевидно, что Π = ∅, так как i^∗ ∈ Π.

Для индексов, не лежащих в Π, слагаемые в последней сумме равны нулю, а для оставшихся

слагаемых эту сумму можно записать в виде

)

∑

⁽G_i

ξ_i)

|G_i(ξ_i) - G_i

ξ_i)|

ε_i

ξ_i|ξ_i

ξ_i|

≤ 0.

ξ_i

|ξ_i

ξ_i|

i∈Π

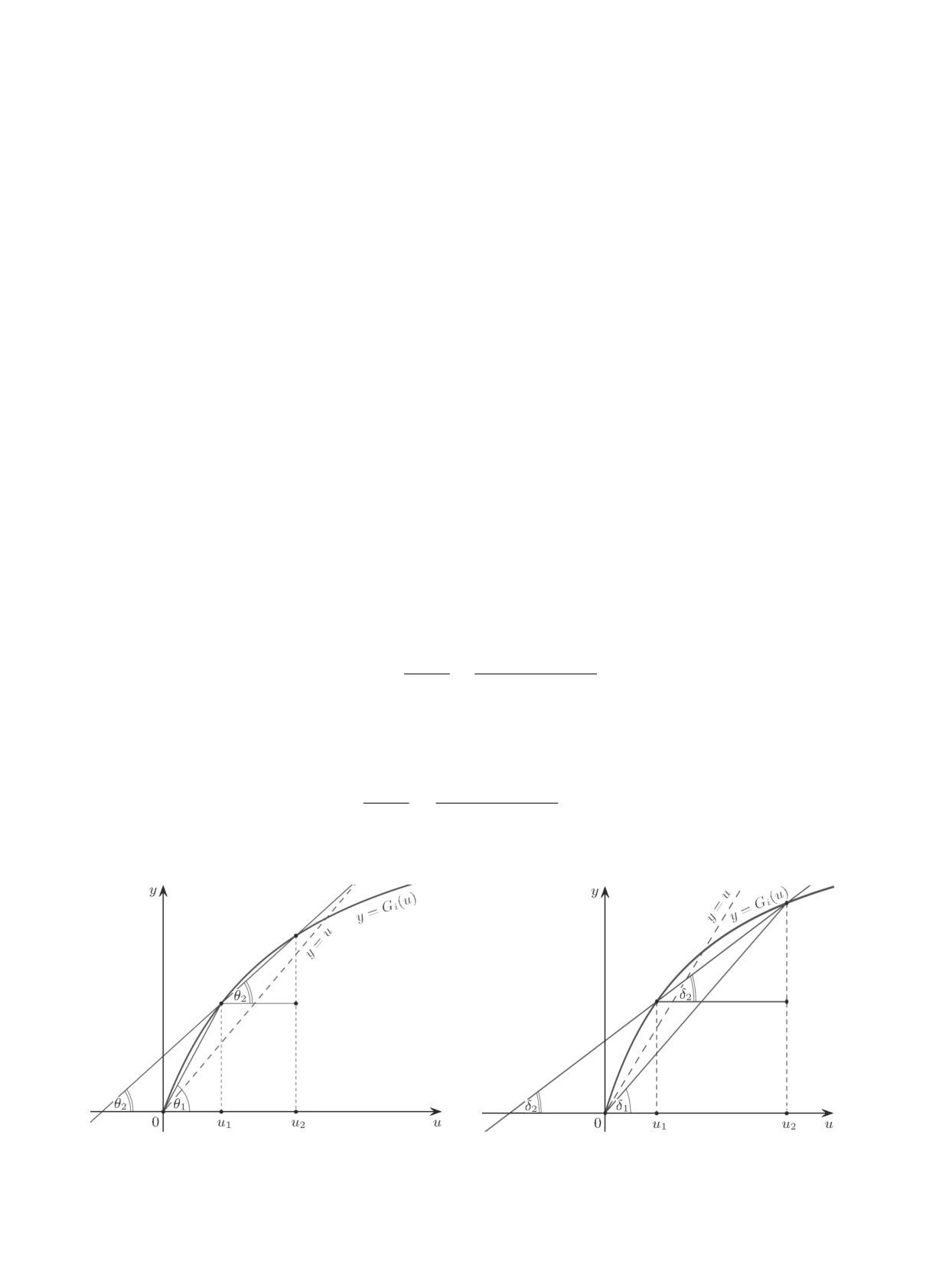
Но последнее неравенство невозможно, поскольку в силу строгой выпуклости функций G_i на

положительной полуоси и равенстве нулю в нуле для всех i ∈ Π имеем строгое неравенство

(рис. 1 и 2)

ξ_i)

|G_i(ξ_i) - G_i

ξ_i)|

ξ_i

|ξ_i

ξ_i|

Следовательно, Π = ∅ и ξ

ξ. Лемма доказана.

Рис. 1. Пересечение графика функции y = Gi(u)

Рис. 2. Пересечение графика функции y = Gi(u)

с прямой, проходящей через точки

(0, 0) и

с прямой, проходящей через точки

(0, 0) и

(u1, Gi(u1)).

(u2, Gi(u2)).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1504

ДАВЫДОВ и др.

Теперь исследуем вопрос существования положительного решения системы (4). Справед-

лива

Лемма 3. В условиях леммы 2 система уравнений (4) имеет положительное решение ξ,

компоненты которого отделены от нуля и меньше соответствующих компонент η, если

либо для некоторого k ∈ {1, 2 . . . , n}

Gk(u)

→ +∞ при u → +0,

(7)

либо для всех этих индексов последний предел конечен (и равен G^′k(0)), а

∑

ε_ja_kjη_jG^′j(0) > η_k,

(8)

j=1

Замечание 1. В частности, компоненты искомого решения удовлетворяют двойному нера-

венству

c^∗η_i ≤ ξ_i < η_i

(9)

с некоторой положительной константой c^∗.

Доказательство. В качестве нулевого приближения к такому решению возьмём ξ⁽⁰⁾ = η,

а за последующие приближения возьмём итерации по системе (4):

∑

ξ(p+1)i =

a_ijε_jG_j(ξ(p)j), p ∈ N⋃ {0}.

(10)

j=1

Эти последовательные приближения монотонно убывают, что легко проверить индукцией по p,

поэтому для доказательства существования предела этих приближений (и тем самым нужного

решения) достаточно показать, что они ограничены снизу положительной константой.

С этой целью рассмотрим следующие функции χ_i на промежутке (0, 1]:

∑

Gj (vηj )

χ_i(v) :=

ε_ja_ijη_j

- 1, v ∈ (0, 1].

η_i

vη_j

j=1

Они непрерывны на (0, 1] в силу непрерывности функций G_i; монотонно убывают на (0, 1],

поскольку из-за строгой выпуклости вверх функций G_i на положительной полуоси отношение

Gj (u)/u монотонно убывает на луче (0, +∞); имеют отрицательные значения в единице:

∑

χ_i(1) =

ε_ja_ijη_j - 1 <

a_ijη_j - 1 = 0,

η_i

j=1

i j=1

поскольку G_j (η_j ) = η_j, ε_j ∈ (0, 1), а Aη = η.

Далее, предел lim

χ_i(v) существует. Он равен +∞ при выполнении условия (7) и поло-

v→0+

жителен при выполнении условия (8). В обоих случаях в силу монотонного убывания функции

χ_i на (0,1] и отрицательности eё значений в единице существует единственное значение c_i ∈

∈ (0, 1) такое, что χ_i(c_i) = 0. Положим

c^∗ := min

c_i

1≤i≤n

и покажем, что итерации ξ(p)i из (10) удовлетворяют двойному неравенству (9). Для этого

воспользуемся индукцией по номеру итерации. При p = 0 это верно в силу выбора первого

приближения ξ⁽⁰⁾ = η. Пусть эта оценка верна для некоторого номера итерации p.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ

1505

Отсюда, учитывая монотонность функций G_i и χ_i, имеем соотношения

∑

ξ(p+1)i =

a_ijε_jG_j(ξ(p)j) ≥

a_ijε_jG_j(c^∗η_j) = (χ_i(c^∗) + 1)c^∗η_i ≥ (χ_i(c_i) + 1)c^∗η_i = c^∗η_i.

j=1

Следовательно, оценка (9) справедлива для итераций (10). Учитывая монотонное убывание

этих итераций, получаем, что они имеют предел при p → ∞ и предельный вектор является

положительным решением системы (4). Лемма доказана.

1.4. Возможные значения {γ_i}ni=1 и {β_i}ni=1 в случаях p₁)-p₄). Покажем, что

в случаях p₁)-p₄) величины γ_i и β_i могут принимать только значения 0 и ±ηi. Точнее,

справедлива следующая

Лемма 4. При выполнении условий a), b), A)-C) и II) величины γ_i и β_i могут принимать

только значения:

1) или нулевые, или η_i в любом сочетании в случае p₁);

2) или нулевые, или -η_i в любом сочетании в случае p₂);

3) γ_i = -η_i, β_i = η_i в случае p₃);

4) γ_i = η_i, β_i = -η_i в случае p₄).

Всюду i ∈ {1, 2, . . . , n}.

Доказательство. Если функция F ∈ L_∞(R) и существуют конечные пределы на ±∞,

то для функции T ∈ L₁(R) верно равенство

∫

∞

∫

∞

lim

T (x - t)F (t) dt =

T (y) dy lim F (x)

x→±∞

-∞

(см. [21]). Отсюда, а также в силу условий lim

λ_j(x) = 1 и A), получаем, что величины

x→±∞

{γ_i}ni=1

и {β_i}ni=1 удовлетворяют системе уравнений

∑

τ_i =

a_ijG_j(τ_j),

(11)

j=1

которая имеет единственное решение τ_i = η_i в классе неотрицательных ненулевых решений

(см. лемму 2.1 в [14]).

Следовательно, справедливо утверждение 1) леммы 4. В силу нечётности функций G_i сис-

тема (11) имеет и решение противоположного знака τ^∗ = -η, и, аналогично, оно единственно

в классе неположительных ненулевых решений. Отсюда получаем справедливость оставшихся

утверждений леммы 4. Лемма доказана.

2. О знакопостоянных ограниченных решениях (1). Изучим существование нетри-

виальных ограниченных решений системы (1) при единичных λ_i. Возможные значения {γ_i}

и {β_i}, при которых могут существовать такие решения, указаны в лемме 4.

2.1. Отсутствие нетривиальных знакопостоянных решений. Имеет место

Теорема 1. При единичных λ_i, выполнении условий a)-c), A)-C) и G^′j (+0) < +∞ сис-

тема (1) в классе знакопостоянных ограниченных функций имеет только нулевое решение,

если γ_i = β_i = 0, i = 1, n.

Доказательство. Докажем для случая неотрицательных решений (для неположительных

рассуждения аналогичны). Рассмотрим произвольное ограниченное неотрицательное непре-

рывное решение f системы (1) с нулевыми пределами на бесконечности. В силу его непре-

рывности и этих пределов существует число δ > 0 такое, что при |x| ≥ δ справедливы

неравенства

0 ≤ f_i(x) ≤ η_i/2.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1506

ДАВЫДОВ и др.

Покажем, что компоненты решения f интегрируемы. Это достаточно сделать на любом

полуинтервале, примыкающем к бесконечности, возьмём [δ, +∞) и произвольное R, R > δ.

В силу условий A)-C) для функции G_i справедливы оценки

Gi(ηi/2)

Gi(u) ≥

u при u ∈ [0, η_i/2], d_i :=

> 1.

(12)

η_i/2

Используя их, оценку из леммы 1, условия a)-c), A)-C) и теорему Фубини (см. [22, с. 317]), из

(1) будем иметь

∫

∑ ∫R

η_i (η_i - f_i(x))dx =

η_i

K_ij(x - t)(η_j - G_j(f_j(t)))dtdx ≤

i=1

δ j⁼¹-∞

∫

≤ η_j η_i

K_ij(x - t)dtdx +

η_j

η_i

K_ij(x - t)dtdx +

j=1

i=1

j=1

i=1

δ -∞

∫

∞

∫

∑

∑ ∫R

+ η_j η_i

K_ij(x - t)dtdx +

η_i

K_ij(x - t)(η_j - G_j(f_j(t)))dtdx ≤

j=1

i=1

j=1 i=1

δ R

δ δ

∫

∞

∫

≤ η_j η_i

K_ij(y)dy dx +

η_j

η_i

K_ij(x - t)dtdx +

j=1

i=1

j=1

i=1

∫

∞

∫

∑∑

+ η_j η_i

K_ij(t - x)dtdx +

η_ia_ij (η_j - G_j(f_j(t)))dtdx ≤

j=1

i=1

j=1 i=1

∫

≤ η_j η_i yK_ij(y)dy + η_j η_i

K_ij(y)dy dx +

j=1

i=1

j=1

i=1

δ x-δ

∫

∞

∑ ∫R

+ η_j η_i

K_ij(y)dy dx +

η_j (η_j - G_j(f_j(t)))dt ≤

j=1

i=1

j=1

0 R-x

∫

∞

≤ η_j η_i yK_ij(y)dy + η_j η_i

K_ij(y)dy dx +

j=1

i=1

j=1

i=1

δ x-δ

∫

∞

∑ ∫R

+ η_j η_i

K_ij(y)dy dt +

η_j (η_j - d_jf_j(t))dt ≤

j=1

i=1

j=1

∫

∑ ∫R

≤3

η_j

η_i

yK_ij(y)dy +

η_j (η_j - d_jf_j(x))dx,

j=1

i=1

j=1

откуда следует, что

∫

∑

η_i(d_i - 1) f_i(x)dx ≤ 3

η_j

η_i

yK_ij(y)dy.

i=1

j=1

i=1

(Аналогично можно доказать, что f_i ∈ L₁(-∞, 0).)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ

1507

Отсюда при R → +∞ получаем интегрируемость компонент решения на луче (δ, +∞),

что и требовалось, а также неравенство

∫

∞

∫

∑

η_i(d_i - 1) f_i(x)dx ≤ 3

η_j

η_i

yK_ij(y)dy.

i=1

j=1

i=1

Тогда в силу непрерывности и интегрируемости ядер K_ij и ограниченности и интегрируемости

f_i из (1) в силу условия A), а также непрерывности свёртки суммируемых и ограниченных

функций (см. [23]) заключаем, что компоненты f_i непрерывны.

Далее в силу G^′j (+0) < +∞, Aη = η, условия a) и теоремы Фубини имеем

∫

∑ ∫∞

η_i

f_i(x)dx =

η_i

K_ij(x - t)G_j(f_j(t))dtdx =

i=1

j=1_-∞

-∞

∫

∞

∑∑

∑ ∫∞

a_ijη_i

Gj (fj(t)) dt =

η_j

Gj (fj (t)) dt.

j=1 i=1

j=1

-∞

Приравнивая крайние выражения в этой цепочке равенств, находим

∑ ∫∞

η_i

(G_i(f_i(x)) - f_i(x)) dx = 0.

i=1

-∞

Подынтегральные выражения в последнем равенстве неотрицательны (поскольку G_i(u) ≥ u

при u ∈ [0, η_i] и 0 ≤ f_i ≤ η_i) и непрерывны. Следовательно, это равенство возможно лишь

при выполнении тождества

Gi(fi(x)) ≡ fi(x)

на всей прямой. Отсюда, учитывая lim

f_i(x) = 0 и выполнение равенства G_i(u) = u лишь

x→±∞

при u = 0, ±η_i, находим f_i ≡ 0. Теорема доказана.

Справедлива также

Теорема 2. При единичных λ_i и выполнении условий a)-c), A)-C) система (1) в классе

знакопостоянных ограниченных функций имеет только постоянное решение f = ±η, если

соответственно γ_i = β_i = ±η_i, i = 1,n.

Доказательство. Для определённости рассмотрим случай неотрицательных решений.

Пусть f - любое решение системы (1) c предельным значением η на ±∞. Существует число

Δ > 0 такое, что при |x| ≥ Δ справедливы неравенства f_i(x) ≥ η_i/2. Отсюда и из леммы 1

при |x| ≥ Δ имеем соотношения

η_i/2 ≤ f_i(x) ≤ η_i.

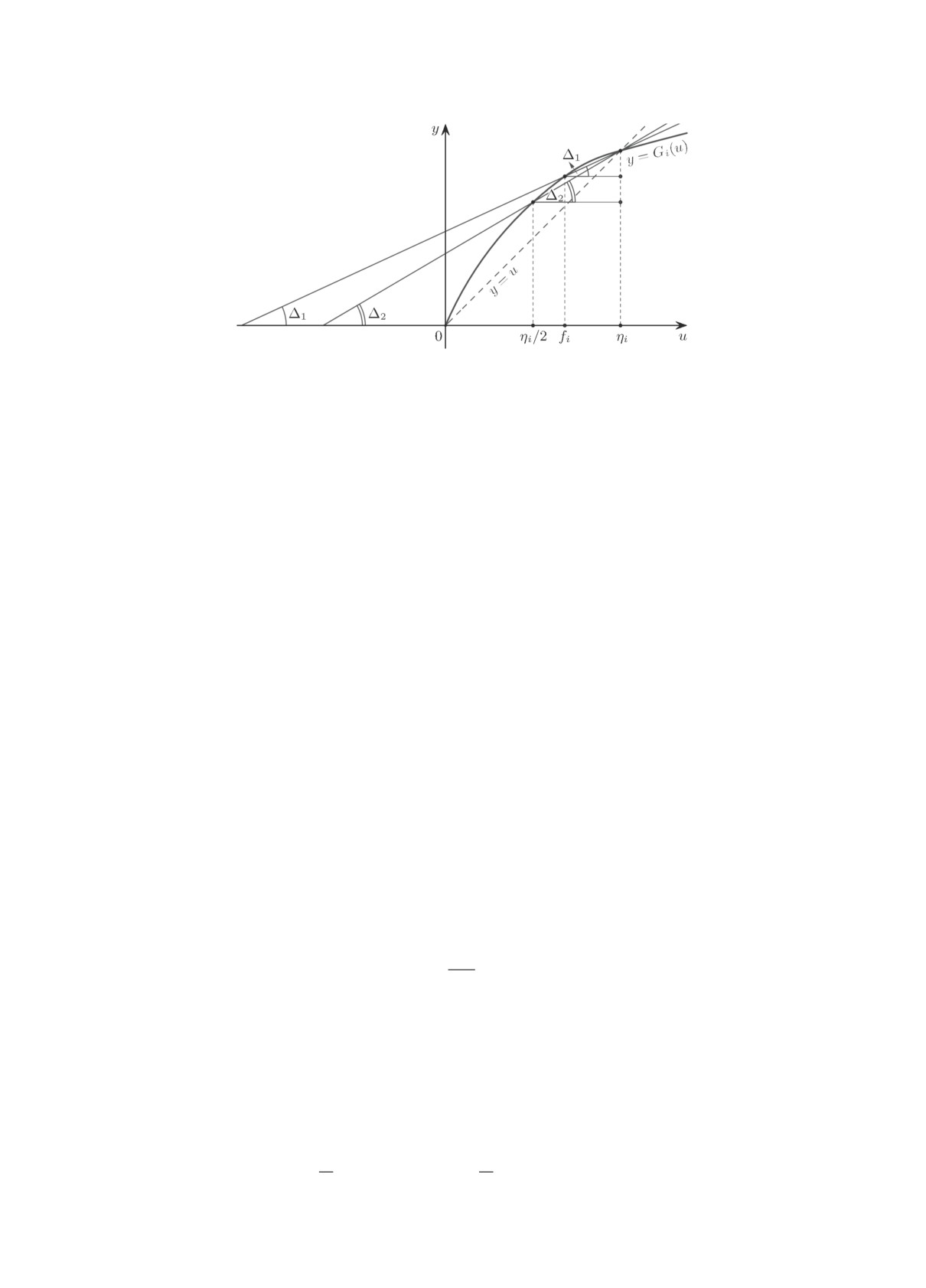
Далее в силу выпуклости вверх функций G_i на R⁺, их нечётности и условия A) при |x| ≥ Δ

справедливы следующие неравенства (рис. 3):

η_i - G_i(η_i/2)

η_i - G_i(f_i(x)) ≤ q_i(η_i - f_i(x)), q_i :=

∈ (0, 1),

(13)

η_i/2

что легко проверить. Используя эти неравенства и рассуждая по аналогии с доказательством

предыдущей теоремы, будем иметь

∫

∞

∫

∑

η_i(1 - q_i) (η_i - f_i(x))dx ≤ 3

η_j

η_i

yK_ij(y)dy.

i=1

j=1

i=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

5^∗

1508

ДАВЫДОВ и др.

Рис. 3. Пересечение графика функции y = Gi(u) с прямой, про-

ходящей через точки (ηi/2, Gi(ηi/2)) и (ηi, ηi).

Аналогично верно

∫

∑

∑ n∑

η_i(1 - q_i)

(η_i - f_i(x)) dx ≤ 3

η_j

η_i

K_ij(y)(-y)dy.

i=1

j=1

i=1

-∞

Отсюда вытекает, что функции η_i - f_i интегрируемы на прямой.

Далее в силу системы (1) и условия Aη = η имеем равенство

∞

∫

∑

η_i - f_i(x) =

K_ij(x - t)(η_j - G_j(f_j(t)))dt, x ∈ R.

j=1_-∞

Умножим обе его части на η_i, проинтегрируем результат по прямой и просуммируем по i.

В результате, учитывая определение матрицы A, условие Aη = η и применяя теорему Фуби-

ни, получаем

∑ ∫∞

η_i

(η_i - f_i(x)) dx =

η_j

(η_j - G_j (f_j(t))) dt

i=1

j=1

-∞

или

∑ ∫∞

η_i

(G_i(f_i(x)) - f_i(x)) dx = 0.

i=1

-∞

Заключительные рассуждения те же, что и в доказательстве предыдущей теоремы, только

теперь будем иметь f_i(x) ≡ η_i. Теорема доказана.

2.2. Об отсутствии знакопостоянных решений системы. Справедлива

Теорема 3. При единичных λ_j и выполнении условий a)-c) и A)-C) система (1) не имеет

знакопостоянных ограниченных решений, если γ_i = 0, β_i = η_i (либо γ_i = 0, β_i = -η_i, либо

γ_i = η_i, β_i = 0, либо γ_i = -η_i, β_i = 0), i = 1,n.

Доказательство. Доказательство проведём лишь для первого случая, поскольку для

остальных рассуждения аналогичны. Допустим противное, что при γ_i = 0, β_i = η_i в условиях

последней теоремы существует знакопостоянное ограниченное решение f системы (1), тогда

оно неотрицательно и по условию

lim

f_i(x) = 0,

lim

f_i(x) = η_i.

x→-∞

x→+∞

Отсюда получаем, что существует положительное число r такое, что

η_i

0 ≤ f_i(x) ≤

при x < -r,

≤ f_i(x) ≤ η_i при x > r.

(14)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ

1509

Теперь проведём рассуждения аналогично как в доказательстве теоремы 2 и получим, что

η_i - f_i ∈ L₁(0,+∞).

(15)

Докажем, что f_i ∈ L₁(-∞, 0). Возьмём отрицательное число R. Учитывая Aη = η, (12),

(14), условия a)-c) и A)-C), из системы (1) будем иметь

∫

η_i (η_i - f_i(x))dx ≤

η_j

η_i

K_ij(x - t)dtdx +

i=1

j=1

i=1

R -∞

∫

∑

η_i

K_ij(x - t)(η_j - G_j(f_j(t)))dtdx +

j=1 i=1

R R

∫

∞

+ η_j η_i

K_ij(x - t)dtdx +

η_j

η_i

K_ij(x - t)dtdx ≤

j=1

i=1

j=1

i=1

R -r

R 0

∫

∑∑

≤ η_j η_i

K_ij(t - x)dtdx +

η_ia_ij (η_j - G_j(f_j(t)))dt +

j=1

i=1

j=1 i=1

R -∞

∫

∑ n∑

+ η_j η_i

K_ij(y)dy dx +

η_j

η_i

K_ij(y)dy dx ≤

j=1

i=1

j=1

i=1

-∞ x

-∞ -∞

∫

∑ n∑

∑∑

≤ η_j η_i

K_ij(y)dy dx +

η_ia_ji (η_j - G_j(f_j(t)))dt +

j=1

i=1

j=1 i=1

R -∞

∫

∑ n∑

+ η_j η_i

K_ij(y)dy dx +

η_j

η_i

K_ij(y)(-y)dy ≤

j=1

i=1

j=1

i=1

-∞ -∞

-∞

∫

∑ n∑

≤ η_j η_i

K_ij(y)dydz +

η_j (η_j - d_jf_j(t))dt + 2

η_j

η_i

K_ij(y)(-y)dy ≤

j=1

i=1

j=1

i=1

R -∞

-∞

∫

∑ n∑

≤ η_j (η_j - d_jf_j(t))dt + 3 η_j η_i K_ij(y)(-y)dy,

j=1

i=1

-∞

откуда получим

∫

∑

∑ n∑

η_i(d_i - 1) f_i(x)dx ≤ 3

η_j

η_i

K_ij(y)(-y)dy = 3

η_j

η_i

K_ij(y)y dy.

(16)

i=1

j=1

i=1

j=1

i=1

-∞

Устремив в (16) число R → -∞, придём к включению f_i ∈ L₁(-∞, -r). Следовательно,

в силу непрерывности f_i получаем нужное включение f_i ∈ L₁(-∞, 0). Отсюда и из (15)

следует, что

f_j(x)(η_j - f_j(x)) ∈ L₁(R).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1510

ДАВЫДОВ и др.

Из последнего включения, учитывая, что f_j(x) ≤ η_j на прямой и, следовательно, f_j(x) ≤

≤ G_j(f_j(x)) на прямой, получаем, что

f_j(x)(η_j - G_j(f_j(x))) ∈ L₁(R).

Умножим теперь обе части (1) на (η_i -G_i(f_i(x))), проинтегрируем по прямой и просуммируем

по всем i. Применяя к результату теорему Фубини с учётом условий Aη = η и a)-c), A)-C),

будем иметь

∫

∞

∫

∞

∑

(η_i - G_i(f_i(x)))f_i(x) dx =

(η_i - G_i(f_i(x)))

K_ij(x - t)G_j(f_j(t))dtdx =

i=1_-∞

j=1_-∞

∫

∞

∫

∞

∑

Gj (fj(t))

K_ij(x - t)(η_i - G_i(f_i(x)))dxdt =

j=1_-∞

i=1_-∞

∫

∞

∫

∞

)

∫

∞

∑

Gj (fj(t))

a_jiη_i -

K_ji(t - x)G_i(f_i(x))dx dt =

(η_j - f_j(t))G_j (f_j(t)) dt.

j=1_-∞

i=1

i=1_-∞

j=1_-∞

Оставив крайние выражения в последней цепочке равенств, найдём

∫

[(η_i - G_i(f_i(x)))f_i(x) - (η_i - f_i(x))G_i(f_i(x))] dx = 0.

(17)

i=1_-∞

В силу непрерывности компоненты f_i и её пределов (0 и η_i на -∞ и +∞ соответственно),

существуют x_i ∈ R и δ_i > 0 такие, что 0 < f_i(x_i) < η_i при x ∈ I_i := (x_i - δ_i, x_i + δ_i).

Определим множества

W_i := {x ∈ R : f_i(x) = 0, f_i(x) = η_i}.

Эти множества непусты, так как I_i ⊂ W_i, и имеют положительную меру (возможно, беско-

нечную). В силу леммы 1 имеем 0 ≤ f_i ≤ η_i, поэтому на этом множестве

0 < f_i(x) < η_i.

Нетрудно видеть, что (17) равносильно равенству

)

∑∫

⁽η_i - G_i(f_i(x))

Gi(fi(x))

f_i(x)(η_i - f_i(x))

dx = 0.

(18)

η_i - f_i(x)

f_i(x)

i=1

Из строгой выпуклости вверх функции G_i на R⁺ имеем

Gi(fi(x))

η_i - G_i(f_i(x))

x∈W_i.

f_i(x)

η_i - f_i(x)

Отсюда получаем, что неотрицательное подынтегральное выражение в равенстве (18) поло-

жительно на I_i, поэтому левая часть этого равенства положительна. Получили противоречие.

Следовательно, наше допущение неверно и теорема доказана.

Замечание 2. Как известно, в одномерном случае система (1) при положительном первом

моменте ядра и достаточно сильных ограничениях на нелинейность и ядро может иметь моно-

тонно возрастающее положительное непрерывное и ограниченное на R решение f с f(-∞) =

= 0 и f(+∞) = η > 0 (см., например, [11, 12]). Отсутствие такого решения для системы (1)

обусловлено свойством чётности ядра K, при которой этот момент равен нулю.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ

1511

Замечание 3. Вопрос существования или отсутствия знакопеременных и ограниченных

на R решений для случаев: 1) γ_i = 0, β_i = η_i; 2) γ_i = η_i, β_i = 0; 3) γ_i = 0, β_i = -η_i;

4) γ_i = -η_i, β_i = 0 остаётся открытым.

Замечание 4. Как было отмечено выше, в случаях p₃) и p₄) система (1) при единичных

λ_i имеет знакопеременное нечётное и ограниченное решение.

3. Разрешимость системы при λ_j ≡ 1.

3.1. Построение знакопостоянного ограниченного решения.

Теорема 4. При выполнении условий a)-c), A)-C), I), II) и λ_j (x) ≡ 1 система (1) имеет

положительное непрерывное и ограниченное на R решение f с предельным значением η на

±∞ и интегрируемыми на прямой разностями η_i - f_i, i = 1,n.

Доказательство. Для поиска решения рассмотрим последовательность итераций по сис-

теме (1):

∞

∫

∑

f(p+1)i(x) =

λ_j(x)

K_ij(x - t)G_j(f(p)j(t))dt, f(0)i(x) ≡ η_i,

(19)

j=1

-∞

где p ∈ N

^⋃ {0}. Индукцией по p легко показать, что это убывающая последовательность, в

частности, на прямой f(p)i(x) ≡ η_i при p ≥ 1. Покажем, что эта последовательность ограни-

чена снизу, а именно всюду

f(p)i(x) ≥ ξ_i

(20)

при всех p, где ξ - единственное неотрицательное ненулевое решение системы уравнений (4)

(см. леммы 2 и 3). Для этого воспользуемся индукцией по номеру итерации.

При p = 0 неравенство (20) справедливо в силу (9). Предположим, что оно имеет место

при некотором возможном p. Отсюда и из (19) в силу условий I), A), B), a), b) с учётом (4)

имеем

∞

∫

∑

f(p+1)i(x) ≥

λ_j(x)G_j(ξ_j)

K_ij(x - t)dt ≥

ε_ja_ijG_j(ξ_j) = ξ_i, x ∈ R⁺.

j=1

-∞

Следовательно, наша последовательность итераций ограничена снизу и, таким образом, имеет

предел f_i при p → +∞. Этот предел положителен, поскольку ограничения ξ_i снизу по-

ложительны, и ввиду предельной теоремы Б. Леви [22, с. 303] удовлетворяет системе (1).

И итерации, и этот предел являются непрерывными функциями на прямой, так как таковыми

являются функции λ_i, K_ij и G_i, есть условие I) и непрерывность свёртки суммируемых и

ограниченных на прямой функций.

Покажем интегрируемость разности η_i - f_i. Имеем оценку

∞

∫

∑

0 ≤ η_i - f(p+1)i(x) =

K_ij(x - t)(η_j - λ_j(x)G_j(f(p)j(t)))dt ≤

j=1_-∞

∫

∞

∑

≤ a_ijη_j(1 - λ_j(x)) +

K_ij(x - t)(η_j - G_j(f(p)j(t)))dt,

j=1

j=1_-∞

из которой и из условий a)-c), A)-C), I) и II) индукцией по p получаем

η_i - f(p)i ∈ L₁(R), p ∈ N⋃ {0}.

Из (4) в силу ε_i ∈ (0, 1) имеем

∑

0 < ξ_i < a_ijG_j(ξ_j) ≤

a_ijG_j(η_j) =

a_ijη_j = η_i,

j=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1512

ДАВЫДОВ и др.

поэтому по аналогии с доказательствами теорем 1 и 3 находим

∞

∫

∑

η_i(1 - l_i)

(η_i - f(p+1)i(x)) dx ≤

i=1

-∞

∫

∞

∫

∑

≤ η²

(1 - λ_j (x)) dx + 6

η_j

η_i

yK_ij(y)dy < +∞,

j=1

i=1

-∞

где l_i := (η_i - G_i(ξ_i))/(η_i - ξ_i) ∈ (0, 1).

Теперь, устремив p → ∞ в последних неравенствах (в их левой части), получаем их c f_i

на месте f(p+1)i. Следовательно, интегрируемость η_i - f_i на прямой имеет место.

Осталось показать, что η_i - предельное значение f_i на бесконечности. Для этого сначала

систему (1) запишем в следующем виде:

∞

∫

∑

η_i - f_i(x) =

a_ijη_j(1 - λ_j(x)) +

λ_j(x)

K_ij(x - t)(η_j - G_j(f_j(t)))dt.

(21)

j=1

-∞

Первое слагаемое в правой части стремится к нулю при x → ±∞, так как все λ_i имеют еди-

ничный предел на бесконечности в силу условия II). В интеграле оба сомножителя ограничены

и интегрируемы на прямой: первый - по условию b), а второй - в силу неравенств

0 ≤ η_j - G_j(f_j(x)) ≤ η_j - f_j(x),

ограниченности и интегрируемости η_j - f_j. Следовательно, сам интеграл как свёртка этих

функций стремится к нулю при x → ±∞ (см. [24]). Отсюда, учитывая ограниченность λ_i,

получаем, что правая часть в (21) стремится к нулю при x → ±∞ и, следовательно, f(x) → η

при x → ±∞. Теорема доказана.

Замечание 5. Единственность решения системы (1) в классе неотрицательных ограничен-

ных функций с отделёнными от нуля значениями вблизи бесконечности доказывается метода-

ми работы [14].

Замечание 6. В силу нечётности функций G_i система (1) имеет также отрицательное

решение f^∗, f^∗(x) := -f(x).

4. Примеры. Приведём примеры функций {G_j(u)}ni=1, {Kij (x)}ni,j=1 и {λj (x)}ni=1, удо-

влетворяющих соответствующим условиям доказанных теорем.

Примеры нелинейностей G_j (u) :

√

g₁) G_j(u) = ηjpj

u/η_j , u ∈ R, где p_j > 1 - нечётные числа, η_j > 0, и удовлетворяют

∑_n

соотношениям

a_ijη_j = η_i;

j=1

{

γ_j(1 - e^-u), если u ≥ 0,

g₂) G_j(u) =

u ∈ R, где γ_j := η_j/(1 - e-ηj) > 1;

γ_j(e^u - 1),

если u < 0,

√

g₃) G_j(u) = (u + ηjpj

u/η_j )/2, u ∈ R.

Подробно остановимся на примере g₂). Сначала заметим, что

Gj (0) = 0, Gj (ηj ) = ηj .

(22)

Так как функция

{

γ_je^-u, если u ≥ 0,

G′j (u) =

γ_je^u,

если u < 0,

непрерывна на всей числовой прямой и G^′j (u) > 0, u ∈ R, то условие A) выполняется.

Поскольку G^′′j(u) = -γ_j e^-u < 0 при u ∈ R⁺, то в силу (22) заключаем, что условие B) также

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

О РЕШЕНИЯХ ОДНОЙ СИСТЕМЫ

1513

справедливо. Выполнение условия C) сразу следует из структуры примера g₂). Заметим

также, что G^′j (+0) = G^′j (-0) = γ_j > 1.

Примеры ядра K(x) = {K_ij (x)}ni,j=1 :

k₁) K_ij(x) = a_ije-x2 /√π, x ∈ R, где aij = aji > 0, A = (aij)ni,j=1 и r(A) = 1;

∫b

k₂) K_ij(x) =

e^-|x|s dσ_ij(s), x ∈ R, где σ_ij(s) = σ_ji(s) - монотонно возрастающие на

[a, b) функции, 0 < a < b ≤ +∞, причём спектральный радиус матрицы

( ∫b

)_n

dσ_ij (s)

i,j=1

равен единице.

Примеры функций λ_j(x) :

Λ₁) λ_j(x) = 1 - (1 - ε_j)e^-|x|, x ∈ R, ε_j ∈ (0,1);

Λ₂) λ_j(x) = 1 - (1 - ε_j)e-x2 , x ∈ R, ε_j ∈ (0,1).

Отметим, что примеры g₁)-g₃), k₁), k₂), Λ₁), Λ₂) удовлетворяют условиям теорем 3, 4,

а примеры g₂), k₁), k₂), Λ₁), Λ₂) - теорем 1 и 2.

Следует также отметить, что примеры g₁), g₂), k₁), k₂) и Λ₂) встречаются в теории p-

адических струн, в эпидемиологии и в кинетической теории газов (см. [2, 3, 6, 7, 11, 12]).

Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-11-

00223).

СПИСОК ЛИТЕРАТУРЫ

1. Ланкастер П. Теория матриц. М., 1973.

2. Cercignani C. The Boltzmann equation and applications // Appl. Math. Sci. V. 67. New York, 1988.

3. Хачатрян А.Х., Хачатрян Х.А. О разрешимости нелинейного модельного уравнения Больцмана в

задаче плоской ударной волны // Журн. теор. и мат. физики. 2016. Т. 189. № 2. С. 239-255.

4. Соболев В.В. Проблема Милна для неоднородной атмосферы // Докл. АН СССР. 1978. Т. 239. № 3.

С. 558-561.

5. Енгибарян Н.Б. Об одной задаче нелинейного переноса излучения // Астрофизика. 1966. Т. 2. № 1.

С. 31-36.

6. Владимиров В.С., Волович Я.И. О нелинейном уравнении динамики в теории p-адической струны

// Журн. теор. и мат. физики. 2004. Т. 138. № 3. С. 355-368.

7. Arefeva I.Ya., Dragovic B.G., Volovich I. V. Open and closed p-adic strings and quadratic extensions of

number fields // Phys. Lett. B. 1988. V. 212. № 3. P. 283-291.

8. Хачатрян Х.А. О разрешимости некоторых классов нелинейных сингулярных краевых задач, воз-

никающих в теории p-адических открыто-замкнутых струн // Журн. теор. и мат. физики. 2019.

Т. 200. № 1. С. 106-117.

9. Sargan J.D. The distribution of wealth // Econometrica. 1957. V. 25. № 4. P. 568-590.

10. Хачатрян А.Х., Хачатрян Х.А. О разрешимости одного нелинейного интегро-дифференциального

уравнения, возникающего в задаче о распределении дохода // Журн. вычислит. математики и мат.

физики. 2010. Т. 50. № 10. С. 1793-1802.

11. Diekmann O. Threshold and travelling waves for the geographical spread of infection // J. of Math.

Biology. 1978. V. 6. P. 109-130.

12. Diekmann O., Kaper H.G. On the bounded solutions of a nonlinear convolution equation // Nonlin.

Anal. Theory Math. Appl. 1978. V. 2. № 6. P. 721-737.

13. Хачатрян Х.А. О разрешимости одной системы нелинейных интегральных уравнений типа Гаммер-

штейна на прямой // Изв. Саратовского ун-та. Нов. сер. Сер. Математика. Механика. Информатика.

2019. Т. 19. № 2. С. 164-181.

14. Хачатрян А.Х., Хачатрян Х.А. Об одной системе интегральных уравнений на всей прямой с вы-

пуклой и монотонной нелинейностью // Изв. НАН Армении. Математика. 2022. Т. 57. № 5. С. 25-40.

15. Хачатрян Х.А., Петросян А.С. О разрешимости одной системы сингулярных интегральных урав-

нений с выпуклой нелинейностью на положительной полупрямой // Изв. вузов. Математика. 2021.

Т. 1. С. 31-51.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1514

ДАВЫДОВ и др.

16. Арабаджян Л.Г. Решения одного интегрального уравнения типа Гаммерштейна // Изв. НАН Ар-

мении. Математика. 1997. Т. 32. № 1. С. 21-28.

17. Banas J. Integrable solutions of Hammerstein and Urysohn integral equations // J. of Austral. Math.

Soc. Ser. A. 1989. V. 46. № 1. P. 61-68.

18. Хачатрян Х.А., Петросян А.С. Асимптотическое поведение решения для одного класса нелиней-

ных интегральных уравнений типа Гаммерштейна на всей прямой // Соврем. математика. Фунд.

направления. 2022. Т. 68. № 2. С. 376-391.

19. Хачатрян Х.А. Существование и единственность решения одной граничной задачи для интеграль-

ного уравнения свёртки с монотонной нелинейностью // Изв. РАН. Сер. мат. 2020. Т. 84. № 4.

С. 198-207.

20. Петросян А.С., Хачатрян Х.А. О единственности решения одного класса интегральных уравнений

с суммарно-разностным ядром и с выпуклой нелинейностью на положительной полупрямой // Мат.

заметки. 2023. Т. 113. № 4. С. 529-543.

21. Енгибарян Н.Б. Уравнения восстановления на полуоси // Изв. РАН. Сер. мат. 1999. Т. 63. № 1.

С. 61-76.

22. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М., 1976.

23. Рудин У. Функциональный анализ. М., 1975.

24. Арабаджян Л.Г., Хачатрян А.С. Об одном классе интегральных уравнений типа свёртки // Мат.

сб. 2007. Т. 198. № 7. С. 45-62.

Московский государственный университет

Поступила в редакцию 13.08.2023 г.

имени М.В. Ломоносова,

После доработки 13.08.2023 г.

Ереванский государственный университет,

Принята к публикации 20.09.2023 г.

Армения,

Национальный аграрный университет Армении,

г. Ереван

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023