ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 11, с. 1566-1570

КРАТКИЕ СООБЩЕНИЯ

УДК 517.925.51

БИФУРКАЦИЯ ХОПФА В СИСТЕМЕ ХИЩНИК-ЖЕРТВА

С ИНФЕКЦИЕЙ

Исследуется модель системы хищник-жертва с возможной инфекцией жертв в виде трёх-

мерной системы обыкновенных дифференциальных уравнений. С помощью метода локали-

зации инвариантных компактов доказывается существование аттрактора и находится ком-

пактное положительно инвариантное множество, оценивающее его положение. Находятся

условия вымирания популяций и существования положений равновесия. Предлагается чис-

ленный метод нахождения бифуркации Хопфа пространственного положения равновесия

и приводится пример возникающего устойчивого предельного цикла.

DOI: 10.31857/S0374064123110122, EDN: PEXCDU

1. Введение. Постановка задачи. Рассмотрим систему обыкновенных дифференциаль-

ных уравнений, описывающую динамику взаимодействия популяций хищников и жертв, при

которой жертвы подвержены заболеванию [1]:

x₁x₃

1 = b1(x1 + x2)(1 - x1) -

-b₄x₁x₂,

b₂ + x₁ + x₂

x₂x₃

2 = b4x1x2 -

- b₅x₂ - b₁(x₁ + x₂)x₂,

b₂ + x₁ + x₂

(x₁ + x₂)x₃

3 =

-b₃x₃,

(1)

b₂ + x₁ + x₂

где

{

} = d{·}/dt, x = (x₁,x₂,x₃) ∈ R3+,0 = {x ≥ 0}, x₁ (x₂) - плотность популяции воспри-

имчивых (инфицированных) жертв, а x₃ - плотность популяции хищников. Параметры b_i,

i = 1,5, этой системы предполагаются положительными.

Для системы (1) докажем, что множество R3+,0 положительно инвариантно, существует

положительно инвариантный компакт, содержащий все инвариантные компакты, все решения

(траектории) продолжаются на неограниченный вправо интервал времени и система имеет ат-

трактор. Кроме того, найдём условия вымирания популяций инфицированных жертв, хищни-

ков и предложим метод нахождения бифуркации Хопфа внутреннего положения равновесия,

в результате которой в системе возникает устойчивый предельный цикл внутри множества

R3+,0. Отметим, что система (1) в инвариантной плоскости {x2 = 0} описывает взаимодей-

ствие хищников и жертв при отсутствии инфекции и известно, что в этой двумерной системе

может происходить другая бифуркация Хопфа, в результате которой появляется предельный

цикл в множестве {x₂ = 0}.

2. Необходимые сведения. Все компактные инвариантные множества системы

x =

= F(x), F ∈ C¹(Rⁿ,Rⁿ), содержащиеся в подмножестве Q ⊂ Rⁿ, содержатся в локали-

зирующем множестве Ω(φ, Q), соответствующем функции φ ∈ C¹(Rⁿ) (локализирующей

функции) и множеству Q ⊂ Rⁿ [2],

Ω(φ, Q) = {x ∈ Q : φ_inf (Q) ≤ φ(x) ≤ φ_sup(Q)},

где

φ_inf(Q) = inf{φ(x) : x ∈ S(φ)

^⋂Q}, φ_sup(Q) = sup{φ(x) : x ∈ S(φ)^⋂ Q},

1566

БИФУРКАЦИЯ ХОПФА В СИСТЕМЕ ХИЩНИК-ЖЕРТВА С ИНФЕКЦИЕЙ

1567

S(φ) = {x ∈ Rⁿ :^φ(x) = 0} - универсальное сечение функции φ, a

- производная функции

φ в силу системы x = F(x). Пусть

Ω(φ, Q, ϵ_-, ϵ₊) = {x ∈ Q : φ_inf (Q) - ϵ_- ≤ φ(x) ≤ φ_sup(Q) + ϵ₊}, ϵ_-, ϵ₊ > 0.

Утверждение 1. Пусть множество Q положительно инвариантно; начинающиеся в

Q траектории системы определены на неограниченном вправо интервале времени; для лю-

бого ϵ > 0 существует δ > 0, что

^φ(x) < -δ < 0 при x ∈ Q^⋂ {φ_sup(Q) + ϵ₊ ≤ φ(x) ≤

≤ φ_sup(Q) + ϵ₊ + ϵ}, и для любого ϵ > 0 существует δ > 0, что

^φ(x) > δ > 0 при x ∈

∈Q

^⋂ {φ_inf (Q)-ϵ_- -ϵ ≤ φ(x) ≤ φ_inf (Q)-ϵ_-}. Тогда любая траектория системы, начинающа-

яся в Q\Ω(φ, Q, ϵ_-, ϵ₊), попадает в положительно инвариантное множество Ω(φ, Q, ϵ_-, ϵ₊)

за конечное время.

3. Локализация инвариантных компактов и её следствия. Множество R3+,0 положи-

тельно инвариантно, так как траектории системы (1) не могут выйти из R3+,0 через его грани-

цу. Действительно, граница множества R3+,0 состоит из точек, у которых одна или более коор-

динат равны нулю, а остальные координаты положительны. Пусть x₀ = (x₁(0), x₂(0), x₃(0)) -

одна из таких точек и она является начальной для траектории x(t) = (x₁(t), x₂(t), x₃(t)), t ∈

∈ [0, T ). Тогда x(t) ∈ R3+,0 при t ∈ [0, ϵ), 0 < ϵ ≪ 1, т.е. xi(t) ≥ 0, i = 1,2,3. Действительно,

это верно для x_i(t), если x_i(0) > 0. Если x₁(0) = 0, то

x₁(0) = b₁x₂(0) и x₁(t) > 0 при

x₂(0) > 0, а при x₂(0) = 0 выполнено равенство

x₂(0) = 0, и поэтому x₂(t) = 0, x₁(t) = 0.

Если x₂(0) = 0, то x2(t) = 0, и аналогично для x3 : если x3(0) = 0, то x3(0) = 0 и x3(t) = 0.

Утверждение 2. Все компактные инвариантные множества системы (1) содержатся

в положительно инвариантных множествах

Ω₁ = {x₁ + x₂ ≤ 1}

⋂R3+,0, Ω₂ = {x₁ + x₂ ≤ 1,x₁ + x₂ + x₃ ≤ 1 + b₁/(4b₃)}⋂ R3+,0

и множество Ω₂ компактно.

Доказательство. Пусть φ₁(x) = x₁ + x₂. Тогда в R3+,0

φ₁(x) = b₁(x₁ + x₂)(1 - x₁ - x₂) -(x1 +x2)x3 - b₅x₂

b₂ + x₁ + x₂

φ₁(x) < 0 при φ₁(x) = x₁ + x₂ > 1. Поэтому множество S(φ₁)⋂ R3+,0 = {φ˙₁ = 0}⋂ R3+,0

содержится в множестве {0 ≤ φ₁(x) ≤ 1}

⋂R3+,0. Поскольку φ₁(x₀) = 1 в точке x₀ = (1,0,0) ∈

∈ S(φ₁)

⋂R3+,0, а φ₁(x_∗) = 0 в точке x_∗ = (0,0,0) ∈ S(φ₁)⋂ R3+,0, то

sup{φ₁(x) : x ∈ S(φ₁)

⋂R3+,0} = 1, inf{φ₁(x) : x ∈ S(φ₁)⋂ R3+,0} = 0,

и локализирующее множество Ω(φ₁, R3+,0) = {0 ≤ φ₁(x) ≤ 1}

⋂R3+,0 = Ω₁. Множество Ω₁

положительно инвариантно, поскольку

φ₁(x) < 0 в R3+,0 \ Ω₁.

Пусть теперь φ₂(x) = x₁ + x₂ + x₃. Тогда

b₁

φ₂(x) = ˙

x₁ + x˙₂ + x˙₃ = b₁(x₁ + x₂)(1 - x₁ - x₂) - b₅x₂ - b₃x₃ ≤

-b₃x₃

и в S(φ₂)

^⋂Ω₁ выполнено неравенство φ₂(x) ≤ 1 + b₁/(4b₃). Следовательно,

sup{φ₂(x) : x ∈ S(φ₂)

^⋂Ω₁} ≤ 1 + b₁/(4b₃), inf{φ₂(x) : x ∈ S(φ₂)^⋂ Ω₁} = 0

и Ω(φ₂,Ω₁) ⊂ {0 ≤ φ₂(x) ≤ 1 + b₁/(4b₃)}

^⋂Ω₁ = Ω₂. Множество Ω₂ положительно инвариант-

но, поскольку

φ₂(x) < 0 в Ω₁ \ Ω₂, и компактно.

Следствие 1. Если a₁, a₂ ≥ 0, то множества Ω1,a1 = {x₁ +x₂ ≤ 1+a₁}

⋂ R3+,0, Ω2,a1,a₂ =

= {x₁ + x₂ ≤ 1 + a₁, x₁ + x₂ + x₃ ≤ 1 + a₁ + b₁/(4b₃) + a₂}

⋂R3+,0 положительно инвариантны,

и множество Ω2,a1,a₂ компактно.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1568

КРИЩЕНКО, ПОДДЕРЕГИН

Следствие 2. Все решения (траектории) системы (1) продолжаются на неограниченный

вправо интервал времени.

Доказательство. Известно, что решение автономной C¹-системы обыкновенных диффе-

ренциальных уравнений в любом компакте продолжается вправо или до границы компакта,

или на неограниченный вправо интервал времени [3, с. 107]. Для любой траектории системы

(1) существуют положительные a₁, a₂, при которых её начальная точка принадлежит ком-

пакту Ω2,a1,a₂ . Этот компакт положительно инвариантен, и траектория не может выйти на

его границу за конечное время. Следовательно, траектория продолжается на неограниченный

вправо интервал времени.

4. Асимптотическое поведение траекторий. Справедливо следующее

Утверждение 3. Любая траектория системы (1), проходящая через лежащую вне мно-

жеств Ω1,ε1 , Ω2,ε1,ε₂ , где ε1 > 0, ε2 > 0, точку, попадает в эти множества за конечное

время и не выходит из них.

Доказательство. В множестве R3+,0\Ω1,ε1 = {φ₁(x) = x₁+x₂ > 1+ε₁} дляφ1 справедливо

φ₁

неравенство

≤ b₁(x₁ + x₂)(1 - x₁ - x₂) ≤ -δ < 0, δ = b₁(1 + ε₁)ε₁ > 0. Таким образом,

согласно утверждению 2, все траектории попадают в множество Ω1,ε1 за конечное время и не

выходят из него.

В множестве Ω1,ε1 \ Ω2,ε1,ε₂ = {φ1(x) = x1 + x2 ≤ 1 + ε1, x1 + x2 + x3 > 1 + ε1 + b1/(4b3) + ε2}

выполнено равенство x₃ = 1 + ε₁ + b₁/(4b₃) + ε₂ - (x₁ + x₂) + d, d > 0, и поэтому в этом

множестве

(

)

b₁

φ₂(x) ≤ b₁(x₁ + x₂)(1 - x₁ - x₂) - b3 1+ε1 +

+ ε₂ - (x₁ + x₂) + d

≤ -b₃(ε₂ + d) < 0.

4b₃

Следовательно, согласно утверждению 2, все траектории попадают в множество Ω1,ε1,ε₂ за

конечное время и не выходят из него.

Следствие 3. Предельные множества всех траекторий системы (1) содержатся в ком-

пактном положительно инвариантном множестве Ω₂, и это множество содержит ат-

трактор системы.

Доказательство. Утверждение следует из того, что множества Ω2,ε1,ε₂ при ε1 > 0, ε2 > 0

компактны, положительно инвариантны и содержат предельные множества всех траекторий,_⋂

a Ω₂ =ε1>0,ε₂>0Ω2,ε₁,ε₂.

5. Вымирание популяций. Теорема Ла-Салля позволяет определить следующие условия

вымирания популяций.

Утверждение 4. При выполнении неравенства

b₃ >

(2)

b₂ + 1

все траектории системы стремятся к множеству {x₃ = 0}

^⋂Ω₂, а при выполнении нера-

венства

b₄ < b₁ + b₅

(3)

– к множеству {x₂ = 0}

^⋂Ω₂.

Доказательство. Достаточно проверить, что при выполнении неравенства (2) ((3)) пре-

дельные множества всех траекторий содержатся в множестве {x₃ = 0}

^⋂Ω₂ ({x₂ = 0}^⋂Ω₂).

Для этого сначала рассмотрим функцию V (x) = x₃. Её производная в силу системы равна

x₃, и в Ω₂ выполнено неравенство

(

)

(

)

x₁ + x₂

=x₃

-b₃

≤x₃

-b₃

≤ 0,

b₂ + x₁ + x₂

b₂

причём

= 0 в Ω₂ при (2) лишь в случае x₃ = 0. Следовательно, предельные множества

всех траекторий содержатся в множестве Ω₂

^⋂ {x₃ = 0}.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

БИФУРКАЦИЯ ХОПФА В СИСТЕМЕ ХИЩНИК-ЖЕРТВА С ИНФЕКЦИЕЙ

1569

Теперь рассмотрим функцию W (x) = x₂. Её производная в силу системы равна

x₂, и в

Ω₂ выполнено неравенство

≤ x₂(b₄x₁ - b₅ - b₁(x₁ + x₂)) ≤ x₂((b₄ - b₁)(x₁ + x₂) - b₅) ≤ x₂((b₄ - b₁) - b₅) ≤ 0,

причём

= 0 в Ω₂ при (3) лишь в случае x₂ = 0. Следовательно, предельные множества

всех траекторий содержатся в множестве Ω₂

^⋂ {x₂ = 0}.

6. Положения равновесия на границе множества R3+,0. Несложно проверить следу-

ющие необходимые и достаточные условия существования этих положений равновесия.

Утверждение 5. У системы (1) при любых значениях параметров существуют положе-

ния равновесия E₁(0,0,0), E₂(1,0,0). При выполнении неравенства b₃ < 1/(1+b₂) существу-

ет положение равновесия E₃(x⁽³⁾¹,0,x⁽³⁾³), x⁽³⁾¹ > 0, x⁽³⁾³ > 0, а при выполнении неравенства

b₄ > b₁ + b₅, - положение равновесия E₄(x⁽⁴⁾¹,x⁽⁴⁾²,0), x⁽⁴⁾¹ > 0, x⁽⁴⁾² > 0.

7. Внутреннее положение равновесия. Из третьего уравнения системы (1) следует,

что для существования положения равновесия E₅(x⁽⁵⁾¹, x⁽⁵⁾², x⁽⁵⁾³) внутри R3+,0 необходимо вы-

полнение неравенства b₃ < 1.

Введём три новых положительных параметра: α = b₁/b₄, β = b₅/b₄, γ = b₂b₃/(1 - b₃).

Утверждение 6. У системы (1) при выполнении неравенств

α + β < γ < γ^∗(α,β),

(4)

где α + β < 1, γ^∗(α, β) ∈ (0, 1) - положительный корень многочлена

g_α,β(γ) = αγ² + ((1 - α)β - α)γ - β²,

существует внутреннее положение равновесия E₅(x⁽⁵⁾¹,x⁽⁵⁾²,x⁽⁵⁾³), где

(

)

αγ

x⁽⁵⁾¹ =^αγ

x⁽⁵⁾² = γ -αγ

x⁽⁵⁾³ = b₄(b₂ + γ)

- αγ - β .

γ-β

Доказательство. Отметим, что α + β ≤ 1, так как иначе популяция x₂ вымирает и

внутреннего положения равновесия нет.

Координаты для точки E₅ находятся после несложных алгебраических преобразований.

Первые две координаты положительны тогда и только тогда, когда α + β < γ, а неравенство

x(5)3 > 0 равносильно условию αγ/(γ - β) - αγ - β > 0, т.е. gα,β(γ) < 0. В результате

получаем условие положительности координат в виде неравенств α+β < γ < γ^∗(α, β), которые

совместны при α + β < 1, так как в этом случае g_α,β(α + β) = α²(α + β - 1) < 0 и γ^∗(α, β) >

> α+β. Если α+β = 1, то g_α,β(α+β) = 0, γ^∗(α,β) = 1 = α+β, и условие положительности

координат не выполняется ни при каком γ.

Замечание. Неравенство γ^∗(α, β) ≥ α + β означает, что в пространстве параметров

поверхность, задаваемая квадратным трёхчленом в области γ > 0, расположена по одну

сторону от плоскости γ = α + β при α > 0, β > 0, α + β < 1.

8. Бифуркация Хопфа. Исследуем поведение собственных чисел внутреннего положе-

ния равновесия с помощью численных расчётов. Для этого построим сетку точек в области

параметров системы, в которой система имеет внутреннее положение равновесия. В каждом

узле сетки вычислим спектр внутреннего положения равновесия. Найдём два узла, в каждом

из которых действительные собственные числа отрицательны, а два других комплексные, при-

чём действительные части этих пар комплексных собственных чисел имеют противоположные

знаки. Соединим эти два узла кривой, которая лежит в области существования внутренних

положений равновесия, и в каждой точке которой действительное собственное значение от-

рицательно. Если существует точка на кривой, в окрестности которой действительная часть

комплексных собственных значений меняет знак с отрицательного на положительный, то она

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023

1570

КРИЩЕНКО, ПОДДЕРЕГИН

соответствует бифуркации Хопфа, что подтвердим наличием соответствующей периодической

траектории.

Сначала задаём сетку точек в области (4) первого октанта в пространстве (α, β, γ) и в

множестве (b₃, b₄) = (0, 1) × (0, B₄), B₄ > 0, первой четверти плоскости параметров (b₃, b₄).

В каждом узле (α_i, β_j , γ_k, b3,l, b4,m) произведения этих сеток перейдём к исходным параметрам

по формулам b₁ = α_ib4,m, b₂ = ((1 - b3,l)/b3,l)γ_k, b₃ = b3,l, b₄ = b4,m, b₅ = β_j b4,m. Для этих

параметров вычисляем спектр внутреннего положения равновесия и выбираем два нужных

узла. Так найден набор значений исходных параметров b⁽¹⁾ = (0.06, 0.2768, 0.5792, 0.6, 0.01),

при котором λ₁ = -0.1563, λ2,3 = -0.0039 ± 0.0859i, и набор значений параметров b⁽²⁾ =

= (0.06, 0.1912, 0.5916, 0.6, 0.01), при котором собственные числа равны λ₁ = -0.0942, λ2,3 =

= 0.0017 ± 0.0958i.

В точках отрезка b(κ) = b⁽¹⁾ + (b⁽²⁾ - b⁽¹⁾)κ, κ ∈ [0, 1], спектр имеет нужную структуру,

а именно: одно собственное число отрицательно, а два других собственных числа комплексно

сопряжённые, и существует значение κ = κ^∗, b(κ^∗) = (0.06, 0.2149, 0.5882, 0.6, 0.01), в окрест-

ности которого действительная часть комплексных собственных чисел меняет знак с ростом

κ с отрицательного на положительный. Это означает, что в системе происходит бифуркация

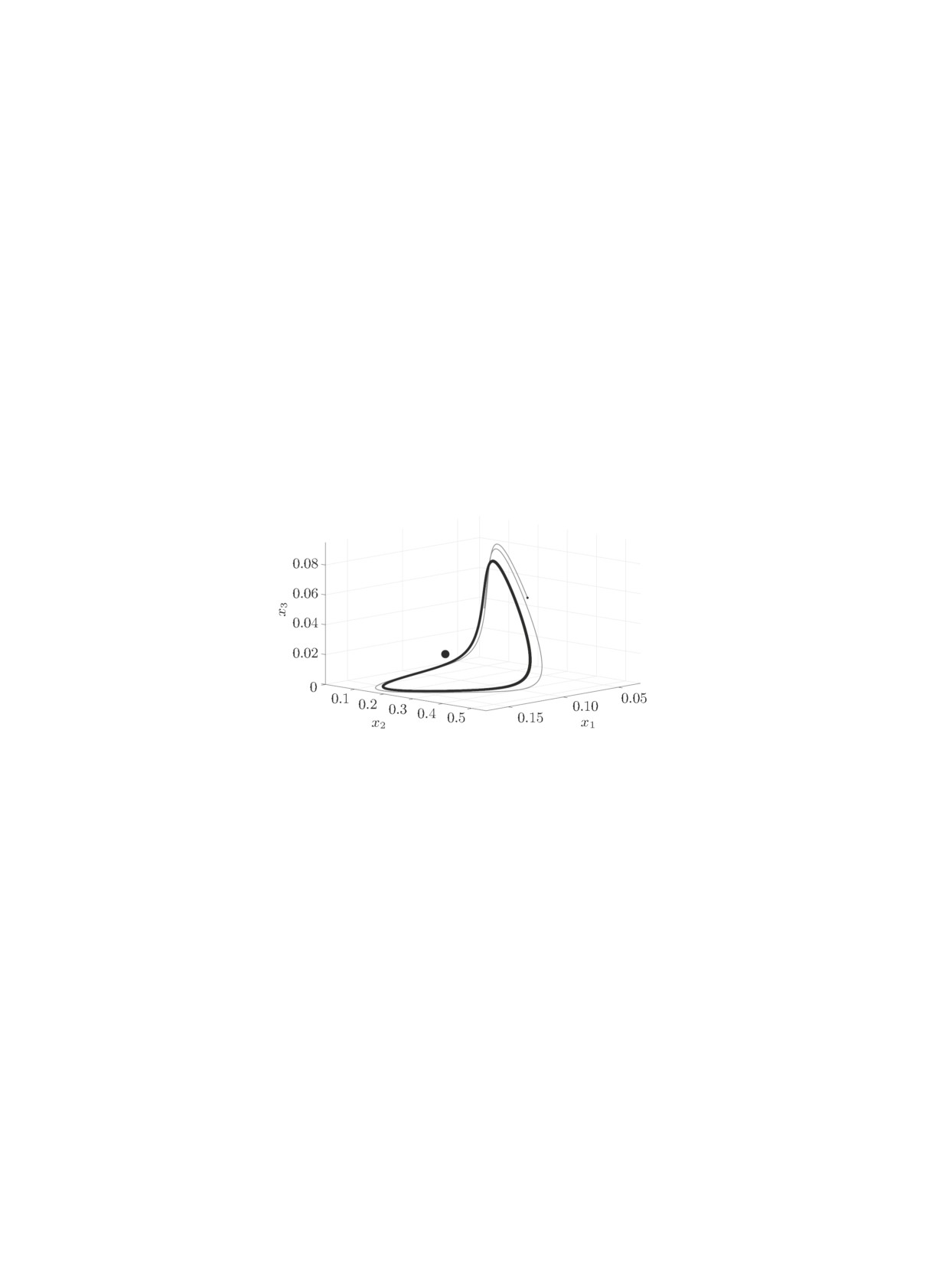
Хопфа, в результате которой появляется устойчивый цикл. Например, система с параметрами

b⁽²⁾ имеет такой цикл с начальными данными (0.1526,0.2366,0.0009) в окрестности внутрен-

него положения равновесия E₅(0.1064, 0.1706, 0.0174) (рисунок).

Рисунок. Устойчивый цикл и внутреннее положение

равновесия системы с параметрами b⁽²⁾.

Заключение. С помощью метода локализации инвариантных компактов найдены условия

вымирания популяций хищников и инфицированных жертв. Они являются необходимыми и

достаточными, что следует из условий существования положений равновесия E₂ и E₃. При

этих положениях равновесия могут существовать внутреннее положение равновесия, простран-

ственная устойчивая периодическая траектория и более сложные аттракторы.

Работа выполнена при поддержке программы “Приоритет 2030” МГТУ имени Н.Э. Бау-

мана.

СПИСОК ЛИТЕРАТУРЫ

1. Bate A.M., Hilkerr F.M. Complex dynamics in an eco-epidemiological model // Bull. Math. Biol. 2013.

V. 75. P. 2059-2078.

2. Крищенко А.П. Локализация инвариантных компактов динамических систем // Дифференц. урав-

нения. 2005. Т. 41. № 12. С. 1597-1604.

3. Арнольд В.И. Обыкновенные дифференциальные уравнения. М., 2012.

Московский государственный технический

Поступила в редакцию 28.04.2023 г.

университет имени Н.Э. Баумана,

После доработки 28.04.2023 г.

Федеральный исследовательский центр

Принята к публикации 20.09.2023 г.

“Информатика и управление” РАН, г. Москва

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 11

2023