ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 11, с. 1571-1574
КРАТКИЕ СООБЩЕНИЯ
УДК 517.977.1
О ВАРИАЦИИ ПАРАМЕТРА НЕЛИНЕЙНОСТИ
В АЛГОРИТМЕ “SUPER-TWISTING”
© 2023 г. В. В. Фомичев, А. О. Высоцкий
Исследована устойчивость модифицированного (при вариации параметра нелинейности)
алгоритма “super-twisting”. Анализ основан на мажорировании траекторий системы с про-
извольным параметром нелинейности траекториями систем классического алгоритма “su-
per-twisting”. Получены условия устойчивости для модифицированных систем, а также
оценки на размеры области устойчивости в зависимости от параметров системы.
DOI: 10.31857/S0374064123110134, EDN: PFBOCN
Введение. Задача стабилизации является одной из центральных в теории управления,
в том числе и для систем с неопределённостью (с неизвестными неизмеряемыми входными
воздействиями). Одним из наиболее популярных алгоритмов управления, используемых для
достижения робастной по отношению к внешним возмущениям устойчивости динамических
систем, является алгоритм “super-twisting” [1, 2]. Для системы уравнений данного алгорит-
ма было доказано существование набора параметров, обеспечивающих устойчивость [2]. Впо-
следствии с помощью метода функций Ляпунова были получены алгебраические достаточные
условия устойчивости [3, 4]. Наконец, в работах [5, 6] с помощью анализа системы при “наи-
худшем возмущении” были найдены необходимые и достаточные условия её устойчивости.
Традиционно при изучении данного алгоритма варьируются только множители перед нели-
нейным и разрывным слагаемыми в первом и втором уравнениях системы соответственно при
одинаковом значении степени, равном 1/2. Целью данной работы является изучение свойства
устойчивости обобщённого (при различных значениях степени) алгоритма “super-twisting”.
Далее используется следующее обозначение: для x ∈ R
⌈x⌋α = sign (x)|x|α.
1. Постановка задачи. Наихудшее возмущение. Рассматривается система
x1 = x2 - k⌈x1⌋α,
x2 = ξ - μ⌈x1⌋0,
(1)
где ξ = ξ(t) - неизвестное ограниченное (|ξ(t)| ≤ ξ0) измеримое входное воздействие, α ∈ R,
0 < α < 1.
Требуется исследовать данную систему на устойчивость в зависимости от значений пара-
метров k, μ и α.
При α=1/2 данная система представляет собой классический [2] алгоритм “super-twisting”.
Для неё с помощью анализа фазового пространства было показано [6], что траектории системы
с любым возмущением из рассматриваемого класса будут ограничены траекторией системы с
“наихудшим” возмущением:
ξ∗ = ξ0 sign ( x1) = ξ0 sign (x2 - k⌈x1⌋α).
(2)
Из ограниченности траекторий следует, что для исследования устойчивости таких систем до-
статочно рассматривать системы с возмущением (2).
Рассуждения о наихудшей помехе из работы [6] могут быть без изменений применены к сис-
теме (1) с произвольным параметром α. Всюду далее в данной статье будет рассматриваться
система (1) с возмущением (2):
x1 = x2 - k⌈x1⌋α,
x2 = ξ∗ - μ⌈x1⌋0.
(3)
1571
9∗
1572
ФОМИЧЕВ, ВЫСОЦКИЙ
2. Анализ устойчивости. Для случая α = 1/2 известны [6] необходимые и достаточные
условия асимптотической устойчивости системы (1) с возмущением (2). Показано, что устой-
чивость системы если достигается, то является глобальной. Кроме того, для любых ξ0 > 0,
μ > ξ0 существует k0 = k0(μ,ξ0) такое, что при любом k > k0 система (3) с параметрами
k,μ,α = 1/2 будет устойчива, при k = k0 система устойчива, но не асимптотически, а при
k < k0 она неустойчива.
Не нарушая общности рассуждений, положим начальные условия для системы (3) равными
(0, x02), x02 > 0. Рассматривать систему, в силу симметричности относительно начала коорди-
нат, достаточно только в правой полуплоскости координатной плоскости, т.е. при x1 ≥ 0.
2.1. Случай α < 1/2. Проанализируем устойчивость системы (3) при 0 < α < 1/2.
Будем сравнивать траекторию системы (3) с произвольными параметрами k, μ, α < 1/2 с
траекторией системы
x1 = x2 - k∗⌈x1⌋1/2,
x2 = ξ∗ - μ⌈x1⌋0,
(4)
где k∗ = k0(μ, ξ0) + ε, ε ∈ R - сколь угодно малое положительное число. В силу приведённых
выше рассуждений система (4) будет глобально асимптотически устойчивой.
Покажем, что существует окрестность начала координат, в которой траектория системы
(4) будет ограничивать траекторию системы (3) с рассматриваемым набором параметров.
Заметим, что в области координатной
плоскости, где
k⌈x1⌋α ≥ k∗⌈x1⌋1/2,
(5)
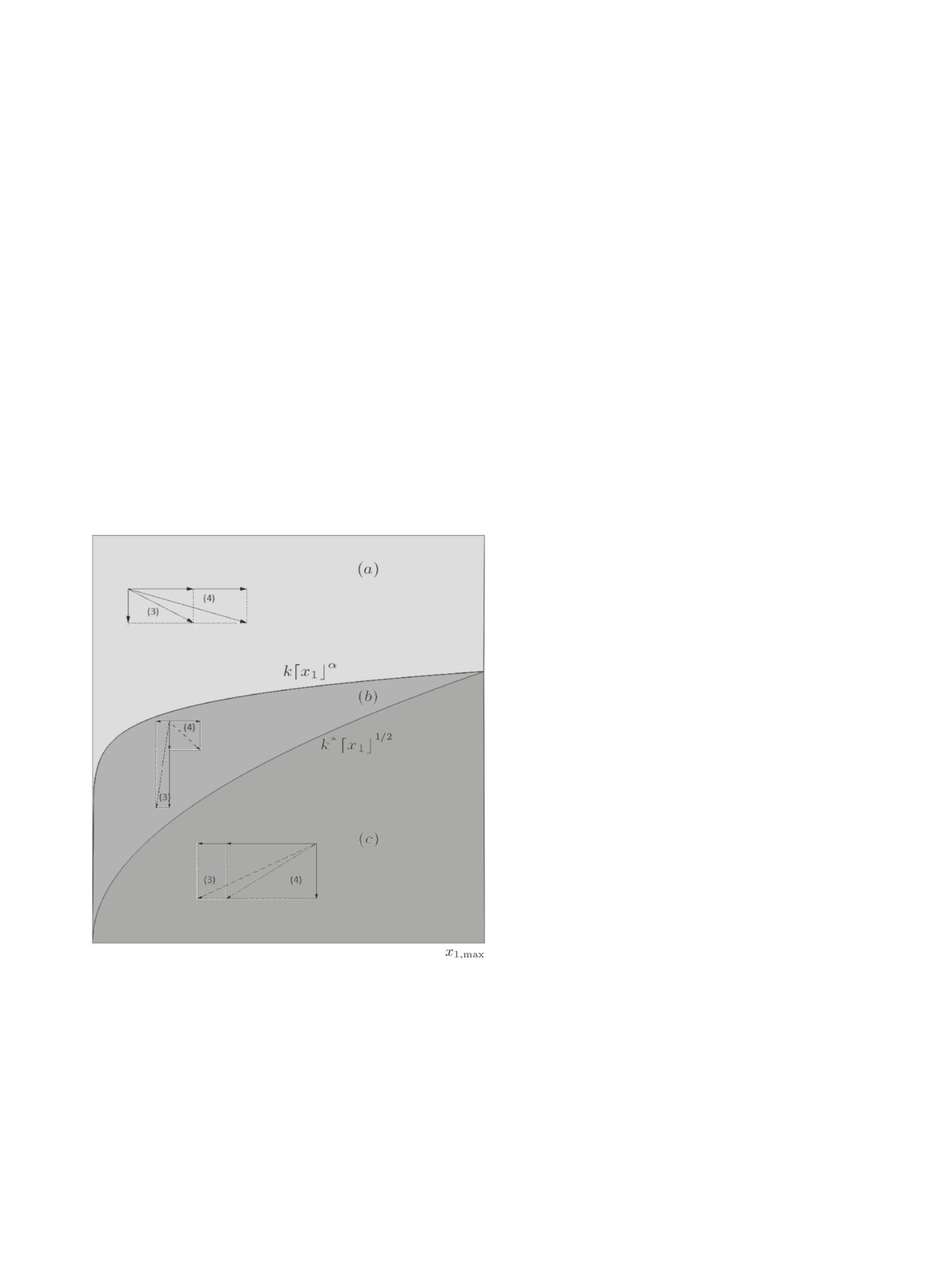
траектория системы (4) будет ограничи-
вать траекторию системы (3). Действи-
тельно, в области, где знаки первой ком-
поненты векторов скорости систем сов-
падают (области (a) и (c) на рисун-
ке), значения второй компоненты векто-
ров скоростей систем совпадают. Значит,
поскольку величина
x1 больше в систе-
ме (4), траектория системы (3) не может
пересечь траекторию системы (4). Слу-
чай когда знаки первых компонент век-
тора скорости двух систем отличаются
возможен только если
x1 < 0 для сис-
темы (3) (область (b) на рисунке). Сле-
довательно, тогда пересечение траекто-
рий невозможно, и траектория системы
(4) будет ограничивать траекторию сис-
темы (3).
Получим оценку на величину началь-
Рисунок. Сравнение векторов скоростей систем (3) и (4). ного условия x02, гарантирующую вы-
полнение неравенства (5). Очевидно, что
поскольку траектории системы (4) огра-
ничивают сверху траектории системы (3) достаточно выбрать такое начальное условие, чтобы
это неравенство выполнялось для системы (4). Неравенство (5) примет вид
|x1| ≤ (k/k∗)2/(1-2α) = x1,max.
(6)
Решение системы (4) было найдено в работе [6]. В частности, была получена зависимость
максимального значения координаты x1 (обозначим его x∗1) от начального условия x02 :
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 11
2023
О ВАРИАЦИИ ПАРАМЕТРА НЕЛИНЕЙНОСТИ
1573
⎧
{
(
)}
⎪(x02)2
-2k∗
k∗
4b - (k∗)2
⎨
exp
√
arctg
√
+ arctg
√
,
(k∗)2 < 8b,
2b
8b - (k∗)2
8b - (k∗)2
k∗
8b - (k∗)2
x∗1 =
(
)2(
)2B
⎪
x02u1
u2(b + k∗u1)
⎩
,
(k∗)2 ≥ 8b,
b+k∗u1
u1(b + k∗u2)
√
где b = μ - ξ0, u1,2 = (-k ±
k2 - 8b)/4, B = -u2/(u1 - u2).
Для системы (4) неравенство (6) равносильно неравенству x∗1 ≤ x1,max. Последнее можно
записать как соотношение для начального условия x02 :
⎧
{
(
)}
√
k0
k0
4b - k20
⎪
2b exp
√
arctg
√
+ arctg
√
√x1,max, k20 < 8b,
⎨
8b - k20
8b - k20
k0
8b - k2
0
x02 <
)B
(7)
⎪b+k0u1
(u1(b + k0u2)
⎩
√x1,max,
k20 ≥ 8b.
u1
u2(b + k0u1)
Если для начальных условий системы (3) выполнено условие (7), то поскольку её траекто-
рия ограничена траекторией системы (4) для неё также будет выполнено и условие (6). Таким
образом, доказана
Теорема 1. Система (1) с 0 < α < 1/2, μ > ξ0 и k > 0 является локально асимптоти-
чески устойчивой. Выполнение условия (7) гарантирует сходимость системы.
Следствие. Если набор параметров k, μ обеспечивает устойчивости системы (3) при
α = 1/2 (т.е. если k > k0(μ,ξ0)), то при α → 1/2 - 0 область устойчивости системы (3)
растёт, заполняя всю координатную плоскость.
2.2. Случай α > 1/2. Перейдём к рассмотрению случая α > 1/2. Аналогично случаю
α < 1/2 будем сравнивать траекторию системы (3) с траекторией неустойчивой системы
x1 = x2 - k∗⌈x1⌋1/2,
x2 = ξ∗ - μ⌈x1⌋0,
(8)
где k∗ = k0(μ, ξ0) - ε, ε > 0 - сколь угодно малое число.
Покажем, что существует окрестность начала координат, внутри которой траектории сис-
темы (8) ограничивают снизу траектории системы (3). Аналогичными случаю α < 1/2 рас-
суждениями легко показать, что такая ограниченность траекторий будет достигаться всюду в
области, где k⌈x1⌋α ≤ k∗⌈x1⌋1/2, т.е. при
|x1| ≤ (k∗/k)2/(2α-1) = x1,min.
(9)
Для системы (8) эквивалентное условию (9) неравенство для начального условия x02 запи-
шется в виде
⎧
{
(
)}
⎪
√
k0
k0
4b - k20
⎨x02 <
2b exp
√
arctg
√
+ arctg
√
√x1,min, k20 < 8b,
2
8b - k20
8b - k20
k0
8b - k
0
(10)
)B
⎪
b+k0u1
(u1(b + k0u2)
⎩x0
<
√x1,min,
k20 ≥ 8b.
2
u1
u2(b + k0u1)
В силу ограниченности траектории системы (8) траекторией системы (3) справедливо сле-
дующее утверждение.
Теорема 2. Система (1) с 1/2 < α < 1 не является устойчивой ни для каких μ > ξ0
и k > 0. При этом если траектории системы сходятся в некую ограниченную область, то
она гарантированно будет содержать область, ограниченную траекториями системы (8) с
начальными условиями, удовлетворяющими условию (10).
Работа выполнена при финансовой поддержке Российского научного фонда (проект 22-21-
00288).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 11
2023
1574
ФОМИЧЕВ, ВЫСОЦКИЙ
СПИСОК ЛИТЕРАТУРЫ
1. Емельянов С.В., Коровин С.К., Левантовский Л.В. Новый класс алгоритмов скольжения второго
порядка // Мат. моделирование. 1990. Т. 2. № 3. С. 89-100.
2. Levant A. Sliding order and sliding accuracy in sliding mode control // Int. J. of Control. 1993. V. 58.
P. 1247-1263.
3. Moreno J., Osorio M. Strict Lyapounov functions for the super-twisting algorithm // IEEE Trans. on
Autom. Contr. 2012. V. 57. P. 1035-1040.
4. Seeber R., Horn M. Stability proof for a well-established super-twisting parameter setting // Automatica.
2017. V. 84. P. 241-243.
5. Seeber R., Horn M. Necessary and sufficient stability criterion for the super-twisting algorithm // 15th
Intern. Workshop on Variable Structure Systems (VSS). 2018. P. 120-125.
6. Фомичев В.В., Высоцкий А.О. Критерий устойчивости и точные оценки для алгоритма “супер-
скручивания”// Дифференц. уравнения. 2023. Т. 59. № 2. С. 252-256.
Электротехнический университет,
Поступила в редакцию 08.09.2023 г.
г. Ханчжоу, Китай,
После доработки 08.09.2023 г.
Московский государственный университет
Принята к публикации 20.09.2023 г.
имени М.В. Ломоносова,
Федеральный исследовательский центр
“Информатика и управление” РАН, г. Москва
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№ 11
2023