ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 12, с. 1692-1701

ТЕОРИЯ УПРАВЛЕНИЯ

УДК 517.977

ПОИСК ПАРАМЕТРОВ МОДЕЛИ

С НАИЛУЧШЕЙ ЛОКАЛЬНОЙ УПРАВЛЯЕМОСТЬЮ

Исследуется задача оптимального выбора параметров модели относительно какого-ли-

бо функционала. Рассматриваются локально управляемые аффинные системы и инте-

гральные функционалы, зависящие от программного управления. Доказывается локальная

управляемость аффинных систем с неотрицательными входами в случае, когда столбцы

при управлениях образуют положительный базис. Для таких систем вводится коэффи-

циент локальной управляемости и ставится задача его максимизации в зависимости от

выбора параметров модели. В качестве примера рассматривается очень упрощённая мо-

дель подводного аппарата и исследуется задача такого расположения его управляющих

винтомоторных агрегатов, при котором энергопотребление аппарата минимально.

DOI: 10.31857/S0374064123120099, EDN: NWKEBC

Введение. В настоящее время существует множество видов автономных необитаемых под-

водных аппаратов, отличающихся размерами, формой, областью применения, видами и рас-

положением управляющих агрегатов и т.д. Задача выбора аппарата, оптимального в том или

ином смысле, решается, как правило, из механических или технических соображений. Напри-

мер, в работах [1, 2] задача снижения энергопотребления подводного аппарата решалась с

использованием обтекаемой конструкции корпуса и разрабатываемой в этих работах системы

управления солнечной энергией и энергией подводного аппарата.

Хорошо известно [3, с. 48], что движение подводного аппарата описывает динамическая

система управления с параметрами. Выбор параметров определяет, в частности, вид и рас-

положение управляющих агрегатов подводного аппарата. Энергия, потребляемая аппаратом,

равна интегральному функционалу, зависящему от управления системы. Задача поиска мо-

дели подводного аппарата с минимальным потреблением энергии формулируется на матема-

тическом языке как задача поиска параметров системы, при которых указанный функцио-

нал минимален. Аналогичные задачи формулируются для летательных аппаратов и наземных

транспортных средств, а также для других функционалов, например, характеризующих время

движения. Задача сравнения однотипных роботов по тому или иному критерию с использова-

нием математических методов актуальна ввиду бурного развития робототехники в настоящее

время.

Отметим, что рассматриваемая в работе задача близка задаче оптимального управления

по какому-либо критерию. Например, задачи оптимального управления по критерию быстро-

действия решались для перехвата движущейся по предписанной траектории цели машиной

Дубинса [4, 5] и для системы, состоящей из двух несинхронных осцилляторов [6].

Цель данной статьи - попытаться разработать математические методы для сравнения од-

нотипных моделей по тому или иному критерию. Мы не используем методы теории оптималь-

ного управления ввиду сложности их применения к данной задаче. Наш подход основан на

предположении, что в малой окрестности каждого допустимого состояния любая траектория

системы возможна и равновероятна. Из этого следует, в частности, локальная управляемость

системы. Кроме того, локальную траекторию системы можно считать случайной величиной.

Тогда значение функционала также есть случайная величина, а поставленную задачу можно

понимать как задачу минимизации математического ожидания значения функционала. Коэф-

фициент локальной управляемости системы относительно заданного функционала, определя-

емый нами как величина обратно пропорциональная указанному математическому ожиданию,

мы предлагаем использовать для сравнения систем с разными значениями параметров.

1692

ПОИСК ПАРАМЕТРОВ МОДЕЛИ

1693

Для упрощения определений и вычислений далее будем рассматривать только аффинные

системы с неотрицательными входами. Локальная управляемость таких систем исследуется с

использованием понятия положительного базиса, введённого в работах [7, 8]. Докажем простой

метод проверки положительного базиса, а также достаточное условие локальной управляемо-

сти систем указанного типа.

В качестве иллюстрации рассмотрен пример движения в вертикальной плоскости подвод-

ного аппарата, управляемого винтомоторными агрегатами (ВМА). Предполагаем, что тяга

каждого ВМА может быть направлена только в одну сторону. Показано, что такое движение

описывает аффинная система с неотрицательными управлениями, параметрами которой явля-

ются количество ВМА и их расположение. Доказано, что данная система локально управляе-

ма только в случае четырёх и более ВМА, расположенных определённым образом. В качестве

функционала, используемого для сравнения систем с разным расположением ВМА, мы рас-

сматриваем потребляемую энергию двигателями аппарата. Коэффициент локальной управля-

емости системы относительно этого функционала вычислен для разных значений параметров.

Найдены несколько точек локального максимума и соответствующие значения функционала

на четырёх выбранных траекториях.

Статья организована следующим образом. В п. 1 ставится задача и формулируется пример.

Определения локально управляемой системы и положительного базиса, а также факты о них

содержатся в п. 2. Алгоритм управления системами с положительным базисом формулируется

в п. 3. В п. 4 определяется коэффициент управляемости и вычисляется для рассматриваемого

примера, сравниваются системы с разными значениями параметров.

1. Постановка задачи. Рассмотрим систему

x = f(x,u,α), x ∈ X ⊂ Rⁿ, u ∈ U ⊂ R^m, α ∈ R^k,

(1)

где x = (x₁, . . . , x_n) - состояние системы, u = (u₁, . . . , u_m) - её управления, X - область

допустимых состояний, U - область допустимых управлений, α = (α₁,... ,α_k) - набор па-

раметров, а x ≡ dx/dt.

Пусть для системы (1) ставится задача выбора таких параметров α, для которых мини-

мален следующий функционал. Рассмотрим гладкую неотрицательную при x ∈ X и u ∈ U

функцию Φ(x, u) и отображение, которое каждому решению (x(t), u(t)) системы (1) ставит в

соответствие интеграл по промежутку [0, T ] функции Φ(x(t), u(t)). Упомянутый функционал

равен максимальному по решениям системы (1) значению этого отображения, т.е.

∫

max

Φ(x(t), u(t)) dt.

(2)

(x(t),u(t))

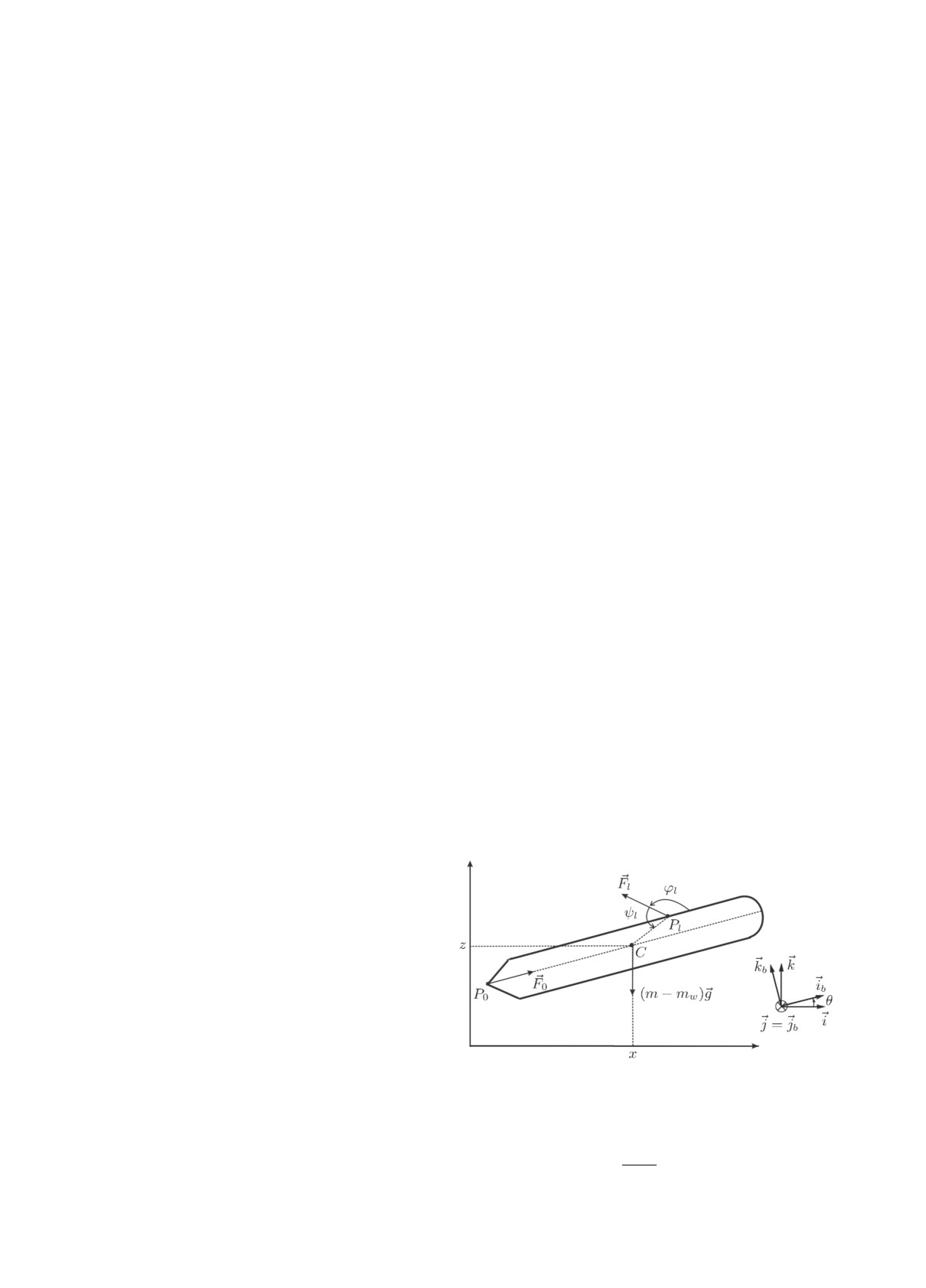
Пример 1. Рассмотрим упрощённую

модель подводного аппарата, эволюция ко-

торого ограничена в вертикальной плоско-

сти (рисунок). Пусть (i,⃗j,k) - ортонорми-

рованный базис неподвижной системы ко-

ординат, а (ib,⃗jb,kb) - ортонормированный

базис подвижной системы координат, при-

креплённой к подводному аппарату. Обо-

значим через θ угол между этими систе-

мами координат. Аппарат имеет один более

мощный винтовой двигатель (с номером 0)

для движения вперед и l_m винтовых двига-

телей малой мощности для разворота. Обо-

Рисунок. Упрощённая модель подводного аппарата.

значим через P₀, P₁, . . . , Plm точки рас-

положения винтов.

На подводный аппарат действуют силы

F₀ = F₀ib,

Fl = Fl(cos φl

⃗i_b + sin φ_l k_b), l = 1,l_m,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

1694

ВЕЛИЩАНСКИЙ, ЧЕТВЕРИКОВ

(m - m_w)g = -(m - m_w)gk,

где m - масса подводного аппарата; m_w - масса воды, вытесненной подводным аппаратом;

--→

φ_l - угол междуib и

Fl, ψl - угол между

Fl и

P_lC. Вес mg и выталкивающая сила -m_wg

прикладываются к центру масс C; сила

Fl прикладывается к точке Pl, l = 0, lm, где

--→

CP_l = -|CPl|(cos(ψl + φl)⃗ib + sin(ψl + φl)kb).

Уравнения движения, записанные в терминах центра масс C, имеют вид

∑

⃗

--→

mvC = (m - m_w)g +

Fl,

L_C =

CP_l

Fl,

l=0

где v_C - скорость,

L_C - угловой момент относительно C. Спроецировав эти уравнения на

неподвижные оси, получим

(

)

∑

x = cosθ u₀ + ul cosφ_l

- sin θ

u_l sin φ_l,

l=1

(

)

∑

z = sinθ u₀ +

u_l cos φ_l

+ cos θ u_l sin φ_l - κg,

θ = κ_lul sinψ_l,

(3)

l=1

где

--→

F₀

m-m_w

m|CPl|

u₀ =

κ=

u_l =

κ_l =

l = 1,l_m,

J - момент инерции подводного аппарата относительно оси Oy. Так как тяга каждого ВМА

может быть направлена только в одну сторону, то u_l ≥ 0, l = 0, l_m.

--→

Параметрами данной системы являются l_m, φ_l, ψ_l,

|CPl|, т.е. количество винтов и их

расположение. В качестве функции Φ(x, u), определяющей функционал (2), возьмём функцию

∑lm

Φ =

u_i. Тогда функционал пропорционален потребляемой энергии всеми двигателями

i=0

аппарата.

2. Условия локальной управляемости. Рассмотрим систему

x = f(x,u), x ∈ X ⊂ Rⁿ, u ∈ U ⊂ R^m.

(4)

Напомним, что состояние x_f ∈ D ⊂ X называют достижимым из состояния x₀ ∈ D ⊂ X в

области D, если существует решение (x(t), u(t)), t ∈ [t₀, t_f ], системы (4), удовлетворяющее

условиям

x(t₀) = x₀, x(t_f ) = x_f ,

x(t) ∈ D, u(t) ∈ U при t ∈ [t₀, t_f ].

(5)

Систему (4) называют управляемой в области D ⊂ X , если любое состояние x_f ∈ D

достижимо из любого состояния x₀ ∈ D в области D.

Пример 2. Запишем систему (3) как

∑

u₀ + u_l cos φ_l = cos θ x + sin θ (z + κg),

u_l sin φ_l = - sin θ x + cos θ (z + κg),

l=1

∑

κ_lu_l sin ψ_l =θ.

(6)

l=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

ПОИСК ПАРАМЕТРОВ МОДЕЛИ

1695

Система (6) имеет вид

∑

u_la_l(x) = ζ(x, x,... , x(s)),

x∈X₀ ⊂Rⁿ,

u = (u₀,...,ulm)^т ∈ U, u_l ≥ 0, l = 0,l_m.

(7)

l=0

А именно, для системы (6) n = 3, s = 2,

x = (x,z,θ)^т, a₀, ..., alm - столбцы высоты 3,

зависящие только от параметров системы.

Для системы (7) обозначим через M матрицу, состоящую из столбцов a₀, a₁, . . . , alm .

Если rang M = n, то для любой векторной функции x(t) ∈ D ⊂ X₀, t ∈ [t₀, t_f ], существует

векторная функция u(t) = (u₀(t), . . . , ulm (t))^т, удовлетворяющая вместе с x(t) системе (7).

Если при этом u(t) ∈ U и u_l(t) ≥ 0 для t ∈ [t₀, t_f ] и l = 0, l_m, то пара векторных функций

(x, u(t)) удовлетворяет всем условиям (7).

Областью достижимости состояния x_f ∈ X за время T > 0 в области D ⊂ X будем

называть множество таких состояний x₀ ∈ X , что существует решение (x(t), u(t)), t ∈ [t₀, t_f ],

системы (4), удовлетворяющее условиям (5) при t_f - t₀ < T.

Систему (4) будем называть локально управляемой в точке x_f ∈ X , если для любого T > 0

область достижимости состояния x_f за время T в области X содержит окрестность точки

x_f (см. [8]). Система (4) локально управляема в области X, если она локально управляема в

любой точке x₀ ∈ X .

Замечание. В определении локальной управляемости рассматриваются траектории сис-

темы, которые начинаются в произвольной точке x₀ ∈ X и заканчиваются в заданной точке

x_f , а не наоборот. Такой выбор объясняется тем, что в начальный момент, как правило, опре-

делены значения u, а в конечный момент мы можем считать компоненты u произвольными.

Существуют системы, которые управляемы, но не локально управляемы.

Пример 3. Рассмотрим подводный аппарат с тремя винтами, т.е. l_m = 2. Пусть винты

расположены так, что φ₁ = π/2, ψ₁ = 0, φ₂ = 3π/4, ψ₂ = π/2. Третье уравнения системы (3)

имеет вид^θ = κ₂u₂. Поскольку u₂ ≥ 0, то угол θ может только расти, т.е. аппарат может

поворачиваться только против часовой стрелки. Чтобы повернуть аппарат на угол θ₀ > 0 по

часовой стрелке, необходимо повернуть его на угол 2π -θ₀ против часовой стрелки. Если угол

θ₀ мал, то угол 2π-θ₀ не является малым, и сколь угодно уменьшать время движения нельзя,

потому что u₂ ограничено сверху. Таким образом, система не локально управляема, хотя

управляема, если нет ограничения на время движения. Например, при движении из начального

состояния в конечное достаточно сначала развернуть аппарат, а потом двигаться по прямой.

Для формулировки условий локальной управляемости в случае u_l ≥ 0, l = 0, l_m, нам пона-

добятся следующие понятия и результаты из работ [7, 8]. Говорят, что векторы a₁, . . . , a_m ∈ R^N

составляют положительный базис пространства R^N , если для каждого a ∈ R^N найдутся та-

кие неотрицательные числа λ₁, . . . , λ_m, что a = λ₁a₁ + . . . + λ_ma_m.

Сформулируем некоторые свойства положительного базиса, доказанные в [7, 8].

Свойство 1. Всегда существует положительный базис размерности N +1, т.е. m = N +1.

Свойство 2. Для любого положительного базиса имеем m ≥ N + 1.

Свойство 3. Пусть векторы a₁, . . . , a_m ∈ R^N составляют положительный базис. Тогда

найдутся такие положительные числа λ₁, . . . , λ_m, что λ₁a₁ + . . . + λ_ma_m = 0.

Свойство 4. Среди векторов, составляющих положительный базис, найдётся N линейно-

независимых, а значит, образующих обычный базис пространства R^N .

Учитывая свойство 1 положительного базиса, далее мы будем рассматривать только случай

m = N + 1. Докажем для этого случая ещё два свойства и теорему, дающую простой метод

проверки положительного базиса.

Свойство 5. В случае m = N + 1 любые N векторов положительного базиса образуют

обычный базис пространства R^N .

Доказательство. Из соображений размерности вытекает, что если N векторов простран-

ства R^N линейно независимы, то они образуют обычный базис этого пространства. Предпо-

ложим существование такого положительного базиса a₀, a₁, . . . , a_N пространства R^N , что

векторы a₁, . . . , a_N линейно зависимы. Из свойства 4 положительного базиса следует, что

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

1696

ВЕЛИЩАНСКИЙ, ЧЕТВЕРИКОВ

среди векторов a₀, a₁, . . . , a_N найдётся обычный базис пространства R^N . Этот базис содер-

жит вектор a₀, пусть он состоит из векторов a₀, a₁, . . . , aN-1. Тогда векторы a₁, . . . , aN-1

линейно независимы. Из линейной зависимости векторов a₁, . . . , a_N следует, что вектор a_N

линейно выражается через векторы a₁, . . . , aN-1. Из определения положительного базиса

следует представление

-a₀ = λ₀a₀ + λ₁a₁ + ... + λ_Na_N ,

где λ_i ≥ 0, i = 0, N . Заменим в этом равенстве вектор a_N на линейную комбинацию векторов

a₁, ..., aN-1 и получим представление

-a₀ = λ₀a₀ + λ′1a₁ + ... + λ′N-1aN-1

с другими коэффициентами λ′1, . . . , λ′N-1, но с тем же λ₀. Так как векторы a₀, a₁, . . . , aN-1

образуют обычный базис пространства R^N , то из полученного представления следует, что

λ₀ = -1, λ′1 = 0, ..., λ′N-1 = 0. Возникает противоречие с условием λ₀ ≥ 0. Поэтому векторы

a₁, ..., a_N не могут быть линейно зависимыми, а значит, они также образуют обычный базис

пространства R^N . Свойство доказано.

Свойство 6. В случае m = N + 1 векторы a₁, . . . , a_m ∈ R^N составляют положительный

базис тогда и только тогда, когда найдутся такие положительные числа α₂, . . . , α_m, что

a₁ + α₂a₂ + ... + α_ma_m = 0, причём числа α₂, ..., α_m определяются однозначно.

Доказательство. Из свойства 3 положительного базиса находим такие положительные

числа λ₁, . . . , λ_m, что λ₁a₁ + . . . + λ_ma_m = 0. Из свойства 5 следует линейная независимость

векторов a₂, . . . , a_m ∈ R^N , а значит, λ₁ = 0 и при α_i = λ_i/λ₁, i = 2, m, получаем равенство

из свойства 6. Набор чисел α₂, . . . , α_m единственен, так как векторы a₂, . . . , a_m линейно

независимы.

Рассмотрим какой-либо набор векторов a₀, a₁, . . . , a_n ∈ Rⁿ и матрицу M размерности n ×

× (n + 1), столбцы которой состоят из координат этих векторов. Минор, полученный из M

удалением i-го столбца, обозначим через M_i.

Теорема 1. Набор векторов a₀, a₁, . . . , a_n ∈ Rⁿ образует положительный базис прост-

ранства Rⁿ тогда и только тогда, когда M₀ = 0, а (-1)ⁱM_i/M₀ > 0 для i = 1, n.

Доказательство. Рассмотрим (n + 1) × (n + 1)-матрицу, первая строка которой есть j-я

строка матрицы M для некоторого j = 1, n, а остальная часть совпадает с матрицей M. По-

лучим вырожденную матрицу. Разложив её определитель по первой строке, получим a0j M₀ -

- a1jM₁ + ... + (-1)ⁿa_njM_n = 0, где a_ij - j-я координата вектора a_i. Так как значение j

произвольно, то получаем соотношение

M₀a₀ - M₁a₁ + ... + (-1)ⁿM_na_n = 0.

(8)

Пусть векторы a₀, a₁, . . . , a_n составляют положительный базис. Из свойства 6 следует,

что M₀ = 0. Поэтому a₀+λ₁a₁+. . .+λ_na_n = 0, где λ_i = (-1)ⁱM_i/M₀, причём это единственное

такое соотношение на векторы a₀, a₁, . . . , a_n ввиду линейной независимости векторов a₁,

..., a_n. Из свойства 6 следует, что (-1)ⁱM_i/M₀ > 0, i = 1,n. Обратное утверждение также

следует из свойства 6 и соотношения (8). Теорема доказана.

Отметим, что разложение a = α₀a₀ + . . . + α_na_n вектора a по положительному базису

a₀, ..., a_n неоднозначное, но всегда существует разложение, для которого хотя бы одно α_i

нулевое, а остальные неотрицательные. Для построения такого разложения достаточно найти

какое-либо соотношение λ₁a₁ + . . . + λ_ma_m = 0 из свойства 3 и получить разложение

a = (α₀ - λ₀αl0/λl0)a₀ + ... + (α_n - λ_nαl0/λl0)a_n,

где αl0 /λl0 - минимальное из чисел α_l/λ_l, l = 0, n. Тогда коэффициент при al0 нулевой, а

остальные неотрицательные. Назовём такое разложение вектора по положительному базису

минимальным. Ввиду свойства 5 оно единственно.

Теорема 2. Пусть для системы (7) с l_m = n столбцы a₀, . . . , a_n ∈ Rⁿ в точке x_f ∈ X₀

образуют положительный базис пространства Rⁿ, коэффициенты u₀, ... , u_n минималь-

ного разложения вектора ζ(x_f,0,... ,0) по этому базису составляют допустимое управ-

ление, функция ζ непрерывна в точке (xf,0,...,0), а компоненты столбцов a0, ..., an

непрерывны в окрестности x_f. Тогда система (7) локально управляема в точке x_f.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

ПОИСК ПАРАМЕТРОВ МОДЕЛИ

1697

Доказательство. Если векторы a₀(x_f ), . . . , alm (x_f ) ∈ Rⁿ образуют положительный базис

пространства Rⁿ, то в силу теоремы 1 и непрерывности функций a_i(x) это свойство выпол-

няется и в некоторой окрестности U точки x_f . Докажем непрерывность в точке (x_f , 0, . . . , 0)

отображения F, которое отображает точку (x, ˙x, . . . , x(s)) в набор коэффициентов u₀, . . . , u_n

минимального разложения вектора ζ(x, ˙x, . . . , x(s)) по положительному базису a₀(x),

...,a_n(x),

x ∈ U. Область определения этого отображение есть объединение множеств X_i,

i = 0,n, где X_j состоит из точек, для которых u_j = 0. Обозначим через A_i(x) квадратную

матрицу, составленную из всех столбцов a₀(x), . . . , a_n(x), кроме a_i(x). Ввиду теоремы 1

матрицы A_i(x), i = 0, n,

x ∈ U, невырождены. Так как каждая такая матрица состоит из

непрерывных функций, то обратные им матрицы также состоят из непрерывных функций.

Ограничение отображения F на X_j есть A_j (x)-1ζ(x, ˙x, . . . , x(s)) и поэтому непрерывно в

точке (x_f , 0, . . . , 0), если эта точка лежит в X_j. Точка (xf,0,...,0) может быть граничной

точкой нескольких множеств X_j , но в силу единственности минимального разложения значе-

ние F (x_f , 0, . . . , 0) не зависит от выбора X_j , а значит, отображение F непрерывно в точке

(x_f,0,...,0).

По условию теоремы точка F (x_f , 0, . . . , 0) принадлежит области допустимых управле-

ний U. Поэтому существует окрестность V точки (xf,0,...,0), образ которой при отоб-

ражении F лежит в U. Выберем такие положительные числа δ₁ и δ₂, что декартово произ-

ведение δ₁-окрестности точки x_f и δ₂-окрестности точки (0, . . . , 0) лежит в V, т.е. Uδ1 (x_f ) ×

× Uδ2(0,...,0) ⊂ V.

Пусть ξ - произвольный единичный вектор, β(t) - какая-либо s раз непрерывно диффе-

ренцируемая, убывающая на отрезке [0, T ] функция, β(T ) = 0,

R = max ∥( ^β(t),...,β(s)(t))∥.

t∈[0,T ]

Рассмотрим траекторию

x(t) = x_f + (δ₂/R)β(t)ξ. Тогда x(T ) = xf , и за счёт выбора ξ и

t в качестве x(t) мы можем получить произвольную точку из δ-окрестности Uδ(xf ) точки

(x_f,0,...,0), где δ = min(δ₁,δ₂β(0)/R). Поэтому окрестность U_δ(x_f) лежит в области дости-

жимости состояния x_f за время T > 0 в U_δ(x_f ), а значит, система (7) локально управляема

в точке x_f . Теорема доказана.

Пример 4. Из свойства 2 положительного базиса следует, что случай, описанный в теоре-

ме 2, возможен только при l_m ≥ 3. Исследуем случай, когда в (3) l_m = 2. Запишем систему (3)

в матричном виде x = T_θM u - B₀, где

⎛

⎞

⎛

⎞

⎛

⎞

⎛

⎞

cos θ

- sin θ

cos φ₁

cos φ₂

u₁

T_θ =^⎝sin θ cos θ

0⎠, M = ⎝0

sin φ₁

sin φ₂

⎠_,

u=^⎝u2⎠, B0 = ⎝κζ⎠.

κ₁ sin ψ₁ κ₂ sin ψ₂

u₃

Рассмотрим функцию h(t, x) = C( x + tB₀), где C - некоторая постоянная строка. Произ-

водная функции h в силу системы (3) равна˙h = CT_θM u. Пусть θ_f - θ-координата состояния

x_f. Если матрица M невырождена, то, положив C = (1 1 1)M-1T-1, где M-1 - обратная к_θ

M матрица, получим равенство

h=(111)M-1Tθ-θ

Mu = u₁ + u₂ + u₃ + α(θ - θ_f),

где α(θ - θ_f ) → 0 при θ → θ_f . Поэтому если u₁ + u₂ + u₃ ≡ 0, то

^h(t, x) > 0 в некото-

рой окрестности точки xf (напомним, что ul ≥ 0 для любого l). Следовательно, значение

функции h в окрестности точки x_f может только расти, а значит, состояния

x, для кото-

рых h(t, x) > h(t, x_f ), не входят в область достижимости состояния

x_f за малое время и

система (3) не является локально управляемой в точке x_f .

Если u₁ + u₂ + u₃ ≡ 0, то u_i ≡ 0, i = 1, 2, 3, и область достижимости состояния x_f есть

кривая (не является открытым множеством), и система (3) не является локально управляемой

в точке x_f и в этом случае.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

1698

ВЕЛИЩАНСКИЙ, ЧЕТВЕРИКОВ

Если матрица M вырождена, то существует такая строка C₀, что C₀M = 0. Рассмотрим

функцию h(t, x) = C₀T-1θ(x + tB), где θf - θ-координата состояния

x_f , а B - некоторый

постоянный столбец. Производная функции h в силу системы (3) равна

= C₀Tθ-θfM u +

+C₀T-1θ

(B - B₀), где первое слагаемое бесконечно малое при θ → θ_f , а второе слагаемое

можно сделать положительным за счёт выбора столбца B. При таком выборе B значение

функции h в окрестности точки x_f может только расти, а значит, система (3) не является

локально управляемой в точке x_f .

Таким образом, мы доказали, что система (3) может быть локально управляема только в

случае l_m ≥ 3.

3. Алгоритм управления системами с положительным базисом. Далее покажем

как построить управления для движения по заданной траектории системы с положительным

базисом. Рассмотрим систему (7) в случае l_m = n. Пусть поставлена задача выбора таких

входов u(t), чтобы система двигалась по траектории x(t), t ∈ [t₀, t_f ], при этом u(t₀) задано.

Шаг 1. Проверяем, что векторы a₀, . . . , a_n ∈ Rⁿ составляют положительный базис. Для

этого находим такие положительные числа λ₀, . . . , λ_n, что λ₀a₀ +. . .+λ_na_n = 0. Обозначаем

через l_d какой-либо номер от 0 до n, а через B - набор, состоящий из всех векторов a_l, кроме

l = l_d. (Из свойства 5 следует, что B образует обычный базис пространства R^N.) Определяем

K - количество шагов для перехода от начальной точки в конечную и шаг Δ = (t_f - t₀)/K.

Полагаем t = t₀.

Шаг 2. Если u(t) ∈ U, то делаем вывод, что движение по заданной траектории при за-

данных ограничениях на управления невозможно и поэтому завершаем вычисления. Иначе

переходим на шаг 3.

Шаг 3. Если t = t_f , то переходим на шаг 6. Иначе вычисляем

t := t + Δ, ζ(t) = ζ(x(t), x(t), . . . , x(s)(t)).

Шаг 4. Раскладываем вектор ζ(t) по базису B :

∑

ζ(t) =

v_la_l, vld = 0.

l=l_d

Шаг 5. Если все полученные v_l неотрицательны, то полагаем u_l(t) = v_l, l = 0, n, а затем

переходим на шаг 2. Иначе находим минимальное из чисел v_l/λ_l, соответствующий номер

обозначаем через l₀ (отметим, что vl0 < 0) и получаем разложение

(

)

∑

vl0

ζ(t) =

v_la_l -

λ_la_l =

v_l -

λ_l a_l.

l₀

λl0

l=l_d

l=0

l=l₀

Заменяем в B вектор al0 на вектор ald и полагаем, что

λ_l

u_l(t) = v_l -

vl0 , l = 0,n,

λl0

и l_d = l₀. Затем переходим на шаг 2.

Шаг 6. Завершаем вычисления и получаем u_l(t), l = 0, n, t ∈ [t₀, t_f ].

4. Коэффициент локальной управляемости и задача его максимизации. Предпо-

ложим, что система (1) приведена к виду (7) и выбран функционал (2). Определим коэффици-

ент локальной управляемости, соответствующий этому функционалу. Для управления систе-

мой (7) будем использовать алгоритм, приведённый выше. Так как мы не обладаем какой-либо

информацией о возможных значениях правой части системы (7) (векторной функции ζ), бу-

дем считать, что любое достаточно малое значение ζ возможно и равновероятно. Понимая

ζ как случайный вектор, равномерно распределённый на шаре радиуса δ, рассмотрим ма-

тематическое ожидание M[Φ(x_f , u)] случайной величины Φ(x_f , u), где x_f - фиксированная

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

ПОИСК ПАРАМЕТРОВ МОДЕЛИ

1699

точка, а компоненты u есть коэффициенты разложения ζ по базису B, составленному из

части векторов a₀, . . . , a_n (см. шаги 4 и 5 алгоритма). Коэффициент локальной управляемо-

сти системы (7) в состоянии x_f относительно функционала (2) определим как величину,

обратную к пределу

k(x_f ) = lim

M [Φ(x_f , u)],

δ→0 δ

т.е. 1/k(xf ). Коэффициентом локальной управляемости системы (7) относительно функци-

онала (2) будем называть точную нижнюю грань коэффициентов локальной управляемости

системы (7) в её допустимых состояниях. Задача поиска параметров модели с наилучшей

управляемостью сводится к нахождению максимума по всем параметрам модели коэффици-

ента локальной управляемости системы, т.е. к поиску min sup k(x_f ).

α x_f

Выведем формулу для k(x). Отметим, что на каждом шаге алгоритма по крайней мере од-

на компонента u равна нулю. Обозначим через ν_i вложение пространства Rⁿ в пространство

Rn+1, которое точку с координатами v = (v₁,... ,v_n) отображает в точку u = (u₀,... ,u_n),

где u_j = vj+1 при j < i, u_i = 0, u_j = v_j при j > i. Пусть A_i - квадратная матрица, полу-

ченная из M удалением i-го столбца. Тогда если ζ раскладывается по базису, полученному

из набора a₀, . . . , a_n удалением a_i, то

ζ = Mν_i(v) = A_iv.

Обозначим также через V_n(δ) объём n-мерного шара радиуса δ, а через B^iδ - часть шара

радиуса δ, состоящую из точек ζ = A_iv. Тогда

∫

∑

M [Φ(x_f , u)] =

Φ(x_f , ν_i(A-1iζ)) dζ.

V_n(δ)

i=0

Bⁱ

В каждом интеграле, сделав замену ζ = δA_iv, получим

∫

∑

|M_i|

M [Φ(x_f , u)] =

Φ(x_f , δν_i(v)) dv,

V_n(1)

i=0

Gⁱ

где M_i = det A_i, а Gⁱ = {v = (v₁, . . . , v_n) ∈ Rⁿ : ∥A_iv∥ ≤ 1, v_j ≥ 0, j = 1, n}.

Пример 5. Рассмотрим подводный аппарат цилиндрической формы с закругленными кон-

цами, причём точки P₁, . . . , Plm расположены на цилиндрической поверхности. В этом случае

--→

|CPl| = d/|sin(ψl + φl)|, где d - радиус цилиндрической поверхности аппарата. Из условия

локальной управляемости следует, что l_m ≥ 3. Рассмотрим случай l_m = 3.

Для упрощения рассуждений разделим последнее уравнение системы (6) на

-J/(md).

Матрица M коэффициентов при управлениях полученной системы (см. теорему 1) имеет вид

⎞

^⎛1

cos φ₁

cos φ₂

cos φ₃

⎜

⎟

⎜0

sin φ₁

sin φ₂

sin φ₃

⎟

M =

⎜

⎟

⎝

sin ψ₁

sin ψ₂

sin ψ₃

⎠

|sin(ψ₁ + φ₁)|

|sin(ψ₂ + φ₂)|

|sin(ψ₃ + φ₃)|

Отметим, что коэффициенты этой матрицы не зависят от x, а значит, коэффициент локальной

управляемости системы во всех состояниях одинаковый. Кроме того, n = 3, поэтому V_n(1) =

= 4π/3 и

∫

∑

3|M_i|

k(x_f ) =

(v₁ + v₂ + v₃) dv.

4π

i=0

Gⁱ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

1700

ВЕЛИЩАНСКИЙ, ЧЕТВЕРИКОВ

Таким образом, задача поиска параметров модели с наилучшей управляемостью сводится

к нахождению минимума k = k(x_f ) по φ₁, ψ₁, φ₂, ψ₂, φ₃, ψ₃, где φ_j ∈ [0, 2π], ψ_j ∈ [0, 2π],

j = 1,2,3.

Указанная экстремальная задача решалась численно. При этом для исключения деления на

малые величины были добавлены следующие ограничения на значения параметров: |tg (ψ_j +

+φ_j)| ≥ 0.2, j = 1,2,3, и |M_i| > 0.1, i = 0,1,2,3. Оказалось, что функция k(φ_i,ψ_i) имеет

большое количество точек локального минимума. Соответствующие значения коэффициента k

указаны в таблице.

Системы с полученными значениями параметров были протестированы на следующих че-

тырёх траекториях:

1) поворот

(

)

t³

t²

x(t) = 0, z(t) = 0, θ(t) = θ_f

-3

t ∈ [0,T], θ_f =

T = 2с;

T³

T²

2) движение по синусоиде вниз

)

⁽πt

2πt

x(t) = 2 sin

z(t) = -

θ(t) = arcsin

√

t ∈ [0,T], T = 18с;

cos²(πt/T ) + 1

3) движение по горизонтальной синусоиде

)

40πt

⁽ 20πt

⁽ 20πt⁾

x(t) =

z(t) = 2 sin

θ(t) = arctg cos

t ∈ [0,T], T = 350с;

4) движение по эллипсу

)

⁽ 2πt

⁽ 2πt⁾

⁽1

⁽ 2πt⁾⁾

x(t)=20 cos

z(t)=10 sin

θ(t)=arctg

ctg

t∈[0,T], T =210с.

Соответствующие значения функционала приведены в таблице.

∑₃

Таблица. Значения функционала

i=0

Траектория

Параметры φ1, φ2, φ3, ψ1, ψ2, ψ3

2.06, 2.16, 4.28, 1.84, 4.33, 2.70

4.68

5.51

61.23

1124.93

115.49

1.15, 1.12, 3.67, 1.79, 4.27, 3.19

7.41

11.64

40.82

1528.06

243.45

2.11, 1.97, 4.28, 1.23, 4.11, 6.26

4.50

5.49

59.51

1114.02

114.14

2.06, 4.17, 4.17, 0, 5.06, 1.92

4.48

5.44

67.26

1105.61

112.94

1.87, 2.35, 4.23, 2.05, 4.13, 2.83

4.86

5.54

58.03

1109.14

113.69

2.11, 2.11, 4.23, 1.23, 4.37, 3.14

4.44

5.53

62.32

1132.80

116.62

2.09, 2.09, 4.19, 1.22, 4.37, 0

4.37

5.47

61.61

1121.26

115.05

1.74, 4.06, 4.14, 0.27, 5.16, 1.89

4.64

6.42

54.70

1186.55

130.13

1.57, 3.14, 4.19, 3.14, 1.57, 4.71

7.87

5.73

47.84

1011.71

119.65

Заключение. В работе рассмотрены локально управляемые системы с положительны-

ми управлениями, введены системы, названные системами с положительным базисом. Для

таких систем доказано достаточное условие локальной управляемости, сформулирован алго-

ритм построения управления для движения по заданной траектории и определён коэффициент

локальной управляемости.

Введённые понятия были исследованы для системы, описывающей движение подводного

аппарата в вертикальной плоскости. Рассмотрен случай, когда аппарат управляется только

винтомоторными агрегатами, винты которых вращаются только в одну сторону. Показано,

что движение такого аппарата описывает система с положительным базисом. Она локально

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023

ПОИСК ПАРАМЕТРОВ МОДЕЛИ

1701

управляема, только если винтомоторных агрегатов не менее четырёх. Задача минимизации по-

требляемой энергии двигателями аппарата эквивалентна задаче максимизации коэффициента

управляемости для соответствующего функционала. Численные расчёты показали, что дан-

ный коэффициент имеет большое количество точек локального максимума. Значения функ-

ционала для некоторых наборов параметров на четырёх выбранных траекториях показали

(см. таблицу), что при движении по конкретной траектории модель с меньшим значением ко-

эффициента управляемости (с большим значением k) может быть более эффективной. Мы

объясняем это тем, что определение коэффициента управляемости основано на вероятност-

ных понятиях, и поэтому эффективность модели с максимальным значением коэффициента

управляемости должна сказаться при движении на продолжительных и разнообразных тра-

екториях.

Отметим также, что в работе рассмотрен только случай, когда сдвиг из любого состояния

в любом направлении возможен и равновероятен. Однако в реальной ситуации вероятность

сдвига в каком-либо направлении зависит от решаемой аппаратом задачи. По нашему мнению,

закон распределения вероятности сдвига в направлении может быть определён при дополни-

тельном исследовании траекторий аппарата с использованием искусственного интеллекта. При

этом изменение закона распределения приведёт к изменению зависимости коэффициента ло-

кальной управляемости от параметров и к другим оптимальным значениям параметров.

Работа выполнена при поддержке программы “Приоритет 2030” МГТУ им. Н.Э. Баумана.

СПИСОК ЛИТЕРАТУРЫ

1. Amory A., Maehle E. SEMBIO-a small energy-efficient swarm AUV // OCEANS 2016 MTS/IEEE

Monterey. Monterey, 2016. P. 1-7.

2. Amory A., Maehle E. Energy efficiency of the swarm-capable micro AUV SEMBIO // OCEANS 2019

Marseille. Marseille, 2019. P. 1-7.

3. Fossen T.I. Guidance and Control of Ocean Vehicles. Chichester, 1994.

4. Buzikov M.E., Galyaev A.A. Time-optimal interception of a moving target by a Dubins car // Automation

and Remote Control. 2021. V. 82. № 5. P. 745-758.

5. Buzikov M.E., Galyaev A.A. Minimum-time lateral interception of a moving target by a Dubins car

// Automatica. 2022. V. 135. Art. 109968.

6. Berlin L., Galyaev A., Lysenko P. Time-optimal control problem of two non-synchronous oscillators

// Mathematics. 2022. V. 10. Art. 3552.

7. Петров Н.Н. Об управляемости автономных систем // Дифференц. уравнения. 1968. Т. 4. № 4.

С. 606-617.

8. Петров Н.Н. Локальная управляемость автономных систем // Дифференц. уравнения. 1968. Т. 4.

№ 7. С. 1218-1232.

Московский государственный технический

Поступила в редакцию 15.06.2023 г.

университет имени Н.Э. Баумана

После доработки 07.10.2023 г.

Принята к публикации 11.10.2023 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№ 12

2023