ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 3, с.303-313

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.925.4+517.988.57

ОБ ОДНОЙ НЕКЛАССИЧЕСКОЙ ЗАДАЧЕ

НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ,

ИМЕЮЩЕЙ НЕЛИНЕАРИЗУЕМЫЕ РЕШЕНИЯ

Исследуется одна нелинейная задача на собственные значения специального вида, возни-

кающая в электродинамике. Задача ставится для системы двух уравнений с краевыми

условиями первого рода и двумя дополнительными локальными условиями. Спектраль-

ный параметр в задаче один, ещё два параметра появляются в указанных выше локаль-

ных условиях, на которые накладывается дополнительное ограничение. Таким образом,

в задаче имеются два неизвестных параметра: один спектральный, второй - некоторый

дополнительный параметр, который подбирается так, чтобы существовало нетривиальное

решение изучаемой задачи. Доказывается существование нелинеаризуемых решений зада-

чи.

DOI: 10.31857/S0374064123030020, EDN: QUAOCW

1. Постановка задачи. Пусть I = (0, 1),

I = [0,1], R₊ = (0,+∞), A = (0,A), где

A > 0 - известная постоянная, λ, A₁, A₂ - вещественные параметры, a₁, a₂, α₁, α₂ > 0 -

вещественные постоянные. На протяжении всей статьи индекс j принимает значения 1,

Рассмотрим систему уравнений

u′′1 = -(a₁ - λ + α₁u²¹)u₁, u′′2 = -(a₂ - λ + α₂u²²)u₂

(1)

с граничными условиями

u₁|x=0 = 0, u₂|x=0 = 0,

(2)

u′1|x=0 = A₁, u′2|x=0 = A₂,

(3)

u₁|x=h = 0, u₂|x=h = 0

(4)

и с дополнительным условием

A²¹ + A²² = A²,

(5)

где x ∈^I, A_j ∈ A и λ, α_j ∈ R₊.

Задача P состоит в том, чтобы определить такие тройки (λ, A₁, A₂), для которых су-

ществуют (нетривиальные) функции u_j ≡ u_j (x; λ, α_j , A_j ), удовлетворяющие системе (1) и

условиям (2)-(5), где u_j дважды непрерывно дифференцируемы по x ∈^I.

Замечание 1. Несмотря на то, что функции u₁, u₂ связаны условием (5):

u′21|x=0 + u′22|x=0 = A²,

уравнения (1) можно изучать отдельно, и поэтому задача P разбивается на две: задача

P₁

для функции u₁ и параметров λ, A₁ и задача P₂ для функции u₂ и параметров λ, A₂, где

λ ≡ λ(A₁) определяется из задачи P₁, параметр A₁ подбирается так, чтобы u₂ удовлетворяло

второму уравнению в (1) и соответствующим условиям из (2)-(4); параметр A₂ определяется

по формуле

√

A₂(A₁) = A² - A²¹ > 0.

Отметим, что поскольку изучаемые уравнения нелинейны относительно искомых функций

стандартных краевых условий (например, первого рода) уже недостаточно для определения

303

304

ВАЛОВИК, МАРТЫНОВА

дискретных собственных значений. Необходимо использовать дополнительные условия, кото-

рые могут быть как локальными, так и нелокальными (нелокальные условия, в частности,

возникают при применении вариационных методов). Мы используем локальные дополнитель-

ные условия (3).

Обратим внимание читателя на то, что хотя уравнения изучаемой задачи и интегрируются

в эллиптических функциях, мы не используем этот факт. В нелинейной оптике (да и в других

разделах нелинейной математической физики) возникают более сложные нелинейности, для

которых подход на основе эллиптических функций невозможен. В то же время используемый

нами подход с некоторыми модификациями может быть применён и к более сложным нелиней-

ностям (необходимо лишь перейти к другой переменной в интеграле и провести необходимые

оценки, см., например, [1]).

2. Разрешимость задачи P. Для удобства введём обозначения v_j = A-1ju_j и β2j = α_jA2j.

В этих обозначениях из (1)-(5) имеем систему

v′′1 = -(a₁ - λ + β²¹v²¹)v₁, v′′2 = -(a₂ - λ + β²²v²²)v₂

(6)

с граничными условиями

v₁(0) = 0, v₂(0) = 0,

(7)

v′1(0) = 1, v′2(0) = 1,

(8)

v₁(1) = 0, v₂(1) = 0

(9)

и с дополнительным условием

β²¹

β²²

=A²,

(10)

α₁

α₂

где β_j ∈ B_j = (0,

√α_jA).

Заметим, что β_j → +0 при A_j → +0 при фиксированном α_j > 0 и наоборот, т.е. β_j → +0

при α_j → +0 при фиксированном A_j > 0. Кроме того, если A₁ → A - 0, то β₂ → +0 (при

фиксированном α₂ > 0), а также если A₂ → A-0, то β₁ → +0 (при фиксированном α₁ > 0).

Фактически задача P была эквивалентно переформулирована в новых обозначениях. Те-

перь задача P состоит в определении троек (λ, β₁, β₂), для которых существуют (нетриви-

альные) функции v_j ≡ v_j (x; λ, β_j ), удовлетворяющие системе (6) и условиям (7)-(10), где v_j

предполагаются дважды непрерывно дифференцируемыми по x ∈I.

Из условий (5), (10) и введённых обозначений видно, что задача P изучается при усло-

вии β_j ∈ (0,

√α_jA). Несмотря на это, некоторые вспомогательные результаты этого пункта

сформулированы (и доказаны) при условии β_j ∈ R₊.

Для начала найдём первые интегралы уравнений системы (6). Умножив на 2v^′j и проин-

тегрировав по [0, x], имеем

β2j

v′j2 = C_j - (a_j - λ)v2j -

v4j.

(11)

Используя условия (7) и (8), находим значения C₁ = C₂ = 1.

Для исследования задачи P будет модифицирован метод интегрального характеристичес-

кого уравнения [1]. Введём новые переменные

v^′j

τ_j = v2j, η_j =

(12)

v_j

Ниже используем обозначения τ_j , τ_j (x), τ_j(x; λ, β_j ), а также η_j, η_j (x), η_j(x; λ, β_j ).

В новых обозначениях система (6) может быть записана в виде

τ′1 = 2τ₁η₁, η′1 = -(η²¹ + a₁ - λ + β²¹τ₁),

τ′2 = 2τ₂η₂, η′2 = -(η²² + a₂ - λ + β²²τ₂).

(13)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

ОБ ОДНОЙ НЕКЛАССИЧЕСКОЙ ЗАДАЧЕ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

305

Соотношения (11) при условиях (7), (8) принимают вид

β2j

τ2j + (η2j + a_j - λ)τ_j - 1 = 0.

(14)

Поскольку τ_j ≥ 0, то, выражая τ_j из (14), получаем

√

-(η2j + a_j - λ) + (η²¹ + a_j - λ)² + 2β2j

τ_j =

β²

Подставив найденные соотношения во второе и четвертое уравнения системы (13), имеем

√

η^′j = - (η2j + a_j - λ)² + 2β2j,

откуда следует, что η^′j < 0 для всех λ ∈ R, т.е. функция η_j (x) монотонно убывает. Из второй

формулы (12) видно, что η_j(x) непрерывна тогда и только тогда, когда v_j не обращается в

нуль. Предположим, что v_j имеет n_j ≥ 0 нулей x_j,i ∈ I, i = 1, n_j , тогда η_j (x) имеет n_j

точек разрыва x_j,i, i = 1, n_j . Если n_j = 0, то v_j не обращается в нуль при x ∈ I.

Очевидно, что если v_j (x) ≡ 0, то v^′j(x_j.i) = 0 для всех i = 1, n_j . Действительно, если

решение v_j задачи (6) обращается в нуль вместе со своей производной v^′j в какой-то точке, то

из классических результатов о (локальном) существовании и единственности решения задачи

Коши для обыкновенного дифференциального уравнения следует, что v_j(x) ≡ 0 [2, c. 73].

Таким образом, все точки разрыва являются точками разрыва второго рода.

Пусть I_j,i = (x_j,i, xj,i+1), где i = 0, n_j , xj,0 = 0, xj,nj+1 = 1; если nj = 0, то Ij,0 = I.

Из условий (7), (8) следует, что

lim

τ_j(x) = 0, lim

η_j(x) = +∞.

(15)

x→+0

Так как η^′j < 0, то получаем условия

lim

τ_j(x) = 0,

lim

η_j(x) = ±∞, i = 1,n_j.

(16)

x→x_j,i

x→x_j,i±0

С учётом (9) имеем

lim

τ_j(x) = 0,

lim

η_j(x) = -∞.

(17)

x→1-0

Подчеркнём, что условия (17) выполняются только на решениях задачи P.

Таким образом, функции τ_j (x) и η_j(x) могут быть определены на каждом интервале I_j,i

как решения уравнений (14) с подходящими условиями, выбранными из (15)-(17).

Теперь рассмотрим уравнение

η^′j = -w_j(η_j;λ,β_j)

(18)

на каждом интервале I_j,i, где

√

w_j(η_j;λ,β_j) ≡ (η2j + a_j - λ)² + 2β2j > 0.

Введём также обозначение

+^∞

T_j(λ,β_j) =

(19)

w_j(s;λ,β_j)

-∞

Имеет место следующее

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

306

ВАЛОВИК, МАРТЫНОВА

Утверждение 1. Задача Коши (6)-(8) глобально однозначно разрешима для x ∈^I, её

(классическое) решение v_j ≡ v_j(x;λ,β_j) непрерывно зависит от точки (x,λ,β_j) ∈^I×R×R₊,

и справедливо равенство

+∞

n_jT_j(λ,β_j) +

= 1,

(20)

w_j(s;λ,β_j)

η_j(1)

где n_j ≥ 0 - количество нулей функции v_j ≡ v_j (x; λ, β_j ), поскольку x ∈ I, а η_j (1) не обяза-

тельно равно -∞.

Доказательство. Учитывая, что w_j (η_j ; λ, β_j ) > 0, интегрируя (18) на каждом интервале

I_j,i, i = 1,n_j, используя условия (15)-(16), приходим к системе

+∞

0<xj,1 =

wj,1(s;λ,β_j)

-∞

+∞

0<x_j,i -xj,i-1 =

i = 2,n_j,

w_j,i(s;λ,β_j)

−∞

+∞

0<1-xnj =

(21)

wj,nj+1(s;λ,βj)

η_j(1)

подробный вывод которой дан, например, в работе [1].

Заметим, что в (21) правые части конечны, так как левые части конечны. Следовательно,

все несобственные интегралы в (21) сходятся. Из этого факта вытекает существование η_j ≡

≡ η_j(x) на каждом интервале I_j,i, i = 1,n_j.

Из соотношений (11) следует, что при фиксированных λ, β_j переменная v_j , а значит, и

переменная v^′j ограничены.

Учитывая существование функции η_j ≡ η_j (x) и ограниченность функций v_j и v^′j, при-

ходим к выводу, что функции v_j(x) и v^′j (x) определены для всех x ∈^I. Другими словами,

доказано, что решение v_j ≡ v_j (x; λ, β_j ) задачи Коши (6)-(8) существует и определено глобаль-

но для x ∈^I. Единственность этого решения и его непрерывность (и дифференцируемость)

по x ∈^I, λ ∈ R и β_j ∈ R₊ являются результатом гладкости правых частей уравнений в (6)

относительно v_j, λ, βj [3, с. 178; 4, с. 118].

Суммируя уравнения в (21), имеем

xj,1 + xj,2 - xj,1 + xj,3 - xj,2 + ... + xj,nj - xj,nj-1 + 1 - xj,n_j =

+∞

∫

=n_j

w_j(s;λ,β_j)

−∞

η_j(1)

Формулы (20) легко получаются из найденного соотношения. Утверждение доказано.

При условиях (9) и (10) формулы (20) приводят к интегральным характеристическим урав-

нениям (ИХУ), для которых имеет место следующая

Теорема 1. Тройка (λ, β₁, β₂) является решением задачи P тогда и только тогда, когда

существуют целые числа n_j ≥ 0 такие, что λ, β₁ и β₂ удовлетворяют системе уравнений

Φ₁(λ,β₁;n₁) ≡ (n₁ + 1)T₁(λ,β₁) = 1,

Φ₂(λ,β₂;n₂) ≡ (n₂ + 1)T₂(λ,β₂) = 1

(22)

при n_j = n_j. В этом случае собственные функции v_j ≡ v_j(x;λ,β_j), соответствующие ре-

шению (λ,β₁,β₂), имеют n_j простых нулей x_j,i = iT_j(λ,β_j) ∈ I, где i = 1, n_j.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

ОБ ОДНОЙ НЕКЛАССИЧЕСКОЙ ЗАДАЧЕ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

307

Доказательство. Из формулы (9) видно, что v_j|x=1 = 0. Так как η^′j < 0, η_j = v^′j/v_j , а

v_j и v^′j не обращаются в нуль в одной и той же точке, то lim

η_j(x) = -∞. Теперь ИХУ (22)

x→1-0

получаются из формулы (20) при условиях (9) и (10). Заметим, что условия (9) приводят к

условиям (17).

Из доказательства утверждения 1 следует, что любое решение задачи P удовлетворяет

системе (22) при некотором n_j = n_j.

Тот факт, что любое решение λ, β₁, β₂ уравнений (22) является решением (λ, β₁, β₂)

задачи P, доказывается аналогично тому, как это сделано в статье [5].

Формула для нулей x_j,i собственной функции v_j получается из формул (21). Теорема

доказана.

С учётом замечания 1 видно, что любое уравнение системы (22) можно изучать независимо

от другого. Докажем несколько фактов о функциях T_j , на которые будем опираться при

дальнейших рассуждениях.

Утверждение 2. Для любого фиксированного β_j ∈ R₊ справедливы следующие свойства:

maxTj(λ,βj) = δj,

(23)

λ∈R

lim

T_j(λ,β_j) = 0,

(24)

λ→±∞

где δ = δ_j (β_j ) является конечной положительной величиной.

Доказательство. Формула (23) получается из следующих рассуждений. Действительно,

подынтегральные выражения в (19) положительны на R. Это означает, что T_j > 0 и можно

найти его максимальное значение, которое обозначим через δ_j . Очевидно, что эти δ_j непре-

рывно зависят от β_j .

Теперь, используя неравенство

√

≤

√

≤

(25)

|p| + q

p² + q²

|p| + q

где p ∈ R, q ∈ R₊, выясним поведение T_j при λ → +∞.

В соответствии с (19) и (25) получаем

√

T_j(λ,β_j) ≤ T_j(λ,β_j) ≤ 2

T_j(λ,β_j),

(26)

где

+∞

T_j(λ,β_j) =

√

(27)

|s² + a_j - λ| +

2β_j

√

В приведённых ниже расчётах используется обозначение s_∗ =

λ - a_j, где предполагает-

√

ся, что λ > a_j +

2β_j. Таким образом, имеем

∫s∗

∫

T_j(λ,β_j) =

√

=I₁ +I₂,

λ-a_j +

2β_j - s

s² - (λ - a_j -

2β_j)

s∗

следовательно,

√

2(I₁ + I₂) ≤ T_j(λ, β_j ) ≤ 2

2(I₁ + I₂)

(28)

√

при условии λ > a_j +

2β_j.

Вычислим интегралы I₁ и I₂ :

√

∫s∗

2 ln( λ - a_j +

2β_j +

λ - a_j) - ln(

2β_j)

I₁ =

√

(29)

√

λ-a_j +

2β_j - s²

λ-a_j +

2β_j

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

308

ВАЛОВИК, МАРТЫНОВА

√

+^∞

2 ln( λ - a_j -

2β_j +

λ - a_j) - ln(

2β_j )

I₂ =

√

(30)

√

s² - (λ - a_j -

2β_j)

λ-a_j -

2β_j

s∗

После элементарных преобразований находим, что

)

⁽ ln λ

I₁ = O

√

и I₂ =O

√

(31)

для достаточно больших положительных λ. Очевидно, что lim

I_j = 0.

λ→+∞

Учитывая неравенство (28), из формул (31) следует, что условие (24) справедливо при

λ → +∞.

Рассмотрим случай λ → -∞. Если λ < 0, то из (27) находим

+^∞

T_j(λ,β_j) =

√

(32)

s² + a_j + |λ| +

2β_j

Интеграл (32) вычисляется точно:

T_j(λ,β_j) =

√

(33)

√

|λ| + a_j +

2β_j

Учитывая неравенство (26), из формулы (33) следует, что (24) имеет место при λ → -∞.

Утверждение доказано.

Утверждение 3. Пусть δ_j (β_j ) = maxTj(λ,βj), где βj ∈ R+. Справедливо следующее

λ∈R

равенство:

lim

δ_j(β_j) = +∞.

(34)

β_j→+0

Доказательство. Пусть λ = a_j . Тогда, очевидно, T_j(a_j , β_j ) ≤ δ_j (β_j ). Учитывая (26) и

вычисляя T_j и

T_j при λ = a_j, получаем неравенства

T_j(a_j,β_j) ≤ T_j(a_j,β_j) ≤ δ_j(β_j),

(35)

где

+∞

T_j(a_j,β_j) =

√

√ .

(36)

s² +

2β_j

2⁴

β_j

Из (36) следует, что lim

T_j(a_j,β_j) = +∞. Формулы (35) и (36) подразумевают выполне-

β_j→+0

ние (34). Утверждение доказано.

Используя утверждение 2, можно получить следующее

Утверждение 4. Для любого β_j ∈ R₊ существует целое число n0j ≥ 0 такое, что урав-

нениеΦj(λ,β_j;n_j) = 1 имеет хотя бы одно отрицательное λ = λ-nj и одно положительное

λ = λnj решения для любых n_j = n0j,n0j +1,..., где λ±nj зависит от β_j и n_j. Кроме того,

lim

λ±nj = ±∞.

n_j→+∞

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

ОБ ОДНОЙ НЕКЛАССИЧЕСКОЙ ЗАДАЧЕ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

309

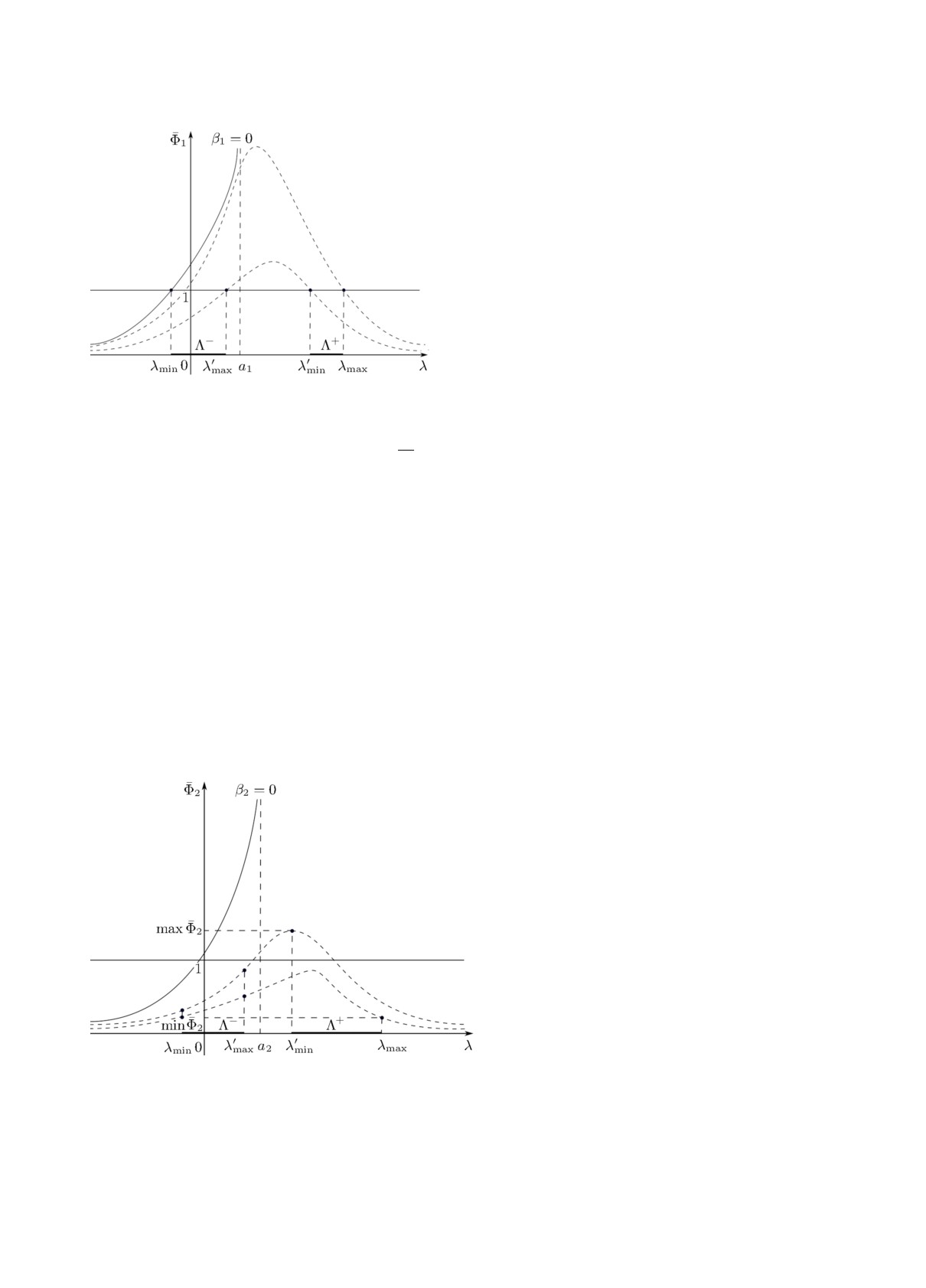
Доказательство. Действительно, всегда суще-

ствует целое число n0j такое, что (n_j + 1)δ_j > 1

при n_j = n0j, n0j + 1, . . . (см. формулу (23)). В то

же время в соответствии с формулой (24) имеем

(n_j + 1)T_j (λ, β_j ) → +0 при λ → ±∞ для любых

n_j = n0j,n0j + 1,... Из этого следует, что уравне-

Φ_j

ние

= 1 имеет по крайней мере два решения

λ = λ при каждом n_j = n0j,n0j + 1,... Очевид-

но, начиная с некоторого целого числа n^′j ≥ n0j,

эти два решения имеют разные знаки. Рис. 1 объ-

ясняет этот факт с геометрической точки зрения.

Утверждение доказано.

Рис. 1. Геометрический смысл доказательства

Итак, рассмотрим функцию

утверждения 4.

λ ≡ λ(β_j;n_j).

Далее важно изучить, что происходит с решением λ ≡ λ(β_j ; n_j) уравнения

Φ_j(λ,β_j;n_j) = 1

при β_j → +0.

Утверждение 5. Пусть λ ≡ λ(β_j ; n_j ) - решение уравненияΦj(λ, β_j ; n_j) = 1. Существу-

ет целое число n^′j ≥ 0 такое, что справедлива формула

lim

λ(β_j ; n_j) = +∞

(37)

β_j→+0

для каждого n_j = n^′j, n^′j + 1, . . .

Доказательство. С учётом оценок (26) и (28) необходимо проанализировать результаты

расчётов (29) и (30). Из (29) и (30) легко видеть, что I₁ и I₂ увеличиваются при уменьшении

β_j > 0. Таким образом, чем меньше положительные β_j, тем больше становится (положитель-

ное) λ, что доказывает (37). Утверждение доказано.

Результаты утверждения 5 можно сформулировать без введения целого числа n^′j. В самом

деле, свойство (37) характеризует решения λ ≡ λ(β_j ; n_j ) уравненияΦj(λ, β_j ; n_j) = 1, которые

не связаны с решениями соответствующей линейной задачи при β_j → +0. Говоря о соответ-

ствующей линейной задаче, имеем в виду ИХУΦj(λ, 0; n_j ) = 1, где λ ∈ (-∞, a_j ), отвечающее

линейной задаче при β_j = 0, т.е. (линейной) задаче Штурма-Лиувилля для уравнения u^′′j =

= -(a_j - λ)u_j при условиях u_j(0) = u_j(1) = 0.

Другой момент, который следует отметить, заключается в следующем. В утверждении 5

говорится только о положительных решениях. Из оценок (26) и (28) и расчётов (32), (33) можно

заметить, что при a_j > 0 свойство (37) не выполняется для всех отрицательных λ. При этом

если брать отрицательные a_j , то свойство (37) будет выполняться лишь для конечного числа

отрицательных λ.

Основной результат этой работы сформулирован в следующей теореме.

Теорема 2 (о разрешимости задачи P). Для любого конечного целого числа n > 0 суще-

ствуют не менее n решений (λ,β₁,β₂) задачи P, где β₂ = β₂(β₁) определяется из (10).

Доказательство. Пусть λ = λ(β₁; n₁) - решение первого уравнения системы (22) при

n₁ = n₁. Пусть λ_min и λ_max - минимальное и максимальное значения λ = λ(β₁; n₁) при β₁ ∈

∈ (0,

√α₁A). Ранее было показано, что lim

λ(β₁; n₁) = +∞. Это означает, что λ_max = +∞.

β₁→+0

Заметим, что функция λ = λ(β₁; n₁) не обязательно непрерывна относительно β₁ для всех

β₁ ∈ (0,

√α₁A). Более того, функция λ = λ(β₁; n₁) может не существовать для некоторых

интервалов (β′1, β′′1) ⊂ (0,

√α₁A). Все это легко видеть из рис. 1.

Тот факт, что λ_max = +∞, даёт возможность выбрать λ_min следующим образом. Пусть

интервал (0, β⁰¹), где β⁰¹ ≤

√α₁A, является максимальным интервалом, для которого функ-

ция λ(β₁; n₁) непрерывна относительно β₁ ∈ (0, β⁰¹), и пусть λ′min - минимальное значение

λ(β₁; n₁) при β₁ ∈ (0, β⁰¹). Заметим, что β⁰¹ > 0 всегда существует. Геометрическая интерпре-

тация приведённого выше рассуждения показана на рис. 2.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

310

ВАЛОВИК, МАРТЫНОВА

Теперь покажем, что можно выбрать удовле-

творяющие (10) λ = λ(β₁; n₁) и β₂ = β₂(β₁) та-

кие, что второе уравнение в системе (22) выпол-

няется при некотором n₂ = n₂.

Подставив λ = λ(β₁; n₁) и β₂ = β₂(β₁), где

β₂ определяется из условия (10) и β₁ ∈ (0,β⁰¹), в

T = T₂(λ(β₁; n₁),β₂(β₁)), оценим его минималь-

ное и максимальное значения.

Итак, пусть

T_min = min

T₂(λ(β₁; n₁),β₂(β₁))

2(β1)

Φ₁

Рис.

2. Графики зависимости

от λ для

T_max = max T₂(λ(β₁; n₁),β₂(β₁))

β₂(β₁)

различных значений β1 и фиксированного n1.

Сплошная кривая соответствует линейному слу-

при β₁ ∈ (0, β⁰¹); в данном случае λ(β₁; n₁) ∈

чаю, т.е. β1 = 0; верхняя штриховая кривая соот-

ветствует β1 вблизи +0, нижняя - β1 =

√α1A.

∈ (λ′min, λ_max).

Интервал (λmin, λmax) всегда остаётся ограничен-

Возможен один из двух случаев.

ным, интервал (λ′min, λmax) можно сделать сколь

Первый случай. Если T_min < 1 < T_max, то в

угодно большим.

силу непрерывной зависимости λ и β₂ от β₁ и

непрерывной зависимости T₂ от λ и β₂ суще-

ствует β₁ ∈ (0, β⁰¹) такое, что для λ = λ(β₁; n₁) и β₂ = β₂(β₁) верно равенство T₂(λ, β₂) = 1.

Таким образом, найдено решение (λ, β₁, β₂) системы (22) при n₁ = n₁ и n₂ = 0.

Второй случай. Если T_max < 1, то существует целое число n₂ такое, что

(n₂ + 1)T_min < 1 < (n₂ + 1)T_max.

Теперь, применяя рассуждения, которые использовали выше, заключаем, что существует β₁ ∈

∈ (0, β⁰¹) такое, что для λ = λ(β₁; n₁) и β₂ = β₂(β₁) верно равенство (n₂ + 1)T₂(λ, β₂) = 1.

Таким образом, находим решение (λ, β₁, β₂) системы (22) при n₁ = n₁ и n₂ = n₂.

При этом случай T_min > 1 невозможен. Действительно, T_j → +0 при λ → +∞ и при

фиксированном β_j > 0, т.е. чтобы получить “маленькие” T_min нужно использовать достаточно

большие λ = λ(β₁, n₁). Как показано вы-

ше, λ = λ(β₁, n₁)→+∞ при β₁ →+0. Од-

нако в этом случае β₂ не стремится к ну-

лю, и, следовательно, можно утверждать,

что при достаточно больших λ функцию

T₂

можно сделать меньше единицы. Та-

ким образом, получаем либо первый слу-

чай, либо второй. Геометрическая интер-

претация приведённого выше рассуждения

показана на рис. 3.

Как сказано в утверждении 4, если рас-

сматривать какое-либо уравнение

Φ_j = 1

отдельно от второго, то можно утвер-

ждать, что оно имеет по крайней мере

два решения λ для любых возможных n_j,

начиная с некоторого n0j. Очевидно так-

Φ₂

Рис. 3. Графики зависимости

от λ для различных

же, что при больших n_j эти два реше-

значений β2 = β2(β1) и фиксированного n2. Сплошная

ния имеют разные знаки. Интересно по-

кривая соответствует линейному случаю, т.е. β2 = 0; две

нять, можно или нет доказать существо-

штриховые кривые соответствуют минимально возмож-

вание по крайней мере двух решений для

ному β2 = β2|β1=β0 (с максимумом, большим единицы)

каждого случая, в котором существует од-

и максимально возможному β2 = β2|β₁=0 (с максимумом,

меньшим единицы).

но решение. Главный факт, который помог

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

ОБ ОДНОЙ НЕКЛАССИЧЕСКОЙ ЗАДАЧЕ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

311

нам доказать существование решений задачи P, заключается в том, что интервал (λ′min, λ_max)

можно сделать сколь угодно большим (см. рис. 2), и он играет ключевую роль для исследо-

вания второго уравнения системы (22). Действительно, это позволяет доказать, что функцию

T2 можно сделать меньше любого фиксированного значения при достаточно больших λ ∈

∈ (λ′min, λ_max). В то же время интервал (λ_min, λ′max), содержащий второе решение уравнения

Φ₁ = 1 (рассматриваемое отдельно от другого уравнения), нельзя выбрать так, чтобы его

длина превышала всякое наперёд заданное число (см. рис. 3). Теорема доказана.

Из теоремы 2 вытекает

Следствие 1 (о разрешимости задачи P). Для любого конечного целого числа n > 0

существует не менее n решений (λ,A₁,A₂) задачи P, где A₂ = A₂(A₁) определяется из (5).

В классической (линейной) теории Штурма-Лиувилля широко используется понятие ха-

рактеристической функции [6, с. 33]. В случае задачи P характеристическая функция может

быть введена аналогичным образом.

Имеем следующее

Утверждение 6. Любая тройка (λ, β₁, β₂) при λ ∈ R, β_j ∈ B_j является решением

задачи P тогда и только тогда, когда она удовлетворяет системе

v₁(1;λ,β₁) = 0, v₂(1;λ,β₂) = 0,

(38)

где v_j (x; λ, β_j ) являются решениями задачи Коши (6)-(8), а β₂ = β₂(β₁) определяется из

условия (10).

Доказательство. Пусть v_j = v_j (x; λ, β_j ) - решение задачи Коши (6)-(8), где β₂ = β₂(β₁)

определяется из формулы (10). Если тройка λ, β₁, β₂ = β₂(β₁) удовлетворяет (38), то, очевид-

но, тройка (λ, β₁, β₂(β₁)) является решением задачи P и v_j(x; λ, β_j ) - собственные функции.

Пусть тройка λ =λ∗ ∈ R, β₁

β∗1 ∈ B₁, β₂

β∗2

β∗1) - решение (38). Рассмотрим задачу

Коши (6)-(8), где λ =λ∗, β₁

β∗1, а β₂

β∗2

определяется из (10) при β₁

β∗1. Соглас-

но утверждению 1 нетривиальное решение v_j = v_j (x;λ∗

β^∗j) этой задачи Коши существует,

единственно и непрерывно зависит от точки (x, λ, β_j ) ∈^I × R × B_j . Если (38) выполняется

для λ =λ∗, β₁

β∗1, β₂

β∗2

β∗1) для этого решения задачи Коши, то тройка (λ∗

β∗1

β∗2

β∗1))

является решением задачи P. Предположим, что для этого решения задачи Коши система

(38) не выполняется при λ =λ∗, β₁

β∗1, β₂

β∗2

β∗1). Следовательно, существует неедин-

ственное решение задачи Коши (6)-(8), где λ =λ∗, β₁

β∗1, β₂

β∗2

β∗1); для одного из них

(38) выполняется, а для другого нет. Этот вывод противоречит утверждению 1. Поэтому пред-

положение о существовании решения задачи Коши (6)-(8), для которой (38) не выполняется,

неверно. Утверждение доказано.

Используя теорему 1 и утверждение 6, получаем следующий результат.

Следствие 2. Любое решение λ ∈ R, β_j ∈ B_j ИХУ (22), где β₂ = β₂(β₁) определяется

из (10), является решением (38) и наоборот.

Объединяя утверждения 2, 3, 5, теорему 2 и следствие 2, получаем

Следствие 3. Для любого целого числа n > 0 задача P имеет не менее n решений

(λ, β₁, β₂), удовлетворяющих следующим условиям:

v₁(1;λ - δ,β₁) · v₁(1;λ + δ,β₁) < 0, v₂(1;λ - δ,β₂) · v₂(1;λ + δ,β₂) < 0,

где v_j(x; λ, β_j ) являются решениями задачи Коши (6)-(8), β₂ = β₂(β₁) определяется из (10),

δ > 0 - достаточно малая постоянная такая, что интервал (λ - δ,λ + δ) не содержит

какого-либо другого решения λ.

Стоит заметить, что вопрос о существовании нелинеаризуемых решений в нелинейных за-

дачах зависит от используемых дополнительных условий.

3. Физический смысл задачи P. Пусть Σ := {(x,y,z) : 0 < x < 1, (y,z) ∈ R²} -

плоский диэлектрический волновод, расположенный в декартовой системе координат Oxyz.

На границах x = 0, x = 1 волновод имеет идеально проводящие экраны.

Задача P описывает распространение двух TE-волн в нелинейном волноводе Σ, которые

связаны условием (5). Одна из волн гармонически зависит от переменной z, а вторая - от y.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

2^∗

312

ВАЛОВИК, МАРТЫНОВА

Введём электромагнитное поле (E, H)e^-iωt, которое представляет собой сумму двух TE-

волн E = E₁ + E₂, H = H₁ + H₂, распространяющихся в волноводе Σ, где ω > 0 - круговая

частота,

E₁ = (0,E_y(x)e^iγz,0)^т, E₂ = (0,0,E_z(x)e^iγy)^т,

H₁ = (Hx1(x)e^iγz,0,H_z(x)e^iγz)^т, H₂ = (Hx2(x)e^iγy,H_y(x)e^iγy,0)^т,

(39)

γ - вещественная постоянная распространения TE-волн. Электромагнитная монохроматиче-

ская ТЕ-волна - это волна, имеющая конфигурацию, определяемую формулой (E₁, H₁)e^-iωt

или (E₂, H₂)e^-iωt, где электрическая и магнитная компоненты электромагнитного поля опре-

делены формулами (39).

Диэлектрическая проницаемость внутри волновода описывается диагональным тензором

⎞

^⎛⋆

ε=^⎝0

ε₁ + β₁E2y

⎠_,

ε₂ + β₁E²

где ε₁, ε₂ > 1, β₁ > 0 - вещественные постоянные, ⋆ - элемент тензора, не влияющий на

распространение волн. Такой тензор соответствует тензорной нелинейности Керра [7, с. 162].

Скалярный случай нелинейности Керра является основным нелинейным законом в нелинейной

оптике [8, 9], а также возникает в других областях нелинейной математической физики [10,

11]. В связи с тем, что основная задача носит векторный характер, логично использовать

тензорную нелинейность.

Уравнения Максвелла имеют вид

rot H = -iωε₀ εE, rot E = iωμ₀H,

(40)

где ε₀ > 0 - диэлектрическая проницаемость вакуума, μ₀ > 0 - магнитная проницаемость

вакуума.

Таким образом, поля E, H удовлетворяют уравнениям (40) и касательные компоненты

E₁, E₂ обращаются в нуль на идеально проводящих экранах (x = 0, x = 1).

Подставляя (39) в уравнения Максвелла (40), получаем

E^′′y = γ²E_y - k²⁰(ε₁ + β₁E2y)E_y, E^′′z = γ²E_z - k²⁰(ε₂ + β₁E2z)E_z,

(41)

где k²⁰ = ω²μ₀ε₀,

Hx1 = -γ(ωμ₀)-1E_y, H_y = -(iωμ₀)-1E^′z,

Hx2 = γ(ωμ₀)-1E_z, H_z = (iωμ₀)-1E^′y.

На границах x = 0, x = 1 имеем следующие граничные условия:

E_y|x=0 = 0, E_z|x=0 = 0,

E^′y|x=0 = A₁, E^′z|x=0 = A₂,

E_y|x=1 = 0, E_z|x=1 = 0.

Таким образом, условия (3) имеют ясный физический смысл - это значение одной из ком-

понент поля на границе волновода (условие вполне естественное с точки зрения теории вол-

новодов). Кроме того, будем считать, что квадрат модуля магнитного поля является фикси-

рованной величиной, т.е. имеют место равенства



(E^′y)² + (E^′z)2

A²



|H|²|x=0 =



ω²μ²⁰

ω²μ²

x=0

Используя обозначения u₁ = E_y, u₂ = E_z, γ² = λ, a_j = k²⁰ε_j , α_j = k²⁰β_j , из (41) получа-

ем систему (6). Сформулированная физическая задача о распространении волн эквивалентна

задаче P. Подобная задача была рассмотрена в работе [12].

Работа выполнена при финансовой поддержке Российского научного фонда (проект 22-71-

00020).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

ОБ ОДНОЙ НЕКЛАССИЧЕСКОЙ ЗАДАЧЕ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

313

СПИСОК ЛИТЕРАТУРЫ

1. Kurseeva V.Yu., Moskaleva M.A., Valovik D.V. Asymptotical analysis of a nonlinear Sturm-Liouville

problem: linearisable and non-linearisable solutions // Asymptot. Anal. 2020. V. 119. № 1-2. P. 39-59.

2. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., 1984.

3. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М., 1961.

4. Хартман Ф. Обыкновенные дифференциальные уравнения. М., 1970.

5. Валовик Д.В. Исследование одной нелинейной задачи на собственные значения методом интеграль-

ного характеристического уравнения // Дифференц. уравнения. 2020. Т. 56. № 2. С. 175-189.

6. Марченко В.А. Операторы Штурма-Лиувилля и их приложения. Киев, 1977.

7. Boardman A.D., Egan P., Lederer F., Langbein U., Mihalache D. Third-Order Nonlinear Electromagnetic

TE and TM Guided Waves / Eds. H.-E. Ponath and G.I. Stegeman. Amsterdam; London; New York;

Tokyo, 1991.

8. Ландау Л.Д., Лившиц Е.М. Элекродинамика сплошных сред. М., 1982.

9. Boyd R.W. Nonlinear Optics. New York; London, 2003.

10. Fibich G. The Nonlinear Schrödinger Equation. Cham; Heidelberg; New York; Dordrecht; London, 2015.

11. Cazenave T. Semilinear Schrödinger equations // Courant lecture notes in mathematics of American

Mathematical Society. V. 10. 2003.

12. Мартынова В.Ю. Распространение гибридных ТЕ-ТЕ-волн в плоском закрытом волноводе, запол-

ненном нелинейной средой // Изв. вузов. Поволжский регион. Физ.-мат. науки. 2021. № 4 (60).

С. 27-45.

Пензенский государственный университет

Поступила в редакцию 18.01.2023 г.

После доработки 18.01.2023 г.

Принята к публикации 14.02.2023 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023