ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 3, с.389-399
ЧИСЛЕННЫЕ МЕТОДЫ
УДК 519.62
МНОГОШАГОВЫЕ МЕТОДЫ
ДЛЯ ДИФФЕРЕНЦИАЛЬНО-АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
© 2023 г. М. В. Булатов, Л. С. Соловарова
Рассмотрена начальная задача для линейных систем обыкновенных дифференциальных
уравнений второго порядка с тождественно вырожденной матрицей перед главной частью.
В терминах матричных полиномов приведены достаточные условия существования един-
ственного решения. Для таких задач предложены многошаговые разностные схемы. Про-
ведены анализ их устойчивости и расчёты модельного примера.
DOI: 10.31857/S037406412303010X, EDN: QVLSII
Введение. Обыкновенные дифференциальные уравнения (ОДУ) различных порядков -
один из основных инструментов для моделирования важных прикладных задач. Если все
уравнения одинакового порядка, то они образуют систему ОДУ. Если процесс можно описать
взаимосвязанными ОДУ различных порядков, а также трансцендентными (конечномерны-
ми) уравнениями, то, объединив их, получим систему с тождественно вырожденной матрицей
перед старшей производной. Такие системы принято называть дифференциально-алгебраиче-
скими уравнениями (ДАУ). Если порядок этой системы выше первого, то их называют ДАУ
высокого порядка.
В настоящее время активно развиваются качественная теория и численные методы ре-
шения ДАУ первого порядка (как для начальной, так и для краевой задачи). Достаточно
общирная и полная библиография по данному вопросу представлена в монографиях [1, 2], из
более ранних можно привести [3, 4]. Для ДАУ высокого порядка обычно применяют следую-
щий стандартный приём: вводят новую вектор-функцию размерности nk (n - размерность
исходной задачи, k - порядок ДАУ) и записывают полученную задачу в виде ДАУ первого
порядка. Такое преобразование имеет ряд недостатков, а именно увеличивает размерность в
k раз и значительно ухудшает свойства полученной задачи - увеличивает индекс, который
является показателем сложности (некорректности) первоначальной задачи.
Приведём одно из понятий индекса для ДАУ первого порядка с заданным начальным ус-
ловием
A(t)x′(t) + B(t)x(t) = ϕ(t), t ∈ [0, 1], x(0) = x0.
(1)
Будем говорить, что система (1) имеет индекс r, если r - минимальное целое неотрица-
тельное число такое, что существует линейный дифференциальный оператор
∑
Pr = Rj(t)(d/dt)j,
j=0
суперпозиция которого с (1) даёт систему ОДУ, т.е.
Pr ◦ (A(t)x′(t) + B(t)x(t)) = x′(t)
B(t)x(t),
где Rj (t), j = 0, r, A(t), B(t),
B(t) - (n × n)-матрицы, причём Rr(t) ≡ 0.
Методы построения оператора Pr с использованием проекторов и различных обобщённых
обратных матриц изложены в [2, 3]. Для ДАУ порядка выше первого можно ввести анало-
гичное понятие индекса или новую переменную и записать рассматриваемую задачу в виде
ДАУ первого порядка. Однако оба эти варианта обладают определёнными недостатками, а
7
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
390
БУЛАТОВ, СОЛОВАРОВА
именно для таких задач индекс не будет отражать сложность создания численных методов.
В частности, для одного класса ДАУ второго порядка ряд различных схем будет неустойчив
или принципиально неприменим, а для других классов ДАУ второго порядка те же самые
алгоритмы сходятся к точному решению. Таким образом, возникает необходимость проводить
исследование на предмет существования и единственности достаточно гладкого решения и со-
здавать методы численного решения ДАУ, не используя редукцию исходной задачи к ДАУ
первого порядка.
Отметим также, что известно очень мало статей, посвящённых численному решению ДАУ
высокого порядка. Из них можно выделить [5], где описано применение неявного метода Эй-
лера для рассматриваемых задач, и [6], в которой данные задачи исследованы с привлечением
техники проекторов.
В настоящей работе выделен класс линейных ДАУ второго порядка (начальная задача),
для которого предложено семейство многошаговых методов. Эти результаты основаны на осо-
бом свойстве матричных полиномов [7].
1. Постановка задачи. Рассмотрим задачу
A(t)x′′(t) + B(t)x′(t) + C(t)x(t) = f(t), t ∈ [0, 1],
(2)
x(0) = x0, x′(t)|t=0 = x′0,
(3)
где A(t), B(t), C(t) - (n × n)-матрицы, f(t) и x(t) - заданная и искомая n-мерные вектор-
функции соответственно, x0, x′0 ∈ Rn. Здесь и далее предполагается, что
det A(t) ≡ 0.
(4)
Систему (2) с условием (4) принято называть дифференциально-алгебраическими уравне-
ниями второго порядка (ДАУ2). Предполагается, что начальные условия (3) согласованы, т.е.
рассматриваемая задача имеет решение. Под решением мы понимаем любую дифференциру-
емую вектор-функцию, которая обращает (2) в тождество и удовлетворяет условиям (3).
Большую роль при исследовании ДАУ первого порядка играет теория регулярных матрич-
ных пучков [4, 8, 9]. Для дальнейшего изложения нам потребуются определения и вспомога-
тельные результаты.
Определение 1 [9]. Выражение вида λA + B, где λ - скалярный параметр, A и B -
матрицы размера m × n, называют матричным пучком. Если m = n и det (λA + B) ≡ 0, где
λ - скаляр, то пучок матриц λA + B называется регулярным. В противном случае (m = n
или det (λA + B) = 0 для любого λ) пучок называется сингулярным.
Определение 2 [7]. Матричный полином λA(t) + μB(t) + C(t), где λ, μ - скалярные па-
раметры, имеет простую структуру на отрезке [0, 1], если для любого t ∈ [0, 1] выполняются
условия:
1) rank A(t) = k = const;
2) rank (A(t)|B(t)) = k + l = const;
3) det (λA(t) + μB(t) + C(t)) = a0(t)λkμl + . . . , a0(t) = 0.
Лемма 1 [4]. Если элементы матриц A(t) и B(t) принадлежат классу Cp[0,1] и rank A(t)=
= k = const, то существует матрица P(t), элементы которой принадлежат классу Cp[0,1]
и detP(t) = 0 для любого t ∈ [0,1], такая, что матричный пучок P(t)(λA(t)+ B(t)) имеет
блочный вид
(
)
(
)
A1(t)
B1(t)
P (t)(λA(t) + B(t)) = λ
+
,
0
B2(t)
где A1(t), B1(t) - (k × n)-матрицы, B2(t) - ((n - k) × n)-матрица, rank A1(t) = k = const
для любого t ∈ [0, 1].
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
МНОГОШАГОВЫЕ МЕТОДЫ
391
Лемма 2 [7]. Если матричный полином λA(t) + μB(t) + C(t) имеет простую структуру
на отрезке [0,1] и элементы матриц принадлежат классу Cp[0,1], то существуют матрицы
R(t), Q(t) с элементами из Cp[0,1] такие, что
⎛
⎞
⎛
⎞
⎛
⎞
A1(t)
B1(t)
C1(t)
R(t)(λA(t) + μB(t) + C(t)) = λ⎝
0
⎠+μ⎝B2(t)⎠+ ⎝C2(t)⎠,
0
0
C3(t)
где A1(t), B1(t), C1(t) - (k × n)-матрицы, B2(t), C2(t) - (l × n)-матрицы, C3(t) - ((n -
- k - l) × n)-матрица, 0 - нулевые матрицы соответствующих размеров, и имеет место
равенство
R(t)(λA(t) + μB(t) + C(t))Q(t) =
⎛
⎞
⎛
⎞
⎛
⎞
Ek
0
A13(t)
B11(t)
0
B22(t)
C11(t) C12(t)
0
=λ⎝ 0
0
0
⎠+μ ⎝
0
El
0
⎠+ ⎝C21(t) C22(t)
0
⎠,
0
0
0
0
0
0
0
0
En-k-l
здесь A13(t), B11(t), B22(t), Cij(t), i, j = 1, 2, - блочные матрицы подходящих размеров, а
Ek, El и En-k-l - единичные матрицы размеров k, l и n - k - l соответственно.
Из данных лемм вытекает
Следствие. Если матричный полином λA(t) + μB(t) + C(t) имеет простую структуру
на отрезке [0,1] и матрицы A(t), B(t), C(t) имеют блочный вид
⎛
⎞
⎛
⎞
⎛
⎞
A1(t)
B1(t)
C1(t)
A(t) =⎝
0
⎠, B(t) = ⎝B2(t)⎠, C(t) = ⎝C2(t)⎠,
0
0
C3(t)
где A1(t), B1(t), C1(t) - (k × n)-матрицы, B2(t), C2(t) - (l × n)-матрицы, C3(t) - ((n -
- k - l) × n)-матрица, то
⎛
⎞
A1(t)
det⎝B2(t)⎠=0
C3(t)
для любого t ∈ [0, 1].
Вернёмся к задаче (2), (3). Одним из подходов к исследованию на предмет единственности
решения (с учётом того, что начальные условия (3) заданы корректно) и построению числен-
ных методов решения является редукция рассматриваемой задачи к системе первого порядка
путём введения новой переменной y(t) = (x′(t)т, x(t)т)т. С учётом данного обозначения задачу
(2), (3) можно записать в виде ДАУ первого порядка
A(t)y′(t) + B(t)y(t) = ϕ(t), y(0) = y0, t ∈ [0, 1],
(5)
где матрицы A(t), B(t) имеют блочный вид
(
)
(
)
A(t) B(t)
0
C(t)
A(t) =
,
B(t) =
,
ϕ(t) = (fт(t), 0)т,
(6)
0
E
-E
0
а начальные условия - вид y(0) = (x′0(t))т, x(t)т0 = y0. Эту задачу исследуют или численно
решают методами, разработанными для ДАУ первого порядка (см., например, [4]).
Другой подход - это построение дифференциального оператора степени r такого, что
Pr ◦ (A(t)x′′(t) + B(t)x′(t) + C(t)x(t)) = x′′ +B(t)x′(t)
C(t)x(t).
(7)
Такие подходы - запись задачи (2), (3) в виде ДАУ первого порядка с матрицами и правой
частью, определёнными по формуле (6), и построение дифференциального оператора (7) -
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
7∗
392
БУЛАТОВ, СОЛОВАРОВА
имеют принципиальный недостаток: индекс ДАУ (5) и r в формуле (7) не всегда являются
показателями сложности создания численных методов решения исходной задачи. Приведём
достаточно простые иллюстративные примеры, в которых предполагается, что входные дан-
ные удовлетворяют тем условиям гладкости, которые необходимы для проведения выкладок.
Пример 1 [1]. Рассмотрим систему
(
)(
)′′
(
)(
)′
(
)
1
αt
u(t)
0
1+α
u
q(t)
+
=
,
(8)
0
0
v(t)
1
αt
v
g(t)
где g(t) ∈ C2[0,1], q(t) ∈ C1[0,1], α - скалярный параметр.
Из второго уравнения имеем u′ = g(t) - αtv′. Подставив это выражение в первое уравне-
ние (8), получим v = q(t) - g′(t).
Достаточно просто можно убедиться в том, что данная система имеет индекс равный двум,
а оператор может быть выбран как
(
)-1 [(
)
(
)
](
)[(
)
(
)
]
1
t
1
0
0
0
d
1
0
1
0
0
0
d
Pr =
+
+
=
0
1-α
0
0
0
1
dt
-1
1
0
0
0
1
dt
(
)
(
)
(
1
0
αt
0
d
0
αt
)(d)2
=
+
+
,
0
0
−1
0
dt
0
-1
dt
здесь r = 2.
Хорошо известно [1, 2, 4, 10, 11], что ряд неявных схем, разработанных для ОДУ, в том
числе и жёстких, для ДАУ (1) часто порождают неустойчивые процессы или принципиально
неприменимые из-за сингулярности матричного пучка λA + B. То же самое можно сказать и
про задачу (2), (3).
Проведём анализ устойчивости простейшей разностной схемы для этого примера. Для
упрощения выкладок положим q(t) = g(t) = 0. Обозначим tj = jh, j = 0, N , uj ≈ u(tj),
vj ≈ v(tj) и рассмотрим алгоритм
(
)(
)
(
)(
)
(
)
1
αti+1
ui+1 - 2ui + ui-1
0
1+α
ui+1 - ui
0
+h
=
,
0
0
vi+1 - 2vi + vi-1
1
αti+1
vi+1 - vi
0
полагая, что u0, u1, v0, v1 заранее заданы. Опуская несложные выкладки, получим, что
данная схема будет устойчива только при |α/(1 + α)| < 1.
Пример 2. ДАУ
(
)(
)′′
(
)(
)
(
)
1
a12(t)
u
c11(t) c12(t)
u
q(t)
+
=
,
t ∈ [0,1],
(9)
0
0
v
0
c22(t)
v
g(t)
при c22(t) = 0 для всех t ∈ [0, 1] и g(t), c22(t) ∈ C2[0,1] также имеет индекс равный двум.
Оператор Pr можно взять в виде
]
(
)-1
[(
)
(
1
a12(t)
1
0
0
0)(d)2
Pr =
+
0
c22(t)
0
0
0
1
dt
Однако в отличие от первого примера простейшая разностная схема
(
)(
)
(
)(
)′
(
)
1
a12(ti+1)
ui+1 - 2ui + ui-1
c11(ti+1) c12(ti+1)
ui+1
q(ti+1)
+h2
=h2
,
0
0
vi+1 - 2vi + vi-1
0
c22(ti+1)
vi+1
g(ti+1)
где i = 1, N - 1, сходится к точному решению с первым порядком при определённой гладкости
элементов входных данных и |uj - u(tj )| = O(h), |vj - v(tj )| = O(h), j = 0, 1. Элементарные,
но громоздкие выкладки показывают, что, записывая системы (8), (9) в виде ДАУ первого
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
МНОГОШАГОВЫЕ МЕТОДЫ
393
порядка с матрицами A(t), B(t) и правой частью, определённой по формуле (6), получим
задачу индекса два.
Приведём в терминах матричных полиномов достаточные условия существования рассмат-
риваемых задач.
Утверждение 1 [7]. Пусть для задачи (2), (3) выполнены следующие условия:
1) матричный полином λA(t) + μB(t) + C(t) имеет простую структуру;
2) элементы входных данных обладают достаточной гладкостью (из класса Cp[0,1]);
3) начальные условия (3) согласованы с правой частью (2).
Тогда данная задача имеет единственное решение из класса Cp[0,1].
Данное утверждение носит только достаточный характер. Проиллюстрируем это. В при-
мере 1 условия утверждения 1 не выполняются, так как rank A(t) = 1, rank (A(t)|B(t)) = 2.
Однако нарушается третье условие определения 1:
(
)
λ λαt + μ(1 + α)
det (λA(t) + μB(t)) = det
= -μ2(1 + α).
μ
μαt
В примере 2 при c22(t) = 0 для любого t ∈ [0, 1] все условия утверждения 1 выполнены:
rank A(t) = rank (A(t)|B(t)) = 1, det (λA(t) + C(t)) = λc22(t) + c11c22(t).
Приведём ещё один пример.
Пример 3. Рассмотрим ДАУ
(
)(
)′′
(
)(
)′
(
)(
)
(
)
a11
0
u
0
b12
u
0
0
u
0
+
+
=
0
0
v
b21
0
v
0
c22
v
0
с условиями u(0) = v(0) = u′(0) = v′(0) = 0. При a11 = 0, b12 = 0, b21 = 0, c22 = 0 и
a11c22 = b12b21 эта задача имеет множество решений x = (u,v) = (ϕ(t),-b221/c22ϕ′(t))т, где
ϕ(t) - функция из C3[0,1], удовлетворяющая условиями ϕ(0) = ϕ′(0) = ϕ′′(0) = 0.
В данном примере матричный полином λA + μB + C не имеет простой структуры, так как
rank A(t) = 1, rank (A|B) = 2,
(
)
λa11
μb12
det (λA + μB + C) = det
= λa11c22 - μ2b12b21.
μb21
c22
Приведём условия согласования начальных условий и построения оператора P2. Для этого
нам потребуется следующее
Определение 3 (см., например, [3]). Матрица A+(t) называется псевдообратной к мат-
рице A(t), если она удовлетворяет уравнениям:
1) A(t)A+(t)A(t) = A(t);
2) A+(t)A(t)A+(t) = A+(t);
3) (A+(t)A(t))т = A+(t)A(t);
4) (A(t)A+(t))т = A(t)A+(t).
Матрица A+(t) определена единственным образом для любой матрицы A(t), её элементы
непрерывны, если rank A(t) = const при любом t и A+(t) = A-1(t); если det A(t) = 0 для
всех t (см., например, [3, 4]), то
V (t)A(t) ≡ 0,
(10)
где V (t) = E - A+(t)A(t).
Продифференцируем (2) и умножим полученную систему на матрицу V (t). В силу (10)
получим систему второго порядка вида
V (t)((A′(t) + B(t))x′′(t) + (B′(t) + C(t))x′(t) + C′(t)x(t)) = V (t)f′(t).
Итогом суммирования данной системы с (2) является система
A1(t)x′′(t) + B1(t)x′(t) + C1(t)x(t) = f1(t), t ∈ [0,1],
(11)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
394
БУЛАТОВ, СОЛОВАРОВА
где матрицы A1(t), B1(t), C1(t) и вектор-функция f1(t) определены по формулам
A1(t) = A(t) + V (t)(A′(t) + B(t)),
(12)
B1(t) = B(t) + V (t)(B′(t) + C(t)),
(13)
C1(t) = C(t) + V (t)C′(t),
(14)
f1(t) = f(t) + V (t)f′(t).
(15)
Аналогичным образом поступим с системой (11): продифференцируем её и умножим на
матрицу V1(t) = E - A1+(t)A1(t). Суммируя полученную систему и систему (11), имеем
A2(t)x′′(t) + B2(t)x′(t) + C2(t)x(t) = f2(t), t ∈ [0,1],
где
A2(t) = A1(t) + V1(t)(A1′ (t) + B1(t)), B2(t) = B1(t) + V1(t)(B1′ (t) + C1(t)),
C2(t) = C1(t) + V1(t)C1′(t), f2(t) = f1(t) + V1(t)f1′ (t).
Если матричный полином λA(t) + μB(t) + C(t) имеет простую структуру, то, используя
технику блочного представления матриц A(t), A1(t), B(t), B1(t), C(t), C1(t) и V (t), V1(t)
(см., например, [12]), лемму 2 и следствие, можно показать, что det A2(t) = 0 при любом t ∈
∈ [0, 1].
Итак, оператор P2 для системы (3) можно выбрать в виде
(
)
d
P2 = (A2(t))-1 E - A1+(t)A1+
(E - A+(t)A(t)).
dt
В этом случае
Pr ◦ (A(t)x′′(t) + B(t)x′(t) + C(t)x(t)) =
= x′′(t) + (A2(t))-1B2(t)x(t) + (A2(t))-1C2(t)x(t) = (A2(t))-1f2(t).
(16)
Отметим, что, используя технику проекторов [2] и операцию дифференцирования, можно
указать другой вид оператора P2. Приведём условия согласования начальных условий (3) для
ДАУ (2).
Утверждение 2. Если для задачи (2), (3) выполнены условия 1) и 2) утверждения 1 и
условия согласования начальных данных:
1) rank A(0) = rank (A(0)|B(0)x′0 + C(0)x0 - f(0));
2) rank A1(0) = rank (A1(0)|B1(0)x′0 + C1(0)x0 - f1(0)),
где A1(0), B1(0), C1(0), f1(0) определены по формулам (12)-(15), то задача (2), (3) имеет
единственное решение.
Доказательство. Подставляя в (2) и в (11) значение t = 0, будем соответственно иметь
системы линейных алгебраических уравнений (СЛАУ)
A(0)x′′(t)|t=0 + B(0)x′0 + C(0)x0 = f(0)
и
A1(0)x′′(t)|t=0 + B1(0)x′0 + C1(0)x0 = f1(0).
Условия согласования начальных данных вытекают из условий 1) и 2) утверждения 1 и тео-
ремы Кронекера-Капелли. В силу утверждения 2 система (2) эквивалентна (16), которая с
условием (3) имеет единственное решение. Утверждение доказано.
Для иллюстрации данного утверждения вернёмся к примеру 2 (формула (9)), для упроще-
ния положив c22(t) = 1. В этом случае компоненты v(t) должны удовлетворять условиям
v(0) = g(0),
(17)
v′(t)|t=0 = g′(t)|t=0.
(18)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
МНОГОШАГОВЫЕ МЕТОДЫ
395
Из условия 1) утверждения 2 вытекает, что v(0) = g(0) (т.е. справедлива формула (17)).
Опуская элементарные выкладки, можно показать, что система (11) имеет вид
(
)(
)′′
(
)(
)′
(
)(
)
(
)
1
a12(t)
u
0
0
u
c11(t) c12(t)
u
q(t)
+
+
=
0
0
v
0
1
v
0
1
v
g(t) + g′(t)
Из условия 2) утверждения 2 вытекает (так как rank A1 = 1 для любого t), что
rank (A1(0)|B1(0)x′0 + C1(0)x0 - f1(0))
должен быть равным единице, т.е.
[(
)(
)(
)′
(
)(
)
(
)
]
1
a12(0)
0
0
u
c11(0) c12(0)
u(0)
q
rank
+
-
= 1.
0
0
0
1
v
0
1
v(0)
g+g′
t=0
t=0
Это возможно только при
v′(t)|t=0 - v(0) - g(0) - g′(t)|t=0 = 0,
а так как v(0) = g(0) (формула (17)), то и v′(t) = g′(t)|t=0 (т.е. формула (18) справедлива).
Следующий пункт посвящён многошаговым методам решения задачи (2), (3).
2. Разностные схемы. Анализ примера 2 показывает, что известные разностные схемы
могут быть использованы для численного решения некоторых классов ДАУ второго поряд-
ка. Зададим на отрезке интегрирования равномерную сетку tj = jh, j = 0, N , h = 1/h и
обозначим
Aj = A(tj), Bj = B(tj), Cj = C(tj), fj = f(tj), xj ≈ x(tj).
С учётом данных обозначений линейные многошаговые (m-шаговые) методы для задачи (2),
(3) имеют вид
∑
∑
∑
1
A
ρjxi+1-j +Bi+1
σjxi+1-j
Ci+1
γjxi+1-j
fi+1, i = m - 1,N - 1.
(19)
i+1 h2
j=0
j=0
j=0
Здесь
Ai+1 = A(t∗i),
Bi+1 = B(t∗i),
Ci+1 = C(t∗i), f∗i+1 = f(t∗i), t∗i ∈ [ti+1-m,ti+1] и
∑
∑
∑
1
1
ρjxi+1-j ≈ x′′(t)|t=t∗
,
σjxi+1-j ≈ x′(t)|t=t∗ ,
γjxi+1-j ≈ x(t)|t=t∗ .
i
i
i
h2
h
j=0
j=0
j=0
Коэффициенты ρj , σj, γj и способы вычисления
Ai+1,
Bi+1,
Ci+1,
fi+1 зависят от вы-
бора точки t∗i. Стандартно предполагается, что при реализации схем (19) заданы или заранее
вычислены стартовые значения x0, x1, . . . , xm-1.
Схемы (19) можно разделить на классы:
1) неявные схемы (ρ0 = 0, σ0 = 0, γ0 = 0);
2) явные схемы (ρ0 = 0, σ0 = γ0 = 0);
3) явно-неявные схемы (ρ0 = 0, σ0 = 0, γ0 = 0 или ρ0 = 0, σ0 = 0, γ0 = 0).
При реализации схем (19) для задачи (2), (3) на каждом шаге интегрирования требуется
решать СЛАУ вида
∑
(ρ0A¯i+1 + hσ0 Bi+1 + h2γ0
Ci+1)xi+1 = (ρjA¯i+1 + hσj Bi+1 + h2γjCi+1)xi+1-j + h2f¯i+1.
(20)
j=1
В силу того, что det A(t) ≡ 0, явные методы (20) для задачи (2), (3) принципиально непри-
менимы. Реализация явно-неявных схем приводит к необходимости решать СЛАУ с матрицей
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
396
БУЛАТОВ, СОЛОВАРОВА
перед ρ0A¯i+1 + hσ0 Bi+1 или ρ0A¯i+1 + hγj
Ci+1. Эти матрицы также могут быть тождественно
вырожденными. Приведём пример: A(t) = diag {a11(t), 0, 0}, B(t) = diag {0, b22(t), 0}, C(t) =
= diag {0,0,c33(t)}, где a11(t), b22(t), c33(t) = 0 для любого t. Поэтому остановимся на
неявных схемах.
Приведём хорошо известные факты (см., например, [13]) из теории разностных схем для
линейных ОДУ второго и первого порядков вида
x′′(t) + B(t)x′(t) + C(t)x(t) = f(t), x(0) = x0, x′(t)|t=0 = x′0, t ∈ [0,1],
(21)
x′(t) + C(t)x(t) = f(t), x(0) = x0, t ∈ [0,1].
(22)
Эти схемы для задач (21) и (22) имеют вид
∑
∑
∑
ρjxi+1-j + hBi+1
σjxi+1-j + h2
Ci+1
γjxi+1-j = h2f¯i+1,
(23)
j=0
j=0
j=0
∑
∑
σjxi+1-j +
Ci+1
γjxi+1-j =
fi+1
(24)
j=0
j=0
соответственно.
В предположении, что элементы входных данных задач (21) и (22) достаточно гладкие,
схемы (23) и (24) аппроксимируют соответствующие задачи с порядком O(hq), начальные
значения ∥xj -x(tj )∥ = O(hq), j = 0, m - 1, и схемы устойчивы, тогда они сходятся к точному
решению и справедливы оценки ∥xi - x(ti)∥ = O(hq), i = m, N.
Для устойчивости разностных схем (23) и (24) для задач (21) и (22) соответственно, как
правило, рассматривают характеристические полиномы
∑
ρjpm-j = 0,
(25)
j=0
∑
σjpm-j = 0,
(26)
j=0
где p - скаляр.
Следуя общепринятой терминологии [14], будем называть схемы ρ-устойчивыми, если ха-
рактеристическое уравнение (25) имеет два кратных корня p1 = p2 = 1, а остальные корни p3,
p4, ..., pm лежат в единичном круге, и на границе круга нет кратных корней; σ-устойчивы-
ми, если характеристическое уравнение (26) имеет корень p1 = 1, а остальные корни p2, p3,
..., pm лежат в единичном круге, и на границе круга нет кратных корней. В силу того, что
рассматриваемая задача может включать в себя и алгебраические уравнения (см. пример 3),
потребуем, чтобы корни характеристического полинома
∑
γjpm-j = 0
j=0
лежали в единичном круге, на границе круга не было кратных корней и не было корня, равно-
го единице. Это условие по аналогии будем называть γ-устойчивостью. Анализ устойчивости
и скорости сходимости многошаговых методов для ДАУ первого порядка (1) проведён в ра-
ботах [1, 2, 11, 14]. Если в исходной системе положим A(t) ≡ 0, то получим задачу (1), и
приведённые выше определения устойчивости схем совпадают с классическими.
Относительно сходимости схем (19) справедливо
Утверждение 3. Пусть для задачи (2), (3) выполнены условия:
1) элементы A(t), B(t), C(t), f(t) принадлежат классу Cq[0,1];
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
МНОГОШАГОВЫЕ МЕТОДЫ
397
2) начальные значения x0, x1, ..., xm-1 удовлетворяют оценке ∥xj - x(tj)∥ = O(hq),
j = 0,m - 1;
3) схема (19) аппроксимирует задачу (2), (3) с порядком q;
4) матричный полином λA(t) + μB(t) + C(t) имеет простую структуру;
5) схема (19) ρ-, σ- и γ-устойчива;
6) матрица Q(t) = Q в лемме 2 постоянная.
Тогда справедлива оценка ∥xj - x(tj)∥ = O(hq).
Ri+1
Доказательство. Умножим каждое из соотношений (19) на матрицу
= R(t∗i) и
произведём замену переменной xi = Qyi, i = 0, N, где матрицы R(t), Q(t) те же, что и в
лемме 2.
В силу условия 6) утверждения 3 и леммы 2 имеем блочные рекуррентные соотношения
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
Ek
0
A13(t∗i)
y1i+1-j
B11(t∗i)
0
B22(t∗i)
y1i+1-j
∑
∑
1
⎝
0
0
0
⎠
ρj ⎝y2i+1-j⎠+1
⎝
0
El
0
⎠
σj ⎝y2i+1-j⎠+
h2
h
0
0
0
j=0
y3i+1-j
0
0
0
j=0
y3
i+1-j
⎛
⎞
⎛
⎞
⎛
⎞
C11(t∗i) C12(t∗i)
0
y1i+1-j
ϕ1(t∗i)
∑
+⎝C21(t∗i) C22(t∗i)
0
⎠
γj ⎝y2i+1-j⎠= ⎝ϕ2(t∗i)⎠,
(27)
0
0
En-k-lj=0
y3i+1-j
ϕ3(t∗i)
где
⎛
⎞
⎛
⎞
y1i+1-j
ϕ1(t∗i
)
⎝
⎝
⎠=R(t∗
y2i+1-j
⎠=Q-1xi+1-j,
ϕ2(t∗i)
i
)f(t∗i).
y3i+1-j
ϕ3(t∗i)
В силу γ-устойчивости разностных схем, условий 2) и 3) утверждения 3 получим
∥y3i - y3(ti)∥ = O(hq).
(28)
Для первой и второй компонент блочной системы (27) будем иметь равенства
∑
∑
(ρj Ek + σjhB11(t∗i) + γj h2C11(t∗i))y1i+1-j +
γjC12(t∗i)y2i+1-j =
j=0
j=0
∑
= h2ϕ1i+1(t∗i) -
(ρj A13(t∗i) + σjB22(t∗i))y3i+1-j ,
j=0
∑
∑
(σj + hγj C22(ti))y2i+1-j +
hγj C21(t∗i)y1i+1-j = ϕ2i+1(t∗i).
j=0
j=0
Из условий ρ- и σ-устойчивости схем, аппроксимации задачи и результатов о сходимости
схем для ОДУ первого и второго порядков [13, 14] следует, что
∥y2i - y2(ti)∥ = O(hq),
∥y1i - y1(ti)∥ = O(hq).
(29)
Вспоминая, что x(t) = Qy(t), и учитывая оценки (28), (29), будем иметь ∥xi - x(ti)∥ =
= O(hq), i = m,N. Утверждение доказано.
Отметим, что условие 6) утверждения 3 для схем вида (19) пока не удалось обойти. Пред-
варительный анализ показывает, что его можно смягчить.
Для иллюстрации приведём двухшаговый метод первого порядка
Ai+1(xi+1 - 2xi + xi-1) + hBi+1(xi+1 - xi) + h2Ci+1xi+1 = h2fi+1
(30)
и трёхшаговый метод второго порядка
h
Ai+1(2xi+1-5xi+4xi-1-xi-2)+
Bi+1(11xi+1-18xi+9xi-1-2xi-2)+h2Ci+1xi+1 = h2fi+1. (31)
6
В следующем пункте будут приведены некоторые расчёты для данных алгоритмов.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
398
БУЛАТОВ, СОЛОВАРОВА
3. Численные расчёты. Проведём расчёты модельных примеров по схемам (30), (31).
В качестве стартовых точек взяты точные значения x(h) и x(2h) соответственно.
Пример 4. Рассмотрим ДАУ
⎛
⎞⎛
⎞′′
⎛
⎞⎛
⎞′
exp(t)
0
0
x1
2α exp(t)
0
0
x1
⎝1
0
0⎠⎝x2⎠ +⎝
2α
exp(-t)
0⎠⎝x2⎠ +
1
0
0
x3
2α
1
0
x3
⎛
⎞⎛
⎞
⎛
⎞
(α2 + β2) exp(t)
0
0
x1
0
+⎝ (α2 + β2)
3γ exp(-t)
0⎠⎝x2⎠= ⎝0
⎠
(α2 + β2)
γ
1
x3
sin t
с начальными условиями x(0) = (0, 1, 0), x′(t)|t=0 = (β, -γ, 1)т. Точное решение имеет вид
x(t) = (exp(-αt) sin(βt), exp(-γt), sin t)т.
Непосредственный проверкой можно убедиться что данный пример удовлетворяет услови-
ям утверждения 1. Варьируя параметры α, β, γ, будем иметь жёсткую систему ОДУ первого
порядка для второй компоненты, жёсткую и быстро осциллирующую систему ОДУ второго
порядка для первой компоненты, и алгебраическую связь для третьей компоненты.
Результаты расчётов представлены в табл. 1, 2 при параметрах α = 20, β = 5, γ = 30.
Погрешности приведены для каждой компоненты в точке t = 1.
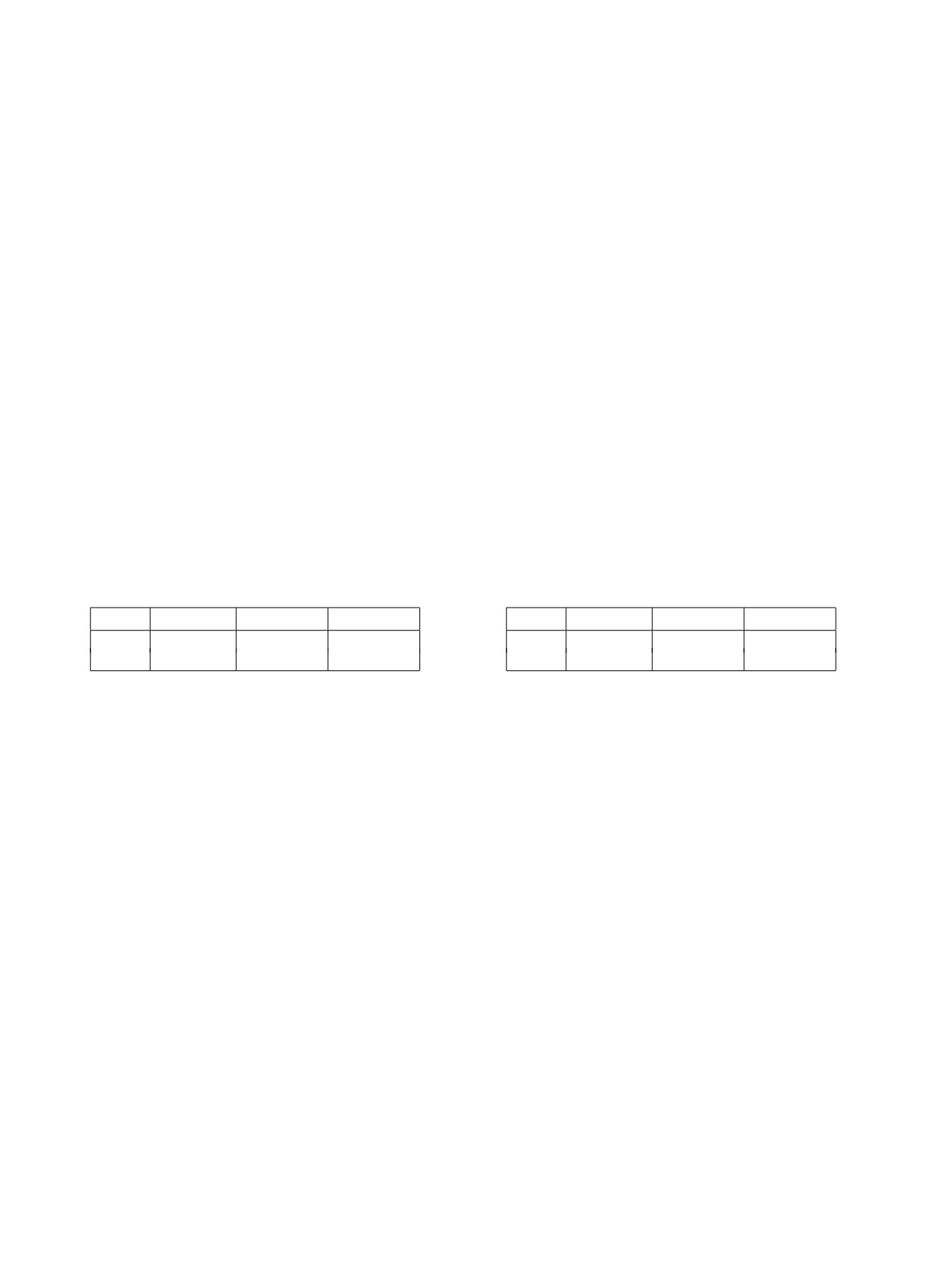
Таблица 1. Результаты применения метода (30)
Таблица 2. Результаты применения метода (31)
для примера 4
для примера 4
h
err1
err2
err3
h
err1
err2
err3
0.05
7.4 · 10-7
6.1 · 10-9
1.1 · 10-16
0.05
4.6 · 10-5
3.5 · 10-7
1.1 · 10-16
0.025
1.8 · 10-8
1.6 · 10-10
1.1 · 10-16
0.025
7.5 · 10-8
4.7 · 10-12
1.1 · 10-16
При увеличении жёсткости или жёсткости и осцилляции, т.е. при увеличении параметров
α, β и γ, предложенные алгоритмы также неплохо работают.
Отметим, что предложенные схемы можно применять и для численного решения более
широкого класса задач.
Пример 5. Точное решение x(t) задачи
⎛
⎞⎛
⎞′′
⎛
⎞⎛
⎞′
exp(t)
0
0
x1
2 exp(t)
1
0
x1
⎝2
0
0⎠⎝x2⎠ +⎝
4
exp(-t)
0⎠⎝x2⎠ +
1
0
0
x3
2
1
0
x3
⎛
⎞⎛
⎞
⎛
⎞
0
3
exp(t)
x1
exp(t) sin t
+⎝0
3 exp(-t)
1
⎠⎝x2⎠= ⎝sint
⎠
0
3
1
x3
sin t
с начальными условиями x(0) = (1, 1, 0), x′(t)|t=0 = (-2, -3, 1)т определяется по формуле
x(t) = (exp(-2t), exp(-3t), sin t)т.
С помощью элементарных преобразований получим систему, эквивалентную данной:
⎛
⎞⎛
⎛
⎞⎛
⎞′
⎛
⎞⎛
⎞ ⎛
⎞
⎞′′
1
0
0
x1
2
exp(-t)
0
x1
0
3 exp(-t)
1
x1
sin t
⎝0
0
0⎠⎝x2⎠ +⎝0
exp(-t)
0⎠⎝x2⎠+⎝0
-3exp(-t)
-1⎠⎝x2⎠=⎝-sint⎠.
0
0
0
x3
0
1 - exp(-t)
0
x3
0
3 - exp(-t)
0
x3
0
Последняя ДАУ при t = 0 не удовлетворяет условиям утверждения 1, так как нарушено
условие 3) определения 2. Численные расчёты этого примера представлены в табл. 3 и 4 для
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023
МНОГОШАГОВЫЕ МЕТОДЫ
399
методов (30), (31). Здесь, также как и в предыдущем примере, погрешности для каждой ком-
поненты приведены при t = 1.
Таблица 3. Результаты применения метода (30)
Таблица 4. Результаты применения метода (31)
для примера 5
для примера 5
h
err1
err2
err3
h
err1
err2
err3
0.05
0.027
0.01
1.7 · 10-14
0.05
0.0043
0.00013
4.8 · 10-14
0.025
0.014
0.0055
2.8 · 10-13
0.025
0.0012
1.6 · 10-5
6.7 · 10-13
Заключение. В статье выделены классы ДАУ второго порядка (начальная задача), ко-
торые имеют единственное решение в классе достаточно гладких функций. Для численного
решения таких задач предложено построение многошаговых методов. Приведены конкретные
двухшаговый и трёхшаговый методы первого и второго порядков соответственно. Их работо-
способность продемонстрирована на расчётах модельных примеров.
Работа выполнена в рамках базового проекта “Теория и методы исследования эволюцион-
ных уравнений и управляемых систем с их приложениями” (проект 121041300060-4).
СПИСОК ЛИТЕРАТУРЫ
1. Brenan K.F., Campbell S.L., Petzold L.R. Numerical Solution of Initial-Value Problems in Differential-
Algebraic Equations. Philadelphia, 1996.
2. Lamour R., März R., Tischendorf C. Differential-Algebraic Equations: a Projector Based Analysis. Berlin;
Heidelberg, 2013.
3. Бояринцев Ю.Е. Регулярные и сингулярные системы линейных обыкновенных дифференциальных
уравнений. Новосибирск, 1980.
4. Чистяков В.Ф. Алгебро-дифференциальные операторы с конечномерным ядром. Новосибирск,
1996.
5. Sand J. On implicit Euler and related methods for high-order high-index DAEes // Appl. Numer. Math.
2002. № 42. P. 411-424.
6. Mehrmann V., Shi C. Transformation of high order linear differential-algebraic systems to first order
// Numer. Algorithms. 2006. № 42. P. 281-307.
7. Булатов М.В., Минг-Гонг Ли. Применение матричных полиномов к исследованию линейных диф-
ференциально-алгебраических уравнений высокого порядка // Дифференц. уравнения. 2008. Т. 44.
№ 10. С. 1299-1306.
8. Бояринцев Ю.Е., Орлова И.В. Пучки матриц и алгебро-дифференциальные системы. Новосибирск,
2006.
9. Гантмахер Ф.Р. Теория матриц. М., 1986.
10. Данилов В.А., Чистяков В.Ф. О препятствиях на пути построения эффективных численных мето-
дов решения алгебро-дифференциальных систем. Иркутск, 1990 (Препринт / ИрВЦ СО АН СССР;
№ 5).
11. Kunkel P., Mehrmann V. Differential-Algebraic Equations: Analysis and Numerical Solution. Zürich,
2006.
12. Булатов М.В. О преобразовании алгебро-дифференциальных систем уравнений // Журн. вычис-
лит. математики и мат. физики. 1994. Т. 34. № 3. С. 360-372.
13. Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения).
М., 1975.
14. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жёсткие и диффе-
ренциально-алгебраические задачи. М., 1999.
Институт динамики систем и теории управления
Поступила в редакцию 19.08.2020 г.
имени В.М. Матросова СО РАН, г. Иркутск
После доработки 11.02.2023 г.
Принята к публикации 14.02.2023 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№3
2023