ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 3, с.422-431

ТЕОРИЯ УПРАВЛЕНИЯ

УДК 517.977+517.925

О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ ЗАДАЧАХ,

СВЯЗАННЫХ С ПЕРЕМЕЩЕНИЕМ В ПОЛЕ СКОРОСТЕЙ

Исследованы экстремали принципа максимума Понтрягина задач, связанных с перемеще-

нием в поле скоростей. Управления являются непрерывными функциями. Показано, что в

фазовом пространстве существует окрестность финальной точки, через каждую точку ко-

торой проходит единственная траектория экстремали, ведущая в финальную точку. Также

показано, что если траектория экстремали содержит точку, через которую проходит дру-

гая экстремаль с таким же значением функционала, то эта точка отсекает от траектории

неоптимальную часть. Доказано, что оставшаяся часть, ведущая в финальную точку, оп-

тимальна.

DOI: 10.31857/S0374064123030135, EDN: QVTYWS

1. Постановка задачи. Рассмотрим перемещения в фазовом пространстве R², подчи-

няющиеся закону

x = v(x) + u. Здесь v: R2 → R2 - векторное поле класса C2, v(0) = 0;

управление u - кусочно-непрерывная, непрерывная справа, с разрывами первого рода вектор-

функция такая, что ∥u∥ ≤ 1, где ∥u∥² = u²¹ + u²². Рассмотрим управления, которые переводят

объект из положения x₀ в начал∫о координат. Пусть поставлен вопрос о выборе управления,

которое минимизирует величину

(1+α∥u∥²)dt. Таким образом, рассматриваются следующие

задачи:

∫0

J (x, u) =

(1 + α∥u(t)∥²) dt → min,

t₀

x = v(x) + u,

∥u∥ ≤ 1,

x(t₀) = x₀, x(0) = 0, α ≥ 0.

(1)

Здесь t = 0 - момент завершения процесса, момент начала процесса t₀ не фиксирован.

При α = 0 получается задача быстродействия. Если α > 0, то экономится не только

время, но и “энергия”, затраченная на перемещение. Варьируя значение α, можем менять

значимость указанных факторов. Для того чтобы выделить экстремали задачи (1), восполь-

зуемся принципом максимума Понтрягина (см. [1, c. 25]).

Пусть (x, u) - оптимальный процесс. Составим функцию Понтрягина

H = ψ₀(1 + α∥u∥²) + ψ(v(x) + u),

где константа ψ₀ принимает значения либо нуль, либо минус единица. Согласно принципу

максимума для некоторого решения системы

ψ=-ψv′(x(t))(v′_{-матрицаЯкобиотображе-}

ния v) функция H принимает максимальное значение по параметру u.

ψ=-ψv′(x),тоψ

Рассмотрим случай ψ₀ = 0. Поскольку вектор (ψ₀, ψ) нетривиален и

не обращается в нуль. Следовательно, H принимает максимальное значение при u = ψ/∥ψ∥.

Так как в финальный момент H = 0 и v(0) = 0, получаем u(0) = 0, что противоречит

условию не обращения в нуль вектора ψ. Таким образом, случай ψ₀ = 0 экстремалей не

выявляет.

Для случая ψ₀ = -1

H = -α∥u∥² + ψu + ψv - 1 = -α∥u∥² + ∥ψ∥∥u∥cos β + ψv - 1,

422

О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ ЗАДАЧАХ

423

где β - угол между векторами ψ и u. Очевидно, что максимальное по u значение величина H

будет достигать при β = 0. При

(

)₂

∥ψ∥

∥ψ∥²

H = -α ∥u∥ -

+ ψv - 1

2α

4α

имеем

{

ψ/(2α), если ∥ψ∥ < 2α,

ψ/∥ψ∥, если ∥ψ∥ ≥ 2α.

Запишем функцию u в виде g(∥ψ∥)ψ, где

{

1/2α при x < 2α,

g(x) =

1/x при x ≥ 2α.

Используем условие H = 0 при t = 0. Поскольку v(0) = 0, имеем равенства

- αg²(∥ψ∥)ψ² + g(∥ψ∥)ψ² - 1 = 0,

ψ²(-αg²(∥ψ∥) + g(∥ψ∥)) = 1.

Если ∥ψ(0)∥ ≤ 2α, то ψ² = 4α, ∥ψ(0)∥ = 2√α при α ≥ 1 (при α < 1 решений нет). Если

∥ψ(0)∥ ≥ 2α, то

(

)

ψ²(0) -α

= 1,

∥ψ(0)∥²

∥ψ(0)∥

откуда получаем, что ∥ψ(0)∥ = 1 + α при α ≤ 1 (при α > 1 решений нет).

Таким образом, экстремали задачи (1) определяются решением следующей задачи Коши

с пятью компонентами фазового пространства и моментом завершения t = 0:

ψ=-ψv′(x),

x₀ = 1 + αg²(∥ψ∥)ψ²,

x = v(x) + g(∥ψ∥)ψ,

x₀(0) = 0, x(0) = (0,0), ψ(0) = b(cos s,sin s),

(2)

где

{

2√α при α ≥ 1,

1 + α при 0 ≤ α < 1.

Решение задачи (2) определяет экстремаль задачи (1): x = (x₁, x₂) - координаты траекто-

рии экстремали, u = g(∥ψ∥)ψ - управление, |x₀| - значение функционала.

Через заданную точку x₀ фазовой плоскости R² могут проходить две (или больше) траек-

тории экстремали. Это может свидетельствовать о том, что хотя бы одна из этих траекторий

содержит неоптимальную часть. Как отделять заведомо неоптимальную часть траектории?

Будет ли оптимален остаток? Могут ли подобные точки x₀ располагаться как угодно близко

от начала координат? Отметим, что этими и другими вопросами, связанными с перемещением

в поле скоростей, занимались разные авторы (см., например, работы [2-4]).

2. Теорема единственности.

Теорема 1. Пусть первые производные отображения υ удовлетворяют условию Липши-

ца в некоторой области, содержащей начало координат. Существует окрестность начала

координат, через каждую точку которой проходит единственная траектория экстремали,

ведущая в начало координат.

Доказательство. Для доказательства потребуются следующие утверждения. Пусть F :

Rⁿ → Rⁿ в области U ограничена константой K и липшицева, т.е. справедливо неравенство

∥F (x) - F (y)∥ ≤ L∥x - y∥; x = x(t) - решение уравнения x = F(x), x(t) ∈ U для t ∈ [0,Δt].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

9^∗

424

НИКОЛЕНКО

Согласно теореме о среднем и следствию из неё (см. [5, c. 148]) выполняются оценки

∥ x(Δt) - x(0)∥ = ∥F(x(Δt)) - F(x(0))∥ ≤

≤ L∥x(Δt) - x(0)∥ ≤ L max ∥ x(ΘΔt)∥|Δt| ≤ LK|Δt|,

(3)

0≤Θ≤1

∥x(Δt) - x(0) - x(0)Δt∥ ≤ max

∥ x(ΘΔt) - x(0)∥|Δt| = max ∥F(x(ΘΔt)) - F(x(0))∥|Δt| ≤

0≤Θ≤1

≤ Lmax∥x(ΘΔt) - x(0)∥|Δt| ≤ L max ∥x(ΘΔt)∥Δ²t ≤ LKΔ²t.

(4)

0≤^Θ≤1

Рассмотрим сначала случай α = 1. Траектория экстремали определяется X-компонентой

решения (X, Ψ) задачи Коши (компоненту x₀ не записываем)

ψ=-ψv′(x),

x = v(x) + g(∥ψ∥)ψ,

x(0) = (0, 0), ψ(0) = b(cos s, sin s),

(5)

где s - действительное число.

При α = 1 b - точка гладкости функции g, поэтому можно указать число δ > 0 такое,

что решение (X(t, s), Ψ(t, s)) является гладким при всех t ∈ [-δ, 0]. Пусть (X(t, s), Ψ(t, s)) -

решение задачи (5). При t ∈ [-δ, 0] рассмотрим отображения

(

)

(

)

(

)

(

)

(

)

t cos s

y₁

x₁(t,s)

ρ:

→

t sin s

y₂

x₂(t,s)

где x_i - компоненты вектора X.

Поскольку X(0, s) = (0, 0)^т при всех s, то отображение Φ(y₁, y₂) = X(t, s) корректно

определено. Для того чтобы записать формулу, задающую отображение Φ, воспользуемся

обозначением (X, Ψ)(t, z) - решение задачи (5) с финальным условием z ∈ R⁴ : (X, Ψ)(0) = z.

Из определения имеем t = -∥y∥, cos s = -y₁/∥y∥, sin s = -y₂/∥y∥ при t < 0.

Тогда

⎧

(

))

-by₁

-by₂

⎨

X -∥y∥,

0, 0,

при y = (0, 0)^т,

∥y∥

Φ(y₁, y₂) =

⎩

(0, 0)^т

при y = (0, 0)^т.

Отображение ρ при t < 0 является локальным диффеоморфизмом. Возьмём окрестность

точки (t, s), которая отображением ρ взаимно-однозначно переводится в окрестность точ-

ки (y₁, y₂). В полученной окрестности отображение Φ можно записать в виде Φ = X(ρ-1).

Проверим, что отображение Φ непрерывно дифференцируемо при ∥y∥ < δ, причём Φ^′(0, 0) -

невырожденная матрица. Отсюда, в силу теоремы об обратной функции, следует утвержде-

ние теоремы при α = 1. Рассмотрим lim Φ^′(λy),

∥y∥ = δ. Убедимся в том, что указанный

λ→0+0

предел есть невырожденная матрица и стремление к ней равномерно по y

(∥y∥ = δ):

lim

Φ^′ = lim X^′(ρ^′)-1,

λ→0+0

t→0

предел в правой части считается при фиксированном s. Запишем матрицы

(

)

(

)

cos s

sin s

cos s

-tsin s

ρ^′ =

(ρ^′)-1

sin s t cos s

sin s

cos s

Для того чтобы записать матрицу X^′, проведём предварительно рассуждения в общем виде.

Пусть F : R⁴ → R⁴, ϕ: R → R⁴ и Y (t, s) - решение задачи Коши

= F(Y ), Y (0) = ϕ(s),

P : R⁴ → R² - проекция на первые две координаты.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ ЗАДАЧАХ

425

Опишем как устроена матрица Якоби отображения P Y : (P Y )^′ = P Y^′. (P Y )^′ состоит

из первых двух строк матрицы Y^′, её первый столбец (Y^′)¹ = Y_t есть F (Y (t, s)), если нас

интересует этот вектор при малых Δt, то можем записать

Y_t(Δt,s) = Y_t(0,s) + O(Δt) = F(ϕ(s)) + O(Δt).

(6)

Второй столбец (Y^′)² = Y_s есть Z-компонента решения системы в вариациях, соответствую-

щих системе

= F(Y ),

= F^′(Y )Z, Y (0) = ϕ(s), Z(0) = ϕ^′(s).

(7)

При малых Δt можем записать

Y (Δt, s) = ϕ(s) + F (ϕ(s))Δt + o(Δt), Z(Δt, s) = ϕ^′(s) + F^′(ϕ(s))ϕ^′(s)Δt + o(Δt).

(8)

Отметим, что если отображение (Y, Z) → (F (Y ), F^′(Y )Z) ограничено константой K и

липшицево с константой L в окрестности образа отображения (ϕ, ϕ^′) и этот образ компактен,

то согласно оценкам (3), (4) можно указать число δ такое, что при |Δt| ≤ δ для величин

O(Δt), o(Δt) из формул (6), (8) выполняются оценки

∥O(Δt)∥ ≤ LK|Δt|,

∥o(Δt)∥ ≤ LKΔ²t.

(9)

В нашем случае вектор из R⁴ записывается в виде (x, ψ),

(

)

v(x) + g(∥ψ∥)ψ

F (x, ψ) =

ϕ(s) = (0, 0, b cos s, b sin s).

-ψv^′(x)

Согласно (6) первый столбец матрицы X^′ определяется по формуле

(

)

cos s

(X^′)¹(Δt, s) = X_t(Δt, s) = P F (ϕ(s)) + O(Δt) = bg(b)

+ O(Δt).

sin s

Второй столбец (X^′)² матрицы X^′ состоит из первых двух компонент вектора Z из фор-

мул (8). Чтобы его записать, потребуются первые две строки матрицы F^′ :

⎛

⎞

ψ₁ψ₂

g^′(∥ψ∥)

+ g(∥ψ∥)

g^′(∥ψ∥)

⎜

⎟

∥ψ∥

⎜

⎟

F^′ =

^′(x)

⎝^v

ψ₁ψ₂

ψ²

⎠^.

g^′(∥ψ∥)

+ g(∥ψ∥)

∥ψ∥

Вычислим

(

)

(X^′)²(Δt, s) = P Z(Δt, s) = υ^′(0)bg′(b)cos2 s+g(b)bg′(b)cosssins

bg^′(b) cos s sin s

bg^′(b) sin² s + g(b)

⎛

⎞

(

)

⎜

⎟

- sin s

⎝

⎠Δt + o(Δt) = bg(b)

Δt + o(Δt).

(10)

-bsin s

cos s

b cos s

Производная отображения Φ в точке y = (Δt cos s, Δt sin s) равна Φ^′(y) = X^′(g^′)-1 =

= bg(b)(E + O(Δt)), где E - единичная матрица. Следовательно, lim Φ^′(λy) = bg(b)E.

λ→0+0

Рассмотрим случай α = 1. Тогда в формулах (5) b = 2,

{

1/2, x ≤ 2,

g(x) =

1/x, x > 2.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

426

НИКОЛЕНКО

Выберем последовательность гладких функций g_n, равномерно сходящуюся к g, такую, что

0 < g_n ≤ 1/2,

|g^′n| ≤ 1/4. Далее убедимся, что можно выбрать числа δ и C таким образом,

что оценки (9) запишутся в виде

∥O(Δt)∥ ≤ C|Δt|,

∥o(Δt)∥ ≤ CΔ²t

(11)

при |Δt| ≤ δ для всех g_n. Чтобы исключить путаницу, функции Φ припишем индекс Φgn , Φ_g.

Функции Φgn равномерно сходятся к Φ_g для |t| ≤ δ. В силу следствия из теоремы о среднем

и вида Φ′gn выполняется неравенство

∥Φgn (b) - Φgn (a) - Φ^′g

(0)(b - a)∥ ≤ sup

∥Φ^′g

g^′n

(0)∥∥(b - a)∥,

c∈[a,b]

следовательно, можно указать d > 0 и δ₁ > 0 такие, что ∥Φgn (b) - Φgn (a)∥ ≥ d∥(b - a)∥

для всех a и b с нормой меньше δ₁. Тогда в силу равномерной сходимости в последнем

неравенстве вместо g_n можно записать g. Следовательно, Φ_g инъективно в круге ∥y∥ <

< δ₁. Кроме того, в силу обратимости отображений Φgn образ шара ∥y∥ < δ₁ содержит шар

∥y∥ < dδ₁ : Φgn (Bδ10 ) ⊃ B0δ2 . Но тогда и Φg(B01 ) ⊃ B0δ1 . Действительно, пусть y ∈ B0δ1 ,

z_n = Φ-1g

y, в силу компактности можем считать, что z_n → z. Тогда Φ_g(z) = y.

Обоснуем теперь оценки (11). Заметим, что в первом неравенстве (9) константы L и K

определяются отображением F, т.е. величинами υ, υ^′, g (но не g^′). Это объясняет первое

из неравенств (11). Чтобы обосновать второе неравенство (11), матрицу F^′ представим в виде

суммы F^′

F^′ + G, где

⎛

⎞

⎛

(

)⎞

υ^′(x) g(∥ψ∥)E

g^′(∥ψ∥)

ψ²¹

ψ₁ψ₂

F^′ =^⎝

⎠, G = ⎝⁰

∥ψ∥

ψ₁ψ₂

ψ²

⎠_.

Если в системе (7) вместо F^′ записать

F^′, то в формулах (9) константы L, K будут

определяться величинами υ, υ^′, константой Липшица для υ^′, g (но не g^′), т.е. можно L и

K взять общими для всех n. Далее, если Y, Z - решение (7), то поскольку G(ϕ(s))ϕ^′(s) =

= 0, можно указать константы A и a такие, что при |t| ≤ A выполняется неравенство

∥G(Y (t))Z(t)∥ ≤ a|t|. Окончательно оценки (11) получаются после применения к сумме

F^′ +

+ G следующего утверждения.

Лемма. Пусть f : Rⁿ → Rⁿ, r : Rⁿ → Rⁿ, x и y - соответственно решения задач Коши

Ż = f(z), z(0) = x⁰

Ż = f(z) + r(z), z(0) = x⁰

на промежутке [-A,A]. Функция f липшицева в достаточно большой окрестности образа

x: ∥f(z₁)-f(z₂)∥ ≤ L∥z1 -z₂∥, для r(y) выполняется неравенство ∥r(y(t))∥ ≤ a|t|. Тогда на

промежутке [-A, A] выполняется неравенство ∥x(t) - y(t)∥ ≤ ct², где c = c(a, A, L).

Доказательство. Проводится аналогично доказательству теоремы 4 из книги [6, гл. 1].

Пусть z = x - y, тогда Ż = f(x) - f(y) - r(y). Умножив на z, получим

1 d

∥z∥² = (f(x) - f(y))z - r(y)z.

2 dt

В силу предположений о свойствах f и r имеем неравенство

1 d

∥z(t)∥² ≤ L∥z(t)∥² + a|t|∥z(t)∥,

2 dt

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ ЗАДАЧАХ

427

после сокращения которого на ∥z(t)∥ получим d∥z(t)∥/dt ≤ L∥z(t)∥+a|t|. Умножив последнее

неравенство на e^-Lt и проинтегрировав в промежутке [0, t], будем иметь соотношения

∫t

∫

(e^-Lτ ∥z(τ)∥)dτ ≤ a τe^-Lτ dτ, e^-Lτ ∥z(t)∥ ≤ -

te^-Lτ -

e^-Lτ +

L²

или

(

)

∥z(t)∥ ≤ -

1 + Lt +

L²t²

L²

Таким образом, ∥z(t)∥ ≤ ct², где c ≤ ae^LA/2. Аналогично оцениваем ∥z(t)∥ для отрица-

тельных t, проводя интегрирование по промежутку [t, 0]. Лемма доказана.

Теорема 1 доказана.

Замечание 1. Отметим, что условия гладкости функции v не могут быть ослаблены.

Так, например, для поля v(x₁, x₂) = (x3/22, 0) из каждой точки вида (p, 0) (p < 0) в начало

координат ведет несколько траекторий (см. [7]).

3. Множество разреза. Если через заданную точку фазовой плоскости проходят две

траектории с одинаковыми значениями функционала, то указанная точка отсекает от тра-

ектории неоптимальную часть. Дадим точную формулировку. Пусть процессы (x, u),

(x, u)

являются экстремалями, определены на промежутках [t₀, t₁],

t₀,

t₁] соответственно, причём

∫t₁

t₀ <

t₀ < t₁, x

t₀) = x

t₀), u

t₀) = u

t₀) и

(1 + α∥u²(t)∥) dt =

t₁ (1 + α∥u²(t)∥)dt. Тогда

t₀

процесс (x, u) на промежутке [t₀, t₁] не оптимален. Действительно, определим процесс (x, u)

на промежутке [t₀,

t₁], положив

x = x,

û=u для t<

t₀,

x = x,

û = ũ для

t₀ ≤ t ≤

t₁.

Значение функционала J для обоих процессов одинаково. Но процесс (x, û) имеет разрыв-

ное управление, а оптимальный процесс, в силу системы (2), имеет непрерывное управление,

поэтому (x, û) не оптимален. Следовательно, не оптимален и (x, u). Таким образом, точка

t₀) отделяет от траектории экстремали неоптимальную часть. Такие точки называют точ-

ками разреза, поиск которых связан с решением следующего уравнения.

Запишем задачу (2), переобозначив (ψ₁, ψ₂) = (x₃, x₄), в виде

= f(X), X(0) = ϕ(s),

(12)

где f : R⁵ → R⁵, ϕ(s) = (0, 0, 0, b cos s, b sin s).

Рассмотрим отображения

Ψ(t, s) = (x₀(t, s), s), Φ(t, s) = (x₁(t, s), x₂(t, s)),

где X(t, s) = (x₀, . . . , x₄)(t, s) - решение задачи (12); g = ΦΨ-1 (отображение Ψ-1 определено,

поскольку

x₀ > 0).

Если g(x₀, τ) = g(x₀, s), τ = s + 2πk, k ∈ Z, то g(x₀, τ) - точка разреза.

Тройку (x₀, τ, s) назовём параметрами разреза. Саму точку g(x₀, τ) назовём правильной,

если два параметра из тройки (x₀, τ, s) являются функцией третьего, причём производные по

третьему параметру отличны от нуля. Кроме того, матрица Φ^′ невырождена на полуинтервале

вдоль траектории между точкой разреза и финальной точкой.

Предельную траекторию для точек разреза, для которой параметры имеют вид (x₀, τ, τ),

назовём особой.

Замечание 2. Отметим, что на траектории экстремали может находиться целый набор то-

чек разреза. Из всей указанной совокупности следует выбрать точку, ближайшую к финаль-

ной, а остальные точки интереса не представляют, поскольку находятся на неоптимальной

части траектории.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

428

НИКОЛЕНКО

Совокупность точек разреза, обладающих указанным в замечании свойством, образуют

множество разреза. Множество разреза рассматриваемых задач изучалось в работах [7-9].

В работе [9] предложена конструкция для численного вычисления множества разреза.

Рассмотрим примеры.

Пример 1. Задача быстродействия с полем v(x₁, x₂) = (x²², 0), α = 0.

Для s ∈ (-π/2, π/2) траектории экстремалей представляют собой “синусоиды”. Из всей

траектории оптимальной может быть лишь последняя полуволна, поскольку начало полувол-

ны - точка на левой полуоси Ox₁, которая является точкой разреза, образуемой пересечением

“синусоиды” с “синусоидой”, симметричной ей относительно оси Ox₁.

Для s ∈ [-π, -π/2]

^⋃ [π/2, π] траектории экстремалей представляют собой кривые, не пе-

ресекающиеся между собой (кривые 12 -16 на рисунке). Особой является точка

√

(-π/

v^′′(0),0) = (-π/

2,0).

Параметры точек разреза могут быть записаны в виде (α(τ), τ, -τ), где τ ∈ (0, π/2), |α(τ)| -

время перемещения по соответствующей полуволне. Производная α^′(τ) < 0, lim α(τ) =

τ→0

√

= -π/

2, lim α(τ) = -∞.

τ→π/2

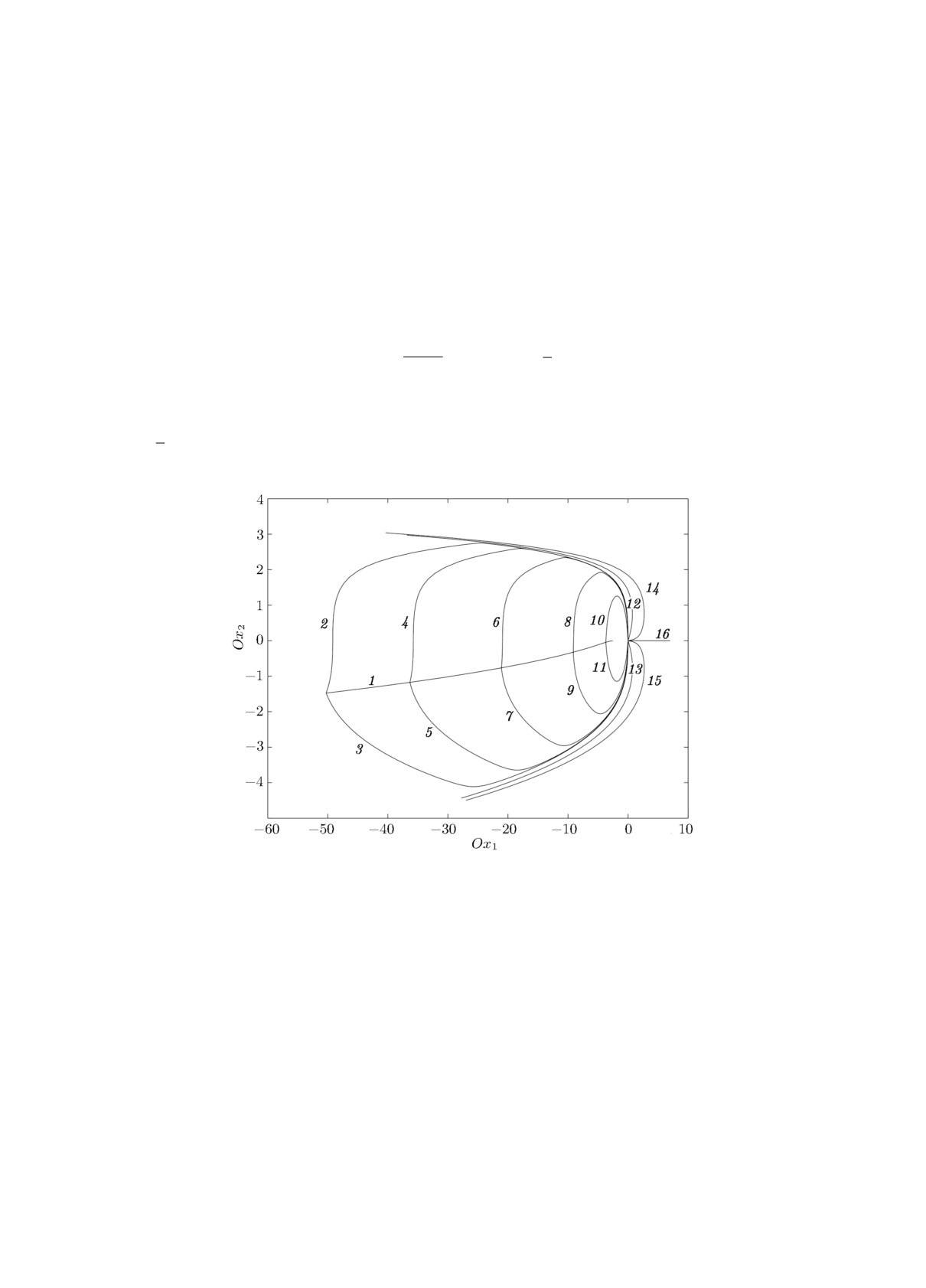
Рисунок. Траектории экстремалей для разных s.

Пусть Ω - часть полосы в пространстве R² :

Ω = {(t,s): t ≤ 0, если s ∈ [-π,-π/2]

^⋃ [π/2, π]; α(s) ≤ t ≤ 0, если s ∈ (-π/2, π/2)}.

Отображение g переводит область Ω в R², причём

g(0, s) = (0, 0), g(t, -π) = g(t, π), g(α(τ), -τ) = g(α(τ), τ)

для 0 < τ < π/2.

Во внутренней части множества Ω отображение g взаимно-однозначно. Введём в Ω отно-

шение эквивалентности, cчитая z₁ ∼ z₂, если g(z₁) = g(z₂). Тогда, поскольку g открыто на

Ω и согласовано с эквивалентностью, оно определяет гомеоморфизм g фактор-пространства

Ω в R². Кроме того, отображение (·)₁ - проекция на первую координату, также согласова-

но с эквивалентностью. Поэтому отображение ω = (g-1)₁ непрерывно. Величина ω(x) есть

время перемещения в начало координат по траектории экстремали.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ ЗАДАЧАХ

429

Пример 2. Рассмотрим задачу быстродействия с полем

Таблица. Значения параметров

задачи быстродействия

{

(x²², 0),

если x₂ < 0,

№ Время t Значение ϕ

v(x₁, x₂) =

α = 0.

(x²² + 0.1x⁶², 0), если x₂ ≥ 0,

Множество разреза

[-7, 0]

-1.55

[-7, 0]

1.51

Вычисления производились для t ∈ [-7, 0] (таблица).

[-6.4, 0]

-1.54

Для значений s ∈ [π/2, 3π/2] траектории экстремалей

[-6.4, 0]

1.49

(кривые 12 -16 на рисунке) не пересекают других траекто-

[-5.5, 0]

-1.52

рий. Для значений s ∈ [-π/2, π/2] траектории экстремалей

[-5.5, 0]

1.45

представляют собой деформированные “синусоиды”. Часть из

[-4.3, 0]

-1.44

точек пересечения “синусоид” между собой и составляют мно-

[-4.3, 0]

1.34

жество разреза, которое на рисунке представлено кривой 1.

[-3.1, 0]

-1.05

Время перемещения от точки разреза до начала координат

[-3.1, 0]

0.98

по траекториям 2 -3, . . . , 10 -11 одинаково. Множество раз-

[-3.5, 0]

реза √остоит из правильных точек. Особой является точка

[-5, 0]

(-π/

2, 0), параметры разреза могут быть записаны в виде

[-5.5, 0]

[-7, 0]

(α(τ), β(τ), τ). Согласно проведённым вычислениям опреде-

[-7, 0]

лим область Ω как часть полосы в R², положив

⎧

⎨(t, s): - 7 ≤ t ≤ 0, если s ∈ [-π,-1.55]

^⋃ [1.51, π],

Ω=

(t, s): α(s) ≤ t ≤ 0, если s ∈ [0, -1.51],

^⎩(t, s): α(τ) ≤ t ≤ 0, если s = β(τ), τ ∈ [0, -1.51].

Как и в предыдущем примере, введём в Ω отношение эквивалентности, полагая, что

z₁ ∼ z₂, если g(z₁) = g(z₂). Получаем гомеоморфизм g фактор-пространства

Ω на область

G в R². Отображение (·)₁ - проекция на первую координату, также согласовано с эквива-

лентностью. Поэтому на G определена и непрерывна величина ω = (g-1(x))₁.

4. Оптимальность траекторий. Установим, что при выполнении некоторых условий

траектории экстремалей, не содержащие точек разреза, оптимальны.

Пусть t₀ < 0 - некоторое число, X(t, s) - решение системы (12). Для каждого s ∈ [-π, π]

определим t(s)

(≥t₀) так, что (x₁(t(s), s), x₂(t(s), s)) - точка разреза либо особая точка, а

если таковых нет, то полагаем t(s) = t₀.

Положим

Ω = {(t,s): t(s) ≤ t ≤ 0,

-π ≤ s ≤ π}.

−→ (x₁(t, s), x₂(t, s)). Бу-

дем предполагать выполненными следующие условия:

- на множествеΩ = {(t, s): t(s) < t < 0, -π ≤ s ≤ π} матрица Φ′ не вырождена;

- множество разреза состоит из правильных точек;

- функция ω = (ΨΦ-1)₁, где (·)₁ обозначает первую компоненту, ω(x₁, x₂) = x₀, опреде-

лённая на Φ(Ω), доопределяется на Φ(Ω) по непрерывности;

- множество с ∥ψ∥ = ∥(x₃, x₄)∥ = 2α - кусочно-гладкая кривая.

Полагаем, что выполняется следующая априорная оценка: пусть x₀ ∈ Φ(Ω) и управление

u переводит x₀ в 0, x - соответствующая траектория, тогда J(x, u) ≥ c.

Теорема 2. Пусть s ∈ [-π, π] и -ω(x₁(t(s), s), x₂(t(s), s)) < c. Тогда оптимальна траек-

тория (x₁(t,s),x₂(t,s)), где t(s) ≤ t ≤ 0.

Доказательство. Установим, что в области Φ(Ω) выполняется (исключая множество раз-

реза и множество, где |ψ∥ = 2α) неравенство Беллмана ω^′ · (f₁, f₂) ≤ f₀, а вдоль траектории

(x₁(t, s), x₂(t, s)), где t(s) < t < 0, выполняется уравнение Беллмана ω^′ · (f₁, f₂) = f₀. Как

показано в [10, c. 241], этого достаточно для оптимальности траектории.

Для доказательства нам потребуются уравнения в вариациях, соответствующие уравнени-

ям (2). Запишем их.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

430

НИКОЛЕНКО

При x²³ + x²⁴ ≥ 4α² имеем

x₃

x₄

x₀ = 1 + α,

x₁ = v₁(x₁,x₂) +

√

x₂ = v₂(x₁,x₂) +

√

x²³ + x²⁴

x²³ + x²

x₃ = -x₃∂₁v₁ - x₄∂₁v₂,

x₄ = -x₃∂₂v₁ - x₄∂₂v₂,

x²⁴y₃

x₃x₄y₄

y₀ = 0,

y₁ = ∂₁v₁y₁ + ∂₂v₁y₂ +

√

x²³ + x²⁴

x²³ + x²

x₃x₄y₃

x²³y₄

y₂ = ∂₁v₂y₁ + ∂₂v₂y₂ -

√

y₃ = ... ,

y₄ = ...

x²³ + x²⁴

x²³ + x²

При x²³ + x²⁴ < 4α² имеем

x²³ + x²⁴

x₃

x₄

x₀ = 1 +

x₁ = v₁(x₁,x₂) +

x₂ = v₂(x₁,x₂) +

4α

2α

x₃ = -x₃∂₁v₁ - x₄∂₁v₂,

x₄ = -x₃∂₂v₁ - x₄∂₂v₂,

y₀ =

(x₃y₃ + x₄y₄),

y₁ = ∂₁v₁y₁ + ∂₂v₁y₂ +

y₃,

2α

y₂ = ∂₁v₂y₁ + ∂₂v₂y₂ +

y₄,

y₃ = ... ,

y₄ = ...

2α

Запишем выражение для ω^′. Значения функций берутся в точках фазового пространства,

соответствующих значениям t, s:

ω^′ = (Ψ^′)₁ · (Φ^′)-1 = (f₀,y₀)(Φ^′)-1,

здесь (·)₁ - первая строка матрицы

(

)-1

(

)-1

(

)

∂_tx₁

∂_sx₁

f₁

y₁

y₂

-y₁

(Φ^′)-1 =

∂_tx₂

∂_sx₂

f₂

y₂

-f₂

f₁

где Δ = f₁y₂ - f₂y₁,

(

)

(

))

f₀

f₂

f₁

f₀

ω^′ =

(f₀y₂ - y₀f₂, -f₀y₁ + y₀f₁) =

det

, det

y₀

y₂

y₁

y₀

Таким образом, согласно формулам Крамера ω^′ является решением системы уравнений

(

)

(

)

(

)

f₁

f₂

f₀

z₁

+z₂

y₁

y₂

y₀

в частности, ω^′ · f = f₀ вдоль экстремалей. Далее увидим, что ω^′ = ψ, где ψ = ψ(t, s) -

компоненты экстремали. Согласно принципу максимума Понтрягина функция H = ψ₁f₁ +

+ ψ₂f₂ - f₀ вдоль экстремалей равна нулю. Таким образом, функция ψ является решением

первого уравнения последней системы. Для проверки верности второго уравнения заметим,

что при t = 0

ψ₁y₁ + ψ₂y₂ - y₀ = 0.

Вычислим d(ψy - y₀)/dt. Если ∥ψ∥ ≥ 2α

((ψ₁, ψ₂) := (x₃, x₄)), то

[

)

)]

⁽x²⁴y₃ - x₃x₄y₄

⁽-x₃x₄y₃ + x²³y₄

ψy + ψ y - y₀ = -ψv^′y + ψv^′y + x₃

√

+x₄

√

= 0.

x²³ + x²⁴

x²³ + x²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023

О НЕКОТОРЫХ ЭКСТРЕМАЛЬНЫХ ЗАДАЧАХ

431

Если ∥ψ∥ ≤ 2α, то

[

]

ψy + ψ y - y₀ = -ψv^′y + ψv^′y +

x₃y₃ +

x₄y₄

(x₃y₃ + x₄y₄) = 0.

2α

Таким образом, вдоль экстремали ψy - y₀ - константа, и она равна нулю.

В силу принципа максимума функция H вдоль траектории принимает максимальное зна-

чение по u, поэтому ω^′(x)f(x, u) ≤ f₀(x, u). Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Арутюнов А.В., Магарил-Ильяев Г.Г., Тихомиров В.М. Принцип максимума Понтрягина. Доказа-

тельство и приложения. М., 2006.

2. Bin Li, Chao Xu, Kok Lay Teo, Jian Chu. Time optimal Zermelo’s navigation problem with moving and

fixed obstacles // Appl. Math. and Comput. 2013. V. 224. P. 866-875.

3. Chertovskih R., Karamzin D., Khalil N.T., Pereira F.L. An indirect numerical method for a time-optimal

state-constrained control problem in a steady two-dimensional fluid flow // Proc. of the 2018 IEEE

Oceanics Engineering Society Autonomous Underwater Vehicle Sympos. 2019. P. 1-6.

4. Chertovskih R., Karamzin D., Khalil N.T., Lobo Pereira F. Regular path-constrained time-optimal

control problems in three-dimensional flow fields // Eur. J. of Control. 2020. V. 56. P. 98-106.

5. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М., 1979.

6. Зубов В.И. Теория колебаний. М., 1979.

7. Николенко П.В. О наискорейших перемещениях в поле скоростей // Дифференц. уравнения. 2011.

Т. 47. № 5. С. 738-745.

8. Николенко П.В. Множество неоднозначности и задача о наискорейших перемещениях в поле ско-

ростей // Дифференц. уравнения. 2014. Т. 50. № 3. С. 372-381.

9. Николенко П.В. О множестве разреза в некоторых экстремальных задачах, связанных с перемеще-

нием в поле скоростей // Изв. вузов. Северо-Кавказский регион. Естеств. науки. 2017. № 4. С. 37-44.

10. Болтянский В.Г. Математические методы оптимального управления. М., 1969.

Ростовский государственный

Поступила в редакцию 26.09.2019 г.

экономический университет

После доработки 17.11.2022 г.

Принята к публикации 20.01.2023 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№3

2023