ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 4, с. 563-566

КРАТКИЕ СООБЩЕНИЯ

УДК 517.929

АСИМПТОТИКА РЕЛАКСАЦИОННЫХ ЦИКЛОВ

В ОБОБЩЁННОМ ЛОГИСТИЧЕСКОМ УРАВНЕНИИ

С ЗАПАЗДЫВАНИЕМ

Асимптотическими методами исследованы решения модифицированного логистического

уравнения с запаздыванием, содержащего большой параметр. Приведён результат о суще-

ствовании и устойчивости релаксационного цикла.

DOI: 10.31857/S037406412304012X, EDN: AOJNDZ

Введение. Исследованию логистического уравнения с запаздыванием

u = λ[1 - u(t - 1)]u

(1)

посвящено множество литературы (см., например, [1-7]). Принято считать, что функция u(t)

описывает динамику изменения плотности популяции, поэтому u(t) ≥ 0. Параметр λ называ-

ют мальтузианским коэффициентом. При значениях λ близких к π/2 наблюдается бифур-

кация Андронова-Хопфа. Асимптотика соответствующего цикла приведена в [7, 8]. При λ ≫ 1

в (1) имеется устойчивый релаксационный цикл u⁰(t, λ) с периодом T⁰(λ). Его асимптотика

рассмотрена в статье [9]. Отметим, что все неотрицательные решения (1) при всех достаточно

больших t удовлетворяют оценке u(t) ≤ exp λ.

В настоящей работе предложены результаты исследования более общего уравнения

u = λ[1 - F(u(t - 1))]u.

(2)

Ограничимся рассмотрением двух наиболее значимых случаев, иллюстрирующих отличия

в динамике уравнения (2) от (1). В одном из них предполагаем, что lim F (u) = ∞, а в другом

u→∞

lim F (u) = A < ∞ (A > 1); функцию F (u) считаем монотонно возрастающей.

u→∞

1. Первый случай. Пусть F (u) = u^α, α > 0. В (2) произведём замену u^α = v и получим

классическое логистическое уравнение с запаздыванием

v = αλ[1 - v(t - 1)]v.

(3)

При выборе подходящим способом параметра λ решениями уравнения (3) могут быть как

устойчивые гармонические колебания (α ∼ λ-1π/2), так и релаксационные колебания (при

α ≫ 1). При αλ < π/2 состояние равновесия u₀ ≡ 1 асимптотически устойчиво. Отметим

ещё (см. [4, 5, 10]), что при αλ ≤ 37/24 все положительные решения уравнения (3) стремятся

к единице при t → ∞.

Интересно рассмотреть случай, когда F (u) = γ ln u, где γ > 0. После замены u = exp v

приходим к линейному уравнению

v = λ[1 - γv(t - 1)].

(4)

При 0 < λγ < π/2 все решения (4) стремятся к состоянию равновесия u₀ ≡ γ-1, а значит,

все решения (3) при t → ∞ стремятся к состоянию равновесия exp(γ-1). При λγ > π/2

решения (4) (и (3)) неограничены при t → ∞. Если же λγ = π/2, то для (4) и (3) имеется

устойчивое однопараметрическое семейство периодических решений v = γ-1 + c cos(tπ/2 + ϕ),

563

9^∗

564

КАЩЕНКО

u = exp(γ-1 + ccos(tπ/2 + ϕ)). Обратим внимание, что в случае когда F(u) = γ ln(1 + u) все

решения уравнения (2) ограничены при t → ∞.

2. Второй случай. В качестве примера для иллюстрации динамических особенностей (2)

фиксируем функцию

F (u) = u(1 + αu)-1, α = A-1 < 1.

(5)

Основное предположение состоит в том, что параметр λ является достаточно большим (λ ≫

≫ 1). Ниже медленно осциллирующим называется такое решение уравнения (2), у которого

расстояние между соседними корнями функции u(t) - 1 = 0 больше, чем время запаздыва-

ния, равное единице. Отметим, что (также как и для (1)) для (2) и (5) имеются и быстро

осциллирующие решения. Их асимптотику при λ ≫ 1 здесь не приводим, поскольку все они

неустойчивы.

Решение u(t, τ) уравнения (3) с начальным условием, заданным в момент t = τ, имеет вид

[ ∫ t

]

u(t, τ) = u(τ, τ) exp λ

(1 - F (u(s - 1, τ))) ds .

(6)

Для того чтобы сформулировать основной результат, введём обозначение t₀ = 1+(A-1)-1.

Теорема. Пусть выполнено равенство (5). Тогда при всех достаточно больших λ урав-

нение (2) имеет асимптотически орбитально устойчивое медленно осциллирующее перио-

дическое решение u₀(t,λ) с периодом T₀(λ), для которого справедливы оценки

⎧

⎨exp(λt(1 + o(1))),

t ∈ [0,1],

u₀(t,λ) =

exp[λ(1 + (1 - A)(t - 1))(1 + o(1))],

t ∈ [1,t₀ + 1],

T₀(λ) = A²(A-1)-1+o(1).

⎩

exp[λ(t - A - t⁰¹)(1 + o(1))],

t ∈ [t₀ + 1,T₀(λ)],

Доказательство. Фиксируем произвольно значение δ ∈ (0, 1/2). Обозначим через S мно-

жество таких функций ϕ(s) ∈ C[-1,0], для которых выполнены условия

ϕ(0) = 1,

0 ≤ ϕ(s) ≤ exp(λδs) для s ∈ [-1,0].

(7)

Исследуем асимптотику всех решений u(t, ϕ) с начальными условиями ϕ(s) ∈ S, задан-

ными при t = 0. Отметим, что все фигурирующие выражения вида o(1) выполняются равно-

мерно по всем ϕ(s) ∈ S. Положим в формуле (6) τ = 0 и используем соотношение (7). Тогда

на отрезке t ∈ [0, 1] имеем асимптотическое равенство

u(t, ϕ) = exp(λ(1 + o(1))t).

Затем положим в (6) τ = 1, тогда при t ∈ [1, t₀ + 1] приходим к формуле

u(t, ϕ) = exp[λ(1 + (1 - A)(t - 1))(1 + o(1))].

(8)

Ниже через t₁(ϕ) и t₂(ϕ) будем обозначать первый и второй положительные корни урав-

нения u(t, ϕ) = 1. Отметим, что для t₁(ϕ) выполнено соотношение t₁(ϕ) = t₀ + o(1). При

t ∈ [t₁(ϕ) + 1,t₂(ϕ)] положим в (6) τ = t₁(ϕ) + 1 и из (8) приходим к равенству

u(t, ϕ) = exp[λ(1 + o(1))(1 - A + t - (t₁(ϕ) + 1))].

Отсюда получаем, что t₂(ϕ) = A²(A - 1)-1 + o(1).

Оператор последования Π введём по правилу

Π(ϕ(s)) = u(s + t₂(ϕ), ϕ).

В итоге

Π(ϕ(s)) ∈ S и ΠS ∈ S,

(9)

где S - множество функций, удовлетворяющих условиям (7).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№4

2023

АСИМПТОТИКА РЕЛАКСАЦИОННЫХ ЦИКЛОВ

565

Воспользуемся общими утверждениями (см., например, [11, с. 227-236]) о существовании

неподвижной точки отображения множества в себя. Тогда из (9) следует существование в S

неподвижной точки ϕ₀(s) оператора Π. Тем самым функция u₀(t, λ) = u(t, ϕ₀) является

периодической с периодом T₀(λ) = t₂(ϕ₀). Простое, но громоздкое обоснование устойчивости

решения u₀(t, λ) здесь не приводим. Детально необходимые для этого построения изложены

в монографии [10, с. 128-136]. Теорема доказана.

Заметим, что явная формула (5) приведена лишь для примера. Утверждение теоремы и её

доказательство сохраняют силу и для произвольной положительной функции F (u), удовле-

творяющей предельному равенству F (u) → A при u → ∞.

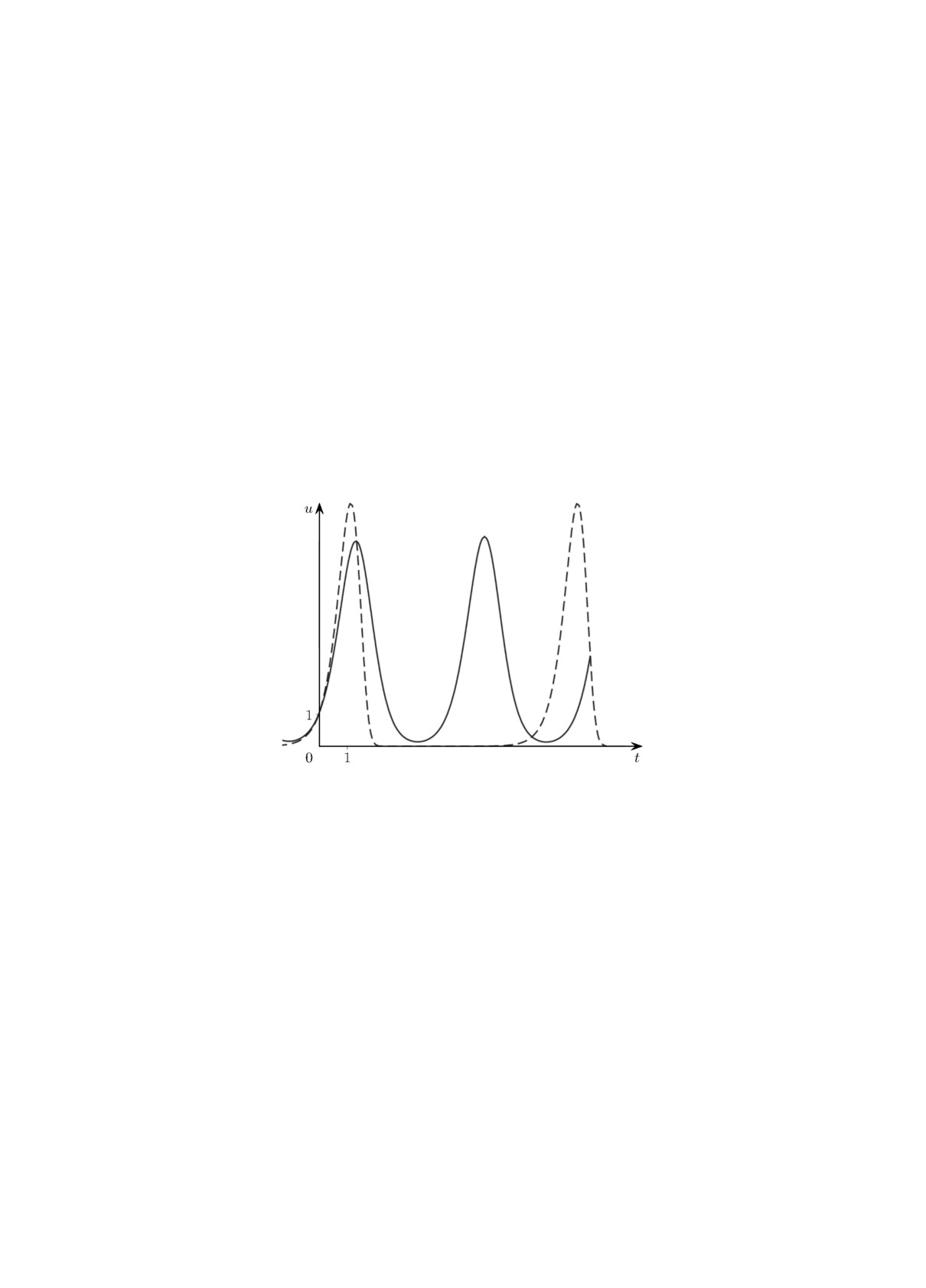
Отметим наиболее важные отличия при λ ≫ 1 цикла u₀(t, λ) уравнения (2) при условии

(5) и релаксационного цикла u⁰(t, λ) уравнения (1). Значения их максимумов примерно одни

и те же, а значения их минимумов и периодов T₀(λ) и T⁰(λ) отличаются существенно:

minu0(t,λ) = exp(λ(1 - A + o(1))), min u0(t,λ) = exp(- exp(λ(1 + o(1)))),

T₀(λ) = A²(A - 1)-1 + o(1), T⁰(λ) = λ-1(1 + o(1))exp λ.

На рисунке приведены графики функций u₀(t, λ) и u⁰(t, λ) при λ = 3, α = 0.4.

Рисунок. Графики функций u0(t, λ) (сплошная кри-

вая) и u⁰(t, λ) (штриховая).

Заключение. В математической экологии функция F (u(t - 1)) в уравнении (2) харак-

теризует сопротивление внешней среды. Нами показано, что ограничение на эту функцию

F (u) ≤ A в экстремальной ситуации при λ ≫ 1 способствует стабилизации колебаний. Име-

ется в виду, что колебания становятся “безопаснее”: наименьшее значение для u₀(t, λ) суще-

ственно больше, чем u⁰(t, λ), период T₀(λ) для u₀(t, λ) существенно меньше, чем период

T⁰(λ) для u⁰(t,λ). Отметим ещё, что в статье [12] приведены результаты динамики решений

для некоторых уравнений с запаздыванием, обобщающих уравнение (1).

Работа выполнена при финансовой поддержке Российского научного фонда (проект 21-71-

30011).

СПИСОК ЛИТЕРАТУРЫ

1. Murray J.D. Mathematical Biology II. Spatial Models and Biomedical Applications. Interdisciplinary

Applied Mathematics. V. 18. New York, 2003.

2. Wu J. Theory and Applications of Partial Functional Differential Equations. Applied Mathematical

Sciences. V. 119. New York, 1996.

3. Kuang Y. Delay Differential Equations with Applications in Population Dynamics. Mathematics in

Science and Engineering. V. 191. Boston, 1993.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№4

2023

566

КАЩЕНКО

4. Wright E.M. A non-linear difference-differential equation // J. für die reine und angewandte Mathematik.

1955. Bd. 194. S. 66-87.

5. Кащенко С.А., Логинов Д.О. Оценка области глобальной устойчивости состояния равновесия ло-

гистического уравнения с запаздыванием // Изв. вузов. Математика. 2020. № 9. C. 39-55.

6. May R.M. Stability and Complexity in Model Ecosystems. Princeton, 1974.

7. Кащенко С.А. Бифуркации в логистическом уравнении с запаздыванием и малыми возмущениями

// Изв. вузов. Математика. 2020. № 10. C. 47-64.

8. Oster G., Guckenheimer J. Bifurcation phenomena in population models // The Hopf Bifurcation and

Its Applications. Appl. Math. Sci. New York, 1976. V. 19. P. 327-353.

9. Kashchenko S.A. Asymptotics of the solutions of the generalized hutchinson equation // Automatic

Control and Computer Sciences. 2013. V. 47. P. 470-494.

10. Кащенко С.А. Динамика моделей на основе логистического уравнения с запаздыванием. М., 2020.

11. Edwards R.E. Functional Analysis. Theory and Applications. New York, 1965.

12. Кащенко С.А. Периодические решения нелинейных уравнений, обобщающих логистические урав-

нения с запаздыванием // Мат. заметки. 2017. Т. 102. С. 216-230.

Региональный научно-образовательный

Поступила в редакцию 21.01.2022 г.

математический центр

После доработки 17.03.2023 г.

“Центр интегрируемых систем”, г. Ярославль,

Принята к публикации 22.03.2023 г.

Ярославский государственный университет

имени П.Г. Демидова

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№4

2023