ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 5, с.569-581

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.929+517.926

АСИМПТОТИЧЕСКИЕ СВОЙСТВА ОДНОГО КЛАССА

СИСТЕМ С ЛИНЕЙНЫМ ЗАПАЗДЫВАНИЕМ

Получены достаточные условия асимптотической устойчивости линейных систем диффе-

ренциальных уравнений, содержащих линейное запаздывание. На основании этих условий

исследованы некоторые системы линейных дифференциальных уравнений, при этом для

одной из них проведена стабилизация на бесконечном промежутке времени.

DOI: 10.31857/S0374064123050011, EDN: CWEAQT

Введение. Будем изучать асимптотические свойства некоторых линейных систем диффе-

ренциальных уравнений с постоянным запаздыванием, к которым приводятся заменой аргу-

мента системы с линейным запаздыванием вида

dx(t)/dt = A(t)x(t) + B(t)x(μt), μ = const,

0 < μ < 1, t ≥ t₀ > 0.

(1)

Здесь A(t), B(t) - непрерывно дифференцируемые m×m-матрицы, x(t) - m-мерная вектор-

функция времени (аргумента) t, запаздывание имеет вид (1 - μ)t. Решение определено в

начальный момент времени t₀ вектор-функцией φ(η), η ∈ [μt₀, t₀].

Системы с линейным запаздыванием встречаются в задачах механики, физики [1, c. 96] и

биологии. Например, при исследовании процесса колебаний токоприёмника движущегося ло-

комотива при взаимодействии с контактным проводом (при учёте воздействия эластичной опо-

ры) в работе [2] задача сводится к исследованию поведения решения линейного неоднородного

дифференциального уравнения первого порядка с линейным запаздыванием. Более сложная

модель, приводящая к исследованию системы четвёртого порядка, предложена в работе [3].

Задача прохождения токоприёмником эластичной опоры имеет практическое применение в

случае изучения устойчивости колебаний движущегося токоприёмника и определения изно-

са контактного провода при различных скоростях движения локомотива, а также в условиях

изменяющейся величины силы нажатия полоза токоприёмника на контактный провод. Учёт

эффекта последействия важен для правильного качественного и количественного описания

данных процессов.

Линейные системы дифференциальных уравнений данного типа, исследуемые в этих ра-

ботах, как правило, имеют постоянные коэффициенты в правой части. При неустойчивости

таких систем возникает проблема их стабилизации на бесконечном промежутке времени. Ста-

билизации подобных систем посвящены работы [4-6]. Следующим этапом является получение

достаточных условий асимптотической устойчивости и построение на этом основании алгорит-

ма стабилизации для некоторых систем с переменными коэффициентами.

Будем рассматривать линейное нормированное пространство R^m, в котором норму вектора

w = {w_j}^т (здесь w_j, j = 1,m, - компоненты вектора w, а^т - знак транспонирования)

∑_m

определим, например, равенством ∥w∥ =

|w_j |. (Норму матрицы D = {d_ij }, i, j = 1, m,

j=1

∑

определим в соответствии с нормой вектора [7, c. 12]: ∥D∥ = max

|.) Решение системы

|d_ij

(1) с начальной функцией φ(η) обозначим через x(t, φ(η), t₀).

Приведём несколько определений, которые будут необходимы в дальнейшем (см. [1, c. 369;

8, c. 114]).

Определение 1. Решение x(t) системы (1), определённое кусочно-непрерывной началь-

ной вектор-функцией φ(η), называется устойчивым, если для любого

C > 0 существуют

569

570

ГРЕБЕНЩИКОВ, ЛОЖНИКОВ

постоянные

C) > 0 и t∗0 = t∗0

C) > 0 такие, что из условия sup∥φ(η)∥

C следует

неравенство sup∥x(t, φ(η), t0)∥

C для всех t₀ ≥ t∗0.

Определение 2. Если решение x(t,φ(η)), наряду с устойчивостью, обладает свойством

lim x(t, φ(η)) = 0, то решение асимптотически устойчиво.

t→∞

1. Получение достаточных условий асимптотической устойчивости для некото-

рых систем вида (1). Рассмотрим линейную систему (1). Сделаем в ней замену τ = ln(t/t₀)

и получим систему с постоянным запаздыванием σ [1, с. 100]:

dz(τ)/dτ = t₀ exp(τ)

A(τ)z(τ) +^B(τ)z(τ - σ)], σ = - ln(μ), σ > 0, τ ≥ 0,

z(η) = φ(t₀ exp(η)), η ∈ [μt₀, t₀],

A(τ) = A(t₀ exp(τ)),

^B(τ) = B(t₀ exp(τ)).

(2)

Начальная вектор-функция

φ(ξ), ξ ∈ [-σ, 0], определяет решение системы (2) в момент вре-

мени τ = 0.

Полагаем, что матрицы

A(τ),

^B(τ) достаточное число раз дифференцируемые и перио-

дические (периода σ). При этом для корней λ_j (τ) характеристического уравнения

det

A(τ) - λE) = 0

(здесь и далее E - единичная m × m-матрица) справедливы неравенства

Re (λ) < -2d, d = const, d > 0,

(3)

и, наряду с этим, для корней ρ_k(τ) характеристического уравнения

det

A-1(τ)^B(τ) - ρE) = 0

выполнены неравенства

|ρ_k(τ)| < γ, γ = const,

0 < γ < 1.

(4)

Чтобы эффективно использовать аппарат теории разностных систем и методов малого

параметра при производной, перейдём от системы (2) к счётной системе обыкновенных диф-

ференциальных уравнений, заданных на конечном промежутке времени τ ∈ [0, σ], полагая [1,

c. 102]

zn+1(τ) = z(τ + nσ), n ∈ N

^⋃ {0}.

Данная счётная система имеет вид

ε_ndzn+1(τ)/dτ = exp(τ)

A(τ)zn+1(τ) +^B(τ)z_n(τ)], ε_n = μⁿ/t₀, n ∈ N⋃ {0},

(5)

при граничных условиях

zn+1(0) = z_n(σ), z₀

φ(τ - σ).

(6)

Введём теперь норму вектор-функции w(τ) на отрезке [0, σ], полагая

∥w∥_σ = sup ∥w(τ)∥.

τ ∈[0,σ]

Далее зададим оператор сдвига T_τ,n следующим образом:

∫τ

exp(s)

T_τ,n(y) = Y0n+1(τ,0,ε_n)y(σ) +

Y0n+1(τ,s,ε_n)^B(s)y(s)ds,

(7)

ε_n

где Y0n+1(τ, s, ε_n) - матрица Коши системы без запаздывающих членов

ε_ndy0n+1(τ)/dτ = exp(τ

A(τ)y0n+1(τ),

0 ≤ τ ≤ σ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

АСИМПТОТИЧЕСКИЕ СВОЙСТВА НЕКОТОРОГО КЛАССА СИСТЕМ

571

Если определить норму оператора сдвига в соответствии с правилом [9, с. 504]

∥T_τ,n(y(s))∥

∥T_τ,n∥ = sup

∥y(s)∥

то при такой нормировке пространство вектор-функций становится пространством Банаха [9,

c. 510], обозначим его C_m.

Известно [10] (ввиду неравенства (3)), что при достаточно малых ε_n имеет место оценка

(

)

∥Y0n+1(τ, s, ε_n)∥ ≤ C₀ exp -

(exp(τ) - exp(s))

C₀ = const, C₀ > 1.

(8)

ε_n

Норма оператора T_τ,n равномерно ограничена числом

M = C₀(1 + b/d), b = max∥ B(τ)∥.

(9)

В банаховом пространстве определено произведение операторов, следовательно, решение

системы (5) можно представить в операторном виде

zn+1(τ) = T_τ,nz_n(s).

Поскольку оценка (9) является достаточно грубой и не позволяет судить об асимптотиче-

ском поведении решения системы (5), для того чтобы установить асимптотические свойства

данной системы (используя малый параметр ε_n), докажем сначала две леммы.

Лемма 1 (оценки на рост производных решения системы (5)). Производные znj)(τ), j =

= 1, 2k, при выполнении неравенства (3) и достаточной “гладкости” матриц

A(τ),

^B(τ)

удовлетворяют следующим (весьма грубым) оценкам роста:

∥z(j)n(τ)∥

C_j(t₀)^j qⁿ sup∥z₀(τ)∥, j = 1,2k,

C_j = const,

C_j > 1,

q= const,

q> 1.

(10)

Доказательство. Оценку для ∥zn+k(τ)∥ (считая начальной вектор-функцией величину

∥z_n(τ)∥) получаем из соотношения (9) (здесь q₀ = M). Рассмотрим теперь поведение величи-

ны ∥z^′n(τ)∥. Продифференцировав обе части системы (5), получим равенство

ε_nd²zn+1(τ)/dτ² = exp(τ)

A(τ)z′n+1(τ) +^B(τ)z^′n(τ)] +

+ exp(τ)

A(τ)zn+1(τ) +^B(τ)z_n(τ)] + exp(τ)

A^′(τ)zn+1(τ) +B′(τ)z_n(τ)]

или, с учётом (5),

ε_nd²zn+1(τ)/dτ² = exp(τ)[

A(τ) + O(ε_n))z′n+1(τ) +^B(τ)z^′n(τ) +

+(B′(τ)

A^′(τ

A-1(τ)^B(τ))z_n(τ)],

(11)

∑

при этом ряд_n ∥O(ε_n)∥ сходится. Запишем решение неоднородной системы (11) в интеграль-

ной форме [1, c. 328], считая неоднородностями члены, содержащие величины O(ε_n)z′n+1(τ),

^B(τ)z^′n(τ),

(B′(τ)

A^′(τ

A-1(τ)^B(τ))z_n(τ). Учитывая (7), имеем соотношение

∫τ

exp(s)

z′n+1(τ) = T_n,τ z^′n(τ) +

Yn+10(τ,s,ε_n)O(ε_n)z′n+1(s)ds +

ε_n

∫τ

exp(s)

Yn+10(τ,s,ε_n)(B′(s)

A^′(s

A-1(s)^B(s))z_n(s)ds.

(12)

ε_n

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

572

ГРЕБЕНЩИКОВ, ЛОЖНИКОВ

Рассмотрим интегралы в правой части (12). Очевидно, что первый интеграл допускает

представление O(ε_n)∥z′n+1(τ)∥_σ. Второй же интеграл в силу оценок (9) и (10) не превосходит

величины α∥z_n(τ)∥_σ, где α = C₀d-1∥B′(τ)

A^′(τ

A-1(τ)^B(τ)∥_σ. С учётом этих оценок из

(12) получаем

∥z′n+1(τ)∥_σ - O(ε_n)∥z′n+1(τ)∥_σ ≤ M∥z^′n(τ)∥_σ + α∥z_n(τ)∥_σ.

(13)

Очевидно, что в данном выражении величины O(ε_n)∥z′n+1(τ)∥_σ можно рассматривать как

“возмущения” по отношению к соответствующей однородной системе первого приближения.

Тогда (ввиду сходимости соответствующего ряда) фундаментальная матрица однородной сис-

темы Z′n+k,n допускает оценку [11, c. 71]



∏



∥Z′n+k,n∥ =^ (M + O(ε_j ))

L₁M^k,

L₁ = const,

L₁ > 1.

(14)

≤

j=n

Из (13), (14), используя формулу вариации постоянных [11, c. 23] (учитывая оценку роста для

∥z_n(τ)∥_σ), имеем неравенство

∥z′n+k(τ)∥_σ ≤L1M^k∥z^′n(τ)∥_σ + αL1M^k∥z_n(τ)∥_σ, k ∈ N.

(15)

Чтобы оценить рост величин ∥z^′n(τ)∥_σ , ∥zn(τ)∥σ (поскольку система (5) является системой

с ограниченной правой частью), применим формулу Гронуола-Беллмана [1, c. 73] и получим

оценку

∥z(τ)∥

β sup

φ(ξ)∥ exp

βτ),

β=t₀exp(nσ(a+b)), a=max

A(τ)∥.

(16)

Оценка (16) будет эффективной при не очень больших величинах t₀ (т.е. при t₀

T ). Далее,

как следует из работы [10], при больших t₀

T справедливо соотношение (9), следовательно,

в этом случае при всех 0 ≤ τ ≤ nσ имеет место экспоненциальная оценка

ln(M)

∥z(τ)∥ ≤ M exp

β₁τ)sup∥φ(s)∥,

β₁ =

(17)

И в том, и в другом случае получаем итоговую оценку (10) на рост решения ∥z_k(τ)∥ при

1 ≤ k ≤ n. Без ограничения общности считаем величину t₀ > 1. Далее рассмотрим поведение

величины ∥z^′k(τ)∥ при 1 ≤ k ≤ n. Из уравнения (5) имеем

t₀

∥z^′k(τ)∥_σ ≤

(a∥z_k(τ)∥_σ + b∥zk-1(τ)∥_σ), a = max

A(τ)∥.

μk+1

Используя последнее неравенство, получаем из (17) итоговую оценку для величины ∥z^′k(τ)∥_σ

(k > 1). Оценки для величин ∥znj)(τ)∥_σ получаются аналогично. Лемма доказана.

Лемма 2 (представление решения через его производные). Величины ∥znj)(τ)∥ для доста-

точно малых ε_n удовлетворяют разностным системам

z(j)n+1(τ) = (

A-1(τ)^B(τ) + O(ε_n))z(j)n(τ) + Yjn+1(τ,0,ε_n)z(j)n(σ) + Π^jj,n(τ,ε_n)z(j)n(0) +

+ F0j,n(τ)z_n(τ) + Π0j,n(τ,ε_n)z_n(0) + F1j,n(τ)z^′n(τ) + Π1j,n(τ,ε_n)z^′n(0) +

... + Fj-1j,n(τ)z(j-1)n(τ) + Πj-1j,n (τ,ε_n)z(j-1)n(0) + O(ε_n)z(j+1)n(τ) + O(ε_n)Πj+1j,n (τ,ε_n)z(j+1)n(0) +

+ ε_nO(ε_n)z(j+2)n(τ) + ε_nO(ε_n)Πj+2j,n (τ,ε_n)z(j+2)n(0) +

... + (ε_n)k-2O(ε_n)z(j+k-1)n(τ) + (ε_n)k-2O(ε_n)Πj+k-1j,n(τ,ε_n)z(j+k-1)n(0) +

+ (t₀)^j O((μ^k q)ⁿ)∥z₀(τ)∥_σ, j = 0, k.

(18)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

АСИМПТОТИЧЕСКИЕ СВОЙСТВА НЕКОТОРОГО КЛАССА СИСТЕМ

573

Здесь F^jl (τ, n) - равномерно ограниченные m × m-матрицы, μ^k q ≤ p, p = const, 0 < p < 1,

= 0, j - 1; матрицы Yjn+1(τ, 0, ε_n), Π^rj,n(τ, ε_n), r = 0, j + k - 1, допускают оценку, анало-

гичную (8).

Отметим, что натуральное число k (которое мы выбираем из приведённого условия) озна-

чает существование и непрерывность производных до 2k-го порядка включительно.

Докажем вначале асимптотическое представление для функций z_n(τ). Как следует из (7),

решение исследуемой системы представимо в интегральной форме

∫τ

zn+1(τ) = Y0n+1(τ,0,ε_n)z_n(σ) + Y0n+1(τ,s,ε_n)^B(s)z_n(s)ds.

(19)

Интегрируя по частям интеграл в правой части данного равенства, получаем

∫τ

I_n =

A-1(τ)^B(τ)z_n(τ)

A-1(0)Y0n+1(τ,0,ε_n)^B(0)z_n(0) +

A-1(s))^′Y0n+1(τ,s,ε_n)^B(s)z_n(s)ds +

∫τ

∫

A-1(s)Y0n+1(τ,s,ε_n)B′(s)z_n(s)ds +

A-1(s)Y0n+1(τ,s,ε_n)^B(s)z^′n(s)ds.

(20)

Рассмотрим последний интеграл I^′n в правой части равенства (20), содержащий величину

z^′n(s). Интегрируя его по частям аналогично интегралу I_n, получаем соотношение

I^′n = O(ε_n)z^′n(τ) + Y0n+1(τ,0,ε_n)O(ε_n)z^′n(0) +

∫τ

∫

+ O(ε_n)Y0n+1(τ,s,ε_n)z^′n(s)ds + O(ε_n)Y0n+1(τ,s,ε_n)z(2)n(s)ds.

(21)

Отметим следующее: интегралы в правой части (21) имеют асимптотическое представление,

соответственно, ε_nO(ε_n)∥z^′n(τ)∥_σ и ε_nO(ε_n)∥zn2)(τ)∥_σ, при этом для оставшихся интегралов

в правой части равенства (19) интегрированием по частям можно получить соотношения, по-

добные (20). Продолжив подобную процедуру, получим в итоге интеграл вида

∫

I^kn = (ε_n)k-1 O(ε_n)Y0n+1(τ,s,ε_n)z(k)n(s)ds.

Учитывая теперь оценку (10) для ∥znk)(τ)∥, ввиду того, что для достаточно большого k

величина μ^k q ≤ p < 1, для I^kn имеем асимптотическое представление

I^kn = O(pⁿ)∥z_n(τ)∥_σ,

(22)

т.е. данный интеграл - “исчезающая” вектор-функция. При этом отметим, что в процессе иссле-

дования асимптотических свойств данного интеграла получаем в правой части (19) выражения

вида

O(ε_n)z^′n(τ), O(ε_n)Π01,n(τ, ε_n)z^′n(0), ε_nO(ε_n)z(2)n(τ), ε_nO(ε_n)Π02,n(τ, ε_n)z(2)n(0),

...,

(ε_n)k-2O(ε_n)z(k-1)n(τ), (ε_n)k-2O(ε_n)Π0k-1,n(τ, ε_n)z(k-1)n(0).

(23)

Асимптотическое представление для величины z_n(τ) доказано.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

574

ГРЕБЕНЩИКОВ, ЛОЖНИКОВ

Для того чтобы исследовать асимптотические свойства величины z^′n(τ), рассмотрим неод-

нородное дифференциально-разностное уравнение (11). Как следует из работ [9, 11], фун-

даментальная матрица Y1n+1(τ, s, ε_n) соответствующей однородной системы для достаточно

больших n допускает оценку

(

)

∥Y1n+1(τ, s, ε_n)∥ ≤ C₀ exp

β_n (exp(τ) - exp(s)) ,

β_n = -d + C₀mε_n, β_n < 0.

(24)

ε_n

Соответствующая вырожденной системе матрица

A(τ) + O(ε_n))-1 B(τ) =

A-1(τ) + O(ε_n) +

+ O(ε_n)²)^B(τ). Следовательно, при достаточно больших n асимптотические свойства со-

ответствующей вырожденной “возмущённой” системы аналогичны свойствам вырожденной

(“невозмущённой”) системы. Ввиду оценки (24) решение соответствующей разностной системы

представляет собой выражение, аналогичное доказанному выше для величины z_n(τ) (полу-

чающаяся в результате исчезающая вектор-функция, аналогичная I^kn, будет иметь оценку,

подобную (22), содержащую множителем величину t₀ ввиду соотношения (10)); при этом

в правой части добавляются члены, найденные в результате интегрирования по частям ве-

личины

∫

exp(s)

Yn+11(τ,s,ε_n)(B′(s)

A^′(s

A-1(s)^B(s))z_n(s)ds.

ε_n

Они имеют вид F11,n(τ, n)z_n(τ), Π11,n(τ, ε_n)z_n(0), остальные члены подобны выражениям ви-

да (23). В итоге для величины z^′n(τ) также можем записать разностное уравнение вида (18).

Далее подобными методами получим соответствующее разностное уравнение для величины

zn2)(τ) и т.д. Лемма доказана.

Теперь, применяя леммы 1 и 2, докажем теорему о достаточных условиях асимптотической

устойчивости решения исходной системы (2).

Теорема 1. При выполнении условий (3), (4) система (2) экспоненциально устойчива,

при этом для решения исходной системы (1) справедлива оценка

)-β

⁽t

∥x(t)∥ ≤ M₀

sup∥φ(η)∥, M₀ = const, M₀ > 1, β = const, β > 0.

t₀

Здесь константы M₀, β одни и те же при всех t₀ ≥ t∗0 > 0, величина t∗0 фиксированная.

Доказательство. Учитывая лемму 2, рассмотрим вначале асимптотическое поведение вы-

рожденной системы

yn+1(τ) =

A-1(τ)^B(τ)y_n(τ).

(25)

Покажем, что существуют такие постоянныеL0 > 1, 0 < q< 1, что для решения разностной

системы (25) будет справедлива оценка [7, с. 40]

sup∥yn(τ)∥ ≤ L0(q)n sup∥y0(τ)∥, n ∈ N.

Ввиду равномерной непрерывности (по τ) матриц

A-1(τ)^B(τ) можно разбить интервал

[0, σ] на конечное число l равных промежутков длины меньше δ₁ таких, что будет выпол-

няться неравенство

A-1(τ)^B(τ)

A-1(τ_j)^B(τ_j)∥ < ε,

|τ - τ_j | < δ₁, j = 1, l,

0 < τ₁ < ... < τ_l = σ.

(26)

Но тогда (вследствие (26)) при достаточно малом ε для каждого промежутка [τ_j, τj+1] найдут-

ся такие постоянные L_j > 1, что будет справедлива оценка соответствующей результирующей

системы, получаемая из (25):



∏



Y0n,1(τ)∥ =^

A-1(τ + jσ)^B(τ + jσ)

L_j γⁿ,

γ = const,

0 < γ < γ < 1, j = 1,l.

(27)

^<

i=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

АСИМПТОТИЧЕСКИЕ СВОЙСТВА НЕКОТОРОГО КЛАССА СИСТЕМ

575

Отсюда следует, что для любых τ ∈ [0, σ] подобное неравенство справедливо при константах

L₀ = maxLj и q = γ, т.е. вырожденная система (25) экспоненциально устойчива.

Пусть в (18) j = k-1 и n достаточно велико. Рассмотрим вначале поведение системы (18)

в точке τ = σ. Очевидно, что при данном τ, ввиду оценок (8), (14) и аналогичных им, члены

в (22), содержащие (t₀)ⁱΠk+i-1k,n(σ, ε_n), будут иметь вид (t₀)^j o(ε_n). Тогда, записав z(k-1)n+i(σ) в

равенстве (18) с помощью формулы вариации постоянных, получим выражение

∑

z(k-1)n+i(σ)

Y k-1n+i,n(σ)y(k-1)n(σ) +

Y k-1n+i,n+j(σ)[Fk-1k-2,n+j-1(σ)z(k-2)n+j-1(σ) +

j=1

+ Fk-1k-3,n+j-1(σ)z(k-3)n+j-1(σ) + ... + Fk-10,n+j-1(σ)zn+j-1(σ) + O(εn+j)z(k)n+j-1(σ) +

+ O(εn+j)εn+jz(k+1)n+j-1(σ) + ... + O(εn+j)(εn+j)k-2z(2k-2)n+j-1(σ)] + (t₀)k-1O(pn+j)∥z₀(τ)∥_σ,

(28)

∑_∞

при этом ряд

∥O(ε_j )∥ сходится. Ввиду сходимости ряда для величины

Y k-1n+i,n(τ)∥ спра-

j=0

ведлива оценка, аналогичная (14).

Если теперь записать подобное равенство уже для величины z(k-2)n+i(σ), учитывая (27), то

получим следующее соотношение:

{

∑

z(k-2)n+i(σ)

Y k-2n+i,n(σ)z(k-2)n(σ) +

Y k-2n+i,n+j(σ) Fk-2k-3,n+j-1(σ)z(k-3)n+j-1(σ) +

j=1

[

+ Fk-2k-4,n+j-1(σ)z(k-4)n+j-1(σ) + ... + Fk-20,n+j-1(σ)zn+j-1(σ) + O(εn+j)

Y k-1n+i,n(σ)z(k-1)n(σ) +

∑

Y k-1n+i,n+j(σ)[Fk-1k-2,n+j-1(σ)z(k-2)n+j-1(σ) + Fk-1k-3,n+j-1(σ)z(k-3)n+j-1(σ) + ...

j=1

... + Fk-10,n+j-1(σ)zn+j-1(σ) + O(εn+j)z(k)n+j-1(σ) + O(εn+j)εn+jz(k+1)n+j-1(σ) + ...

]

... + O(εn+j)(εn+j)k-2z(2k-2)n+j-1(σ) + (t₀)k-1O(pn+j)∥z₀(τ)∥_σ] +

+ O(εn+j)εn+jz(k)n+j-1(σ) + O(εn+j)(εn+j)²z(k+1)n+j-1(σ) + ...

}

... + O(εn+j)(εn+j)k-2z(2k-3)n+j-1(σ) + (t₀)(k-2)O(pn+j)∥z₀(τ)∥σ ,

(29)

где есть члены, содержащие z(2k-2)n+j(σ). Нетрудно видеть, что они имеют порядок (t₀)(k-1) ×

× O(pn+j)∥z₀(τ)∥_σ. С другой стороны, члены, содержащие z(k-1)n+j(σ), отсутствуют, так как

вместо них входят выражения, содержащие величины znr)(σ), r = k - 1, k - 2. Далее, в со-

отношении (28) имеются члены, содержащие множители z(k-2)n+j(σ). Коэффициенты при них

имеют порядок O(εn+j ). Члены же, содержащие величины znr)(σ), r = k - 1, k - 2, . . . ,

стремятся к нулю как экспоненты. Учитывая теперь асимптотическую устойчивость соот-

ветствующей однородной разностной системы и вид её неоднородности, обусловленной “воз-

мущениями” (ввиду наличия величин zn+j(σ), z′n+j (σ), . . . , z(k-3)n+j(σ)), а также перемен-

ные z(k)n+j(σ), z(k+1)n+j(σ), . . . , z(2k-3)n+j(σ), получаем, что величина z(k-2)n+i(σ) (общее решение

неоднородной системы) состоит из экспоненциально устойчивого решения (имеющего оценку

O(γn+i(∥z(k-1)(σ)∥ + ∥z(k-2)(σ)∥)), и решения, обусловленного “возмущениями”, и решения,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

576

ГРЕБЕНЩИКОВ, ЛОЖНИКОВ

обусловленного “исчезающей” вектор-функцией (t₀)(k-1)O(pn+j)∥z₀(τ)∥_σ. Покажем, что ре-

шение, обусловленное “исчезающей” вектор-функцией, также экспоненциально устойчиво.

Без ограничения общности полагаем, что q < p, т.е. справедливо равенство q = δp, δ =

= const,

0 < δ < 1. Тогда из соотношения (29), учитывая последнее равенство, получаем

оценку



 ∑i



∑



Y k-2n+i,n+j(σ)(t₀)(k-1)O(pn+j)

z₀(τ)∥_σ ≤^L(t₀)(k-1)pn

δi-1p^i-jp^j∥z₀(τ)∥_σ <



^∥

j=1

n+j

∥z₀(τ)∥_σ,

L= const,

L> 1,

(30)

1-δ

откуда и следует экспоненциальная оценка для составляющей, обусловленной “исчезающей”

вектор-функцией.

Далее исследуя свойства вектор-функции z(k-3)n+i(σ) методами, аналогичными применён-

ным при исследовании величины z(k-2)n+i(σ), получим, что её “возмущения” зависят лишь от

величин zn+j(σ), z′n+j(σ), . . . , z(k-2)n+j(σ); z(k)n+j(σ), z(k+1)n+j(σ), . . . , z(2k-4)n+j(σ).

Продолжив процесс изучения поведения величин z(r)(σ), r = 1, k - 4, получим в резуль-

тате неоднородную разностную систему

zn+i(σ) = [

A-1(σ)^B(σ) + O(ε_n)]z_n(σ) + O(pⁿ)∥z₀(τ)∥_σ,

(31)

обладающую следующим свойством: соответствующая однородная “возмущённая” система экс-

поненциально устойчива, при этом неоднородность является “исчезающей” вектор-функцией,

для которой справедлива оценка, подобная O(pn+j)∥y₀(τ)∥_σ.

Решение системы (31) стремится к нулю при n → ∞ как экспонента (это доказывается

точно так же, как и при получении оценки (30)).

Рассмотрим теперь поведение решения разностной системы (18) на всём интервале [0, σ] :

j = 0. Ввиду условий (6) её решение экспоненциально устойчиво и при τ = 0. Следовательно,

члены, содержащие z_n(0), являются “исчезающей” вектор-функцией. Но тогда исследование

асимптотических свойств при любых τ ∈ (0, σ) ничем не отличается от приведённого выше,

и решение системы (5) экспоненциально устойчиво. Теорема доказана.

2. Получение достаточных условий экспоненциальной устойчивости системы,

содержащей постоянное запаздывание. Рассмотрим теперь систему вида

dx(τ)/dτ = A₁(τ)x(τ) + B₁(τ)x(τ - σ) + A₂(τ)y(τ) + B₂(τ)y(τ - σ),

dy(τ)/dτ = t₀ exp(τ)(A₃(τ)x(τ) + B₃(τ)x(τ - σ) + A₄(τ)y(τ) + B₄(τ)y(τ - σ)), τ ≥ 0.

(32)

Полагаем, что m × m-матрицы A_j (τ), B_j (τ), j = 1, 4, периодические (периода σ) и доста-

точное число раз дифференцируемые.

Вновь перейдём к счётной дифференциально-разностной системе на конечном промежутке

времени [0, σ]. Имеем соотношения

dxn+1(τ)/dτ = A₁(τ)xn+1(τ) + B₁(τ)x_n(τ) + A₂(τ)yn+1(τ) + B₂(τ)y_n(τ),

ε_ndyn+1(τ)/dτ = exp(τ)(A₃(τ)xn+1(τ) + B₃(τ)x_n(τ) + A₄(τ)yn+1(τ) + B₄(τ)y_n(τ)),

ε_n = μⁿ/t₀, τ ∈ [0,σ],

(33)

при краевых условиях

xn+1(0) = x_n(σ), yn+1(0) = y_n(σ).

Начальная вектор-функция есть выражение {x₀(τ), y₀(τ)}^т.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

АСИМПТОТИЧЕСКИЕ СВОЙСТВА НЕКОТОРОГО КЛАССА СИСТЕМ

577

В работе [12] показано, что системой первого приближения для (33) является дифферен-

циально-разностная система

dx0n+1(τ)/dτ = 0.5[(A⁰¹ + B⁰¹)x0n+1(τ) + A⁰²y0n+1(τ) + B⁰²y0n(τ)],

ε_ndy0n+1(τ)/dτ = exp(τ)[(A₃(τ) + B₃(τ))x0n+1(τ) + A₄(τ)y0n+1(τ) + B₄(τ)y0n(τ)],

∫

2σ

∫

2σ

μⁿ

A0j =

A_j(ξ)dξ, B0j =

B_j(ξ)dξ, j = 1,2, ε_n =

τ ∈ [0,σ].

(34)

t₀

Рассмотрим асимптотическое поведение системы (34) при достаточно больших n. Сделаем в

ней замену τ = θ_nε_n [13, c. 204] и получим систему

dx0n+1(θ_n)/dθ_n = 0.5ε_n[(A⁰¹ + B⁰¹)x0n+1(θ_n) + A⁰²y0n+1(θ_n) + B⁰²y0n(θ_n)],

dy0n+1(θ_n)/dθ_n = exp(θ_nε_n)[Aεn3 (θn) + B3n (θn)xⁿ+1(θn) + A4n (θn)yⁿ+1(θn) + B4n (θn)yⁿ(θn)],

(35)

Aεnj(θn)=Aj(θn^εn),Bjn(^θn)=Bj(θn^εn),j=3,4.

Из того, что в первой подсистеме (35) правая часть имеет множитель ε_n, следует (из первой

подсистемы в (34)), что величина xn+1(τ) удовлетворяет асимптотическому равенству

xn+1(τ)=-2(A⁰¹ + B⁰¹)-1(A⁰²y0n+1(τ) + B⁰²y0n(τ)) +

+ O(∥xn+1(τ)∥_σ + ∥yn+1(τ)∥_σ + ∥y_n(τ)∥_σ).

(36)

Рассматривая теперь систему первого приближения, полагаем, что собственные значения

λ0i матрицы A⁰¹ + B⁰¹ удовлетворяют неравенству

Re (λ0i) < -2β₁, β₁ = const, β₁ > 0.

(37)

Наряду с этим считаем, что для собственных чисел^λ(τ) матрицы A₄(τ) справедливо нера-

венство, аналогичное (3), т.е.

Re(^λ(τ)) < -2β₂, β₂ = const, β₂ > 0.

(38)

В силу соотношения (36) имеем приближённое равенство

xn+1(τ) ≈ -2(A⁰¹ + B⁰¹)-1(A⁰²y0n+1(τ) + B⁰²y0n(τ)).

Подставив данное выражение во вторую подсистему в (35), получим систему m-го порядка

ε_ndy0n+1(τ)/dτ = exp(τ){[A₄(τ) - 2(A₃(τ) + B₃(τ))(A⁰¹ + B⁰¹)-1A⁰²]y0n+1(τ) +

+ [B₄(τ) - 2(A₃(τ) + B₃(τ))(A⁰¹ + B⁰¹)-1B⁰²]y0n(τ)}.

(39)

Полагаем, что собственные числа ν матрицы

H₁ = A₄(τ) - 2(A₃(τ) + B₃(τ))(A⁰¹ + B⁰¹)-1A⁰²

удовлетворяют неравенству

Re(ν) < -2d₁,

(40)

и, наряду с этим, собственные числа ρ_h матрицы

H₂ = (H₁)-1[B₄(τ) - 2(A₃(τ) + B₃(τ))(A⁰¹ + B⁰¹)-1B⁰²]

удовлетворяют условию

|ρ_h| < γ_h, γ_h = const,

0 < γ_h < 1.

(41)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

578

ГРЕБЕНЩИКОВ, ЛОЖНИКОВ

Теорема 2. Пусть справедливы неравенства (37), (38), (40), (41). Тогда дифференциаль-

но-разностная система (33) (а следовательно, и исходная система (32)) экспоненциально

устойчива.

Доказательство. Очевидно (в силу теоремы 1), что система (39) экспоненциально устой-

чива, т.е. справедлива оценка

∥y⁰(τ)∥ ≤^K exp(-δ(τ - T )) sup ∥y(η)∥,

K= const,

δ = const,

δ > 0.

0≤η≤T

Рассмотрим теперь поведение первой подсистемы в (34) на бесконечном промежутке вре-

мени при достаточно больших τ. Она имеет вид

dx⁰(τ)/dt = 0.5[(A⁰¹ + B⁰¹)x0τ + A⁰²y⁰(τ) + B⁰²y⁰(τ - σ)], τ ≥ τ,

τ - достаточно большое положительное число. Записывая решение данной системы в инте-

гральной форме

⁽ (A⁰¹ + B⁰¹)(τ - τ)⁾

x⁰(τ) = exp

x⁰(τ) +

∫τ

⁽ (A⁰¹ + B⁰¹)(τ - s)⁾

+ exp

[A⁰²y⁰(s) + B⁰²y⁰(s - σ)] ds,

(42)

учитывая, что ввиду неравенства (37) справедлива оценка

∥ exp(0.5(A⁰¹ + B⁰¹)(τ - s))∥ ≤

M₁ exp(-β₁(τ - s)),

M₁ = const,

M₁ > 1,

получаем, что первый член в правой части в (42) стремится к нулю при τ → ∞.

Рассмотрим теперь поведение интегрального члена. Без ограничения общности считаем,

чтоδ < β₁. Тогда имеем оценку

∫



xp(0.5(A⁰¹ + B⁰¹)(τ - s))[A⁰²y⁰(s) + B⁰²y⁰(s - σ)] ds

 e

≤

M₁ K(∥A0

∥ + exp(δσ)∥B⁰²∥)

≤

exp(-β₁(τ - τ)) sup

∥y⁰(η)∥,

β₁ -δ

0≤η≤T

откуда следует экспоненциальная устойчивость величины x⁰(τ), а значит, система первого

приближения экспоненциально устойчива.

Рассмотрим теперь исходную (“возмущённую”) систему при достаточно большом n. Если

в первой из подсистем ввести “медленную” переменную θ_n, то при достаточно малом ε_n, как

следует из [13, c. 67], матрица Коши Kεn (θ_n, s) однородной системы имеет вид

Kεn (θ_n,s) ≈ exp{0.5ε_n(A⁰¹ + B⁰¹)(θ_n - s)}.

Данное соотношение тем точнее, чем меньше ε_n. Более того, если рассматривать неоднород-

ную усреднённую систему

dx0n(θ_n)/dθ_n = ε_n[0.5ε_n(A⁰¹ + B⁰¹)x0n(θ_n) + A⁰²yn+1(θ_n + B⁰²y_n(θ_n))],

то она является первым приближением для исходной первой подсистемы.

Если теперь рассмотреть вторую из подсистем в (33), то ввиду соотношения (36) и оценки,

аналогичной (26), имеем, что вторая из подсистем в (34) является первым приближением для

исходной подсистемы. Как следует из [9, c. 258] (учитывая экспоненциальную устойчивость

системы (34)), “возмущённая” система (33) экспоненциально устойчива. Теорема доказана.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

АСИМПТОТИЧЕСКИЕ СВОЙСТВА НЕКОТОРОГО КЛАССА СИСТЕМ

579

3. Примеры. Мы исследовали асимптотические свойства некоторых систем, решение ко-

торых экспоненциально устойчиво. Приведём конкретные примеры, которые иллюстрируют

достаточную точность методов исследования устойчивости, предложенных нами. Вначале рас-

смотрим пример экспоненциально устойчивой системы второго порядка:

dx₁(τ)/dτ = exp(τ){-(1 + 2 cos(2πτ))x₁(τ) - 2(1 - sin(2πτ))x₂(τ) +

+ 0.5(1 + 2 cos(2πτ))x₁(τ - 1) + 0.5(1 - sin(2πτ))x₂(τ - 1)},

dx₂(τ)/dτ = exp(τ){2(1 + sin(2πτ))x₁(τ) - (1 - 2 cos(2πτ))x₂(τ) -

- (1 + sin(2πτ))x₁(τ - 1) + 0.25(1 - 2 cos(2πτ))x₂(τ - 1)}, τ ≥ 0.

(43)

Здесь матрица A(τ) периодическая (период равен единице), имеет собственные значения

λ₁(τ) = λ2(τ) = -1, cледовательно, система без запаздывающих членов асимптотически

устойчива; матрица B(τ) также периодическая (период равен единице), при этом матрица

-A-1(τ)B(τ) имеет вид

(

)

0.5

-A(τ)-1B(τ) =

0.25

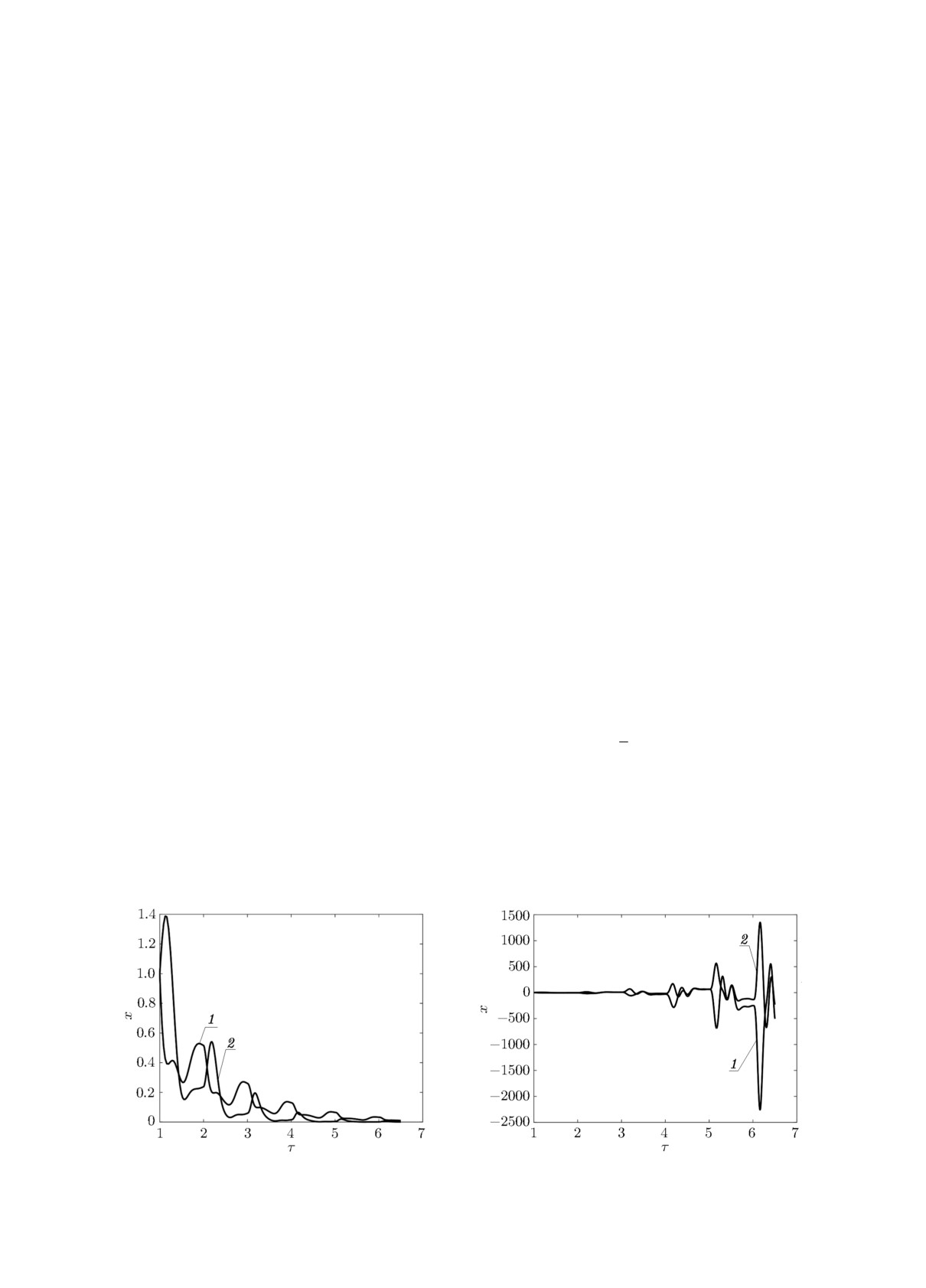
её собственные значения ρ₁ = 0.5, ρ₂ = 0.25. Система (43) экспоненциально устойчива, что

иллюстрируется графиком решения на рис. 1 при начальной вектор-функции φ(ξ) = (1, 1)^т,

заданной на отрезке [0, 1].

Рассмотрим теперь управляемую систему

dx(τ)/dτ = exp(τ)[A(τ)x(τ) +^B(τ)x(τ - 1) + C(τ)u(τ)],

(44)

где управляющее воздействие u(τ) - скалярная величина, матрица

^B(τ) и вектор C(τ) опре-

делены следующим образом:

(

)

(

)

-4(1 - sin(2πτ))

-4(1 + 2 cos(2πτ))

1 + 2cos(2πτ)

B(τ)=

C(τ) =

−2(1 - 2 cos(2πτ))

8(1 + sin(2πτ))

-2(1 + 2 sin(2πτ))

Следовательно,

(

)

√

-4

-A(τ)-1 B(τ) =

ρ1,2 = ±2

(45)

-2

Собственными значениями этой “вырожденной” матрицы являются величины, большие по мо-

дулю единицы, следовательно, “вырожденная” система неустойчива, но неустойчива и исход-

ная система (44) (при u(τ) ≡ 0), что видно из графика на рис. 2. (Отметим, что достаточные

условия неустойчивости могут быть получены с помощью знакопеременных функционалов

Ляпунова-Красовского [4].)

Рис. 1. Решение системы (43): 1 - x1(τ ),

Рис. 2. Решение системы (44) при u(τ ) ≡ 0 :

2 - x2(τ).

1 - x1(τ), 2 - x2(τ).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

580

ГРЕБЕНЩИКОВ, ЛОЖНИКОВ

Возникает проблема стабилизации. Осуществить её традиционными методами весьма не-

просто ввиду того, что правая часть системы содержит экспоненциальный множитель. Поэто-

му поступаем следующим образом: будем стабилизировать вырожденную (разностную) систе-

му второго порядка

z(τ) = -A-1(τ)^B(τ)z(τ - 1)

Cv(τ),

C = (1,0)^т.

(46)

Ввиду того, что матрица -A-1(τ)^B(τ) = A₁ имеет обратную, стабилизацию разностной сис-

темы (45) можно осуществить следующим образом [14, с. 107]:

u(τ) = (1

C^т

C)-1

CA₁z(τ - 1).

(47)

Здесь R - положительная 2×2-матрица, при этом матрица R-1 является решением линейного

матричного уравнения

(

)

0.0064

R-1

C^т = (1/0.64)A₁R-1(A₁)^т, R-1 =

(48)

0.048

Из (47) и (48) получаем стабилизированную матрицу

(

)

-0.25

A_s = A₁ + (1

C^т

C)-1

CA₁ =

ρ1,2 = ±0.707.

−2

Если теперь в исходной управляемой системе (44) положить управление u(τ) =Rx(τ - 1),

то полученная (стабилизированная) система будет иметь вид

dx(τ)/dτ = exp(τ)[A(τ)x(τ) + (^B(τ) + C(τ)R(τ))x(τ - 1)],

(

)

-4 + 4sin(2πτ)

-0.25 - 0.5 cos(2πτ)

^B(τ) + C(τ)R(τ) =

(49)

−2 + 4cos(2πτ)

0.5 + 0.5 sin(2πτ)

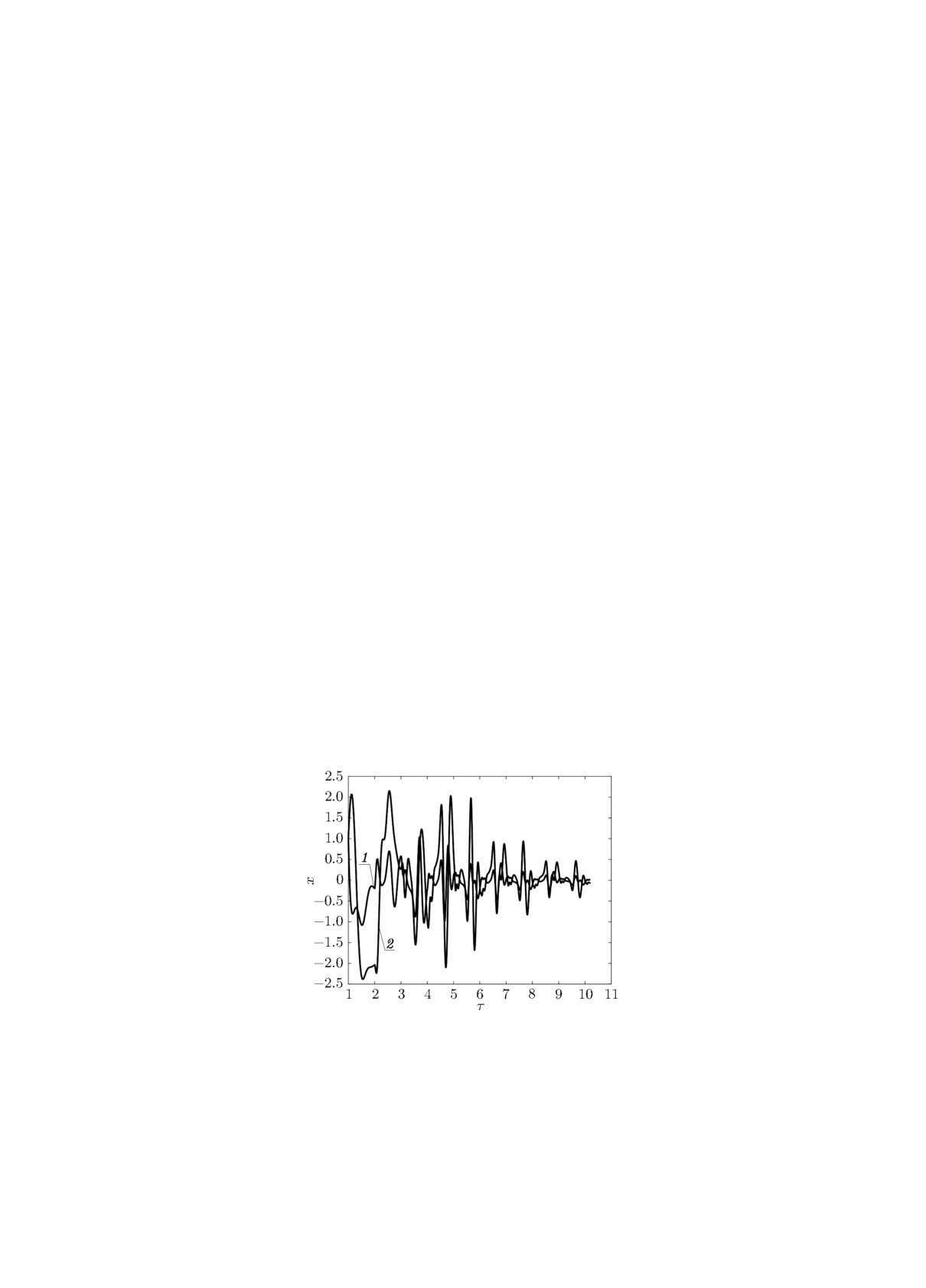
откуда, учитывая соотношения (44) и (46), получаем, что решение стабилизированной системы

(49) экспоненциально устойчиво, что иллюстрирует график, приведённый на рис. 3.

Рис. 3. Решение стабилизированной системы

(49): 1 - x1(τ ), 2 - x2(τ).

Последний пример показывает, что условие экспоненциальной устойчивости “вырожден-

ной” системы существенно.

Заключение. Достаточные условия асимптотической устойчивости, сформулированные

в теореме 1, в случае постоянных матриц A и B аналогичны условиям, полученным ранее

(см. [15]) с помощью преобразования Лапласа [1, c. 11]. В статье [16] показано, что в случае

существования у матрицы -A-1B собственных чисел ρ, | ρ| > 1, решение соответствующей

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023

АСИМПТОТИЧЕСКИЕ СВОЙСТВА НЕКОТОРОГО КЛАССА СИСТЕМ

581

системы неустойчиво. Преобразование Лапласа неприменимо для исследования асимптотиче-

ской устойчивости систем вида (2), следовательно, метод, предложенный авторами, является

более общим и позволяет решать задачи стабилизации традиционными методами некоторых

нестационарных систем.

СПИСОК ЛИТЕРАТУРЫ

1. Беллман Р., Кук К. Дифференциально-разностные уравнения. М., 1967.

2. Fox L., Mayers D.F., Ockendon J.R., Tayler A.B. On functional differential equation // Inst. Math.

Appl. 1972. V. 8. P. 271-307.

3. Ockendon J.R., Tayler A.B. The dynamics of a current collection system for an electric locomotive

// Proc. Soc. London. Ser. A. 1971. V. 322. P. 447-468.

4. Гребенщиков Б.Г., Ложников А.Б. Устойчивость и стабилизация одного класса линейных неста-

ционарных систем с постоянным запаздыванием // Изв. РАН. Теория и системы управления. 2017.

№ 2. С. 3-15.

5. Sesekin A.N., Shlyakov A.S. On the stability of discontinuous solutions of bilinear systems with impulse

action, constant and linear delays // Proc. of the 45th Intern. Conf. on Application of Mathematics in

Engineering and Economics. 2019. P. 2172(1):030009.

6. Жабко А.П., Тихомиров О.Г., Чижова О.Н. О стабилизации одного класса систем с пропорцио-

нальным запаздыванием // Вестн. Санкт-Петербургского ун-та. Сер. А. Прикл. математика. Ин-

форматика. Процессы управления. 2018. Т. 14. Вып. 2. С. 165-172.

7. Барбашин Е.А. Введение в теорию устойчивости. М., 1967.

8. Эльсгольц Л.Э., Норкин С.Б. Введение в теорию дифференциальных уравнений с отклоняющимся

аргументом. M., 1971.

9. Былов Б.Ф., Виноград Р.Э., Гробман Д.М., Немыцкий В.В. Теория показателей Ляпунова и ее

приложение к вопросам устойчивости. M., 1966.

10. Гребенщиков Б.Г. Об устойчивости нестационарных систем с большим запаздыванием // Устойчи-

вость и нелинейные колебания. Свердловск, 1984. С. 18-29.

11. Халанай А., Векслер Д. Качественная теория импульсных систем. М., 1971.

12. Гребенщиков Б.Г. Об устойчивости по первому приближению одной нестационарной системы с

запаздыванием // Изв. вузов. Математика. 2012. № 2. С. 34-42.

13. Митропольский Ю.А. Метод усреднения в нелинейной механике. Киев, 1971.

14. Фурасов В.Д. Устойчивость и стабилизация дискретных систем. M., 1982.

15. Гребенщиков Б.Г. Устойчивость систем с переменным запаздыванием, линейно зависящим от вре-

мени // Устойчивость и нелинейные колебания. Свердловск, 1983. С. 25-34.

16. Гребенщиков Б.Г., Новиков С.И. О неустойчивости некоторой системы с линейным запаздыванием

// Изв. вузов. Математика. 2010. № 2. С. 3-13.

Южно-Уральский государственный университет,

Поступила в редакцию 27.05.2021 г.

г. Челябинск,

После доработки 01.03.2023 г.

Институт математики и механики

Принята к публикации 16.03.2023 г.

имени Н.Н. Красовского УрО РАН, г. Екатеринбург,

Уральский федеральный университет,

г. Екатеринбург

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№5

2023