ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 6, с.780-790

ЧИСЛЕННЫЕ МЕТОДЫ

УДК 519.63

О КВАЗИАКУСТИЧЕСКОЙ СХЕМЕ А.П. ФАВОРСКОГО

Рассматривается явная консервативная квазимонотонная разностная схема второго поряд-

ка точности для численного решения уравнений газовой динамики, предложенная А.П. Фа-

ворским. Приводятся обоснования основных методов и подходов, лежащих в основе её по-

строения.

DOI: 10.31857/S0374064123060080, EDN: FGLOLL

Введение. Численным методам решения гиперболических уравнений и систем посвящено

огромное количество работ (см., например, обзоры [1, 2]). Интерес к постоянному развитию

этого направления прикладной математики обусловлен тем, что такие уравнения, в частности

система уравнений Эйлера газовой динамики, являются базовой составляющей математиче-

ских моделей, описывающих многие практически значимые задачи. При этом в силу нелиней-

ности уравнений нахождение их решений аналитическими методами возможно лишь в редких

частных случаях.

При построении разностных методов приближённого решения системы уравнений газовой

динамики используются различные идеи и подходы, которые зачастую перекликаются между

собой, однако имеют существенные отличия в определённых аспектах. В настоящей работе

речь пойдет о так называемой квазиакустической разностной схеме, предложенной А.П. Фа-

ворским, которую сам автор позиционировал как комбинацию консервативного метода Году-

нова [3] и сеточно-характеристического подхода [4]. Схема [5-9] является явной, имеет второй

порядок точности на монотонных участках гладких решений, не содержит искусственных регу-

ляризаторов и при этом сохраняет монотонность профиля решений, в том числе в окрестности

разрывов. В указанных статьях основное внимание уделено численным исследованиям квази-

акустической схемы. Чтобы дополнить эти исследования, в данной работе авторы постарались

привести более детальные обоснования методов и подходов, использованных при построении

вычислительного алгоритма, поскольку заложенные в них идеи по-прежнему представляются

перспективными.

Работа посвящена памяти замечательного человека и талантливого ученого Антона Пав-

ловича Фаворского (29.08.1940-17.06.2013), который навсегда останется в сердцах его благо-

дарных учеников, к которым, безусловно, относят себя и авторы статьи.

1. Разностная схема для уравнения переноса. Рассматривается начально-краевая

задача для уравнения переноса

∂u

= 0,

0<x<l,

0<t≤T,

∂t

∂x

u(x, 0) = u₀(x).

Предполагается, что функция u₀(x) является финитной на интервале (0, l), а значение T

таково, что решение u(x, t), где t - время, x - пространственная переменная, остаётся фи-

нитным на том же интервале при всех t ∈ (0, T ]. Это позволяет рассматривать однородные

граничные условия

u(0, t) = u(l, t) = 0.

Далее для определённости будем считать, что a > 0.

На отрезках [0, l] и [0, T ] вводится равномерная сетка

ω_h = {x_i = ih, i = 0,1,... ,N, Nh = l}, ω_τ = {t_n = nτ, n = 0,1,... ,K, Kτ = T}.

780

О КВАЗИАКУСТИЧЕСКОЙ СХЕМЕ А.П. ФАВОРСКОГО

781

Помимо узлов x_i пространственной сетки определяются границы разностных ячеек xi+1/2 =

= (i + 1/2)h. В соответствии с общей идеологией построения конечно-объёмных разностных

схем [2] вводится сеточная функция yⁿⁱ = y(x_i, t_n), определяемая в узлах сетки как интеграль-

ное среднее по разностной ячейке при t = t_n :

xi+1/2∫

yⁿⁱ =

u(x, t_n) dx.

(1)

xi-1/2

Разностная схема строится интегро-интерполяционным методом [10, с. 114]. Для этого уравне-

ние переноса интегрируется по пространственно-временной ячейке xi-1/2 ≤ x ≤ xi+1/2, t_n ≤

≤ t ≤ tn+1. В результате получается соотношение

h(yn+1i - yⁿⁱ) + wni+1/2 - wni-1/2 = 0,

∫tn+1

где wni+1/2 = a

u(xi+1/2, t) dt. Величины wni+1/2 представляют собой интегральные потоки

через границы ячеек за время τ = tn+1 - t_n.

Поскольку решение u(x, t), фигурирующее в подынтегральных выражениях для потоков,

заранее неизвестно, для их приближённого вычисления в каждой ячейке сетки используется

линейная реконструкция [2] функции u(x, t) по значениям сеточной функции yⁿⁱ. При t = t_n

реконструированная функция имеет вид

ũⁿⁱ(x,t_n) = yⁿⁱ + (x - x_i)Dⁿⁱ, xi-1/2 ≤ x ≤ xi+1/2.

(2)

Здесь коэффициенты Dⁿⁱ задают наклоны реконструкции и будут определены далее. Считая,

что реконструированная функция удовлетворяет уравнению переноса, в соответствии с его

характеристическими свойствами [10] при t > t_n имеем

ũⁿⁱ(x,t) = yⁿⁱ + (x - a(t - t_n) - x_i)Dⁿⁱ

и, в частности,

ũⁿⁱ(xi+1/2,t) = yⁿⁱ + (0.5h - a(t - t_n))Dⁿⁱ.

Последнее выражение справедливо при всех t ∈ [t_n, tn+1] при ограничении на число Куран-

та [11]

aτ

≤ 1.

Замена неизвестной функции uⁿⁱ(xi+1/2, t) на ũⁿⁱ(xi+1/2, t) позволяет вычислить приближён-

ные выражения для потоков

∫

wni+1/2 ≈ wni+1/2 =

aũ(xi+1/2, t) dt = aτ(yⁿⁱ + 0.5(h - aτ)Dⁿⁱ).

В результате приближённое равенство

h(yn+1i - yⁿⁱ) + wni+1/2 - wni-1/2 ≈ 0

определяет семейство разностных схем

y^nt,i + ayn¯x,i +

(h - aτ)Dn¯x,i = 0.

(3)

Здесь и далее используются краткие обозначения (см. [12]) для разностных производных y^nt,i =

= (yn+1i - yni )/τ, yn¯x,i = (yⁿⁱ - yni-1)/h и др. Различные схемы из этого семейства определяются

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

782

АБАКУМОВ, ИСАКОВ

выбором коэффициентов наклона линейных реконструкций Dⁿⁱ. Так, например, при Dⁿⁱ =

= 0 получим схему первого порядка, монотонную [12] при q ≤ 1, а при Dⁿⁱ = y^nx,i - схему

Лакса-Вендроффа [13]

y^nt,i + ay^◦

=a²

yn¯xx,i

x,i

второго порядка аппроксимации, которая не является монотонной.

А.П. Фаворским была предложена разностная схема [6], которая может быть отнесена к

описанному выше семейству, имеющая второй порядок аппроксимации на гладких монотонных

участках решения исходной задачи, сохраняющая монотонность его профиля. В предложенной

схеме наклоны линейных реконструкций выбираются следующим образом:

y_x|y_x| + y_x|y_x|

Dⁿⁱ =

(4)

|y_x| + |y_x|

Здесь и далее индексы у разностных производных опущены. Как легко видеть, в точках ло-

кального экстремума численного решения, где знаки y_x, y_x различны, наклоны Dⁿⁱ = 0, как

в схеме первого порядка. В противном случае

2y_xy_x

Dⁿⁱ =

y_x + y_x

При этом для гладкой функции u(x), обозначая u_i = u(x_i),

2(u_i - ui-1)(ui+1 - u_i)

D_i(u) =

= u^′x + O(h²),

h(ui+1 - ui-1)

т.е. разностное отношение аппроксимирует пространственную производную, что, как извест-

но [2], приводит к повышению порядка аппроксимации схемы. Покажем, что схема аппрок-

симирует гладкое решение исходной задачи на его монотонном участке со вторым порядком.

Далее будем обозначать yx ≡ yx,i-1.

Теорема 1. Пусть в узле сетки (x_i, t_n) знаки разностных производных yx, yx, yx совпа-

дают. Тогда погрешность аппроксимации схемы (3) с наклонами (4) на достаточно гладком

решении исходной задачи Ψⁿⁱ = O(h² + τ² + τh).

Доказательство. Запишем погрешность аппроксимации на решении u(x, t) в узле (x_i, t_n),

опуская аргументы функции u и её производных:

(

) (

)

Ψⁿⁱ = u^′t +

u^′′

+a u^′x -

u^′′

(h - aτ)D_x(u) + O(h² + τ²).

Учитывая, что при условии теоремы (опуская выкладки)

(

)

u_i - ui-1

ui+1 - u_i

ui-1 - ui-2

D_x(u) = 2

=u^′′xx -

u^′′′xxx + O(h²),

h²

ui+1 - ui-1

u_i - ui-2

получим (с учётом равенства u^′t + au^′x = 0)

(

)

Ψⁿⁱ =

u^′′tt -

u^′′xx +

(h - aτ)

u^′′xx + O(h)

+ O(h² + τ²) =

(u^′′tt - a²u^′′xx) + O(h² + τ² + τh).

Первое слагаемое обращается в нуль вследствие уравнения переноса.

Далее покажем, что схема удовлетворяет условиям принципа максимума (условиям поло-

жительности коэффициентов), что и обеспечивает сохранение монотонности профиля числен-

ного решения [12, с. 40].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

О КВАЗИАКУСТИЧЕСКОЙ СХЕМЕ А.П. ФАВОРСКОГО

783

Теорема 2. Схема (3) с наклонами (4) удовлетворяет условиям принципа максимума.

Доказательство. Сначала будем считать, что разностные производные yx, yx, yx в узле

(x_i, t_n) имеют одинаковые знаки. Тогда разностную схему можно записать в виде

(

)

(

)

y_xy_x

yxyx

yn+1i - yⁿⁱ + q yⁿⁱ + (1 - q)h

- q yni-1 + (1 - q)h

= 0.

y_x + y_x

yx + yx

Учитывая равенство hy_x = y_i - yi-1 и вводя обозначения

y_x

α=

β =

y_x + y_x

yx + yx

перепишем разностное уравнение в виде

yn+1i = (1 - q)(1 - q(α - β))yⁿⁱ + q(1 + (1 - q)(α - β))yni-1.

Учитывая, что α, β ∈ [0, 1], q ≤ 1, условия принципа максимума выполняются. Это остаёт-

ся верным, если при наличии локальных экстремумов численного решения Dⁿⁱ = 0 или(и)

Dni-1 = 0, соответственно α = 0 или(и) β = 0.

Подводя промежуточные итоги, целесообразно отметить, что описанную схему А.П. Фа-

ворского следует отнести к классу нелинейных монотонных разностных методов, в которых

осуществляется “переключение” между аппроксимацией первого и второго порядков.

2. Разностная схема для квазилинейного уравнения переноса. Далее рассмотрим

начально-краевую задачу для квазилинейного уравнения переноса (уравнения Хопфа):

∂u

= 0,

0<x<l,

0<t≤T,

∂t

∂x

u(0, t) = u(l, t) = 0, u(x, 0) = u₀(x).

Здесь также считается, что функция u₀(x) является финитной на интервале (0, l), а решение

u(x, t) остаётся финитным на том же интервале при всех t ∈ (0, T ]. Временно будем полагать,

что u₀(x) ≥ 0, т.е. перенос осуществляется в положительном направлении оси x.

В точности также, как и для линейного уравнения, на равномерной разностной сетке ω_h ×

×ω_τ введём сеточную функцию yⁿⁱ вида (1), определим её линейную реконструкцию ũni (x,t_n)

вида (2) и рассмотрим разностную схему

h(yn+1i - yⁿⁱ) + wni+1/2 - wni-1/2 = 0.

Отличие состоит в том, что выражение для приближённых интегральных потоков теперь при-

мет вид

∫

wni+1/2 =

ũ²(xi+1/2,t)dt.

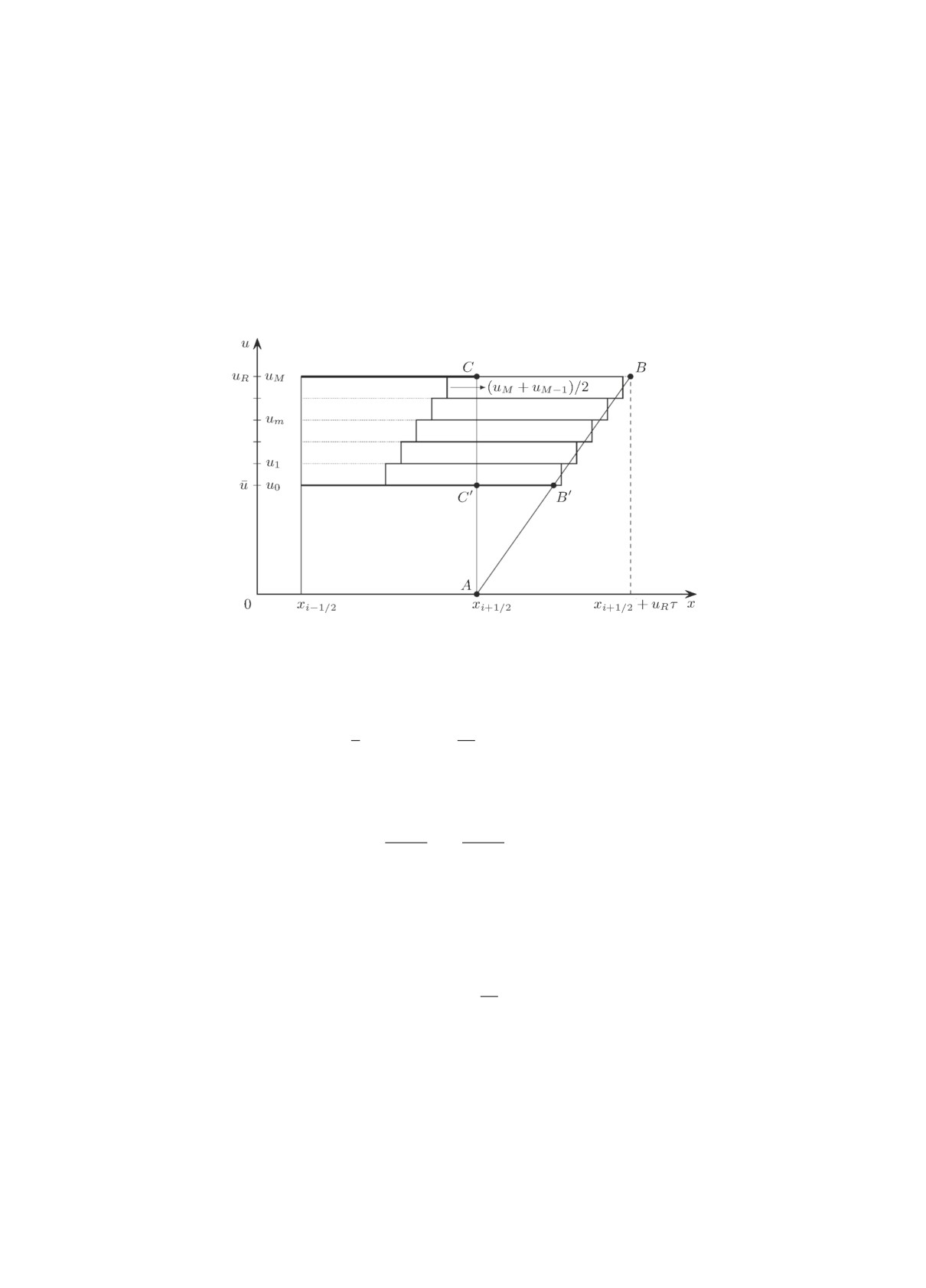
Записав уравнение прямой, проходящей через точки B и E (рис. 1), несложно построить

автомодельное решение квазилинейного уравнения

)

x - xi-1/2 - u_L(t - t_n

ũ(x, t) = Dⁿ

+u_L,

(5)

1 + Dni (t - t_n)

где u_L,R = yⁿⁱ ± hDⁿⁱ/2, совпадающее с реконструированной функцией ũⁿⁱ(x, t_n) при t = t_n.

В частности,

u_R

ũ(xi+1/2, t) =

1 + Dni (t - t_n)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

784

АБАКУМОВ, ИСАКОВ

Рис. 1. Декомпозиция интегрального потока.

Последнее равенство справедливо при всех t ∈ [t_n, tn+1] при ограничении τ ≤ h/u_L (если

временно не рассматривать влияние соседней слева ячейки, например, считая, что в ней значе-

ние реконструированной функции постоянно и равняется u_L). Тогда можно явно вычислить

выражение для приближённых интегральных потоков

u2R

(yⁿⁱ + hDⁿⁱ/2)

wni+1/2 =

(6)

2 1+Dⁿⁱτ

1+Dⁿⁱτ

Выбрав наклоны линейных реконструкций Dⁿⁱ в виде (4), получим аналог разностной

схемы, подробно описанной в п. 1. Однако важно отметить, что при построении обеих схем

использовалась возможность явно записать решения задач Коши для уравнений переноса на

отрезке t ∈ [t_n, tn+1] с начальными данными в виде реконструированного линейного профи-

ля. В случае уравнений газовой динамики это уже не представляется возможным. В связи

с этим для дальнейшего обобщения схемы на указанный случай проведём дополнительные

построения.

Заметим, что решение u(x, t) квазилинейного уравнения переноса (до момента возможной

“градиентной катастрофы”) удовлетворяет соотношению

u(x + u(x, t) dt, t + dt) = u(x, t),

которое иллюстрирует перенос решения в неизменном виде вдоль прямолинейной характери-

стики dx/dt = u [14, с. 76]. Это, в частности, позволяет записать автомодельное решение,

использованное выше. Кроме того, соотношение даёт основание интерпретировать решение

задачи Коши как “послойную трансляцию” начального профиля, при которой каждое значе-

ние u переносится с той же скоростью параллельно оси x. Это соображение и лежит в основе

идеи декомпозиции интегрального потока, которую опишем далее.

Целесообразно начать со случая, когда наклон линейной реконструкции Dⁿⁱ = 0, тогда

u_L = u_R, а выражение для приближённого интегрального потока примет вид

u2R

wni+1/2 =

τ.

Указанное значение равно площади треугольника ABC (рис. 2). На интервале (0, u_R) вы-

берем произвольное (фоновое) значение u, а отрезок [u, u_R] разобьем на одинаковые проме-

жутки [um-1, u_m], m = 1, M. Значения u_m определяют набор “прямоугольных возмущений”

относительно фонового значения

u внутри ячейки [xi-1/2, xi+1/2]. Площадь треугольника

ABC может быть записана в виде

∑

u_m + um-1

S_ABC = S_AB′_C′ + S_C′_B′_BC =

τ + (u_m - um-1)

τ.

(7)

m=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

О КВАЗИАКУСТИЧЕСКОЙ СХЕМЕ А.П. ФАВОРСКОГО

785

Слагаемые под знаком суммы, в свою очередь, можно интерпретировать как площади тех

частей соответствующих прямоугольных возмущений, которые, двигаясь со скоростью (u_m +

+ um-1)/2, пересекли границу ячейки xi+1/2 за время τ. Важно отметить, что в точном

решении квазилинейного уравнения переноса с начальными данными u(x, 0) = u_m при x <

< xi+1/2

и u(x, 0) = um-1 при x > xi+1/2 разрыв перемещается со временем как раз с

указанной скоростью [14, с. 510]. Равенство (7) по сути определяет выражение для точной (в

рассматриваемом случае Dⁿⁱ = 0) декомпозиции интегрального потока wni+1/2, который, как

уместно напомнить, сам по себе точным не является. Далее получим приближённый аналог

этого равенства иным способом, который более удобен для обобщения декомпозиции на случай

уравнений газовой динамики.

Рис. 2. Точная декомпозиция потока при Dⁿⁱ = 0.

Пусть u - некоторое постоянное фоновое значение, а δu - его малое возмущение. Предста-

вим потоковую комбинацию W в виде

W =

(u + δu)² ≈

+ uδu =^W + δW.

Здесь отброшено слагаемое второго порядка малости относительно δu. Считая, что δu удо-

влетворяет линеаризованному уравнению

∂(δu)

= 0,

∂t

∂x

приходим к тому, что вклад возмущения в потоковый интеграл равен площади части профи-

ля δu, которая пересекла границу ячейки, двигаясь с постоянной скоростью u за время τ.

Для набора прямоугольных возмущений, введённого выше, приходим к следующей формуле

декомпозиции потока:

∫

∑

u²

wni+1/2 ≈Wτ +

δW_m dt =

τ+

(u_m - um-1)um-1τ.

(8)

m=1

m=1 tn

Здесь слагаемые под знаком суммы соответствуют перемещениям каждого прямоугольного

возмущения по индивидуальному фону um-1 с той же (акустической) скоростью.

Заметим, что приближённое выражение (8) для wni+1/2 отличается от точного (7) на вели-

чину τ(Δu)²/(2M), где Δu - длина отрезка u, разбиваемого значениями u_m. Общее фоновое

значение u выбирается (см. далее) таким образом, что значения Δu сравнимы с величиной

Dⁿⁱh, поэтому выражение обеспечивает достаточную для схемы второго порядка точность да-

же при небольших значениях M.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

786

АБАКУМОВ, ИСАКОВ

Вернёмся к более общему случаю Dⁿⁱ = 0. Отметим, что значение полученного ранее точ-

ного выражения (6) для

wni+1/2 по-прежнему совпадает с площадью треугольника ABC при

t = tn+1, который теперь не является прямоугольным (см. рис. 1). В качестве фонового зна-

чения выберем u = u_R (при положительном наклоне u = u_L). Отрезок [u_R, u_L], как и ранее,

разобьем на одинаковые промежутки (слои) значениями u₀, u₁, . . . , u_M . В пределах каждого

слоя заменим трапециевидную (или треугольную) часть профиля реконструированной функ-

ции прямоугольником той же площади (см. рис. 1). Декомпозиция потока осуществляется

аналогично предыдущему. Фоновая составляющая u²/2 соответствует площади треугольника

ABC^′. А площадь треугольника BCC^′ представляется (точно или приближённо) суммой тех

частей прямоугольников (прямоугольных возмущений), которые, двигаясь со своими скоростя-

ми, пересекли границу ячейки xi+1/2 за время τ. При этом, как уже отмечалось, в качестве

скорости на слое с номером m можно выбирать как значение (u_m + um-1)/2, так и значение

um-1 (акустическая скорость).

Как уже отмечалось, проведённые построения справедливы в предположении, что линей-

ный профиль автомодельного решения (5) на промежутке времени t ∈ [t_n, tn+1] не искажает-

ся вследствие влияния данных соседней слева (относительно рассматриваемой [xi-1/2, xi+1/2])

ячейки. Чтобы исключить подобное влияние, достаточно проводить те же построения не на

целых ячейках, а на их половинах [x_i, xi+1/2]. Дополнительно необходимо потребовать выпол-

нения условия

τ ≤ 0.5h/max|ũ|,

где максимум берётся по всем значениям реконструированных функций во всех ячейках.

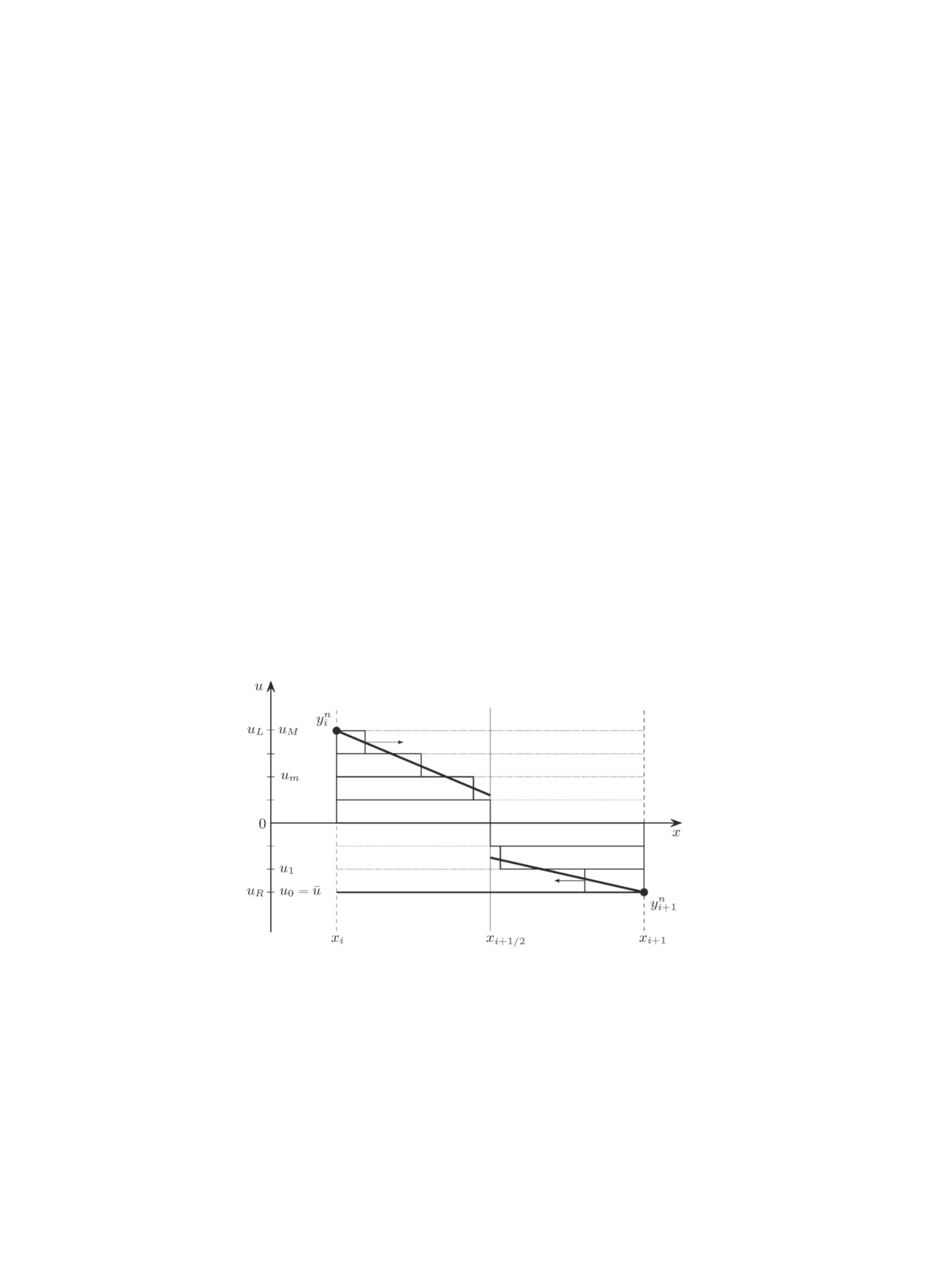
И, наконец, в наиболее общем случае (не предполагая, что u₀(x) ≥ 0) может оказаться,

что реконструированные функции в соседних ячейках принимают значения разных знаков.

Тогда необходимо рассматривать две “полуячейки”, примыкающие к общей границе xi+1/2,

т.е. отрезок [x_i, xi+1] (рис. 3).

Рис. 3. Случай различных знаков реконструированных функций.

Общее фоновое значение

u можно выбирать различными способами. Например, в каче-

стве такового может выступать минимальное из значений двух реконструированных функций,

определённых на соответствующих полуячейках. Далее промежуток между общим минимумом

и максимумом двух функций ([u_R, u_L] для профилей, представленных на рис. 3) разбивается

на слои значениями u₀, u₁, . . . , u_M , и в каждой полуячейке определяются прямоуголь-

ные возмущения аналогично описанному выше. Фоновая составляющая интегрального потока

wni+1/2 по-прежнему равна u2/2. Вклады прямоугольных возмущений учитываются так же,

как описано ранее, только площади частей прямоугольников, пересекающих границу xi+1/2 в

отрицательном направлении оси x, не суммируются, а вычитаются.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

О КВАЗИАКУСТИЧЕСКОЙ СХЕМЕ А.П. ФАВОРСКОГО

787

3. Схема для уравнений газовой динамики. Рассмотрим систему уравнений газовой

динамики [15] в пространственно одномерном приближении совместно с уравнением состояния

идеального газа:

∂ρ

∂(ρu)

∂(ρu² + p)

∂(ρe)

∂(ρue + up)

= 0,

∂t

∂x

∂t

∂x

∂t

∂x

e=ε+

p = (γ - 1)ρε.

(9)

Здесь t - время, x - пространственная координата, ρ - плотность газа, u - скорость, p -

давление, ε - удельная внутренняя энергия, e - полная удельная энергия, γ - показатель

адиабаты.

Система уравнений (9), записанная в консервативной форме, может быть преобразована

к следующему виду, содержащему исключительно “примитивные” переменные ρ, u, p и их

производные:

⎡

⎤

u ρ

∂q

= 0, q = (ρ, u, p)^т, A = ⎣0 u

1/ρ⎦.

(10)

∂t

∂x

ρc²

√

Здесь c =

γp/ρ - скорость звука. Несложно проверить, что матрица A имеет собственные

значения λ_± = u ± c, λ₀ = u и отвечающие им собственные векторы

l_± = (0,±1,1/(cρ)), l₀ = (1,0,-1/c²),

определённые с точностью до нормирующих множителей.

Наряду с “примитивными”, также будем использовать характеристические переменные

r_± = l_±q = ±u + p/(cρ), r₀ = l₀q = ρ - p/c².

Обратное преобразование, как легко видеть, даёт равенства

cρ

ρ=

(r₊ + r_-) + r₀, u =

(r₊ - r_-), p =

(r₊ + r_-).

В предположении, что решение системы (10) имеет вид

ρ = ρ+ δρ, u = u + δu, p = p+ δp,

где ρ,

p - постоянные значения, а δρ, δu, δp - функции малых возмущений, получим

систему линеаризованных уравнений

⎡

⎤

∂(δq)

+A¯∂(δq)

= 0, δq = (δρ, δu, δp)^т ,

A=^⎣0

1/ρ⎦,

∂t

∂x

ρc²

√

где

γ p/ρ. Отметим, что матрица

A получается из матрицы A системы (10) заменой

функций ρ, u, p на постоянные

ρ,

p. Поэтому выражения для характеристических

переменных получаются из записанных ранее путём аналогичных модификаций.

В характеристических переменных

δr_± = ±δu + δp/(cρ), δr₀ = δρ - δp/c²

линеаризованная система распадается на три независимых друг от друга уравнения переноса

∂(δr_±)

∂(δr₀)

+λ_±

= 0,

+λ₀

= 0,

∂t

∂x

∂t

∂x

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

6^∗

788

АБАКУМОВ, ИСАКОВ

где

λ_± = u ± c,

λ₀ = u. Это позволяет записать известное решение задачи Коши для ли-

неаризованной системы с начальными данными δρ⁰(x), δu⁰(x), δp⁰(x) и отвечающими им

начальными распределениями характеристических переменных δr0±(x), δr⁰⁰(x):

δρ(x, t) =

(δr⁰⁺

ξ₊) + δr0-

ξ_-)) + δr⁰⁰

ξ₀),

cρ

δu(x, t) =

(δr⁰⁺

ξ₊) - δr0-

ξ_-)), δp(x,t) =

(δr⁰⁺

ξ₊) + δr0-

ξ_-)),

гд

ξ_± = x-(u±c)t,

ξ₀ = x-ut. Отметим, что выражения в правых частях равенств несложно

записать через функции δρ⁰, δu⁰ и δp⁰.

Как вытекает из результатов предыдущего пункта, для построения разностной схемы необ-

ходимо записать приближённые выражения для потоков массы, импульса и энергии, фигури-

рующих в исходной системе (9). Для этого также воспользуемся процедурой расщепления

потоков на общую фоновую составляющую и вклады малых прямоугольных возмущений, ко-

торые А.П. Фаворский для краткости именовал “кирпичами”. Чтобы получить формулы при-

ближённого вычисления вкладов возмущений в подынтегральные выражения для потоков, как

и ранее представим потоковые комбинации в виде (на примере потока импульса)

W^I = ρu² + p = (ρ+ δρ)(u + δu)² + p+ δp ≈ ρu² + p+ u²δρ + 2ρuδu + δp = W_I + δW^I.

Выражение для вклада возмущений, в котором отброшены слагаемые второго и третьего по-

рядка малости относительно δρ и δu, запишем на основе известного решения линеаризован-

ной системы:

cρ

δW^I = u²δρ + 2ρuδu + δp = u²

(δr⁰⁺ + δr0-) + u²δr⁰⁰ + ρu(δr⁰⁺ - δr0-) +

(δr⁰⁺ + δr0-) =

ρ(u + c)

ρ(u - c)²

δr⁰⁺ +

δr0- + u²δr⁰⁰.

Здесь аргумент

ξ_±

ξ0 функций δr0± и δr00, отвечающих начальным возмущениям прими-

тивных переменных, опущены. Аналогично получаются формулы приближённого вычисления

вкладов возмущений в подынтегральные выражения для потоков массы и энергии:

ρ(u + c)

ρ(u - c)

δW^M =

δr⁰⁺ +

δr0- + uδr⁰⁰,

)

ρ(u + c)

⁽u

c²

ρ(u - c)

⁽u²

c²

u³

δW^E =

+ uc+

δr⁰⁺ +

- uc+

δr0- +

δr⁰⁰.

γ-1

Отметим, что полученные выражения для вкладов возмущений несложно записать через

функции δρ⁰, δu⁰ и δp⁰. Так, например,

(

)

ρ(u ± c)

δp⁰

ξ_±)

δW^I = δWI+ + δW^I- + δWI0, W^I± =

±δu⁰

ξ_±) +

cρ

(

)

δp⁰

ξ₀)

WI0 = u²

δρ⁰

ξ₀) -

(11)

c²

Это может быть удобным, поскольку в оригинальной схеме А.П. Фаворского реконструируют-

ся функции примитивных переменных.

Сама же схема строится аналогично описанному выше. На той же равномерной простран-

ственно-временной сетке определяется векторная сеточная функция

xi+1/2∫

yⁿⁱ =

u(x, t_n) dx, u = (ρ, ρu, ρe)^т.

xi-1/2

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

О КВАЗИАКУСТИЧЕСКОЙ СХЕМЕ А.П. ФАВОРСКОГО

789

В точном интегральном соотношении

h(yn+1i - yⁿⁱ) + wni+1/2 - wni-1/2 = 0,

где

∫

wni+1/2 =

W(xi+1/2, t) dt, W = (ρu, ρu² + p, ρue + up),

интегральные по времени потоки wni+1/2 заменяются на их приближённые выражения wni+1/2.

Эти выражения получаются путём реконструкции каждой из примитивных переменных f ∈

∈ {ρ, u, p} в ячейках сетки:

f_x|f_x| + f_x|f_x|

fⁿⁱ(x,t_n) = fⁿⁱ + (x - x_i)Dⁿⁱ, Dⁿⁱ =

|f_x| + |f_x|

Здесь fⁿⁱ выражаются через известные значения компонент yⁿⁱ. Далее для каждой пере-

менной выбирается фоновое значение

fni+1/2 и разбиваются реконструированные профили по

разные стороны от границы ячеек xi+1/2 на малые прямоугольные возмущения так же, как

описано в п. 2. Важно отметить, что количество слоёв разбиения M для всех переменных одно

и то же. Приближённые выражения для интегральных потоков в соответствии с проведёнными

выше построениями имеют вид

∫

∑

wni+1/2 =

τ+

(δW₊ + δW_- + δW₀)nm,i+1/2 dt,

i+1/2

m=1 tn

= (ρu, ρu² + p,γup/(γ - 1) + ρu³/2)ni+1/2.

i+1/2

Здесь индекс m по-прежнему обозначает номер слоя разбиения. Интегрирование сводится к

нахождению площадей тех частей прямоугольных возмущений, которые, двигаясь с соответ-

ствующей характеристической скоростью по своему индивидуальному фону (т.е. значения ρ,

ξ в выражениях (11) различны для разных номеров m), пересекли границу ячейки

xi+1/2 за время τ = tn+1 - tn.

Заключение. В работе приведены обоснования основных подходов, использованных при

построении квазиакустической разностной схемы для уравнений газовой динамики, предло-

женной А.П. Фаворским. Результаты численных расчётов (некоторые содержатся в работах

А.П. Фаворского, перечисленных во введении), а также возможные модификации описанной

схемы в рамках данной статьи не обсуждаются. Указанные вопросы предполагается рассмот-

реть в последующих публикациях.

СПИСОК ЛИТЕРАТУРЫ

1. Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. Berlin, 1999.

2. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения

гиперболических систем уравнений. М., 2001.

3. Годунов С.К. Разностный метод численного расчёта разрывных решений гидродинамики // Мат.

сб. 1959. Т. 47 (89). № 3. С. 271-306.

4. Магомедов К.М., Холодов А.С. Сеточно-характеристические численные методы. М., 1988.

5. Фаворский А.П., Тыглиян М.А., Тюрина Н.Н., Галанина А.М., Исаков В.А. Численное моделиро-

вание распространения акустических импульсов в гемодинамике // Дифференц. уравнения. 2009.

Т. 45. № 8. С. 1179-1187

6. Фаворский А.П., Тыглиян М.А., Тюрина Н.Н., Галанина А.М., Исаков В.А. Численное моделиро-

вание распространения гемодинамических импульсов // Мат. моделирование. 2009. Т. 21. № 12.

С. 21-34.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023

790

АБАКУМОВ, ИСАКОВ

7. Абакумов М.В., Галанина А.М., Исаков В.А., Тюрина Н.Н., Фаворский А.П., Хруленко А.Б. Ква-

зиакустическая схема для уравнений Эйлера газовой динамики // Дифференц. уравнения. 2011.

Т. 47. № 8. С. 1092-1098.

8. Исаков В.А., Фаворский А.П. Квазиакустическая схема для уравнений Эйлера газовой динамики в

случае двух пространственных измерений // Мат. моделирование. 2012. Т. 24. № 12. С. 55-59.

9. Галанина А.М., Исаков В.А., Тюрина Н.Н., Фаворский А.П. Конструктивный подход к численному

решению квазилинейных уравнений переноса // Мат. моделирование. 2013. Т. 25. № 8. С. 80-88.

10. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М., 2004.

11. Courant R., Friedrichs K., Lewy H. Uber die partiellen Differenzengleichungen der mathematischen

Physik // Mathematische Annalen. 1928. Bd. 100. № 1. S. 32-74.

12. Самарский А.А. Теория разностных схем. М., 1989.

13. Lax P.D., Wendroff B. Difference schemes for hyperbolic equations with high order of accuracy // Comm.

on Pure and Appl. Math. 1964. V. 17. № 3. P. 381-398.

14. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой

динамике. М., 1978.

15. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 4. Гидродинамика. М., 1986.

Московский государственный университет

Поступила в редакцию 20.02.2023 г.

имени М.В. Ломоносова

После доработки 30.03.2023 г.

Принята к публикации 18.04.2023 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59

№6

2023