ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 6, с.791-802
ЧИСЛЕННЫЕ МЕТОДЫ
УДК 519.63
ЗАДАЧА О НЕИДЕАЛЬНОМ ТЕПЛОВОМ КОНТАКТЕ
© 2023 г. М. П. Галанин, А. С. Родин
Рассмотрена задача определения термомеханического состояния твэла в ядерном реакто-
ре. Описан конечно-элементный алгоритм решения тепловой задачи совместно с задачей
о механическом контакте, для выяснения основных особенностей и численного алгорит-
ма решения которой исследована модельная одномерная задача. Построены главный член
асимптотического разложения решения такой задачи и разностная схема для её решения,
в том числе итерационные методы. Выполнен цикл тестовых расчётов, подтверждающих
теоретические оценки. Сопоставление расчётов реальных задач с теоретическими пред-
сказаниями показало, что алгоритм решения многомерной нелинейной задачи качественно
соответствует поведению одномерных вычислений.
DOI: 10.31857/S0374064123060092, EDN: FHVDJZ
1. Введение и постановка задачи. Рассмотрим в многомерном пространстве конструк-
⋃N
цию из N тел, занимающую область G =
Gα с границей ∂G
(G = G⋃ ∂G). Нас
α=1
интересует температура этих тел.
Начально-краевая задача для нелинейного уравнения теплопроводности задана следующи-
ми соотношениями [1, c. 159]:
∂T
c(x, T )
= (λij (x, T )T,j),i + φ(x, t), (x, t) ∈ G × (0, tM ],
∂t
T (x, 0) = T0(x), x ∈G,
T (x, t)|S1 = Tw(x, t), x ∈ S1 ⊂ ∂G, t > 0,
-niλij(x,T)T,j|S2 = qw(x,t), x ∈ S2 ⊂ ∂G, t > 0.
(1)
Здесь xi - компоненты радиус-вектора x, t - время, T (x, t) - температура, T,j = ∂T /∂xj ,
T0(x) - начальная температура, λij(x,T) - компоненты тензора теплопроводности среды (для
изотропного случая λij(x, T ) = λ(x, T )δij ), φ(x, t) - мощность внутренних источников (сто-
ков) тепла, c(x, T ) - объёмная теплоёмкость среды, Tw(x, t) - температура поверхности S1,
на которой задано условие первого рода, qw(x, t) - плотность теплового потока на поверхности
S2, на которой задано условие второго рода, ni - компоненты единичного вектора внешней
нормали n = niei к границе ∂G.
На поверхности S3 заданы условия третьего рода
-niλij(x,T)T,j|S3 = α(x,T,χ)(T(x,t) - Tf(x,t)), x ∈ S3 ⊂ ∂G, t > 0,
(2)
где α(x, T, χ) - коэффициент теплоотдачи, Tf (x, t) - температура среды у поверхности S3.
При решении тепловой контактной задачи в качестве температуры среды Tf (x, t) будем
рассматривать температуру в противолежащей точке x соседнего контактирующего тела. Ко-
эффициент теплоотдачи α может зависеть от ряда дополнительных параметров, обозначен-
ных χ (в роли подобных параметров выступают величина зазора между телами, контактное
давление, размер шероховатости поверхности и т.д.).
Наряду с неидеальным тепловым контактом между телами, также рассмотрим ситуацию
идеального теплового контакта на поверхности, когда в противолежащих точках контактиру-
ющих поверхностей должны совпадать и температуры, и тепловые потоки [2]:
T (x, t) = T (x, t) = Tcont(x, t),
-niλij(x,T)T,j|S3 = niλij(x,T)T,j|S3 = qcont(x,t), x ∈ S3 ⊂ ∂G, t > 0.
(3)
Величины Tcont и qcont в условиях (3) заранее неизвестны и должны быть определены
в ходе решения задачи. В случае неидеального контакта неизвестны температуры на обеих
контактных поверхностях, а тепловой поток связан с температурами соотношением (2).
791
792
ГАЛАНИН, РОДИН
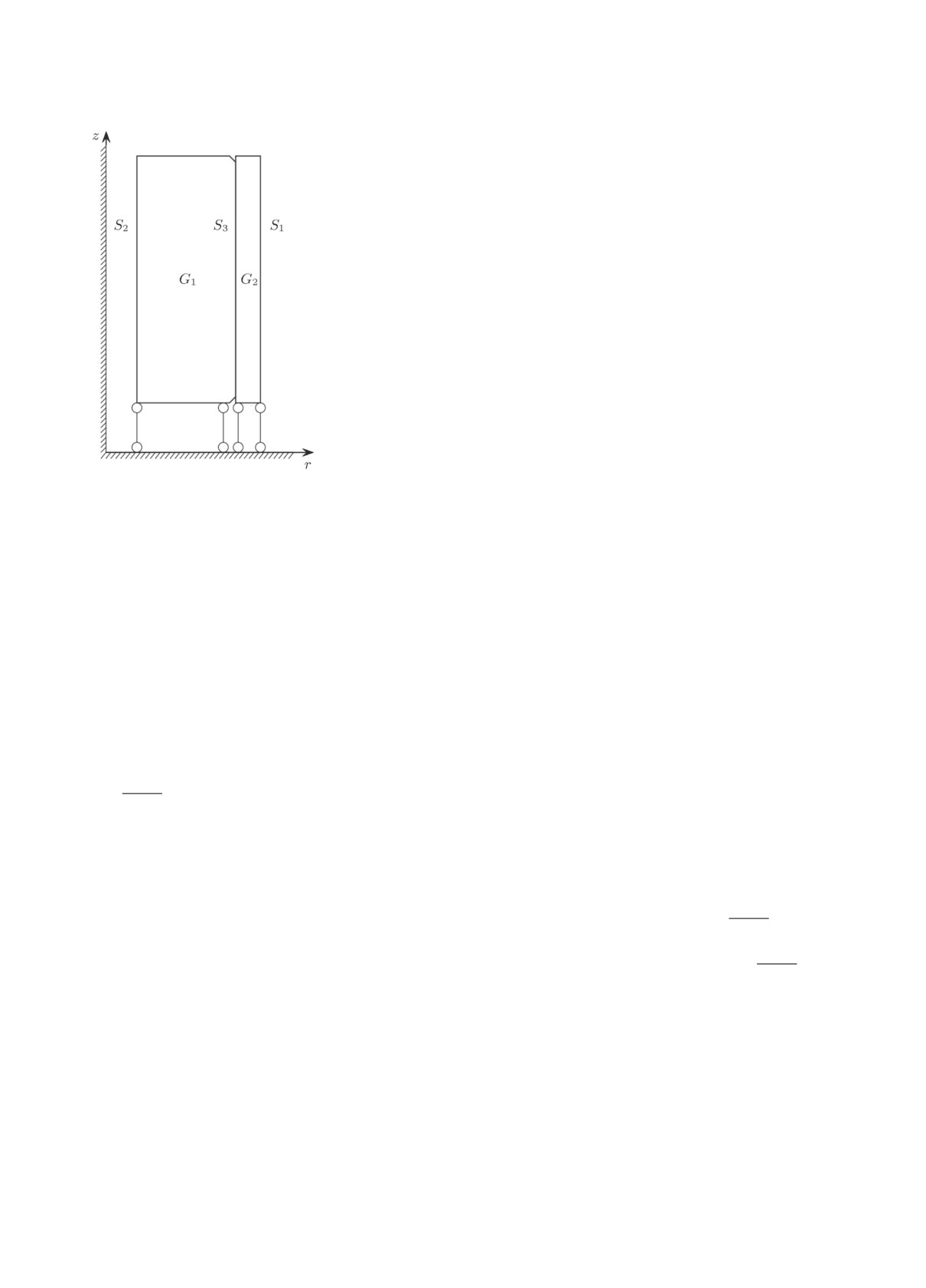
В дальнейшем нас будет интересовать задача моделирова-
ния термомеханического состояния участка тепловыделяющего
элемента (твэла). Область моделирования представляет собой
участок цилиндрической оболочки GN , внутри которой распо-
ложен столб из одинаковых цилиндрических топливных табле-
ток G1, . . . , GN-1, имеющих внутреннее отверстие и фаски
на обоих торцах. Задача часто решается в осесимметричной
постановке. Пример расчётной области для случая N = 2 (по-
ловина продольного сечения) показан на рис. 1. При моделиро-
вании твэла важную роль играет учёт тепловыделения в топ-
ливных таблетках и процесс теплообмена между таблетками и
оболочкой (на рис. 1 соответствующие поверхности обозначены
S3), а также между оболочкой и теплоносителем, находящим-
ся снаружи элемента. Теплофизические характеристики мате-
риалов топливной таблетки и оболочки существенно зависят
от температуры. При определённых допущениях можно счи-
тать, что температура теплоносителя является постоянной (и
известной) и совпадает с температурой внешней поверхности
Рис. 1. Схема участка твэла с
оболочки (обозначена S1 на рис. 1). На других поверхностях
одной таблеткой.
таблеток, кроме внешней, обычно ставятся условия теплоизо-
ляции (нулевого потока).
В начальной конфигурации твэла между таблетками и оболочкой, как правило, существует
зазор. При нагревании таблетки расширяются, зазор уменьшается, а затем чаще всего происхо-
дит механический контакт между таблетками и оболочкой. Значения коэффициента теплоот-
дачи для случая, когда механического контакта нет, и случая, когда он есть, могут отличаться
на два порядка. Поэтому тепловая и механическая задачи являются связанными и их нужно
решать вместе. В данной работе основное внимание будет уделено решению тепловой задачи.
Постановка механической задачи контактного взаимодействия элементов твэла и описание
различных численных методов решения поставленной задачи приведены в статьях [3, 4].
Целью работы является исследование решения задачи о неидеальном тепловом контакте,
разработка и применение методов её численного решения.
2. Численная модель. Для дискретизации задачи (1), (2) по пространству используем
метод конечных элементов (МКЭ) [5]. Построим в расчётной области четырёхугольную сетку
и каждому узлу p (в глобальной нумерации) поставим в соответствие финитную функцию Np,
p = 1,Ku, Ku - глобальное число узлов сетки конечно-элементной модели. Тогда температуру
˜
и её производные по координатам и времени
T,
T,i,
T) на сетке можно интерполировать с
помощью следующих соотношений:
˜
T = [N]{T},
T,i = [N,i]{T},
T =[N]
T }.
Здесь [N] - матрица-строка, составленная из финитных функций Np, p = 1, Ku;
{T } -
вектор-столбец, составленный из узловых значений температуры Tp;
T} - вектор-столбец,
˙
составленный из узловых значений производных температуры по времени
T
p, p = 1,Ku.
После дискретизации по пространству задачу (1) можно свести к системе обыкновенных
дифференциальных уравнений [5]
[C]
T} + [K]{T} = {R}
(4)
с начальным условием
{T }|t=0 = {T0}.
Здесь использованы следующие стандартные обозначения [5]: [C] - глобальная матрица теп-
лоёмкости, [K] - глобальная матрица теплопроводности, {R} - глобальный вектор узловых
тепловых усилий.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЗАДАЧА О НЕИДЕАЛЬНОМ ТЕПЛОВОМ КОНТАКТЕ
793
Для решения системы (4) выберем неявную схему дискретизации по времени:
}
T -T
C]
+[K]
T} = { R},
(5)
τ
где величины с “крышкой” относятся к новому шагу по времени, а величины без “крышки” -
к предыдущему.
Система уравнений (5) является нелинейной из-за зависимости характеристик материала
от температуры. Для линеаризации применим метод простой итерации [6, с. 88].
При наличии теплового контакта значения величины Tf в точках численного интегри-
рования поверхностного элемента соответствуют значениям температуры в противолежащих
точках, относящихся к другим телам. Возможны два алгоритма учёта теплового контакта. В
первом алгоритме значения Tf берутся из новой итерации, поэтому соответствующие слагае-
мые войдут в матрицу системы (5), при этом получается одна система линейных уравнений для
всей конструкции (блоки, относящиеся к разным телам, будут взаимно связаны). Во втором
алгоритме значения Tf берутся из предыдущей итерации, тогда итоговая система линейных
уравнений на (s + 1)-й итерации принимает вид
}
T(s+1) - T
C](s)
+[K](s)
T}(s+1) ={R}(s).
(6)
τ
Система (6) разбивается на N независимых подсистем уравнений (для каждого тела),
которые можно решать отдельно друг от друга. Для конструкций, которые включают в се-
бя большое количество тел (например, для твэла количество топливных таблеток достигает
нескольких сотен), данное свойство второго алгоритма представляется весьма перспектив-
ным, но эффективность его применения зависит от особенностей сходимости итерационного
процесса.
При численном решении задачи с идеальным тепловым контактом (1), (3) можно использо-
вать итерационные алгоритмы, являющиеся аналогами методов декомпозиции области (МДО)
[7]. В МДО единое тело разбивается на ряд непересекающихся подобластей (есть варианты и
для случаев пересекающихся подобластей), исходное уравнение в частных производных реша-
ется отдельно в каждой подобласти, а граничные условия на внутренних границах подобластей
корректируются на каждой итерации таким образом, чтобы общее решение задачи и его про-
изводные по нормали к данным границам менялись непрерывным образом при переходе из
одной подобласти в другую.
В качестве подобного метода используем аналог метода Дирихле-Неймана, который за-
ключается в том, что на (s + 1)-й итерации для пары контактирующих тел последовательно
решаются следующие задачи:
а) для первого тела
(s+1)
}
T1
−T1
C1](s)
+[K1](s)
T1}(s+1) = {R1}(s)
(7)
τ
с условием, что в узлах на поверхности S3 первого тела выполнены равенства
T(s)2,i - темпе-
ратура второго тела в точке, противолежащей узлу с номером i)
T(s+1)1,i
T(s)2,i;
(8)
б) для второго тела
(s+1)
}
T2
−T2
C2](s)
+[K2](s)
T2}(s+1) = {R2}(s) + {Rcont}(s+1),
(9)
τ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
794
ГАЛАНИН, РОДИН
где
{Rcont}(s+1) - глобальный вектор узловых контактных тепловых усилий, учитывающий
интеграл от теплового потока q(s+1)cont по поверхностным элементам, относящимся к контактной
поверхности S3 второго тела.
В узлах численного интегрирования поверхностного элемента с номером (e) тепловой по-
ток равен (с обратным знаком) значению теплового потока в противолежащей точке первого
тела:
q(e),(s+1)cont,i = -q(s+1)1,i.
(10)
Таким образом, на поверхности S3 всегда выполнено второе условие (3), а в ходе итераци-
онного процесса с нужной точностью достигается и выполнение первого условия (3) (равенство
температур).
Аналогичный итерационный алгоритм применён в статье [2] для решения задачи об иде-
альном тепловом контакте между летательным аппаратом и газовой средой. В расчётах ис-
пользовались линейные конечные элементы на четырёхугольной сетке.
Для изучения особенностей задачи (1), (2) рассмотрим более простую модельную задачу.
3. Модельная одномерная задача. Рассмотрим следующую одномерную задачу о теп-
лообмене между двумя областями:
c1T1,t = λ1T1,xx,
-l < x < 0, t > 0,
T1(x,0) = T10(x), T1,x(-l,t) = 0,
c2T2,t = λ2T2,xx,
0 < x < L, t > 0,
T2(x,0) = T20(x), T2,x(L,t) = 0,
λ1T1,x(0,t) = λ2T2,x(0,t) = α(T2(0,t) - T1(0,t)).
(11)
Далее участок x ∈ (-l, 0) будем называть областью 1, а участок x ∈ (0, L) - областью 2.
Все теплофизические параметры (ci, λi, i = 1, 2, α) постоянны. Делаем допущение, что
коэффициент теплообмена α = 1/ε велик, т.е. ε мало. Все величины считаем безразмерными.
Решение задачи (11) для произвольных начальных данных может быть получено мето-
дом Фурье в виде бесконечных рядов по системе собственных функций. Однако анализ этого
решения и его применение для численного решения более сложных задач представляется за-
труднительным, поэтому воспользуемся асимптотическими методами [8] с учётом малости ε.
Дальнейшее изложение будем вести в основном (по возможности) в терминах задачи (11)
в области 1.
Введём новые переменные:
τ = t/ε2, ξ = x/ε, ξl = (l + x)/ε, ξL = (L - x)/ε.
Будем искать T1 - часть решения задачи (11) в области 1 - в виде
T1(x,t) = U1(x,τ) + Π1(ξ,τ) + P1(ξl,τ).
(12)
Аналогичное представление будем использовать для части решения T2 с заменой индекса 1
на 2 и ξl на ξL.
Подставив такие решения в (11) и разделив соответствующие выражения по переменным,
от которых зависят части решения (12), получим задачи
c1U1,τ = ε2λ1U1,xx,
-l < x < 0, τ > 0,
U1(x,0) = T10(x);
(13)
c1Π1,τ = λ1Π1,ξξ,
-∞ < ξ < 0, τ > 0,
Π1(ξ,0) = 0,
ελ1U1,x(0, τ) + λ1Π1,ξ(0, τ) = U2(0, τ) + Π2(0, τ) - U1(0, τ) - Π1(0, τ);
(14)
c1P1,τ = λ1P1,ξlξl ,
0 < ξl < ∞, τ > 0,
P1(ξl,0) = 0, εU1,x(-l,τ) + P1,ξl (0,τ) = 0.
(15)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЗАДАЧА О НЕИДЕАЛЬНОМ ТЕПЛОВОМ КОНТАКТЕ
795
Погранслойные функции Π1 и P1 появились в (12) вследствие необходимости обеспечить
условия (11) на границах x = -l и x = 0. Задача (14) должна решаться одновременно с
соответствующей задачей в области 2, поскольку функции Π1(0, τ) и Π2(0, τ) фигурируют в
условии теплообмена на границе ξ = 0.
Будем далее искать решения задач (13)-(15) в виде
∑
∑
∑
U1 = Ui1εi, Π1 =
Πi1εi, P1 =
Pi1εi.
(16)
i=0
i=0
i=0
Решение в области 2 представим аналогичным образом.
Как и в работе [8], от погранслойных функций потребуем стремления к нулю на бесконеч-
ности (по ξ, ξl и ξL).
Для коэффициентов при i = 0 из (13)-(16) получим
U01(x,τ) = T10(x), P01(ξl,τ) = 0.
Условие на границе раздела областей 1 и 2 из (14) запишется в виде
λ1Π01,ξ(0,τ) = T20(0) + Π02(0,τ) - T10(0) - Π01(0,τ).
(17)
Аналогичное условие можно записать и для Π02.
Обе функции Π01 и Π02 удовлетворяют однородным уравнениям теплопроводности с ну-
левыми начальными условиями. Решения этих задач могут быть получены, например, с по-
мощью преобразования Лапласа либо взяты в готовом виде из [9, с. 27]. Они имеют вид
[ (
)
(
)]
T20(0) - T10(0)
k1
ξ
ξ
Π01(ξ,τ) =
erfc
-
- exp(-βk1ξ + β2τ) erfc β
√τ -k1
,
1+κ
2
√τ
2
√τ
[
)
(
)]
T20(0) - T10(0)
(k2
ξ
ξ
Π02(ξ,τ) = -κ
erfc
- exp(-βk2ξ + β2τ) erfc β
√τ +k2
(18)
1+κ
2
√τ
2
√τ
Здесь использованы обозначения функции из [10] и
√
∫
∞
c1λ1
1+κ
√ci
2
κ=
,
β =
,
i = 1,2, erfc(z) =
c2λ2
√c1λ1 ,ki =
λi
√πe-t2 dt.
z
Для коэффициентов при i = 1 из (16) получим, что U11(x, τ) = 0, P11(ξl, τ) - решение
начально-краевой задачи для уравнения теплопроводности на полубесконечном участке. Оно
определяется значением T10,x(-l) и может быть легко получено. Коэффициенты Π11 и Π12
находятся совместно из решения задач на бесконечном участке. При этом на границе областей
будет выполнено условие типа (17). Решение этой задачи весьма громоздко, поэтому мы его
не приводим.
Справедливо следующее
Утверждение 1. Для задачи теплообмена между двумя полубесконечными участками
(l → +∞, L → +∞) с постоянными начальными данными (T10(x) = T01, T20(x) = T02)
точное решение задачи (11) задаётся формулами
T1(x,t) = T01 + Π01(ξ,τ), T2(x,t) = T02 + Π02(ξ,τ).
(19)
Как упоминалось ранее, решение задачи (11) для произвольных начальных данных может
быть получено методом Фурье в виде бесконечных рядов по системе собственных функций.
Для специально подобранных начальных условий решение можно представить в компактной
форме.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
796
ГАЛАНИН, РОДИН
Утверждение 2. Для задачи (11) с начальными условиями
)
(√
)
(√ c1
c2
T10(x) = A1 cos
ω(x + l)
,
T20(x) = A2 cos
ω(L - x)
λ1
λ2
точное решение задаётся формулами
)
(√
)
(√ c1
c2
T1(x,t) = A1e-ω2t cos
ω(x + l)
,
T2(x,t) = A2e-ω2t cos
ω(L - x)
(20)
λ1
λ2
В (20) коэффициенты A1 и A2 связаны соотношением
)∕
(√
)
√
(√ c1
c2
A2 = -A1
1λ1 sin
ωl
sin
ωL ,
λ1
λ2
а ω - это решение уравнения, являющегося условием нетривиальности решения (20). Оно
есть следствие подстановки (20) в граничное условие (11) в точке контакта.
Исследуем алгоритм численного решения модельной задачи, чтобы оценить его особенно-
сти. Применим метод конечных разностей [11]. Используем следующие обозначения для i-го
тела [8]: τ - шаг сетки по времени, hi - постоянный шаг пространственной сетки,
ŷi,0
-
значение сеточной функции для температуры в узле с номером 0, относящееся к новому вре-
менному слою, yi,0 - аналогичное значение сеточной функции, относящееся к предыдущему
временному слою. Обозначения сеточных функций и операторов соответствуют [11].
Возьмём полностью неявную разностную схему, записав её интегро-интерполяционным спо-
собом в граничных точках. Уравнения в нулевых точках областей 1 и 2 имеют вид
0.5h1c1y1,0,t = α(ŷ2,0 - ŷ1,0) - λ1(ŷ1,0 - ŷ1,1)/h1,
0.5h2c2y2,0,t = -α(ŷ2,0 - ŷ1,0) + λ2(ŷ2,0 - ŷ2,1)/h2.
(21)
Справедливо следующее
Утверждение 3. Построенная разностная схема (21) удовлетворяет условиям принципа
максимума [11, с. 226] со строгим диагональным преобладанием коэффициентов. Её решение
существует, единственно и непрерывно зависит от входных данных.
В ситуации, когда численное решение для каждого тела находится по отдельности, необхо-
димо проводить итерационный учёт условия неидеального теплового контакта (21). Обозначим
индексом s вверху итерационные приближения для ŷ1,
ŷ2 на s-й итерации. Во всех уравне-
ниях разностной схемы (21), кроме граничных условий, будем разыскивать
y2 . Первое
уравнение (21) заменим на следующее:
0.5h1c1(s+1y1,0 - y1,0)/τ = α(sy2,0 -
y1,0 -
s+1y1,1)/h1.
(22)
Аналогичным образом заменим второе уравнение в (21).
Введём обозначения:
s
s
s
s
s
s
s
δyi = ŷi -
yi,
∥δyi∥c = max {|δyi,j|},
∥δ
y∥c = max{∥δy1∥c,∥δy2∥c}.
0≤j≤ni
Вычитая из (21) уравнение (22) (и так же для второго тела) и поступая аналогично с
другими уравнениями схемы, получаем следующее
Утверждение 4. Имеет место оценка
{
}
α
α
∥δ
s+1y∥c ≤ q1∥δsy∥c,q1 = max
,
(23)
α + 0.5h1c1/τ
α + 0.5h2c2/τ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЗАДАЧА О НЕИДЕАЛЬНОМ ТЕПЛОВОМ КОНТАКТЕ
797
Из данной оценки следует сходимость алгоритма для любых значений параметров. Однако
для больших значений α сходимость будет медленной, если только τ не берётся достаточно
малым.
Можно рассмотреть ситуацию, когда тепловой поток между телами в уравнении (22) пол-
ностью берётся из предыдущей итерации. Тогда (22) принимает вид (для второго тела анало-
гично)
0.5h1c1(
y1,1)/h1.
(24)
Для подобного алгоритма справедливо
Утверждение 5. Имеет место оценка
}
{ 4ατ
4ατ
∥δ
s+1y∥c ≤ q2∥δsy∥c, q2 = max
,
(25)
h1c1
h2c2
Из этой оценки следует очень жёсткое условие на сходимость итерационного процесса (q2 <
< 1), которое при больших значениях α, скорее всего, не позволит проводить расчёт с жела-
емыми значениями шагов по времени.
В [6] отмечено, что для случаев простых областей и регулярных сеток численные схемы,
полученные на основе применения МКЭ, аналогичны соответствующим численным схемам,
полученным на основе конечно-разностного подхода. Можно ожидать, что на качественном
уровне утверждения о сходимости итерационных алгоритмов (23) и (25) будут справедливы и
для конечно-элементного алгоритма, изложенного в п. 2.
4. Результаты расчётов.
4.1. Решение тестовых задач. Рассмотрим решение задачи теплообмена между одной
топливной таблеткой (тело 1) и участком оболочки (тело 2), имеющим такую же высоту, что
и таблетка (см. рис. 1). Считаем, что на всех участках поверхности задан нулевой поток,
кроме внешней поверхности таблетки и внутренней поверхности оболочки, на которых постав-
лено условие телообмена (2). Для сравнения с аналитическими решениями, полученными в
п. 3, полагаем, что у таблетки нет фасок, мощность тепловыделения равна нулю, тепловые
характеристики не зависят от температуры (ci(T ) = ci(T0), λi(T ) = λi(T0)), коэффициент
теплоотдачи является постоянным, а вся задача рассматривается в плоской постановке. С
принятыми допущениями полученное численное решение не зависит от второй координаты и
соответствует модельной одномерной задаче (11).
Тест 1. Выполним серию расчётов на различных сетках, чтобы исследовать поведение
погрешности численного решения относительно аналитического решения, заданного в (18),
(19). Значения параметров, использованных в расчётах (в безразмерных величинах): протя-
жённость первого тела l = 3.0, протяжённость второго тела L = 0.7, c1 = 2467, λ1 = 8380,
c2 = 20960, λ2 = 17600, начальные температуры T10 = 300, T20 = 623. Моделировался ин-
тервал времени продолжительностью 0.02, существенно меньший, чем характерное время, за
которое изменение температуры доходит от левого края оболочки до правого (L2c2/λ2 ≈ 0.58).
Можно считать, что задача для областей конечных размеров на рассматриваемых временах
соответствует задаче о теплообмене между двумя полубесконечными областями.
Были использованы сетки:
расчёт 1 (h1 = h2 = 0.1, τ = 10-3);
расчёт 2 (h1 = h2 = 0.05, τ = 2.5 · 10-4);
расчёт 3 (h1 = h2 = 0.025, τ = 6.25 · 10-5).
В табл. 1 приведены абсолютные погрешности решения в момент времени t = 0.02 для
разных сеток и разных значений коэффициента теплоотдачи α.
Таблица 1. Погрешности численного решения. Тест 1
Расчёт 1
Расчёт 2
Расчёт 3
α
error1/error2
error2/error3
(error1)
(error2)
(error3)
2.5 · 104
1.050
0.245
0.062
4.28
3.95
2.5 · 106
1.502
0.330
0.085
4.54
3.88
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
798
ГАЛАНИН, РОДИН
Из приведённых в табл. 1 ошибок для разных расчётов видно, что погрешность численного
решения убывает по зависимости, близкой к O(h2 + τ). Это соответствует теоретическим
представлениям о схеме с использованием линейных конечных элементов для дискретизации
по пространству и схеме 1 порядка для дискретизации по времени.
Тест 2. Выполним серию расчётов на различных сетках, чтобы исследовать поведение
погрешности численного решения относительно аналитического решения, заданного (20). Па-
раметры расчётов и использованные сетки соответствуют тесту 1. В аналитическом решении
выбрано значение свободного параметра A1 = 1. Моделировался интервал времени продолжи-
тельностью 0.05, за это время максимальное значение температуры в областях уменьшилось
примерно в 7 раз. В табл. 2 приведены абсолютные погрешности решения в момент времени
t = 0.05 для разных сеток и разных значений α.
Из приведённых в табл. 2 соотношений ошибок для разных расчётов видно, что для зна-
чения α = 2.5 · 104 погрешность численного решения по-прежнему убывает по зависимости,
близкой к O(h2 + τ), но для α = 2.5 · 106 скорость уменьшения ошибки замедляется.
Таблица 2. Погрешности численного решения. Тест 2
Расчёт 1
Расчёт 2
Расчёт 3
α
error1/error2
error2/error3
(error1)
(error2)
(error3)
2.5 · 104
8.07 · 10-3
2.03 · 10-3
5.09 · 10-4
3.97
3.99
2.5 · 106
1.21 · 10-2
5.06 · 10-3
3.61 · 10-3
2.39
1.41
Тест 3. Выполним серию расчётов, чтобы исследовать характер сходимости итерационно-
го процесса, учитывающего условия неидеального теплового контакта между двумя телами.
Считаем, что на внешней поверхности оболочки поставлено условие первого рода (T = 623),
мощность тепловыделения в таблетке постоянна по пространству, по времени меняется по ли-
нейному закону от нуля до номинального значения за интервал времени, равный 3600, а затем
остаётся постоянной. Моделировался интервал времени продолжительностью 3600. Задача
решалась в осесимметричной постановке, все остальные параметры такие же, как в тесте 1.
В расчётах применялась сетка с шагами h1 = h2 = 0.1, τ = 360. Для контроля сходимости
использовалась оценка
Ts+1
Ts∥c ≤ ε0.
В табл. 3 приведено характерное количество итераций за один шаг по времени для различ-
ных значений ε0 и α.
Таблица 3. Количество итераций в тепло-
вой задаче за один шаг по времени. Тест 3
ε0
α = 104
α = 105
α = 106
10-2
12
46
236
10-3
16
66
414
10-4
20
86
594
Выясним, как в проведённых расчётах при увеличении α меняется количество итераций,
необходимых для уменьшения величины
Ts+1
T∥c в 10 раз. Сравним полученный резуль-
тат с теоретической оценкой, приведённой в (23). Согласно (23) нас интересует количество
итераций k такое, что qk1 = 10-1, т.е. k = -(lg q1)-1. Для использованных параметров за-
дачи при увеличении коэффициента α от 104 до 105 количество итераций из оценки (23)
должно возрасти примерно в 10 раз. Аналогичная ситуация наблюдается при увеличении ко-
эффициента α от 105 до 106. В проведённых расчётах при повышении коэффициента α
от 104 до 105 количество итераций изменилось с 4 до 20, т.е. возросло в 5 раз. При изме-
нении коэффициента α от 105 до 106 количество итераций увеличилось в 9 раз - с 20 до
180. Таким образом, на качественном уровне зависимость скорости сходимости алгоритма от
коэффициента α соответствует формуле (23), полученной для тестовой одномерной задачи.
При попытке решить задачу по алгоритму, в котором тепловой поток целиком брался из
предыдущей итерации (аналогично (24)), численное решение разваливалось. Это соответству-
ет оценке сходимости (25), поскольку в таком случае коэффициент q2 значительно больше
единицы.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЗАДАЧА О НЕИДЕАЛЬНОМ ТЕПЛОВОМ КОНТАКТЕ
799
Если решать задачу с условием идеального теплового контакта с использованием итераци-
онного алгоритма (7)-(10), то для достижения точности, соответствующей величине ε0 = 10-4,
требовалось 6 итераций.
В табл. 4 приведены значения следующих характеристик расчётов с неидеальным теп-
ловым контактом (для различных α) и с идеальным тепловым контактом в момент времени
t = 3600: температура на внешней поверхности таблетки (Tp), температура на внутренней по-
верхности оболочки (Tc), значение модуля теплового потока (для неидеального контакта он
равен α|Tp - Tc|). Из табл. 4 следует, что для рассмотренного интервала времени при условии
неидеального теплового контакта значение теплового потока между таблеткой и оболочкой,
а также значение температуры на внутренней поверхности оболочки практически не зависят
от коэффициента α и отличаются от соответствующих значений, полученных для условия
идеального теплового контакта, не более чем на 0.013 % (для потока) и на 0.0016 % (для
температуры). В то же время температура внешней поверхности таблетки при уменьшении
значения α может существенно отличаться от температуры оболочки.
Таблица 4. Результаты расчётов с неидеальными и с идеальными
тепловыми контактами
Тепловой контакт
α
Tp
Tc
|qcont |
Неидеальный
104
884.6825
696.2676
1.88416 · 106
Неидеальный
105
715.1190
696.2754
1.88436 · 106
Неидеальный
106
698.1606
696.2762
1.88438 · 106
Идеальный
-
696.2767
696.2767
1.88439 · 106
Выполненный анализ позволяет сделать вывод, что при моделировании твэла в определён-
ных ситуациях для больших значений коэффициента α с вычислительной точки зрения более
предпочтительным является расчёт с идеальным тепловым контактом по алгоритму (7)-(10),
чем расчёт с неидеальным тепловым контактом по алгоритму (5).
4.2. Результаты моделирования участка твэла. Рассмотрим решение связанной тер-
момеханической задачи взаимодействия элементов твэла. В расчётную область (см. рис. 1)
входят M топливных таблеток с фасками и находящийся напротив них участок оболочки
(N = M + 1). Считаем, что между внешними поверхностями таблеток и внутренней поверх-
ностью оболочки происходит теплообмен. Коэффициент теплоотдачи α зависит от величины
зазора, разности температур в двух противолежащих точках, контактного давления и ряда
иных факторов. Другие тепловые характеристики зависят от температуры (ci(T ),λi(T )). Со-
ответствующие зависимости взяты из библиотеки MATPRO [12]. Остальные тепловые условия
задачи такие же, как в тесте 3. Моделировался интервал времени продолжительностью 3600.
Для решения механической задачи контактного взаимодействия таблеток друг с другом и
с оболочкой использован метод Дирихле-Неймана [3].
В первой серии расчётов полагалось, что в начальный момент времени между таблетка-
ми и оболочкой существует зазор δ0 = 0.04. В результате нагрева в таблетках образуются
тепловые деформации и зазор уменьшается (это происходит неравномерно относительно оси
z), но механического контакта между таблетками и оболочкой нет (в расчётах учитывает-
ся механический контакт между таблетками). Выполнены расчёты для случаев M = 1, 4, 10.
На каждом шаге по времени итерационный процесс продолжался до выполнения критерия
Ts+1
Ts∥c ≤ 10-2.
В табл. 5 приведены значения следующих характеристик расчёта с одной таблеткой в че-
тыре момента времени: количество итераций в тепловой задаче (в скобках указано количество
итераций для расчёта с десятью таблетками), величина зазора, коэффициент теплоотдачи и
разность температур между двумя противолежащими точками на двух поверхностях для узла
сетки, расположенного вблизи центра боковой поверхности таблетки.
Видно, что с уменьшением зазора значение коэффициента теплоотдачи увеличивается, но
температуры в противолежащих точках могут значительно отличаться. Таким образом, теп-
ловой контакт остаётся существенно неидеальным. Количество итераций в тепловой задаче
для различного количества таблеток изменялось незначительно.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
800
ГАЛАНИН, РОДИН
Таблица 5. Характеристики первой серии расчётов
Количество Величина Коэффициент
Разность
Время
итераций
зазора
теплоотдачи
температур
720
10(10)
0.029
7.61 · 103
48.83
1800
12(12)
0.022
9.93 · 103
93.37
2880
13(13)
0.014
1.39 · 104
106.14
3600
17(18)
0.009
1.90 · 104
97.44
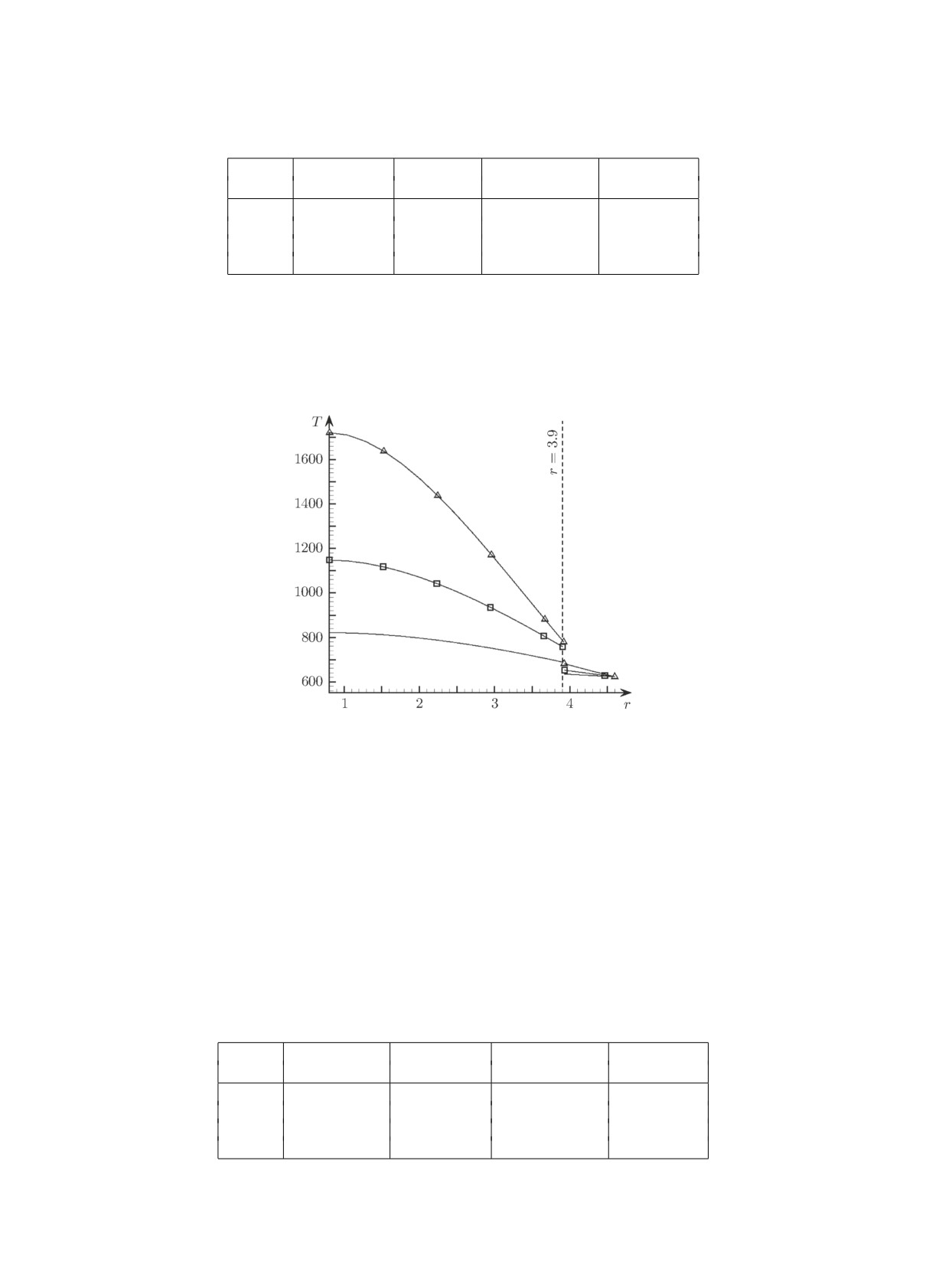
На рис. 2 приведены графики изменения температуры вдоль поперечного сечения, соот-
ветствующего половине высоты таблетки: три для таблетки (Tp, область r < 3.9) и три для
оболочки (Tc, область r ≥ 3.9). Хорошо заметен разрыв по температуре между внешней по-
верхностью таблетки и внутренней поверхностью оболочки вследствие использования условий
неидеального теплового контакта между телами.
Рис. 2. Изменение температуры таблеток Tp (в
области r
< 3.9) и оболочек Tc (в области
r ≥ 3.9) вдоль поперечного сечения для разных
моментов времени: t = 720 (графики без марке-
ра), t = 1800 (графики с квадратным маркером)
и t = 3600 (графики с треугольным маркером).
Во второй серии расчётов полагалось, что в начальный момент времени зазор между таб-
летками и оболочкой равен нулю. В результате нагрева таблетки вступают в механический
контакт с оболочкой. Выполнены расчёты для случаев M = 1, 4, 10.
В табл. 6 приведены значения следующих характеристик расчёта с одной таблеткой в че-
тыре момента времени: количество итераций в тепловой задаче (в скобках указаны количества
итераций для расчётов с четырьмя и десятью таблетками), контактное давление, коэффици-
ент теплоотдачи и разность температур между двумя противолежащими точками на двух
поверхностях для узла сетки, расположенного вблизи центра боковой поверхности таблетки.
Таблица 6. Характеристики второй серии расчётов
Количество Контактное Коэффициент
Разность
Время
итераций
давление
теплоотдачи
температур
720
387(393, 393)
26.43
1.04 · 106
0.36
1800
196(262, 498)
38.07
1.44 · 106
0.64
2880
249(398, 701)
52.47
1.94 · 106
0.75
3600
297(438, 499)
64.02
2.33 · 106
0.78
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЗАДАЧА О НЕИДЕАЛЬНОМ ТЕПЛОВОМ КОНТАКТЕ
801
Из проведённых расчётов следует, что с увеличением контактного давления значение ко-
эффициента теплоотдачи возрастает, при этом температуры в противолежащих точках по-
верхностей практически не отличаются друг от друга, т.е. фактически реализуется случай
идеального теплового контакта. Количество итераций в тепловой задаче в расчётах для одной
таблетки и для десяти таблеток отличалось в среднем в 2-2.5 раза.
Если решать задачу с условием идеального теплового контакта с использованием итераци-
онного алгоритма (7)-(10), то для достижения точности, соответствующей величине ε0 = 10-4,
в расчётах с M = 1, 4, 10 требовалось от 14 до 16 итераций на каждом шаге по времени. Зна-
чения температур в узлах на внутренней поверхности оболочки и тепловых потоков между
таблетками и оболочкой в расчётах с разными условиями теплового контакта практически
не отличаются друг от друга на участках вблизи центров поверхностей таблеток. На участ-
ках, расположенных ближе к фаскам таблеток, температуры в разных расчётах отличаются
на 2-3 %.
Приведённые в табл. 5 и 6 данные свидетельствуют, что и для более сложной задачи харак-
тер зависимости сходимости итерационного процесса от величины коэффициента теплоотдачи
качественно соответствует оценке (23).
Заключение. Представлена нелинейная задача о тепловом взаимодействии системы тел.
В качестве граничных условий на противолежащих поверхностях контактирующих тел рас-
смотрены условия как неидеального, так и идеального теплового контакта. Для дискретизации
задачи по пространству использован метод конечных элементов, для дискретизации по вре-
мени применена полностью неявная конечно-разностная схема. Представлены итерационные
алгоритмы, позволяющие свести решение общей задачи к решению систем линейных урав-
нений для каждого тела по отдельности. Для выяснения основных особенностей решения и
численного алгоритма для случая неидеального теплового контакта рассмотрена модельная
одномерная задача, для которой построен главный член асимптотического разложения и ис-
следована разностная схема, в том числе получены оценки скорости сходимости различных
итерационных алгоритмов. Выполнена серия тестовых расчётов на сгущающихся сетках по
пространству и времени. Полученные результаты подтвердили, что численное решение схо-
дится к выведенным точным решениям с ожидаемой скоростью. При увеличении значения
коэффициента теплоотдачи наблюдается кратное увеличение количества итераций, нужное
для достижения требуемой точности. В то же время значения температур и тепловых потоков
на контактирующих поверхностях стремятся к значениям соответствующих величин в задаче
с идеальным тепловым контактом.
С помощью построенных численных алгоритмов решена связанная термомеханическая за-
дача взаимодействия элементов в участке твэла в ядерном реакторе в осесимметричной по-
становке с использованием реалистичных зависимостей для теплофизических характеристик
материалов топливной таблетки и оболочки, взятых из библиотеки MATPRO. Проведена се-
рия расчётов, в которых рассматривался участок, включающий в себя от одной до десяти таб-
леток. Сопоставление расчётов реальных задач с теоретическими предсказаниями показало,
что алгоритм решения многомерной нелинейной задачи качественно соответствует поведению
одномерных вычислений.
Работа выполнена при финансовой поддержке Российского научного фонда (проект 22-21-
00260).
СПИСОК ЛИТЕРАТУРЫ
1. Зарубин В.С., Кувыркин Г.Н. Математические модели механики и электродинамики сплошной сре-
ды. М., 2008.
2. Galanin M.P., Zhukov V.T., Klyushev N.N. Implementation of an iterative algorithm for the coupled heat
transfer in case of high-speed flow around a body // Computers and Fluids. 2018. V. 172. P. 483-491.
3. Галанин М.П., Родин А.С. Исследование и применение метода декомпозиции области для модели-
рования тепловыделяющего элемента // Журн. вычислит. математики и мат. физики. 2022. Т. 62.
№ 4. С. 659-676.
7
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
802
ГАЛАНИН, РОДИН
4. Аронов П.С., Галанин М.П., Родин А.С. Численное решение задачи контактного взаимодействия
элементов твэла с помощью mortar-метода и метода декомпозиции области // Вестн. МГТУ
им. Н.Э. Баумана. Сер. Естественные науки. 2021. № 3. С. 4-22.
5. Бате К.-Ю. Методы конечных элементов. М., 2010.
6. Галанин М.П., Савенков Е.Б. Методы численного анализа математических моделей. М., 2010.
7. Toselli A., Widlund O. Domain Decomposition Methods - Algorithms and Theory. Berlin; Heidelberg,
2005.
8. Васильева А.Б., Бутузов В.Ф. Асимптотические методы теории сингулярных возмущений. М.,
1990.
9. Беляков Н.С., Носко А.П. Неидеальный тепловой контакт тел при трении. М., 2010.
10. Абрамовиц М., Стиган И. Справочник по специальным функциям с формулами, графиками и
математическими таблицами. М., 1979.
11. Самарский А.А. Теория разностных схем. М., 1989.
12. Hagrman D.L., Reymann G.A. A Handbook of Materials Properties for Use in the Analysis of Lightwater
Reactor Fuel Rod Behavior. Idaho, 1979.
Институт прикладной математики
Поступила в редакцию 22.02.2023 г.
имени М.В. Келдыша РАН, г. Москва
После доработки 22.02.2023 г.
Принята к публикации 18.04.2023 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023