ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 6, с.803-813
ЧИСЛЕННЫЕ МЕТОДЫ
УДК 519.633
ЯВНО-НЕЯВНЫЕ СХЕМЫ РАСЧЁТА ДИНАМИКИ
УПРУГОВЯЗКОПЛАСТИЧЕСКИХ СРЕД
С МАЛЫМ ВРЕМЕНЕМ РЕЛАКСАЦИИ
© 2023 г. В. И. Голубев, И. С. Никитин,
Н. Г. Бураго, Ю. A. Голубева
Рассматривается динамическое поведение упруговязкопластических сред под действием
внешней нагрузки. Для общего случая нелинейной функции вязкости, описывающей ско-
ростное упрочнение, строится явно-неявная расчётная схема второго порядка аппроксима-
ции, позволяющая получать численное решение исходной полулинейной гиперболической
задачи. Отличительной особенностью данного подхода является не использование метода
расщепления по физическим процессам. Несмотря на это, был получен явный вычисли-
тельный алгоритм, допускающий эффективную реализацию на современных вычислитель-
ных системах.
DOI: 10.31857/S0374064123060109, EDN: FHXWZC
Введение. Дифференциальная часть систем уравнений, описывающих динамику упруго-
вязкопластических сред [1-4], совпадает с системой уравнений динамической теории упруго-
сти, однако в эти системы входят уравнения (для девиаторных или касательных напряжений,
соответственно), содержащие сильно нелинейный свободный член с характерным временем
релаксации τ в знаменателе.
В нестационарных (и тем более квазистатических) процессах с характерным временем мно-
го большим чем τ упруговязкопластические (УВП) среды ведут себя как упругопластические
(УП), т.е. при τ → 0 УВП системы уравнений переходят в системы типа Прандтля-Рейса [5-7].
Этот факт отмечается во многих работах на физико-механическом [6, 7] или математическом
[8, 9] уровне строгости.
Однако для сильно динамических процессов с характерными временами (≤τ) эффекты
скоростного упрочнения и резкого роста динамического предела текучести проявляют себя в
полной мере [4, 7]. Для их описания требуется использовать полную УВП систему того или
иного типа. Кроме того, УВП системы по своей дифференциальной части заведомо являют-
ся гиперболическими, приводимыми к дивергентному виду, и допускают численное решение
сеточно-характеристическими [10] или конечно-объёмными [11] методами. В то же время УП
системы, к которым сводятся теории пластического течения, не являются дивергентными и
для построения решений, допускающих сильные разрывы, приходится расширять формули-
ровки и классы решений [9, 12], в частности, использовать предельные переходы от УВП к УП
обобщённому решению, при этом результат зависит от выбора “переходной” УВП модели [12,
13]. Таким образом, УВП системы уравнений, с одной стороны, отражают физику динамиче-
ских процессов деформирования, а с другой - обеспечивают регуляризацию недивергентных
УП систем уравнений.
Устойчивое интегрирование определяющих соотношений связи напряжений и деформаций
в УВП системах уравнений по явной схеме для малых времен релаксации τ требует более
сильного ограничения величины временного шага, чем обычное курантовское ограничение.
Устранить это дополнительное ограничение можно с помощью неявных схем расчёта опре-
деляющих соотношений (“жёсткой” части общей УВП системы уравнений). Важно, что опи-
сываемые ниже неявные схемы расчёта определяющих уравнений для УВП сред не требуют
решения систем алгебраических уравнений, и расчёт каждого шага по времени проводится
явно с обычным курантовским шагом по времени.
803
7∗
804
ГОЛУБЕВ и др.
1. Изотропные и анизотропные модели упруговязкопластических сплошных
сред.
1.1. Система уравнений изотропной упруговязкопластической среды. В декар-
товой прямоугольной системе координат xi, i = 1, 2, 3, система уравнений изотропной УВП
среды при малых деформациях имеет вид [1, 4]
(
#
∂vi
∂σij
∂σ
2
)∂vk
∂sij
sij
(√sklskl
)$1
ρ
=
,
= λ+
μ
,
= 2μe′ij - 2μ
F
-1
,
∂t
∂xj
∂t
3
∂xk
∂t
√sklskl
σs
τ
)
)
1
(∂vi
∂vj
1
(∂vi
∂vj
1 ∂vk
eij =
+
,
e′ij =
+
-
δij,
2
∂xj
∂xi
2
∂xj
∂xi
3 ∂xk
sij = σij - σδij, σ = σkk/3, i,j = 1,2,3,
(1)
vi - компоненты вектора скорости, σij - компоненты тензора напряжений, sij - компоненты
девиатора напряжений, σ - среднее напряжение, eij - компоненты тензора скорости дефор-
мации, e′ij - компоненты девиатора скорости деформации,
√sklskl - второй инвариант девиа-
тора напряжений, σs - предел текучести, F (√sklskl/σs - 1) - нелинейная функция вязкости,
описывающая скоростное упрочнение, F ≥ 0, F (0) = 0,
〈F 〉 = F H(F ), H(F ) - функция
Хевисайда, τ - характерное время релаксации компонент девиатора напряжений на поверх-
ность текучести, ρ - плотность среды, λ и μ - модули упругости Ламе. По повторяющимся
индексам проводится суммирование.
1.2. Система уравнений анизотропной упруговязкопластической среды. Система
уравнений анизотропной УВП среды, описывающая динамику слоистой среды с вязкопласти-
ческими условиями скольжения на межслойных контактных границах, перпендикулярных оси
x3, имеет вид [2, 3]
∂vi
∂σij
∂σij
∂vk
∂σ33
∂vk
∂v3
ρ
=
,
=λ
δij + 2μeij, i,j = 3,
=λ
+ 2μ
,
∂t
∂xj
∂t
∂xk
∂t
∂xk
∂x3
#
∂σ3j
σ3j
(√σ3kσ3k
)$1
= 2μe3j - 2μ
F
-1
,
j = 3, k = 1,2.
(2)
∂t
√σ3kσ3k
σs
τ
Обе УВП системы уравнений (1) и (2) являются полулинейными гиперболическими сис-
темами первого порядка дивергентного вида. Вся характерного вида нелинейность сосредо-
точена в свободных не дифференциальных членах уравнений для компонент девиаторов или
касательных напряжений.
2. Общие построения неявных аппроксимаций второго порядка для полулиней-
ных уравнений. Обоснуем аппроксимации второго порядка для полулинейных уравнений
систем, описывающих динамику изотропной и анизотропной упруговязкопластической сред
и содержащих нелинейные свободные члены. В обоих случаях эти выделенные уравнения из
общей системы в векторной записи имеют следующий вид:
∂S
= LxV - SF(|S|),
(3)
∂t
где S - вектор-столбец неизвестных девиаторных или касательных компонент напряжений Sk
и |S| =
√SkSk , V - вектор скорости, Lx - линейный матричный оператор пространственного
дифференцирования, соответствующий закону Гука для упругой среды. В дальнейшем также
понадобится эта совокупность уравнений, продифференцированная по времени:
∂2S
∂V
∂(SF (|S|))
=Lx
-
∂t2
∂t
∂t
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЯВНО-НЕЯВНЫЕ СХЕМЫ РАСЧЁТА ДИНАМИКИ
805
Индексами n+1 и n будем помечать значения искомых величин на верхнем и нижнем сло-
ях разбиения по времени, Δt - шаг по времени. Запишем неявную разностную аппроксимацию
вида
Sn+1 - Sn
1
1
=
Lh(Vn+1 + Vn) -
(Sn+1Fn+1 + SnFn)
Δt
2
2
или
1
1
Sn+1 - Sn =
Lh(Vn+1 + Vn)Δt -
(Sn+1Fn+1 + SnFn)Δt.
(4)
2
2
Утверждение 1. Разностная задача (4) аппроксимирует исходную дифференциальную
задачу (3) со вторым порядком малости по временному шагу.
Доказательство. Пусть оператор пространственного дифференцирования Lx аппрокси-
мирован со вторым порядком по пространственному шагу разностным оператором Lh, не
уточняя конкретный вид этой аппроксимации и оставляя для неё свободу выбора, т.е.
LhVn = LxVn + O(Δx2).
Для решений исходной дифференциальной системы уравнений на (n + 1)-м шаге по времени
справедливы разложения
∂S
1∂2S
Sn+1 = Sn +
Δt +
t2 + O(Δt3),
Δ
∂t
2 ∂t2
tn
tn
∂V
∂F
Vn+1 = Vn +
Δt + O(Δt2), Fn+1 = Fn +
t + O(Δt2).
Δ
∂t
∂t
tn
tn
Подставив эти разложения в разностные уравнения с неявной аппроксимацией, получим
(
)
∂S
1∂2S
1
∂V
Δt +
Δt2 + O(Δt3) =
Lh Vn +
t + O(Δt2) + Vn Δt -
Δ
∂t
2 ∂t2
2
∂t
tn
tn
tn
((
)(
)
)
1
∂S
∂F
-
Sn +
Δt + O(Δt2) Fn +
t + O(Δt2)
+ SnFn Δt.
Δ
2
∂t
∂t
tn
tn
Применяя формулу для разностного оператора пространственного дифференцирования
LhVn = LxVn + O(Δx2),
после выкладок и приведения подобных слагаемых получим равенство
∂S
1∂2S
+
t + O(Δt2) =
Δ
∂t
2 ∂t2
tn
tn
1
∂V
1 ∂(SF)
=LxVn +
Lx
Δt + O(Δx2) - SnFn -
t + O(Δt2).
Δ
2
∂t
2
∂t
tn
tn
С учётом исходной полулинейной системы и её продифференцированного по времени след-
ствия получаем, что рассмотренная неявная разностная схема выполняется на решении этой
системы со вторым порядком аппроксимации. Утверждение доказано.
3. Неявная схема второго порядка аппроксимации для определяющих уравне-
ний упруговязкопластической среды с нелинейными свободными членами. Посколь-
ку системы (1) и (2), по существу, аналогичны друг другу, будем вести построение численной
схемы на примере изотропной УВП системы (1). Особый интерес представляет схема расчё-
та части системы уравнений для девиаторов с нелинейным свободным членом и возможным
малым параметром в его знаменателе. Что касается остальных уравнений системы (1) - ли-
нейных уравнений движения для компонент скорости и уравнений для среднего напряжения,
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
806
ГОЛУБЕВ и др.
то их численная аппроксимация по какой-либо явной схеме требуемого (второго) порядка не
вызывает затруднений [14]. Будем считать, что такая аппроксимация проведена, значения ско-
ростей и среднего напряжения на верхнем временном слое определены с учётом необходимых
по постановке начальных и граничных условий.
Построим неявную аппроксимацию второго порядка уравнения для девиаторов тензора
напряжений с нелинейным свободным членом из УВП системы (1) указанного выше типа:
sn+1ij - snij
e′n+1ij + e′nij
= 2μ
-
Δt
2
√
(
#
)$
#
)$)
sn+1
( sn+1klsn+1kl
snij
2μ
ij
(√snklsnkl
1
-
√
F
-1
+
F
-1
τ
σs
√snklsnkl
σs
2
sn+1klsn+1kl
Эту нелинейную систему уравнений для sn+1ij можно записать в виде
(
# (√
)$
)
sn+1
snij
√
1
ij
sn+1ij = sn+1ije -
√
F sn+1klsn+1kl - 1
+
snklsnkl - 1)〉
δ
√snklsn〈F(
sn+1klsn+1kl
kl
Здесь введены безразмерные компоненты sn+1ij = sn+1ij/σs, snij = snij/σs, sn+1ije = sn+1ije/σs, где
sn+1ije = snij + μ(e′n+1ij + e′nij)Δt - компоненты девиатора после “упругого” шага по времени, δ =
= τσs/(μΔt) - безразмерный малый параметр системы уравнений.
Отметим, что с учётом проведённого ранее расчёта значений компонент скорости на верх-
нем временном слое компоненты “упругого” девиатора sn+1ije также можно считать известными,
как и значения snij на n-м слое.
Нелинейную систему, из которой необходимо найти неизвестные компоненты девиатора на
верхнем слое sn+1ij, можно записать следующим образом:
(
#
√
$)
1
〈F (
√snklsnkl - 1)〉
sn+1ij δ +
√
F( sn+1klsn+1kl - 1)
+snij
= δsn+1ije.
(5)
√snklsn
sn+1klsn+1kl
kl
Свернём эти уравнения последовательно с sn+1ij, snij, sn+1ije и введём обозначения для возни-
кающих сверток с неизвестными значениями
√
√
√
X = sn+1klsn+1kl, Y = sn+1klsnkl, Z = sn+1klsn+1kle
и с уже вычисленными значениями
√
√
√
T =
snklsnkl, S = snklsn+1kle, Σ = sn+1klesn+1kle.
Получим нелинейную систему трёх уравнений с тремя неизвестными:
(
)
〈F (X - 1)〉
〈F (T - 1)〉
X2 δ+
+Y2
= δZ2,
X
T
(
)
〈F (X - 1)〉
〈F (T - 1)〉
Y2 δ+
+T2
= δS2,
X
T
(
)
〈F (X - 1)〉
〈F (T - 1)〉
Z2 δ+
+S2
= δΣ2.
X
T
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЯВНО-НЕЯВНЫЕ СХЕМЫ РАСЧЁТА ДИНАМИКИ
807
Исключив неизвестные Y и Z, запишем уравнение для X2 :
(
)2
〈F (X - 1)〉
X2 δ+
= ΔP2,
X
где
2
〈F (T - 1)〉
( 〈F (T - 1)〉)
ΔP2 = δ2sn+1ijesn+1ije - 2δsn+1ijesn
ij
+snijsn
ij
=δ
S2 ≥ 0,
T
T
snij 〈F(T - 1)〉
√
S2 = sn+1ijsn+1ij,
sn+1ij = sn+1ije -
,
T =
snklsnkl.
T
δ
Нетрудно видеть, что промежуточный девиатор
sn+1ij и его свёртка
S вычисляются по
результатам “упругого” шага по времени.
Поскольку для свёртк
S2 всегда выполняетс
S2 ≥ 0, получаем окончательное уравнение
для неизвестной свёртки X :
δX + 〈F(X - 1)〉 =
S.
(6)
Отметим, что из (5) следует формула для искомых компонент девиатора на верхнем вре-
менном слое в следующем виде:
(
)-1
〈F (X - 1)〉
δsn+1ijX
sn+1ij = δsn+1ij δ +
=
=sn+1
X.
(7)
ij
X
δX + 〈F(X - 1)〉
S
Таким образом, для полного определения величин sn+1ij следует решить уравнение (6) и
подставить результат в (7). Уточним диапазоны допустимых значений для X. При X < 1
решение (6) тривиально: X
S. Следовательно, sn+1ij = sn+1ij с критерием применимости
S < 1 после “упругого” шага. При X ≥ 1 следует решить уравнение
δX + F(X - 1) =
S.
(8)
Для этого нужно конкретизировать функцию вязкости с учётом её упомянутых выше свойств
F ≥ 0, F(0) = 0, 〈F 〉 = F H(F ).
4. Неявная схема второго порядка аппроксимации для определяющих уравне-
ний УВП среды с нелинейными свободными членами. Как правило, для функции
вязкости используются степенные или полиномиальные аппроксимации, построенные по ре-
зультатам экспериментальных исследований [4, 7, 15].
Утверждение 2. Для случая линейной функции вязкости F (x) = x уравнение (8) имеет
точное аналитическое решение.
В этом случае решение уравнения (8), условие X ≥ 1 и искомые компоненты девиатора
соответственно имеют вид
1+
S
sn+1ij 1 + δS
X =
,
S ≥ 1, sn+1ij =
1+δ
S
1+δ
При малых δ
sn+1ij
sn+1ij ≈
(1 + δ
S - 1)).
(9)
S
Утверждение 3. Для случая квадратичной функции вязкости F (x) = x2 уравнение (8)
имеет точное аналитическое решение.
Уравнение (8) выглядит следующим образом:
δX + (X - 1)2 =
S.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
808
ГОЛУБЕВ и др.
Его решение, дополнительное условие и девиатор напряжения на верхнем слое определяются
соотношениями
√
√
(
)
2
sn+1ij
δ
δ
δ
δ2
X =1-
+ δ
S - 1) +
,
S ≥ 1, sn+1ij =
1-
+ δ
S - 1) +
2
4
S
2
4
При малых δ
√
)
sn+1ij (
sn+1ij ≈
1+ δ
S - 1)
(10)
S
Утверждение 4. Для случая корневой функции вязкости F (x) =
√x уравнение (8) име-
ет точное аналитическое √шение.
Решим уравнение δX +
X-1=
S сдополнительными условиям
S ≥ X ≥ 1. Опуская
выкладки и проверку условий, запишем результат:
2(1 + δ2
S2)
sn+1ij
2(1 + δ2
S2)
X =
√
,
S ≥ 1, sn+1ij =
√
S
1+2δ
S+
1+4δ2
S - 1)
1+2δ
S+
1+4δ2
S - 1)
При малых δ справедливо
sn+1ij
sn+1ij ≈
(1 + δ2
S - 1)2).
(11)
S
Если уравнение (4) не имеет аналитического решения, то его можно решить в предполо-
жении, что параметр δ является малым (δ ≪ 1), и воспользовавшись методом разложения
по малому параметру. Достаточно общим примером может служить степенное представление
функции F (x) = xq. Необходимо при δ ≪ 1 решить уравнение
δX + (X - 1)q =
S, X ≥ 1, q > 0.
Будем искать решение в виде асимптотического ряда по степеням δ1/q с точностью до
первого малого члена: X = 1 + C1δ1/q + . . . Подставляя это разложение и приравнивая коэф-
фициенты при одинаковых степенях q, получаем значение неизвестного коэффициента раз-
ложения
C1 =
S-1)1/q, X ≈1+
S - 1)1/q,
S ≥ 1.
Отсюда следует решение для девиаторов при произвольном положительном q :
sn+1ij
sn+1ij ≈
(1 + δ1/q
S - 1)1/q).
(12)
S
Легко видеть, что рассмотренные выше частные точные решения δ совпадают с полу-
ченным приближённым решением. Обсудим также вопрос предельного перехода при δ → 0,
поскольку формула для промежуточного девиатора sn+1ij содержит малый параметр в знаме-
нателе:
snij 〈F (T - 1)〉
sn+1ij = sn+1ije -
(13)
T
δ
Утверждение 5. Корректировочная формула (13) при δ → 0 допускает представление
в форме, не содержащей в явном виде параметр δ.
Доказательство. Уравнение (8), справедливое на (n+1)-м слое по времени, запишем для
n-го слоя:
√
δT + 〈F(T - 1)〉 = δ
snij snij .
Отсюда имеем
$
#√
√
〈F (T - 1)〉 = δ
snij snij -
snklsn
,
kl
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЯВНО-НЕЯВНЫЕ СХЕМЫ РАСЧЁТА ДИНАМИКИ
809
и в формуле для промежуточного девиатора удаётся снять особенность при δ → 0:
$
snij
#√
√
sn+1ij
sn+1ij = sn+1ije -
snij snij -
snklsn
,
sn+1ij =
(14)
kl
√snklsnkl
S
Утверждение доказано.
Что касается системы уравнений (2) для анизотропной УВП среды, описывающей динами-
ку слоистой среды с вязкопластическими условиями скольжения на межслойных контактных
границах, то для её численного решения корректировку касательных напряжений, например,
аналог формулы (12), можем записать следующим образом:
(
(√
)1/q
)
σn+13j
σn3j
〈F (
√σn3kσn3k - 1)〉
σn+13j ≈
√
1+
σn+13kσn+1
δ1/q
,
σn+13j = σn+13je -
3k
√σn3kσn
δ
σn+13kσn+13k
3k
Аналогичные замены следует произвести и для всех остальных рассмотренных случаев
(9)-(11) и (14).
Таким образом, показано, что полученные решения неявной аппроксимации второго поряд-
ка для девиаторов напряжений УВП системы уравнений допускают предельный переход при
малом времени релаксации. Следовательно, формулы (9)-(12) для различных представлений
функций вязкости при малых δ можно трактовать как регуляризаторы численных решений
УП систем. Сами эти формулы представляют собой алгебраические корректировки компонент
девиаторов напряжений, полученных в результате расчёта “упругого” шага по времени.
Этот приём, предложенный в работах [16, 17], широко использовался в вычислительной
практике (см., например, [18-20]), но трактовался как корректировка первого порядка в про-
цессе физического расщепления упругопластического процесса на упругий шаг и приведение
девиаторов напряжений на круг текучести, которая имеет вид
sn+1ije
sn+1ij =
√
sn+1klesn+1
kle
В данной статье специфические корректировки девиаторов напряжений за пределом те-
кучести второго порядка возникают как обоснованный результат построения явно-неявной
схемы второго порядка для УВП системы уравнений, а корректировка (14) - для УП системы
уравнений.
5. Численная схема для нестационарной упругой системы. В прямоугольной сис-
теме координат (x, y, z) система уравнений линейной изотропной теории упругости является
гиперболической и может быть записана в каноническом виде
qt + Axqx + Ayqy + Azqz = f.
Здесь вектор q = (vx, vy, vz, σxx, σyy, σzz, σyz , σxz, σxy)т содержит компоненты тензора напря-
жений и вектора скорости смещений точек среды, f - вектор внешних сил. Матрицы Ax, Ay
и Az разреженные и зависят от параметров среды λ, μ и ρ. С помощью метода расщепления
по физическим процессам решение исходной задачи сводится к последовательному решению
однородной линейной гиперболической системы уравнений и последующему решению системы
обыкновенных дифференциальных уравнений первого порядка. Дальнейшее применение ме-
тода расщепления по пространственным направлениям приводит к набору из трёх одномерных
гиперболических систем уравнений [21]
qt + Axqx = 0, qt + Ayqy = 0, qt + Azqz = 0.
Для определённости рассмотрим первую из них. Ввиду гиперболичности матрицы Ax, она
может быть представлена в виде
Ax = Ω-1xΛΩx,
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
810
ГОЛУБЕВ и др.
где матрица Ω-1x состоит из правых собственных векторов, матрица Ωx - обратная к ней, а
матрица Λ - диагональная, состоящая из собственных значений матрицы Ax. Опустим далее
индекс x и введём обозначение ω = Ωq. Умножение одномерной системы уравнений на матри-
цу Ω и внесение её под операторы дифференцирования по времени и по координате приводит
к набору независимых линейных уравнений переноса с постоянными коэффициентами
ωt + Λωx = 0.
(15)
Для каждой компоненты вектора ω справедливы соотношения
ωi(t + Δt,x,y,z) = ωi(t,x - λiΔt,y,z).
С использованием пространственной интерполяции заданного порядка на выбранном сеточ-
ном шаблоне получается восстановить значения ωi(t, x - λiΔt, y, z). В дальнейшем, с учётом
невырожденности матрицы Ω, восстанавливаются значения искомых функций задачи на сле-
дующем временном слое qn+1 = Ω-1ωn+1.
При использовании пространственного шаблона (xm-2, xm-1, xm, xm+1) для решения ли-
нейного одномерного уравнения переноса возможно построить схему третьего порядка аппрок-
симации по времени и по пространству. Однако, как известно, невозможно построить линейную
монотонную схему выше первого порядка аппроксимации. Преимуществом применяемой в ра-
боте схемы является её квазимонотонность. В статье [22] показано, что её близость к области
монотонных по Фридрихсу схем в пространстве неопределённых коэффициентов приводит к
наименьшему развитию осцилляций на разрывных решениях. Таким образом, для решения
уравнения (15) на компоненте ωi использовалось выражение
2
σ
σ
ωn+1m = ωnm -
(ωnm+1 - ωnm-1) +
(ωnm-1 - 2ωnm + ωnm+1) +
2
2
σ(σ2 - 1)
+
(ωnm-2 - 3ωnm-1 + 3ωnm - ωnm+1),
6
где σ = λiΔt/h < 1 - число Куранта, h - пространственный шаг расчётной сетки. Отметим,
что сеточно-характеристический метод ранее успешно применялся для решения ряда динами-
ческих задач деформируемого твёрдого тела [23-25].
6. Примеры расчётов. На примерах расчётов покажем, что полученные универсаль-
ные формулы корректировки девиаторов напряжений при различных значениях времени ре-
лаксации, сравнимых или меньших шага по времени, могут быть успешно использованы для
моделирования быстропротекающих процессов в упруговязкопластической среде. Применение
обычных явных схем при малых значениях времени релаксации для численного решения полу-
линейных упруговязкопластических систем уравнений привело бы к неустойчивости решения.
В настоящей работе был проведён расчёт процесса нагружения изотропной упруговязко-
пластической среды. Рассматривалась полная трёхмерная постановка. Область интегрирова-
ния имела размеры 50×50×10000 м и покрывалась кубической расчётной сеткой с шагом 5 м.
Для задания упругих констант среды использовались следующие физические параметры: ско-
√
√
рость продольных волн Cp =
(λ + 2μ)/ρ = 4500 м/c, Cs =
μ/ρ = 2250 м/c, плотность
ρ = 2500 кг/м3, σs = 112500 Па. Исходя из условия устойчивости Куранта для сеточно-
характеристической схемы, используемой для решения линейной упругой задачи, шаг по вре-
мени задавался равным 1 мс. При этом общее время расчёта составляло 2 с. К нижней час-
ти области равномерно по всей поверхности прикладывалось постоянное внешнее давление
в 337 500 Па. Согласно аналитическому исследованию исходных определяющих уравнений, в
среде при данном типе нагружения распространяются упругая волна сжатия со скоростью Cp
и пластическая волна со скоростью
√
Cf =
ρ-1(λ + 2μ/3) ≈ 3674м/с.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЯВНО-НЕЯВНЫЕ СХЕМЫ РАСЧЁТА ДИНАМИКИ
811
Аналитически значение напряжения σ∗1 на полке между волнами сильных разрывов можно
вычислить из условия текучести Мизеса при определённом соотношении между компонентами
напряжений σ2 = σ3 = λ(λ + 2μ)-1σ1 :
(
)2
(
)2
(
)2
σ
σ
σ
3λ + 2μ
σ1 -
+ σ2 -
+ σ3 -
=σ2s, σ = σ1 + σ2 + σ3 =
σ1.
3
3
3
λ + 2μ
После алгебраических преобразований получаем:
√
λ + 2μ
6
σ∗1 =
σs.
μ
4
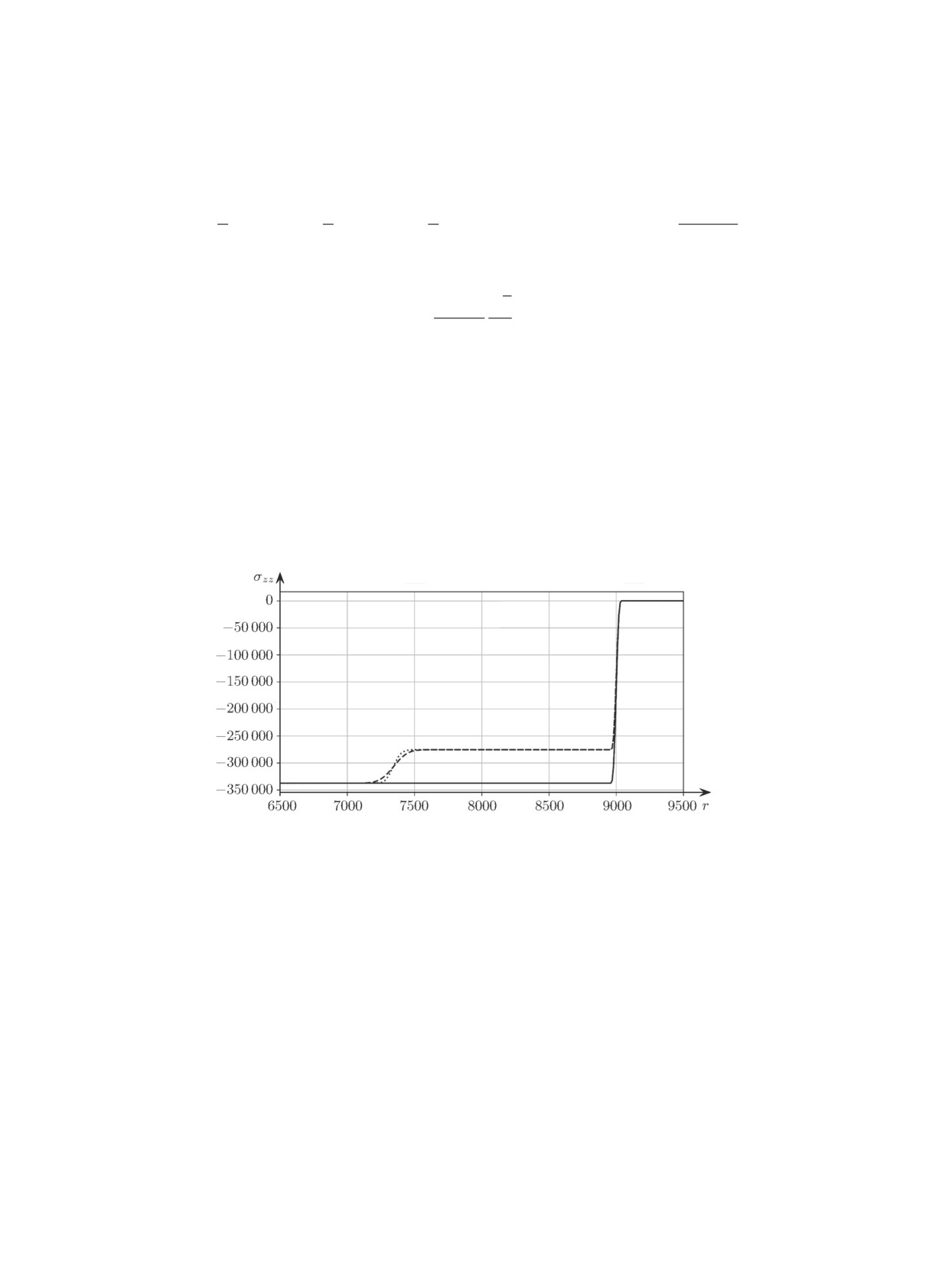
На рис. 1 представлены численные решения, полученные для линейной упругой среды
(сплошная линия), а также для изотропной упругопластической среды по схеме Wilkins [17]
(штиховая линия) и по предложенной в работе явно-неявной схеме (пунктирная линия). Его
анализ показывает, что во всех трёх случаях корректно воспроизводится процесс распростра-
нения продольной волны нагружения. Расчётная скорость распространения этой волны в среде
совпадает с аналитическими оценками. Отметим также, что не возникают численные осцил-
ляции на разрывах решения. На обоих численных решениях для упругопластической среды
чётко прослеживается пластическая волна. Скорость её распространения, измеренная по точке
перегиба на фронте, совпадает с аналитическими оценками. При этом предложенная в насто-
ящей работе схема гораздо точнее разрешает сам волновой фронт (разрыв решения).
Рис. 1. Пространственное распределение вертикальной компоненты тен-
зора напряжений σzz в момент времени t = 2 с (r - расстояние вдоль
оси Oz).
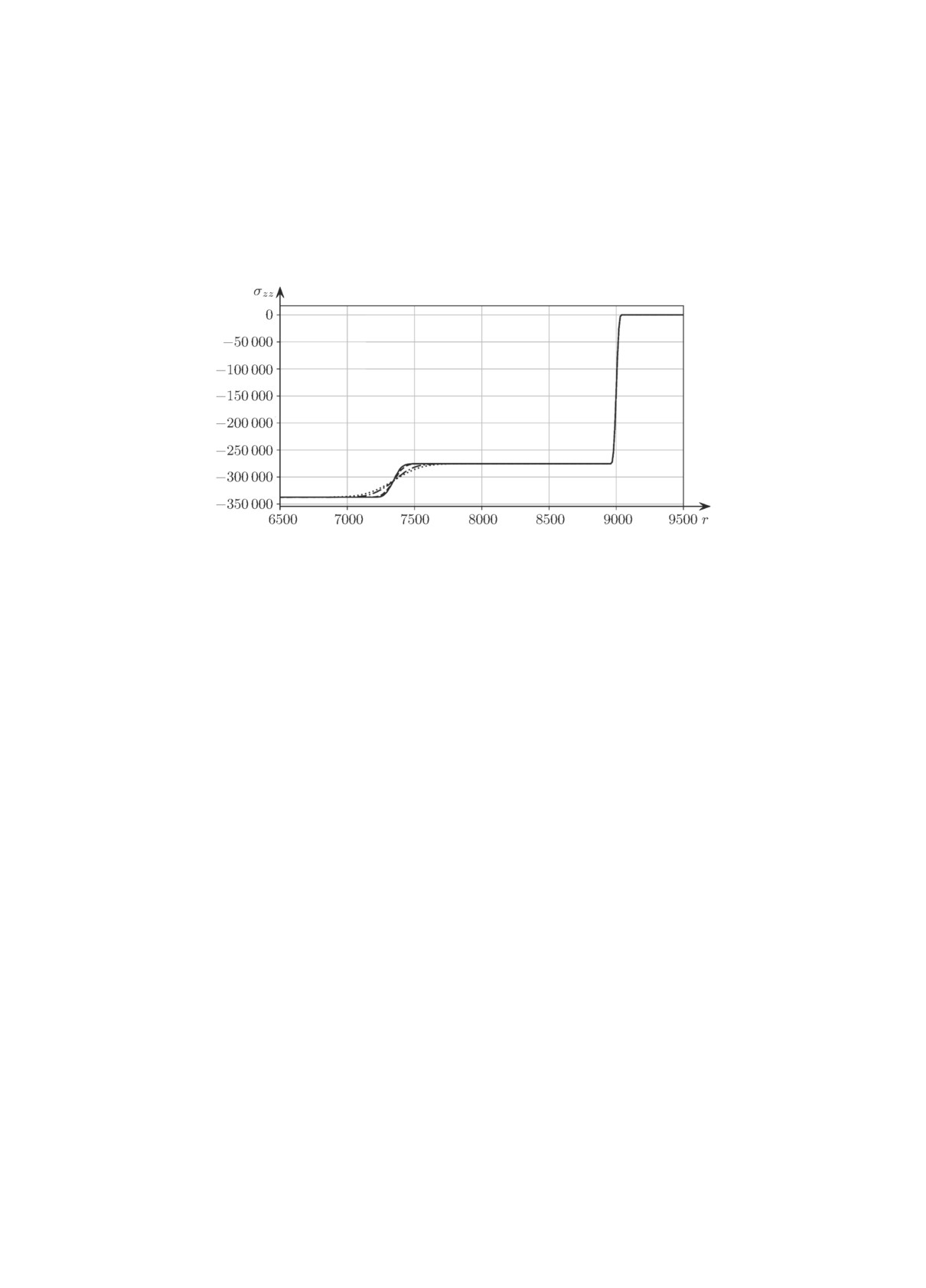
На рис. 2 приведены численные решения, полученные для линейной упругой среды с ли-
нейной функцией вязкости при различных значениях параметра δ ∈ [0.01, 10]. Все остальные
значения характеристик рассматриваемой среды и параметры вычислительного алгоритма
оставались без изменений. Видно, что увеличение характерного времени релаксации компо-
нент девиатора напряжений на поверхность текучести размывает фронт пластической волны.
Заключение. Для устойчивого численного решения определяющей системы упруговяз-
копластической модели сплошной среды предложена явно-неявная схема второго порядка с
явной аппроксимацией уравнений движения и неявной аппроксимацией определяющих соот-
ношений, содержащих малый параметр в знаменателе нелинейных свободных членов. Для
согласования порядков аппроксимации явного упругого и неявного корректировочного шагов
построена неявная аппроксимация второго порядка для изотропной и анизотропной моделей
упруговязкопластической модели сплошной среды. Получены уточнённые корректировочные
формулы после “упругого” шага расчёта.
Найденные решения неявной аппроксимации второго порядка для девиаторов напряжений
упруговязкопластической системы уравнений допускают предельный переход при стремлении
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
812
ГОЛУБЕВ и др.
времени релаксации к нулю. Корректировочные формулы, полученные таким предельным
переходом, можно трактовать как регуляризаторы численных решений упругопластических
систем. Поскольку упруговязкопластические системы уравнений по своей дифференциальной
части заведомо являются гиперболическими, приводимыми к дивергентному виду, предложен-
ный численный алгоритм в указанном выше смысле обеспечивает консервативность сеточно-
характеристических и конечно-объёмных методов при расчёте разрывных решений, в том чис-
ле и недивергентных упругопластических систем уравнений.
Рис. 2. Пространственное распределение вертикальной компоненты тен-
зора напряжений σzz в момент времени t = 2 с при δ = 10 (пунктирная
линия), δ = 1 (штрихпунктирная), δ = 0.1 (штриховая) и δ = 0.01
(сплошная).
Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-71-
10060).
СПИСОК ЛИТЕРАТУРЫ
1. Кукуджанов В.Н. Вычислительная механика сплошных сред. М., 2008.
2. Никитин И.С. Динамические модели слоистых и блочных сред с проскальзыванием, трением и
отслоением // Изв. РАН. Механика твердого тела. 2008. № 4. С. 154-165.
3. Никитин И.С. Теория неупругих слоистых и блочных сред. М., 2019.
4. Новацкий В.К. Волновые задачи теории пластичности. М., 1978.
5. Фрейденталь А., Гейрингер Х. Математические теории неупругой сплошной среды. М., 1962.
6. Кукуджанов В.Н. Распространение волн в упруговязкопластических материалах с диаграммой об-
щего вида // Изв. РАН. Механика твердого тела. 2001. № 5. С. 96-111.
7. Коларов Д., Балтов А., Бончева Н. Механика пластических сред. М., 1979.
8. Дюво Г., Лионс Н. Неравенства в механике и физике. М., 1980.
9. Садовский В.М. Разрывные решения в задачах динамики упругопластических сред. М., 1997.
10. Golubev V.I., Shevchenko A.V., Khokhlov N.I., Petrov I.B., Malovichko M.S. Compact grid-characteristic
scheme for the acoustic system with the piece-wise constant coefficients // Int. J. of Appl. Mech. 2022.
P. 2250002.
11. LeVeque R.J. Finite Volume Methods for Hyperbolic Problems. Cambridge, 2002.
12. Dal Maso G., LeFloch P.G., Murat F. Definition and weak stability of nonconservative products // J.
de Math. Pur. et Appl. 1995. V. 74. № 6. P. 483-548.
13. Pares C. Numerical methods for nonconservative hyperbolic systems: a theoretical framework // SIAM
J. on Numer. Anal. 2006. V. 44. № 1. P. 300-321.
14. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения
гиперболических систем уравнений. М., 2001.
15. Кукуджанов В.Н. Численное моделирование динамических процессов деформирования и разруше-
ния упругопластических сред // Успехи механики. 1985. Т. 8. № 4. С. 21-65.
16. Уилкинс М.Л. Расчет упругопластических течений. Вычислительные методы в гидродинамике. М.,
1967.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023
ЯВНО-НЕЯВНЫЕ СХЕМЫ РАСЧЁТА ДИНАМИКИ
813
17. Wilkins M.L. Computer Simulation of Dynamic Phenomena. Berlin; Heidelberg; New York, 1999.
18. Кукуджанов В.Н. Метод расщепления упругопластических уравнений // Механика твердого тела.
2004. № 1. С. 98-108.
19. Абузяров М.Х., Баженов В.Г., Котов В.Л. и др. Метод распада разрывов в динамике упругопла-
стических сред // Журн. вычислит. математики и мат. физики. 2000. Т. 40. № 6. С. 940-953.
20. Бураго Н.Г. Моделирование разрушения упругопластических тел // Вычислит. механика сплошных
сред. 2008. Т. 1. № 4. С. 5-20.
21. Golubev V.I., Shevchenko A.V., Petrov I.B. Raising convergence order of grid-characteristic schemes for
2D linear elasticity problems using operator splitting // Computer Research and Modeling. 2022. V. 14.
№ 4. P. 899-910.
22. Kholodov A.S., Kholodov Ya.A. Monotonicity criteria for difference schemes designed for hyperbolic
equations // Comput. Math. Math. Phys. 2006. V. 46. С. 1560-1588.
23. Golubev V.I., Nikitin I.S., Vasyukov A.V., Nikitin A.D. Fractured inclusion localization and charac-
terization based on deep convolutional neural networks // Procedia Structural Integrity. 2023. V. 43.
P. 29-34.
24. Golubev V., Vasykov A., Nikitin I. et al. Continuum model of fractured media in direct and inverse
25. Guseva E.K., Beklemysheva K.A., Golubev V.I., Epifanov V.P., Petrov I.B. Investigation of ice rheology
based on computer simulation of low-speed impact // Mathematical Modeling and Supercomputer
Technologies. MMST 2022. Communications in Computer and Information Science / Eds. D. Balandin,
K. Barkalov, I. Meyerov. Cham, 2022. V. 1750. P. 176-184.
Московский физико-технический институт
Поступила в редакцию 16.02.2023 г.
(национальный исследовательский университет),
После доработки 27.03.2023 г.
Институт автоматизации проектирования РАН, г. Москва,
Принята к публикации 18.04.2023 г.
Институт проблем механики
имени А.Ю. Ишлинского РАН, г. Москва
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№6
2023