ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2023, том 59, № 9, с.1260-1265
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
УДК 517.968.21+517.956.22
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ФРЕДГОЛЬМА
ДЛЯ ЗАДАЧ АКУСТИЧЕСКОГО РАССЕЯНИЯ
НА ТРЁХМЕРНЫХ ПРОЗРАЧНЫХ СТРУКТУРАХ
© 2023 г. А. Б. Самохин, А. С. Самохина, И. А. Юрченков
Рассмотрены дифференциальные и интегральные постановки задач акустического рассе-
яния на трёхмерных ограниченных прозрачных структурах, описываемых интегральным
уравнением. Приведены результаты численного решения интегрального уравнения, описы-
вающего рассматриваемый класс задач. Доказана теорема существования и единственно-
сти решения.
DOI: 10.31857/S0374064123090108, EDN: WSGPTN
Введение. Решаются задачи акустического рассеяния на трёхмерных ограниченных про-
зрачных структурах. Исходная дифференциальная постановка задачи сводится к объёмному
интегральному уравнению Фредгольма второго рода. Доказывается теорема существования
и единственности решения, в том числе для “сред без потерь”. Используя метод коллокации
на тетраэдальной сетке, интегральное уравнение аппроксимируется системой линейных ал-
гебраических уравнений (СЛАУ). Для решения СЛАУ применяются итерационные методы.
Приводятся и анализируются численные результаты решения.
1. Интегральное уравнение. Рассмотрим следующий класс задач акустики. В ограни-
ченной трёхмерной области Q, окружённой свободным пространством, материальная среда
характеризуется индексом рефракции n(x), x ∈ Q, который является кусочно-дифференци-
руемой функцией координат, причём вне Q индекс рефракции равен единице. Требуется опре-
делить акустическое поле в евклидовом пространстве E3, порождаемое внешним источником
f0(x) с временной зависимостью в виде множителя exp(-iωt), ω - частота акустического по-
ля. В такой постановке соответствующая математическая задача формулируется следующим
образом: найти функцию акустического поля U(x), удовлетворяющую уравнению
ΔU(x) + k2n(x)U(x) = f0(x), k = ω/c,
(1)
где c - скорость звука в свободном пространстве, и U(x) должна удовлетворять условию
излучения на бесконечности
[
(
)]
√
∂U
lim
r
- ikU
= 0, r := |x| = x21 + x22 + x23.
(2)
r→∞
∂r
Кроме того, функция U(x) на границах раздела параметров среды должна быть непрерывной.
Пусть f(x) - финитная функция в E3 относительно x. Тогда интегральное представление
∫
V (x) = - f(y)G(R) dy
(3)
удовлетворяет в пространстве E3 уравнению Гельмгольца
ΔV (x) + k2V (x) = f(x)
(4)
и условию излучения на бесконечности вида (2). В (3) G(R) - функция Грина уравнения
Гельмгольца, которая в декартовой системе координат имеет вид
G(R) = exp(ikR)/(4πR), R = |x - y|, x = (x1, x2, x3), y = (y1, y2, y3).
(5)
1260
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ФРЕДГОЛЬМА
1261
Запишем уравнение (1) в виде
ΔU + k2U = f0 - k2(n - 1)U.
(6)
Из (1)-(6) следует, что неизвестное поле U(x) имеет следующее интегральное представление:
∫
∫
U (x) = - f0(y)G(R) dy + k2 (n(y) - 1)U(y)G(R) dy, x ∈ E3.
(7)
Q
Первый интеграл в правой части (7) описывает поле U0(x), создаваемое источником f0(x) в
свободном пространстве. Далее, поскольку n(x) = 1 вне Q, из (7) следует уравнение Фред-
гольма второго рода относительно неизвестного поля U(x) в области Q [1, с. 116]
∫
U (x) - k2 (n(y) - 1)U(y)G(R) dy = U0(x), x ∈ Q.
(8)
Q
Из выражения (7), зная поле U(x) в области Q, можно найти поле в любой точке про-
странства.
2. Теорема существования и единственности. Рассмотрим сначала дифференциаль-
ную постановку задачи. Однородное уравнение (1) запишем в виде
div grad U(x) + k2n(x)U(x) = 0.
(9)
Справедливо следующее тождество:
div (U∗ grad U) = U∗ div grad U + grad U∗ · grad U,
(10)
где символ∗ обозначает комплексное сопряжение, а · - скалярное умножение.
Проинтегрировав (10) по всему пространству и использовав формулу Грина и уравнение
(9), получим равенство
∫
∫
∫
∂U
lim
U∗
dS = -k2
n|U|2 dν +
|grad U|2 dν,
(11)
r→∞
∂r
Sr
где Sr - сфера радиуса r c центром в точке x ∈ Q.
Выбрав мнимую часть от выражения (11), с учётом условия излучения (2) будем иметь
∫
∫
k lim
|U|2 dS + k2 Im n|U|2 dν = 0.
(12)
r→∞
Sr
Q
Ниже будем полагать, что Im n ≥ 0 в области Q, а значит, каждое слагаемое в (12) равно
нулю. Тогда в сферической системе координат
2π
π
∫
∫
lim
|U|2r2 sin θ dθ dϕ = 0.
(13)
r→∞
0
0
Обозначим через ΩR шар радиусом R, содержащий область Q, причём граничные точки
Q находятся вне поверхности шара. Вне области ΩR поле удовлетворяет уравнению Гельм-
гольца
ΔU(x) + k2U(x) = 0
(14)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№9
2023
1262
САМОХИН и др.
и условию излучения (2). Общее решение задачи (14), (2) описывается рядом собственных
функций уравнения Гельмгольца, которые представляются в виде произведения функций Ган-
келя, зависящих от r ≥ R, и ортогональных сферических функций (см. [2, с. 375]). При боль-
ших значениях r функции Ганкеля пропорциональны, с точностью членов большего порядка
малости, exp(ikr)/r. Поэтому из (13), учитывая ортогональность сферических функций на
сфере, получаем, что коэффициенты ряда по собственным функциям уравнения Гельмгольца
(14) равны нулю. Значит, акустическое поле для задачи (14), (2) в области E3 \ ΩR равно
нулю.
Уравнение (14) является эллиптическим в области E3 \ Q, и все коэффициенты уравнения
являются дифференцируемыми функциями. Тогда можно воспользоваться принципом продол-
жения решения по непрерывности [3, с. 291] из области E3 \ ΩR в область ΩR \ Q. Поэтому,
поскольку поле равно нулю и в области E3 \ ΩR, оно равно нулю в области E3 \ Q. Если
Im n(x) > 0 в Q, то из (12) следует, что в области Q, а значит и во всем пространстве, поле
равно нулю.
Далее, пусть n(x) является всюду дифференцируемой функцией, в том числе на границе
Q. Тогда аналогично изложенному выше получим, что поле тождественно равно нулю во всем
пространстве.
Рассмотрим следующий случай. Пусть n(x) - дифференцируемая функция координат в
области Q, а на границе функция терпит скачок. В области Q находится сколь угодно малая
область Q1, в которой Im n(x) > 0, а в области Q \ Q1 Im n(x) = 0. Из равенства (12)
следует, что поле равно нулю в области Q1. Используя принцип продолжения решения по
непрерывности из области Q1 в область Q \ Q1, получаем, что во всей области Q поле равно
нулю.
Любое решение однородного уравнения (8) из гильбертова пространства интегрируемых
с квадратом функций удовлетворяет однородной задаче (1), (2). Следовательно, однородное
интегральное уравнение (8) будет иметь только нулевое решение в пространстве L2(Q), если
однородная дифференциальная задача (1), (2) имеет только нулевое решение. Поскольку опе-
ратор уравнения (8) является фредгольмовым, то решение уравнения (8) существует, если оно
единственно. Если правая часть уравнения (8) выражается через (7), то решение интеграль-
ного уравнения будет являться решением исходной задачи (1), (2). Таким образом, доказана
следующая
Теорема. Пусть в ограниченной области Q определена функция индекса рефракции n(x),
а вне Q n(x) = 1. Тогда решение интегрального уравнения (8) существует и единственно в
гильбертовом пространстве L2(Q), если выполняется одно из следующих условий:
1) Im n(x) > 0 в области Q;
2) n(x) является дифференцируемой функцией координат в Q, а на границе Q терпит
разрыв; в области Q находится сколь угодно малая область Q1, в которой Im n(x) > 0, а
в области Q \ Q1 Im n(x) = 0;
3) n(x) является всюду, в том числе и на границе Q, дифференцируемой функцией ко-
ординат и Im n(x) = 0 в области Q.
Если правая часть (8) представима через функцию источника f0(x), то решение урав-
нения (8) будет являться единственным решением задачи (1), (2).
3. Метод решения. Для аппроксимации интегрального уравнения (8) будем использовать
метод коллокации на неравномерной сетке. Представим область Q в виде объединения NQ
ячеек Ωn, n = 1, NQ. Узловые точки в этих ячейках будем выбирать в их центрах xcn =
= (xcn1 , xcn2 , xcn3 ), n = 1, NQ, которые определяются формулами
∫
1
xci =
xi dx1 dx2 dx3, i = 1,2,3,
mes Ω
Ω
где mes Ω - объём ячейки Ωn. Если в качестве ячеек рассматриваются тетраэдры произволь-
ной формы, то можно достаточно точно описать многие сложные конфигурации области Q и
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№9
2023
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ФРЕДГОЛЬМА
1263
среды. Центр тетраэдра определяется простой формулой xcni = (x(1)ni + x(2)ni + x(3)ni + x(4)ni)/4,
i = 1,2,3, в которой (x(k)n1,x(k)n2,x(k)n3) - декартовы координаты k-й вершины тетраэдра.
Будем аппроксимировать интегральное уравнение (8) системой линейных алгебраических
уравнений размерности NQ относительно значений неизвестного поля в узловых точках об-
ласти Q, находящихся в центрах ячеек Ωn [4]:
NQ
∫
∑
exp(ik|xcn - y|)
un +
A(n, m)ηmum = u0n, n = 1, NQ,
A(n, m) = k2
dy,
4π|xcn - y|
m=1
Ωm
un = U(xcn), u0n = U0(xcn), ηn = n(xcn) - 1.
(15)
Отметим, что поскольку узловые точки находятся в центре ячеек, точность аппроксимации
интегральных операторов порядка h2, где h - максимальный диаметр ячеек (диаметром
называем максимальное расстояние между точками границы). В работе [5] доказано, что при
сгущении сетки в методе коллокации, т.е. при увеличении числа ячеек NQ, приближённые
решения на основе СЛАУ стремятся к точному решению интегрального уравнения.
Опишем основные проблемы, которые возникают при численном решении СЛАУ (15). В си-
лу трёхмерности уравнения (8) после дискретизации возникают СЛАУ большой размерности
N ≫ 1000. Очевидно, что использование прямых методов практически невозможно, посколь-
ку в памяти компьютера необходимо хранить M ∼ N2 чисел, а для решения СЛАУ нужно
выполнить T ∼ N3 арифметических операций. Поэтому возможно использование только ите-
рационных методов. В этом случае параметры M и T оцениваются формулами
M ∼ MA, T ∼ LTA.
(16)
В (16) MA - количество элементов массива чисел, которые необходимы для алгоритма умно-
жения матрицы СЛАУ на вектор; L - количество итераций для получения решения с заданной
точностью; TA - число арифметических операций для умножения матрицы СЛАУ на вектор.
Для плотных матриц произвольного вида MA ∼ N2, TA ∼ N2.
В настоящей работе для численного решения СЛАУ (15) будем использовать двухшаговый
метод градиентного спуска [6]:
2
∥H∗r0∥
z1 = z0 -
H∗r0, r0 = Hz0 - f,
∥HH∗r0∥2
zk+1 = zk - tk(zk - zk-1) - hkH∗rk, rk = Hzk - f, k ∈ N,
tk∥rk - rk-1∥2 + hk∥H∗rk∥2 = 0,
tk∥H∗rk∥2 + hk∥HH∗rk∥2 = ∥H∗rk∥2,
где H - комплексная матрица системы уравнений Hz = f, а символ∗ обозначает сопря-
жённую матрицу, т.е. транспонированную матрицу с комплексно-сопряжёнными элементами.
Отметим, что, в отличии от других итерационных методов, приведённый метод сходится толь-
ко при одном условии - если матрица СЛАУ невырожденная.
Помимо двухшагового метода градиентного спуска для численного решения СЛАУ (15),
также рассматриваются итерационные методы бисопряжённых градиентов [7] и минимальных
невязок [8, с. 130].
4. Численные результаты. Проведём численное моделирование на области Q, которая
задана кубом с центром в точке xcQ = (0, 0, 0) и длиной стороны LQ = 2.4, коэффициент ре-
фракции области nQ(x) = 2. Внутри куба находится сфера S единичного радиуса RS = 1 с
центром в точке (0, 0, 0), коэффициент рефракции сферы nS(x) = 3. Триангуляционную сет-
ку для поставленной задачи построим в системе построения сеток gmsh: количество разбиений
NQ ≈ 10000, максимальный диаметр разбиения h = 0.430.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№9
2023
1264
САМОХИН и др.
Вне√ ий √точн√к излучения задан амплитудой колебаний A = 1, вектором направления
d = (1/
3, 1/
3,1/
3), а также волновым числом k, который будет варьироваться в ходе
сравнения.
Решать задачу будем с помощью двухшагового метода градиентного спуска (MSGD), ста-
билизированного метода бисопряжённых градиентов (BICGStab) и метода минимальных невя-
зок (MRES). Критерий остановки метода будем определять исходя из относительной разности
приближений на соседних шагах метода:
∥un - un-1∥
< ε.
(17)
∥f∥
Таким образом, при достижении заданной точности изменения приближаемого вектора
итерационный метод окончательно определит приближённое численное решение ul исходной
задачи.
В таблице представлены результаты работы итерационных методов на задаче (15). Варьи-
руя значения волнового числа k при фиксированном ε = 10-7, для каждого итерационного
метода определены число mv умножений матрицы на вектор m для достижения цели сходи-
мости и конечная норма невязки
∥rL∥ = ∥AuL - f∥
на последнем шаге L.
Видно, что при увеличении k решения на основе итерационных методов расходятся по
конечной норме невязки и числу итераций, а норма невязки ∥rL∥ на последнем шаге для
каждого метода при адекватных значениях волнового числа в методах различается не сильно.
По точности сходимости на конкретной задаче лучшим является двухшаговый метод градиент-
ного спуска. При достижении k ≥ 4 решение в заданных условиях становится нестабильным и
количество итераций для методов достигает максимального заранее заданного значения. При
переходе через критическое значение волнового числа для данной задачи сравнение методов
не является репрезентативным.
Таблица. Сравнительная таблица методов MSGD, BICGStab,
MRES при различных значениях k и ε = 10-7, NQ = 10 000
MSGD
BICGStab
MRES
k
mv
∥rL∥
mv
∥rL∥
mv
∥rL∥
0.1
12
3.75E-08
7
1.67E-13
8
1.13E-07
0.5
21
3.23E-06
9
1.13E-08
18
9.75E-06
1
42
8.28E-06
17
1.40E-06
82
0.000107
2
201
0.001906
87
4.02E-06
2000
0.028508
3
276
0.000209
255
4.83E-05
68
19.9611
4
2226
0.022816
2001
1.070618
70
12.56881
5
3003
0.006033
2001
45.78722
112
10.29263
6
3003
0.035198
2001
106.9764
80
7.641037
7
3003
0.055716
2001
0.814367
110
6.08206
8
3003
0.071086
2001
0.437052
108
4.956859
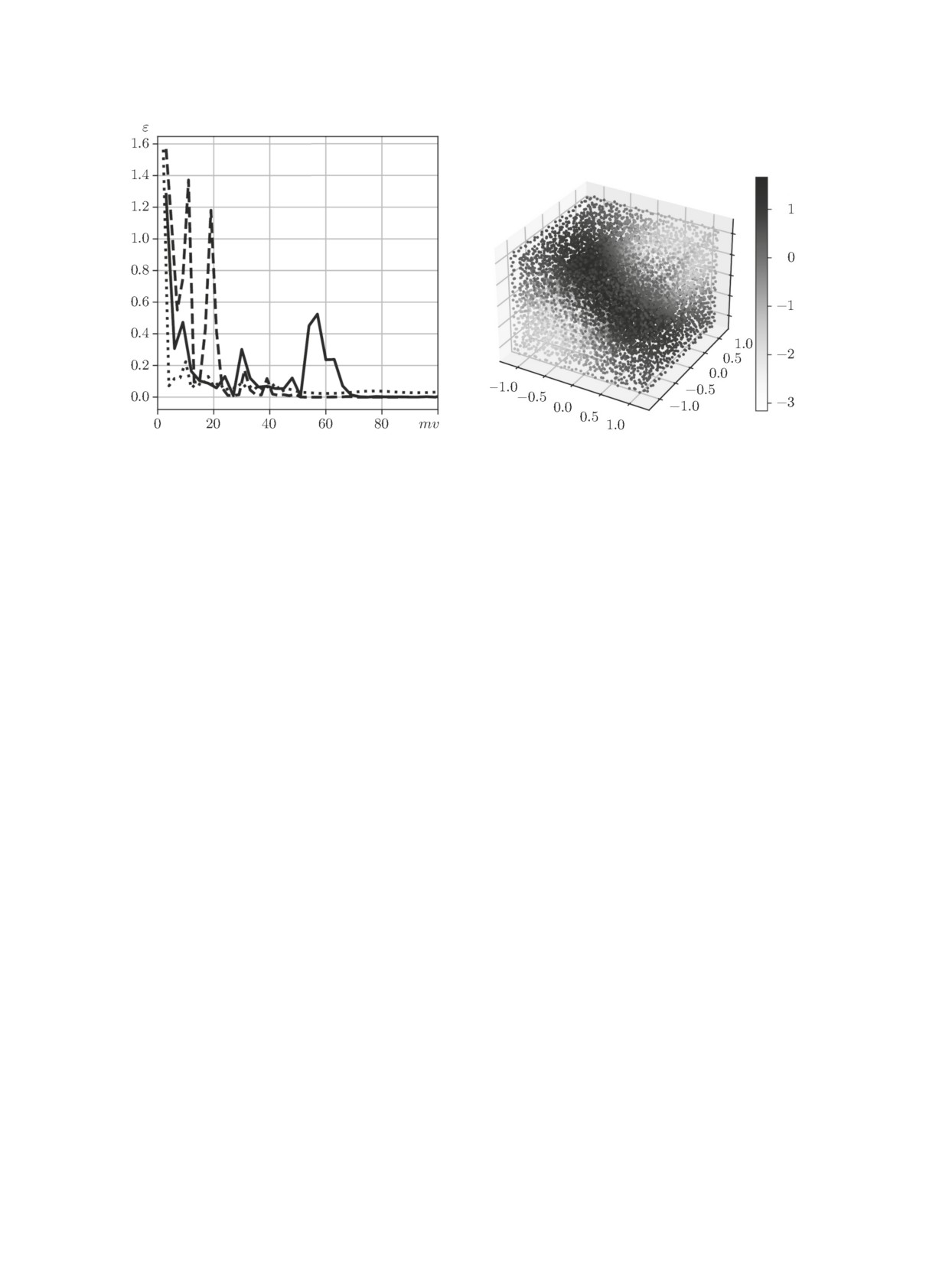
На рис. 1 показана динамика (17) на итерациях при k = 2.
Для каждого итерационного метода конечный результат распределения значений U(xcn)
в области Q в центрах разбиений xcn на основе трёхмерного графика разброса визуально
представлен на рис. 2. Значения функции в точке центра каждого тетраэдра соответствуют
значению на цветовой шкале напряжённости. Трёхмерная визуализация потенциального поля
U (x) в области Q при значениях k = 2 справедлива для всех рассматриваемых итерационных
методов с точностью до значения конечной нормы невязки на последней итерации.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№9
2023
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ФРЕДГОЛЬМА
1265
Рис. 1. Сравнение по относительной норме
Рис. 2. Распределение значений приближён-
разницы приближения итерационных методов
ного решения для неизвестной функции U(x)
BICGStab (штриховая линия), MRES (m = 1)
в центрах тетраэдров Ωn.
(пунктирная) и MSGD (сплошная).
Заключение. В статье рассмотрено объёмное интегральное уравнение Фредгольма второ-
го рода, описывающее задачи акустического рассеяния на ограниченных прозрачных струк-
турах. При выполнении ряда условий доказана теорема существования и единственности ре-
шений рассматриваемых задач. Описан численный метод решения интегрального уравнения
на основе метода коллокации и итерационных методов. Приведены результаты численного
решения конкретных задач.
СПИСОК ЛИТЕРАТУРЫ
1. Колтон Д., Кресс Р. Методы интегральных уравнений в теории рассеяния. М., 1990.
2. Кошляков Н.С., Глинер Э.Б., Смирнов M.M. Уравнения в частных производных математической
физики. М., 1970.
3. Хермандер Л. Анализ линейных дифференциальных уравнений с частичными производными. M.,
1986.
4. Самохин А.Б. Методы и эффективные алгоритмы решения многомерных интегральных уравнений
// Russ. Technological J. 2022. V. 10. № 6. P. 70-77.
5. Vainikko G. Multidimensional Weakly Singular Integral Equations. Heidelberg, 1993.
6. Самохин A.Б., Самохина А.С., Скляр А.С., Шестопалов Ю.В. Итерационные методы градиентного
спуска для решения линейных уравнений // Журн. вычислит. математики и мат. физики. 2019.
T. 59. № 8. C. 1331-1339.
7. Henk A., van der Vorst. Iterative Krylov Methods for Large Linear System. Cambridge, 2003.
8. Самохин А.Б. Объёмные сингулярные интегральные уравнения электродинамики М., 2021.
МИРЭА - Российский технологический университет,
Поступила в редакцию 29.03.2023 г.
г. Москва,
После доработки 29.03.2023 г.
Институт проблем управления
Принята к публикации 20.07.2023 г.
имени В.А. Трапезникова РАН, г. Москва
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 59
№9
2023