Актуальность исследования аминокислот обусловлена тем, что они являются жизненно важными молекулами: входят в состав белков как структурные мономеры, участвуют в биохимических процессах в организме (обмене веществ, синтезировании белка, передаче межклеточных импульсов, регуляции экспрессии генов и др.) [1, 2]. Особое значение приобретает развитие физико-химических основ для определения конформационной стабильности и функциональной активности белковых образований, активизирующихся при изменении состояния среды (под действием температуры, рН, ионной силы). Взаимодействие белковых молекул с молекулами растворителя является важным фактором, влияющим на их состояние в растворе [3, 4], что способствовало увеличению числа работ по изучению сольватационных эффектов при моделировании молекулярных свойств и реакций в растворе, включая биологические среды [5–8]. Несмотря на имеющиеся литературные данные [9–12], в настоящее время ощущается недостаток исследований по влиянию температуры и кислотности среды как на ионное состояние молекул биологически активных соединений, так и на их термодинамические свойства, что существенно сужает возможности теоретической базы для изучения характера и движущих сил межмолекулярных взаимодействий в реальных физиологических условиях.

Лизин (2S-2,6-диаминогексановая кислота, H₂N–(CH₂)₄–C_αH(NH₂)COOH, Lys) является незаменимой основной аминокислотой, молекула которой содержит концевые α-амино и α-карбоксильную группы, а также дополнительную сильноосновную боковую NH₂-группу, которые являются потенциальными сайтами для взаимодействия с молекулами растворителя и других веществ. Лизин участвует во многих биологических и химических процессах, включая расщепления протеаз, хелатирование тяжелых металлов, сохранение эндоплазматического ретикулума; играет важную роль в выработке различных ферментов и гормонов, а также при формировании костей и мышц [13–15]. Кроме того, лизин является структурным блоком полилизинового пептида, обладающего широким антимикробным действием в отношении дрожжевых грибков, грамположительных и грамотрицательных бактерий [16]. Полилизин может применяться в качестве безопасного консерванта для пищевых продуктов и входить в состав антимикробной упаковки [17].

Как известно [18], объемные свойства растворов наиболее чувствительны к взаимодействиям растворенного вещества с растворителем, а также к изменению гидратации под действием температуры и среды. В литературе имеется всего несколько работ по экспериментальному исследованию плотности водных растворов L-лизина [19–21] и практически отсутствуют данные по влиянию температуры на объемные свойства Lys в буферных растворах. Задачей настоящего исследования является использование методов денсиметрии для определения влияния температуры и среды на объемные свойства и межмолекулярные взаимодействия L-лизина в воде (рН 5.4) и водном буферном растворе (рН 7.4) в изученном интервале температур и концентраций. Обсуждение рассчитанных кажущихся молярных объемов и предельных парциальных молярных объемов проведено на основе рассмотрения взаимодействий (растворенное вещество – растворитель) в рамках подхода Гэрни [22].

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

В работе использовали L-лизин (Sigma-Aldrich, Switzeland, CAS 56-87-1). Содержание основного вещества составляло >98%. Аминокислоту сушили в вакуумном шкафу при 343 К в течение 24 ч и выдерживали в эксикаторе (над P₂O₅) не менее 48 ч непосредственно перед использованием. Методом К. Фишера (Volumetric KF Titrator V30, Mettler Toledo) было определено содержание воды в аминокислоте, которое составляло менее 0.8 мас. %.

Для приготовления водных растворов использовали бидистиллированную воду (с рН 5.4). Измерения плотности проводили в чистой воде и фосфатном буферном растворе. Водный буферный раствор, содержащий 0.0416 моль кг^–1 NaH₂PO₄ и 0.2049 моль кг^–1 Na₂HPO₄, обеспечивал постоянство кислотности среды (рН 7.4) в условиях эксперимента. Значения рН растворов фиксировали цифровым рН-метром Mettler Toledo, модель Five-Easy. Все растворы приготовлены весовым методом, используя весы Sartorius-ME215S (с точностью взвешивания 1 × 10^–5 г). Концентрацию (моляльность – m) аминокислоты варьировали от ~(0.0030 до 0.0318) моль кг^–1. Погрешность приготовления растворов указанной концентрации не превышала ±2 × 10^–4 моль кг^–1.

Измерения плотности исследуемых растворов выполнены на цифровом вибрационном денсиметре DMA-5000M (Anton Paar, Австрия) при температурах (288.15, 293.15, 298.15, 303.15, 308.15 и 313.15) K. Прибор имеет встроенный термостат, включающий два платиновых термометра Pt100 в сочетании с элементами Пельтье, что обеспечивало термостатирование образца внутри ячейки с погрешностью 5 × 10^–3 К. Перед каждой серией измерений проводили калибровку ячейки сухим воздухом и дважды дистиллированной дегазированной водой при атмосферном давлении. Денсиметр обладает точностью измерения ±1.0 × × 10^–3 кг м^–3 и воспроизводимостью ±3.0 × 10^–3 кг м^–3. Подробное описание процедуры измерения дано ранее [23]. Совокупная стандартная погрешность измерения плотности исследуемых растворов не превышала ±1.24 × 10^–2 кг м^–3. Экспериментальные данные по плотности (ρ) исследуемых растворов приведены в табл. 1 и 2 . Как видно из таблиц, значения ρ уменьшаются с температурой и возрастают с концентрацией аминокислоты. Необходимо отметить, что сравнение экспериментальных значений плотности растворов L‑лизина в воде и буфере с литературными данными затруднительно. Имеющиеся измерения плотности водных растворов L-лизина были выполнены для другой области концентраций аминокислоты [24] или для моногидрохлорида [25, 26] и моногидрата [27] L-лизина, а в случае буферных растворов Lys они были получены при одной температуре 298.15 К [28].

Таблица 1.

Плотность водных растворов L-лизина (ρ, г cм^‒3) при разных концентрациях и температурах

m, моль кг^–1	288.15 K	293.15 К	298.15 К	303.15 К	308.15 К	313.15 К
0.00000	0.999099	0.998203	0.997043	0.995645	0.994029	0.992212
0.00364	0.999241	0.998344	0.997182	0.995784	0.994167	0.992349
0.00713	0.999376	0.998477	0.997315	0.995916	0.994298	0.992481
0.01230	0.999573	0.998674	0.997510	0.996111	0.994493	0.992672
0.01783	0.999781	0.998882	0.997718	0.996316	0.994697	0.992875
0.02163	0.999922	0.999021	0.997858	0.996458	0.994835	0.993012
0.03182	1.000293	0.999391	0.998226	0.996823	0.995202	0.993376

Таблица 2.

Плотность водных буферных растворов L-лизина (ρ, г cм^–3) при разных концентрациях и температурах

m, моль кг^–1	288.15 K	293.15 К	298.15 К	303.15 К	308.15 К	313.15 К
0.00000	1.030005	1.028839	1.027473	1.025604	1.023353	1.021925
0.00263	1.030097	1.028926	1.027556	1.025684	1.023431	1.022002
0.00808	1.030260	1.029074	1.027693	1.025816	1.023557	1.022125
0.01236	1.030361	1.029161	1.027767	1.025887	1.023621	1.022186
0.01610	1.030422	1.029220	1.027823	1.025940	1.023678	1.022231
0.02120	1.030494	1.029277	1.027877	1.025975	1.023707	1.022259
0.03120	1.030590	1.029354	1.027918	1.025999	1.023716	1.022267

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

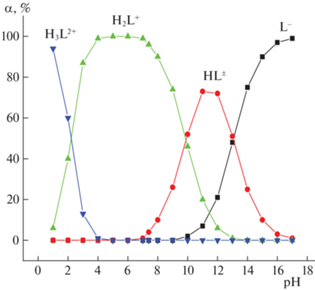
В водных растворах лизин может существовать в двух катионных ([H₃L]²⁺, [H₂L]⁺), цвиттерионной ([HL]^±) или анионной ([L]^–) формах. Диссоциацию лизина в водных растворах можно представить схемой:

${{{\text{H}}}_{{\text{3}}}}{{{\text{L}}}^{{2 + }}} \leftrightarrow {{{\text{H}}}^{ + }} + {{{\text{H}}}_{{\text{2}}}}{{{\text{L}}}^{ + }},$

${{{\text{H}}}_{{\text{2}}}}{{{\text{L}}}^{ + }} \leftrightarrow {{{\text{H}}}^{ + }} + {\text{H}}{{{\text{L}}}^{ \pm }},$

${\text{H}}{{{\text{L}}}^{ \pm }} \leftrightarrow {{{\text{H}}}^{ + }} + {{{\text{L}}}^{--}}.$

Соотношение форм определяется кислотно-основными характеристиками (${\text{р}}{{K}_{{a(\alpha {\text{ - СООН}})}}}$, ${\text{p}}{{K}_{a}}_{{(\alpha {\text{ - N}}{{{\text{H}}}_{{\text{2}}}})}}$, ${\text{p}}{{K}_{{{\text{side}}(\varepsilon {\text{ - N}}{{{\text{H}}}_{2}})}}}$) соединения и значением рН раствора. В литературе имеются данные по константам ионизации лизина [29], с учетом которых проведен расчет равновесного состава растворов аминокислоты при различных значениях рН с помощью программы “RRSU”, в основу которой заложен модифицированный метод Бринкли [30–33]. На рис. 1 представлена полученная диаграмма долевого распределения ионных форм аминокислоты при изменении рН среды. Лизин относится к основным аминокислотам, молекулы которых содержат в боковой цепи группы, проявляющие основные свойства; изоэлектрическая точка Lys соответствует щелочной среде (pI = 9.82 [29]). Хорошо видно (рис. 1), что в кислой среде при рН < < 3 Lys существует в виде дикатиона ([H₃L]²⁺) и является трехосновной кислотой; в широкой области рН (от 4 до 9) преобладает форма монокатиона ([H₂L]⁺); а цвиттерионная ([HL]^±) и анионная ([L]^–) формы Lys начинают доминировать при рН >11. В изученной области концентраций аминокислоты экспериментальное значение рН ее водного раствора составило 9.7 ± 0.1, при котором Lys существует в виде смеси монокатиона (66%) и цвиттериона (34%). В условиях фосфатной буферной среды (рН 7.4) Lys находится преимущественно в монокатионной форме ([H₂L]⁺), при этом вероятность наличия цвиттерионных частиц ([HL]^±) составляет менее 4%.

Рис. 1.

Долевое распределение ионных форм L-лизина в зависимости от рН раствора.

Кажущийся молярный объем Lys (^φV) вычислен по уравнению на основе экспериментальных данных по плотности:

(1)

$^{\varphi }V = 1000({{\rho }_{0}}--\rho ){\text{/}}\rho {{\rho }_{0}}m + M{\text{/}}\rho ,$

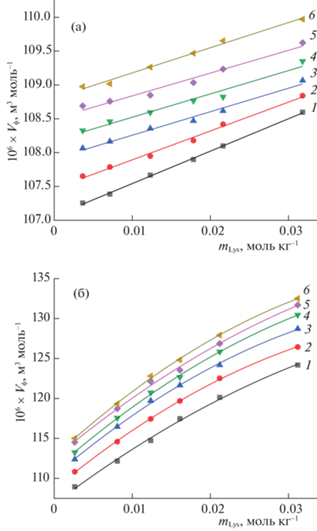
где ρ₀ и ρ – плотности растворителя и раствора, m – моляльная концентрация аминокислоты, М – молекулярная масса. Средняя погрешность значений ^φV с учетом погрешности измерения плотности составила ≈0.7 × 10^–6 м³ моль^–1. На рис. 2 представлены графики концентрационных зависимостей кажущихся молярных объемов аминокислоты в воде и буферном растворе при разных температурах. Показано, что зависимости ^φV = = f(m) для Lys в воде описываются линейной функцией, а в буферном растворе хорошо аппроксимируются полиномом второй степени:

(2)

$^{\varphi }V = {}^{\varphi }V^\circ + {{a}_{1}}m + {{a}_{2}}{{m}^{2}},$

где ^φV° – предельное значение кажущегося молярного объема Lys, равное парциальному молярному объему при бесконечном разбавлении, a₁, a₂ – постоянные коэффициенты. Значения ^φV увеличиваются с ростом концентрации аминокислоты и температуры.

Рис. 2.

Концентрационные зависимости кажущихся молярных объемов L-лизина (^φV) в воде (а) и водном буферном растворе (б) при температурах: 1 – 288.15, 2 – 293.15, 3 – 298.15, 4 – 303.15, 5 – 308.15, 6 – 313.15 К.

В табл. 3 представлены парциальные молярные объемы при бесконечном разбавлении ^φV°, полученные из уравнения (2), положительные значения которых указывают на присутствие взаимодействий между аминокислотой и растворителем. Насколько нам известно, в литературе отсутствуют сведения о парциальных молярных объемах Lys в фосфатном буферном растворе при разных температурах (кроме 298.15 К). В случае водных растворов полученные нами значения ^φV° согласуются в пределах экспериментальной погрешности с имеющимися данными для Lys при 298.15 К (108.71 ± 0.16) × 10^–6 м³моль^–1 [21] и 108.50 × 10^-6 м³моль^–1 [19]), но отличаются от значений ^φV° для моногидрата лизина (118.15 ± 0.06) × × 10^–6 м³моль^–1 [20].

Таблица 3.

Предельные кажущиеся молярные объемы (^φV°) L-лизина (Lys) при бесконечном разбавлении, парциальные молярные расширяемости ($E_{\varphi }^{^\circ }$) и значения парциальных молярных объемов переноса (${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$) Lys из воды в буферный раствор при разных температурах

T, K	Lys – вода		Lys – буфер		${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ × 10⁶, м³ моль^–1
T, K	^φV° × 10⁶, м³ моль^–1	$E_{\varphi }^{^\circ }$ × 10⁶, ^а м³ моль^–1 K^–1	^φV° × 10⁶, м³ моль^–1	$E_{\varphi }^{^\circ }$ × 10⁶, ^а м³ моль^–1 K^–1
288.15	107.06	0.0912	107.43	0.3327	0.36
293.15	107.54	0.0801	108.79	0.2860	1.24
298.15	107.98	0.0688	110.31	0.2393	2.33
303.15	108.17	0.0576	111.22	0.1926	3.04
308.15	108.50	0.0464	112.35	0.1459	3.85
313.15	108.76	0.0352	112.71	0.0992	3.95

^а$E_{\varphi }^{^\circ }$ = (∂^φV°/∂T)_p вычислено по уравнению (5).

Парциальные молярные объемы ^φV° чувствительны к сольватации растворенного вещества Lys, молекулы которого содержат как зарядные и полярные гидрофильные группы, так и гидрофобные фрагменты. В водных растворах происходит гидратация ионизацированных α‑карбоксильной и α-амино-групп молекулы Lys, протонирование боковой ε-амино-группы и гидратация неполярных (–CH₂–) фрагментов. Значение рН водного раствора аминокислоты в изученной области концентраций равнялось 9.7 ± 0.1, при этом образуется смесь двух ионных форм Lys – монокатиона ([H₂L]^++–) и цвиттериона ([HL]^±) в соотношении ~2 : 1. В случае растворов Lys в фосфатном буфере гидратированные ионы электролита (Na⁺, H₂PO$_{4}^{ - }$, HPO$_{4}^{{2 - }}$) взаимодействуют с гидратированными тремя зарядными центрами (α-NH$_{3}^{ + }$, α-COO^–, ε-NH$_{3}^{ + }$) монокатионов Lys, которые доминируют в условиях рН 7.4. Также диполи молекул воды попадают под воздействие электростатических сил вблизи катионов, анионов и монокатионов. В результате происходит усиление взаимодействий, обусловленных, прежде всего, электростатическими силами и образованием водородных связей между аминокислотой и компонентами растворителя.

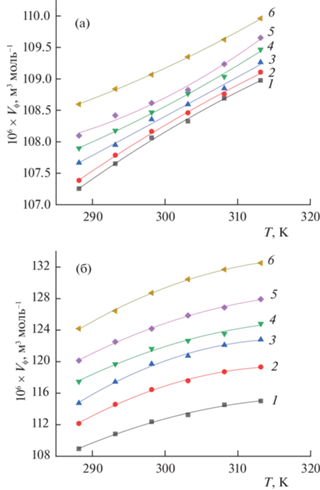
Температурные зависимости кажущихся молярных объемов ^φV = f(T) для Lys в воде и буферном растворе приведены на рис. 3. Наблюдается монотонная последовательность в расположении изоконцентрационных кривых ^φV(T) с ростом концентрации аминокислоты, что указывает на отсутствие процессов образования комплексов между Lys и компонентами буферного растворителя. Отметим, что изоконцентраты аминокислоты как в воде, так и буферном растворе описываются полиномом второй степени: ^φV = b₀ + b₁T + + b₂T², где b₀, b₁, b₂ – константы.

Рис. 3.

Температурные зависимости кажущихся молярных объемов ^φV L-лизина при разных концентрациях: (а) в воде (1 – 0.0036, 2 – 0.0071, 3 – 0.0123, 4 – 0.0178, 5 – 0.0216, 6 – 0.0318 m) и (б) в водном буферном растворе (1 – 0.0026, 2 – 0.0081, 3 – 0.0124, 4 – 0.0161, 5 – 0.0212, 6 – 0.0312 m).

Парциальные молярные объемы переноса при бесконечном разбавлении (${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$) аминокислоты из воды в буферный раствор вычислены по соотношению (3) и приведены в табл. 3:

(3)

${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ } = {}^{\varphi }V^\circ ({\text{Lys}}{\kern 1pt} --{\kern 1pt} {\text{буфер}}) - {}^{\varphi }V^\circ ({\text{Lys}}{\kern 1pt} --{\kern 1pt} {\text{вода}}).$

Применение модели Гэрни о перекрывания ко-сфер [22] позволяет рассмотреть ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ с точки зрения взаимодействий растворенных веществ. Согласно этой модели, когда частицы растворенного вещества сближаются настолько, что их ко-сферы перекрываются, то часть молекул воды из ко-сфер вытесняется, что сопровождается изменением термодинамических параметров (таких как объем, теплоемкость, энтальпия, энтропия и т.д.). В исследуемых буферных растворах перекрыванию гидратных ко-сфер молекул растворенных веществ способствуют взаимодействия: (i) между зарядными (α-NH$_{3}^{ + }$, α-COO^–, ε-NH$_{3}^{ + }$) группами лизина и ионами (Na⁺, H₂PO$_{4}^{ - }$, HPO$_{4}^{{2 - }}$) электролита, (ii) между гидрофобными группами молекул аминокислоты и ионами электролита. Взаимодействия первого типа приводят к увеличению объема ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ > 0, тогда как во втором случае наблюдается понижение значений ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ < 0 [22, 34–37]. Полученные нами положительные значения ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ отражают, прежде всего, эффекты электростатического взаимодействия ионов электролита буфера с зарядными центрами аминокислоты и образования водородных связей, которые приводят к понижению электрострикции молекул воды, вытесненных из гидратных сфер, и увеличению парциального молярного объема переноса. Сравнение значений ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$, приведенных в табл. 3, с данными, полученными для другой основной аминокислоты L-гистидина [38], показывает, что значения ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$(Lys) > ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$(His) и возрастают, соответственно, от (2.32 до 3.95) × × 10^–6 м³ моль^–1 и от (1.2 до 2.79) × 10^–6 м³ моль^–1 с ростом температуры в интервале (298.15–313.15) К. По-видимому, это является следствием влияния на объемные свойства более высокой основности боковой цепи Lys по сравнению с боковой цепью His: pK_side(Lys) > pK_side(His) [29]; Lys выступает в роли трехзарядных (++–) частиц, а His сохраняет цвиттерионную (+–) форму преобладающей в буферном растворе (рН 7.4). Кроме того, это согласуется с гидрофобностью аминокислот: более гидрофильная аминокислота имеет большее значение объема переноса [39]. Степень гидрофобности аминокислоты увеличивается при переходе от Lys к His [40]. Таким образом, уменьшение величины ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ в случае His свидетельствует о нарастании ион-гидрофобных взаимодействий, вносящих отрицательный вклад в значения ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$. Полученные результаты указывают на больший вклад ионной боковой цепи Lys в совокупный эффект взаимодействия компонентов буфера с трехзарядной формой Lys по сравнению с цвиттерионом His.

Как видно из табл. 3, значения ^φV° увеличиваются с ростом температуры, что согласуется с данными для других аминокислот в водных растворах [20, 41–43]. Изменение парциального молярного объема ^φV° с температурой может быть вызвано разными причинами, такими как тепловое расширение, ослабление сетки Н-связей, высвобождение молекул воды из сольватных слоев и т.д. Учитывая наличие сольватных (гидратных) сфер вокруг монокатионов и цвиттерионов аминокислоты в растворе, увеличение значений ^φV° с повышением температуры обусловлено, прежде всего, высвобождением части электрострикционно сжатой воды из рыхлых гидратных сфер растворенного вещества в объем раствора [34]. При более высоких температурах этот процесс происходит легче, что приводит к расширению раствора, о чем свидетельствуют более высокие значения ^φV° при более высоких температурах. Следует отметить, что в интервале температур от 288.15 до 313.15 К изменение объема Δ^φV° составило 1.7 × × 10^–6 м³ моль^–1 и 5.28 × 10^–6 м³ моль^–1 для Lys в воде и буфере соответственно. Можно полагать, что влияние температуры на ^φV° более выражено для буферных растворов Lys.

Изменения предельного кажущегося молярного объема ^φV° с температурой в воде и буфере, представленные в графической форме на рис. 4, описываются полиномом второй степени:

(4)

$^{\varphi }V^\circ = \alpha + \beta T + \gamma {{T}^{2}},$

где α, β и γ – константы, T – температура. Значения коэффициентов уравнения (4) приведены в табл. 4. Парциальная молярная расширяемость ($E_{\varphi }^{^\circ }$) при бесконечном разбавлении в исследуемых растворах вычислена по соотношению, полученному путем дифференцирования уравнения (4) по температуре:

(5)

$E_{\varphi }^{^\circ } = {{({{\partial }^{\varphi }}V^\circ {\text{/}}\partial T)}_{p}} = \beta + 2\gamma T.$

Величины $E_{\varphi }^{^\circ }$, представленные в табл. 4 для исследуемых растворов Lys, положительны и понижаются с ростом температуры, при этом их значения больше для растворов аминокислоты в буфере, чем в воде. Согласно подходу Хеплера [44], знак производной парциальной молярной расширяемости по температуре (∂$E_{\varphi }^{^\circ }$/∂T)_p = (∂^2φV°/∂T²)_p может служить критерием для характеристики структурно-образующей или структурно-разрушающей способности растворенных веществ в растворе. Полученные отрицательные значения (∂$E_{\varphi }^{^\circ }$/∂T)_p для Lys как в воде (–0.00224 см³ моль^–1 K^–2), так и в буферном растворе (–0.00934 см³ моль^–1 K^–2) свидетельствуют о склонности этой аминокислоты к нарушению структуры растворителя, причем более выраженное воздействие Lys оказывает на структуру буферного раствора.

Рис. 4.

Температурные зависимости парциальных молярных объемов ^φV° L-лизина в воде (1) и буферном растворе (2).

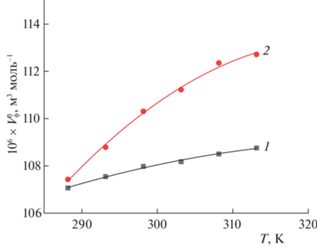
Таблица 4.

Коэффициенты α, β, γ уравнения (4) для L‑лизина в воде и водном буферном растворе

Система	α, см³ моль^–1	β, см³ моль^–1 К^–1	γ, см³ моль^–1 К^–2
Lys–вода	–12.581	0.7367	–0.00112
Lys–буфер	–376.443	3.0241	–0.00467

Таким образом, методом денсиметрии получены экспериментальные значения плотности растворов L-лизина в воде и фосфатном буферном растворе (рН 7.4) в интервале концентраций (~0.003–0.031 моль кг^–1) и температур (288.15–313.15) К. Определены кажущиеся и парциальные молярные объемы (^φV, ^φV°) L-лизина, а также предельные кажущиеся молярные объемы переноса (${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$) Lys из воды в буферный раствор. Положительные значения ^φV и ^φV° предполагают присутствие взаимодействий растворенного вещества с растворителем и характеризуют поведение Lys в растворах как гидрофильного растворенного вещества. Установлено увеличение значений ^φV, ^φV° и ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ Lys в воде и буферном растворе с повышением температуры, что обусловлено, прежде всего, высвобождением части электрострикционно сжатой воды из гидратных сфер монокатионной и цвиттерионной форм аминокислоты и ионов электролита в объем раствора. Показано, что влияние температуры на значения ^φV° более выражено для буферных растворов Lys, чем для воды. Монотонная последовательность в расположении изоконцентрационных кривых ^φV(T) с ростом концентрации аминокислоты указывает на отсутствие процессов образования комплексов между Lys и компонентами буферного растворителя.

Наблюдаемые положительные значения объема ${{\Delta }_{{{\text{tr}}}}}V_{\varphi }^{^\circ }$ переноса Lys из воды в буфер при всех изученных температурах являются результатом, прежде всего, эффектов гидратации и взаимодействия между гидратированными ионными формами Lys и ионами электролитов буферного раствора через электростатические силы и образование водородных связей. Иными словами, ион-гидрофильные и гидрофильно-гидрофильные взаимодействия доминируют над гидрофобно-гидрофобными и ион-гидрофобными взаимодействиями в исследуемых растворах L-лизина.

Определены парциальные молярные расширяемости ($E_{\varphi }^{^\circ }$) и их производные по температуре (∂$E_{\varphi }^{^\circ }$/∂T)_p при бесконечном разбавлении в водном и буферном растворах L-лизина. Показано, что полученные положительные значения $E_{\varphi }^{^\circ }$ понижаются с ростом температуры. L-лизин не способствует укреплению структуры раствора, что отражается в отрицательных значениях параметра (∂$E_{\varphi }^{^\circ }$/∂T)_p. Выявлено, что по сравнению с водным раствором, структурно-разрушающие эффекты Lys усиливаются в водном буферном растворе.

Измерения плотности выполнены на оборудовании центра коллективного пользования “Верхневолжский региональный центр физико-химических исследований” ИХР РАН (http://www.isc-ras.ru/ru/struktura/ckp).