ВВЕДЕНИЕ
В последнее десятилетие исследователей привлекают структуры, называемые вихревыми оптическими солитонами или вихрями. Оптическим вихрем является солитон, в волновом фронте которого содержится фазовая сингулярность. При этом он имеет характерное распределение интенсивности (например, похожее на кольцо) и фазы (в виде спирали). Исследования солитонов, в том числе, имеющих фазовую сингулярность, проводятся, в основном, в средах с керровской (кубической) нелинейностью. Обзор современного состояния исследований оптических вихревых структур приведен в статье [1].
Работа Б.А. Маломеда [1] посвящена рассмотрению последних теоретических и экспериментальных результатов, полученных при изучении двумерных и трехмерных солитонов, обладающих орбитальным угловым моментом. Двумерные и трехмерные солитоны, также называемые световыми пулями, в отличие от одномерных, которые обычно стабильны, подвержены нестабильностям, вызванным эффектами, возникающими в кубически нелинейных средах. Соответственно главной задачей, стоящей перед исследователем оптических многомерных солитонов является поиск физических сред и моделей, в которых световые пули могут распространяться стабильно. Вместе с уже известными методами стабилизации солитонов Б.А. Маломед описывает две относительно новые возможности, возникшие благодаря исследованию процессов, происходящих в бозе-эйнштейновских конденсатах (БЭК). Первую из них, обнаружили в гибридной модели БЭК, описываемой системой из двух уравнений Гросс-Питаевского, где уравнения были связаны между собой микроволновым полем через магнитно-дипольный переход [2]. В рамках данной модели исследователям удалось добиться стабилизации двумерных вихревых солитонов. Более того, как показали авторы [2], в гибридной модели БЭК вихревые солитоны могут обладать достаточно высоким топологическим зарядом, при этом сохраняя свою устойчивость. Вторая идея стабилизации импульсов/пучков стала основой для настоящей работы и будет описана ниже.
Вихревые солитоны, а также импульсы/пучки, с помощью которых они генерируются, имеют множество практических применений: оптические системы связи, захват и перемещение частиц вихревыми пучками, микроскопия c высоким разрешением и другие [3]. Для полноценного использования оптических солитонов с фазовой сингулярностью требуется преодолеть проблему азимутальной неустойчивости, характерную для пучков, обладающих орбитальным угловым моментом. Азимутальная неустойчивость ведет к распаду оптических вихрей на некоторое количество фундаментальных солитонов, которые также являются неустойчивыми в кубически нелинейных средах. Для стабилизации вихрей существует несколько способов, например, использование сред с конкурирующими нелинейностями [4, 5], сред с захватывающими потенциалами [6] или сред с нелокальной нелинейностью [7]. Новую возможность преодоления азимутальной неустойчивости обнаружили в бинарных БЭК. Стабильные двумерные и трехмерные оптические вихри были получены в БЭК с (псевдо) спин-орбитальной связью (СОС), которая является эффективной имитацией СОС, порождаемой связью магнитного момента электрона с магнитным полем, создаваемым собственным электростатическим полем ионной решетки [8], в полупроводниках. Авторы [9] использовали оптическую аналогию СОС в структуре, представляющей собой двужильный волновод с керровской нелинейностью, для стабилизации фундаментальных двумерных солитонов.
В настоящей работе мы изучаем возможность использования аналога оптической СОС [9] для стабилизации двумерных оптических вихрей.
ПОСТАНОВКА ЗАДАЧИ
Мы рассматриваем распространение оптических пучков в двужильном волноводе с фокусирующей кубичной нелинейностью и аномальной дисперсией групповых скоростей. Из-за небольшой модуляции показателя преломления происходит взаимное проникновение полей между жилами за счет туннельного эффекта. Такой волновод можно представить, как два связанных волновода, и описать двумя связанными НУШ, которые выглядят следующим образом:
(1)
$\begin{gathered} \frac{{\partial {{q}_{1}}}}{{\partial z~}} = \frac{i}{2}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + ~\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right){{q}_{1}} + i{{\left| {{{q}_{1}}} \right|}^{2}}{{q}_{1}} + \left( {ic - \delta \frac{\partial }{{\partial t}}} \right){{q}_{2}} + i\beta {{q}_{1}}~{\text{,}} \\ \frac{{\partial {{q}_{2}}}}{{\partial z~}} = \frac{i}{2}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + ~\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right){{q}_{2}} + i{{\left| {{{q}_{2}}} \right|}^{2}}{{q}_{2}} + \left( {ic - \delta \frac{\partial }{{\partial t}}} \right){{q}_{1}} - i\beta {{q}_{2}}~{\text{.}} \\ \end{gathered} $Здесь ${{q}_{{1,2}}}$ – комплексные амплитуды пучков в первом и втором волноводах, поперечная координата $x$ и продольная координата $z$ нормированы, соответственно, на ширину пучка ${{x}_{0}}$ и дифракционную длину ${{L}_{{diff}}} = kx_{0}^{2},$ где k – волновое число, t – локальное время, нормированное на величину (${{t}_{0}} = {{\left( {{{L}_{{diff}}}\left| {{{{{\partial }^{2}}k} \mathord{\left/ {\vphantom {{{{\partial }^{2}}k} {\partial {{\omega }^{2}}}}} \right. \kern-0em} {\partial {{\omega }^{2}}}}} \right|} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$). За аналог СОС, названный в [9] связывающей дисперсией (СД), отвечает коэффициент $\delta \approx \left( {{c \mathord{\left/ {\vphantom {c {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}} \right)~\left[ {{2 \mathord{\left/ {\vphantom {2 \omega }} \right. \kern-0em} \omega } + {{\chi _{l}^{{ - 1}}\partial {{\chi }_{l}}} \mathord{\left/ {\vphantom {{\chi _{l}^{{ - 1}}\partial {{\chi }_{l}}} {\partial \omega }}} \right. \kern-0em} {\partial \omega }}} \right],$ где ${{\chi }_{l}}$ – амплитуда модуляции диэлектрической проницаемости, $c$ – величина линейной связи между волноводами, $\beta $ описывает разность показателя преломления в волноводах.
Система (1) обладает следующими интегралами движения:
(3)
$\begin{gathered} H = \int {\int {\left[ {\beta \left( {\left| q \right|_{2}^{2} - \left| q \right|_{1}^{2}} \right) - cRe\left( {{{q}_{1}}q_{2}^{*} + {{q}_{2}}q_{1}^{*}} \right) + } \right.} } \\ + \,\,\delta Im\left( {q_{1}^{*}\frac{{\partial {{q}_{2}}}}{{\partial t}} + q_{2}^{*}\frac{{\partial {{q}_{1}}}}{{\partial t}}} \right) + \\ + \,\,\left. {\sum\limits_{n = 1,2} {{{\left( {{{{\left| {{{\partial {{q}_{n}}} \mathord{\left/ {\vphantom {{\partial {{q}_{n}}} {\partial x}}} \right. \kern-0em} {\partial x}}} \right|}}^{2}} + {{{\left| {\partial {{q}_{n}}/\partial x} \right|}}^{2}} - {{{\left| {{{q}_{n}}} \right|}}^{4}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\left| {{{\partial {{q}_{n}}} \mathord{\left/ {\vphantom {{\partial {{q}_{n}}} {\partial x}}} \right. \kern-0em} {\partial x}}} \right|}}^{2}} + {{{\left| {\partial {{q}_{n}}/\partial x} \right|}}^{2}} - {{{\left| {{{q}_{n}}} \right|}}^{4}}} \right)} 2}} \right. \kern-0em} 2}} } \right]dxdt, \\ \end{gathered} $На вход волновода подаются импульсы-пучки, содержащие пространственно-временные оптические вихри. Начальные условия в этом случае имеют вид:
(4)
${{\left. {{{q}_{{1,2}}}\left( {x,t} \right)} \right|}_{{z = 0}}} = {{A}_{{10,20}}}{\text{exp}}\left( {{{x}^{2}} + {{t}^{2}} + i\phi } \right),$Мы проводили компьютерное моделирование на основе системы (1) совместно с начальными условиями (4), используя численный псевдоспектральный метод, реализуемый с помощью итераций. На каждом шаге по z проводилось преобразование комплексных амплитуд q1,2 в Фурье-образы, проводился расчет новой итерации и затем обратно преобразовывался Фурье-прообраз. Данный процесс проводился до тех пор, пока максимальная разница между предыдущей и новой итерациями не превышала некоторого заданного числа, обычно порядка 10–10–10–12. При этом контролировалось сохранение интегралов (2) и (3). В качестве результата расчета получалась зависимость изменения комплексной амплитуды от продольной координаты z. Анализировалось сохранение формы импульса-пучка и наличие оптических вихрей в нем.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Перед рассмотрением процессов формирования и распространения вихревых солитонов в двужильном волноводе, мы рассчитали стабильное солитонное решение в такой структуре, основываясь на данных статьи [9]. При значениях ${{A}_{{10}}} = 1.75,$ ${{A}_{{20}}} = 0,$ $\delta = 2,$ $~с = 1,$ $\beta = 3$ происходит формирование и затем стабильное распространение фундаментального солитона. Далее мы использовали эти параметры, как параметры пробного решения вида (4), запускаемого в среду.
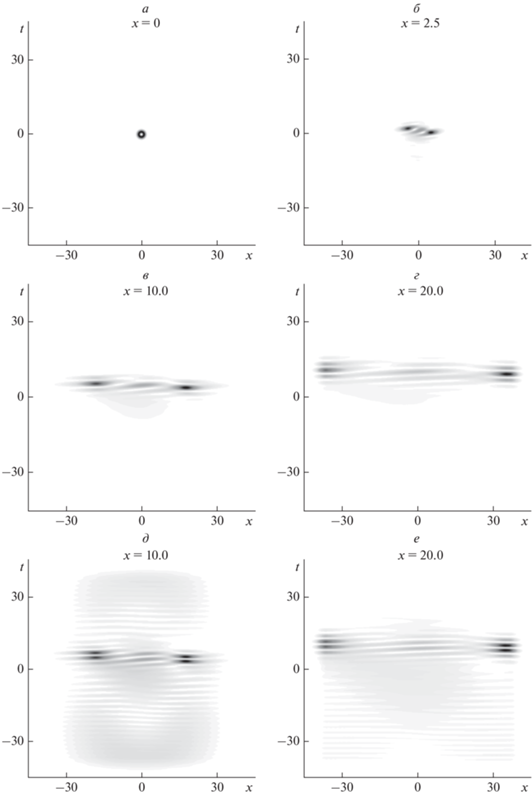
На вход первого волновода был подан импульс-пучок с пространственно-временным оптическим вихрем вида (4), в результате во время распространения, благодаря линейной связи волноводов структуры, во втором волноводе генерируется импульс-пучок, который также имеет особенности волнового фронта. В расчетах использованы следующие параметры: ${{A}_{{10}}} = 1.75,$ ${{A}_{{20}}} = 0,$ $~\delta = 0,$ $с = 1,$ $\beta = 5.$ При $\delta = 0$ в системе отсутствует СД, импульсы-пучки в обеих жилах разрушаются из-за не скомпенсированного влияния дифракции и дисперсии (рис. 1а). При постепенном увеличении $\delta $ (с шагом 0.5), в системе начинает действовать СД, импульс-пучок продолжает расширяться в пространстве и времени, но с другим “паттерном” распада (рис. 1а–1г). Распределение амплитуды и фазы в плоскости xt также меняется с ростом $\delta $ (рис. 2). Можно видеть, что при δ = 0 и $\delta = 1$ импульс-пучок сохраняет кольцевую структуру на расстоянии двух нелинейных длин (рис. 2а и 2в). Фазовая особенность при этом также сохраняется (рис. 2б и 2г). При $\delta = 2$ импульс-пучок конденсируется в два больших и несколько небольших локализаций (рис. 2д), причем, фазовый фронт сохраняет сложную структуру (рис. 2е). Можно видеть возникновение множества пар оптических вихрей низкой интенсивности, но солитонный характер распространения нарушается.
Рис. 1.
Профиль амплитуды в tz-плоскости для импульса-пучка во втором волноводе для разных значений $\delta $ = 0 (а), 0.5 (б), 1 (в), 1.5 (г) при постоянных $с = 1,$ ${{\beta }} = 5,$ ${{A}_{{10}}} = 1.75,$ ${{A}_{{20}}} = 0.$
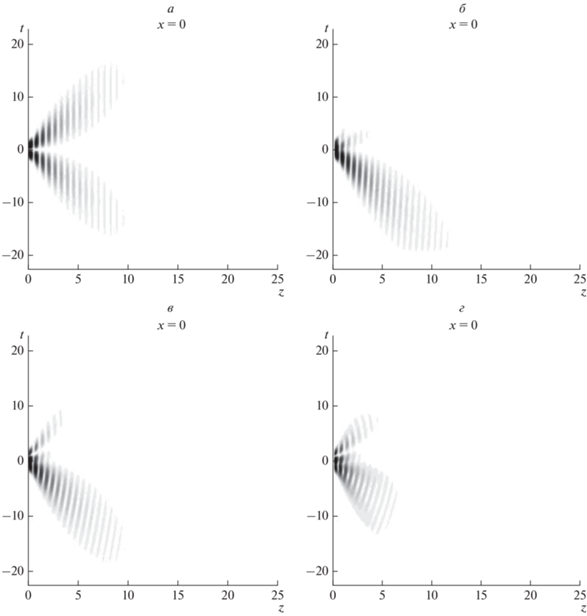
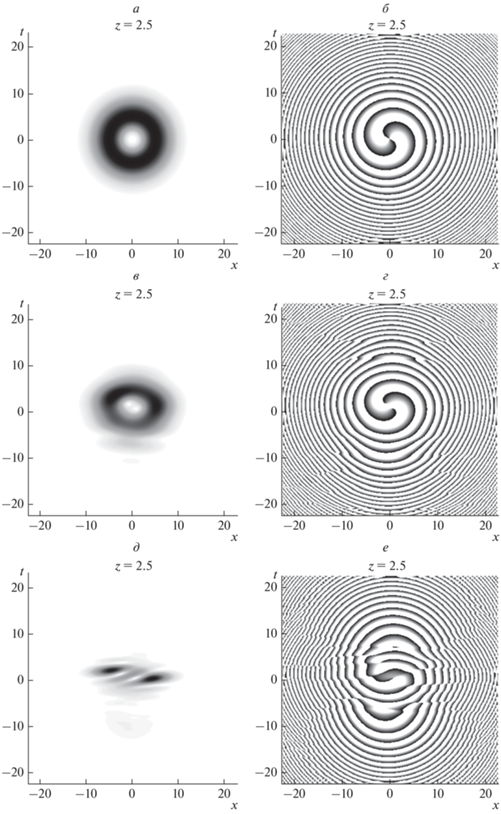
Рис. 2.
Распределение амплитуды (а, в, д) и фазы (б, г, е) импульса-пучка в первом волноводе при разных значениях параметра $\delta $ = 0 (а, б), 1 (в, г), 2 (д, е) при постоянных $с = 1,$ ${{\beta }} = 3,$ ${{A}_{{10}}} = 1.75,$ ${{A}_{{20}}} = 0.$
При вариации других параметров ($с,~{{\beta }}$) форма импульсов-пучков в первом и втором волноводе изменяется, но они распадаются на несколько небольших быстро затухающих кластеров. При достаточно высоком значении амплитуды начальный вихревой импульс-пучок в первом волноводе распадается на фундаментальные солитоны, которые распространяются без изменений в своей форме на всей дистанции распространения (рис. 3а–3г). Фундаментальные солитоны в первом волноводе также генерируют пары солитонов во втором волноводе, которые остаются стабильными на всей дистанции распространения (рис. 3д и 3е).
ЗАКЛЮЧЕНИЕ
Проанализировано распространение оптических вихревых импульсов-пучков в системе двух туннельно-связанных кубично-нелинейных волноводов. С помощью численного моделирования показано, что вихревые солитоны в данном случае неустойчивы при различных комбинациях амплитуды модуляции диэлектрической проницаемости, величины линейной связи между волноводами и разности показателя преломления в волноводах. Однако импульсы-пучки сохраняют пространственно-временную вихревую структуру на протяжении нескольких дисперсионных и дифракционных длин.
Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского государственного университета “Фотонные и квантовые технологии. Цифровая медицина”.