ВВЕДЕНИЕ
В настоящее время многослойные неоднородные голографические дифракционные структуры (МНГДС) привлекают свое внимание множество исследователей своими уникальными дифракционными характеристиками [1–11]. Селективный отклик таких структур отличается от стандартных одиночных голографических дифракционных структур (ГДС) наличием локальных максимумов, заключенных в общий контур селективности, который при этом аналогичен одиночной ГДС [3–6]. Варьируя соотношением толщин буферных и дифракционных слоев, а также их количеством, возможно изменять вид селективного отклика [3–6, 12–14]. Данная особенность позволяет рассматривать данные структуры, например, в качестве элементов спектральных фильтров или же для генерации последовательности фемтосекундных лазерных импульсов [7–11].
В предыдущей работе [14] была продемонстрирована возможность управления дифракционными характеристиками МНГДС, сформированных в капсулированных полимером жидких кристаллах (КПЖК), с помощью внешнего электрического воздействия. При электрическом воздействии на определенные дифракционные слои появлялась возможность “отключать” дифракцию на необыкновенных собственных волнах, что в итоге приводило к трансформации селективного отклика на выходе всей МНГДС. Следовательно, на основе таких структур появляется возможность построения уже электрически управляемых дифракционных оптических элементов для спектральной фильтрации оптического излучения.
Однако, проведенные исследования с КПЖК показывают, что среда является оптически однородной, происходит полное разделение фаз, и при управлении внешним электрическим полем директор капсул жидких кристаллов (ЖК) поворачивается по толщине слоев ГДС одинаково. При рассмотрении же случая, когда концентрация ЖК достаточно велика (более 90%), среда имеет плавную оптическую неоднородность [15, 16], что необходимо учитывать при решении задачи дифракции.
Таким образом, целью данной работы является разработка аналитической модели дифракции света на МНГДС в ФПМ-ЖК, которые имеют плавную оптическую неоднородность по толщине слоев.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
При значительно большой концентрации ЖК (более 90%) по сравнению с фотополимерным материалом (ФПМ), их ориентация определяется границами дифракционного слоя и описывается уравнением Фредерикса [15, 16]:
(1)
$\begin{gathered} \frac{1}{{{{\xi }_{E}}(E)}}\left( {\frac{{{{d}_{n}}}}{2} + y} \right) = \\ = \,\,\int\limits_0^{\varphi (\vec {r},E)} {{{{\left( {{{{\sin }}^{2}}{{\varphi }_{m}}(\vec {r},E) - {{{\sin }}^{2}}\varphi } \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}d\varphi } , \\ \end{gathered} $Для начала поворота директора ЖК необходимо достичь уровня критической напряженности Фредерикса, которое определяется как [14–16]:
(2)
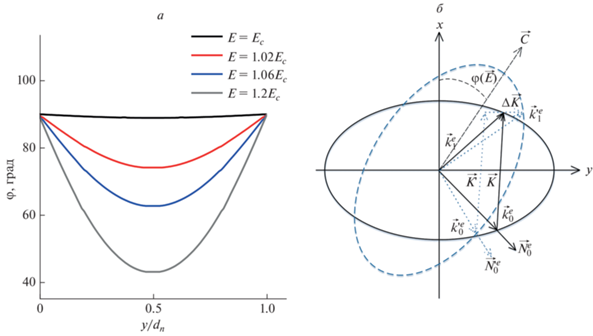
${{E}_{c}} = {{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} {{{d}_{n}}}}} \right. \kern-0em} {{{d}_{n}}}}\sqrt {{{4{{\pi }}{{K}_{{33}}}} \mathord{\left/ {\vphantom {{4{{\pi }}{{K}_{{33}}}} {\Delta {{\varepsilon }}}}} \right. \kern-0em} {\Delta {{\varepsilon }}}}} .$Для демонстрации причины возникновения плавной оптической неоднородности по глубине ФПМ-ЖК слоя, на рис. 1а приведен численный расчет угла поворота директора ЖК от прикладываемого внешнего электрического поля. Из представленного рисунка хорошо видно, что угол поворота директора ЖК имеет разные значения по глубине дифракционного слоя, что в итоге и обуславливает оптическую неоднородность среды. На рис. 1б также продемонстрирована векторная диаграмма дифракции света на необыкновенных волнах при изменении угла поворота директора ЖК.
Рис. 1.
Зависимость угла поворота директора ЖК по толщине ФПМ-ЖК слоя (а) и векторная диаграмма дифракции (б).
Учитывая угол поворота директора ЖК из выражения (1), тензор диэлектрической проницаемости для $n$-го слоя с ФПМ-ЖК записывается как [16]:
(3)
${{{{\varepsilon }}}^{n}} = (1 - {{\rho }})\left( {{{\varepsilon }}_{p}^{n} \cdot \hat {I} + \Delta {{\varepsilon }}_{p}^{n}} \right) + {{\rho }}\left( {{{\varepsilon }}_{{LC}}^{n} + \Delta {{\varepsilon }}_{{LC}}^{n}} \right),$Изменение тензора диэлектрической проницаемости можно представить в виде ряда Фурье по пространственным гармоникам решеток, учитывая, что ${{\Delta \varepsilon }}_{p}^{n}{{\delta }} \ll {{\varepsilon }}_{p}^{n}$ и ${{\Delta \varepsilon }}_{{LC}}^{n}{{\delta }} \ll {{\varepsilon }}_{{LC}}^{n}{\text{:}}$
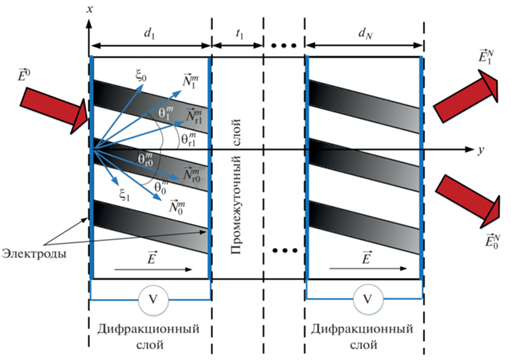
При решении задачи дифракции будем предполагать, что на МНГДС, у которой каждый дифракционный слой с ФПМ-ЖК расположен между двумя пластинами, выполненными ${\text{из}}$ оптически прозрачного материала (стекло), где на внутреннюю сторону каждой пластины нанесены электроды из проводящего оптически прозрачного материала (оксид индия-олова), падает произвольно поляризованный квазимонохроматический световой пучок ${{\vec {E}}^{0}}$ с волновым вектором ${{\vec {k}}_{0}}$ и единичным комплексным вектором поляризации ${{\vec {e}}_{0}}$ (рис. 2). Для схемы дифракции будем также рассматривать обобщенный случай, когда дифракционная структура наклонена, вследствие возможной последовательной записи нескольких наложенных решеток (рис. 2) [17].
Следуя методу медленноменяющихся амплитуд в случае брэгговской дифракции световых пучков на МНГДС в оптически неоднородных слоях ФПМ-ЖК (рис. 2), амплитуды взаимодействующих волн определяются системами уравнений связанных волн в частных производных [14–16]:
(4)
$\begin{gathered} \vec {N}_{{r{\text{0}}}}^{{m,n}} \cdot \nabla E_{0}^{{m,n}}\left( {\omega ,\vec {r}} \right) = \\ = \,\, - iС_{1}^{{m,n}}\left( E \right) \cdot n_{1}^{{m,n}}\left( {\vec {r},E} \right) \cdot E_{1}^{{m,n}}\left( {\omega ,\vec {r}} \right) \times \\ \times \,\,\exp \left[ { + i{{\Theta }^{{m,n}}}(\vec {r},E)} \right], \\ \vec {N}_{{r1}}^{{m,n}} \cdot \nabla E_{1}^{{m,n}}\left( {\omega ,\vec {r}} \right) = - iС_{0}^{{m,n}}\left( E \right) \times \\ \times \,\,n_{1}^{{m,n}}\left( {\vec {r},E} \right) \cdot E_{0}^{{m,n}}\left( {\omega ,\vec {r}} \right) \cdot \exp \left[ { - i{{\Theta }^{{m,n}}}(\vec {r},E)} \right], \\ \end{gathered} $(5)
${{\Theta }^{{m,n}}}(\vec {r},E) = \int\limits_0^{{{d}_{n}}} {\Delta {{{\vec {K}}}^{{m,n}}}\left( {\vec {r},E} \right)} d\vec {r},$Однако, согласно результатам, приведенным в работе [16], зависимость ${{\Theta }^{{m,n}}}(\vec {r},E)$ имеет сложный вид, что делает получение решений для (4) в случае высокой эффективности дифракции невозможным. Вместе с тем, каждый ФПМ-ЖК слой можно аппроксимировать параболической функцией, тогда интегральную фазовую расстройку ${{\Theta }^{{m,n}}}(\vec {r},E)$ для каждого n-го слоя можно представить в аналитическом виде [16]:
(6)
$\begin{gathered} {{\Theta }^{{m,n}}}(\vec {r},E) = \int {\Delta {{{\vec {K}}}^{{m,n}}}\left( {\vec {r}} \right)d\vec {r}} = \int {\left( {\Delta {{K}^{{m,n}}}{{{\vec {y}}}_{0}}} \right)d\left( {{{{\vec {y}}}_{0}}y} \right)} = \\ = \Delta {{K}_{0}}^{{m,n}}y + \frac{{t_{y}^{n}}}{2}{{y}^{2}}, \\ \end{gathered} $И если ввести коэффициенты аппроксимации для интегральной фазовой расстройки для каждого ФПМ-ЖК слоя вида:
(7)
$\begin{gathered} {{\Theta }^{{m,1}}}({{y}_{1}},E) = {{\Theta }_{{\text{н}}}} + {{a}_{1}}(E){{y}_{1}} + {{b}_{1}}(E)y_{1}^{2}{\text{,}} \\ {\text{при}}\,\,\,\,n = 1, \\ {{\Theta }^{{m,n}}}({{y}_{n}},E) = {{\Theta }^{{n - 1}}} + {{a}_{n}}(E){{y}_{n}} + {{b}_{n}}(E)y_{n}^{2}, \\ {\text{при}}\,\,\,\,n = 2,...,N, \\ \end{gathered} $Таким образом, связь между слоями задается ${{\Theta }^{{m,n - 1}}}$ и для определения решения уравнений (4) необходимо произвести аппроксимацию параметра ${{\Theta }^{{m,n}}}(\vec {r})$ для каждого слоя и определить коэффициенты ${{a}_{n}}$ и ${{b}_{n}}$ из (7) путем минимизации интегральной среднеквадратической ошибки аппроксимации [16]:
Возвращаясь к схеме дифракции (рис. 2), определим выражения для пространственных распределений световых полей для 0-го и 1-го дифракционного порядка на выходе МНГДС [14, 16]:
Для описания преобразования плоских световых волн в многослойных средах воспользуемся матричным методом. Для этого перейдем от амплитудных распределений частотных Фурье-компонент дифрагирующих пучков к их угловым спектрам [6, 14]:
В результате процесс преобразования частотно-угловых спектров взаимодействующих световых пучков для необыкновенных волн на выходе МНГДС представится в виде [6, 14]:
где${{\vec {T}}^{N}} = {{\vec {T}}^{{e,N}}} \cdot {{\vec {A}}^{{e,N - 1}}} \cdot {{\vec {T}}^{{e,N - 1}}} \cdot ... \cdot {{\vec {A}}^{{e,n}}} \cdot {{\vec {T}}^{{e,n}}} \cdot ...$ $ \ldots \cdot {{\vec {A}}^{{e,1}}} \cdot {{\vec {T}}^{{e,1}}}$ – матричная передаточная функция всей МНГДС, ${{\vec {E}}^{{e,n}}} = \left[ {\begin{array}{*{20}{c}} {E_{0}^{{e,n}}({{\omega }},{{\theta }})} \\ {E_{1}^{{e,n}}({{\omega }},{{\theta }})} \end{array}} \right],$ ${{\vec {T}}^{{n,m}}} = \left[ {\begin{array}{*{20}{c}} {T_{{00}}^{{n,m}}\left( {{{\omega }},{{\theta }}} \right)}&{T_{{10}}^{{n,m}}\left( {{{\omega }},{{\theta }}} \right)} \\ {T_{{01}}^{{n,m}}\left( {{{\omega }},{{\theta }}} \right)}&{T_{{11}}^{{n,m}}\left( {{{\omega }},{{\theta }}} \right)} \end{array}} \right]$ – матричная передаточная функция, ${{\vec {E}}^{0}} = \left[ {\begin{array}{*{20}{c}} {{{E}_{0}}({{\omega }},{{\theta }})} \\ 0 \end{array}} \right],$ ${{\vec {A}}^{{e,n}}}$ – матрица перехода для промежуточного слоя, которая представлена в работах [6, 14].Компоненты матрицы ${{\vec {T}}^{{e,n}}}$ определяются как [16]:
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
При численном расчете будем полагать, что поляризация падающего излучения совпадает с поляризацией собственных необыкновенных волн для каждого слоя. Световые пучки являются плоскими монохроматическими с единичной амплитудой. Дифракционная эффективность на выходе МНГДС можно определить по известному выражению:
(9)
$\begin{gathered} {{\eta }}_{d}^{{e,n}}(E,\Delta K) = \\ = {{{{{\left| {E_{1}^{{e,n}}(E,\Delta K)} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {E_{1}^{{e,n}}(E,\Delta K)} \right|}}^{2}}} {\left( {{{{\left| {E_{1}^{{e,n}}(E,\Delta K)} \right|}}^{2}} + {{{\left| {E_{0}^{{e,n}}(E,\Delta K)} \right|}}^{2}}} \right)}}} \right. \kern-0em} {\left( {{{{\left| {E_{1}^{{e,n}}(E,\Delta K)} \right|}}^{2}} + {{{\left| {E_{0}^{{e,n}}(E,\Delta K)} \right|}}^{2}}} \right)}}, \\ \end{gathered} $При численном расчете будет использована трехслойная ГДС с однородными профилями показателя преломления. Параметры для моделирования: ${{\lambda }} = 633$ нм; ${{d}_{n}} = 20$ мкм; ${{t}_{n}} = 160$ мкм; $n_{{lc}}^{o} = 1.535$ и $n_{{lc}}^{e} = 1.68$ являются обыкновенными и необыкновенными показателями преломления для ЖК соответственно; ${{n}_{p}} = 1.535$ является показателем преломления для полимера; угол Брэгга составляет ${{{{\theta }}}_{b}} = 15$ градусов; период дифракционной структуры 1.2 мкм; параметры для аппроксимации пространственной амплитуды первой гармоники показателя преломления для ФПМ-ЖК слоев функцией вида $n(y,c,s,t) = \cosh {{\left( {c(sy - t)} \right)}^{{ - 1}}}$ равны $\left\{ {с,s,t} \right\} = \left\{ {{\text{0}}{\text{.058}}, - {\text{1}}{\text{.867}}, - {\text{0}}{\text{.688}}} \right\}.$
На рис. 3 и 4 приведены зависимости дифракционной эффективности для трехслойной ГДС с ФПМ-ЖК от угла считывания и приложенного электрического поля только на второй слой.
Рис. 3.
Зависимость дифракционной эффективности для трехслойной ГДС с ФПМ-ЖК от угла считывания и значения внешнего электрического поля на втором слое.
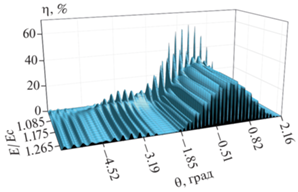
Рис. 4.
Зависимость дифракционной эффективности для трехслойной ГДС с ФПМ-ЖК от угла считывания и дискретных значений внешнего электрического поля на втором слое.
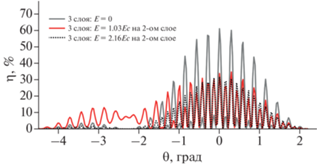
Как видно из рис. 3 и 4, при подаче напряжения только на второй дифракционный слой селективный отклик трехслойной ГДС начинает трансформироваться до вида двухслойной ГДС, но с увеличенным промежуточным слоем, что обуславливает добавление локальных максимумов контура селективности. Однако, кроме трансформации, из-за плавной оптической неоднородности в ФПМ-ЖК слоях, наблюдается смещение угловой селективности даже при небольшом увеличении значения внешнего электрического воздействия, относительно критической напряженности Фредерикса, что не было так характерно для случая с КПЖК [14].
На рис. 5 и 6 приведены зависимости дифракционной эффективности для трехслойной ГДС в случае электрического воздействия на всех слоях.
Рис. 5.
Зависимость дифракционной эффективности для трехслойной ГДС с ФПМ-ЖК от угла считывания и значения внешнего электрического поля на всех слоях.
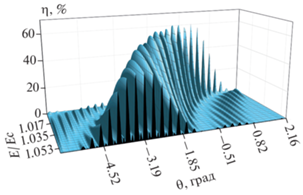
Рис. 6.
Зависимость дифракционной эффективности для трехслойной ГДС с ФПМ-ЖК от угла считывания и дискретных значений внешнего электрического поля на всех слоях.
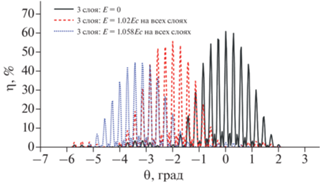
Как видно из рис. 5 и 6, при электрическом воздействии на всех слоях происходит существенное смещение угловой селективности вследствие увеличения интегральной фазовой расстройки в каждом дифракционном слое. В общем случае, при дальнейшем увеличении значения электрического поля дифракция отключится. Однако, при небольшом увеличении значения электрического поля, относительно критической напряженности Фредерикса, появляется возможность плавно смещать угловую селективность, что в случае с МНГДС можно интерпретировать как канальную перестройку, если рассматривать такие структуры в качестве спектральных фильтров.
Также стоит отметить, что в случае увеличения числа и толщины дифракционных слоев при электрическом воздействии на всех слоях, произойдет увеличение коэффициента смещения угловой селективности, что обусловлено ростом интегральной фазовой расстройки из-за плавной оптической неоднородности от каждого дифракционного слоя с ФПМ-ЖК.
Приведенные закономерности необходимо учитывать при построении управляемых оптических спектральных фильтров на основе МНГДС с ФПМ-ЖК, так как это позволяет не только иметь возможность трансформации селективного отклика, но и осуществлять канальную перестройку с помощью внешнего электрического воздействия.
ЗАКЛЮЧЕНИЕ
Представлена новая аналитическая модель дифракции света на пропускающих электрически управляемых многослойных неоднородных голографических дифракционных структурах в фотополимерных композициях с жидкокристаллической компонентой, которая учитывает плавную оптическую неоднородность вдоль глубины решеток. Представленные передаточные функции описывают эволюцию частотно-угловых спектров световых пучков при их дифракции на многослойных неоднородных голографических дифракционных структурах.
С помощью численного расчета было продемонстрировано, что при воздействии электрического поля на выбранный ФПМ-ЖК слой селективный отклик МНГДС может трансформироваться. При этом, вследствие плавной оптической неоднородности ФПМ-ЖК слоев, трансформация протекает со смещением угловой селективности, направление которого зависит от направления приложенного электрического поля.
Выявленные закономерности можно использовать для осуществления перестройки каналов, если рассматривать многослойные неоднородные голографические дифракционные структуры в качестве электрически управляемых элементов оптических спектральных фильтров.
Работа выполнена в рамках программы стратегического академического лидерства “Приоритет-2030”.