ВВЕДЕНИЕ

В последнее время наблюдается большой интерес к разработке компактных структур нанофотоники для дифференцирования оптических сигналов, а также для реализации более сложных дифференциальных операторов. Указанные дифференцирующие структуры являются перспективными в задачах обработки информации в режиме реального времени [1, 2].

Преобразование оптического сигнала, происходящее при его отражении или прохождении через дифракционную структуру, может быть описано как преобразование сигнала линейной системой, у которой передаточная функция (ПФ) задается коэффициентом отражения или пропускания структуры, рассматриваемым как функция угловой и/или пространственной частоты [2–4]. В частности, выполнение операции оптического дифференцирования во времени соответствует в Фурье-пространстве умножению спектра падающего импульса на $ - i\omega $, где $\omega $ – угловая частота. Аналогичным образом, в случае пространственного дифференцирования пространственный спектр падающего пучка умножается на $i{{k}_{{x,0}}},$ где ${{k}_{{x,0}}}$ – пространственная частота (тангенциальная компонента волнового вектора падающей волны). Таким образом, ПФ идеального дифференциатора имеет нуль на центральной частоте (угловой или пространственной). В этой связи необходимым условием для оптического дифференцирования является наличие нуля в спектре отражения или пропускания дифракционной структуры. Поскольку нули в спектре отражения (пропускания), как правило, обусловлены резонансными эффектами возбуждения собственных мод структуры, то для дифференцирования широко используются резонансные структуры фотоники, в частности, резонансные дифракционные решетки [2, 3], слоистые структуры [4, 5] и микро-резонаторы [6].

В недавней работе авторов настоящей статьи было показано, что простая трехслойная структура металл-диэлектрик-металл (МДМ-структура) позволяет в отражении реализовать вычисление первой производной по пространственной переменной или во времени [7]. При этом было строго показано, что в спектре МДМ-структуры всегда можно получить нуль отражения за счет выбора толщин металлических и диэлектрического слоев. Отметим, что, в отличие от дифференциаторов в [5, 8], МДМ-структура не требует призмы для ввода излучения и поэтому является существенно более компактной.

В настоящей работе впервые теоретически описано и численно продемонстрировано применение композитной МДМ-структуры для реализации операции “пространственно-временного” дифференцирования второго порядка. Под “пространственно-временным” дифференцированием при этом понимается вычисление дифференциального оператора, равного линейной комбинации производных соответствующего порядка по времени и по пространственной координате.

ОДИНОЧНАЯ И КОМПОЗИТНАЯ СТРУКТУРЫ МЕТАЛЛ–ДИЭЛЕКТРИК–МЕТАЛЛ

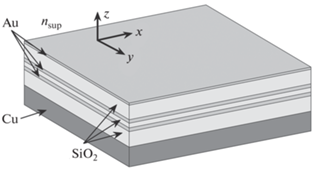
Одиночная структура металл–диэлектрик–металл состоит из верхнего металлического слоя, диэлектрического слоя и нижнего металлического слоя [7] (на рис. 1 схематично показана геометрия аналогичной композитной МДМ-структуры, рассмотренной ниже). Пусть на МДМ-структуру падает плоская волна, имеющая единичную амплитуду и некоторую фиксированную поляризацию (поперечную электрическую (ТЕ) или поперечную магнитную (ТМ)). Обозначим ${{k}_{{x,0}}} = {{k}_{0}}{{n}_{{{\text{sup}}}}}\sin {{\theta }_{0}}$ тангенциальную компоненту волнового вектора падающей волны, где ${{\theta }_{0}}$ – угол падения, ${{k}_{0}} = {{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} c}} \right. \kern-0em} c}$ – волновое число, ${{\omega }_{0}}$ – частота волны, $c$ – скорость света, ${{n}_{{{\text{sup}}}}}$ – показатель преломления области над структурой.

С использованием модели многолучевой интерференции коэффициент отражения МДМ-структуры несложно получить в виде [7]

где ${{r}_{1}},$ ${{r}_{2}}$ – комплексные коэффициенты отражения верхнего металлического слоя для плоских волн, падающих на слой сверху из области над структурой и снизу со стороны диэлектрического слоя, $t$ – коэффициент пропускания верхнего металлического слоя, $\rho $ – коэффициент отражения нижнего металлического слоя, ${{k}_{{z,0}}} = \sqrt {k_{0}^{2}n_{d}^{2} - k_{{x,0}}^{2}} $ – $z$-компонента волнового вектора плоской волны в диэлектрическом слое, отраженной от нижнего слоя металла, ${{n}_{d}}$ и ${{h}_{d}}$ – показатель преломления и толщина диэлектрического слоя соответственно. Коэффициенты отражения и пропускания металлических слоев в (1) зависят от их толщины и частоты, угла падения и поляризации падающей волны и рассчитываются по формулам, описывающим отражение и прохождение плоской волны через плоскопараллельный слой однородного материала.

Отметим, что рассматриваемая МДМ-структура является резонансной, поскольку в ней могут существовать вытекающие моды, локализованные в диэлектрическом слое [7]. В ряде случаев в резонансных структурах коэффициент отражения может обращаться в нуль. Данное свойство является важным с практической точки зрения, и, в частности, позволяет использовать резонансные структуры в качестве оптических дифференциаторов.

Приравнивая к нулю числитель выражения для коэффициента отражения в (1), получим, что коэффициент отражения МДМ-структуры обращается в нуль при выполнении равенства

В работе [7] было доказано, что при фиксированной толщине нижнего металлического слоя соотношение (2) всегда может быть выполнено за счет выбора толщин верхнего металлического и диэлектрического слоев. Таким образом, при заданных материалах, частоте $\omega = {{\omega }_{0}}$ и угле падения (тангенциальной компоненте волнового вектора) в МДМ-структуре всегда можно получить нулевое отражение. Отметим, что при нормальном падении $({{k}_{{x,0}}} = 0)$ коэффициент отражения МДМ-структуры в силу симметрии задачи дифракции является четной функцией от ${{k}_{x}},$ и поэтому структура, имеющая нуль отражения 1-го порядка по $\omega $ при $\omega = {{\omega }_{0}},$ будет иметь нуль отражения 2-го порядка по ${{k}_{x}}.$

Покажем, что, “комбинируя” две МДМ-структуры, имеющие нуль отражения и разделенные промежуточным слоем диэлектрика, можно получить в спектре отражения нуль 2-го порядка по $\omega \,.$ Геометрия композитной МДМ-структуры показана на рис. 1. Действительно, используя модель многолучевой интерференции, коэффициент отражения композитной МДМ-структуры можно также получить в виде (1), только коэффициенты ${{r}_{1}},$ ${{r}_{2}},$ $\rho ,$ $t$ теперь уже следует рассматривать не как коэффициенты отражения и пропускания верхнего и нижнего металлических слоев, а как коэффициенты отражения и пропускания верхней и нижней МДМ-структур. При этом толщина диэлектрического слоя ${{h}_{d}}$ в (1) теперь соответствует толщине диэлектрического слоя, разделяющего МДМ-структуры. Если МДМ-структуры, образующие композитную МДМ-структуру, имеют нули отражения при ω = ω₀, то коэффициенты ${{r}_{1}},$ ${{r}_{2}},$ $\rho ,$ $t$ могут быть записаны в виде

Подставляя (3) в (1) и проводя несложные преобразования, коэффициент отражения композитной МДМ-структуры можно получить в виде

где $h$ – толщина диэлектрического слоя, разделяющего МДМ-структуры. Соответственно, при выполнении условия композитная структура будет иметь нуль отражения 2-го порядка по $\omega $ при $\omega = {{\omega }_{0}}.$ При нормальном падении композитная МДМ-структура, удовлетворяющая условию (5), будет иметь нули 2-го порядка как по $\omega ,$ так и по ${{k}_{x}}.$

ПРЕОБРАЗОВАНИЕ ОПТИЧЕСКИХ СИГНАЛОВ

Рассмотрим пространственно-временное преобразование двумерного оптического импульса с центральной частотой $\omega = {{\omega }_{0}},$ происходящее при отражении от многослойной структуры при нормальном падении (${{\theta }_{0}} = 0$). Пространственно-временную огибающую падающего импульса в системе координат $\left( {x,z} \right)$ (ось z перпендикулярна структуре, рис. 1), можно представить в виде суперпозиции плоских волн с различными угловыми ($\omega = {{\omega }_{0}} + {{\omega }_{{inc}}}$) и пространственными (${{k}_{x}}$) частотами:

где $G\left( {{{k}_{x}},{{\omega }_{{inc}}}} \right)$ – спектр огибающей, заданный в некоторой области $\Omega ,$ $\nu = {c \mathord{\left/ {\vphantom {c {{{n}_{{sup}}}}}} \right. \kern-0em} {{{n}_{{sup}}}}}$ – скорость распространения импульса.

Преобразование пространственно-временной огибающей импульса (6), происходящее при отражении импульса от слоистой структуры, описывается линейной системой с передаточной функцией (ПФ) [9]

Таким образом, огибающая отраженного импульса примет вид

Если в качестве слоистой структуры используется композитная МДМ-структура, удовлетворяющая условию (5), т.е. имеющая нули отражения второго порядка и по $\omega $ и по ${{k}_{x}}$ при $\omega = {{\omega }_{0}}$ и ${{k}_{x}} = 0,$ то ПФ (7) может быть записана в виде

Главные члены разложения в (9) пропорциональны ПФ идеальных дифференциаторов 2-го порядка по пространственной переменной и во времени, и поэтому композитная МДМ-структура позволяет реализовать вычисление следующего дифференциального оператора, которое будем называть пространственно-временным дифференцированием 2-го порядка:

Отметим, что, как будет продемонстрировано в следующем разделе, различные соотношения между коэффициентами ряда Тейлора ${{с}_{{x,2}}}$ и ${{c}_{{t,2}}}$ в (9), (10) позволяют получить различные профили огибающих отраженного пространственно-временного импульса.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Рассмотрим возможность использования исследуемой композитной МДМ-структуры для выполнения операций пространственно-временного дифференцирования второго порядка (10) на примере падающих ТЕ- и TM-поляризованных пространственно-временных оптических импульсов с центральной частотой ${{\omega }_{0}} = {\text{2}}{\text{.99 ф}}{{{\text{с}}}^{{ - 1}}}$ (длиной волны ${{\lambda }_{0}} = 630{\text{ нм}}$) и гауссовым профилем огибающей ${{P}_{{inc}}}\left( {x,t} \right) = \exp \left[ { - {{{\left( {{x \mathord{\left/ {\vphantom {x {{{\sigma }_{x}}}}} \right. \kern-0em} {{{\sigma }_{x}}}}} \right)}}^{2}} - {{{\left( {{t \mathord{\left/ {\vphantom {t {{{\sigma }_{t}}}}} \right. \kern-0em} {{{\sigma }_{t}}}}} \right)}}^{2}}} \right],$ где σ_x = 18 мкм, ${{\sigma }_{t}} = 5800\,\,{\text{фс}}{\text{.}}$

Для реализации дифференциального оператора (10) была рассчитана композитная МДМ-структура, удовлетворяющая условию (5) и состоящая из слоев золота (Au), меди (Cu) и диоксида кремния (SiO₂). Конфигурация слоев структуры, перечисленных сверху вниз, имеет вид Au–SiO₂–Au–SiO₂–Au–SiO₂–Cu. Стоит отметить, что для рассматриваемого примера использование меди в качестве материала нижнего слоя обеспечило лучшие рабочие характеристики структуры (соотношения между коэффициентами в выражениях (9) и (10), приведенными ниже) по сравнению со случаем, когда все металлические слои структуры выполнены из золота. Указанная структура расположена на подложке из кварца (SiO₂), над структурой – воздух. Для показателей преломления материалов использовались справочные данные [10, 11]. Толщины слоев рассчитанной структуры, имеющей нули второго порядка по $\omega $ и по ${{k}_{x}},$ описываются следующим массивом: [21.6, 146.5, 33.8, 46.0, 34.5, 156.3, 100.0] нм.

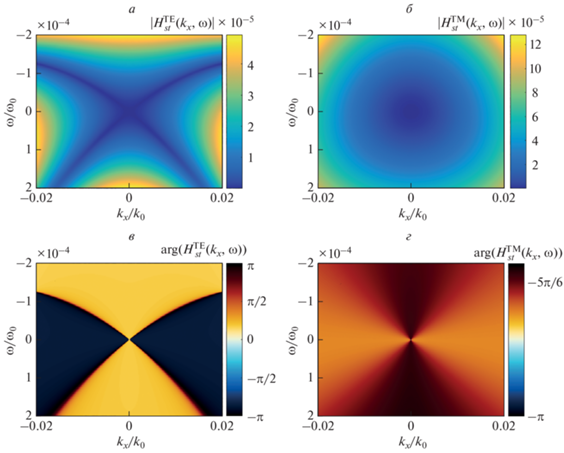
На рис. 2 показаны рассчитанные с помощью строгого метода решения задачи дифракции на слоистых структурах [12] модуль и фаза (аргумент) пространственно-временных ПФ структуры $H_{{st}}^{{{\text{TE}}}}$ – для TE-поляризованных волн (рис. 2а и 2в) и $H_{{st}}^{{{\text{TM}}}}$ – для TM-поляризованных волн (рис. 2б и 2г). Представленные ПФ хорошо аппроксимируются главными (квадратичными) членами разложения в (9) при ${{c}_{{x,2}}} = {\text{0}}{\text{.0024}}{{e}^{{ - {\text{2}}{\text{.69}}i}}}\,\,{\text{мк}}{{{\text{м}}}^{2}},$ ${{c}_{{t,2}}} = {\text{ 276}}{\text{.9}}{{e}^{{{\text{0}}{\text{.45}}i}}}\,\,{\text{ф}}{{{\text{с}}}^{2}}$ (для ТЕ-поляризации) и ${{c}_{{x,2}}} = {\text{0}}{\text{.0031}}{{e}^{{ - {\text{2}}{\text{.74}}i}}}\,\,{\text{мк}}{{{\text{м}}}^{2}},$ ${{c}_{{t,2}}} = {\text{276}}{\text{.9}}{{e}^{{ - {\text{2}}{\text{.69}}i}}}\,\,{\text{ф}}{{{\text{с}}}^{2}}$ (для ТМ-поляризации).

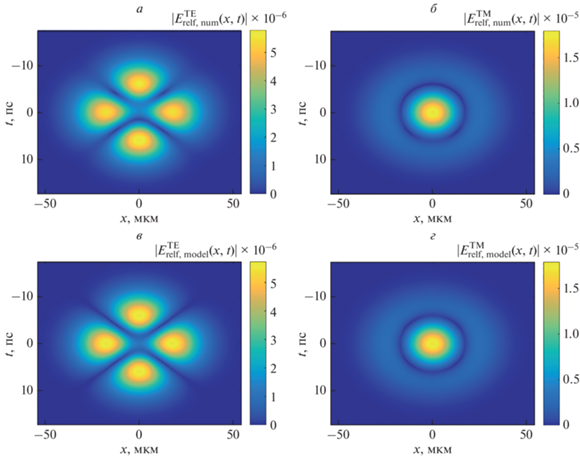
Верхний ряд на рис. 3 показывает амплитуды отраженных TE- (рис. 3, левый столбец) и TM- (рис. 3, правый столбец) поляризованных пространственно-временных импульсов ($\left| {E_{{{\text{refl,}}\,\,{\text{num}}}}^{{{\text{TE}}}}} \right|$ и $\left| {E_{{{\text{refl,}}\,\,{\text{num}}}}^{{{\text{TM}}}}} \right|$ соответственно), рассчитанных численно на основе формулы (8). Нижний ряд рис. 3 показывает аналитически полученные по формуле (10) “модельные” амплитуды отраженных импульсов $\left| {E_{{{\text{refl,}}\,\,{\text{model}}}}^{{{\text{TE}}}}} \right|$ и $\left| {E_{{{\text{refl,}}\,\,{\text{model}}}}^{{{\text{TM}}}}} \right|.$ Из рис. 3 видно, что численно рассчитанные огибающие отраженных импульсов хорошо описываются выражениями (10) при соответствующих значениях коэффициентов ${{c}_{{x,2}}},$ ${{c}_{{t,2}}}.$ Действительно, нормированное среднеквадратическое отклонение численно рассчитанной огибающей отраженного импульса от “модельной” огибающей (10) для случая ТЕ-поляризации (рис. 3а и 3в) составляет 1.6%, а аналогичное значение для случая TM-поляризованного импульса (рис. 3б и 3г) – всего лишь 0.2%.

Отметим, что существенно различный вид огибающих отраженных импульсов на рис. 3 обусловлен различным соотношением между аргументами комплексных коэффициентов ${{c}_{{x,2}}},$ ${{c}_{{t,2}}}$ в случаях ТЕ- и ТМ-поляризации. Для TE-поляризации (рис. 2а и 2в) разность фаз указанных коэффициентов близка к $\pi ,$ а для TM-поляризации (рис. 2б и 2г) – близка к нулю.

ЗАКЛЮЧЕНИЕ

Рассмотрены условия нулевого отражения для одиночной и композитной МДМ-структур. С использованием теории линейных систем показано, что композитная МДМ-структура, имеющая при нормальном падении нуль отражения 2-го порядка по угловой и пространственной частотам, позволяет реализовывать операцию “пространственно-временного” дифференцирования 2-го порядка.

В рамках численного моделирования показано, что операция пространственно-временного дифференцирования 2-го порядка реализуется с высоким качеством (при среднеквадратичной ошибке менее 2%). При этом показано, что композитная МДМ-структура позволяет формировать различные оптические импульсы в зависимости от поляризации падающего излучения.

Полученные результаты могут найти применение при создании систем аналоговых оптических вычислений и оптической обработки информации.

Работа выполнена при поддержке Российского научного фонда (проект № 19-19-00514) в части исследования МДМ-структур и Министерства науки и высшего образования Российской Федерации (государственное задание ФНИЦ “Кристаллография и фотоника” РАН) в части реализации моделирующего программного обеспечения.