ВВЕДЕНИЕ

Изучение оптических свойств графеновых структур – важное и актуальное направление современных исследований физики графена. Несмотря на пока еще существующие сложности технологического плана в получении графеновых сверхструктур, активно ведутся теоретические и экспериментальные исследования одномерных [1, 2] и двумерных (2D) [3–9] сверхрешеток на основе графена (ГСР). На сегодняшний день в данной области получено множество интересных результатов. В ГСР возможна генерация и усиление электромагнитных волн, в частности уединенных электромагнитных импульсов [10–15], что уже в недалеком будущем несомненно будет иметь важное практическое значение [16, 17]. Одномерная ГСР представляет собой слой графена на полосчатой подложке из чередующихся полос, например, оксида и карбида кремния (SiO₂ и SiC) соответственно. Подложка из SiO₂ не влияет на энергетический спектр графена, а в результате взаимодействия графена с подложкой из SiC появляется запрещенная зона (“щель”) шириной 0.26 эВ. Чередование щелевой и бесщелевой модификации графена приводит к образованию минизонного спектра. Ось сверхрешетки в этом случае направленно перпендикулярно чередующимся полосам SiO₂ и SiC. Если же вместо полосчатой взять подложку, образуемую периодически чередующимися в шахматном порядке прямоугольными областями оксида и карбида кремния, то получится 2D ГСР. Модельный энергетический спектр такой сверхрешетки предложен в работе [3], а в работах [5, 6] исследовалось распространение электромагнитных импульсов в 2D ГСР. В данной работе численно исследовано взаимодействие уединенных электромагнитных импульсов (УЭИ), распространяющихся вдоль осей 2D ГСР по взаимоперпендикулярным направлениям.

ОСНОВНЫЕ УРАВНЕНИЯ

Спектр 2D ГСР, состоящей из чередующихся в шахматном порядке прямоугольных областей щелевого и бесщелевого графена, в одноминизонном приближении имеет вид [3]

(1)

$\begin{gathered} \varepsilon (\vec {p}) = \\ = \,\, \pm \sqrt {\Delta _{0}^{2} + \Delta _{1}^{2}\left( {1 - \cos ({{p}_{x}}{{d}_{1}})} \right) + \Delta _{2}^{2}\left( {1 - \cos ({{p}_{у}}{{d}_{2}})} \right)} , \\ \end{gathered} $

где p_x, p_y – проекции квазиимпульса электрона на оси СР, а параметры Δ₀, Δ₁ и Δ₂ были выбираются путем численного решения дисперсионного уравнения (здесь и далее $\hbar = 1$). Подробное исследование свойств спектра 2D ГСР было предпринято в работах [4–7]. Отметим, что присущая данному спектру непараболичность предопределяет нелинейные свойства двумерной ГСР, в частности возможность распространения в ней уединенных электромагнитных импульсов (УЭИ) [18].

Эволюция УЭИ описывается уравнением д’Аламбера для векторного потенциала с учетом столкновений

(2)

$\begin{gathered} \frac{{{{\partial }^{2}}{{\vec {A}}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\vec {A}}}}}{{\partial {{y}^{2}}}} - \frac{{\text{1}}}{{{{{\text{V}}}^{{\text{2}}}}}}\frac{{{{\partial }^{2}}{{\vec {A}}}}}{{\partial {{t}^{2}}}} + \\ + \,\,\frac{{4\pi }}{c}{{{\vec {j}}}_{0}}({{{\text{A}}}_{x}}{\text{,}}{{{\text{A}}}_{y}}) = - \frac{{4\pi }}{c}{{{\vec {j}}}_{{st}}}({{{\text{A}}}_{x}}{\text{,}}{{{\text{A}}}_{y}}), \\ \end{gathered} $

где V = cχ^–1/2, χ – эффективная диэлектрическая проницаемость среды. Векторный потенциал связан с напряженностью электрического поля $\vec {E} = - {{({1 \mathord{\left/ {\vphantom {1 c}} \right. \kern-0em} c})\partial{ \vec {A}}} \mathord{\left/ {\vphantom {{({1 \mathord{\left/ {\vphantom {1 c}} \right. \kern-0em} c})\partial{ \vec {A}}} {\partial t}}} \right. \kern-0em} {\partial t}}.$ При решении задачи мы выбираем кулоновскую калибровку векторного потенциала.

Плотность электрического тока определяется в виде

(3)

$\vec {j} = - e\sum {n(\vec {p})\vec {\upsilon }\left( {\vec {p} + \frac{e}{c}{{\vec {A}}}(\vec {r},t)} \right)} ,$

где $n(\vec {p})$ – функция распределения электронов, ${{\upsilon }}\left( {\vec {p}} \right)$ = (∂ε/∂p_x, ∂ε/∂p_y) – скорость электронов. В бесстолкновительном пределе из (3) получаем j₀(A_x,A_y). Величина, стоящая в правой части уравнения (2) ${{j}_{{st}}}({{{\text{A}}}_{x}}{\text{,}}{{{\text{A}}}_{y}})$ является нелинейным функционалом возмущения плотности тока ${{j}_{0}}({{{\text{A}}}_{x}}{\text{,}}{{{\text{A}}}_{y}})$ при учете столкновений. Для нахождения функции распределения носителей использовано классическое уравнение Больцмана с модельным интегралом столкновений в приближении постоянной частоты релаксации (ν = const)

(4)

$\frac{{\partial п{\text{(}}\vec {p}{\text{)}}}}{{\partial t}} - \frac{e}{с}\frac{{\partial {{\vec {A}}}}}{{\partial t}}\frac{{\partial n{\text{(}}\vec {p}{\text{)}}}}{{\partial{ \vec {p}}}} = - \nu \left( {n\left( {\vec {p}} \right) - {{n}_{0}}\left( {\vec {p}} \right)} \right).$

Разлагая скорость электронов в двумерный ряд Фурье и предполагая электронный газ невырожденным, имеем выражение для плотности тока

(5)

$\begin{gathered} {{{\vec {j}}}_{0}} = - \frac{{e{{n}_{0}}}}{a}\left( {\sum\limits_{n = 1}^\infty {\sum\limits_{m = - \infty }^\infty {{{В}_{{nm}}}\sin (n{{\varphi }_{x}})\cos (m{{\varphi }_{y}})} } } \right., \\ \left. {\sum\limits_{n = 1}^\infty {\sum\limits_{m = - \infty }^\infty {{{C}_{{nm}}}\sin (n{{\varphi }_{y}})\cos (m{{\varphi }_{x}})} } } \right), \\ \end{gathered} $

где n₀ – концентрация 2D электронов, а – толщина графена, $\vec {\varphi } = \frac{e}{c}{\text{(}}{{{\text{A}}}_{x}}{{d}_{1}},{{{\text{A}}}_{y}}{{d}_{2}})$ – безразмерный векторный потенциал, B_nm = a_nmI_nm/I₀₀,

${{I}_{{nm}}} = \int\limits_{{\text{ - }}\pi }^\pi {\int\limits_{{\text{ - }}\pi }^\pi {\cos (nx)\cos (my)\exp } } \left[ {{{ - \sqrt {\Delta _{0}^{2}\, + \,\Delta _{1}^{2}\left( {1\, - \,\cos (x)} \right)\, + \,\Delta _{2}^{2}\left( {1\, - \,\cos (y)} \right)} } \mathord{\left/ {\vphantom {{ - \sqrt {\Delta _{0}^{2}\, + \,\Delta _{1}^{2}\left( {1\, - \,\cos (x)} \right)\, + \,\Delta _{2}^{2}\left( {1\, - \,\cos (y)} \right)} } {kT}}} \right. \kern-0em} {kT}}} \right]dxdy,$

${{a}_{{nm}}}\, = \,\frac{{\Delta _{1}^{2}{{d}_{1}}}}{{2{{\pi }^{2}}}}\int\limits_{ - \pi }^\pi {\int\limits_{ - \pi }^\pi {\frac{{\sin (x)\sin (nx)\cos (my)dxdy}}{{\sqrt {\Delta _{0}^{2}\, + \,\Delta _{1}^{2}\left( {1 - \cos (x)} \right)\, + \,\Delta _{2}^{2}\left( {1 - \cos (y)} \right)} }}} } .$ C_nm вычисляется аналогично B_nm посредством разложения в ряд Фурье проекции скорости электронов на ось y.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Решение уравнения (2) производится численно с использованием схемы типа “крест”. Периоды сверхрешетки выбираются равными d₁= d₂= = d = 2 ⋅ 10^–6 см, при таком выборе параметры энергетического спектра (1) составляют Δ₀ = = 0.4217Δ (для SiC Δ = 0.13 эВ), Δ₁ = Δ₂ = 0.3318Δ. Степень неаддитивности спектра будет определяться количеством перекрестных членов в его разложении в ряд Фурье.

(6)

$\begin{gathered} \varepsilon (\vec {p}) = \Delta \left\{ {{{g}_{1}} - \frac{{{{g}_{2}}}}{2}\left[ {\cos \left( {{{p}_{x}}d} \right) + \cos \left( {{{p}_{у}}d} \right)} \right] - } \right. \\ \left. { - _{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}^{{}}{{g}_{3}}\cos \left( {{{p}_{x}}d} \right)\cos \left( {{{p}_{у}}d} \right)} \right\}. \\ \end{gathered} $

где g₁ = 0.624475, g₂ = 0.1787, g₃ = 0.01306. При решении данной задачи мы ограничивались лишь первыми членами. Такой подход дает относительное отклонение спектров в 2%, что вполне соответствует случаю слабой неаддитивности. В декартовых координатах система уравнений для компонент безразмерного векторного потенциала приобретает вид:

(7)

$\begin{gathered} \frac{{{{\partial }^{2}}{{\varphi }_{x}}}}{{\partial {{{\tilde {t}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{x}}}}{{\partial {{{\tilde {x}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{x}}}}{{\partial {{{\tilde {y}}}^{2}}}} + \sin {{\varphi }_{x}}(1 + \beta \cos {{\varphi }_{y}}) = 0, \\ \frac{{{{\partial }^{2}}{{\varphi }_{y}}}}{{\partial {{{\tilde {t}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{y}}}}{{\partial {{{\tilde {x}}}^{2}}}} - \frac{{{{\partial }^{2}}{{\varphi }_{y}}}}{{\partial {{{\tilde {y}}}^{2}}}} + \sin {{\varphi }_{y}}(1 + \beta \cos {{\varphi }_{x}}) = 0, \\ \end{gathered} $

где $\tilde {t} = {{t\varpi } \mathord{\left/ {\vphantom {{t\varpi } {\sqrt \chi }}} \right. \kern-0em} {\sqrt \chi }},$ $\tilde {x} = {{x\varpi } \mathord{\left/ {\vphantom {{x\varpi } c}} \right. \kern-0em} c},$ $\tilde {y} = {{y\varpi } \mathord{\left/ {\vphantom {{y\varpi } c}} \right. \kern-0em} c},$ ${{\varpi }^{2}} = {{2\pi {{n}_{0}}{{e}^{2}}{{B}_{{10}}}d} \mathord{\left/ {\vphantom {{2\pi {{n}_{0}}{{e}^{2}}{{B}_{{10}}}d} a}} \right. \kern-0em} a},$ $\beta = {{2{{B}_{{11}}}} \mathord{\left/ {\vphantom {{2{{B}_{{11}}}} {{{B}_{{10}}}}}} \right. \kern-0em} {{{B}_{{10}}}}}.$ В предельном случае аддитивного энергетического спектра (при β = 0) уравнения (5) представляют собой двумерные уравнения синус-Гордона. В случае слабой неаддитивности спектра ГСР система (7) допускает точное аналитическое решение для некоторых выделенных направлений [5]. При учете столкновений правая часть уравнения (7) модифицируется и вместо нее появляется нелинейный функционал от векторного потенциала, выражающийся через диссипативный ток.

Большой интерес представляет исследование взаимодействия нелинейных уединенных импульсов. В отсутствие неаддитивности спектра, когда параметр β = 0, солитоны, распространяющиеся вдоль взаимно перпендикулярных направлений, не взаимодействуют, вследствие чего их форма сохраняется. Однако в случае слабой неаддитивности результаты численного расчета показывают взаимное влияние распространяющихся уединенных волн даже в случае малых потенциалов.

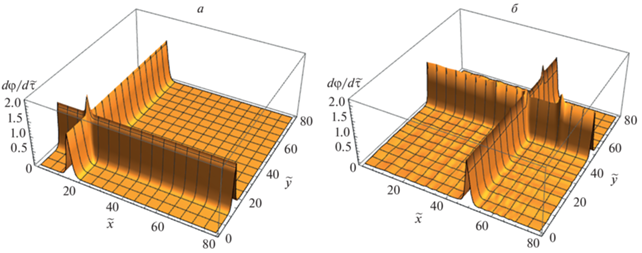
Непосредственно результаты численного моделирования столкновений солитонов в 2D ГСР показаны на рис. 1. По горизонтальным осям отложены безразмерные координаты, по вертикальной – модуль напряженности электрического поля, также выраженный в безразмерных единицах. На рис. 1б хорошо виден результат взаимного влияния солитонов друг на друга. В области перекрытия солитонов наблюдается уменьшение амплитуды с одновременным образованием двух импульсов, со значительной скоростью распространяющихся вдоль фронтов уединенных волн.

Рис. 1.

Взаимодействие солитонов для $\tilde {t} = 0$ (a), 60 (б).

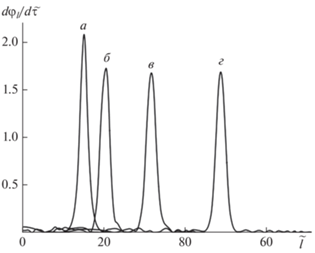
Для анализа картины эволюции УЭИ удобно выбрать направление под углом 45° к осям ГСР и наблюдать за изменением потенциала и напряженности электрического поля вдоль этого направления. Результаты моделирования изменения формы УЭИ представлены на рис. 2. Хорошо заметно быстрое уменьшение амплитуды на начальном этапе распространения, а также то, что по достижении амплитудой определенного значения в дальнейшем она перестает изменяться. В процессе распространения изменяется также и форма импульса. В целом картина эволюции формы УЭИ выглядит как подстраивание импульса под среду, в которой происходит его распространение.

Рис. 2.

Профиль импульса (срез под углом 45° к осям ГСР) для $\tilde {t} = 0$ (a), 10 (б), 30 (в), 60 (г).

При учете столкновений электронов с решеткой амплитуды УЭИ быстро уменьшаются, поэтому основной задачей является увеличение времени его жизни. Для увеличения времени жизни солитонной системы необходимо осуществить подпитку энергии с помощью внешнего электрического поля или тока [5, 6].

ЗАКЛЮЧЕНИЕ

Численно исследовано распространение двух взаимодействующих нелинейных УЭИ в 2D ГСР в бесстолкновительном приближении и с учетом столкновений. Получена картина взаимного влияния и эволюции солитонов, распространяющихся вдоль осей сверхрешетки во взаимно перпендикулярных направлениях. В бесстолкновительном режиме после переходного процесса наблюдается состояние с установившейся амплитудой в области перекрытия солитонов и образование импульсов, бегущих вдоль фронтов уединенных волн. Такая эволюция рассматриваемой пары солитонов вызвана неаддитивностью энергетического спектра, приводящей к взаимосвязи ортогональных составляющих векторного потенциала. Разработан программный комплекс для численного моделирования распространения уединенных электромагнитных волн в 2D ГСР.