ВВЕДЕНИЕ

В последнее время в ряде теоретических исследований обращается внимание на необычные явления, связанные с неаддитивностью энергетического спектра графеновых структур. Взаимное влияние на носители тока в щелевом графене двух электромагнитных волн разной частоты со взаимно перпендикулярными векторами напряженности изучено в [1]. В графеновых сверхрешетках (ГСР) электрическое поле, приложенное поперек оси сверхрешетки, способно модифицировать продольную вольт-амперную характеристику этого материала [2–7].

Изучение двумерных (2D) ГСР привлекает внимание исследователей в связи с необычностью их свойств, в том числе и электронных, что связано с особенностями энергетического спектра графена и структур на его основе. В работах [8–11] рассматриваются новые подходы к созданию 2D ГСР. Вызывает значительный интерес модель 2D ГСР, в которой графен осажден на подложку из периодически чередующихся в шахматном порядке прямоугольных ячеек, например оксида и карбида кремния (SiO₂ и SiC) [10]. В результате взаимодействия графена с подложкой из SiC в энергетическом спектре носителей заряда появляется запрещенная зона (щель), а подложка из SiO₂ не вызывает изменение спектра графена (щель отсутствует). Чередование в шахматном порядке так называемых щелевой и бесщелевой модификаций графена [2] приводит к образованию 2D сверхрешеточного минизонного спектра. В [10, 11] исследуется влияние внешних постоянного и переменного электрических полей на транспортные свойства такой структуры. Показано, что наличие постоянного поперечного электрического поля приводит к появлению дополнительного пика в вольт-амперных характеристиках. Для такой 2D ГСР исследован коэффициент поглощения электромагнитной волны в присутствии постоянного электрического поля для случая квазиклассически сильных электрических полей [12], выявлено влияние неаддитивности спектра 2D ГСР на распространение уединенного электромагнитного импульса вдоль произвольных направлений образца [13], а также показана возможность управления амплитудами высших гармоник поперечными электрическими полями [14].

В рамках настоящей работы исследованы особенности управления проводимостью поперечными электрическими полями в 2D ГСР, состоящей из чередующихся в шахматном порядке прямоугольных областей щелевого и бесщелевого графена.

ОСНОВНЫЕ УРАВНЕНИЯ

Энергетический спектр электронов в 2D ГСР в одноминизонном приближении выбран в модельном виде [10]

где $\vec {p}$ – квазиимпульс электрона, d_i = a_i + b_i – период ГСР, a_i и b_i – ширины ячеек бесщелевого и щелевого графена. Из формулы (1) видно, что полная энергия электронов не может быть представлена алгебраической суммой ее компонент по двум взаимно перпендикулярным направлениям, то есть энергетический спектр 2D ГСР неаддитивен. Неаддитивность энергетического спектра сверхрешетки на основе графена приводит к взаимной зависимости движений носителей заряда вдоль перпендикулярных друг другу направлений, что приводит к дополнительной возможности управления током вдоль оси сверхрешетки приложением поперечного напряжения [4].

Рассмотрим случай, когда в плоскости 2D ГСР приложено постоянное и переменное электрические поля $\vec {E} = \left( {{{E}_{{1x}}} + {{E}_{{0x}}}\cos \omega t,\,\,\,\,{{E}_{{1y}}} + {{E}_{{0y}}}\cos \omega t} \right),$ где E₀ и ω – амплитуда и частота переменного электрического поля, Е₁ – модуль напряженности постоянного электрического поля.

Для невырожденного электронного газа в работе [14] была получена постоянная составляющая плотности тока, текущего вдоль оси одной из осей 2D ГСР

где ${{j}_{0}} = {{ - e{{d}_{1}}n\Delta } \mathord{\left/ {\vphantom {{ - e{{d}_{1}}n\Delta } 2}} \right. \kern-0em} 2},$ n – концентрация электронов в зоне проводимости, J_n(x) –функция Бесселя 1-го рода n-го порядка, ν – частота столкновений, ${{\alpha }_{x}} = {{e{{E}_{{0x}}}{{d}_{1}}} \mathord{\left/ {\vphantom {{e{{E}_{{0x}}}{{d}_{1}}} {\hbar \omega }}} \right. \kern-0em} {\hbar \omega }},$ ${{\alpha }_{y}} = {{e{{E}_{{0y}}}{{d}_{2}}} \mathord{\left/ {\vphantom {{e{{E}_{{0y}}}{{d}_{2}}} {\hbar \omega }}} \right. \kern-0em} {\hbar \omega }},$ ${{\Omega }_{x}} = e{{E}_{{1x}}}{{d}_{1}},$ ${{\Omega }_{y}} = e{{E}_{{1y}}}{{d}_{2}},$ $\sin \kappa _{{knm}}^{ \pm } = \frac{\nu }{{\sqrt {{{\nu }^{2}} + {{{(m{{\Omega }_{x}} \pm n{{\Omega }_{y}} + k\omega )}}^{2}}} }},$ ${{A}_{{nm}}}\, = \,{{\Delta }_{0}}\int_{ - \pi }^\pi {\int_{ - \pi }^\pi {\frac{{\cos \left( y \right)\sin \left( x \right)\sin (mx)\cos (ny)dxdy}}{{\sqrt {\Delta _{0}^{2}\, + \,\Delta _{1}^{2}\left( {1\, - \,\cos {\text{(}}x{\text{)}}} \right)\, + \,\Delta _{2}^{2}\left( {1\, - \,\cos {\text{(}}y{\text{)}}} \right)} }}} } ,$

Вычисление плотности тока проведено с использованием решения кинетического уравнения Больцмана с модельным интегралом столкновений в приближении постоянного времени релаксации.

Из анализа формулы (2) можно увидеть, что вследствие неаддитивности энергетического спектра 2D ГСР, постоянная составляющая плотности тока, текущего вдоль оси х, зависит не только от полей, ориентированных вдоль этой оси (продольных), но и от полей, ориентированных перпендикулярно (поперечных).

Для численного расчета также, как и в [14] выбрана симметричная 2D ГСР (d₁= d₂= d = 2 ⋅ 10^–6 см).

ОСНОВНЫЕ РЕЗУЛЬТАТЫ

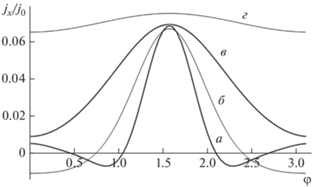
Приведем один из примеров исследования плотности тока в 2D ГСР. Выберем направление вектора напряженности постоянного электрического поля вдоль одной из осей СР, для определенности вдоль оси x. Частота и амплитуда переменного электрического поля постоянны, а направление вектора поляризации этого поля задается углом φ относительно оси х. Зависимость плотности тока от угла поворота φ вектора поляризации переменного электрического поля, при фиксированных значениях параметров внешних электрических полей показана на рис. 1. Максимального значения плотность тока достигает, когда переменное поле поляризовано перпендикулярно оси 2D ГСР. С увеличением напряженности поля плотность тока, протекающего вдоль оси x, уменьшается. При сильных полях также можно наблюдать на графике смену знака тока, протекающего в продольном направлении (рис. 1а и 1б), эффект абсолютной отрицательной проводимости [15]. Для значения угла φ = π/2 ярко прослеживается возможность управления проводимостью поперечными полями. Результаты данного исследования могут быть использованы для детектирования электромагнитного излучения, если, поворачивая образец с 2D ГСР, находящийся под воздействием постоянного электрического поля, измерять угол поворота и величину электрического тока.

Следующей частью исследования являлось определение параметров внешних электрических полей, при которых будет наиболее эффективно изменяться плотность тока. В этом случае будем варьировать продольные и поперечные по отношению к исследуемому направлению тока компоненты электрических полей. На первом этапе численно определили диапазон возможных значений плотности тока (максимальное и минимальное значение) при фиксированной частоте и при изменении остальных параметров полей.

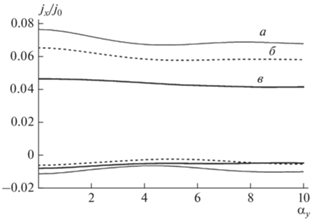
Обнаружено, что наибольший размах между возможными значениями тока наблюдается при равенстве нулю поперечной составляющей постоянного поля (E_1y = 0), когда анализируется зависимость от этой характеристики. Далее проводился численный анализ зависимости плотности тока от поперечной составляющей переменного поля при фиксированной частоте ω и E_1y = 0. Результат такого расчета приведен на рис. 2. Здесь наблюдается уменьшение диапазона изменения значений плотности тока при увеличении продольной составляющей постоянного электрического поля. Аналогичные результаты получены при построении зависимости плотности тока от поперечной составляющей переменного поля при прочих равных условиях.

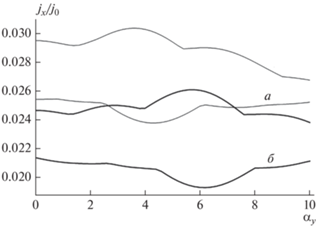
На следующем этапе было определено (рис. 3), что наибольший размах максимумов и минимумов плотности тока, проявляется при равных значениях продольной E_1x и поперечной E_1y составляющих переменного электрического поля, если анализируется зависимость плотности тока от E_1y. При исследовании зависимости от поперечной оставляющей постоянного электрического поля E_0y, при равенстве E_0x = E_0y выявлено, что размах минимален. При увеличении частоты этот эффект становится менее выраженным.

Предложенная в работе методика численного определения диапазона значений плотности тока интересна тем, что, варьируя сразу несколько параметров, можно выяснить, в каких границах может изменяться исследуемая величина.

В рассматриваемом в работе частном случае энергетический спектр обладает слабой неаддитивностью, что и проявляется в слабой зависимости плотности тока от поперечного электрического поля. Отметим, что при уменьшении периода 2D ГСР возможность управления проводимостью поперечными электрическими полями увеличивается, поскольку с уменьшением периода увеличивается неаддитивность энергетического спектра [13].

Приведем оценку параметров рассматриваемой системы в связи с использованными моделями и приближениями. В работе пренебрегалось межминизонными переходами, выбрано одноминизонное приближение, что соответствует выполнению условий: $\hbar \omega $ $ \ll $ ε_g, ε_g12 (ω $ \ll $ 1.2 ⋅ 10¹⁴ с^–1), k_bT $ \ll $ ε_g, ε_g12 (T $ \ll $ 10³ K). При расчете плотности тока использован квазиклассический подход, приводящий к условиям на параметры полей: ω < < 10¹³ с^–1; ${{ed{{E}_{0}}} \mathord{\left/ {\vphantom {{ed{{E}_{0}}} {\hbar \nu }}} \right. \kern-0em} {\hbar \nu }},$ ${{ed{{E}_{1}}} \mathord{\left/ {\vphantom {{ed{{E}_{1}}} {\hbar \nu }}} \right. \kern-0em} {\hbar \nu }}$ $ \ll $ 1.2 ⋅ 10³. Для численных расчетов использованы следующие параметры: n = 10¹¹ см^–2, τ = ${{\nu }^{{ - 1}}}$ ≈ 10^–11 с, T = 70 К. Численная оценка величины поля E при ${{edE} \mathord{\left/ {\vphantom {{edE} {\hbar \nu }}} \right. \kern-0em} {\hbar \nu }}$ = 1 составляет 33 В/см.

ЗАКЛЮЧЕНИЕ

Неаддитивность энергетического спектра структур на основе графена, и, в частности, 2D ГСР, приводит к существенному отличию кинетических явлений в таких электронных системах от структур с аддитивным спектром. По сравнению со щелевым графеном [4], энергетический спектр 2D ГСР обладает более слабой неаддитивностью и значительно меньшей шириной зон (минизон) проводимости, что и определяет ее отклик на внешние электрические поля. Использование квазиклассического подхода для нахождения плотности тока в условиях воздействия произвольно поляризованных статического и переменного электрических полей позволяет получить аналитическую зависимость плотности тока от параметров полей. Проведено исследование зависимости плотности тока от параметров поперечно ориентированных электрических полей. Определены соотношения между параметрами приложенных полей, при которых наблюдается существенное различие между возможными значениями плотности тока, и, соответственно, управление проводимостью наиболее эффективно. Выявленные зависимости могут быть использованы для управления проводимостью в двумерных графеновых сверхрешетках и в устройствах детектирования электромагнитного излучения.